Радиотехника и электроника, 2019, T. 64, № 5, стр. 490-497

ВВЕДЕНИЕ

В последние годы активно исследуются особенности взаимодействия слоев графена и слоистых структур на его основе с электромагнитными полями. Высокие подвижность носителей заряда и проводимость при практическом отсутствии поглощения в широкой частотной области делают графен одним из наиболее перспективных материалов фотоники и оптоэлектроники [1–5]. Ввиду особенностей дисперсии проводимости графена физические свойства периодических структур на его основе могут существенно отличаться от свойств периодических структур на основе других материалов [6–10].

Для практических применений важную роль играют направляющие свойства структур, выполненных на основе графеновых слоев. В работе [11] была показана возможность распространения локализованных на монослое графена волн, дисперсия которых лежит в терагерцовой частотной области. Активно исследуется способность слоистых структур на основе двух и более слоев графена, разделенных слоями диэлектрика, удерживать распространяющиеся волны границами раздела сред; разрабатывается возможность создания устройств волноводного типа [12–19]. Для управления поверхностными волнами в такой структуре существенной является возможность воздействия внешними полями (в частности, магнитным полем) на материальные параметры сред, составляющих структуру [20, 21].

В связи с этим в данной работе исследуются особенности распространения волн ТМ- и ТЕ-поляризаций вдоль плоской границы раздела изотропного диэлектрика и слоистой среды “магнетик–графен” при наличии внешнего магнитного поля, которое будем считать поперечным по отношению к направлению распространения. Диэлектрическая и магнитная проницаемости такой слоистой среды получены в длинноволновом приближении (приближении мелкослоистой среды) в работах [22, 23].

1. МАТЕРИАЛЬНЫЕ ПАРАМЕТРЫ

Рассмотрим волноведущую структуру, у которой областью $z > 0$ является немагнитный диэлектрик, а областью $z < 0$ – слоистая среда, состоящая из чередующихся слоев феррита – железо-иттриевого граната (ЖИГ) и графенa с толщинами ${{d}_{f}}$ и ${{d}_{g}}.$ Будем считать, что длина распространяющихся в структуре волн существенно больше периода слоистой среды, поэтому для описания ее оптических свойств может быть использовано приближение эффективной среды. В исследуемом диапазоне частот диэлектрик и феррит считаются непоглощающими и их диэлектрические проницаемости (ДП) ${{\varepsilon }_{d}}$ и ${{\varepsilon }_{f}}$ не обладает частотной зависимостью.

Для слоев графена ДП связана с его поверхностной проводимостью соотношением

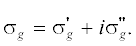где Частотная зависимость проводимости определяется выражением [1–6] где ${{\sigma }_{0}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {4\hbar }}} \right. \kern-0em} {4\hbar }},$ $e$ – заряд электрона, $\hbar $ – постоянная Планка, $\omega $ – частота распространяющейся волны, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $T$ – температура, химический потенциал $\mu = \hbar {{v}_{{\text{F}}}}\sqrt {\pi {{n}_{0}}} $ (${{n}_{0}}$ и ${{v}_{{\text{F}}}}$ – концентрация носителей заряда и скорость Ферми).

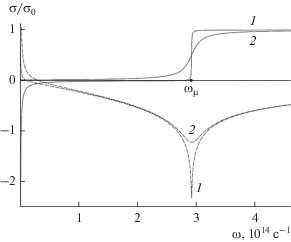
Как показывает анализ выражения (1), при понижении температуры от комнатной до экстремально низкой характер проводимости графена в широкой области частот изменяется незначительно. При температурах $T \approx 10\,\,{\text{K}}$ и ниже действительная часть проводимости $\sigma {\text{'}}$ при $\omega \approx {{\omega }_{\mu }} = {{2\mu } \mathord{\left/ {\vphantom {{2\mu } \hbar }} \right. \kern-0em} \hbar }$ испытывает быстрый рост (практически – скачок) от нулевого значения до величины ${{\sigma }_{0}}.$ При более высоких температурах с ростом частоты скачок величины $\sigma {\text{'}}$ сменяется достаточно плавной асимптотической зависимостью с $\sigma {\text{'}} \to {{\sigma }_{0}}.$ Мнимая часть проводимости 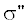в широкой частотной области принимает отрицательные значения и в области скачка величины $\sigma {\text{'}}$ достигает минимума, который также с ростом температуры сглаживается. Для иллюстрации сказанного на рис. 1 представлены частотные зависимости действительной и мнимой частей проводимости графена при температурах $T = 10,\,\,300\,\,{\text{K}}{\text{.}}$ При численном анализе использованы следующие значения параметров графена: ${{\sigma }_{0}} \simeq 5.5 \times {{10}^{7}}\,\,{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}}{\text{,}}$ ${{v}_{{\text{F}}}} = {{10}^{8}}\,\,{{{\text{с м }}} \mathord{\left/ {\vphantom {{{\text{с м }}} {\text{с }}}} \right. \kern-0em} {\text{с }}},$ $\mu = 0.6\,\,{\text{э В ,}}$ ${{d}_{g}} \simeq 0.335$ нм [5–7].

Мелкослоистая среда обладает выделенным направлением, которым является ось периодичности $Oz.$ Управление волновым процессом в структуре осуществляется постоянным магнитным полем, лежащим в плоскости границы раздела слоистой среды и диэлектрика (вдоль оси $Oy$). При направлении распространения вдоль оси $Ox$ собственными являются волны ТМ- и ТЕ- поляризации, причем только ТЕ-волна является магнитоуправляемой. Компоненты диагонального тензора эффективной ДП слоистой среды ${{\bar {\varepsilon }}_{{xх }}} = {{\bar {\varepsilon }}_{{yу }}} = \bar {\varepsilon },$ ${{\bar {\varepsilon }}_{{zz}}} = {{\bar {\varepsilon }}_{0}},$ полученные в работах [7, 15–18], отвечают используемому приближению мелкослоистости и имеют вид

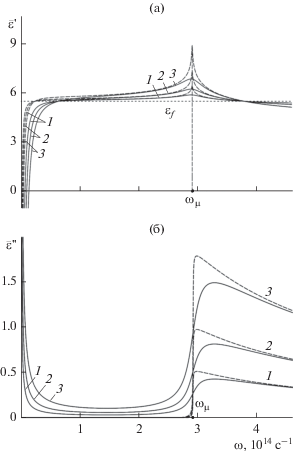
где $\theta = {{{{d}_{g}}} \mathord{\left/ {\vphantom {{{{d}_{g}}} {{{d}_{f}}}}} \right. \kern-0em} {{{d}_{f}}}}.$

На рис. 2 представлены частотные зависимости действительной и мнимой частей компоненты $\bar {\varepsilon }$ тензора эффективной ДП слоистой среды с ДП ферритовых слоев ${{\varepsilon }_{f}} = 5.5$ и параметром $\theta = 0.05,\,\,0.1,\,\,0.2,$ полученные при $T = (10,\,\,300)\,\,{\text{K}}{\text{.}}$ Видно, что в области скачка величины $\sigma _{g}^{'}$ (при $\omega \simeq {{\omega }_{\mu }}$) величина $\operatorname{Re} \bar {\varepsilon }$ достигает максимального значения. С увеличением вклада графена (т.е. с уменьшением периода $d = {{d}_{g}} + {{d}_{f}}$) растут максимальные значения как реальной, так и мнимой части эффективной ДП. Далее будем рассматривать только область $\omega < {{\omega }_{\mu }},$ а точнее, область вблизи плазменного резонанса структуры, где в мелкослоистой среде поглощение либо практически отсутствует (при $T = 10\,\,{\text{K}}$), либо достаточно мало (при $T = 300\,{\text{K}}$). Наличие такой области существенно отличает рассматриваемую проводящую структуру на основе графена от структуры металл–диэлектрик. В области малых частот ($\omega \ll {{\omega }_{\mu }}$) реальная часть ДП становится отрицательной, что позволяет реализовать в структуре поверхностную волну. На частотах $\omega > {{\omega }_{\mu }}$ поглощение в структуре существенно возрастает даже при достаточно низких температурах.

Магнитные проницаемости (МП) диэлектрика и графена приняты равными единице (${{\mu }_{d}} = 1\,,\,\,{{\mu }_{g}} = 1$). Тензор МП изотропного феррита при направлении внешнего поля вдоль оси $Oу $ имеет следующие отличные от нуля компоненты: ${{\mu }_{{х х }}} = {{\mu }_{{zz}}} = {{\mu }_{f}},$ ${{\mu }_{{yy}}} = {{\mu }_{0}},$ ${{\mu }_{{х z}}} = - {{\mu }_{{zx}}} = i{{\mu }_{a}}.$ Их частотная зависимость может быть представлена следующим образом [24]:

где ${{\omega }_{H}} = \gamma {{H}_{0}},$ ${{\omega }_{M}} = 4\pi \gamma {{M}_{0}},$ ${{\omega }_{r}} = \xi {{\omega }_{H}},$ $\gamma = 1.76 \times {{10}^{7}}\,\,\,{{({\text{Э }}\,{\text{с }})}^{{ - 1}}}$ и характерные значения материальных параметров: $4\pi {{M}_{0}} = 1787\,\,{\text{Г с ,}}$ $\xi = 0.02$ [25]. Отличные от нуля компоненты тензора эффективной МП мелкослоистой среды ${{\hat {\mu }}_{{{\text{э ф }}}}}$ определяются выражениями [23]

2. ДИСПЕРСИЯ ТМ-ВОЛН

Рассмотрим сначала особенности распространения поверхностной волны ТМ-поляризации с компонентами волнового поля (${{E}_{x}}\,,{{H}_{y}}\,,{{E}_{z}}$), которая не управляется внешним магнитным полем. Зависимость от времени и продольной координаты указанных компонент будем считать пропорциональной фактору $\exp \left[ {i(\omega t - \beta x)} \right],$ где $\beta $ – константа распространения. Их зависимость от поперечной координаты в слоистой среде определяется уравнениями

где ${{k}_{0}} = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c},$ c – скорость света в вакууме. Соответствующие уравнения для компонент волны в диэлектрике имеют аналогичный вид при замене ${{q}_{s}} \to {{q}_{d}}$ и $\bar {\varepsilon },\,\,{{\bar {\varepsilon }}_{0}} \to {{\varepsilon }_{d}},$ Здесь ${{q}_{s}}$ и ${{q}_{d}}$ – поперечные компоненты волнового вектора в каждой из сред. Решение этих уравнений приводит к следующей зависимости магнитного поля поверхностной волны (ПВ) от времени и координат: где ${{Н }_{0}}$ – амплитуда магнитного поля при $z = 0,$ а

Компоненты электрического поля ${{E}_{x}}$ и ${{E}_{z}}$ находятся с помощью подстановки соотношений (6) в уравнения (5).

В общем случае константа распространения является комплексной величиной (т.е. 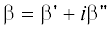), поэтому комплексными являются и поперечные компоненты волнового вектора в каждой из сред. Необходимым условием существования поверхностной (т.е. локализованной на границе раздела сред) волны является выполнение в каждой из сред неравенств $\operatorname{Re} (q_{{d,s}}^{2}) > 0\,$ и $q_{{d,s}}^{'} > 0,$ которые обеспечивают экспоненциальный спад амплитуды волнового поля при удалении от границы раздела. Также требуется выполнение неравенств $\beta {\text{'}} > 0$ и 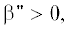первое из которых указывает на положительность фазовой скорости волны, второе – на отсутствие ее усиления. Согласно (6) плоскость постоянной амплитуды 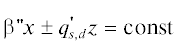волнового поля пересекает границу раздела сред под углами 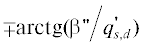в каждой из сред. Плоскость постоянной фазы 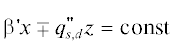пересекает границу раздела под углами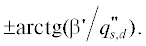

Учет непрерывности компоненты электрического поля ${{E}_{x}}$ приводит к дисперсионным соотношениям для поверхностной ТМ-волны в рассматриваемой структуре:

Особенности дисперсии ПВ данного типа во многом определяются особенностями компоненты $\bar {\varepsilon }(\omega )$ эффективной ДП мелкослоистой среды. При действительных значениях входящих в (8) величин существование ПВ в структуре возможно лишь в области отрицательности диэлектрической функции $\bar {\varepsilon }(\omega ).$ Для комплексных величин область существования поверхностной волны определяется областью отрицательности функции $\bar {\varepsilon }{\kern 1pt} {\text{'}}(\omega ).$ Частота, на которой $\bar {\varepsilon }{\kern 1pt} {\text{'}}(\omega ) = 0,$ может считаться плазменной частотой мелкослоистой проводящей среды. На этой частоте в рассматриваемой структуре имеет место плазменный резонанс.

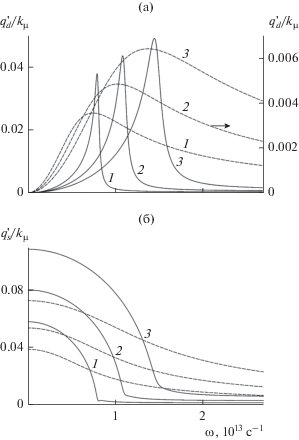
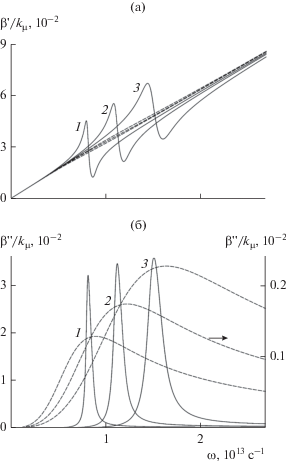
На рис. 3 приведены частотные зависимости действительной и мнимой части константы распространения (нормированной на величину k_μ = $ = {{{{\omega }_{\mu }}} \mathord{\left/ {\vphantom {{{{\omega }_{\mu }}} c}} \right. \kern-0em} c} = {\text{6}}{\text{.1}} \times {\text{1}}{{{\text{0}}}^{4}}\,\,{\text{с }}{{{\text{м }}}^{{ - 1}}},$ ${{\omega }_{\mu }} = {{2\mu } \mathord{\left/ {\vphantom {{2\mu } \hbar }} \right. \kern-0em} \hbar }$ = $1.83 \times {{10}^{{15}}}\,\,{{{\text{с }}}^{{ - 1}}}$), отвечающие значениям параметра $\theta = 0.05,\,\,0.1,\,\,0.2$ при температурах $T = (10,\,\,300)\,\,{\text{K}}{\text{.}}$ В случае низких температур поглощение в структуре крайне мало по сравнению с комнатной температурой. При наличии потерь в структуре дисперсия поверхностных и объемных (нелокализованных) волн описывается разными частями одной непрерывной кривой, представляемой зависимостью (8). В резонансной области наблюдается наиболее быстрое изменение величины $\beta {\text{'}}(\omega ),$ т.е. в этой области максимальны значения модуля величины ${{d\beta {\text{'}}} \mathord{\left/ {\vphantom {{d\beta {\text{'}}} {d\omega }}} \right. \kern-0em} {d\omega }},$ что указывает на существенное замедление ПВ. Вблизи резонансной частоты наблюдается также резкое возрастание мнимой части константы распространения ПВ и, следовательно, убывание длины ее пробега.

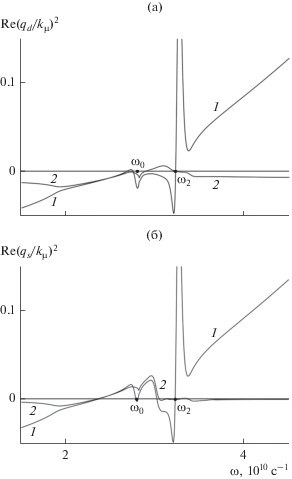
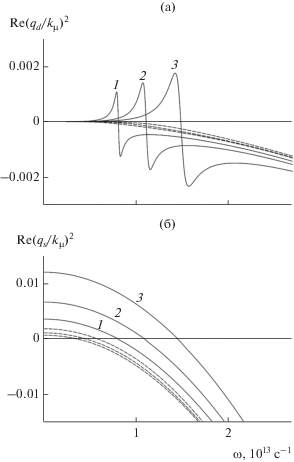
На рис. 4 приведены частотные зависимости действительной части квадрата поперечной компоненты волнового вектора в диэлектрике $\operatorname{Re} (q_{d}^{2})$ и слоистой среде $\operatorname{Re} (q_{s}^{2})$ при температурах $T = (10,\,\,300)\,\,{\text{K}}$ (штриховая и сплошная линии). Знак величины 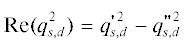указывает на характер режима распространения волны в структуре, т.е. какой из режимов преобладает – волноводный или излучательный. Если в рассматриваемой области частот $\operatorname{Re} (q_{{d,s}}^{2}) > 0,$ то распространяющуюся волну можно считать локализованной на границе раздела сред. В противоположном случае волна является нелокализованной, т.е. излучательной.

На рис. 5 приведены частотные зависимости действительных частей поперечной компоненты волнового вектора $q_{{s,d}}^{'}$ в диэлектрике и слоистой среде при температурах $T = (10,\,\,300)\,\,{\text{K}}$ (штриховая и сплошная линии). В обеих средах ПВ является локализованной вблизи границы в резонансной области. Глубина проникновения ПВ в каждую из сред определяется величинами ${{\delta }_{d}} = {1 \mathord{\left/ {\vphantom {1 {q_{d}^{'}}}} \right. \kern-0em} {q_{d}^{'}}}$ и ${{\delta }_{s}} = {1 \mathord{\left/ {\vphantom {1 {q_{s}^{'}}}} \right. \kern-0em} {q_{s}^{'}}}.$ В области отрицательности $\bar {\varepsilon }$ с ростом частоты степень локализации поля волны в диэлектрике растет, а в слоистой среде уменьшается. При дальнейшем увеличении частоты ПВ превращается в объемную. Если энергия фотона превышает химический потенциал, то волна из объемной и однородной превращается в затухающую. При температуре $T = 300\,\,{\text{K}}$ можно выделить две области частот. В первой $\bar {\varepsilon }{\text{'}}$ имеет отрицательное значение, во второй – положительное. В первой области электромагнитная волна ведет себя подобно волне в металле, поле сильнее локализовано в слоистой среде. При температуре $T = 10\,\,{\text{K}}$ поле сильно локализуется в слоистой среде вблизи границы и почти не локализуется в диэлектрике.

3. ДИСПЕРСИЯ ТЕ-ВОЛН

Рассмотрим теперь локализованные на границе раздела сред волны ТЕ-поляризации с компонентами волнового поля (${{H}_{x}}\,,{{E}_{y}}\,,{{H}_{z}}$). Именно эти волны управляются внешним магнитным полем. В случае ориентации внешнего поля вдоль оси $Oу $ (перпендикулярно направлению распространения волны) уравнения волнового поля в слоистой среде принимают вид

где $q_{s}^{2} = {{\beta }^{2}} - k_{0}^{2}{{\bar {\mu }}_{ \bot }}\bar {\varepsilon },$ а ${{\bar {\mu }}_{ \bot }} = \bar {\mu } - {{\bar {\mu }_{а }^{2}} \mathord{\left/ {\vphantom {{\bar {\mu }_{а }^{2}} {\bar {\mu }}}} \right. \kern-0em} {\bar {\mu }}}.$ В диэлектрике поле определяется уравнениями где ${{q}_{d}}$ дается выражением (7). Решая граничную задачу, приходим к дисперсионному уравнению для ПВ рассматриваемого типа:

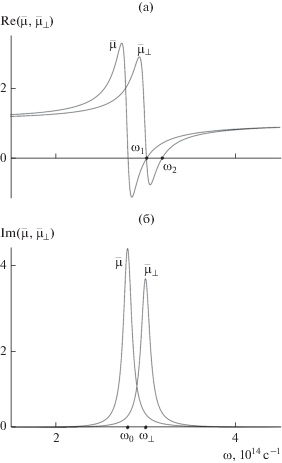
На рис. 6 приведены зависимости от частоты действительной и мнимой части проницаемостей $\bar {\mu }$ и ${{\bar {\mu }}_{ \bot }}$ мелкослоистой среды “графен–магнетик” при значении внешнего поля ${{H}_{0}} = 1000\,\,{\text{Э }}$. Именно эти величины определяют особенности поведения как поверхностных, так и объемных волн ТЕ-поляризации в рассматриваемой структуре. На оси частот отмечены характерные частоты ${{\omega }_{0}},$ ${{\omega }_{ \bot }}$ и ${{\omega }_{{1,2}}},$ где первые две частоты являются резонансными для величин $\operatorname{Im} \bar {\mu }$ и $\operatorname{Im} {{\bar {\mu }}_{ \bot }},$ а две другие отвечают нулям функции $\operatorname{Re} {{\bar {\mu }}_{ \bot }}.$ В области частот (${{\omega }_{1}}$,${{\omega }_{2}}$) величина $\operatorname{Re} {{\bar {\mu }}_{ \bot }}$ отрицательна. При уменьшении поля ${{H}_{0}}$ резонансные кривые смещаются в область более низких частот.

Дисперсионное уравнение (11) можно преобразовать к следующему биквадратному уравнению относительно константы распространения:

где введены обозначения

Решение уравнения (12) дает две пары корней с противоположными знаками. Для константы распространения волн, бегущих вдоль оси $Ox,$ получаем

На рис. 7 приведены частотные зависимости действительной и мнимой части константы распространения двух собственных ТЕ-волн, для которых $\beta {\text{'}} > 0$ и 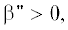т.е. бегущих вдоль положительного направления оси $Ox$ и затухающих в этом же направлении. Температура и отношение толщин слоев в мелкослоистой структуре выбраны равными $T = 300\,K$ и $\theta = 0.1.$ На указанных зависимостях вблизи частот ${{\omega }_{0}}$ и ${{\omega }_{2}}$ отмечаются две резонансные области с характерным значительным ростом мнимой части константы распространения. Следовательно, вблизи указанных частот должна убывать длина пробега собственных волн. Вблизи частот, где $({{d\beta {\text{'}}} \mathord{\left/ {\vphantom {{d\beta {\text{'}}} {d\omega }}} \right. \kern-0em} {d\omega }}) \to 0,$ имеет место также существенное замедление распространяющихся волн.

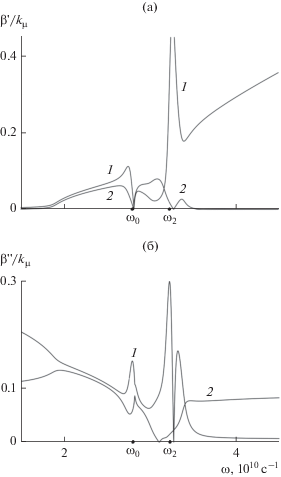
Для выяснения характера распространяющихся волн на рис. 8 приведены частотные зависимости реальной части квадратов поперечных компонент волнового вектора в каждой из граничащих сред. Локализация волны на границе раздела в каждой из сред имеет место в области частот, где $\operatorname{Re} (q_{{d,s}}^{2}) > 0.$ Так, на частотах $\omega > {{\omega }_{2}}$ волна 1 является локализованной в обоих средах, тогда как волна 2 в диэлектрике является излучательной, а в мелкослоистой среде эта волна либо слабо локализована (вблизи частоты ${{\omega }_{2}}$), либо является излучательной (вне резонансной области). В области $\omega < {{\omega }_{2}}$ характер каждой волны в обоих средах зависит от близости к резонансной области, положение которой зависит от доли графена в среде.

ЗАКЛЮЧЕНИЕ

Исследованы направляющие свойства и способность локализации ТМ- и ТЕ-волн плоской границы раздела диэлектрика и мелкослоистой среды, состоящей из чередующихся слоев железо-итриевого граната и графена. В приближении “мелкослоистости” получены частотные зависимости компонент тензоров эффективной ДП и МП. В результате решения граничной электродинамической задачи получены выражения для волновых полей в структуре и дисперсионные соотношения для ТМ- и ТЕ-волн. На основе численного анализа дисперсионного соотношения построены частотные зависимости константы распространения и поперечных компонент волнового вектора. Для ТМ-поляризации показано наличие двух частотных областей, в одной из которых реализуется режим распространения ПВ, во второй – объемной (излучательный). Для волн ТЕ-типа возможно управление дисперсионными характеристиками внешним магнитным полем. Наличие графена в структуре позволяет реализовать условия существования ПВ при практическом отсутствии поглощения. Изменение доли графена в слоистой подложке позволяет управлять режимами распространения. Для неуправляемой магнитным полем волны ТМ-поляризации рабочий диапазон частот лежит в области сотен терагерц. Для управляемой полем ТЕ-поляризации рабочий частотный диапазон смещается в область сотен гигагерц.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (госзадание № 3.6825.2017//БЧ).