Радиотехника и электроника, 2019, T. 64, № 9, стр. 866-873

ВВЕДЕНИЕ

Предыдущие работы [1–4] были посвящены численному моделированию удаленной регистрации в магнитосфере и на земной поверхности низкочастотных волн от искусственных возмущений в ионосфере. В качестве конкретного объекта исследований были выбраны волны низкой частоты (НЧ), генерируемые в результате демодуляции мощного коротковолнового (КВ) излучения станции HAARP (Аляска, США).

Характерной особенностью ионосферы с точки зрения распространения радиоволн является ее высотная неоднородность и одноосная анизотропия, обусловленная присутствием постоянного геомагнитного поля, направление и величина которого зависят от географического положения и высоты. На средних широтах в ионосфере гирочастота электрона f_He ~ 1 МГц и убывает ~r^–3, где r – расстояние от центра Земли. Таким образом, в ионосфере и плазмосфере собственные частоты электромагнитных процессов находятся, как правило, в НЧ-диапазоне. Низкими частотами в этом случае будем условно называть частоты   f < f_He/2. Это те частоты, свойства генерации и распространения которых определяются поведением составляющих плазму заряженных частиц [5].

Одной из важнейших научных задач, решаемых при помощи станций типа HAARP, является задача построения эффективных “виртуальных” НЧ-излучателей, расположенных непосредственно в ионосфере. Создание мощных наземных излучающих вверх антенн затруднено из-за их сравнительно больших геометрических размеров и относительно высокой проводимости земли на низких частотах.

Закономерно возникает вопрос о возможности размещения НЧ-передатчика непосредственно в нижней ионосфере. Один из таких проектов был доведен до стадии реального пуска и раскрытия антенны на грузовом корабле “Прогресс” [6]. На рис. 1 приведен увеличенный фрагмент рисунка из работы [6]. На фоне облачности отчетливо виден грузовик с двумя рамочными антеннами диаметром 20 м каждая.

В такого рода проекте первоочередным является обоснованный выбор типа излучающей антенны, поскольку возможности лабораторного моделирования свойств НЧ-излучателя больши́х размеров крайне ограничены [7]. В наземных передатчиках используются электрические дипольные антенны, поскольку рамочные антенны имеют малую эффективную длину. В ионосфере ситуация радикально меняется. Электрический диполь становится малопригодным для использования. Любое металлическое тело, помещенное в ионизованную среду, заряжается отрицательно вследствие бо́льшей подвижности электронов в сравнении с подвижностью ионов. Вокруг тела образуется обедненный электронами слой – “ионный экран”. Толщина такого слоя нелинейно меняется в зависимости от приложенного напряжения сигнала. В результате входной емкостной импеданс диполя непредсказуемо изменяется в широких пределах при движении космического аппарата (КА) и зависит от амплитуды НЧ-сигнала даже в линейном приближении.

Ионный экран образуется и вокруг проводника рамочной антенны. Однако входной импеданс рамки имеет индуктивный характер и не зависит от параметров ионосферной плазмы, магнитная проницаемость которой равна магнитной проницаемости свободного пространства. Наши оценки показывают, что в НЧ-диапазоне относительный вклад окружающей среды в величину индуктивности рамочной антенны не превышает 0.1%. Это позволяет надежно согласовать такую антенну с передатчиком в ходе полета КА. Модельные измерения в лабораторных условиях подтверждают этот вывод [7]. Кроме того, НЧ-волны в интервале частот 1…10 кГц (основной НЧ-интервал HAARP) имеют в ионосфере показатель преломления n, составляющий десятки и сотни единиц. Соответственно, значительно сокращается длина волны и резко возрастает эффективность излучения рамки.

Цель данной работы состоит в численной оценке напряженности ближнего поля рамочной антенны и в ее сравнении с напряженностью поля, создаваемой “демодулятором” мощного передатчика станции HAARP. Антенна расположена на борту низкоорбитального искусственного спутника Земли (ИСЗ), имеющего соответствующую приполярную орбиту. Оценки величины поля станции в нижней ионосфере опубликованы ранее.

1. БЛИЖНЕЕ ПОЛЕ БОРТОВОЙ РАМОЧНОЙ АНТЕННЫ В ИОНОСФЕРЕ

Для расчетов напряженности поля антенны мы используем уравнения Максвелла совместно с моделью среды в виде однородной холодной многокомпонентной магнитоактивной плазмы. Такая среда описывается тензором диэлектрической проницаемости $\hat {\varepsilon }$. Как уже отмечалось выше, магнитная проницаемость ионосферной плазмы равна магнитной проницаемости вакуума μ₀. Тензор $\hat {\varepsilon }$ имеет вид [5]:

где ν_k – эффективная частота соударений частиц сорта k; f – частота волны, ω = 2πf, i – мнимая единица. Суммирование ведется по сорту k заряженных частиц, составляющих плазму, с учетом знака заряда в величинах Y_k: где f_Hk и f_pk – гиро- и плазменная частота частицы сорта k: k = 1 (электроны), 2,… Предполагается, что волновая нормаль $\vec {k}$ составляет с вектором геомагнитного поля $\overrightarrow {{{B}_{0}}} $ угол ψ. Введем комплексный фазовый показатель преломления плоской волны с волновым вектором $\vec {k}$: где k₀ = ω/c = 2πf/c – волновое число (c – скорость света в вакууме). Для электронов имеем где N_e измеряется в см^–3; e, m_e – заряд и масса электрона; ε₀ – диэлектрическая проницаемость вакуума. В максимуме слоя F2 ионосферы имеем днем f_pe ≈ 10 МГц, ночью – f_pe ≈ 2…5 МГц в зависимости от условий (времени суток, сезона, географического положения и активности Солнца). Для ионов сорта k в формуле (4) следует использовать соответствующие значения концентрации N_k и массы m_k. Для гирочастоты электронов имеем выражение

В пределах ионосферы пространственная структура вектора геомагнитного поля ${{\vec {B}}_{0}}$ хорошо описывается моделью точечного магнитного диполя, расположенного вблизи центра Земли с осью, наклоненной под некоторым углом к оси вращения Земли. По аналогии с географическими координатами вводятся понятия геомагнитной широты Φ и долготы Λ. Если взять точку на высоте h и широте Φ, то значение гирочастоты можно оценить так:

где R₀ – средний радиус Земли (~6370 км). В северном полушарии вектор ${{\vec {B}}_{0}}$ направлен вниз к северу и составляет с вертикалью острый угол γ:

Для холодной магнитоактивной плазмы величину n фазового показателя преломления волны можно найти как корень биквадратного уравнения [8]:

где A = S sin² ψ + P cos² ψ ; B = RL sin² ψ + PS(1 + + cos² ψ); C = PRL.

Формально решение уравнения (8) можно записать в виде

где знаки “±” соответствуют необыкновенной и обыкновенной волнам. Известно, что в гиротропной среде понятие “обыкновенная” волна является условным. Обе характеристические волны имеют в общем случае эллиптическую поляризацию и их свойства зависят от угла ψ. Можно показать, что на низких частотах в ионосфере и магнитосфере условие μ $ \gg $ χ выполняется только для “необыкновенной” волны (“свистовой моды”). Обыкновенная НЧ-волна испытывает сильное поглощение, особенно в нижней ионосфере, и обычно не учитывается.

Из уравнения (9) видно, что величина n имеет сингулярность при A = 0, которая соответствует резонансному углу ψ = ψ_рез такому, что (см. (1) и (8)) в результате получаем

Такие углы соответствуют повышенному поглощению энергии НЧ-волн. В данной точке ионосферы при ее фиксированных параметрах значение выражения (10) зависит от частоты. Можно показать [8], что в многокомпонентной плазме имеется набор резонансов, которые служат границами различных типов распространения НЧ-волн. Отметим, что благодаря наличию соударений величина вещественной части n не имеет истинных сингулярностей.

Для низкочастотной свистовой моды понятие частоты нижнего гибридного резонанса (НГР) f_НГР, имеет простой наглядный смысл. При f < f_НГР поверхность n(ψ) замкнута на рассматриваемом частотном интервале, а при f > f_НГР – разомкнута и остается таковой вплоть до частоты f_He/2. Действительно, зависимость n(ψ) является поверхностью вращения с осью, совпадающей с направлением ${{\vec {B}}_{0}}$ и симметричной относительно своего “экватора” ψ = 90°. Поэтому достаточно изобразить один квадрант сечения такой поверхности любой плоскостью, содержащей ${{\vec {B}}_{0}}$. Направим ось n_∥ декартовой системы координат вдоль оси вращения, а ось n_⊥ – перпендикулярно этой оси в плоскости сечения. Очевидно, что во всех четырех квадрантах будет присутствовать одна и та же кривая. Для наглядности изобразим только первый квадрант.

Далее везде будем использовать численные значения параметров плазмы, которые соответствуют приполярной ионосфере над станцией HAARP [9] на широте 60° и высоте 200 км (таблица 1).

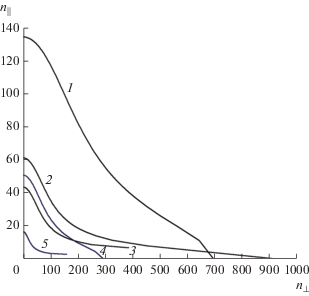
На рис. 2 приведены сечения n(ψ), рассчитанные для приведенных в таблице параметров ионосферы в виде зависимостей величины n_∥ при ψ = 0 от величины n_⊥ при ψ = 90° на частотах 1, 5 и 10 кГц. Нижняя гибридная частота для дневной и ночной ионосферы равна соответственно f_НГР ≈ 7.48 и 5.55 кГц. Из рисунка видно, что, как отмечалось выше, величины n могут быть сравнительно велики и возрастают с уменьшением частоты. С увеличением частоты величина n_⊥ растет и с приближением f к f_НГР снизу становится чрезвычайно велика. При f > f_НГР величина ψ_рез становится меньше 90°, т.е. поверхность фазового показателя преломления становится “открытой”. Распространение НЧ-волн в пределах углов 90° – ψ_рез < ψ < 90° + ψ_рез становится практически невозможным: энергия излучателя трансформируется в тепло [8].

В качестве модели источника выберем рамку с осью, параллельной внешнему магнитному полю. Это делает вычисления более ясными и компактными. Выберем в физическом пространстве и в пространстве волновых векторов сферические системы координат, центр которых совпадает с центром рамки. Тогда радиус-вектор и вектор волновой нормали можно записать в виде

Предположим, что рамка имеет радиус a, и по ней протекает синфазный гармонический ток с амплитудным значением I₀. Простейшая модель такой рамки соответствует элементарному точечному диполю:

где δ(x) – дельта-функция Дирака, ${{\vec {e}}_{\alpha }}$ – единичный вектор в азимутальном направлении. Для элементарной рамки a → 0, и для фурье-образа плотности тока в пространстве волновых нормалей имеем где M₀ = πa²I₀ – дипольный момент рамки.

Из выражения (13) видно, что в пространстве волновых векторов спектр элементарного источника неограниченно растет, если Γ → ∞. В анизотропной ионосфере существуют резонансные направления, в которых величина n чрезвычайно велика, даже с учетом соударений. В результате расчеты напряженности поля элементарного источника могут дать физически нереалистичные результаты [10]. По этой причине для источника, находящегося в ионосфере, необходимо использовать модель, явно учитывающую конечные размеры антенны [11]. Для плотности магнитного тока имеем

где a и b – эффективные радиус и толщина антенны. Выражение записано во вспомогательной цилиндрической системе координат: ось z направлена вдоль магнитного поля, центр этой системы совпадает с центром рамки, плоскость z = 0 совпадает с плоскостью рамки; ${{\vec {e}}_{z}}$ – единичный вектор вдоль оси z. Для подстановки в уравнения Максвелла удобнее использовать плотность электрического тока

Вычисляя ротор (14), получим

где ${{\vec {e}}_{{\varphi }}}$ – азимутальный единичный вектор. Этот ток распределен, вообще говоря, по всему пространству. Для прояснения ситуации вычислим средний квадрат радиуса такого тока R_эф: т.е. a – радиус эквивалентного кольцевого тока бесконечно малого сечения. Фурье-образ (16) в сферических координатах в пространстве волновых векторов (11б) вычисляется явно: где вектор ${\vec {v}}$ имеет компоненты: ${\vec {v}}$ = {sinα, –cosα, 0}. Из выражения (17) видно, что спектр источника конечных размеров имеет экспоненциальный обрезающий множитель, устраняющей проблему сингулярности напряженности поля в резонансах. Кроме того, легко видеть, что в случае элементарной рамки (a = b = 0) выражение (17) совпадает с (13).

Уравнения Максвелла для стационарного гармонического тока и зависимости от времени вида exp(+iωt) имеют вид

где $\vec {E}$ и $\vec {H}$ – напряженности электрического и магнитного полей волны. Для напряженности электрического поля волны имеем

Используем фурье-преобразование в пространство волновых нормалей:

В этом случае дифференциальные уравнения (19) преобразуются в алгебраические и их легко разрешить относительно $\vec {\mathbb{E}}$:

где ∆ = $ - k_{0}^{2}A(\psi )$(Γ² – $n_{1}^{2}$) (Γ² – $n_{2}^{2}$) – см. выражения (8), (9). Элементы 3 × 3 матрицы ${\mathbf{\hat {a}}}$ имеют вид

Выражения (21), (22) можно использовать в обратном преобразовании Фурье для получения компонент напряженности электрического поля в реальном пространстве. При этом величина ∆ находится в знаменателе подынтегральных выражений, и для получения ближнего поля необходимо использовать процедуру выделения не сингулярных частей соответствующих интегралов [12]. Результат получается почти в аналитическом виде, если считать интегралы от функции ошибок такими же функциями, как синус или косинус:

где

В общем случае интегралы вида (24) не берутся аналитически. Однако при R > a можно использовать асимптотику вида [13]

В случае элементарного точечного источника нужно оставить только первое слагаемое в (25) при m = 1, причем интегралы (24) берутся явно, и мы получим аналитические выражения для напряженности ближнего поля элементарного точечного источника. Это поле спадает при увеличении расстояния как ~r^–2, так же как и поле рамки конечных размеров (23) при r $ \gg $ a.

2. РЕЗУЛЬТАТЫ РАСЧЕТОВ БЛИЖНЕГО ПОЛЯ

Результаты расчетов величины E = ($E_{R}^{2}$ + $E_{\theta }^{2}$ + + $E_{\varphi }^{2}$)^1/2 получены для дневной и ночной моделей нижней приполярной ионосферы. Параметры моделей были приведены в таблице. На рис. 3а и 3б представлены зависимости E(f) на расстоянии 1 км от источника для дневной и ночной моделей ионосферы соответственно для различных значений углов θ = 0, 5, 10, 15 и 90 град. Параметры излучателя взяты из реального эксперимента [6]: I₀ = 100 А, a = 10 м, b = 0.2 м. По оценкам авторов [6], выходная мощность бортового НЧ-передатчика составляла примерно 1 кВт. В узком диапазоне высот нижней ионосферы можно считать мощность излучения неизменной по порядку величины.

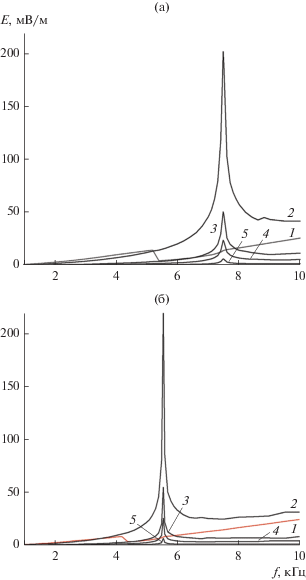
Напомним, что частоты нижнего гибридного резонанса для дня и ночи в рамках нашей модели ионосферы равны соответственно 7.48 и 5.55 кГц. В изотропной среде поле рамки вдоль ее оси равно 0. При наличии анизотропии кривая n(θ) отличается от окружности (см. рис. 2) и возникает поле рамки вдоль направления ${{\vec {B}}_{0}}$ (кривая 1 для θ = 0). В зависимости от частоты и времени суток напряженность продольного поля может достигать 20…30 мВ/м. При f ~ f_НГР поверхность фазового показателя преломления сильно вытягивается в направлении θ = 90° , при этом нормаль к поверхности на вытянутых участках составляет малый угол с направлением ${{\vec {B}}_{0}}$. Это объясняет появление резких пиков напряженности поля вблизи f_НГР при малых θ. В целом из рис. 3а и 3б видно, что картины распределения напряженности НЧ-поля рамки в магнитоактивной плазме и в пустом пространстве качественно различаются. В плазме поле в направлении θ = 90° имеет заметно меньшую величину по сравнению с полем при малых углах θ.

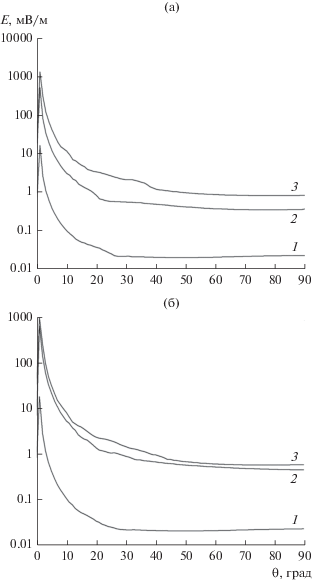
На рис. 4а и 4б приведены зависимости E(θ) на расстоянии 1 км от источника соответственно для дневной и ночной моделей ионосферы для частот 1, 5 и 10 кГц (параметры рамки те же, что и для рис. 3). На рисунках отчетливо видны максимумы напряженности поля при малых значениях угла θ, о которых говорилось выше при обсуждении рис. 3. При θ $ \gtrsim $ 30° кривые E(θ) для данной частоты изменяются относительно слабо. Соответствующие величины E находятся в интервале от десятков микровольт на метр до единиц микровольт на метр. В работе [6] экспериментально были измерены поля при малых θ на расстоянии 12 км от источника на почти вдвое большей высоте (N_e ~ 5…6 × 10⁵ см^–3); максимальные напряженности поля составляли ~30 мВ/м на частоте 5 кГц.

Полученные числовые значения напряженности поля E сравним с аналогичными значениями НЧ-поля ионосферного демодулятора над станцией HAARP. Подобное сравнение неизбежно носит качественный характер, поскольку на процессы генерации и распределения НЧ-поля в пространстве и во времени существенно влияют локальные текущие гелио- и геофизические условия [14].

Спутниковые измерения НЧ-излучения ионосферного демодулятора в рамках проекта HAARP проводили при помощи аппаратуры спутника европейского проекта DEMETER [15]. Спутник выведен с орбиты 17 марта 2012 г. Высота его полета составляла ~670 км, наклонение орбиты ~98.3°, средняя горизонтальная орбитальная скорость ~7.6 км/с. Измерения электрического и магнитного НЧ-поля HAARP проводились в 2007 г. [16–18].

Было, в частности, показано, что эквивалентная мощность НЧ-демодулятора, излучаемая вверх, составляет ~4 Вт на частоте около 1 кГц. Примерно столько же излучается вниз в волновод “Земля-ионосфера” [19]. Напомним, что полная излучаемая мощность КВ-передатчика составляет ~3.6 МВт, а с учетом диаграммы направленности достигает 1 ГВт. Таким образом, спектральный коэффициент преобразования КВ-мощности в НЧ-мощность составляет ничтожно малую величину, порядка 4 × 10^–7%. Аналогичные данные получены и для частоты 2 кГц. Кроме того, и теоретически, и экспериментально показано [1, 16], что демодулированная НЧ энергия распространяется в ионосферу в виде относительно узкого (шириной 10…20 км) пучка. Приведенные выше значения мощности источника относятся именно к этому пучку, за пределами которого и поток мощности, и напряженность поля резко уменьшаются по величине.

В нижней ионосфере прямые измерения напряженности поля НЧ-демодулятора практически отсутствуют, поэтому оценки делаются путем пересчета результатов измерений на бо́льших высотах, в связи с чем у разных авторов получаемые значения заметно различаются. В целом, по результатам оценок [16–18], в нижней ионосфере следует ожидать значений напряженности НЧ‑поля от ~1 до ~30 мВ/м.

ЗАКЛЮЧЕНИЕ

Приведены результаты компьютерного моделирования одного из возможных способов генерации и воздействия НЧ-излучения на ионосферу Земли. Рассмотренный способ заключается в установке на борту искусственного спутника Земли низкочастотного передатчика, нагруженного на внешнюю рамочную антенну относительно большого диаметра. Расчеты велись в приближении “холодной” плазмы. Для исключения резонансных особенностей в распределении напряженности излучаемого НЧ-поля использовалась модель источника “конечных” размеров [10, 11]. Строго говоря, в резонансных областях приближение холодной плазмы не справедливо. С учетом “тепловых” добавок поверхность фазового показателя преломления остается замкнутой, и резонансные особенности также исчезают [8, 20]. На наш взгляд, в рамках данной задачи введение тепловых поправок неоправданно усложняет процедуру расчетов и не дает каких-либо значимых результатов в сравнении с относительно простой моделью источника конечных размеров.

Приведены результаты расчетов, пригодные для сравнения с характеристиками излучения НЧ-демодулятора станции HAARP (Аляска). Рассмотрен характерный диапазон частот модуляции от 1 до 10 кГц.

Показано, что НЧ-волны указанного диапазона в нижней ионосфере на высоте ~200 км имеют показатель преломления ~50…100 днем и ~20…50 ночью, что соответствует длинам волн ~3..5 и ~6…15 км. Следовательно, в ночное время, когда работает демодулятор HAARP, для ИСЗ на высоте 200 км область возмущения в нижней ионосфере находится в ближней зоне источника. В дневное время – это ближняя и промежуточная зоны.

Получены соотношения, описывающие ближнее поле рамки конечных размеров, ось которой параллельна внешнему геомагнитному полю ${{\vec {B}}_{0}}$. Проведены расчеты напряженности электрического поля такого источника в зависимости от угла наблюдения относительно направления ${{\vec {B}}_{0}}$ и в зависимости от частоты.

Показано, что НЧ-поле рамки распределено крайне неравномерно. В пространстве максимальные значения напряженности поля сосредоточены вблизи локального направления ${{\vec {B}}_{0}}$. В зависимости от частоты напряженность поля имеет острый максимум вблизи локального значения частоты нижнего гибридного резонанса.

Сравнение с опубликованными данными показывает, что бортовой НЧ-передатчик мощностью ~1 кВт способен обеспечить в нижней ионосфере по порядку величины ту же напряженность НЧ-поля, что и НЧ-демодулятор HAARP, который создается наземным КВ-передатчиком мощностью 3.6 МВт.