1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 64, № 9, 2019

Радиотехника и электроника, 2019, T. 64, № 9, стр. 910-915

Исследование помехоустойчивости алгоритма оптимального посимвольного приема сигналов, соответствующих кодам с проверкой на четность в недвоичных полях

Л. Е. Назаров 1, *, П. В. Шишкин 1

1 Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино Московской обл., пл. Введенского, 1, Российская Федерация

* E-mail: levnaz2008@mail.ru

Поступила в редакцию 20.02.2019
После доработки 20.02.2019
Принята к публикации 18.03.2019

Полный текст (PDF)

Аннотация

Рассмотрен алгоритм оптимального посимвольного приема сигнальных конструкций на основе блоковых помехоустойчивых кодов в недвоичных полях. Показано, что основу разработанного алгоритма посимвольного приема составляет спектральное преобразование в базисе Уолша–Адамара. Показано, что результирующая сложность разработанного алгоритма приема определяется размерностью дуального кода, что обусловливает перспективность его применения для блоковых помехоустойчивых кодов с высокой кодовой скоростью. Приведены результаты моделирования разработанного алгоритма приема с целью исследования помехоустойчивости для сигналов на основе кодов с проверкой на четность.

ВВЕДЕНИЕ

Коды с проверкой на четность находят широкое применение в схемах помехоустойчивого кодирования, например, в блоковых турбокодах в качестве составляющих кодов, в каскадных схемах кодирования [1, 2]. Для этих кодовых схем разработаны процедуры итеративного приема на основе алгоритмов посимвольного приема составляющих кодов, реализующих вычисление выходных “мягких” (многоуровневых) решений для кодовых символов с использованием входных “мягких” решений с выхода демодулятора сигналов [1, 3–5]. Это определяет низкую сложность результирующих алгоритмов итеративного приема данных кодовых схем, что обусловливает их практическое применение в системах связи различного назначения, в частности, блоковые турбокоды на основе рассматриваемых составляющих кодов с проверкой на четность применяются в оптических системах связи, в системах магнитной записи [6, 7].

Правило оптимального посимвольного приема минимизирует вероятность ошибки на кодовый символ в отличие от правила приема максимального правдоподобия, минимизирующего вероятность ошибки на кодовое слово [8]. Известен ряд алгоритмов посимвольного приема сигналов на основе помехоустойчивых линейных кодов в двоичном поле $GF(2)$, например, на основе использования решетчатой структуры дуальных кодов, а также на основе использования спектрального преобразования в базисе Уолша–Адамара [9, 10]. Актуальной является проблема разработки и исследования алгоритмов посимвольного приема для сигналов, соответствующих кодам в недвоичных полях $GF({{2}^{m}})$ [1, 2]. Этот подход позволяет расширить класс эффективных сигнальных и кодовых конструкций и согласуется с направлением развития теории класса помехоустойчивых кодов в недвоичных полях [1, 2, 8, 11–14]. В этот класс входят коды Рида-Соломона и низкоплотностные коды [15–18], интенсивно используемые в приложениях.

В статье рассматривается алгоритм оптимального посимвольного приема, реализующий вычисление “мягких” решений для кодовых символов с использованием входных “мягких” решений для сигнальных конструкций, соответствующих кодам в недвоичных полях $GF({{2}^{m}}).$ Исследование помехоустойчивости этого алгоритма произведено для сигнальных конструкций, соответствующих кодам с проверкой на четность.

1. ПОСТАНОВКА ЗАДАЧИ

Пусть $\vec {A} = ({{a}_{i}};0 \leqslant i \leqslant k - 1)$ – последовательность информационных символов – элементов поля $GF({{2}^{m}}).$ Проверочный символ ${{a}_{k}}$ кодового слова $\vec {B}$ кода с проверкой на четность задается в виде суммы [14, 19]

(1)
${{a}_{k}} = \sum\limits_{i = 0}^{k - 1} {{{a}_{i}}} .$

Суммирование в (1) осуществляется в поле $GF({{2}^{m}}),$ элементы поля ${{a}_{i}}$ представляются многочленами [18]

(2)
${{a}_{i}}(x) = \sum\limits_{p = 0}^{m - 1} {{{\alpha }_{p}}({{a}_{i}})} {{x}^{p}},\,\,\,\,{{\alpha }_{p}}({{a}_{i}}) \in GF(2).$

Кодовые символы ${{a}_{i}},$ $i = 0,1,...,k$ сопоставляются сигналам, которые передаются по физическим каналам. На вход приемного устройства поступает реализация $\vec {Y} = ({{\dot {y}}_{l}};\,\,0 \leqslant l \leqslant k),$ где ${{\dot {y}}_{l}}$ – “мягкие” решения (в общем случае комплексные), поступающие с демодулятора сигналов.

Оптимальное посимвольное правило приема заключается в вычислении апостериорных вероятностей $\Pr ({{a}_{i}} = \beta \left| {\vec {Y}} \right.),$ $\beta \in GF({{2}^{m}})$ и коэффициентов ${{\alpha }_{p}}({{a}_{i}}) \in GF(2),$ $p = 0,1,...,m - 1,$ на основе которых вычисляются “мягкие” решения ${{x}_{\beta }}(i)$ [1, 9]

(3)
${{x}_{\beta }}(i) = \ln \left( {\frac{{\Pr ({{a}_{i}} = \beta \left| {\vec {Y})} \right.}}{{\Pr ({{\alpha }_{i}} = 0\left| {\vec {Y})} \right.}}} \right).$

С использованием ${{x}_{\beta }}(i)$ принимаются “жесткие” решения относительно оценки символов ${{\hat {a}}_{i}}$ и значений коэффициентов ${{\hat {\alpha }}_{p}}({{a}_{i}})$

(4)
${{\hat {a}}_{i}} = \mathop {\max }\limits_{\beta \in GF({{2}^{m}})} (\arg ({{x}_{\beta }}(i))).$

Апостериорные вероятности кодовых символов ${{a}_{i}}$ задаются выражением [9]

(5)
$\begin{gathered} \Pr ({{a}_{i}} = \beta \left| {\vec {Y}} \right.) = \sum\limits_{\vec {B}:{{a}_{i}} = \beta } {\Pr (\vec {B}\left| {\vec {Y})} \right.} = \\ = \sum\limits_{\vec {B}:{{a}_{i}} = \beta } {\frac{{\Pr (\vec {A})}}{{p(\vec {Y})}}p(\vec {Y}\left| {\vec {B})} \right.} , \\ \end{gathered} $

где $\Pr (\vec {B}\left| {\vec {Y})} \right.$ – условная вероятность кодового слова $\vec {B}$ для реализации $\vec {Y}$.

Функция правдоподобия $\Pr (\vec {Y}\left| {\vec {B})} \right.$ в (5) определяется моделью физического канала, для канала без памяти –

$p(\vec {Y}\left| {\vec {B})} \right. = \prod\limits_{i = 0}^k {p(\vec {Y}\left| {{{a}_{i}})} \right.} .$

Априорные вероятности сообщений $\vec {A}$ полагаются равными $\Pr (\vec {A}) = {1 \mathord{\left/ {\vphantom {1 {{{2}^{{mk}}}}}} \right. \kern-0em} {{{2}^{{mk}}}}}.$

Сложность реализации (5), определяемая требуемым объемом вычислительных операций, оценивается соотношением ${{P}_{1}} \approx {{2}^{{mk}}},$ и даже для малых значений $m,k$ вычисление (5) представляет трудноразрешимую проблему.

Суть задачи – дать описание разработанного эффективного относительно сложности реализации алгоритма оптимального посимвольного приема с входными и выходными “мягкими” решениями для сигнальных конструкций, соответствующих помехоустойчивым кодам в недвоичных полях $GF({{2}^{m}}),$ а также привести результаты моделирования разработанного алгоритма приема с целью оценки вероятностных характеристик для ряда сигнальных конструкций, соответствующих кодам с проверкой на четность.

2. АЛГОРИТМ ОПТИМАЛЬНОГО ПОСИМВОЛЬНОГО ПРИЕМА СИГНАЛОВ

Введем в рассмотрение функции [13]

(6)
${{\omega }_{b}}(a) = \exp (j\pi (a \times b)d),$

где $a,b,d$ – элементы поля $GF({{2}^{m}});$ a × b = $ = \left[ {a(x)b(x)} \right]$ – произведение элементов $a,b$ в поле $GF({{2}^{m}}),$ задаваемого по модулю неприводимого многочлена $\gamma (x)$ степени m; $ad = \sum\nolimits_{i = 0}^{m - 1} {{{a}_{i}}{{b}_{i}}} .$

Функции ${{\omega }_{b}}(a)$ принимают значения $ \pm 1$. Полагаем, что элементы b, a определяют номер и аргумент функции ${{\omega }_{b}}(a).$ При фиксированном $b \ne 0$ и для ${{a}_{i}},$ $i = 0,1,...,{{2}^{m}} - 1$ произведения ${{a}_{i}} \times b$ принимают все значения поля $GF({{2}^{m}})$ и функции ${{\omega }_{b}}(a)$ эквивалентны функциям Уолша ${{W}_{b}}(a)$ с перемеженными значениями номеров и аргументов. Функции Уолша с длительностью ${{2}^{m}}$ определяются соотношением

${{W}_{b}}(a) = \exp (j\pi ab) = \exp \left( {\sum\limits_{i = 0}^{m - 1} {{{a}_{i}}{{b}_{i}}} } \right),$

где ${{a}_{i}}$, ${{b}_{i}}$ – двоичное представление чисел a и b. Справедливы условия ортогональности [13]

(7)
$\sum\limits_{a \in GF({{2}^{m}})} {{{W}_{b}}(a) = \left\{ {\begin{array}{*{20}{c}} {0,b \ne 0,} \\ {{{2}^{m}},b = 0} \end{array}} \right.} ,$
(8)
$\sum\limits_{a \in GF({{2}^{m}})} {{{W}_{b}}(a){{W}_{c}}(a) = \sum\limits_{a \in GF({{2}^{m}})} {{{W}_{{b + c}}}(a)} = \left\{ {\begin{array}{*{20}{c}} {0,b \ne 0,} \\ {{{2}^{m}},b = 0} \end{array}} \right.} .$

Функции ${{\omega }_{b}}(a)$ также ортогональны в области их определения, их полное множество представляет ортогональный базис, по которому можно разложить дискретные функции длительностью ${{2}^{m}}$ в ряд.

Для базисной системы функций Уолша разработаны производительные алгоритмы быстрого спектрального преобразования, которые также могут быть применены к перемеженной базисной системе (6).

Утверждение. Пусть неприводимый многочлен, порождающий поле $GF({{2}^{m}})$, имеет вид $\gamma (x) = 1 + {{x}^{k}} + {{x}^{m}}$ ($1 \leqslant k \leqslant m - 1$), элемент поля $d$ имеет единичную компоненту на ($k - 1$)-й позиции (${{d}_{{k - 1}}} = 1$) и нулевые на остальных позициях (${{d}_{i}} = 0;i \ne k - 1$). В этом случае закон перемежения номеров $b,b{\text{'}}$ для функций ${{W}_{b}}(a) = {{w}_{{b'}}}(a)$ определяется соотношением для компонент ${{b}_{i}},b_{i}^{'},$ $i = 0,1,...,m - 1$

(9)
$b_{i}^{'} = \left\{ {\begin{array}{*{20}{c}} {{{b}_{{k - i - 1}}},\,\,\,\,0 \leqslant i \leqslant k - 1} \\ {{{b}_{{m + k - i - 1}}},\,\,k \leqslant i \leqslant m - 1} \end{array}} \right..$

Для доказательства утверждения представим произведение $[a \times b]$ в виде

(10)
$[a(x) \times b(x)] = \sum\limits_{l = 0}^{2(m - 1)} {[{{x}^{l}}]\sum\limits_{i + \nu = l} {{{a}_{i}}{{b}_{\nu }}} } .$

С использованием соотношения (10) имеем

(11)
$(a \times b)d = \sum\limits_{l = 0}^{2(m - 1)} {{{T}_{{k - 1}}}(l)\sum\limits_{i + \nu = l} {{{a}_{i}}{{b}_{\nu }}} } ,$

где ${{T}_{{k - 1}}}(l)$ – ($k - 1)$-я компонента многочлена $[{{x}^{l}}]$.

Для значений $0 \leqslant l \leqslant m - 1$ выполняется условие $[{{x}^{l}}] = {{x}^{l}}$ и справедливо соотношение ${{T}_{{k - 1}}}(l) = \left\{ {\begin{array}{*{20}{c}} {1,\,\,l = k - 1} \\ {0,\,\,l \ne k - 1} \end{array}} \right..$ В этом случае имеем $\nu = k - i - 1.$ Верхнее соотношение (10) утверждения доказано.

Для значений $m \leqslant l \leqslant 2(m - 1)$ имеем

(12)
$\begin{gathered} \text{[}{{x}^{l}}] = [{{x}^{{j + m}}}] = [{{x}^{j}}(1 + {{x}^{k}})] = [{{x}^{j}} + {{x}^{{j + k}}}], \\ 0 \leqslant j \leqslant m - 2. \\ \end{gathered} $

При $j = k - 1$ первое слагаемое в (13) имеет вид $[{{x}^{{k - 1}}}].$ Второе слагаемое в (12) имеет подобное составляющее при условии $j = m - 1,$ однако в соответствии с предположением $j \leqslant m - 2.$ Поэтому имеем результирующее выражение $\nu = l - i$ = $m + k - 1 - i.$ Нижнее соотношение в (9) доказано.

Алгоритм оптимального посимвольного приема сигналов в поле $GF({{2}^{m}})$ включает три этапа [13].

На первом этапе выполняется спектральное преобразование в базисе ${{\omega }_{b}}(a)$ с размерностью ${{2}^{m}}$ над последовательностью “мягких” решений $p({{y}_{l}}\left| {b(l))} \right.$

(13)
${{C}_{l}}(r) = \sum\limits_{b(l) \in GF({{2}^{m}})} {p({{y}_{l}}\left| {b(l)} \right.){{w}_{{b(l)}}}(r)} .$

Здесь $l = 0,1,...,n - 1$ – номер позиции кодовых символов.

Верным является обратное преобразование

$p({{y}_{l}}\left| {b(l)} \right.) = \frac{1}{{{{2}^{m}}}}\sum\limits_{r \in GF({{2}^{m}})} {{{C}_{l}}(r){{w}_{{b(l)}}}(r)} .$

На втором этапе вычисляется спектральное множество $\{ {{T}_{l}}(\lambda )\} $

(14)
$\begin{gathered} {{T}_{l}}(\lambda ) = \sum\limits_{\beta \in GF({{2}^{m}})} {\Pr (b(l) = \beta \left| {\vec {\dot {Y}}){{w}_{\beta }}(\lambda )} \right.} , \\ \lambda \in GF({{2}^{m}}). \\ \end{gathered} $

Cпектральное множество $\{ {{T}_{l}}(\lambda )\} $ вычисляется с использованием величин ${{С}_{l}}(r)$ (13) и множества кодовых слов $R$ дуального кода ${{С}_{H}}$ с параметрами $(n,n - k)$

(15)
${{T}_{l}}(\lambda ) = \frac{1}{{\sum\limits_{{{r}_{p}}:R \in {{C}_{H}}} {\prod\limits_{p = 0}^{n - 1} {{{C}_{p}}({{r}_{p}})} } }}\sum\limits_{{{r}_{p}}:R \in {{C}_{H}}} {\prod\limits_{p = 0}^{n - 1} {{{C}_{p}}({{r}_{p}})\frac{{{{C}_{l}}({{r}_{l}} - \lambda )}}{{{{C}_{l}}({{r}_{l}})}}} } .$

Сложность вычисления соотношения (14) оценивается приведенным выше значением ${{P}_{1}}$, сложность вычисления (15) оценивается как ${{P}_{2}} \cong {{2}^{{m(n - k)}}},$ для значений $n - k \ll k$ справедливо условие ${{P}_{2}} \ll {{P}_{1}}.$

Доказательство соотношения (15) основано на использовании свойств ортогональности (7), (8) для функций ${{\omega }_{b}}(a).$ Запишем (15) в виде

(16)
$\begin{gathered} {{T}_{l}}(\lambda ) = \sum\limits_{\beta \in GF({{2}^{m}})} {\sum\limits_B {\delta (b(l) - \beta )} \Pr (b(l)} = \\ = \beta \left| {\vec {Y})} \right.\exp (j\pi (\lambda \times \beta )d). \\ \end{gathered} $

Здесь $\delta (x) = 1,$ если $x = 0,$ иначе $\delta (x) = 0.$

Выражение (16) преобразуется к следующему виду:

(17)
$\begin{gathered} {{T}_{l}}(\lambda ) = \frac{1}{{{{2}^{{m(k + n)}}}}}\frac{1}{{p(\vec {\dot {Y}})}}\sum\limits_A {\sum\limits_{{{r}_{0}}} {...\sum\limits_{{{r}_{{n - 1}}}} {{{C}_{0}}({{r}_{0}})} } } ...{{C}_{{n - 1}}}({{r}_{{n - 1}}}) \times \\ \times \,\,\prod\limits_{i = 0}^{k - 1} {\exp \left( {j\pi \left[ {a(i) \times \sum\limits_{t = 0}^{n - 1} {g(i,t) \times {{r}_{t}}} } \right]} \right.} {\kern 1pt} d + \\ \left. {\frac{{^{{^{{}}}}}}{{_{{_{{}}}}}} + j\pi (\lambda \times a[i] \times g(i,l))d)} \right). \\ \end{gathered} $

Рассмотрим выражение для $\Pr (B\left| {\vec {Y})} \right.,$ входящего в состав (17):

(18)
$\begin{gathered} \Pr (B\left| {\vec {Y})} \right. = \frac{1}{{{{2}^{{m(k + n)}}}p(\vec {\dot {Y}})}}\sum\limits_{{{r}_{0}}} {...\sum\limits_{{{r}_{{n - 1}}}} {{{C}_{0}}({{r}_{0}})} } ...{{C}_{{n - 1}}}({{r}_{{n - 1}}}) \times \\ \times \,\,\prod\limits_{i = 0}^{k - 1} {\exp \left( {j\pi \left[ {a(i) \times \sum\limits_{t = 0}^{n - 1} {g(i,t) \times {{r}_{t}}} } \right]d} \right)} . \\ \end{gathered} $

Учитывая условие $\sum\nolimits_B {\Pr (B\left| {\vec {\dot {Y}})} \right. = 1} $ и свойство ортогональности (8)

(19)
$\begin{gathered} \sum\limits_A {\exp \left( {j\pi \left[ {a(i) \times \sum\limits_{t = 0}^{n - 1} {g(i,t) \times {{r}_{t}}} } \right]d} \right)} = \\ = {{2}^{m}}\delta \left( {\sum\limits_{t = 0}^{n - 1} {g(i,t) \times {{r}_{t}}} } \right), \\ \end{gathered} $

имеем соотношение

$p(\vec {Y}) = \frac{1}{{{{2}^{{mn}}}}}\sum\limits_{{{r}_{p}}:R \in {{C}_{H}}} {\prod\limits_{p = 0}^{n - 1} {{{C}_{p}}({{r}_{p}})} } .$

Суммирование в соотношении производится для кодовых слов $R = ({{r}_{l}};0 \leqslant l \leqslant n - 1)$ дуального кода ${{С}_{H}}$. С использованием (17)–(19) получается результирующее выражение (15) относительно ${{T}_{l}}(\lambda )$.

На третьем этапе вычисляются апостериорные вероятности $\Pr (b(l) = \beta \left| {\vec {\dot {Y}})} \right.$ с использованием обратного спектрального преобразования над ${{T}_{l}}(\lambda )$ (16)

(20)
$\Pr (b(l) = \beta \left| {\vec {Y})} \right. = \sum\limits_{\lambda \in GF({{2}^{m}})} {{{T}_{l}}(\lambda )} {{\omega }_{\beta }}(\lambda ).$

Наиболее простым является рассматриваемый алгоритм посимвольного приема для сигнальных конструкций на основе кодов с проверкой на четность. В этом случае множество кодовых слов ${{R}_{i}}$ дуального кода ${{C}_{H}}$ с параметрами ($k + 1,1$) содержит ${{2}^{m}}$ последовательностей кодовых символов одинаковых элементов $\alpha \in GF({{2}^{m}})$ длительностью $k + 1$ [19].

Для двоичного поля $GF(2)$ множество кодовых слов $R$ дуального кода содержит лишь два кодовых слова с элементами $\alpha = 0$ и $\alpha = 1.$ Для канала с аддитивным белым гауссовским шумом (АБГШ) с односторонней спектральной плотностью ${{N}_{0}}$ и для сигналов длительностью $T$ с двоичной фазовой манипуляцией (ФМ2) условная плотность вероятности $p({{y}_{l}}\left| \alpha \right.)$ задается выражением

$p({{y}_{l}}\left| \alpha \right.) = \frac{1}{{\sqrt {2\pi } {{N}_{0}}{N \mathord{\left/ {\vphantom {N 4}} \right. \kern-0em} 4}}}exp\left( { - \frac{{{{{({{y}_{l}} - {{{( - 1)}}^{\alpha }}{{AT} \mathord{\left/ {\vphantom {{AT} 2}} \right. \kern-0em} 2})}}^{2}}}}{{{{{{N}_{{\text{0}}}}T} \mathord{\left/ {\vphantom {{{{N}_{{\text{0}}}}T} 2}} \right. \kern-0em} 2}}}} \right).$

Подставляя это выражение в соотношения (13), (15) и (20), получаем результирующее выражение для отношения правдоподобия

(21)
$\begin{gathered} x(l) = \frac{{\Pr (b(l) = 0\left| {\vec {Y})} \right.}}{{\Pr (b(l) = 1\left| {\vec {Y})} \right.}}, \\ x(l) = exp(2{{y}_{l}})\frac{{1 + \prod\limits_{p = 0,p \ne l}^{n - 1} {\operatorname{th} ({{y}_{p}})} }}{{1 - \prod\limits_{p = 0,p \ne l}^{n - 1} {\operatorname{th} ({{y}_{p}})} }}. \\ \end{gathered} $

Значения $x(l)$ эквивалентны выходным “мягким” решениям, при условии $x(l) \geqslant 1$ принимается “жесткое” решение $b(l) = 0,$ иначе $b(l) = 1.$ Здесь $\operatorname{th} (x)$ – функция тангенс гиперболический.

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

На рис. 1 и 2 приведены вероятностные характеристики (вероятности ошибки ${{P}_{{{\text{ош}}}}}$ на кодовое слово в зависимости от отношения сигнал/помеха ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$ (${{E}_{{\text{б}}}}$ – энергия сигналов на информационный бит)) для АБГШ-канала при приеме сигнальных конструкций на основе сигналов ФМ2 и кодов с проверкой на четность в полях $GF({{2}^{3}}),$ $GF({{2}^{4}})$ и $GF({{2}^{6}}),$ порождающие многочлены которых приведены в таблице [19].

Рис. 1.

Зависимости вероятности ошибки ${{P}_{{{\text{ош}}}}}$ от отношения сигнал/помеха при посимвольном приеме сигнальных конструкций на основе сигналов ФМ2 и кода с проверкой на четность в поле $GF(2)$ (кривая 1), $GF({{2}^{3}})$ (кривая 2), $GF({{2}^{6}})$ (кривая 3).

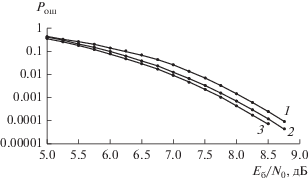
Рис. 2.

Зависимости вероятности ошибки ${{P}_{{{\text{ош}}}}}$ от отношения сигнал/помеха при посимвольном приеме сигнальных конструкций на основе ортогональных функций Уолша и кода с проверкой на четность в поле $GF({{2}^{3}})$ (кривая 1), $GF({{2}^{4}})$ (кривая 2), $GF({{2}^{6}})$ (кривая 3).

Порождающие многочлены $\gamma (x)$ для полей $GF({{2}^{3}}),$ $GF({{2}^{4}}),$ $GF({{2}^{6}})$

Поле $\gamma (x)$
$GF({{2}^{3}})$ ${{x}^{3}} + x + 1$
$GF({{2}^{4}})$ ${{x}^{4}} + x + 1$
$GF({{2}^{6}})$ ${{x}^{4}} + x + 1$

Вероятностные характеристики получены путем моделирования приведенного алгоритма оптимального посимвольного приема с вычислением выходных “мягких” решений при передаче кодовых слов с информационным объемом ≈150 битов. При этом число информационных символов, эквивалентных элементам полей $GF(2)$, $GF({{2}^{3}}),$ $GF({{2}^{4}})$ и $GF({{2}^{6}})$, равно $k = 150,$ 50, 38 и 25 соответственно.

При выполнении моделирования производится интервальная оценка вероятности ${{P}_{{{\text{ош}}}}}$ путем вычисления частости $w = {x \mathord{\left/ {\vphantom {x u}} \right. \kern-0em} u},$ где$x$ – число ошибочных решений в последовательности испытаний $u$. Требуемое количество вычислительных экспериментов $u$ определяется размером доверительного интервала, вероятностью ${{P}_{{{\text{ош}}}}}$, доверительной вероятностью ${{P}_{{{\text{дов}}}}}$ [20]. Например, для значения ${{P}_{{{\text{ош}}}}} = {{10}^{{ - 4}}},$ доверительного интервала [$0.5{{P}_{{{\text{ош}}}}},1.5{{P}_{{{\text{ош}}}}}$] и ${{P}_{{{\text{дов}}}}} = 0.95$ требуемое количество экспериментов оценивается значением 1540000.

На рис. 1 вероятностная кривая 1 соответствует результату моделирования алгоритма посимвольного приема (23) ФМ2 сигналов на основе кода с проверкой на четность в поле $GF(2)$. Вероятностные кривые 2 и 3 получены в результате моделирования алгоритма посимвольного приема (13), (15), (20) сигналов на основе кода с проверкой на четность в поле $GF({{2}^{3}})$ и $GF({{2}^{6}}).$ Видно, что при увеличении объема полей вероятности ошибки ${{P}_{{{\text{ош}}}}}$ монотонно уменьшаются для фиксированных значений ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}\,:$ вероятность ${{P}_{{{\text{ош}}}}} = {{10}^{{ - 4}}}$ достигается при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 8.75$ дБ для поля $GF(2)$, при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 8.5$ дБ для поля $GF({{2}^{3}})$ и при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 8.35$ дБ для поля $GF({{2}^{6}}).$

На рис. 2 приведены вероятностные кривые, полученные в результате моделирования алгоритма (13), (15), (20) посимвольного приема сигнальных конструкций на основе ортогональных функций Уолша с объемом 8, 16 и 64 и на основе кода с проверкой на четность в полях $GF({{2}^{3}}),$ $GF({{2}^{4}})$ и $GF({{2}^{6}}).$ В этом случае условная плотность вероятности $p({{y}_{{l0,}}}{{y}_{{l1}}},...,{{y}_{{l(m - 1)}}}\left| \alpha \right.),$ $\alpha \in GF({{2}^{m}})$ определяется выражением

$\begin{gathered} p({{y}_{{l0,}}}{{y}_{{l1}}},...,{{y}_{{l(m - 1)}}}\left| \alpha \right.) = \\ = \prod\limits_{p = 0}^{m - 1} {\frac{1}{{\sqrt {2\pi } {{N}_{0}}{N \mathord{\left/ {\vphantom {N 4}} \right. \kern-0em} 4}}}\exp \left( { - \frac{{{{{({{y}_{{lp}}} - {{{( - 1)}}^{{{{\alpha }_{p}}}}}{{AT} \mathord{\left/ {\vphantom {{AT} 2}} \right. \kern-0em} 2})}}^{2}}}}{{{{{{N}_{0}}T} \mathord{\left/ {\vphantom {{{{N}_{0}}T} 2}} \right. \kern-0em} 2}}}} \right)} , \\ \end{gathered} $

где ${{\alpha }_{p}},$ $p = 0,1,...,m - 1$ – двоичные коэффициенты при представлении соотношением (2) элемента поля α в виде многочлена степени m. Видно, что при увеличении объема полей (при увеличении объема ортогональных функций Уолша) вероятности ошибки ${{P}_{{{\text{ош}}}}}$ монотонно уменьшаются для фиксированных значений ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}\,:$ вероятность ${{P}_{{{\text{ош}}}}} = {{10}^{{ - 4}}}$ достигается при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 7.25$ дБ для поля $GF({{2}^{3}})$, при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 6.1$ дБ для поля $GF({{2}^{4}})$ и при ${{{{E}_{{\text{б}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{б}}}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 4.5$ дБ для поля $GF({{2}^{6}})$.

ЗАКЛЮЧЕНИЕ

Приведено описание алгоритма оптимального посимвольного приема сигнальных конструкций на основе сигнальных “созвездий” и блоковых помехоустойчивых кодов в недвоичных полях $GF({{2}^{m}})$, формируемых по модулю неприводимого многочлена степени m. Правило посимвольного приема минимизирует вероятность ошибки на кодовый символ в отличие от известного правила максимального правдоподобия, минимизирующего вероятность ошибки на кодовое слово. При реализации правила посимвольного приема вычисляются апостериорные вероятности кодовых символов, эквивалентные “мягким” решениям, используемым в алгоритмах итеративного приема наиболее эффективных кодовых конструкций, например, блоковых турбокодов, турбоподобных кодов.

Основу разработанного алгоритма посимвольного приема составляет спектральное преобразование в базисе Уолша-Адамара, размерность которого определяется размерностью поля ${{2}^{m}}$. Результирующая сложность разработанного алгоритма посимвольного приема определяется размерностью дуального кода, что обусловливает перспективность его применения для блоковых помехоустойчивых кодов с высокой кодовой скоростью (с низкой избыточностью).

Исследование вероятностных характеристик рассматриваемого алгоритма посимвольного приема произведено путем его моделирования для сигнальных конструкций на основе “созвездия” ФМ2 сигналов и ортогональных функций Уолша и высокоскоростных кодов с проверкой на четность в полях $GF(2),$ $GF({{2}^{3}}),$ $GF({{2}^{4}}),$ $GF({{2}^{6}}).$ Показано, что при увеличении размерности поля $m$ повышается помехоустойчивость передачи информации по каналу АБГШ, в частности, для вероятности ошибки на кодовое слово ${{P}_{{{\text{ош}}}}} = {{10}^{{ - 4}}}$ энергетический выигрыш достигает 0.4 дБ для поля $GF({{2}^{6}})$ по отношению к полю $GF(2)$.

Разработка алгоритмов итеративного приема на основе рассмотренного алгоритма оптимального посимвольного приема для эффективных кодовых конструкций, например для блоковых турбокодов, формируемых на основе блоковых кодов в недвоичных полях $GF({{2}^{m}}),$ представляет перспективное направление исследований.

Список литературы

  1. Johnson S.J. Iterative Error Correction: Turbo, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge: Univ. Press, 2010.

  2. Бакулин М.Г., Крейнделин В.Б., Панкратов Д.Ю. Технологии в системах радиосвязи на пути к 5G. М.: Горячая линия-Телеком, 2018.

  3. Ping Li, Chan S., Yeng K.L. // Electronic Lett. 1997. V. 33. № 19. P. 1614.

  4. Назаров Л.Е., Головкин И.В. // Журн. радиоэлектроники. 2011. № 1. http://jre.cplire.ru/jan11/3/ text.pdf.

  5. Назаров Л.Е., Батанов В.В., Кузнецов О.О. // Журн. радиоэлектроники. 2014. № 9. http://jre.cplire.ru/ jre/sep14/1/text.pdf.

  6. Li J., Narayanan R., Kurtas E., Georghiades C.N. // IEEE Trans. 2002. V. COM-50. № 5. P. 723.

  7. Farhadi G., Jamali S.H. // IEEE Trans. 2006. V. COM-54. № 9. P. 1643.

  8. Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.: Эко-Трендз, 2005.

  9. Bahl L.R., Cocke J., Jelinek F., Raviv J. // IEEE Trans. 1974. V. IT-20. № 3. P. 284.

  10. Haзapoв Л.E. // PЭ. 2002. T. 47. № 12. C. 1474.

  11. Kaipa K. // IEEE Commun. Lett. 2018. V. 22. № 11. P. 2210.

  12. Ben-Haim X., Litsyn S.A. // Adv. Mathem. Commun. 2007. V. 1. № 1. P. 83.

  13. Смольянинов В.М., Назаров Л.Е. // РЭ. 1999. Т. 44. № 7. С. 838.

  14. Назаров Л.Е., Шишкин П.В. // Журн. радиоэлектроники. 2018. № 12. http://jre.cplire.ru/jre/dec18/ 10/text.pdf.

  15. Lin S.-J. // IEEE Trans. 2018. V. COM-66. № 8. P. 3235.

  16. Steiner F., Bocherer G., Liva G. // IEEE Commun.Lett. 2018. V. 22. № 11. P. 2210.

  17. Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера, 2005.

  18. Yeo S., Park I.-C. // IEEE Trans. 2018. V. IT-64. № 7. P. 5170.

  19. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир, 1976.

  20. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М.: Гостехтеориздат, 1955.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал