Радиотехника и электроника, 2020, T. 65, № 11, стр. 1101-1108

ВВЕДЕНИЕ

Под сегментацией сигнала в задачах автоматического распознавания речи (АРР) традиционно понимают [1, 2] ее фонемную или, иными словами [3], фонологическую разновидность, целью которой является on-line-членение речевого потока на последовательность минимальных (не делимых далее) речевых единиц типа фонем и их аллофонов. Это важнейшая составная часть обработки речевого сигнала в системах самого разного назначения [4–6]: от голосового управления и идентификации дикторов до речевой аналитики, и биометрии, которая между тем зачастую недооценивается специалистами. Причина сказанного кроется в самом понятии фонологической сегментации, предшествующей этапу распознавания (парадигматической идентификации [3]) вычлененных сегментов сигнала в рамках “отложенной” [7] сегментации речи. Так, например, в работах [8, 9] применен простейший способ фонологической сегментации: членение речевого сигнала на речевые фреймы (отрезки сигнала) предельно малой длительности τ = 10…20 мс, которая согласована с периодом основного тона устной речи типичного диктора [9]. Однако в этом случае возникает [10] острая проблема малых выборок наблюдений и вслед за ней обостряется проблема множественных сравнений [11]. Как следствие, приходится констатировать [7, 12], что применительно к русской слитной речи с большим словарем указанная задача до настоящего времени не решена совсем или решена недостаточно эффективно. Между тем, как это показано в работах [13, 14] на ряде примеров из практики, при применении сегментации речевого сигнала с объединением однородных фреймов в однофонемные сегменты речи удается в значительной степени преодолеть проблему малых выборок, а вслед за ней – и множественных сравнений в задачах АРР. Поэтому можно утверждать [15–17], что полноценная фонологическая сегментация является в настоящее время наиболее перспективным способом повышения эффективности АРР на стадии первичной обработки речевого сигнала [7]. Первостепенное значение при этом имеет вопрос о выборе критерия сегментации [3]. Поэтому актуальность темы проведенного далее исследования представляется очевидной.

В основу предложенного в статье критерия положен принцип его гарантированного уровня значимости в задаче обнаружения “разладки” случайного сигнала [18–21] на интервале длительностью в один речевой фрейм. В отличие от известных критериев [13–17] он напрямую не связан с понятием случайной погрешности статистических оценок параметров распределений и нацелен на применение в условиях априорной неопределенности в отношении тонкой структуры речевого сигнала [22].

1. ПОСТАНОВКА ЗАДАЧИ

Следуя статистической теории “разладки” [19], воспользуемся универсальной [9–11] гауссовой аппроксимацией $P({{X}_{k}}) = {\text{Nor}}{{{\text{m}}}_{n}}{\text{(}}{{{\mathbf{R}}}_{k}}{\text{) }}$ многомерного (n-мерного) закона распределения наблюдаемого сигнала $x(t)$ в пределах одного (текущего) речевого фрейма ${{X}_{k}}$ фиксированной длительности τ = const, где k = 1, 2, …. Здесь ${{{\mathbf{R}}}_{k}} \triangleq {\mathbf{E}}\left( {{{{\mathbf{x}}}_{k}}{\mathbf{x}}_{k}^{Т}} \right)$ – автокорреляционная ($n \times n$)-матрица (АКМ) речевого сигнала, который предполагается предварительно центрированным; ${{{\mathbf{x}}}_{k}}$ – n-вектор (столбец) его последовательных отсчетов (символами ${\mathbf{E}}\left( \cdot \right),$ $ \triangleq $ и ${{( \cdot )}^{T}}$ обозначены соответственно математическое ожидание, равенство по определению и операция транспонирования векторов). Задача формулируется в терминах проверки статистических гипотез

о равенстве друг другу АКМ речевого сигнала в двух соседних фреймах X_k – 1 и X_k. Она решается пошагово. Здесь k – номер шага с инициализацией в виде равенства k = 1. По результатам решения задачи (1) на каждом очередном шаге k текущий речевой фрейм X_k либо объединяется с предыдущим фреймом X_k – 1 в один однородный сегмент речевого сигнала, либо, напротив, обособляется в качестве первого фрейма очередного сегмента в речи диктора. Во втором случае номер k текущего речевого фрейма вновь устанавливается равным единице.

Задача состоит, таким образом, в последовательной – от фрейма к фрейму – проверке статистических гипотез (1) в пределах интервала наблюдения над речевым сигналом $x(t).$ При этом инициализацией вычислительной процедуры (1) может служить равенство ${{{\mathbf{R}}}_{0}} = {\text{dia}}{{{\text{g}}}_{n}}\left( {\sigma _{0}^{2}} \right),$ где символом ${\text{dia}}{{{\text{g}}}_{n}}{\text{(}} \cdot )$ обозначена диагональная $(n \times n)$-матрица с дисперсией $\sigma _{0}^{2}$ фонового (из речевых пауз) шума на главной диагонали.

В условиях априорной неопределенности, когда матрицы ${{{\mathbf{R}}}_{k}}$ и ${{{\mathbf{R}}}_{{k - 1}}}$ заранее неизвестны, воспользуемся их оценками максимального правдоподобия по формуле корреляционного выборочного момента [22–24]

где x_k,i – i-й (парциальный) n-вектор последовательных отсчетов речевого сигнала; M $ \triangleq $ [N/n] (целая часть числа) – количество непересекающихся парциальных векторов в пределах одного (наблюдаемого) фрейма; N = Fτ – суммарный объем выборки из речевого сигнала на интервале в один фрейм; F – частота его дискретизации. При этом размерность векторов ${{{\mathbf{x}}}_{{k,i}}},$ i ≤ M, определяется наблюдателем в зависимости от полосы частот [F_min; F_max] в спектре речевого сигнала [4]: n = 0.5F_max/F_min = 0.25F/F_min. Так, при частоте дискретизации F = 8 кГц (согласована с полосой частот стандартного телефонного канала связи [11]), F_min. = (100…200) Гц и длительности фрейма τ = 10 мс будем иметь n = 10…20, N = 80 и, следовательно, получаем M = (4…8) парциальных выборок для вычислений матрицы ${{{\mathbf{S}}}_{j}}.$ А это явный признак остроты проблемы малых выборок наблюдений [10]. Поэтому воспользуемся для решения задачи (1) асимптотически минимаксным критерием отношения правдоподобия с гарантированным уровнем значимости [22].

2. СИНТЕЗ АЛГОРИТМА

Определим в рамках указанного критерия критическую область n-мерного выборочного пространства согласно решающему правилу общего вида [19]:

где $p({{X}_{0}}{\text{|}}{{H}_{0}}) = p({{X}_{{k - 1}}}{\text{|}}{{H}_{0}})p({{X}_{k}}{\text{|}}{{H}_{0}}),$ $p({{X}_{0}}{\text{|}}{{H}_{1}}) = $ $ = p({{X}_{{k - 1}}}{\text{|}}{{H}_{1}})p({{X}_{k}}{\text{|}}{{H}_{1}})$ – функции правдоподобия соответственно гипотез H₀ и H₁ для объединенной выборки наблюдений ($P\left( { \cdot | \cdot } \right)$ – условная вероятность случайного события, символом sup обозначена верхняя граница функции на множестве допустимых АКМ R_j, j = k – 1, k). Уровень значимости данного критерия $\alpha \triangleq P\left( {W{\text{|}}{{H}_{0}}} \right)$ регулируется выбором порогового уровня ${{{\lambda }}_{0}}$ в правой части выражения (3). Применительно к рассматриваемой задаче автоматической сегментации речи такая регулировка позволяет менять в широких пределах и при этом гарантировать выполнение требований наблюдателя [6] к степени однородности речевого сигнала в пределах каждого отдельного фонетического сегмента данных.

В условиях априорной неопределенности наблюдателю неизвестны распределения $p({{X}_{j}}{\text{|}}{{H}_{1}})$ и $p({{X}_{j}}{\text{|}}{{H}_{0}}).$ Поэтому, следуя общесистемному принципу максимума энтропии [23–26], раскроем правило принятия решений (3) в расчете на максимально неопределенный случай: статистической независимости выборок x_j, i, i ≤ M, в совокупности. Для этого случая запишем систему равенств [5]

Или, после логарифмирования, будем иметь

Здесь ${{{\mathbf{S}}}_{0}} = 0.5\left( {{{{\mathbf{S}}}_{{k - 1}}} + {{{\mathbf{S}}}_{k}}} \right)$ – оценка максимума правдоподобия для АКМ речевого сигнала по объединенной выборке наблюдений X₀, где c = = ln(2π) = const (символами |·| и tr(·) обозначены соответственно определитель и след квадратной (n × n)-матрицы). Путем несложных вычислений [19] отсюда получаем

При этом было учтено [22], что на множестве допустимых ковариаций выборочных данных X_k и X_k – 1 верхняя граница функций правдоподобия достигается при выборе АКМ R_k и R_{k– 1} равными их оценкам максимума правдоподобия S_k и S_{k– 1} соответственно, если справедлива гипотеза H₁, и R = S₀ – в противном случае. Здесь все АКМ, как и их выборочные оценки, предполагаются неособенными. Проблема их обусловленности на практике преодолевается [4] путем оптимизации параметров n и M и применением современных вычислительных процедур корреляционно-спектрального анализа [23].

Полученные выражения (4) определяют общую формулировку для оптимальной решающей статистики вида

где ${{H}_{n}}({{{\mathbf{S}}}_{j}}) = 0.5\left( {ln\left| {{{{\mathbf{S}}}_{j}}} \right| + nc} \right)$ – дифференциальная (по Шеннону) энтропия [24] n-мерного гауссова распределения вероятностей с АКМ, равной ${{{\mathbf{S}}}_{j}},$ $j = 0,$ $k - 1,$ $k.$ Решение здесь принимается по принципу допустимых различий между двумя эмпирическими распределениями, ${\text{Nor}}{{{\text{m}}}_{n}}{\text{(}}{{{\mathbf{S}}}_{{k - 1}}}{\text{)}}$ и ${\text{Nor}}{{{\text{m}}}_{n}}{\text{(}}{{{\mathbf{S}}}_{k}}{\text{),}}$ в теоретико-информационном смысле._. В идеальном случае, когда выполняется система равенств S₀ = S_{k– 1} = S_k, имеем равенство $\widetilde {\lambda }({{X}_{0}}) = 0.$ Но это, повторяем, только в идеальном случае. В реальности будем иметь S_{k– 1} ≠ S_k и, следовательно, выполняется неравенство ${\tilde {\lambda }}({{X}_{0}}) \ne 0.$ Его характер уточняется в следующем теоретическом положении.

Утверждение. В условиях вывода равенства (5) выполняется соотношение ${\tilde {\lambda }}({{X}_{0}}) \geqslant 0.$

Доказательство. Отталкиваясь от выражения (5), запишем

где

– величина информационного рассогласования по Кульбаку–Лейблеру [24] двух гауссовых распределений с АКМ ${{{\mathbf{S}}}_{0}}$ и ${{{\mathbf{S}}}_{j}},$ $j = k - 1,$ $k,$ обладающая свойством ${{\Theta }_{{{0 \mathord{\left/ {\vphantom {0 j}} \right. \kern-0em} j}}}} \geqslant 0$ и с равенством нулю в случае равенства двух рассматриваемых АКМ друг другу. Отсюда вытекает справедливость сформулированного выше утверждения.

Следствие. Доказанное утверждение приводит к следующей импликации: $\widetilde {\lambda }({{X}_{0}}) \geqslant 0 \Rightarrow $ $ \Rightarrow \left\{ {ln\left| {{{{\mathbf{S}}}_{0}}} \right| \geqslant \ln \left| {{{{\mathbf{S}}}_{{k - 1}}}} \right|} \right\} \vee \left\{ {{\text{l}}n\left| {{{{\mathbf{S}}}_{0}}} \right| \geqslant \ln \left| {{{{\mathbf{S}}}_{k}}} \right|} \right\}$ – достоверное событие, где символом $ \vee $ обозначен квантор объединения двух случайных событий, или их дизъюнкция.

На основании последнего утверждения и выражения (5) подоптимальное правило принятия решений в задаче проверки статистических гипотез (1) может быть представлено в виде

При этом учитываются оба возможных варианта проявления различий в эмпирических распределениях ${\text{Nor}}{{{\text{m}}}_{n}}{\text{(}}{{{\mathbf{S}}}_{{k - 1}}}{\text{)}}$ и ${\text{Nor}}{{{\text{m}}}_{n}}{\text{(}}{{{\mathbf{S}}}_{k}}{\text{):}}$ в сторону как увеличения, так и уменьшения их энтропий ${{H}_{n}}({{{\mathbf{S}}}_{k}})$ и ${{H}_{n}}({{{\mathbf{S}}}_{{k - 1}}})$ по отношению к энтропии ${{H}_{n}}({{{\mathbf{S}}}_{0}})$ распределения объединенной выборки ${{X}_{0}}.$ Пороговый уровень ${{{\tilde {\lambda }}}_{0}} > 0$ служит здесь регулятором уровня значимости $\alpha ({{\delta }_{0}}).$ Указанная регулировка является существенным преимуществом решающего правила (6) по сравнению с его известными аналогами. Проиллюстрируем данное преимущество на конкретном примере практической реализации алгоритма (6) с использованием авторегрессионной модели речевого сигнала и математического аппарата авторегрессионного анализа [23, 25].

3. ПРИМЕР ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ

Авторегрессионная модель (АР-модель) речевого сигнала [23]

в пределах j-го речевого фрейма X_j однозначно определяется своим вектором АР-коэффициентов $\left\{ {{{a}_{q}}(i),\,\,i = \overline {1,q} } \right\}$ заданного порядка q ≤ n и дисперсией $\sigma _{j}^{2} = {\text{const}}$ порождающего процесса $\left\{ {{{{\eta }}_{j}}(t)} \right\}$ типа белого гауссова шума в дискретном времени $t = {\text{1,2,}}....$ С одной стороны, модель (7) органично сочетается с голосовым механизмом человека (имеется в виду известная [4, 6] модель “акустической трубы”), с другой – существенно расширяет возможности программно-аппаратной реализации критерия (6). С указанной точки зрения представляет интерес асимптотическое равенство [25, 26]: ${{\left. {{{n}^{{ - 1}}}\ln \left| {{{{\mathbf{S}}}_{j}}} \right|} \right|}_{{n \to \infty }}} = {\text{ln}}\sigma _{j}^{2}.$ Величина ${\sigma }_{j}^{2}$ здесь характеризует [23] минимально достижимую дисперсию погрешности линейного предсказания случайного временного ряда (7) на один шаг в будущее. Теоретически данное равенство с достаточной степенью точности обусловлено соотношением N $ \gg $ q [25].

В самом деле, порядок АР-модели на практике [10, 11] не превышает q = 10…20, притом что размер АКМ речевого сигнала в задачах АРР ограничен только объемом N = 80…120 речевого фрейма. Критерий (6) в таком случае может быть переписан следующим образом:

– через объединение двух случайных событий ${{A}_{{k - 1}}}$ и ${{A}_{k}}$ для принятия гипотезы ${{H}_{1}}.$ Или, что эквивалентно, – в виде условия к максимуму отношения двух дисперсий

погрешности линейного предсказания речевого сигнала в текущем времени k = 1, 2, … Здесь ${{\tilde {\delta }}_{0}} > 1$ – пороговый уровень, а символом $\left( \cdot \right)$ обозначена выборочная оценка дисперсии погрешности

линейного предсказания q-го порядка в пределах j-го речевого фрейма.

Полученный результат (8), (9) – это известная [26] формулировка критерия проверки статистических гипотез о равенстве дисперсий откликов двух обеляющих фильтров на речевой сигнал. Их назначение – декорреляция сигнала ${{{\varepsilon }}_{j}}(t)$ на выходе. Указанная декорреляция достигается, если вектор АР-коэффициентов $\left\{ {{{a}_{q}}(i)} \right\}$ фильтра (9) предварительно адаптирован под анализируемый сигнал $\left\{ {x(t)} \right\}$ на интервале его наблюдения в один или два фрейма подряд (при равенстве j = 0). Для этого в теории авторегрессионного анализа разработан эффективный математический аппарат. В качестве примера можно привести высокоскоростную вычислительную процедуру Берга–Левинсона вида [23]

при ее инициализации системой равенств ν₀(t) = $ = {{{\eta }}_{0}}(t - 1) = x(t),$ $t = 1,2,...$ Финальные значения данной рекурсии (10) при m = q составят необходимую базу априорных данных $\left\{ {{{a}_{m}}(i)} \right\}$ для вычисления погрешности линейного предсказания согласно выражению (9). Оценка ее дисперсии может быть получена по формуле средней квадратичной величины:

– в зависимости от анализируемого отрезка речевого сигнала $x(t).$

Полученный результат (11) совместно с выражениями (8)–(10) определяет адаптивный алгоритм сегментации речевого сигнала $x(t)$ в пределах каждого отдельного речевого фрейма X_k. Его эффективность характеризуется главным образом гарантированным уровнем значимости.

4. АНАЛИЗ ЭФФЕКТИВНОСТИ

Следуя известной методике вычислений [19, 26] и учитывая при этом ${{{\chi }}^{2}}$-распределение статистик под знаком суммы в правой части (11), а также пренебрежимо малую вероятность случайного события $P\left( {\left. {{{A}_{{k - 1}}} \wedge {{A}_{k}}} \right|{{H}_{0}}} \right),$ где $ \wedge $ – символ логической конъюнкции, запишем выражение для вероятности ошибки первого рода

при применении критерия (8). Здесь ${{F}_{{2N - q;{\text{ }}N - q}}}({{\tilde {\delta }}_{0}})$ – интегральная функция F-распределения (Фишера) с (2N – q; N – q) степенями свободы, ${{\tilde {\delta }}_{0}}$ – установленный наблюдателем пороговый уровень решающей статистики. Указанное распределение подробно табулировано и широко представлено в самых разных источниках, включая электронные таблицы Excel. Например, при N = 80, q = 20 для уровня значимости ${{\alpha }_{0}}$ = 0.10 (10%) по этим таблицам с помощью функции FРАСПОБР(0.05; 2N – q; N – q) получим порог ${{\tilde {\delta }}_{0}},$ равный квантилю ${{F}_{{140;\,60;\,0.95}}}$ = 1.46 заданного порядка ${{1 - {{\alpha }_{0}}} \mathord{\left/ {\vphantom {{1 - {{\alpha }_{0}}} 2}} \right. \kern-0em} 2} = 0.95.$ При увеличении объема выборки до N = 120 (при длительности речевого фрейма 15 мс) и при сохранении прежнего уровня значимости пороговый уровень может быть понижен до 1.33. Чем меньше величина ${{\tilde {\delta }}_{0}},$ тем строже требования наблюдателя к степени однородности объединенной выборки $\left\{ {{{X}_{{k - 1}}};{{X}_{k}}} \right\}.$ А установленный при этом уровень значимости ${{{\alpha }}_{0}}$ характеризует требования наблюдателя иного рода, а именно: к вероятности ложной отбраковки текущего речевого фрейма ${{X}_{k}}$ как недостаточно четкого, маргинального.

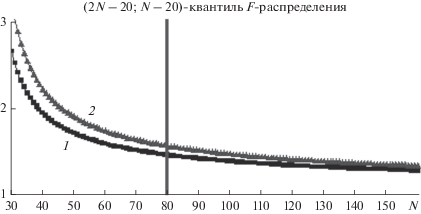
В идеале следует стремиться к минимизации одновременно и ${{\tilde {\delta }}_{0}},$ и ${{{\alpha }}_{0}}.$ Однако эти требования противоречат друг другу, и поэтому необходимо найти компромисс. Обычно поиск такого компромисса – это самостоятельная задача [7], но только не в нашем случае, когда искомый компромисс очевиден: равенство (12) связывает между собой обе рассматриваемые величины. Отметим при этом монотонность функции распределения ${{F}_{{2N - q;{\text{ }}N - q}}}({{\tilde {\delta }}_{0}}).$ Поэтому, устанавливая значение ${{\tilde {\delta }}_{0}}$ в правой части (12) из условия достижения равенства ${{{\alpha }}_{k}} = {{{\alpha }}_{0}},$ наблюдатель гарантирует требуемый уровень значимости критерия (8) при минимальном пороговом уровне. О качестве достигаемого в данном случае компромисса свидетельствует рис. 1. На нем представлены два графика зависимости ($2N - q;$ $N - q$)-квантиля F-распределения от объема выборки N при заданном порядке q = 20 АР-модели речевого сигнала (7) для двух значений уровня значимости ${{\alpha }_{0}}:$ 5% и 10%. Хорошо видно, что уже при N = 80 обе кривые практически утрачивают свою динамику. А это означает, что конечного объема выборки N = 80 на интервале наблюдения речевого сигнала в один стандартный фрейм¹¹ оказывается вполне достаточно для достижения эффекта гарантированного уровня значимости без существенных потерь в точности сегментации. Сделанный вывод подтверждается результатами проведенного эксперимента (см. далее).

Рис. 1.

Зависимости квантиля F-распределения от объема выборки N при различном уровне значимости: ${{\alpha }_{0}}$ = 0.1 (кривая 1) и 0.05 (кривая 2).

5. ПРОГРАММА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ

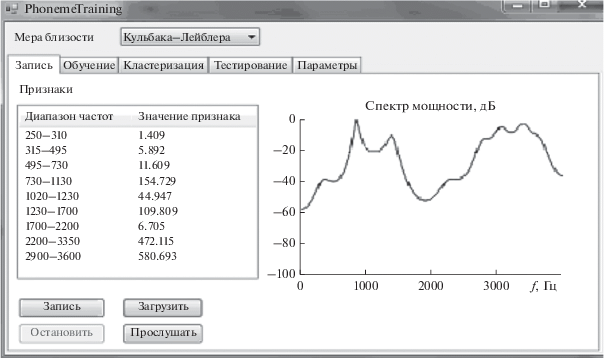
В подтверждение результатов теоретического анализа был поставлен и проведен эксперимент с использованием авторской компьютерной программы “Phoneme Training”²². На рис. 2 показан скриншот ее главного окна. В правой части отображен график оценки спектра мощности гласного звука русской речи “а” методом Берга [23]. При учете его высоких динамических свойств сначала была исследована степень однородности реальных речевых сигналов в обоснование актуальности проведенного выше исследования.

Рис. 2.

Скриншот главного окна компьютерной программы “Phoneme Training”.

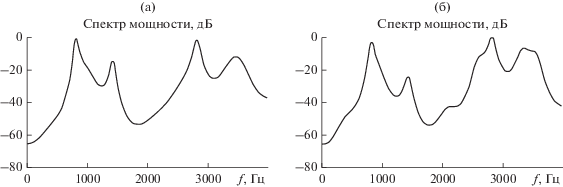
С этой целью в пределах гласных звуков речи достаточно большой длительности (секунды) от контрольного диктора (автора статьи) была сформирована представительная [27] последовательность речевых фреймов длительностью 10 мс каждый. По ним с использованием рекуррентной процедуры (10) были рассчитаны спектральные оценки Берга достаточно большого порядка q = 20, которые затем сопоставлялись между собой. Типичные две из них для фонемы “а” представлены на рис. 3. Из их сравнения друг с другом можно сделать вывод о существенной неоднородности речевого сигнала в пределах даже одного звука речи диктора. Это следствие известного [28] эффекта внутридикторской вариативности устной речи. Задача сегментации речевого сигнала приобретает в свете сказанного очевидное практическое значение.

Рис. 3.

Скриншот фрагмента главного окна программы “Phoneme Training” с графиком оценки спектра мощности сигнала фонемы “А” в пределах двух разнесенных во времени фреймов.

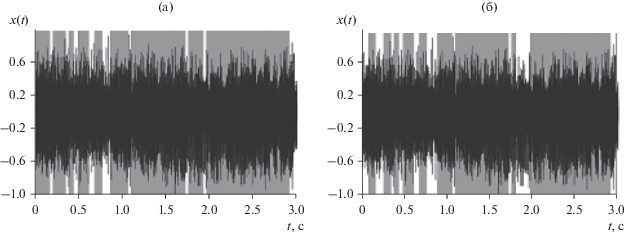
На втором этапе эксперимента программа “Phoneme Training” была переведена для работы в режим “Тестирование”, в котором однофонемные сигналы были подвергнуты автоматической сегментации согласно алгоритму (8)–(11). При этом пороговый уровень разладки ${{\tilde {\delta }}_{0}}$ варьировался в широких пределах с помощью вкладки “Параметры” в меню главного окна (см. рис. 2). Полученные результаты отражены в виде двух временных диаграмм фонемы “а” на рис. 4а, 4б: при ${{\tilde {\delta }}_{0}}$ = 1.45 и ${{\tilde {\delta }}_{0}}$ = 1.35 соответственно. Светлым фоном на рисунке отмечены маргинальные фреймы речевого сигнала, которые не прошли проверку на требуемую степень однородности согласно критерию (8). Их относительная доля в речевом сигнале примерно равна 10% в первом, менее строгом варианте критерия, и 20% – во втором варианте. Оба полученных результата хорошо согласуются с их теоретическими оценками из выражения (12): α_k = 0.11 и α_k = 0.19 соответственно. При этом статистическая погрешность измерений в ее относительном выражении ${\varepsilon } = {2 \mathord{\left/ {\vphantom {2 {\sqrt {{{10T} \mathord{\left/ {\vphantom {{10T} \tau }} \right. \kern-0em} \tau }} }}} \right. \kern-0em} {\sqrt {{{10T} \mathord{\left/ {\vphantom {{10T} \tau }} \right. \kern-0em} \tau }} }}$ [27] с доверительной вероятностью 0.95 (почти достоверное событие) не превысила в данном случае 3.6%.

Рис. 4.

Скриншот рабочего окна программы в режиме “Тестирование” при двух разных значениях порогового уровня: ${{\tilde {\delta }}_{0}}$ = 1.45 (а) и ${{\tilde {\delta }}_{0}}$ = 1.35 (б).

6. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

При анализе письменного текста на русском языке мы опираемся на наши точные знания в отношении количественного и качественного состава используемой фонологической системы, а также закономерностей ее функционирования в разговорной речи. Этими знаниями мы пользуемся, например, при транскрибации потока речи. Однако если мы анализируем звучащий текст на неизвестном языке и нам недоступна полная информация, относящаяся к его тонкой структуре, то можно либо, опираясь на наш лингвистический опыт, давать участкам речевого потока приблизительную интерпретацию в рамках Международного фонетического алфавита³³, либо, обратившись к акустическим понятиям [4], линейно членить речевой сигнал на некие повторяющиеся минимальные единицы и давать им определенные метки. Очевидно, что второй подход со всех точек зрения наиболее информативен и универсален. Именно он и был применен в рамках проведенного выше исследования.

Основная проблема при таком подходе состоит в том [28], что разговорная речь по своим акустическим характеристикам широко варьируется, причем не регулярным образом, не только от одного носителя языка к другому, но и в пределах одного речевого потока от одного диктора. В указанных условиях становится проблематичной сама идея выделения повторяющегося набора фонетических единиц. Кроме того, их длительность не превышает на практике нескольких десятков миллисекунд, и это главное препятствие для применения традиционных методов теоретической информатики к разговорной речи.

В поисках путей решения перечисленных выше проблем в работах [5, 6] само понятие “фонема” было строго определено в теоретико-информационном смысле как множество однородных фонетических единиц, объединенных в кластер по критерию минимального информационного рассогласования в метрике Кульбака–Лейблера. Условно говоря, человеческий мозг объединяет и запоминает в себе как нечто целое (в виде абстрактного образа) разные образцы (произношения) каждой отдельной фонемы в соответствующей “сфере” своей памяти вокруг абстрактного “центра” с заданным “радиусом”. Этот радиус и определяет в конечном итоге [10] величину порогового уровня ${{\tilde {\delta }}_{0}}$ в предложенном критерии (8). Нетрудно понять, что благодаря такому определению одновременно решается множество проблем в области автоматической обработки речи: и ее вариативности, и априорной неопределенности, и, наконец, проблемы малых выборок наблюдений.

ЗАКЛЮЧЕНИЕ

Таким образом, предложен новый критерий автоматической сегментации речевого сигнала для систем АРР повышенной точности и надежности. Этот критерий без существенных потерь в степени однородности выделяемых сегментов речи гарантирует стабильный уровень значимости при обработке речевых фреймов малой длительности в предположении, что парциальные выборки в совокупности статистически независимы.

Работа выполнена в рамках Программы фундаментальных исследований Национального исследовательского университета “Высшая школа экономики” (НИУ ВШЭ).