Радиотехника и электроника, 2020, T. 65, № 2, стр. 107-117
Замедляющая система типа диафрагмированный прямоугольный волновод
М. В. Давидович *
Саратовский национальный исследовательский государственный университет им. Н.Г. Чернышевского
410012 Саратов, ул. Астраханская, 83, Российская Федерация
* E-mail: davidovichmv@info.sgu.ru
Поступила в редакцию 11.12.2018
После доработки 11.12.2018
Принята к публикации 10.01.2019
Аннотация
Предложены быстрые и достаточно точные модели для замедляющих систем (ЗС) типа двойные сдвинутые гребенки в прямоугольном экране и ЗС типа петляющий волновод на основе вычисления проводимости диафрагм в прямоугольном волноводе (ПВ). Получена проводимость емкостной диафрагмы в ПВ при электрической и магнитной широких стенках. Также предложены многомодовые модели на основе функционалов электрического и магнитного типов. Модели позволяют корректно учитывать потери. Рассчитана дисперсия двойной гребенки и петляющего волновода с бесконечно тонкими стенками.
1. ПОСТАНОВКА ЗАДАЧИ
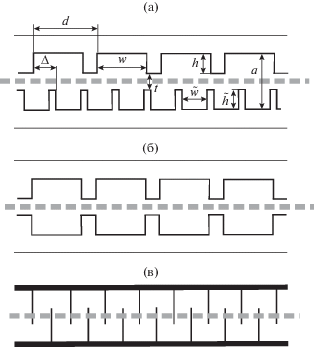
В лампах бегущего волновода (ЛБВ) терагерцового (ТГц) диапазона перспективны ленточные электронные пучки большой ширины и малой толщины с токами порядка 0.1…1.0 А и более, которые должны проходить через узкие в одном из поперечных направлений каналы [1‒6]. Для достижения приемлемой мощности в ТГц-микроэлектронике необходимы релятивистские ЛБВ (с анодным напряжением 20 кВ и более), поэтому высоких замедлений не требуется, и задача проектирования замедляющих систем (ЗС) состоит в увеличении рабочей полосы и сопротивления связи ${{R}_{с}}.$ Перспективными и достаточно технологичными ЗС для этого являются широкие двусторонние гребенки с симметричными относительно осевой плоскости $x = 0$ и со сдвинутыми по оси z гребнями в прямоугольном экране [1‒9]. На рис. 1а приведен вид такой ЗС со сдвигом гребенок и отношением их периодов 2 : 1, а на рис. 1в дан вид диафрагмированного волновода со сдвигом диафрагм на противоположных стенках на полпериода. Рис. 1б соответствует симметричной гребенке с конечной толщиной гребня. Сдвиг гребней на половину периода ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ (см. рис. 1в) приводит к ЗС с плоскостью зеркальной симметрии, что существенно расширяет полосу. Анализ ЗС на основе коммерческих пакетов программ требует весьма больших ресурсов, что делает оптимизацию достаточно затруднительной [5]. Поэтому задача получения быстрых алгоритмов важна. Ранее ЗС типа одиночная гребенка с бесконечно тонкими гребнями в прямоугольном волноводе (ПВ) рассматривалась в ряде работ, например [10‒12], где использовано разложение по пространственным гармоникам и сшивание в продольной плоскости. Метод также формулируется с использованием стационарных свойств функционала. В работах [7, 8] предложен метод периодически продолженных функций Грина (ФГ) ПВ и рассмотрен метод частичных областей (ЧО), приводящий к поверхностным интегральным уравнениям (ИУ) в продольных и поперечных сечениях. Модель и результаты расчета для двойной сдвинутой гребенки получены в работах [4, 6]. В них использован подход на основе разложения по пространственным гармоникам [10, 11] с учетом условия на ребре, что позволило получить быстрый алгоритм. Задача решена методом ЧО, приводящем к ИУ в продольном сечении. Для ЗС из сдвинутых гребенок (см. рис. 1а) несколько электродинамических моделей приведено в работе [9].
Рис. 1.
Виды ЗС типа гребенка: а – двойная сдвинутая гребенка с отношением периодов 2 : 1; б – симметричная гребенка; в – двойная сдвинутая гребенка с бесконечно тонкими диафрагмами и с перекрытием канала (петляющий волновод).
Цель данной работы – получение моделей на основе аналитических результатов, обладающих высокой точностью (существенно лучшей, чем у импедансных моделей типа [12, 13]) и меньшими вычислительными затратами, чем строгие модели типа [4, 6‒9], а также получение быстрых и строгих алгоритмов, позволяющих учитывать потери. В работе использованы как импедансный, так и адмитансный подходы для получения ИУ и функционалов двух типов: импедансных (относительно магнитного поля или поверхностной плотности тока на диафрагме), и адмитансных (относительно электрического поля в апертуре). Строгие модели получены для бесконечно тонких диафрагм, хотя метод с некоторыми усложнениями может быть распространен и на протяженные диафрагмы. Реально при учете диссипации считаем, что “бесконечно тонкая” диафрагма имеет толщину не менее нескольких скин-слоев.
1. БЫСТРАЯ ПРИБЛИЖЕННАЯ МОДЕЛЬ
Замедляющая система рис. 1 а может быть использована для управления полосой и повышения ${{R}_{с}}$. Для периодичности периоды гребенок кратные (для ЗС1 их отношение 2 : 1). Более мелкую гребенку можно рассматривать как импедансную поверхность [13], управляющую дисперсией и ${{R}_{с}}$. Области брегговских резонансов второй гребенки более высокочастотные, что и объясняет расширение полосы. ЗС, представленные на рис. 1а–1в, можно рассматривать как диафрагмированные прямоугольные волноводы (ПВ). Простые модели таких ЗС получаются для бесконечно тонких диафрагм, для которых ${{R}_{с}}$ максимально. Пренебречь толщиной $\delta $ диафрагм вполне можно, если ${\delta \mathord{\left/ {\vphantom {\delta d}} \right. \kern-0em} d} < 0.1.$ Сдвинутые на ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ гребенки (верхняя относительно нижней) обладают плоскостью скользящей симметрии. Это приводит к пересечению прямых и обратных дисперсионных ветвей при фазовом сдвиге ${{k}_{z}}d = \Psi = \pi $ и к существенному расширению полосы [3‒6]. У симметричной гребенки (рис. 1б) при $\Psi = \pi $ возникает запрещенная зона [4]. В случае $h < {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ при сдвиге возникает перекрытие канала (рис. 1в). В этом случае двойная симметричная сдвинутая на ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ гребенка с диафрагмами толщины $\delta = {d \mathord{\left/ {\vphantom {d 8}} \right. \kern-0em} 8}$ есть ЗС типа петляющий волновод. В диафрагмах необходим пролетный канал (см. штриховые прямые на рис. 1а–1в). При меньших толщинах диафрагм ЗС также ведет себя как петляющий волновод с существенно большим замедлением, при этом толщину диафрагм-стенок желательно уменьшать. Это также ведет к увеличению ${{R}_{c}}$, поскольку увеличивается область пространства взаимодействия. По оси y ПВ имеет размер $b \gg a,$ что приводит к низкочастотной отсечке при волновом числе ${{k}_{0}} = {{k}_{y}} = {\pi \mathord{\left/ {\vphantom {\pi b}} \right. \kern-0em} b}.$ ЗС без отсечки в виде металлизированной сверху диэлектрической гребенки рассмотрена в работах [7, 8]. Для симметричной ЗС2 возможны решения с электрической и магнитной стенками в центре при $x = 0.$ Первый случай эквивалентен одиночной гребенке в ПВ с половинным размером ${a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ [14], а второй – одиночной гребенке в ПВ с половинным размером и с широкой магнитной стенкой. Первый случай имеет меньшую величину ${{R}_{с}}$ и не интересен. Второй требует решения для диафрагмы, которое отсутствует в литературе и далее будет получено. Для моды в симметричной ЗС2 с магнитной стенкой в центре отсечка имеет место при ${{k}_{0}} = \pi \sqrt {{{b}^{{ - 2}}} + {{a}^{{ - 2}}}} .$ Она возбуждается высшей модой ПВ, поэтому более интересна ЗС3.
В приближенной модели рассматриваем бесконечно тонкие диафрагмы без диссипации и не учитываем взаимодействие по высшим затухающим (эванесцентным) модам. При существенном расстоянии между диафрагмами этим взаимодействием можно пренебречь. При уменьшении расстояния взаимодействие растет, и при соединении диафрагм в одну приводит к следующему результату: вместо суммарной проводимости $2y$ от двух диафрагм в схеме реально имеем проводимость одиночной диафрагмы $y$. Поэтому корректируем проводимости взаимодействующих на расстоянии $\Delta $ двух одинаковых диафрагм как $\tilde {y} = y\left( {{{1 - \exp \left( { - \alpha \Delta } \right)} \mathord{\left/ {\vphantom {{1 - \exp \left( { - \alpha \Delta } \right)} 2}} \right. \kern-0em} 2}} \right),$ где $y = iB$ ‒ проводимость одиночной диафрагмы. Величина $\alpha $ определяет затухание, и в качестве нее удобно взять коэффициент затухания первой высшей моды ПВ, например,
Физический смысл введенной поправки ${\text{в}}$ том, что запасенная около отдельной диафрагмы реактивная мощность уменьшается в промежутке между двумя диафрагмами и делится между ними. Для периодических диафрагм этого нет. Строгая полевая модель приведена в конце работы. Она показывает, что в периодическом случае коррекция имеет другой вид. В случае $h < {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ при сближении диафрагм, расположенных на противоположных стенках, до нулевого расстояния проводимость каждой растет, поскольку апертура $s = a - h$ уменьшается до значения $s{\kern 1pt} ' = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2} - h$ при $\Delta = 0,$ при этом в зазоре возникает электрическая стенка. Если ${{y}_{0}}$ ‒ нормированная проводимость такой диафрагмы, то коррекцию можно сделать в виде $\tilde {y} = y + \left( {{{y}_{0}} - y} \right){{\exp }^{{ - \alpha \Delta }}}.$ Модель не работает, когда $h > {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ (диафрагмы пересекаются). (Более строгая коррекция приведена далее.) Для моды в симметричной ЗС2 с магнитной стенкой в центре отсечка имеет место при ${{k}_{0}} = \pi \sqrt {{{b}^{{ - 2}}} + {{a}^{{ - 2}}}} .$
Рассмотрим периодический диафрагмированный ПВ с LE-волнами [10, 14], для которых ${{E}_{y}} = 0$. Соответственно, вводим магнитный вектор Герца ${{{\mathbf{\Pi }}}^{m}} = {{{\mathbf{y}}}_{0}}\left( {{{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} \right){{H}_{y}},$ $k = \sqrt {k_{0}^{2} - k_{y}^{2}} .$ Зависимости от y компонент ${{E}_{x}}$, ${{H}_{y}}$ и ${{E}_{z}}$ в виде множителей $\sin \left( {{{k}_{y}}y} \right)$ и в виде $\cos \left( {{{k}_{y}}y} \right)$ у компонент ${{H}_{x}}$, ${{H}_{z}}$ опускаем. Тогда зависящие от x и z поля имеют вид
(1)
$\begin{gathered} {{E}_{x}}\left( {x,y} \right) = \frac{{i{{k}_{0}}{{Z}_{0}}}}{{{{k}^{2}}}}\frac{{\partial {{H}_{y}}\left( {x,z} \right)}}{{\partial z}}, \\ {{E}_{z}}\left( {x,y} \right) = \frac{{ - i{{k}_{0}}{{Z}_{0}}}}{{{{k}^{2}}}}\frac{{\partial {{H}_{y}}\left( {x,z} \right)}}{{\partial x}}, \\ \end{gathered} $(2)
$\begin{gathered} {{H}_{x}}\left( {x,y} \right) = \frac{{{{k}_{y}}}}{{{{k}^{2}}}}\frac{{\partial {{H}_{y}}\left( {x,z} \right)}}{{\partial x}}, \\ {{H}_{z}}\left( {x,y} \right) = \frac{{{{k}_{y}}}}{{{{k}^{2}}}}\frac{{\partial {{H}_{y}}\left( {x,z} \right)}}{{\partial z}}. \\ \end{gathered} $Согласно (1) импеданс LEm1-моды ${{\tilde {Z}}_{m}} = $ $ = \left( {{{{{k}_{0}}{{k}_{{zm}}}} \mathord{\left/ {\vphantom {{{{k}_{0}}{{k}_{{zm}}}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}} \right){{Z}_{0}},$ ${{Z}_{0}} = {{\left( {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Решение для регулярных по y неоднородностей ПВ следует из решения задачи для плоскопараллельного волновода (ППВ) (для которого ${{k}_{y}} = 0$) путем замены ${{k}_{0}} \to k = {{k}_{{z0}}}$ [14], что справедливо только для плоских неоднородностей. Для них нормированные адмитансы пропорциональны ${{{{{\tilde {Z}}}_{0}}} \mathord{\left/ {\vphantom {{{{{\tilde {Z}}}_{0}}} {{{{\tilde {Z}}}_{m}}}}} \right. \kern-0em} {{{{\tilde {Z}}}_{m}}}} = {k \mathord{\left/ {\vphantom {k {{{k}_{{zm}}}}}} \right. \kern-0em} {{{k}_{{zm}}}}}$ в ПВ и ${{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{{\tilde {Z}}}_{m}}}}} \right. \kern-0em} {{{{\tilde {Z}}}_{m}}}} = {{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} {{{k}_{{zm}}}}}} \right. \kern-0em} {{{k}_{{zm}}}}}$ в ППВ. Проводимость емкостной диафрагмы $y = iB$ с размером выступа h с центром апертуры при ${{x}_{0}}$ берем в виде $B = - \left( {{{2ka} \mathord{\left/ {\vphantom {{2ka} \pi }} \right. \kern-0em} \pi }} \right)$$\ln \left[ {\sin \left( {{{\pi h} \mathord{\left/ {\vphantom {{\pi h} {\left( {2a} \right)}}} \right. \kern-0em} {\left( {2a} \right)}}} \right)\sin \left( {{{\pi {{x}_{0}}} \mathord{\left/ {\vphantom {{\pi {{x}_{0}}} a}} \right. \kern-0em} a}} \right)} \right]$ [14]. Для нахождения проводимости симметричной емкостной диафрагмы с магнитной стенкой при $x = 0$ берем разложение ${{H}_{y}}$ по функциям sin(kxmx) × $ \times \,\,\exp \left( { \pm i{{k}_{{zm}}}z} \right),$ kzm = $\sqrt {k_{0}^{2} - k_{{xm}}^{2} - k_{y}^{2}} ,$ ${{k}_{{xm}}} = {{\left( {2m - 1} \right)} \mathord{\left/ {\vphantom {{\left( {2m - 1} \right)} a}} \right. \kern-0em} a}$ с учетом условий излучения. Выражая компоненты полей из (1), (2) и сшивая по методике [14], получаем нормированную на импеданс ${{\tilde {Z}}_{1}} = {{{{Z}_{0}}{{k}_{0}}{{k}_{{z1}}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}{{k}_{0}}{{k}_{{z1}}}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}$ моды LE11 входную проводимость ${{Y}_{{{\text{in}}}}} = {{\left( {1 - R} \right)} \mathord{\left/ {\vphantom {{\left( {1 - R} \right)} {\left( {1 + R} \right)}}} \right. \kern-0em} {\left( {1 + R} \right)}}$ = = $1 + iB,$ где
(3)
$\begin{gathered} B\sin \left( {{{k}_{{x1}}}x} \right)\int\limits_{{{ - t} \mathord{\left/ {\vphantom {{ - t} 2}} \right. \kern-0em} 2}}^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {E\left( x \right)\sin \left( {{{k}_{{x1}}}x} \right)dx} = \\ = \int\limits_{{{ - t} \mathord{\left/ {\vphantom {{ - t} 2}} \right. \kern-0em} 2}}^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {K\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} , \\ \end{gathered} $(4)
$K\left( {x,x{\kern 1pt} '} \right) = 4{{k}_{{z1}}}\sum\limits_{m = 2}^\infty {{{{\left| {{{k}_{{zm}}}} \right|}}^{{ - 1}}}\sin \left( {{{k}_{{xm}}}x} \right)\sin \left( {{{k}_{{xm}}}x{\kern 1pt} '} \right)} .$В (4) произошло сокращение на ${{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}.$ Вместо ИУ (4) можно использовать функционал
(5)
$B = {С \mathord{\left/ {\vphantom {С D}} \right. \kern-0em} D} = {{\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {E\left( x \right)K\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx} } \mathord{\left/ {\vphantom {{\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {E\left( x \right)K\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx} } {{{{\left[ {\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {E\left( x \right)\sin \left( {{{k}_{{x1}}}x} \right)dx} } \right]}}^{2}}}}} \right. \kern-0em} {{{{\left[ {\int\limits_0^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {E\left( x \right)\sin \left( {{{k}_{{x1}}}x} \right)dx} } \right]}}^{2}}}}.$В (5) учтена нечетность $E\left( x \right) = {{E}_{x}}\left( {x,0} \right)$ и нечетность ядра $K\left( {x,x{\kern 1pt} '} \right).$ Обозначим $\tau = {{\pi t} \mathord{\left/ {\vphantom {{\pi t} {\left( {2a} \right)}}} \right. \kern-0em} {\left( {2a} \right)}},$ $\chi = {{\pi x} \mathord{\left/ {\vphantom {{\pi x} a}} \right. \kern-0em} a},$ $n = 2m - 1.$ Для вычисления (5) используем замену Швингера $\sin \left( \chi \right) = \sin \left( \tau \right)\sin \left( \theta \right)$ [14], приводящую к распределению электрического поля в виде $E\left( x \right) = {{E}_{0}}{\text{tg}}\left( \theta \right)$$\sqrt {1 - {{{\sin }}^{2}}\left( \tau \right){{{\sin }}^{2}}\left( \theta \right)} ,$ удовлетворяющему условию на ребре. Это распределение можно использовать в (5) для непосредственного получения значения B. Приведенная замена преобразует интегрирование в интегралах (3) к области ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2} < \theta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ а в интегралах (5) – к области $0 < \theta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Получим квазистатическое решение ИУ (3). Имеем
Используя формулу суммирования [15] и замену $\sin \left( {y{\kern 1pt} '} \right) = \sin \left( {{{\pi t} \mathord{\left/ {\vphantom {{\pi t} {\left( {2a} \right)}}} \right. \kern-0em} {\left( {2a} \right)}}} \right)\sin \left( {\theta {\kern 1pt} '} \right),$ получаем
(6)
$\begin{gathered} 4S\left( {x,x{\kern 1pt} '} \right) = \ln \left( {\frac{{{\text{tg}}\left( {{{\left( {\chi + \chi {\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{\left( {\chi + \chi {\kern 1pt} '} \right)} 2}} \right. \kern-0em} 2}} \right)}}{{{\text{tg}}\left( {{{\left( {\chi - \chi {\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{\left( {\chi - \chi {\kern 1pt} '} \right)} 2}} \right. \kern-0em} 2}} \right)}}} \right) = \\ = \ln \left( {\frac{{\sin \left( \chi \right) + \sin \left( {\chi {\kern 1pt} '} \right)}}{{\sin \left( \chi \right) - \sin \left( {\chi {\kern 1pt} '} \right)}}} \right) = \ln \left( {\frac{{{\text{tg}}\left( {{{\left( {\theta + \theta {\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{\left( {\theta + \theta {\kern 1pt} '} \right)} 2}} \right. \kern-0em} 2}} \right)}}{{{\text{tg}}\left( {{{\left( {\theta - \theta {\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{\left( {\theta - \theta {\kern 1pt} '} \right)} 2}} \right. \kern-0em} 2}} \right)}}} \right), \\ \sum\limits_{m = 2}^\infty {\frac{{\sin \left( {{{k}_{{xm}}}\chi } \right)\sin \left( {{{k}_{{xm}}}\chi {\kern 1pt} '} \right)}}{{\left| {{{k}_{{zm}}}} \right|}}} \approx \\ \approx \frac{a}{\pi }\left[ {\sum\limits_{m = 1}^\infty {\frac{{\sin \left( {n\theta } \right)\sin \left( {n\theta {\kern 1pt} '} \right)}}{n}} - \sin \left( \theta \right)\sin \left( {\theta {\kern 1pt} '} \right)} \right]. \\ \end{gathered} $Используя (6) в ИУ (3), получаем приведенное квазистатическое решение $E\left( x \right)$ и квазистатическое значение проводимости
Для его уточнения подставим $E\left( x \right)$ в (5). Квадрат интеграла в знаменателе равен $D = E_{0}^{2}{{a}^{2}}{{\sin }^{4}}{{\left( \tau \right)} \mathord{\left/ {\vphantom {{\left( \tau \right)} 4}} \right. \kern-0em} 4}.$ Рассмотрим интеграл
(7)
$\begin{gathered} {{I}_{n}} = \int\limits_{{{ - t} \mathord{\left/ {\vphantom {{ - t} 2}} \right. \kern-0em} 2}}^{{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} {\frac{{\sin \left( {n\chi } \right)\sin \left( \chi \right)\cos \left( \chi \right)}}{{\sqrt {{{{\sin }}^{2}}\left( \tau \right) - {{{\sin }}^{2}}\left( \chi \right)} }}dx} = \\ = \frac{{2a}}{\pi }\int\limits_0^\tau {\frac{{\sin \left( {n\chi } \right)\sin \left( \chi \right)\cos \left( \chi \right)}}{{\sqrt {{{{\sin }}^{2}}\left( \tau \right) - {{{\sin }}^{2}}\left( \chi \right)} }}d\chi } . \\ \end{gathered} $Очевидно, числитель (5) равен
После замены $\sin \left( \chi \right) = \sin \left( \tau \right)\sin \left( \theta \right)$ и ϑ(θ) = $ = \arcsin \left( {\sin \left( \tau \right)\sin \left( \theta \right)} \right)$ имеем интеграл
(8)
$\begin{gathered} {{I}_{{2m - 1}}} = 2\left( {{a \mathord{\left/ {\vphantom {a \pi }} \right. \kern-0em} \pi }} \right)\sin \left( \tau \right) \times \\ \times \,\,\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\sin \left( {\left( {2m - 1} \right)\vartheta \left( \theta \right)} \right)\sin \left( \theta \right)d\theta } . \\ \end{gathered} $Для его вычисления воспользуемся формулой из работы [15, ф-ла (1.332.2)]:
В ней положим ${{\sin }^{{2k + 1}}}\left( \vartheta \right) = {{\sin }^{{2k + 1}}}\left( \tau \right){{\sin }^{{2k + 1}}}\left( \theta \right).$ Таким образом, получаем
(9)
$\begin{gathered} {{I}_{{2m - 1}}} = \left( {2m - 1} \right)a \times \\ \times \,\,\sum\limits_{k = 0}^{m - 1} {\frac{{{{{\left( { - 1} \right)}}^{k}}\left( {2k + 1} \right)!!{{{\sin }}^{{2k + 2}}}\left( \tau \right){{{\sin }}^{{2k + 2}}}\left( \theta \right)}}{{\left( {2k + 1} \right)!\left( {2k + 2} \right)!!}}} \times \\ \times \,\,\prod\limits_{l = 1}^k {\left[ {{{{\left( {2m - 1} \right)}}^{2}} - {{{\left( {2l - 1} \right)}}^{2}}} \right]} . \\ \end{gathered} $Области применимости формул: для несимметричной и симметричной диафрагм соответственно
В случае расположения одинаковых диафрагм на расстояниях ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ в ПВ значения их проводимостей корректируем множителями, приведенными далее в разд. 3. Отметим, что симметричную диафрагму можно возбудить волной H10, и тогда в центре ее апертуры возникает электрическая стенка [14]. Но симметричный электронный пучок ее не возбуждает, и мы это не рассматриваем. Для работы с симметричным пучком следует использовать трансформатор мод от H10 к LE11.
В приближенной модели считаем, что в волновод периодически включены диафрагмы с проводимостями ${{y}_{1}}$, ${{y}_{2}}$, ${{y}_{3}}$. Это значит, что следующая за диафрагмой ${{y}_{3}}$ будет ${{y}_{1}}$. Одномодовое рассмотрение не различает наличие несимметричной диафрагмы на конкретной стенке ПВ, однако это делает наложение условия Флоке. Если ${{y}_{1}} = {{y}_{2}} = {{y}_{3}},$ то периодичность возможна, только если вторая диафрагма находится на противоположной стенке (иначе период будет ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$). Вводим расстояния между диафрагмами ${{\Delta }_{1}}$, ${{\Delta }_{2}}$ и ${{\Delta }_{3}} = d - {{\Delta }_{1}} - {{\Delta }_{2}}$ соответственно от первой до второй, от второй до третьей и от третьей до следующей. Перемножая нормированные матрицы передачи диафрагмы и отрезка волновода, получаем матрицу звена диафрагма-отрезок волновода
в которой ${{B}_{n}} = \left| {{{y}_{n}}} \right|.$ Полная матрица периода ЗС $\hat {a} = {{\hat {a}}_{1}}{{\hat {a}}_{2}}{{\hat {a}}_{3}}$ связывает комплексные амплитуды ${{E}_{x}}\left( 0 \right) = {{E}_{x}}\left( d \right)\exp \left( {i\Psi } \right)$ и ${{Z}_{0}}{{H}_{y}}\left( 0 \right) = {{Z}_{0}}{{H}_{y}}\left( d \right) \times $ $ \times \,\,\exp \left( {i\Psi } \right)$ при $z = 0$ с такими же амплитудами ${{E}_{x}}\left( d \right)$ и $Z{{H}_{y}}\left( d \right)$ при $z = d$ компонент электрического и магнитного полей в этих поперечных сечениях. Условия Флоке явно наложены: $\Psi = {{k}_{z}}d$ ‒ фазовый сдвиг на период. В результате получаем дисперсионное уравнение (ДУ) Флоке-Блоха в виде $\cos \left( \Psi \right) = X$ и его явное решение: $\Psi = \arccos \left( X \right)$ = $ = - i\ln \left( {X \pm \sqrt {{{X}^{2}} - 1} } \right),$ где $X = {{\left( {{{a}_{{11}}} + {{a}_{{22}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{11}}} + {{a}_{{22}}}} \right)} 2}} \right. \kern-0em} 2}.$ Решение $ - \Psi $ также дается этой формулой, что означает взаимный переход (неразличимость) прямых и обратных волн в периодических недиссипативных ЗС подобно взаимно противоположным волнам в волноводе. Для выделения прямой волны периодичность ЗС должна быть нарушена введением либо источника, либо диссипации. Тогда движение энергии идет или в сторону от источника, или в сторону затухания волны. Волна прямая, если фаза движется также в сторону движения энергии, и обратная – в противном случае. Рассмотрим учет влияния конечной толщины диафрагмы. Пусть также на периоде имеем три диафрагмы с толщинами ${{\delta }_{n}}$. Рассчитываем проводимость бесконечно тонкой диафрагмы ${{y}_{n}}$ и выполняем корректировку ${{\tilde {y}}_{n}}$. Толстую диафрагму рассматриваем как две диафрагмы ${{\tilde {y}}_{n}}$, разделенные отрезком волновода с матрицей
В ней ${{\rho }_{n}}$ есть отношение волновых сопротивлений каналов ПВ.
2. БЫСТРЫЕ МНОГОМОДОВЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МОДЕЛИ
Рассмотрим получение строгих электродинамических моделей для диафрагм с одинаковыми высотами h и апертурами $s = a - h$ (в симметричном случае $2s = a - 2h$). Интересен также более простой случай ППВ с диафрагмами. Для него зависимость от координаты y отсутствует, поэтому возможны другие представления полей, например, через одну компоненту $\Pi _{x}^{e}\left( {x,z} \right)$ электрического вектора Герца. Оно эквивалентно (1), (2), поскольку в обоих случаях ненулевыми компонентами являются ${{E}_{x}}$, ${{E}_{z}}$ и ${{H}_{y}}$. Возможно и представление полей через одну продольную компоненту $\Pi _{z}^{e}\left( {x,z} \right)$ вектора Герца. Оно также приводит к ненулевым компонентам ${{E}_{x}}$, ${{E}_{z}}$, ${{H}_{y}}$ и удобно при решении задачи о возбуждении ЗС. Однако при таком формальном представлении для компонент ${{E}_{x}}$ и ${{H}_{y}}$ выпадает член, не зависящий от координаты x (соответствующий T-волне), который следует добавлять (при возбуждении пучком он не возникает, однако участок такой ЗС можно запитать коаксиальной линией). Если рассматривать ПВ и добавлять одну пространственную вариацию по y в виде $\cos \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} b}} \right. \kern-0em} b}} \right)$ к соответствующим компонентам полей, то выбор представления (1), (2) становится однозначным: только он дает отсутствие компоненты ${{E}_{y}}$ и малую величину ${{H}_{x}}$, т.е. малую y-компоненту поверхностного тока на диафрагме, что имеет место при возбуждении диафрагмированного ПВ симметричным по y пучком с плотностью тока ${{J}_{z}}\left( {x,y,z} \right)$ = ${{J}_{z}}\left( {x,z} \right)\cos \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} b}} \right. \kern-0em} b}} \right).$ При больших $b \gg a$ указанное различие становится несущественным, а в пределе $b \to \infty $ пропадает. Случай ППВ реализуется при $k = {{k}_{0}}$.
В случае двух одинаковых бесконечно тонких диафрагм в ППВ берем разложение
(10)
$\begin{gathered} {{H}_{y}}\left( {x,z} \right) = \sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} {\sin \left( {{{k}_{{xm}}}x} \right)} \\ {\cos \left( {{{k}_{{xm}}}x} \right)} \end{array}} \right)} \times \\ \times \,\,\left[ {{{\alpha }_{m}}\cos \left( {{{k}_{{zm}}}z} \right) + {{\beta }_{m}}\cos \left( {{{k}_{{zm}}}\left( {z - d} \right)} \right)} \right]. \\ \end{gathered} $Для симметричных диафрагм ${{k}_{{xm}}} = \left( {2m - 1} \right){{\pi x} \mathord{\left/ {\vphantom {{\pi x} a}} \right. \kern-0em} a},$ $m = 1,2,...,$ ${{k}_{{zm}}} = \sqrt {{{k}^{2}} - k_{{xm}}^{2}} ,$ и выбираем синус (магнитная стенка при $x = 0$). Для несимметричных диафрагм выбираем косинус и ${{k}_{{xm}}} = {{m\pi x} \mathord{\left/ {\vphantom {{m\pi x} a}} \right. \kern-0em} a},$ $m = 0,1,2,...,$ а отсчет x ведем от нижней стенки. Определяя ${{E}_{x}}\left( {x,z} \right)$ и коэффициенты разложения через ${{E}_{x}}\left( {x,0} \right) = E\left( x \right),$ ${{E}_{x}}\left( {x,d} \right) = E\left( x \right)\exp \left( { - i\Psi } \right),$ получаем ИУ (несимметричный случай)
(11)
$\begin{gathered} \int\limits_0^a {K\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} ' = \cos \left( \Psi \right)\int\limits_0^a {\tilde {K}\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} ', \\ K\left( {x,x{\kern 1pt} '} \right) = \sum\limits_{m = 0}^\infty {\frac{{\cos \left( {{{k}_{{xm}}}x} \right)\cos \left( {{{k}_{{xm}}}x{\kern 1pt} '} \right)}}{{{{\varepsilon }_{m}}{{k}_{{zm}}}\tan \left( {{{k}_{{zm}}}d} \right)}}} , \\ \tilde {K}\left( {x,x{\kern 1pt} '} \right) = \sum\limits_{m = 0}^\infty {\frac{{\cos \left( {{{k}_{{xm}}}x} \right)\cos \left( {{{k}_{{xm}}}x{\kern 1pt} '} \right)}}{{{{\varepsilon }_{m}}{{k}_{{zm}}}\sin \left( {{{k}_{{zm}}}d} \right)}}} . \\ \end{gathered} $Здесь ${{\varepsilon }_{m}} = 1 + {{\delta }_{{m0}}}.$ Если $E\left( x \right)$ есть решение ИУ (11), то фазовый сдвиг определяется как экстремум функционала
(12)
$\begin{gathered} \cos \left( \Psi \right) = \\ = {{\int\limits_0^a {E\left( x \right)K\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} \mathord{\left/ {\vphantom {{\int\limits_0^a {E\left( x \right)K\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} {\int\limits_0^a {E\left( x \right)\tilde {K}\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)}}} \right. \kern-0em} {\int\limits_0^a {E\left( x \right)\tilde {K}\left( {x,x{\kern 1pt} '} \right)} E\left( {x{\kern 1pt} '} \right)}}. \\ \end{gathered} $В симметричном случае в ядра входят синусы, а пределы интегрирования симметричные. В этом случае используем $E\left( x \right) = {{E}_{0}}{\text{tg}}\left( \theta \right)$$\sqrt {1 - {{{\sin }}^{2}}\left( \tau \right){{{\sin }}^{2}}\left( \theta \right)} ,$ а в несимметричном случае берем $E\left( x \right)$ из [14]. Интегрирование идет по апертуре $0 \leqslant x \leqslant s$ или $ - s \leqslant x \leqslant s.$ Явная модель для $\Psi $ и ЗС в рис. 1 также легко получается путем использования двух ЧО. В этом случае плоскости симметрии нет (плоскость симметрии зеркальная), поэтому используем несимметричное представление в первой области ($0 < z < {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$):
(13)
$\begin{gathered} {{H}_{y}}\left( {x,z} \right) = \sum\limits_{m = 0}^\infty {\cos \left( {{{k}_{{xm}}}x} \right)} \times \\ \times \,\,\left[ {{{\alpha }_{m}}\cos \left( {{{k}_{{zm}}}z} \right) + {{\beta }_{m}}\cos \left( {{{k}_{{zm}}}\left( {z - {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \right)} \right], \\ \end{gathered} $и аналогичное представление во второй области (${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2} < z < d$):
(14)
$\begin{gathered} {{H}_{y}}\left( {x,z} \right) = \sum\limits_{m = 0}^\infty {\cos \left( {{{k}_{{xm}}}x} \right)} \times \\ \times \,\,\left[ {{{\gamma }_{m}}\cos \left( {{{k}_{{zm}}}z - {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) + {{\delta }_{m}}\cos \left( {{{k}_{{zm}}}\left( {z - d} \right)} \right)} \right]. \\ \end{gathered} $Выражаем коэффициенты разложения через электрические поля на диафрагмах:
Сшивая компоненты (13), (14) на апертурах, имеем систему ИУ
(15)
$\int\limits_0^s {{{K}_{{11}}}\left( {x,x{\kern 1pt} '} \right){{E}_{1}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} - \frac{{\left( {1 + \exp \left( {i\Psi } \right)} \right)}}{2}\,\int\limits_h^a {{{K}_{{12}}}\left( {x,x{\kern 1pt} '} \right){{E}_{2}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} = 0,\,\,\,\,\,0 < x < s,$(16)
$ - \frac{{\left( {1 + \exp \left( { - i\Psi } \right)} \right)}}{2}\int\limits_0^s {{{K}_{{21}}}\left( {x,x{\kern 1pt} '} \right){{E}_{1}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} + \,\,\int\limits_h^a {{{K}_{{22}}}\left( {x,x{\kern 1pt} '} \right){{E}_{2}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} = 0,\,\,\,\,h < x < a,$в которую входят симметричные ядра:
В силу однородности (15) и (16) общий множитель ${{2{{k}^{2}}} \mathord{\left/ {\vphantom {{2{{k}^{2}}} {\left( {i{{k}_{0}}a{{Z}_{0}}} \right)}}} \right. \kern-0em} {\left( {i{{k}_{0}}a{{Z}_{0}}} \right)}}$ сокращен. В пренебрежении диссипацией решая эту систему методом Бубнова–Галеркина, получаем систему однородных алгебраических уравнений с эрмитовой матрицей. Ее определитель дает ДУ, из равенства нулю которого находятся действительные значения $\Psi = {{k}_{z}}d.$ Для получения быстрого алгоритма возьмем поля на апертурах в виде ${{E}_{1}}\left( x \right) = \alpha E\left( x \right),$ ${{E}_{2}}\left( x \right) = $ $ = \beta E\left( {a - x} \right),$ где $E\left( x \right)$ ‒ распределение поля на одиночной диафрагме [14]. В результате вычисления определителя имеем ДУ
(17)
${{\cos }^{2}}\left( {{\Psi \mathord{\left/ {\vphantom {\Psi 2}} \right. \kern-0em} 2}} \right) = \frac{{\int\limits_0^s {\int\limits_0^s {E\left( x \right)} {{K}_{{11}}}\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx\int\limits_h^a {\int\limits_h^a {E\left( {a - x} \right){{K}_{{11}}}\left( {x,x{\kern 1pt} '} \right)E\left( {a - x{\kern 1pt} '} \right)dx{\kern 1pt} 'dx} } }}{{{{{\left[ {\int\limits_h^a {E\left( {a - x} \right)} \int\limits_0^s {{{K}_{{12}}}\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx} \right]}}^{2}}}}.$В общем случае (17) следует понимать как функционал и искать его стационарное значение
при разложении функции $E\left( x \right)$ по базисным функциям. В интеграле знаменателя и в двойном интеграле числителя удобно
сделать замену переменных 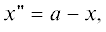 $x{\kern 1pt} ''' = a - x{\kern 1pt} ',$ что приводит к единым пределам интегрирования $\left( {0,s} \right)$. При такой замене в сдвинутых ядрах имеем
$x{\kern 1pt} ''' = a - x{\kern 1pt} ',$ что приводит к единым пределам интегрирования $\left( {0,s} \right)$. При такой замене в сдвинутых ядрах имеем 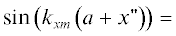 =
= 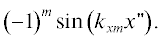 После замен лишние штрихи можно опустить. Двойной сдвиг не приводит к изменению ядра.
В результате имеем
После замен лишние штрихи можно опустить. Двойной сдвиг не приводит к изменению ядра.
В результате имеем
(18)
$\cos \left( {{\Psi \mathord{\left/ {\vphantom {\Psi 2}} \right. \kern-0em} 2}} \right) = \pm \frac{{\int\limits_0^s {\int\limits_0^s {E\left( x \right)} {{K}_{{11}}}\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx}}{{\int\limits_0^s {\int\limits_0^s {E\left( x \right)} {{{\tilde {K}}}_{{12}}}\left( {x,x{\kern 1pt} '} \right)E\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} dx}},$где тильда означает однократно сдвинутое ядро, т.е. наличие множителя ${{\left( { - 1} \right)}^{m}}$ в сумме. Для получения быстрой модели осталось вычислить интеграл
Заменой переменных $t = \cos \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} a}} \right. \kern-0em} a}} \right)$ он сводится к интегралу
(19)
$\begin{gathered} {{I}_{m}}\left( {{{t}_{s}}} \right) = \frac{a}{\pi }\int\limits_{{{t}_{s}}}^1 {\frac{{{{T}_{m}}\left( t \right)dt}}{{\sqrt {\left( {1 - t} \right)\left( {t - {{t}_{s}}} \right)} }}} = \\ = \frac{a}{2}\left[ {{{P}_{m}}\left( {{{t}_{s}}} \right) + {{P}_{{m - 1}}}\left( {{{t}_{s}}} \right)} \right], \\ \end{gathered} $где ${{t}_{s}} = \cos \left( {{{\pi s} \mathord{\left/ {\vphantom {{\pi s} a}} \right. \kern-0em} a}} \right),$ ${{T}_{m}}\left( t \right)$ ‒ полином Чебышева первого рода, ${{P}_{m}}$ ‒ полином Лежандра. Для вычисления (19) использована формула из [16, (2.18.1.1)]. Результат справа в (19) верен для $m \geqslant 1.$ Для $m = 1$ имеем ${{I}_{m}}\left( {{{t}_{s}}} \right) = aB{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \pi }} \right. \kern-0em} \pi } = a$ (формула из [17, (2.5.2.1)]). При $s = 0$ (перекрытие канала) формула (19) не применима. При $s = a$ (отсутствие диафрагм) ${{t}_{s}} = - 1,$ поэтому ${{I}_{m}}\left( { - 1} \right) = 0,$ ${{I}_{0}}\left( { - 1} \right) = \pi .$ В этом случае $\Psi = 0.$
Рассмотрим импедансный алгоритм, выразив коэффициенты в (13), (14) через ${{H}_{y}}$:
Магнитное поле терпит скачок на диафрагмах с поверхностными плотностями тока в виде
В последнем соотношении мы воспользовались условием Флоке. В силу непрерывности ${{E}_{x}}$ имеем ${{\alpha }_{m}} = - {{\delta }_{m}},$ ${{\gamma }_{m}} = - \exp \left( { - i\Psi } \right){{\beta }_{m}}.$ Подставим выражения $H_{y}^{ - }$ в приведенные соотношения и исключим интегралы с $H_{y}^{ + }$:
Имеем ${{\Delta }_{m}} = 4\left[ {{{{\cos }}^{2}}\left( {{\Psi \mathord{\left/ {\vphantom {\Psi 2}} \right. \kern-0em} 2}} \right) - {{{\cos }}^{2}}\left( {{{k}_{{zm}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \right]$ и
(20)
${{\delta }_{m}} = \frac{2}{{a{{\varepsilon }_{m}}{{\Delta }_{m}}}}\int\limits_0^a {\left[ {{{j}_{{x2}}}\left( x \right)\left( {1 + \exp \left( { - i\Psi } \right)} \right) + 2{{j}_{{x1}}}\left( x \right)\cos \left( {{{k}_{{zm}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \right]} \cos \left( {{{k}_{{xm}}}x} \right)dx,$(21)
${{\beta }_{m}} = \frac{2}{{a{{\varepsilon }_{m}}{{\Delta }_{m}}}}\int\limits_0^a {\left[ {2{{j}_{{x1}}}\left( x \right)\cos \left( {{{k}_{{zm}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) + {{j}_{{x2}}}\left( x \right)\left( {1 + \exp \left( {i\Psi } \right)} \right)} \right]} \cos \left( {{{k}_{{xm}}}x} \right)dx.$Теперь можно найти поля на диафрагмах и апертурах:
(22)
${{E}_{{x1}}}\left( x \right) = \frac{{i{{k}_{0}}{{Z}_{0}}}}{{{{k}^{2}}}}\sum\limits_{m = 0}^\infty {{{\beta }_{m}}{{k}_{{zm}}}\sin \left( {{{k}_{{zm}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)\cos \left( {{{k}_{{xm}}}x} \right)} ,$(23)
${{E}_{{x2}}}\left( x \right) = \frac{{i{{k}_{0}}{{Z}_{0}}}}{{{{k}^{2}}}}\sum\limits_{m = 0}^\infty {{{\delta }_{m}}{{k}_{{zm}}}\sin \left( {{{k}_{{zm}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)\cos \left( {{{k}_{{xm}}}x} \right)} .$С учетом (20) и (21) на диафрагмах они являются ИУ, если на них наложить импедансные условия ${{E}_{{x1}}}\left( x \right) = Z{{j}_{{x1}}}\left( x \right)$ и ${{E}_{{x2}}}\left( x \right) = Z{{j}_{{x2}}}\left( x \right).$ Здесь $Z = {{Z}_{0}}\rho = {{{{Z}_{s}}} \mathord{\left/ {\vphantom {{{{Z}_{s}}} 2}} \right. \kern-0em} 2} = \left( {1 + i} \right){{{{R}_{s}}} \mathord{\left/ {\vphantom {{{{R}_{s}}} 2}} \right. \kern-0em} 2},$ ${{Z}_{s}}$ ‒ поверхностный импеданс Леонтовича, а двойка возникла в силу двустороннего поверхностного тока на каждой диафрагме. Пусть первая диафрагма расположена в области $0 < x < h,$ а следующая в области $a - h < x < a.$ Интегралы следует брать по указанным областям, при этом ${{j}_{{x1}}}\left( x \right) = \alpha {{j}_{x}}\left( x \right),$ ${{j}_{{x2}}}\left( x \right) = \beta {{j}_{x}}\left( {a - x} \right).$ Хорошей аппроксимацией для функции jx(x), удовлетворяющей условию на ребре, служит функция ${{j}_{x}}\left( x \right) = \cos \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right).$ Используя ее, получаем систему уравнений
В ней обозначены ядра:
Проецируем эту систему уравнений на функции ${{j}_{{x1}}}$, ${{j}_{{x2}}}$ (т.е. умножаем первое на ${{j}_{x}}\left( x \right)$ и интегрируем, а второе – на ${{j}_{x}}\left( {a - x} \right)$ и интегрируем). В силу произвольности $\alpha $ и $\beta $ имеем ДУ в виде равенства нулю определителя второго порядка, из которого находится $\Psi $, при этом матричные элементы вычисляются аналитически. Указанный подход не позволяет явно определить фазовый сдвиг $\Psi $, поскольку он входит в ${{\Delta }_{m}}$, что требует нахождения корней определителя (в общем случае комплексных). Однако если $k_{0}^{2} < {{\left( {{{m\pi } \mathord{\left/ {\vphantom {{m\pi } a}} \right. \kern-0em} a}} \right)}^{2}} + k_{y}^{2},$ $m \geqslant 1,$ то ${{\Delta }_{m}} \approx - 4{{\operatorname{ch} }^{2}}\left( {\left| {{{k}_{{zm}}}} \right|{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right),$ и $\Psi $ входит только в члены с $m = 0$. Для импедансной диафрагмы имеем однородную систему ИУ Фредгольма второго рода. В случае $\rho = 0$ получаем систему ИУ Фредгольма первого рода. Полученные алгоритмы быстрые, поскольку необходимо вычислять быстро сходящиеся ряды. Указанные ряды можно асимптотически суммировать, и тогда достаточно вычислять несколько их членов, т.е. ДУ приобретают аналитический вид. Указанные формулы для модели (22) и (23) можно получить, вычисляя определитель системы уравнений
и входящие в него интегралы, выражающиеся через интеграл
Рассмотрим метод ИУ на основе ФГ. Также расположим ось z на нижней стенке. Объемную плотность тока представим формально через поверхностную плотность тока на диафрагмах с помощью дельта-функций: ${{J}_{x}}\left( {x,z} \right) = {{j}_{{xl}}}\left( x \right)\delta \left( {z - {{z}_{l}}} \right),$ $l = 1,2,3,$ ${{z}_{1}} = 0,$ ${{z}_{2}} = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2},$ ${{z}_{3}} = d.$ Для поверхностной плотности тока пишем ${{j}_{{x1}}}\left( x \right) = \alpha \cos \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right),$ ${{j}_{{x2}}}\left( x \right) = \beta \cos \left( {\pi {{\left( {x - a} \right)} \mathord{\left/ {\vphantom {{\left( {x - a} \right)} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right),$ ${{j}_{{x3}}}\left( x \right) = {{j}_{{x1}}}\left( x \right) \times $ $ \times \,\,\exp \left( { - i\Psi } \right)$ соответственно для первой, второй и сдвинутой на период диафрагм. Компонента функции Грина ${{G}_{{xx}}}$, связывающая компоненту ${{A}_{x}}$ вектор-потенциала с компонентой плотности тока ${{J}_{x}}$, имеет вид
(24)
$\begin{gathered} {{G}_{{xx}}}\left( {x,\left. z \right|x{\kern 1pt} ',z{\kern 1pt} '} \right) = \frac{2}{{ad}} \times \\ \times \,\,\sum\limits_{m = 0}^\infty {\sum\limits_{n = - \infty }^\infty {\frac{{\cos \left( {{{k}_{{xm}}}x} \right)\cos \left( {{{k}_{{xm}}}x{\kern 1pt} '} \right)\exp \left( { - i{{{\tilde {k}}}_{n}}\left( {z - z{\kern 1pt} '} \right)} \right)}}{{\left( {1 + {{\delta }_{{m0}}}} \right)\left( {k_{{xm}}^{2} + \tilde {k}_{n}^{2} - k_{0}^{2}} \right)}}} } , \\ \end{gathered} $где ${{k}_{{xm}}} = {{m\pi } \mathord{\left/ {\vphantom {{m\pi } a}} \right. \kern-0em} a},$ ${{\tilde {k}}_{n}} = {{k}_{z}} + {{2n\pi } \mathord{\left/ {\vphantom {{2n\pi } d}} \right. \kern-0em} d}.$ Если экран не плоскопараллельный, а прямоугольный с размером b по оси y, то в (24) возникает еще одна сумма по функциям $\cos \left( {{{k}_{{yl}}}y} \right)\cos \left( {{{k}_{{yl}}}y{\kern 1pt} '} \right),$ с членом $k_{{yl}}^{2}$ в сумме знаменателя и множителем перед суммами ${4 \mathord{\left/ {\vphantom {4 {\left( {abd} \right)}}} \right. \kern-0em} {\left( {abd} \right)}}.$ Здесь ${{k}_{{yl}}} = \left( {2l - 1} \right){\pi \mathord{\left/ {\vphantom {\pi b}} \right. \kern-0em} b}.$ Это соответствует симметричной (четной) по y волне, которая возбуждается симметричным электронным пучком. В первом приближении можно взять только один член $\cos \left( {{{k}_{{y1}}}y} \right)\cos \left( {{{k}_{{y1}}}y{\kern 1pt} '} \right)$ в последней сумме, что соответствует замене $k_{0}^{2} \to {{k}^{2}}$ в (24). Если электронный пучок имеет распределение $\cos \left( {{{k}_{{y1}}}y} \right),$ то удержание одного члена дает точный результат. Система ИУ имеет вид
(25)
$\begin{gathered} {{E}_{x}}\left( {x,0} \right) = \alpha \rho \cos \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right) = \frac{{k_{0}^{2} + \partial _{x}^{2}}}{{i{{k}_{0}}}}\,\, \times \\ \times \,\,\int\limits_0^h {\left[ {\alpha {{G}_{{xx}}}\left( {x,\left. 0 \right|x{\kern 1pt} ',0} \right) + \beta {{G}_{{xx}}}\left( {x,\left. 0 \right|a - x{\kern 1pt} ',{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \right]} \times \\ \times \,\,\cos \left( {{{\pi x{\kern 1pt} '} \mathord{\left/ {\vphantom {{\pi x{\kern 1pt} '} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right)dx{\kern 1pt} ', \\ \end{gathered} $(26)
$\begin{gathered} {{E}_{x}}\left( {x,{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = \beta \rho \cos \left( {\pi {{\left( {a - x} \right)} \mathord{\left/ {\vphantom {{\left( {a - x} \right)} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right) = \\ = \frac{{k_{0}^{2} + \partial _{x}^{2}}}{{i{{k}_{0}}}}\int\limits_0^h {\left[ {\alpha {{G}_{{xx}}}\left( {x,\left. {{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right|x{\kern 1pt} ',0} \right) + \beta {{G}_{{xx}}}\left( {x,\left. {{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right|a - x{\kern 1pt} ',{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \right]} \cos \left( {{{\pi x{\kern 1pt} '} \mathord{\left/ {\vphantom {{\pi x{\kern 1pt} '} {\left( {2h} \right)}}} \right. \kern-0em} {\left( {2h} \right)}}} \right)dx{\kern 1pt} '. \\ \end{gathered} $Действие оператора перед интегралами дает множитель $k_{0}^{2} - k_{{xm}}^{2},$ который модифицирует ядро указанных ИУ по сравнению с ФГ (24). Быстрый алгоритм получаем, проецируя (25) и (26) на введенные базисные функции поверхностной плотности тока. Он также требует нахождения комплексных корней определителя второго порядка, матричные элементы которого имеют аналитический вид. Здесь ищется комплексное значение ${{k}_{z}} = {\Psi \mathord{\left/ {\vphantom {\Psi d}} \right. \kern-0em} d}.$ Соотношения упрощаются, а потери отсутствуют, если $\rho = 0.$ Отметим, что если сшивать компоненты ${{H}_{y}}$ с учетом их скачка в виде поверхностной плотности тока на диафрагмах, для модели ИУ (15), (16) также можно учесть потери. Только теперь соотношение ${{E}_{x}} = Z{{j}_{x}}$ следует использовать под интегралами на диафрагмах, а интегрирование вести по всему сечению. Если использовать два близко расположенных на расстоянии Δ одинаковых поверхностных тока, можно моделировать диафрагму конечной толщины Δ. При этом следует использовать импеданс ${{Z}_{s}}$. Поскольку он мал или при пренебрежении диссипацией нулевой, поле между лепестками малó и носит квазистатический характер. Для снижения размерности можно вводить фазовый сдвиг между указанными токами, связанный с толщиной и задаваемый множителем $\exp \left( { - i{{k}_{{0z}}}\Delta } \right)$. Получение строгой модели для толстых диафрагм требует использования компоненты ${{G}_{{zz}}}$ и учета торцевой плотности ${{j}_{z}}$. Это сильно усложняет алгоритм. При малой толщине диафрагмы это влияние малó, поскольку в средней точке ее торца ${{j}_{z}} = 0$, и влияние торца можно учесть как небольшое увеличение h.
3. ОДНОМОДОВАЯ МОДЕЛЬ С КОРРЕКЦИЕЙ
Одномодовая модель ЗС в виде диафрагм на одной широкой стенке имеет вид
(27)
$\cos \left( \Psi \right) = X = \cos \left( {{{k}_{{z0}}}d} \right) - B\sin \left( {{{k}_{{z0}}}d} \right),$где B – нормированная (умноженная) на волновое сопротивление H10-волны проводимость диафрагмы в ПВ. Отсутствие диафрагм ($B = 0$) означает ${{k}_{z}} = {{k}_{{z0}}}.$ Фазовый сдвиг $\Psi = \pi $ получается на частоте, определяемой из уравнения $B{\text{tg}}\left( {{{k}_{{z0}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = 1,$ а сама частота определяется выражением
Сравнивая (27) с (12), пишем (12) в форме
(28)
$\begin{gathered} \cos \left( \Psi \right) = \\ = \frac{{\cos \left( {{{k}_{{z0}}}d} \right) - \sin \left( {{{k}_{{z0}}}d} \right)\frac{{4{{k}_{{z0}}}}}{{{{\pi }^{2}}}}\sum\limits_{m = 1}^\infty {\frac{{I_{m}^{2}}}{{\left| {{{k}_{{zm}}}} \right|\operatorname{th} \left( {\left| {{{k}_{{zm}}}} \right|d} \right)}}} }}{{1 - \sin \left( {{{k}_{{z0}}}d} \right)\frac{{4{{k}_{{z0}}}}}{{{{\pi }^{2}}}}\sum\limits_{m = 1}^\infty {\frac{{I_{m}^{2}}}{{\left| {{{k}_{{zm}}}} \right|\operatorname{th} \left( {\left| {{{k}_{{zm}}}} \right|d} \right)}}} }}. \\ \end{gathered} $Как видно, (28) соответствует (27), лишь если член с суммой перед синусом мал. Считая этот член существенно меньше, чем единица, имеем
(29)
$\begin{gathered} \cos \left( \Psi \right) \approx \cos \left( {{{k}_{{z0}}}d} \right) - \sin \left( {{{k}_{{z0}}}d} \right) \times \\ \times \,\,\frac{{4{{k}_{{z0}}}}}{{{{\pi }^{2}}}}\sum\limits_{m = 1}^\infty {\frac{{I_{m}^{2}}}{{\left| {{{k}_{{zm}}}} \right|\operatorname{th} \left( {\left| {{{k}_{{zm}}}} \right|d} \right)}}} . \\ \end{gathered} $В знаменателе значения $\operatorname{th} \left( {\left| {{{k}_{{zm}}}} \right|d} \right)$ при больших m близки к единице. Тогда в пределе $d \to \infty $ выражение (29) соответствует (27). Наименьшее значение имеет $\operatorname{th} \left( {d\sqrt {{{{\left( {{\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0em} a}} \right)}}^{2}} + {{{\left( {{\pi \mathord{\left/ {\vphantom {\pi b}} \right. \kern-0em} b}} \right)}}^{2}} - k_{0}^{2}} } \right).$ Если следующие значения почти равны единице, что имеет место при ${{\pi d} \mathord{\left/ {\vphantom {{\pi d} a}} \right. \kern-0em} a}\sim 1,$ а основной вклад в B вносит первый член, то скорректированная проводимость есть $\tilde {B} = {B \mathord{\left/ {\vphantom {B {\operatorname{th} }}} \right. \kern-0em} {\operatorname{th} }}\left( {\left| {{{k}_{{z1}}}} \right|d} \right),$ что приводит к увеличению замедления. Если ${{k}_{{z0}}}d = \pi $ (диафрагмы в противофазе), то $\Psi = \pi ,$ что имеет место на частоте резонанса ${{\omega }_{r}} = c\sqrt {{{{\left( {{\pi \mathord{\left/ {\vphantom {\pi d}} \right. \kern-0em} d}} \right)}}^{2}} + {{{\left( {{\pi \mathord{\left/ {\vphantom {\pi b}} \right. \kern-0em} b}} \right)}}^{2}}} ,$ когда в плоскости обеих диафрагмах находится электрическая стенка. В соответствии с ранее полученным результатом это может быть только при B = ∞, т.е. при отсутствии зазора s. Вместе с тем из $\Psi = \pi $ в (28) следует
что в сравнении с $\tilde {B}{\text{tg}}\left( {{{k}_{{z0}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = 1$ дает $\tilde {B} = {{2B} \mathord{\left/ {\vphantom {{2B} {\operatorname{th} }}} \right. \kern-0em} {\operatorname{th} }}\left( {\left| {{{k}_{{z1}}}} \right|d} \right).$ Это и есть правильное скорректированное значение.
Рассмотрим теперь случай одинаковых диафрагм, включенных на расстояниях ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ на разных стенках ПВ (см. рис. 1, 3 ). Одномодовая модель дает ${{\cos }^{2}}\left( {{\Psi \mathord{\left/ {\vphantom {\Psi 2}} \right. \kern-0em} 2}} \right) = Y,$ где
При $\Psi = \pi $ имеем ${\text{tg}}\left( {{{k}_{{z0}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = {2 \mathord{\left/ {\vphantom {2 B}} \right. \kern-0em} B}.$ Из уравнения (18) имеем
Условие $\Psi = \pi $ дает ${\text{tg}}\left( {{{k}_{{z0}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)$ = $\operatorname{th} {{\left( {\left| {{{k}_{{z1}}}} \right|{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {{{k}_{{z1}}}} \right|{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right)} B}} \right. \kern-0em} B}.$ Сравнивая с предыдущим одномодовым результатом, получаем условие коррекции $\tilde {B} = $ $ = {{2B} \mathord{\left/ {\vphantom {{2B} {\operatorname{th} }}} \right. \kern-0em} {\operatorname{th} }}\left( {\left| {{{k}_{{z1}}}} \right|{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right).$ Частоту загиба (разрыва) дисперсионной характеристики при $\Psi = 2\pi $ можно получить из условия
Также следует условие $\cos \left( {{{k}_{{z0}}}{d \mathord{\left/ {\vphantom {d 4}} \right. \kern-0em} 4}} \right) = 0,$ которое означает наличие электрической стенки при ${d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}.$
ЗАКЛЮЧЕНИЕ
В работе предложены быстрые приближенные (одномодовые) модели для диафрагмированных ПВ и ППВ на основе вычисления проводимости диафрагм с приближенным учетом их взаимодействия по первой высшей моде, а также быстрые многомодовые модели импедансного и адмитансного типов. Модели учитывают все моды между диафрагмами и позволяют рассчитывать потери, а малое время счета связано с использованием функционалов и функций, достаточно точно удовлетворяющих строгим ИУ. Полученные результаты позволяют моделировать сдвинутые гребенки и ЗС типа петляющий волновод, обладающие зеркальной плоскостью симметрии и более широкой рабочей полосой. Строгие модели на основе функционалов типа (12), (18) могут быть получены для диафрагм конечной толщины. Это требует использования в два раза большего числа ЧО (двух для несдвинутых диафрагм и четырех для сдвинутых диафрагм), что несколько усложняет получаемые функционалы. При моделировании ЗС с диафрагмами конечной толщины методом ФГ удобно использовать соответствующие каждой границе два близко расположенных лепестка поверхностного тока с наложением на каждом из них импедансных условий. Получены формулы коррекции, для которых соответствие приближенной и многомодовой моделей лучше, поскольку учтено взаимодействие между диафрагмами по первой высшей моде. На рис. 2 приведены результаты моделирования на основе приближенной модели с проводимостями и на основе функционала (18). Результаты показывают возможность использовать быстрые приближенные модели для оптимизации и получения приближенных конфигураций ЗС, которые затем следует уточнять по строгим моделям. В быстрых моделях следует использовать коррекцию. Взаимодействие диафрагм приводит к тому, что поле в зазоре несколько отличается от использованного квазистатического решения Швингера для одиночной диафрагмы. Однако это отличие не должно приводить к существенному отличию полученных строгих функционалов от приведенных. Тем не менее, полученные функционалы можно использовать в строгих алгоритмах с применением большого числа разложений ${{E}_{x}}$ на апертурах и ${{j}_{x}}$ на диафрагмах. Но такие модели уже не являются быстрыми и сложны для определения комплексных корней ${{k}_{z}}$ с высокой точностью.
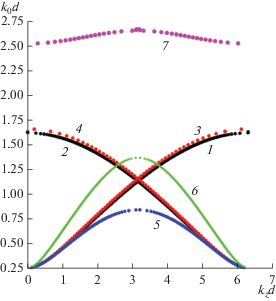
Рис. 2.
Дисперсия ЗС3: прямая ветвь (кривые 1, 3) и обратная ветвь (2, 4) при $h = 0.8a$ по строгой (1, 2) и приближенной (3, 4) моделям, а также дисперсия низшей моды симметричной ЗС с нулевой толщиной диафрагм и электрической стенкой в канале $t = 0.1a$ (5), $t = 0.2a$ (6), а также моды с магнитной стенкой (7) в канале $t = 0.3a.$ Использованы параметры: ${d \mathord{\left/ {\vphantom {d a}} \right. \kern-0em} a} = 0.8,$ ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a} = 10.$
Список литературы
Алехин Ю.В., Апин М.П., Бурцев А.А. и др. Сверхширокополосные лампы бегущей волны. Исследование в СВЧ-, КВЧ- и ТГЧ-диапазонах. Внедрение в производство. М.: Радиотехника, 2016.
Carlsten B.E. // Phys. Plasmas. 2002. V. 9. № 12. P. 5088.
Shin Y.-M., Barnett L.R., Luhmann N.C. // Appl. Phys. Lett. 2008. V. 93. № 22. P. 221504.
Рожнёв А.Г., Рыскин Н.М., Каретникова Т.А. и др. // Изв. вузов. Радиофизика. 2013. Т. 56. № 8‒9. С. 601.
Deng G., Chen P., Yang J., Yin Z., Ruan J. // J. Comput. Electron. 2015. V. 15. № 2. P. 634.
Каретникова Т.А., Рожнев А.Г., Рыскин Н.М. и др. // РЭ. 2016. Т. 61. № 1. С. 54.
Бушуев Н.А., Давидович М.В., Шиловский П.А. // Изв. Сарат. ун-та. Новая серия. Сер. Физика. 2012. Т. 12. Вып. 2. С. 64.
Давидович М.В., Бушуев Н.А. // Антенны. 2014. № 8. С. 49.
Давидович М.В. Замедляющая система “двойная сдвинутая импедансная гребенка” // ЖТФ. 2019. Т. 89. Вып. 2. С. 280.
Самохин Г.С., Силин Р.А. // Электрон. техника. Сер. 1. “Электроника СВЧ”. 1973. Вып. 5. С. 3.
Самохин Г.С., Силин Р.А. // Электрон. техника. Сер. 1. “Электроника СВЧ”. 1973. Вып. 6. С. 11.
Силин Р.А., Сазонов В.П. Замедляющие системы. М.: Сов. радио, 1966.
Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
Левин Л. Современная теория волноводов. М.: Изд-во иностр. лит., 1954.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов, и произведений. М.: Физматгиз, 1962.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Специальные функции. М.: Наука, 1983.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. М.: Наука, 1981.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


