Радиотехника и электроника, 2020, T. 65, № 5, стр. 487-494
Дважды стохастическая фильтрация пространственно неоднородных изображений
К. К. Васильев a, В. Е. Дементьев a, *
a Ульяновский государственный технический университет
432027 Ульяновск,
ул. Сев. Венец, 32, Российская Федерация
* E-mail: dve@ulntc.ru
Поступила в редакцию 15.04.2019
После доработки 26.07.2019
Принята к публикации 26.07.2019
Аннотация
Рассмотрено представление пространственно неоднородных изображений на основе дважды стохастических авторегрессионных моделей. Показана возможность синтеза полукаузальных дважды стохастических алгоритмов фильтрации изображений на базе таких моделей. Рассмотрены варианты сокращения вычислительных затрат, необходимых для реализации дважды стохастических фильтров, на основе использования каскадов скользящих окон. Проведен сравнительный анализ предлагаемых алгоритмов с известными аналогами, подтверждающий практическую возможность использования дважды стохастических фильтров для обработки реальных двумерных изображений.
ВВЕДЕНИЕ
Несмотря на достигнутые успехи при разработке систем обработки изображений, в настоящее время остается ряд значимых нерешенных проблем, препятствующих дальнейшему развитию методов машинного зрения. Среди этих проблем можно выделить вопросы описания многомерных массивов неоднородных коррелированных данных и их оптимальной и квазиоптимальной обработки.
Математические модели многомерных сигналов можно разделить на два класса [1]. К случайным полям (СП), заданным в непрерывном пространстве–времени, можно отнести гауссовские и марковские СП, полученные либо с помощью спектральных преобразований, либо с использованием методов формирующего фильтра [1–5]. Второй класс представляют СП на многомерных пространственно-временных сетках [2–9]. Наиболее общего описания при этом можно добиться, если использовать тензорные разностные стохастические уравнения [7, 8]. Частным случаем тензорных моделей случайных полей являются каузальные авторегрессионные (АР) [2, 5, 7, 8] и некаузальные гиббсовские модели [2, 5, 10]. Существенным недостатком таких моделей являются сложности описания пространственно неоднородного материала, например, спутниковых изображений поверхности Земли.
В связи с этим представляет особый интерес поиск механизмов, позволяющих выполнять имитацию изображений с изменяющимися статистическими и корреляционными характеристиками. Примером может служить аппликативно-сплайновая модель [11]. Однако на основе таких моделей затруднительно выполнять синтез алгоритмов обработки изображений. Еще одним вариантом имитации неоднородных СП является моделирование изображений с заданным энергетическим спектром, в том числе и фрактальным [7, 12–14]. Недостатком данной модели является ограниченное число реальных изображений, которые могут быть рассмотрены как фрактальные. В работе [13] моделирование многоспектральных пространственно неоднородных динамических полей яркости осуществляется на основании использования методов синтеза случайных текстур. Недостатком этого подхода являются сложности идентификации параметров модели по реальным изображениям и временным последовательностям таких изображений.
Приведенный краткий анализ показывает, что в настоящее время удовлетворительного описания неоднородных изображений не получено. В связи с этим целью данной работы является синтез математических моделей, адекватных реальному материалу и позволяющих формировать на своей основе эффективные алгоритмы обработки.
1. ДВАЖДЫ СТОХАСТИЧЕСКАЯ МОДЕЛЬ ИЗОБРАЖЕНИЯ
Для решения поставленной задачи будем считать многомерное изображение реализацией СП ${{x}_{{\bar {i}}}} = F\left( {{{x}_{{\bar {j}}}},{{\alpha }_{{\bar {i}}}},{{\xi }_{{\bar {i}}}}} \right),$ $\bar {i} \in {\Omega }$, $\bar {j} \in D$, заданного на прямоугольной сетке Ω, где D – окрестность точки ${{x}_{{\bar {i}}}}$; ${{\xi }_{{\bar {i}}}}$ – вспомогательное гауссовское СП; $F\left( \ldots \right)$ – некоторое преобразование; ${{\alpha }_{{\bar {i}}}}$ – параметры модели, представляющие собой реализации независимого от ${{\xi }_{{\bar {i}}}}$ СП. Математические модели, параметрами которых являются реализации вспомогательных СП, называют смешанными или дважды стохастическими (ДС) [5, 16]. Их важное преимущество заключается в том, что совокупность СП параметров $\left\{ {{{\alpha }_{{\bar {i}}}}} \right\}$ позволяет формировать разнообразные, в том числе и близкие по свойствам к неоднородным, реализации СП $\left\{ {{{x}_{{\bar {i}}}}} \right\}$, оказывающиеся адекватными реальным многомерным наблюдениям [17].
В качестве важного примера рассмотрим следующую авторегрессионную ДС-модель СП, заданного на прямоугольной N-мерной сетке ${\Omega } = {\text{\{ }}\bar {i} = ({{i}_{1}},({{i}_{2}},..,{{i}_{N}}{\text{)}}:$ $\left( {{{i}_{k}} = 1,2,..,{{M}_{k}}} \right),$ k = 1, 2, ..., N}:
(1)
${{x}_{{\bar {i}}}} = {{\alpha }_{{\bar {i}}}} + \sum\limits_{\bar {j} \in {{D}_{{\bar {i}}}}} {{{\rho }_{{\bar {i},\bar {j}}}}{{x}_{{\bar {i} - \bar {j}}}}} + {{\beta }_{{\bar {i}}}}{{\xi }_{{\bar {i}}}},\,\,\,\,\bar {i},\bar {j} \in {\Omega },$где $\left\{ {{{x}_{{\bar {i}}}},\bar {i} \in {\Omega }} \right\}$ – моделируемое СП, определенное на ${\Omega }$, $\left\{ {{{\rho }_{{\bar {i},\bar {j}}}},{{\alpha }_{{\bar {i}}}},{{\beta }_{{\bar {i}}}}:\bar {i} \in \Omega ,\bar {j} \in {{D}_{{\bar {i}}}}} \right\}$ – коэффициенты модели; ${\Xi } = \left\{ {{{\xi }_{{\bar {i}}}},\bar {i} \in {\Omega }} \right\}$ – порождающее белое СП; ${{D}_{{\bar {i}}}}$ – каузальная область локальных состояний [8] для точки $\bar {i}$.
Предположим, что коэффициенты ${{\rho }_{{\bar {i},\bar {j}}}}$ и ${{\alpha }_{{\bar {i}}}}$, ${{\beta }_{{\bar {i}}}}$ являются СП, определяемыми следующими соотношениями:
(2)
$\begin{gathered} {{\rho }_{{\bar {i},\bar {j}}}} = \mathop \sum \limits_{\bar {l} \in {{D}_{{\rho \bar {i},\bar {j}}}}} {{r}_{{\bar {l},\bar {j}}}}{{\rho }_{{\bar {i} - \bar {l},\bar {j}}}} + {{\gamma }_{{\bar {i},\bar {j}}}}{{\zeta }_{{\bar {i},\overline {j,} }}}{{\alpha }_{{\bar {i}}}} = \\ = \mathop \sum \limits_{\bar {l} \in {{D}_{{\alpha \bar {i}}}}} {{r}_{{\alpha \bar {l}}}}{{\alpha }_{{\bar {i} - \bar {l}}}} + {{\gamma }_{{\alpha \bar {i},}}}{{\zeta }_{{\alpha \bar {i}}}}; \\ {{\beta }_{{\bar {i}}}} = \mathop \sum \limits_{\bar {l} \in {{D}_{{\beta \bar {i}}}}} {{r}_{{\beta \bar {l}}}}{{\beta }_{{\bar {i} - \bar {l}}}} + {{\gamma }_{{\beta \bar {i},}}}{{\zeta }_{{\beta \bar {i}}}},~\,\,\,\,\bar {i},\bar {j} \in \Omega , \\ \end{gathered} $где $~\left\{ {{{r}_{{\bar {l},\bar {j}}}},{{\gamma }_{{\bar {i},\bar {j}}}},{{r}_{{\alpha \bar {l},\bar {j}}}},{{\gamma }_{{\alpha \bar {i},}}},{{r}_{{\beta \bar {l},\bar {j}}}},{{\gamma }_{{\beta \bar {i},}}}:\bar {i} \in \Omega ,\bar {l} \in {{D}_{{\bar {i}}}}} \right\}$ – постоянные коэффициенты; ${{D}_{{\rho \bar {i},\bar {j}}}},$ ${{D}_{{\alpha \bar {i}}}},{{D}_{{\beta \bar {i}}}}$ – области локальных состояний СП $\left\{ {{{\rho }_{{\bar {i},\bar {j}}}}} \right\}$, $\left\{ \alpha \right\}$ и $\left\{ {{{\beta }_{{\bar {i}}}}} \right\};$ $\left\{ {{{\zeta }_{{\bar {i},\bar {j}}}},\bar {i},\bar {j} \in {\Omega }} \right\},$ $\left\{ {{{\zeta }_{{\alpha \bar {i}}}},\bar {i} \in {\Omega }} \right\},$ ${{{\Sigma }}_{\beta }} = \left\{ {{{\zeta }_{{\beta \bar {i}}}},\bar {i} \in {\Omega }} \right\}$ – вспомогательные белые СП.
Недостатком модели (1), определяемым ее АР-природой, является анизотропность порождаемых СП. Кроме того, специфическим для предложенной модели является наличие большого количества параметров, определяющих поведение имитируемых СП. Однако анализ показал, что из всего многообразия порождающих многомерных АР-моделей возможно выделить группу, позволяющую формировать СП, близкие к изотропным. Такой группой являются АР-модели с кратными корнями характеристических уравнений (АРКК-модели). Для многомерной сетки ${\Omega }$ в операторной форме такие модели будут иметь следующий вид [8, 18]:
(3)
$\prod\limits_{k = 1}^N {{{{\left( {1 - {{\rho }_{k}}z_{k}^{{ - 1}}} \right)}}^{{{{n}_{k}}}}}} {{x}_{{\bar {i}}}} = \beta {{\xi }_{{\bar {i}}}},\,\,\,\,\bar {i} \in {\Omega },$где ${{\rho }_{k}},$ $\beta $ – коэффициенты модели; ${{n}_{k}}$ – кратность корней характеристических уравнений по k-му измерению; $z_{k}^{{ - 1}}$ – оператор сдвига: $z_{k}^{{ - l}}\left( {{{x}_{{{{i}_{1}},{{i}_{2}}, \ldots ,{{i}_{k}}, \ldots ,{{i}_{N}}}}}} \right)$ = = ${{x}_{{{{i}_{1}},{{i}_{2}}, \ldots ,{{i}_{k}} - l, \ldots ,{{i}_{N}}}}}.$
Ковариационная функция (КФ) для рассматриваемой модели является разделимой, т.е.
где ${{B}_{k}}\left( {{{i}_{k}}} \right)$ – КФ соответствующих одномерных АР:
Например, для важного случая $n$-мерной АРКК модели кратности 2 получим
(4)
$B\left( {{{i}_{1}},{{i}_{2}},..,{{i}_{N}}} \right) = \sigma _{x}^{2}\prod\limits_{k = 1}^N {\left( {1 + \frac{{1 - \rho _{k}^{2}}}{{1 + \rho _{k}^{2}}}\left| {{{i}_{k}}} \right|} \right)} \rho _{k}^{{\left| {{{i}_{k}}} \right|}}.$Можно показать [18], что при $1 - {{\rho }_{i}} \ll 1$ такая КФ может быть описана уравнениями, близкими к эллиптическим. При этом ее сечения высоких уровней $B\left( {{{i}_{1}},{{i}_{2}},..,{{i}_{N}}} \right)\sim \sigma _{x}^{2}$ имеют вид
где ${{a}_{k}} = \sqrt {\frac{{1 + \rho _{k}^{2}}}{{\left( {1 - \rho _{k}^{2}} \right)\left( {1 - {{\rho }_{k}}} \right)}}} ;$ $A\left( {{{\rho }_{k}}} \right) = \frac{{1 + {{\rho }_{k}}}}{{1 + \rho _{k}^{2}}}.$
Очевидно, сечения $B\left( {{{i}_{1}},{{i}_{2}},..,{{i}_{k}}} \right)$ близкого к $B\left( {{{i}_{1}},{{i}_{2}},..,{{i}_{k}}} \right) = 1$ уровня асимптотически, при $1 - {{\rho }_{i}} \to 0$ и больших значениях кратности ${{n}_{1}}$ и ${{n}_{2}}$, являются гиперэллипсоидами. Практика показывает, что близости к изотропности можно достичь уже при ${{n}_{1}} = {{n}_{2}} = \ldots = {{n}_{N}} = 2$. Также обратим внимание, что любая АРКК-модель определяется всего $3N$-параметрами, где $N$ – размерность описываемого СП. Для сравнения отметим, чтобы описать стандартную многомерную АР-модель требуется $\sum\nolimits_{k = 1}^N {\left( {{{K}_{k}} + 1} \right)} $-параметр, где ${{K}_{k}}$ – размер каузального окна по каждому измерению. При использовании АРКК-модели (3) в качестве основы для ДС-модели (1) в случае, если ${{D}_{{\bar {i}}}} = {{D}_{{\rho \bar {i},\bar {j}}}}$ = = ${{D}_{{\alpha \bar {i}}}} = {{D}_{{\beta \bar {i}}}}$ для всех $\bar {i},\bar {j} \in {\Omega ,}$ число параметров ДС-модели составит всего $10 + 3N$ и не будет зависеть от количества элементов в ${{D}_{{\bar {i}}}}$.
Следует отметить еще одно достоинство моделей с кратными корнями характеристических уравнений – простоту идентификации параметров СП любой размерности. Действительно, для идентификации можно использовать двухэтапную процедуру, проводимую независимо по каждой из осей. На первом этапе необходимо определить значения кратности характеристических корней АР-уравнений. Эта задача может быть решена на основе методики определения порядка одномерной АР-последовательности. На втором этапе определяются значения параметра $~{{\rho }_{k}}$, например, на основе выборочных значений КФ [8].
2. ДВАЖДЫ СТОХАСТИЧЕСКАЯ ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ
Использование ДС-модели на базе АРКК-модели позволяет формировать эффективные алгоритмы фильтрации реальных изображений. Действительно, пусть двумерное изображение может быть описано с помощью ДС-модели (1), так что и основное, и вспомогательное СП может быть описано двумерными АРКК-моделями (3) кратности 2. Такая модель может быть записана в виде
(5)
${{x}_{{i,j}}} = {{F}_{{{\text{АРКК}}\left( {2,2} \right)}}}\left( {{{P}_{1}} + {{\rho }_{{1i,j}}},{{P}_{2}} + {{\rho }_{{2i,j}}},B{{\xi }_{{i,j}}}} \right),$где $A,$ ${{P}_{1}},$ ${{P}_{2}},B$ – некоторые числа, характеризующие среднее математическое ожидание, корреляционные свойства и дисперсию изображения; $~{{F}_{{{\text{АРКК}}\left( {{{K}_{1}},{{K}_{2}}} \right)}}}\left( {{{\rho }_{1}},{{\rho }_{2}},b} \right)$ – преобразование, соответствующее двумерной АРКК-модели (3); $~{{K}_{1}} = 2,$ ${{K}_{2}} = 2$ – коэффициенты, определяющие кратность модели; $~\beta $ – нормирующий коэффициент; ${{\rho }_{{1i,j}}}$ = ${{F}_{{ARMR\left( {2,2} \right)}}}\left( {{{r}_{{11}}},{{r}_{{12}}},{{\gamma }_{1}}{{\xi }_{{1i,j}}}} \right),$ ${{\rho }_{{2i,j}}}$ = $ = {{F}_{{{\text{АРКК}}\left( {2,2} \right)}}}\left( {{{r}_{{21}}},{{r}_{{22}}},{{\gamma }_{2}}{{\xi }_{{2i,j}}}} \right)$ – случайные величины, определяемые АРКК-моделью; ${{\xi }_{{i,j}}},$ ${{\xi }_{{1i,j}}},{\text{\;}}$ ${{\xi }_{{2i,j}}}$ – гауссовские белые СП; $i = 1,..,{{M}_{1}},$ $j = 1, \ldots ,{{M}_{2}}$.
Пусть производятся наблюдения смеси ${{z}_{{i,j}}} = {{x}_{{i,j}}} + {{n}_{{i,j}}}$ информационного СП и аддитивного белого гауссовского СП $~\{ {{n}_{{i,j}}}\} $ с дисперсией $\sigma _{n}^{2}.~$ Решим задачу восстановления отчетов $\{ {{x}_{{i,j}}}\} $ по наблюдениям $\{ {{z}_{{i,j}}}\} $. Для этого составим следующий вектор элементов длиной $6{{M}_{1}} + 6$:
где
Тогда модель (5) можно записать в компактном векторном виде
где ${{\varphi }_{{i,j}}}\left( {{{{\bar {x}}}_{{i,j}}}} \right)$ – матричное нелинейное преобразование [17]; $~{{\bar {\xi }}_{{i,j}}} = \left( {{{\xi }_{{i,j}}},{{\xi }_{{\rho 1i,j}}},{{\xi }_{{\rho 2i,j}}}} \right).$
Обратим внимание, что к такой форме можно привести любую модель (1). Варьируя сложность ДС-модели, можно получить необходимую точность оценивания.
Используя эти соотношения и методы рекуррентной нелинейной фильтрации [9], можно получить следующий двумерный ДС-фильтр:
(6)
${{\hat {\bar {x}}}_{{i,j}}} = {{\hat {\bar {x}}}_{{{\text{Э}}i,j}}} + {{{\mathbf{B}}}_{{i,j}}}\left( {{{z}_{{i,j}}} - {{{\hat {x}}}_{{{\text{Э}}i,j}}}} \right),$где ${{\hat {x}}_{{{\text{Э}}i,j}}}$ – первый элемент вектора ${{\hat {\bar {x}}}_{{{\text{Э}}i,j}}}$, соответствующий прогнозу в точку $\left( {i,j} \right)$ по всем предшествующим элементам; $~{{{\mathbf{B}}}_{{i,j}}} = {{{\mathbf{P}}}_{{{\text{Э}}i,j}}}{{C}^{T}}{\mathbf{D}}_{{i,j}}^{{ - 1}};$ $~C = \left( {1,0,..,0} \right);$ ${{{\mathbf{D}}}_{{i,j}}} = C{{{\mathbf{P}}}_{{{\text{Э}}i,j}}}{{C}^{T}} + \sigma _{n}^{2};$ ${{{\mathbf{P}}}_{{{\text{Э}}i,j}}} = \varphi _{{i,j - 1}}^{'}\left( {{{{\hat {\bar {x}}}}_{{i,j - 1}}}} \right){{{\mathbf{P}}}_{{i,j - 1}}}\varphi _{{i,j - 1}}^{'}$ × $ \times \,\,{{\left( {{{{\hat {\bar {x}}}}_{{i,j - 1}}}} \right)}^{T}} + {{{\mathbf{V}}}_{{\xi i,j}}}.$
Ошибки фильтрации на каждом шаге определяются матрицей ${{{\mathbf{P}}}_{{i,j}}} = \left( {{\mathbf{E}} - {{{\mathbf{B}}}_{{i,j}}}{\mathbf{C}}} \right){{{\mathbf{P}}}_{{Ei,j}}}$ размером $\left( {6{{M}_{1}} + 6 \times 6{{M}_{1}} + 6} \right).$ Состоятельность и сходимость подобных нелинейных фильтров исследована в работах [9, 17]. Полученный алгоритм обладает важными особенностями. Во-первых, несмотря на внешнюю громоздкость, он не требует обращения матриц большого размера, как при построчном калмановском оценивании [17]. Во-вторых, при формировании оценки в точке $\left( {i,j} \right)~$ используются все элементы слева и сверху от этой точки, а входящие в вектор ${{\overline {\hat {x}} }_{{i,j}}}$ элементы, предшествующие ${{\hat {x}}_{{i,j}}},$ переоцениваются. Таким образом, это нивелирует недостаток каузальности авторегрессионной конструкции, используемой в ДС-модели (2). В-третьих, результатом фильтрации является не только совокупность оценок ${{\hat {x}}_{{i,j}}}$, но и оценки корреляционных связей ${{\hat {\rho }}_{{1i,j}}}$ и ${{\hat {\rho }}_{{2i,j}}}.$ Такая особенность позволяет использовать ДС-фильтр и для компенсации шума и как элемент алгоритмов текстурно-корреляционного анализа, например, при сегментации изображений. Кроме этого, использование полученных значений ${{\hat {\rho }}_{{1i,j}}}$ и ${{\hat {\rho }}_{{2i,j}}}$ для расчета и уточнения последующих оценок ${{\hat {x}}_{{i,j}}}$ наделяет ДС-фильтр ярко выраженными адаптивными свойствами, схожими со свойствами фильтров, предложенных в работах [19, 20]. На рис. 1 представлены примеры фильтрации искусственно зашумленного спутникового изображения.
Рис. 1.
Фильтрация спутниковых изображений: а – исходное изображение; б – искаженное изображение; в – результат фильтрации.

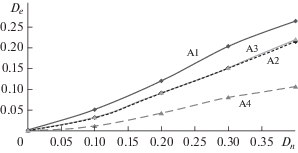
На рис. 2 представлены зависимости дисперсии ошибки фильтрации изображения De от дисперсии шума Dn, полученные с использованием векторного фильтра Калмана без интерполяции [5] и с интерполяцией [9], дискретного фильтра Винера [8] и ДС-фильтра.
Анализ кривых показывает эффективность предложенного метода фильтрации, выигрыш которого по сравнению с остальными фильтрами составляет до 120% по уровню дисперсии ошибки оценивания. Более того, имеет место еще более сильный результат. ДС-фильтр в среднем выигрывает до 15…20% по уровню дисперсии ошибки оценивания у фильтров A1-A3 даже в том случае, если последние применяются уже к сегментированному человеком изображению. Это объясняется возможностью адаптивной подстройки параметров ДС-фильтра под изменяющиеся вероятностные и корреляционные параметры изображения.
3. КВАЗИОПТИМАЛЬНЫЕ ДВАЖДЫ СТОХАСТИЧЕСКИЕ ФИЛЬТРЫ
Предложенное выше решение задачи фильтрации пространственно неоднородных изображений на фоне белого шума представляется незаконченным, поскольку предполагает полукаузальный характер фильтрации и значительное количество операций, необходимых для реализации фильтра. В связи с этим рассмотрим возможности построения ДС-моделей и алгоритмов фильтрации поля $~\left\{ {{{{\bar {x}}}_{{\bar {i}}}}} \right\}$ на фоне аддитивной помехи в скользящих по сетке ${\Omega \;}$ окнах. Для определенности будем считать вначале, что сетка ${\Omega }$ является двумерной размером ${{M}_{1}} \times {{M}_{2}}$ элементов, а используемые окна прямоугольными одинаковыми размерами ${{W}_{1}} \times {{W}_{2}}$. Окно, геометрический центр которого располагается в точке $\left( {i,j} \right),$ будем обозначать через ${{\bar {X}}_{{i,j}}}.$ Также будем считать, что в результате перемещения этого окна на одну позицию по вертикали и по горизонтали область ${{D}_{{i + 1j + 1}}},$ построенная для точки $\left( {i + 1,j + 1} \right),$ состоит из элементов ${{\bar {X}}_{{ij}}} \cup {{\bar {X}}_{{i - 1j}}} \cup {{\bar {X}}_{{ij - 1}}}$ для любых пар $\left( {i,j} \right)$. Очевидно, всегда можно выбрать ${{W}_{1}}$ и ${{W}_{2}}$ таким образом, что указанные условия будут выполняться.
Предположим, что определены W1 × W2 элементов вектора ${{\bar {X}}_{{i,j - 1}}}$ = $\left( {\bar {x}_{{i,j - 1}}^{1},\bar {x}_{{i,j - 1}}^{2},..,\bar {x}_{{i,j - 1}}^{{{{W}_{1}}{{W}_{2}}}}} \right),$ входящие в окно на позиции $\left( {i,j - 1} \right)$. Будем также считать, что порядок заполнения элементов вектора ${{\bar {X}}_{{i,j - 1}}}$ определяется линейной разверткой (построчно) в пределах текущего расположения окна. Сдвинем окно на одну позицию и сформируем вектор ${{\bar {X}}_{{i,j}}}$ $ = \left( {\bar {x}_{{i,j}}^{1},\bar {x}_{{i,j}}^{2},..,\bar {x}_{{i,j}}^{{{{W}_{1}}{{W}_{2}}}}} \right).$ Обратим внимание, что в силу особенностей ДС-модели, элементами ${{\bar {X}}_{{i,j}}}$ являются векторы, вообще говоря, разной длины. Также отметим, что позиции, на которые сдвигается окно по каждому измерению, не обязательно соответствуют отсчетам самого СП. Так можно описать перемещение окна на любое целое количество отсчетов вдоль каждого из измерений.
Используя предлагаемую выше методику, нетрудно записать следующее выражение, определяющее поведение произвольного ${{\bar {X}}_{{i,j}}}$:
(7)
${{\bar {X}}_{{i,j}}} = {{{\mathbf{{\rm P}}}}_{{i,j - 1}}}{{\bar {X}}_{{i,j - 1}}} + {{{\mathbf{{\rm P}}}}_{{i - 1,j}}}{{\bar {X}}_{{i - 1,j}}} + {{\vartheta }_{{ij}}}{{\bar {\xi }}_{{ij}}}.$Обратим особое внимание, что в выражении (7) вектор ${{\bar {\xi }}_{{ij}}}$ составлен только из случайных величин, принадлежащих точке $\left( {i + \left[ {\frac{{{{W}_{1}}}}{2}} \right],j + \left[ {\frac{{{{W}_{2}}}}{2}} \right]} \right)$, поcкольку
Среди различных вариантов обработки двумерного изображения на основе соотношения (7) особое место занимает фильтрация в параллельно скользящих окнах. При этом начальные параметры фильтрации каждой последующей строки определяются результатами фильтрации предыдущей строки. Подобная фильтрация представляется весьма перспективной, поскольку она может быть очень просто распараллелена на процедуры построчной оконной рекуррентной фильтрации. Так как каждая такая процедура включает в себя значительный объем повторяющихся тензорных вычислений, ее удобно реализовывать на графических процессорах с параллельной архитектурой (дискретных графических ускорителях, поддерживающих архитектуру Compute Unified Device Architecture (CUDA) и последующих).
Для иллюстрации указанного способа обработки предположим, что изображение может быть описано моделью (5). Для определенности будем считать, что фильтрация осуществляется в скользящих окнах размером 3 × 3 элемента. Тогда не сложно показать, что четырехмерный тензор ${{{\mathbf{{\rm P}}}}_{{i,j}}}$ в формуле (7) можно представить в виде матрицы размером 9 × 9, элементами которой в свою очередь являются матрицы размером 3 × 3. При этом почти все эти вложенные матрицы являются нулевыми, за исключением
Тензор ${{{\mathbf{Q}}}_{{i,j}}}$ можно представить аналогичным образом. При этом
Указанные соотношения позволяют реализовать построчную процедуру фильтрации. При этом
(8)
${{\hat {\bar {X}}}_{{i,j}}} = {{\hat {\bar {X}}}_{{{\text{Э}}i,j}}} + {{{\mathbf{P}}}_{{Dij}}}{\mathbf{V}}_{n}^{{ - 1}}\left( {{{z}_{{i + 1,j + 1}}} - {\mathbf{\Upsilon }}{{{\hat {\bar {X}}}}_{{{\text{Э}}ij}}}} \right).$Здесь ${{\hat {\bar {X}}}_{{{\text{Э}}i,j}}} = {{{\mathbf{{\rm P}}}}_{{i,j}}}{{\bar {X}}_{{i - 1,j}}} + {{{\mathbf{Q}}}_{{i,j}}}{{\bar {X}}_{{i,j - 1}}},$ ${{{\mathbf{P}}}_{{Di,j}}} = $ $ = {{{\mathbf{P}}}_{{{\text{Э}}i,j}}}{{\left( {{\mathbf{E}} + {\mathbf{V}}_{n}^{{ - 1}}{{{\mathbf{P}}}_{{{\text{Э}}i,j}}}} \right)}^{{ - 1}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}i,j}}} = {{{\mathbf{P}}}_{{{\text{Э}}1i,j}}} + {{{\mathbf{P}}}_{{{\text{Э}}2i,j}}} + {{{\mathbf{V}}}_{{\xi i,j}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}1i,j}}} = {{{\mathbf{P}}}_{{i,j}}}{{{\mathbf{P}}}_{{Di,j - 1}}}{\mathbf{P}}_{{i,j}}^{T},$ ${{{\mathbf{P}}}_{{{\text{Э}}2i,j}}} = {{{\mathbf{Q}}}_{{i,j}}}{{{\mathbf{P}}}_{{Di - 1,j}}}{\mathbf{Q}}_{{i,j}}^{T},~$ где ${{{\mathbf{P}}}_{{{\text{Э}}ij}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}1ij}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}2ij}}},$ ${{{\mathbf{P}}}_{{Di,j - 1}}}$ – $9 \times 9 \times 3 \times 3$-тензоры; ${\mathbf{V}}_{n}^{{ - 1}} = {1 \mathord{\left/ {\vphantom {1 {\sigma _{n}^{2}}}} \right. \kern-0em} {\sigma _{n}^{2}}};$ ${\mathbf{\Upsilon }}$ – $~9 \times 3 \times 3$-тензор, первый слой которого
а второй и третий слои тензора ${\mathbf{\Upsilon }}$ являются нулевыми. Выражение (8) предполагает переоценку всех элементов вектора ${{\bar {X}}_{{i,j}}},$ за исключением последнего, на каждой итерации по результатам обработки одного-единственного наблюдения ${{z}_{{i + 1j + 1}}}.$ При этом важно, что выражение (8) дает возможность простого распараллеливания процессов обработки. Действительно, для оценки ${{\hat {\bar {X}}}_{{i,j}}}$ требуется только оценка, сделанная на предыдущем шаге ${{\hat {\bar {X}}}_{{i,j - 1}}}$ и в предыдущей строке ${{\hat {\bar {X}}}_{{i - 1,j}}}.$ Соответственно, возможно организовать параллельную обработку “строк” изображения с задержкой на условной такт каждой последующей строки.
Основные сложности применения рассмотренных фильтров, связаны с необходимостью осуществления тензорных операций. Рассмотрим возможности упрощения процедур. Для этого будем считать, что корреляционные характеристики одинаковы во всех направлениях, в том числе по условным вертикали и горизонтали изображения. Будем также полагать, что скорость изменения корреляционных характеристик незначительна и в пределах окна фильтрации эти корреляционные характеристики можно считать одинаковыми. Тогда рассмотрим следующие векторы:
и построим для них соотношение вида
где ${{{\mathbf{{\rm P}}}}_{{i - 1,j}}}$ и ${{{\mathbf{Q}}}_{{i,j - 1}}}$ – двумерные матрицы размером 10 × 10, элементы которых равны нулю почти всюду, за исключением
Использование такого подхода позволяет реализовать построчную процедуру фильтрации. При этом
(9)
${{\hat {\bar {X}}}_{{i,j}}} = {{\hat {\bar {X}}}_{{{\text{Э}}i,j}}} + {{{\mathbf{P}}}_{{Dij}}}{\mathbf{V}}_{n}^{{ - 1}}\left( {{{z}_{{i + 1,j + 1}}} - {\mathbf{\Upsilon }}{{{\hat {\bar {X}}}}_{{{\text{Э}}ij}}}} \right),$где ${{\hat {\bar {X}}}_{{{\text{Э}}i,j}}} = {{{\mathbf{{\rm P}}}}_{{i,j}}}{{\bar {X}}_{{i - 1,j}}} + {{{\mathbf{Q}}}_{{i,j}}}{{\bar {X}}_{{i,j - 1}}},$ ${{{\mathbf{P}}}_{{Di,j}}} = {{{\mathbf{P}}}_{{{\text{Э}}i,j}}} \times $ $ \times \,\,{{\left( {{\mathbf{E}} + {\mathbf{V}}_{n}^{{ - 1}}{{{\mathbf{P}}}_{{{\text{Э}}i,j}}}} \right)}^{{ - 1}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}i,j}}} = {{{\mathbf{P}}}_{{{\text{Э}}1i,j}}} + {{{\mathbf{P}}}_{{{\text{Э}}2i,j}}} + {{{\mathbf{V}}}_{{\xi i,j}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}1i,j}}} = $ $ = {{{\mathbf{P}}}_{{i,j}}}{{{\mathbf{P}}}_{{Di,j - 1}}}{\mathbf{P}}_{{i,j}}^{T},$ ${{{\mathbf{P}}}_{{{\text{Э}}2i,j}}} = {{{\mathbf{Q}}}_{{i,j}}}{{{\mathbf{P}}}_{{Di - 1,j}}}{\mathbf{Q}}_{{i,j}}^{T}.$ Здесь ${{{\mathbf{P}}}_{{{\text{Э}}ij}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}1ij}}},$ ${{{\mathbf{P}}}_{{{\text{Э}}2ij}}},$ ${{{\mathbf{P}}}_{{Di,j - 1}}}$ – матрицы размером $10 \times 10$;
Найденные процедуры несложно обобщить на произвольный размер окна фильтрации. Например, для размера окна 5 × 5 длина вектора ${{\bar {X}}_{{i,j}}}$ увеличится с 10 элементов до 26. Соответственно, размер матриц ${{{\mathbf{{\rm P}}}}_{{i,j}}}$, ${{{\mathbf{Q}}}_{{i,j}}}$, ${{{\mathbf{P}}}_{{{\text{Э}}ij}}},$ ${{{\mathbf{P}}}_{{Di,j}}}$ составит 26 × 26, матрица ${\mathbf{\Upsilon }}$ будет иметь размер 5 × 26, однако структура всех этих матриц останется без каких-либо изменений.
Обратим внимание, что все перечисленные фильтры позволяют на каждом шаге получать в том числе локальную оценку корреляционных характеристик изображения. Например, для последнего фильтра такой характеристикой является элемент ${{\bar {X}}_{{i,j}}}\left( {10} \right)$ для каждой точки$~\left( {i,j} \right)$. Это дает возможность адаптировать размер окна фильтрации под оцененные локальные корреляционные характеристики в процессе самой фильтрации. Такую адаптацию можно интерпретировать как определение для каждой точки $\left( {i,j} \right)$ некаузальной области, определяющей значение СП в данной точке.
На рис. 3 представлены фрагменты отдельных кадров трех тестовых спутниковых изображений, полученных с космического аппарата Landsat-8. С целью анализа эффективности найденных алгоритмов изображения были смешаны с белым шумом разной интенсивности так, что отношение сигнал/шум $q = {{{\sigma }_{x}^{2}} \mathord{\left/ {\vphantom {{{\sigma }_{x}^{2}} {{\sigma }_{n}^{2}}}} \right. \kern-0em} {{\sigma }_{n}^{2}}}$ изменялось в диапазоне от 2 до 10, и была выполнена фильтрация.
В табл. 1 представлены результаты анализа эффективности описанных процедур в сравнении c LPA/ICI-алгоритмом (Local Polynomial Approximation/Intersection Confidence Interval) [21 ] , вейвлет-фильтром с SURE (Stein’s Unbiased Risk Estimation) порогом [22, 23], разделимым билатеральным фильтром [24] и дважды стохастическим фильтром (6) по относительной дисперсии ошибки фильтрации ($\sum\nolimits_{i,j \in D} {{{{{{\left( {{{x}_{{i,j}}} - {{{\hat {x}}}_{{i,j}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{x}_{{i,j}}} - {{{\hat {x}}}_{{i,j}}}} \right)}}^{2}}} {{\sigma }_{x}^{2}}}} \right. \kern-0em} {{\sigma }_{x}^{2}}}} $).
Таблица 1.
Сравнительные результаты качества фильтрации спутниковых изображений
| Алгоритм фильтрации | Номер изображения | Время обработки | q | ||
|---|---|---|---|---|---|
| 2 | 5 | 10 | |||
| LPA/ICI фильтр | 1 | 23 с | 0.076 | 0.042 | 0.031 |
| 2 | 18 с | 0.067 | 0.036 | 0.028 | |
| 3 | 28 с | 0.083 | 0.045 | 0.032 | |
| Вeйвлет-фильтpaция c SURЕ-пopoгом | 1 | 14 с | 0.083 | 0.065 | 0.053 |
| 2 | 13.5 с | 0.081 | 0.061 | 0.049 | |
| 3 | 14 с | 0.087 | 0.064 | 0.051 | |
| Билатеральный фильтр (на основе параллельной декомпозиции на пространственные фильтры) | 1 | 0.8 с | 0.112 | 0.091 | 0.071 |
| 2 | 0.7 с | 0.097 | 0.083 | 0.063 | |
| 3 | 0.8 с | 0.107 | 0.089 | 0.076 | |
| Дважды стохастический фильтр | 1 | 17 мин 56 с | 0.089 | 0.048 | 0.036 |
| 2 | 17 мин 39 с | 0.083 | 0.042 | 0.033 | |
| 3 | 18 мин 19 с | 0.092 | 0.051 | 0.041 | |
| Дважды стохастический фильтр с интерполяцией | 1 | 6 ч 3 мин 9 с | 0.071 | 0.038 | 0.027 |
| 2 | 6 ч 1 мин 11 с | 0.063 | 0.033 | 0.024 | |
| 3 | 6 ч 4 мин 53 с | 0.079 | 0.043 | 0.030 | |
| Дважды стохастическая фильтрация в параллельно скользящих окнах в соответствии с соотношением (8) | 1 | 16 с | 0.068 | 0.035 | 0.027 |
| 2 | 15 с | 0.059 | 0.033 | 0.025 | |
| 3 | 16 с | 0.074 | 0.04 | 0.028 | |
| Дважды стохастическая фильтрация в параллельно скользящих окнах в соответствии с соотношением (9) | 1 | 4.4 с | 0.076 | 0.04 | 0.03 |
| 2 | 4.3 с | 0.064 | 0.035 | 0.026 | |
| 3 | 4.4 с | 0.083 | 0.045 | 0.031 | |
Представленные результаты свидетельствуют о меньших значениях относительной дисперсии ошибок предложенных алгоритмов фильтрации при различных уровнях сигнал/шум q. Это связано с наличием протяженных областей на зашумленном изображении, в пределах которых ДС-фильтры адаптируются к локальным особенностям. При этом качество обработки при использовании параллельно скользящих и взаимосвязанных окон оказывается даже выше, чем у формально оптимальных ДС-фильтров. Проведенные исследования показывают, что это связано с наличием четких границ на исходных изображениях, приводящих к локальному рассогласованию оптимального ДС-фильтра. Его аналог для обработки в некаузальных окнах имеет существенно более компактную рабочую область и быстрее адаптируется к резким изменениям свойств изображения. Кроме того, имеется значительный выигрыш в количестве требуемых на реализацию вычислительных ресурсов (на два-три порядка). В результате реализованные на CUDA-архитектуре алгоритмы оказываются существенно быстрее, чем процедуры, применяемые в графических редакторах. При этом выигрыш может быть намного увеличен в случае использования специальных методик оптимизации тензорных операций с учетом разреженности используемых тензоров.
ЗАКЛЮЧЕНИЕ
Таким образом, рассмотрена модификация ДС-фильтра, основанная на применении скользящих окон фильтрации. Такая модификация выгодно отличается от обычного ДС-фильтра существенно более высокой скоростью обработки и некаузальными свойствами, позволяющими уменьшить время адаптации при переходе границ между объектами. Отмеченные свойства позволяют рекомендовать предложенную модификацию ДС-фильтра для обработки реальных пространственно неоднородных сигналов.
Список литературы
Ширман Я.Д., Манжос В.Н. Теория и техника обработки радиолокационной информации на фоне помех. М.: Радио и связь, 1981.
Винклер Г. Анализ изображений, случайные поля и динамические методы Монте-Карло. Новосибирск: Гео, 2002.
Гонсалес Р., Вудс Р. Цифровая обработка изображений. М.: Техносфера, 2012.
Шовенгердт Р.А. Дистанционное зондирование. Методы и модели обработки изображений. М.: Техносфера, 2013.
Bouman C.A. Model Based Imaging Processing. West Lafayette: Purdue Univ., 2013.
Jensen J. Introductory Digital Image Processing: a remote sensing perspective. London: Pearson Education, 2015.
Потапов А.А. Новейшие методы обработки изображений. М.: Физматлит, 2008.
Васильев К.К., Крашенинников В.Р. Статистический анализ последовательностей изображений. М.: Радиотехника, 2017.
Васильев К.К. Оптимальная обработка сигналов в дискретном времени: учебное пособие. М.: Радиотехника, 2016.
Петюшко А.А. // Интеллектуальные системы. Теория и приложения. 2010. Т. 14. № 1. С. 225.
Бондур Н.И., Аржененко В.Н., Линник В.Г. и др. // Исследование Земли из космоса. 2003. № 2. С. 3.
Сергеев В.В., Денисова А.Ю. // Компьютерная оптика. 2013. Т. 37. № 2. С. 239.
Болгов А.Н. // Вестник Сибирского гос. аэрокосмического ун-та. 2014. № 5. С. 44.
Грудин Б.Н., Плотников В.С., Смольянинов Н.А. // Автометрия. 2010. Т. 46. № 3. С. 13.
Vasil'ev K.K., Dement’ev V.E., Andriyanov N.A. // Pattern Recognition and Image Analysis. 2016. V. 26. № 1. P. 240.
Vasiliev K.K., Dementiev V.E., Andriyanov N.A. // CEUR Workshop Proc. 2017. V. 1814. P. 10.
Дементьев В.Е. // Радиотехника. 2017. № 6. С. 18.
Vasil'ev K.K., Popov O.V. // Pattern Recognition and Image Analysis. 1999. V. 9. № 2. P. 327.
Котов В.М., Шкердин Г.Н., Шкердин Д.Г. и др. // РЭ. 2008. Т. 53. № 3. С. 333.
Caмoйлин E.A. // PЭ. 2007. T. 52. № 7. C. 831.
Paliy D., Katkovnik V., Bilcu R. et al. // Int. J. Imaging Sys. Tech., Sp. Iss. Appl. Color Image Process. 2008. V. 17. № 3. P. 105.
Воскобойников Ю.Е., Гочаков А.В. // Автометрия. 2011. № 1. С. 17.
Ясин А.С., Павлов А.Н., Храмов А.Е. // РЭ. 2016. Т. 61. № 2. С. 149.
Беляева О.В., Пащенко О.Б., Филиппов М.В. // Труды МАИ. 2017. № 94. С. 1.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника