1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 65, № 5, 2020

Радиотехника и электроника, 2020, T. 65, № 5, стр. 479-486

Нижняя граница Рао–Крамера дисперсий совместных оценок параметров смеси узкополосного и широкополосного сигналов с белым шумом

В. Н. Жураковский a, *, А. С. Логвиненко a, **

a Московский государственный технический университет им. Н.Э. Баумана
Москва, 2-я Бауманская ул., д. 5, стр. 1, Российская Федерация

* E-mail: vnzh521@yandex.ru
** E-mail: anna.logvinenko.bmstu@mail.ru

Поступила в редакцию 07.09.2018
После доработки 27.11.2018
Принята к публикации 17.01.2019

Полный текст (PDF)

Аннотация

Решена задача определения минимума дисперсий совместных оценок параметров сигнала, представляющего смесь узкополосного и широкополосного сигналов и белого гауссовского шума, представленных в виде комплексного суммарного сигнала. Получено выражение для расчета элементов матрицы Фишера, необходимой для установления нижней границы Рао–Крамера. Приведены графики зависимости среднеквадратических отклонений оценок (СКО) от отношения сигнал/шум, длины выборки и от исходных параметров сигнала – центральных частот составляющих сигнала, ширины широкополосной составляющей. Проведено сравнение с минимальными СКО, полученными для модели сигнала, включающей только широкополосную составляющую. Проведен анализ полученных результатов, позволяющий оценить требования, которые могут быть предъявлены к разрабатываемым алгоритмам совместной оценки параметров смеси сигналов рассматриваемого типа, в зависимости от установленных значений частоты дискретизации и объема выборки.

ВВЕДЕНИЕ

При синтезе различных алгоритмов цифровой обработки сигналов, разработчикам часто приходится сталкиваться с проблемой определения параметров смеси узкополосного (УП) и широкополосного (ШП) сигналов [1, 2]. В радиолокации, в частности, к таким алгоритмам можно отнести спектральные алгоритмы селекции движущихся целей (СДЦ) на фоне пассивных широкополосных помех [3–9]. Среди многообразия таких алгоритмов СДЦ существует класс адаптивных [6–9], составляющей частью которых в том или ином виде является оценка параметров сигнала со спектром Доплера от точечной цели (спектр Доплера которой – узкополосный сигнал на частоте, соответствующей скорости цели) и широкополосной помехи. В зависимости от типа радиолокационных систем (РЛС) (обзора, обнаружения, целеуказания) и их назначения в вектор оцениваемых информативных параметров включаются разные составляющие и предъявляются различные требования к точности его оценки [10–13].

С развитием информационных технологий для решения перечисленных типов задач продолжают разрабатываться новые, более совершенные алгоритмы оценки. Однако для выдвижения корректных требований к синтезируемым алгоритмам необходимо знать потенциальную точность оценки параметров сигналов рассматриваемого типа. Одним из методов установления предела достижимой точности оценок является нахождение границ Рао–Крамера (ГРК) [14].

В отечественной и зарубежной литературе выражения нижней границы Рао–Крамера для рассматриваемых типов сигналов приводятся для различных комбинаций составляющих вектора оцениваемых параметров, однако, как правило, ГРК вычисляется либо для узкополосных, либо для широкополосных сигналов в отдельности [15–18]. Также в приведенных статьях часто в качестве модели сигналов используются вещественные сигналы, вычисление же ГРК для комплексных сигналов приводится редко в виду более сложной процедуры вывода итоговых выражений. В связи с этим целью данной работы являлось установление нижней границы Рао–Крамера совместных оценок смеси узкополосного и широкополосного сигналов, представленных в комплексном виде. В качестве информационных параметров были выбраны: центральная частота и ширина спектра ШП сигнала и частота УП сигнала.

1. МОДЕЛЬ СИГНАЛА

Модель рассматриваемого сигнала представляет собой широкополосный сигнал:

$s\left( n \right) = {{s}_{B}}\left( n \right) + {{s}_{N}}\left( n \right),$
где $n~$ – номер дискретного отcчета сигнала,
(1)
${{s}_{B}}\left( n \right) = {{A}_{B}}\int\limits_{{{ - {{W}_{B}}} \mathord{\left/ {\vphantom {{ - {{W}_{B}}} 2}} \right. \kern-0em} 2}}^{{{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} 2}} \right. \kern-0em} 2}} {{\text{exp}}(j2\pi {{t}_{d}}n\left( {{{F}_{B}} + w)} \right)dw} $
– модель ШП-сигнала (${{A}_{B}}$ – спектральная плотность ШП-сигнала,${{F}_{B}}$ – центральная частота спектра ШП-сигнала, Гц, ${{W}_{B}}$ – ширина спектра сигнала, Гц, ${{t}_{d}}$ – период дискретизации, c),
${{s}_{N}}\left( n \right) = {{A}_{N}}{\text{exp}}\left( {j2\pi {{t}_{d}}n{{F}_{N}}} \right),$
– модель УП-сигнала (${{A}_{N}}$ – амплитуда УП-сигнала, ${{F}_{N}}$ – частота УП-сигнала, Гц).

Модель наблюдения имеет вид

$x\left( n \right) = s\left( n \right) + w\left( n \right),$
где $x\left( n \right)$ – наблюдаемый комплексный сигнал, $w\left( n \right)$ – комплексный белый гауссовый шум. Представим модель наблюдения в векторном виде
(2)
$\vec {x} = \vec {s} + \vec {w},$
где $\vec {x} = ~{{[{{x}_{1}}, \ldots ,{{x}_{K}}]}^{T}},$ $\vec {s} = ~{{[{{s}_{1}}, \ldots ,{{s}_{K}}]}^{T}},$ $\vec {w} = ~{{[{{w}_{1}}, \ldots ,{{w}_{K}}]}^{T}},$ $K$ – длина выборки.

2. ВЫВОД НИЖНЕЙ ГРАНИЦЫ РАО–КРАМЕРА

Для определения потенциальной точности совместной оценки центральной частоты и ширины спектра ШП-сигнала и частоты УП-сигнала (2) воспользуемся многомерным неравенством Рао–Крамера, устанавливающим нижнюю границу для матрицы ковариаций несмещенной оценки [15]:

${\mathbf{co}}{{{\mathbf{v}}}_{{\vec {\xi }}}}\left( {\vec {\hat {\xi }}} \right) \geqslant {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}^{{ - 1}}},$
где $\vec {\xi }$ – вектор оцениваемых параметров, $~\vec {\hat {\xi }}$ – несмещенная оценка вектора параметров $\vec {\xi }$, $~{\mathbf{I}}\left( {\vec {\xi }} \right)$ – информационная матрица Фишера, ${{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}^{{ - 1}}}$ – матрица, обратная к матрице Фишера.

Для случая совместной оценки центральной частоты широкополосного сигнала (${{F}_{B}}$), ширины его спектра (${{W}_{B}}$) и частоты УП-сигнала (${{F}_{N}}$) нижняя граница ковариационной матрицы рассчитывается следующим образом:

(3)
${\mathbf{co}}{{{\mathbf{v}}}_{{{{{\vec {\xi }}}_{{\min }}}}}}\left( {\overrightarrow {\hat {\xi }} } \right) = {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}^{{ - 1}}}{\text{\;,}}$
где

(4)
$\vec {\xi } = {{[{{F}_{B}},{{W}_{B}},{{F}_{N}}]}^{T}}.$

Соответственно, минимальные дисперсии оценок являются элементами главной диагонали матрицы, определяемой выражением (3):

(5)
${{D}_{{{\text{min}}}}}\left( {{{{\overrightarrow {\hat {\xi }} }}_{m}}} \right) = {{\left[ {{\mathbf{co}}{{{\mathbf{v}}}_{{{{{\vec {\xi }}}_{{\min }}}}}}(\vec {\hat {\xi }})} \right]}_{{mm}}} = ~\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]_{{mm}}^{{ - 1~}},$
где $m = 1, \ldots ,M$ ($M$ – размерность вектора параметров).

Найдем информационную матрицу Фишера ${\mathbf{I}}\left( {\vec {\xi }} \right).$ Элементы матрицы Фишера для комплексного сигнала $\vec {x}$, представленного моделью (2), и для вектора оцениваемых параметров $\vec {\xi }$ (4) рассчитываются следующим образом [15]:

(6)
${{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{ij}}} = \frac{2}{{{{\sigma }^{2}}}}{\text{\;Re}}\left[ {\mathop \sum \limits_{n = 1}^K \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{{\vec {\xi }}}_{i}}}}\frac{{\partial s\left( n \right)}}{{\partial {{{\vec {\xi }}}_{j}}}}} \right],$
где ${\text{Re}}$ – знак вещественной части, $s{\text{*}}\left( n \right)$ – сопряженное к $~s\left( n \right)~$ выражение.

Найдем частные производные от $s\left( n \right)$ по составляющим вектора параметров $\vec {\xi }$.

Перепишем (1) в виде

$\begin{gathered} {{s}_{B}}\left( n \right) = {{A}_{B}}\int\limits_{{{ - {{W}_{B}}} \mathord{\left/ {\vphantom {{ - {{W}_{B}}} 2}} \right. \kern-0em} 2}}^{{{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} 2}} \right. \kern-0em} 2}} {{\text{exp}}\left( {j2\pi {{t}_{d}}n\left( {{{F}_{B}} + w} \right)} \right)dw} = \\ = \frac{{ - 2{{A}_{B}}j}}{{{{C}_{n}}}}{\text{exp}}(j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right), \\ \end{gathered} $
где ${{C}_{n}} = 2\pi {{t}_{d}}n.$

Частные производные от $s\left( n \right)$ имеют вид

$\frac{{\partial s\left( n \right)}}{{\partial {{F}_{B}}}} = \frac{{\partial {{s}_{B}}\left( n \right)}}{{\partial {{F}_{B}}}} = 2{{A}_{B}}{\text{exp(}}j{{C}_{n}}{{F}_{B}}){\text{sin}}\left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right),$
$\frac{{\partial s\left( n \right)}}{{\partial {{W}_{B}}}} = \frac{{\partial {{s}_{B}}\left( n \right)}}{{\partial {{W}_{B}}}} = - {{A}_{B}}j{\text{exp(}}j{{C}_{n}}{{F}_{B}})\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right),$
$\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}} = \frac{{\partial {{s}_{N}}\left( n \right)}}{{\partial {{F}_{N}}}} = j{{C}_{n}}{{A}_{N}}\left[ {{\text{exp}}\left( {j{{C}_{n}}{{F}_{N}}} \right)} \right].$

Теперь найдем частные производные от $s{\text{*}}\left( n \right).$ Выражение для $s{\text{*}}\left( n \right)~$имеет вид

$s{\text{*}}\left( n \right) = s_{B}^{*}\left( n \right) + s_{N}^{*}\left( n \right),$
где

$s_{B}^{*}\left( n \right) = \frac{{2{{A}_{B}}j}}{{{{C}_{n}}}}{\text{exp}}( - j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right),$
$s_{N}^{*}\left( n \right) = {{A}_{N}}{\text{exp}}\left( { - j{{C}_{n}}{{F}_{N}}} \right).$

Далее находим частные производные от $s{\text{*}}\left( n \right)$:

$\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}} = \frac{{\partial s_{B}^{*}\left( n \right)}}{{\partial {{F}_{B}}}} = 2{{A}_{B}}{\text{exp}}( - j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right),$
$\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{W}_{B}}}} = \frac{{\partial s_{B}^{*}\left( n \right)}}{{\partial {{W}_{B}}}} = {{A}_{B}}j{\text{exp(--}}j{{C}_{n}}{{F}_{B}})\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right),$
$\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{N}}}} = \frac{{\partial s_{N}^{*}\left( n \right)}}{{\partial {{F}_{N}}}} = - j{{C}_{n}}{{A}_{N}}{\text{exp}}\left( { - j{{C}_{n}}{{F}_{N}}} \right).$

Таким образом, можем найти произведения соответствующих производных, использующихся для расчета элементов матрицы Фишера (6):

1) для элементов главной диагонали матрицы Фишера –

$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{B}}}} = 2{{A}_{B}}\exp ( - j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) \times \\ \times \,\,2{{A}_{B}}\exp (j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) = 4{{A}_{B}}^{2}{{\left[ {\sin ({{C}_{n}}\frac{{{{W}_{B}}}}{2})} \right]}^{2}}, \\ \end{gathered} $
$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{W}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{W}_{B}}}} = j{{A}_{B}}{\text{exp}}\left( { - j{{C}_{n}}{{F}_{B}}_{~}} \right)\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) \times \\ \times \,\,j{{C}_{n}}{{A}_{N}}{\text{exp}}\left( {j{{C}_{n}}{{F}_{N}}} \right)\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) = \\ = A_{B}^{2}{{\left[ {\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \right]}^{2}}, \\ \end{gathered} $
$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{N}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}} = - j{{C}_{n}}{{A}_{N}}{\text{exp}}\left( { - j{{C}_{n}}{{F}_{N}}} \right) \times \\ \times \,\,j{{C}_{n}}{{A}_{N}}{\text{exp}}\left( {j{{C}_{n}}{{F}_{N}}} \right) = C_{n}^{2}A_{N}^{2} \\ \end{gathered} $

2) для остальных элементов матрицы Фишера –

$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{W}_{B}}}} = 2{{A}_{B}}\exp ( - j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) \times \\ \times \,\,{{A}_{B}}j\exp (j{{C}_{n}}{{F}_{B}})\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) = A_{B}^{2}j\sin ({{C}_{n}}{{W}_{B}}), \\ \end{gathered} $
$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}} = 2{{A}_{B}}\exp ( - j{{C}_{n}}{{F}_{B}})\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) \times \\ \times \,\,j{{C}_{n}}{{A}_{N}}\left[ {{\text{exp}}\left( {j{{C}_{n}}{{F}_{N}}} \right)} \right] = \\ = j{{C}_{n}}{{A}_{N}}{{A}_{B}}\exp [j{{C}_{n}}\left( {{{F}_{N}} - {{F}_{B}}} \right)]\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right), \\ \end{gathered} $
$\begin{gathered} \frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{W}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}} = {{A}_{B}}j\exp ( - j{{C}_{n}}{{F}_{B}})\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right) \times \\ \times \,\,j{{C}_{n}}{{A}_{N}}\left[ {{\text{exp}}\left( {j{{C}_{n}}{{F}_{N}}} \right)} \right] = \\ = - {{C}_{n}}{{A}_{N}}{{A}_{B}}\left[ {{\text{exp}}j{{C}_{n}}\left( {{{F}_{N}} - {{F}_{B}}} \right)} \right]\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right). \\ \end{gathered} $

Тогда элементы главной диагонали матрицы Фишера (6) соответственно будут равны:

$\begin{gathered} {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{11}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} } \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{B}}}}} \right] = \\ = \frac{{8A_{B}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{{\left[ {\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \right]}}^{2}}} , \\ \end{gathered} $
$\begin{gathered} {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{22}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{W}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{W}_{B}}}}} \right]} = \\ = \frac{{2A_{B}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{{\left[ {\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \right]}}^{2}}} , \\ \end{gathered} $
${{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{33}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{N}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}}} \right]} = \frac{{2A_{N}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {C_{n}^{2}} ,$

остальные элементы матрицы Фишера:

${{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{12}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{W}_{B}}}}} \right]} = 0,$
$\begin{gathered} {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{13}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{F}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}}} \right] = } \\ = \frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{C}_{n}}} \sin \left[ {{{C}_{n}}\left( {{{F}_{N}} - {{F}_{B}}} \right)} \right]\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right), \\ \end{gathered} $
$\begin{gathered} {{\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]}_{{23}}} = \frac{2}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {\operatorname{Re} } \left[ {\frac{{\partial s{\text{*}}\left( n \right)}}{{\partial {{W}_{B}}}}\frac{{\partial s\left( n \right)}}{{\partial {{F}_{N}}}}} \right] = \frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}} \times \\ \times \,\,\sum\limits_{n = 1}^K {{{C}_{n}}} \cos \left[ {{{C}_{n}}\left( {{{F}_{N}} - {{F}_{B}}} \right)} \right]\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right). \\ \end{gathered} $

Матрица Фишера имеет вид

$\left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{8A_{B}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{{\left[ {\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \right]}}^{2}}} }&0&{\frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{C}_{n}}\sin \left[ {{{C}_{n}}({{F}_{N}} - {{F}_{B}})} \right]\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} } \\ 0&{\frac{{ - 2A_{B}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{{\left[ {\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \right]}}^{2}}} }&{\frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{C}_{n}}\cos \left[ {{{C}_{n}}({{F}_{N}} - {{F}_{B}})} \right]\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} } \\ {\frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{C}_{n}}\sin \left[ {{{C}_{n}}({{F}_{N}} - {{F}_{B}})} \right]\sin \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} \,}&{\,\frac{{ - 2{{A}_{N}}{{A}_{B}}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {{{C}_{n}}\cos \left[ {{{C}_{n}}({{F}_{N}} - {{F}_{B}})} \right]\cos \left( {{{C}_{n}}\frac{{{{W}_{B}}}}{2}} \right)} }&{\frac{{2A_{N}^{2}}}{{{{\sigma }^{2}}}}\sum\limits_{n = 1}^K {C_{n}^{2}} } \end{array}} \right]$

Используя полученное выражение, а также (4), (5), можем рассчитать минимальные среднеквадратические отклонения (СКО) оценок параметров:

${{\sigma }_{{{{\theta }_{{\min }}}}}}\left( {{{F}_{B}}} \right) = \left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]_{{{\text{11}}}}^{{ - 1~}} = \sqrt {\frac{{{{M}_{{11}}}}}{{\det \left( {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right)}}} ,$
${{\sigma }_{{{{\theta }_{{\min }}}}}}\left( {{{W}_{B}}} \right) = \left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]_{{22}}^{{ - 1}} = \sqrt {\frac{{{{M}_{{22}}}}}{{\det \left( {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right)}}} ,$
${{\sigma }_{{{{\theta }_{{\min }}}}}}\left( {{{F}_{N}}} \right) = \left[ {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right]_{{33}}^{{ - 1}} = \sqrt {\frac{{{{M}_{{33}}}}}{{\det \left( {{\mathbf{I}}\left( {\vec {\xi }} \right)} \right)}}} .$

Для проверки правильности выведенных формул были сделаны аналогичные описанным выше преобразования в среде MATLAB с использованием пакета символьных вычислений [19]. Однако скорость вычислений в символьном виде значительно ниже. Поэтому путем численного моделирования было проведено сравнение результатов двух способов вычисления и была подтверждена корректность полученных аналитически формул.

3. АНАЛИЗ ЗАВИСИМОСТИ ГРК ОТ ПАРАМЕТРОВ ВХОДНОГО СИГНАЛА

Для упрощения понимания влияния различных параметров входного сигнала на значения минимальных СКО оценок сначала рассмотрим ГРК ШП-составляющей отдельно, а затем совместную ГРК с учетом наличия УП-составляющей в смеси.

Рассмотрим ГРК оценки параметров помехи. Минимальные СКО оценок ширины и центральной частоты помехи для этого случая определяются следующими выражениями [20]:

${{\sigma }_{{\min }}}\left( {{{F}_{B}}} \right) = ~\frac{1}{{2q{\text{*}}\sqrt {\left[ {K - \sum\limits_{n = 1}^K {\left( {\cos \left( {{{2\pi n~{{W}_{B}}} \mathord{\left/ {\vphantom {{2\pi n~{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}~} \right)} \right)} } \right]} ~}},$
${{\sigma }_{{\min }}}\left( {{{W}_{B}}} \right) = \,\,~\frac{1}{{q{\text{*}}\sqrt {\left[ {K + \sum\limits_{n = 1}^K {\left( {\cos \left( {{{2\pi n~{{W}_{B}}} \mathord{\left/ {\vphantom {{2\pi n~{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}~} \right)} \right)} } \right]} ~}}.$

Таким образом, можем рассмотреть зависимости от трех параметров исходного сигнала: $q$ – отношения сигнал/шум, $K$ – объема выборки, ${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$ – отношения ширины сигнала к частоте дискретизации.

На рис. 1а–1г приведены полученные в среде MATLAB зависимости минимальных СКО оценки параметров помехи (σmin(FB) и σmin(WB) от K и ${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$ при $q = 1$.

Рис. 1.

Зависимость ГРК оценки ширины помехи (а, б) и центральной частоты (в, г) от объема выборки и отношения ширины помехи к частоте дискретизации выборки при К = 2 (1), 6 (2), 20 (3) и 100 (4).

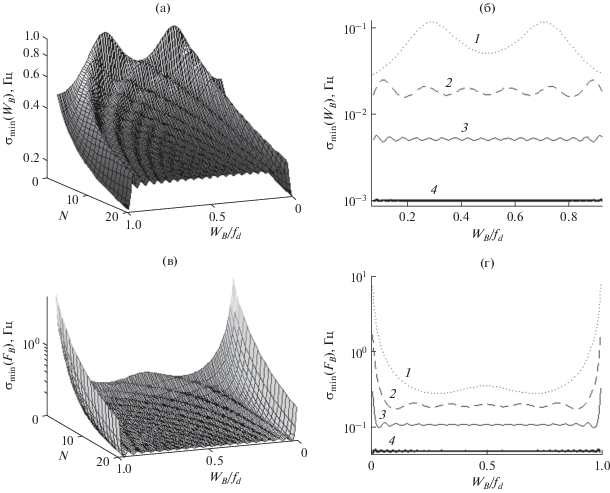
Как видно из рисунков, влияние отношения ширины помехи к частоте дискретизации (${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$) на величину минимального значения СКО оценки параметров помехи незначительно при больших объемах выборок (20 и более отсчетов), и им можно пренебречь при составлении требований к алгоритмам оценки параметров помехи и при сравнении разработанных алгоритмов с ГРК. Однако в случае маленьких выборок (от двух до десяти отсчетов) влияние величины ${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$ на минимальные СКО оценок необходимо учитывать.

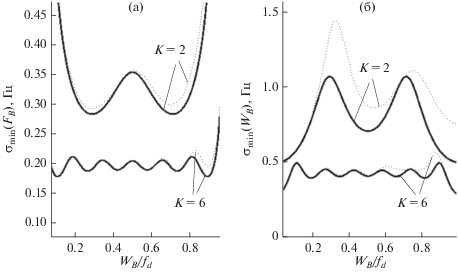
Теперь рассмотрим изменение вида данных зависимостей при добавлении к широкополосной помехе узкополосного сигнала от цели. Рассмотрим случай равенства амплитуд сигналов от цели и помехи. При следующих параметрах сигнала: q = 1, FN = 100 Гц, FB = 700 Гц, fd = 1400 Гц были получены зависимости ГРК оценок помехи при малых объемах выборок ($K$ = 2 и $K$ = 10 отсчетов) для случаев совместной оценки только параметров помехи (два параметра – FB, WB) и параметров суммарного сигнала от цели и помехи (три параметра – FB, WB, FN) (рис. 2). Из графиков, представленных на рис. 2, можно сделать вывод о том, насколько сильно зависит минимум СКО оценки выбранного параметра от значения ${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$.

Рис. 2.

Зависимость ГРК параметров помехи от W/fd при малых объемах выборки в случае совместной оценки как только параметров помехи (сплошные кривые), так и параметров суммарного сигнала (пунктирные) при q = 1, FN = = 100 Гц, FB = 700 Гц. На правом рисунке – увеличенный масштаб оси ординат.

Проанализируем зависимость ГРК оценок от ${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}$ при различных значениях FN/fd и при фиксированных q = 1, $K$ = 6, FB/fd = 0.5 (рис. 3).

Рис. 3.

Зависимость ГРК оценки от WB/fd при малых объемах выборки в случае совместной оценки только параметров помехи (а), и параметров суммарного сигнала (б) при q = 1, K = 6, FB/fd = 0.5, (в) – совместный график зависимостей, изображенных на рис. (а) – черный фон и рис. (б) – серый фон.

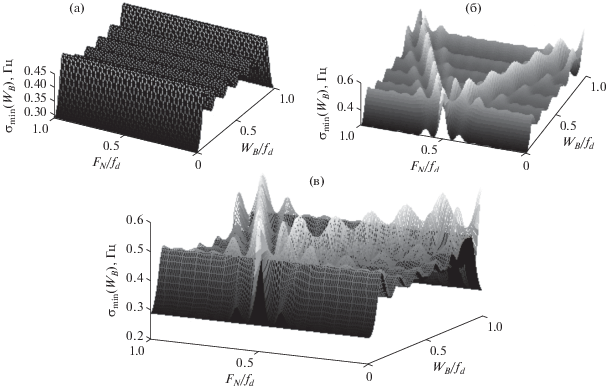
Приведены зависимости ГРК оценки WB отдельно для случая оценки только параметров помехи (рис. 3а), параметров смеси помехи с целью (рис. 3б), и совместный график, отражающий изменение характера зависимости ГРК оценки ширины помехи при добавлении к широкополосной помехе сигнала от цели (рис. 3в). Видно, что в целом зависимости на рис. 3а и 3б одинаковы, за исключением областей, расположенных возле прямых, которые можно описать уравнением

${{{{W}_{B}}} \mathord{\left/ {\vphantom {{{{W}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}} = 2\left| {{{{{F}_{N}}} \mathord{\left/ {\vphantom {{{{F}_{N}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}--{{{{F}_{B}}} \mathord{\left/ {\vphantom {{{{F}_{B}}} {{{f}_{d}}}}} \right. \kern-0em} {{{f}_{d}}}}} \right|.$

Вблизи значений, удовлетворяющих решению данного уравнения минимальные СКО оценок начинают бесконечно возрастать. Ширина данных областей определяется в свою очередь объемом выборки (рис. 4).

Рис. 4.

Зависимость ГРК оценки от WB/fd и FN/fd при N = 6 (а) и 100 (б) в случае совместной оценки как только параметров помехи (темный фон), так и параметров суммарного сигнала (светлый фон).

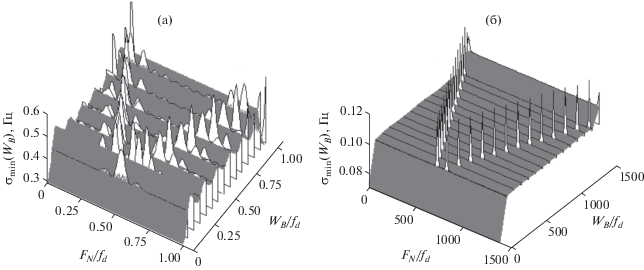
Из рис. 4 видно, что по мере увеличения объема выборки зависимости ГРК оценки ширины помехи для двух и трех параметров все больше совпадают, за исключением узких областей вблизи решений уравнения (7). Зависимости ГРК оценки центральной частоты ШП составляющей и частоты УП составляющей от WB/fd и FN/fd по характеру аналогичны, поэтому в статье не приводятся.

Далее рассмотрим зависимость ГРК оценки всех трех составляющих вектора параметров от центральной частоты помехи для случая маленькой ($K$ = 6) и большой выборки ($K$ = 100) при фиксированных значениях WB/fd, FB/fd и $q$ (рис. 5 и 6).

Рис. 5.

Зависимость ГРК оценки вектора параметров $\xi = {{[{{F}_{B}}~{{W}_{B}}{{F}_{N}}]}^{T}}$ от FB/fd при WB = 100 Гц и $K$ = 6 (пунктирная кривая) и 100 (сплошная); FN = 700 Гц, AN = 1, AB = 1, fd = 1400 Гц, q = 10. На вставках – зависимость ГРК оценки параметров от длины выборки K.

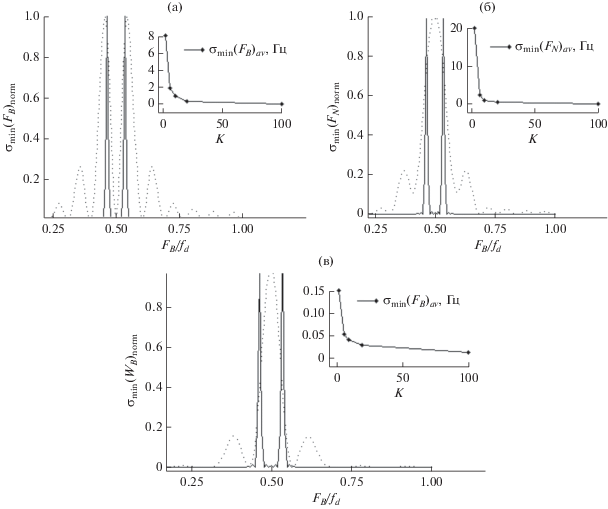
Рис. 6.

Зависимость ГРК оценки вектора параметров $\xi = {{[{{F}_{B}}~{{W}_{B}}{{F}_{N}}]}^{T}}$от FB/fd при WB = 1 Гц и $K$ = 6 (пунктирная кривая) и 100 (сплошная); FN = 700 Гц, AN = 1, AB = 1, fd = 1400 Гц, q = 10. На вставках – зависимость ГРК оценки параметров от длины выборки K.

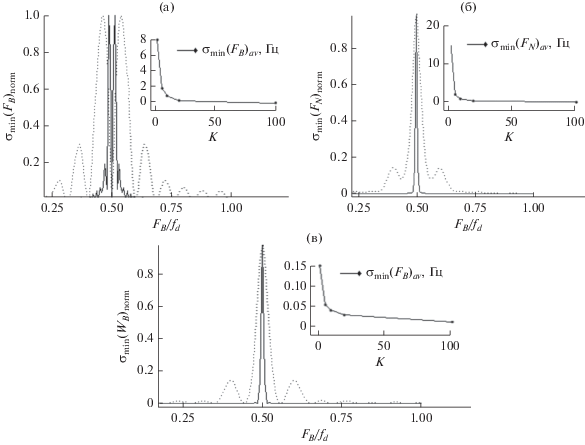
На рис. 5 и 6, ${{\sigma }_{{{\text{min}}}}}{{\left( {{{F}_{B}}} \right)}_{{{\text{av}}}}}~\left( {\text{а}} \right)$, ${\text{\;}}{{\sigma }_{{{\text{min}}}}}{{\left( {{{F}_{N}}} \right)}_{{{\text{av}}}}}~~\left( {\text{б}} \right),$ ${{\sigma }_{{{\text{min}}}}}{{\left( {{{W}_{B}}} \right)}_{{{\text{av}}}}}$ (в) – усредненные по FB/fd, а ${{\sigma }_{{{\text{min}}}}}{{\left( {{{F}_{B}}} \right)}_{{{\text{norm}}}}}$ (а), ${\text{\;}}{{\sigma }_{{{\text{min}}}}}{{\left( {{{F}_{N}}} \right)}_{{{\text{norm}}}}}$ (б), ${{\sigma }_{{{\text{min}}}}}{{\left( {{{W}_{B}}} \right)}_{{{\text{norm}}}}}$ (в) – соответственно нормированные значения ${{\sigma }_{{{\text{min}}}}}\left( {{{F}_{B}}} \right)$, ${{\sigma }_{{{\text{min}}}}}\left( {{{F}_{N}}} \right){\text{\;}}$, ${{\sigma }_{{{\text{min}}}}}\left( {{{W}_{B}}} \right)$. Из рис. 5 и 6 видим, что с увеличением объема выборки влияние FB/fd на ГРК параметров проявляется лишь в узких областях относительно всего диапазона значений. Также можно видеть, как ширина помехи WB влияет на характер данных зависимостей.

ЗАКЛЮЧЕНИЕ

Получено выражение для расчета элементов матрицы Фишера, необходимой для установления минимальных значений СКО совместных оценок параметров смеси узкополосного и широкополосного сигналов и белого гауссовского шума, представленных в виде комплексного суммарного сигнала, с помощью многомерного неравенства Крамера–Рао. Приведены графики зависимости СКО оценок от отношения сигнал/шум, длины выборки и от исходных параметров сигнала – центральных частот составляющих сигнала, ширины широкополосной составляющей. Проведено сравнение с минимальными СКО, полученными для модели сигнала, включающей только широкополосную составляющую. Проведен анализ полученных результатов, позволяющий оценить требования, которые могут быть предъявлены к разрабатываемым алгоритмам совместной оценки параметров смеси сигналов рассматриваемого типа, в зависимости от установленных значений частоты дискретизации и объема выборки.

Список литературы

  1. Principles of Modern Radar: Basic Principles / Eds. by Richards M.A., Scheer J.A., Holm W.A. Edison: SciTech Publishing Inc., 2010.

  2. Van Trees H.L. Detection, Estimation and Modulation Theory, N.Y.: Wiley, 2001. Pt 3.

  3. Горбунов Ю.Н. // Сборник научных трудов Междунар. научно-техн. конф. “Научно-технические проблемы построения систем и комплексов землеобзора, дозора и управления и комплексов с беспилотными ЛА”, Москва, 23 мая 2013 г. С. 55.

  4. Бакулев П.А., Степин В.М. Методы и устройства селекции движущихся целей. М.: Радио и связь, 1986.

  5. Гордеев А.Ю., Яцышен В.В. // Электромагнитные волны и электронные системы. 2015. Т. 20. № 3. С. 40.

  6. Горбунов Ю.Н. Цифровые системы СДЦ и их оптимизация. М.: МИРЭА, 2008.

  7. Бартенев В.Г. // 10-я Междунар. конф. DSPA-2008. Москва, 26–28 марта, 2008. С. 26.

  8. Уидроу Б., Стирнз С. Адаптивная обработка сигналов / Пер. с англ. М.: Радио и связь, 1989.

  9. Adve R.S., Wicks M., Hale T., Antonik P. // Record 2000 IEEE Intern. Radar Conf. Alexandria USA, May 2000. P. 735.

  10. Попов Д.И. // Изв. вузов. Радиоэлектроника. 2003. № 3. С. 71.

  11. Артюшенко В.М., Воловач В.И. // Изв. вузов. Приборостроение. 2012. № 9. С. 62.

  12. Соболев В.С., Журавель Ф.А. // РЭ. 2014. Т. 59. № 4. С. 322.

  13. Жураковский В.Н., Логвиненко А.С. // Радиотехника. 2017. № 11. С. 78.

  14. Турчин В.И. Введение в современную теорию оценки параметров сигналов. Н. Новгород: ИПФ РАН, 2005.

  15. Kay S.M. Fundamentals of Statistical Signal Processing, V. I: Estimation Theory. Upper Saddle River: Prentice Hall, 1993.

  16. Novak L.M. On the Estimation of Spectral Parameters Using Burst Waveforms. MIT Lincoln Laboratory Technical Report 672. Lexinghton: Defense Technical Information Center, 1983. 60 p.

  17. Frelich R.G. // IEEE Trans. 1993. V. GRS-31. № 6. P. 1123.

  18. Sobolev V.S., Feshenko A.A. // IEEE Trans. 2006. V. IM-55. № 2. P. 659.

  19. Дъяконов В., Круглов В. Математические пакеты расширения MATLAB. Спец. справочник. СПб.: Питер, 2001.

  20. Жураковский В.Н., Логвиненко А.С. // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2018. № 5. С. 26. https://doi.org/10.18698/0236-3933-2018-5-26-35

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал