Радиотехника и электроника, 2020, T. 65, № 6, стр. 578-586

1. ПОСТАНОВКА ЗАДАЧИ

Для точного определения дальности и скорости совокупности малоразмерных космических объектов на околоземной орбите, разрешения отдельных элементов сложных космических объектов, а также малоразмерных объектов на земной поверхности, необходимо использовать широкополосные зондирующие сигналы, имеющие высокие разрешающие способности по наклонной дальности $\Delta r = {c \mathord{\left/ {\vphantom {c {2{{F}_{{\text{с}}}}}}} \right. \kern-0em} {2{{F}_{{\text{с}}}}}}$ (${{F}_{{\text{с}}}}$ – ширина спектра сигнала) и радиальной скорости. Для получения высокого углового разрешения $\Delta \theta $ элементов земной поверхности и расположенных на ней целей используют радиолокаторы, расположенные на быстро движущихся воздушно-космических носителях с прямым синтезом апертуры. Высокие разрешения по наклонной и поперечной $\Delta {{r}_{ \bot }} = {{r}_{0}}\Delta \theta $ дальностям (${{r}_{0}}$ – наклонная дальность до наблюдаемого элемента разрешения) позволяют получать двумерные дальностные портреты целей. Получение высокого углового разрешения малоразмерных космических объектов или элементов сложных космических объектов основано на эффекте инверсного (обратного) синтеза апертуры антенны [1–4]. При разрешающей способности по доплеровской частоте $\Delta {{F}_{{\text{Д}}}} = {1 \mathord{\left/ {\vphantom {1 {{{T}_{{\text{с}}}}}}} \right. \kern-0em} {{{T}_{{\text{с}}}}}}$ (${{T}_{{\text{с}}}}$ – длительность зондирующего сигнала (время когерентного накопления)), обеспечивается угловая разрешающая способность $\Delta \theta = \left( {{\lambda \mathord{\left/ {\vphantom {\lambda {2V\sin {{\theta }_{0}}}}} \right. \kern-0em} {2V\sin {{\theta }_{0}}}}} \right)\Delta {{F}_{{\text{Д}}}},$ где V – путевая скорость движения объекта, ${{\theta }_{0}}$ – угол между вектором путевой скорости и линией визирования [2, 3]. Поперечное разрешение обеспечивается поворотом вектора скорости цели относительно линии визирования и реализуется обработкой последовательности комплексных отсчетов, приходящих от каждого разрешаемого по наклонной дальности элемента цели.

Из сказанного выше следует, что для обеспечения высоких разрешающих способностей по наклонной $\Delta r$ и поперечной $\Delta {{r}_{ \bot }}$ дальностям необходимо использовать зондирующие сигналы с широким спектром и большой длительностью.

В литературе для этих целей используется пачка линейно-частотно-модулированных (ЛЧМ) импульсов с высокой частотой повторения их следования, а также “разомкнутые” частотно-манипулированные когерентные сигналы, представляющие собой пачку из $M \gg 1$ прямоугольных радиоимпульсов длительностью ${{T}_{{\text{и}}}}$ с шагом изменения частоты от импульса к импульсу ${1 \mathord{\left/ {\vphantom {1 {{{T}_{{\text{и}}}}}}} \right. \kern-0em} {{{T}_{{\text{и}}}}}}$ и скважностью $q > 2$ [1–3]. Однако, как известно, частотно-модулированные и манипулированные сигналы имеют скошенную функцию рассогласования, в результате чего появляется неоднозначность по дальности. Автокорреляционная функция (АКФ) пачки ЛЧМ-импульсов имеет пики неоднозначности.

Тема выбора зондирующего сигнала актуальна также в связи с проблемой разрешения перекрывающихся по времени эхо-сигналов, амплитуда которых меняется в значительном диапазоне, т.е. с проблемой обнаружения слабых эхо-сигналов, закрытых боковыми лепестками АКФ сильных сигналов. Для подавления боковых лепестков корреляционной функции эхо-сигналов применяют внутриимпульсное и межимпульсное взвешивание [5, 6]. Однако при этом происходит расширение основного лепестка АКФ и потеря его величины в отношении сигнал–шум.

Для решения названных задач можно использовать фазокодоманипулированные (ФКМ) сигналы, свободные от недостатков частотно-модулированных и манипулированных сигналов. В работах [6–9] были рассмотрены радиолокационные ФКМ-сигналы, имеющие нулевую зону корреляции в области центрального пика апериодической АКФ (НЗ АКФ). Данные сигналы представляют собой периодическую последовательность из $M \gg 1$ когерентных импульсов, кодированных (манипулированных по фазе) ансамблями комплементарных или ортогональных последовательностей. ФКМ-сигналы с НЗ АКФ решают проблему обнаружения слабых эхо-сигналов на фоне сильных. Однако относительная ширина НЗ АКФ ФКМ-сигналов, рассмотренных в [6–9], много меньше единицы:

где Z – ширина НЗ АКФ; L – длительность сигнала [10].

Кроме того, при формировании и обработке ФКМ-сигналов с большим количеством импульсов в пачке довольно сложно выдерживать их когерентность. Рассмотренные в [6–9] полифазные ФКМ-сигналы, например, сигналы Фрэнка или P4, также имеют большой алфавит фаз, равный числу дискрет в импульсе.

В последнее время особое внимание уделяется тому, чтобы снизить возможности обнаружения радиолокационных станций (РЛС) средствами радиотехнической разведки и самонаводящимися противорадиолокационными ракетами [11–13]. В РЛС с малой вероятностью обнаружения излучения предусмотрены следующие специальные меры для повышения скрытности их работы: низкая спектральная плотность излучения, изменение параметров зондирующих сигналов по случайному закону, работа в широкой полосе частот, управление мощностью излучения. Применяемые широкополосные зондирующие сигналы – ЛЧМ-сигналы или бифазные ФКМ-сигналы – не обеспечивают скрытности работы РЛС. Так, ЛЧМ-сигналы могут быть легко распознаны средствами разведки по скорости изменения фазы; бифазные ФКМ-сигналы – с помощью схем квадратурного детектирования. В значительной степени скрытность излучения можно повысить при использовании полифазных ФКМ-сигналов [13]. Полифазные импульсные сигналы могут формироваться широким набором p-ичных кодов, отличаются малой спектральной плотностью и низким уровнем боковых лепестков АКФ.

Цель данной работы – синтезировать полифазный (p-фазный, где p-простое число) радиолокационный сигнал, имеющий НЗ АКФ, для решения задач высокого разрешения совокупности малоразмерных космических объектов на околоземной орбите, отдельных элементов сложных космических объектов, а также малоразмерных объектов на земной поверхности. Данный сигнал представляет собой пачку из p когерентных ФКМ-импульсов, кодированных комплементарными последовательностями p-ичного D-кода. Он имеет малое количество импульсов p в пачке, небольшой алфавит фаз, равный p, а способ формирования кода позволяет для его сжатия в согласованном фильтре использовать алгоритм быстрого преобразования.

2. СИНТЕЗ p-ИЧНОГО D-КОДА И ПОЛИФАЗНОГО КОГЕРЕНТНОГО ДОПОЛНИТЕЛЬНОГО СИГНАЛА

Последовательности $\left\{ {d_{n}^{1}} \right\},\left\{ {d_{n}^{2}} \right\},...,\left\{ {d_{n}^{i}} \right\},...,\left\{ {d_{n}^{p}} \right\},$ n = 1, 2, …, N, длиной $N = {{p}^{k}}$ ($k \geqslant 2$ – целое число) называются комплементарными [8, 14–16], если

где $r_{m}^{i} = r_{m}^{{i,i}} = \sum\nolimits_{n = m + 1}^N {d_{n}^{i}d_{{n - m}}^{{{\text{*}}i}}} $ – апериодическая АКФ последовательности $\left\{ {d_{n}^{i}} \right\}$, * – операция комплексного сопряжения.

Удовлетворяющие (2) ${N \mathord{\left/ {\vphantom {N p}} \right. \kern-0em} p}$ наборов комплементарных (дополнительных) последовательностей длиной N образуют матрицу p-фазных дополнительных последовательностей (МДП) размером $N \times N$, которая называется ансамблем p-фазных комплементарных последовательностей Голея [8, 14, 15], или p-ичным D-кодом [16] (введем обобщенное понятие ансамбля последовательностей Голея и D-кода для $p > 2$ [17]).

Пусть ${{{\mathbf{\tilde {D}}}}_{N}} = \left\| {{{{\tilde {d}}}_{{i,n}}}} \right\|_{1}^{N}$ – матрица p-ичных D-кодов, ${{\tilde {d}}_{{i,n}}} = 0,1,...,p - 1$; $N = {{p}^{k}}$. Тогда МДП порядка k (размером $N \times N$) будет иметь вид

Назовем последовательности ${\mathbf{D}}_{{1,N}}^{i} = \left\| {{{d}_{{i,n}}}} \right\|_{{n = 1}}^{N}$ и ${\mathbf{D}}_{{1,N}}^{j} = \left\| {{{d}_{{j,n}}}} \right\|_{{n = 1}}^{N}$ p-парными, если

где i, j – номера последовательностей в D-коде или номера строк МДП; ${{\left( a \right)}_{p}}$ – число a в p-ичном виде; $ \oplus $ – операции сложения по модулю p; $\Delta = {{p}^{{k - 1}}}$; p-парные последовательности являются комплементарными, т.е. для них выполняется (2).

Пусть ${{{\mathbf{D}}}_{N}}$ – МДП (3), а ${{{\mathbf{H}}}_{N}} = \left\| {{{h}_{{i,n}}}} \right\|_{1}^{N}$ – матрица системы функций Виленкина–Крестенсона–Кронекера (ВКК) [18]. Известно, что система функций ВКК является мультипликативной абелевой группой [18, 19]. Так как множество, состоящее из строк МДП, является смежным классом по подгруппе, элементами которой являются строки матрицы ВКК, а первая строка МДП – лидером смежного класса, то можно записать:

где ${{{\mathbf{d}}}_{N}} = {\text{diag}}\left\{ {{{d}_{{1,1}}},{{d}_{{1,2}}},...,{{d}_{{1,n}}},...,{{d}_{{1,N}}}} \right\}$ – диагональная матрица с элементами из первой строки ${{{\mathbf{D}}}_{N}}$.

При $p = 2$ матрица ВКК преобразуется в матрицу Адамара [20].

Из (5) следует, что для построения МДП ${{{\mathbf{D}}}_{N}}$ необходимо сформировать ее первую строку ${\mathbf{D}}_{{1,N}}^{1}$.

Элементы первой строки МДП определяются следующим образом [21]:

где $y + 1 = n$ – номер столбца МДП; (y)_p = $ = \left( {\begin{array}{*{20}{c}} {{{y}_{k}}}&{{{y}_{{k - 1}}}}&{...}&{{{y}_{i}}}&{...}&{{{y}_{1}}} \end{array}} \right)$ – номер столбца МДП в p-ичном виде; ${{y}_{i}} = 0,1,...,p - 1$; $y = 0,1,...,{{p}^{k}} - 1$; ${{l}_{i}} = 1,2,...,i$; $i = 1,2,...,k - 1$; ${{l}_{{k - 1}}} \ne {{l}_{{k - 2}}} \ne \ldots \ne {{l}_{2}}.$

Сложение в выражении (6) выполняется по модулю p. Данный способ позволяет сформировать $\gamma = {{2}^{{k - 2}}}$ ансамблей D-кода порядка k.

Следует отметить, что данный способ формирования D-кода рассмотрен нами ранее в [20] при $p = 2$, а в [21] рассмотрен пример формирования D-кода при $p = 3$ и $k = 3$.

Последовательности ${\mathbf{D}}_{{1,N}}^{i} = \left\| {{{d}_{{i,n}}}} \right\|_{{n = 1}}^{N}$ и ${\mathbf{D}}_{{1,N}}^{j} = $ $ = \left\| {{{d}_{{j,n}}}} \right\|_{{n = 1}}^{N}$ называются смежными, если

где i, j – номера последовательностей в D-коде или номера строк МДП; $\delta = {{p}^{{{{l}_{{k - 1}}} - 1}}}$; ${{l}_{{k - 1}}} = 1,2,...,k - 1$ из (6).

Смежные последовательности также являются комплементарными, и для них справедливо соотношение (2).

Назовем полифазным когерентным дополнительным сигналом (КДС) пачку из p ФКМ-импульсов, кодированных p-парными или смежными последовательностями D-кода [17].

Аналитическое выражение комплексной огибающей (КО) КДС имеет вид

где – огибающая n-го дискрета КДС; ${{T}_{{\text{0}}}}$ – длительность дискрета; $q \geqslant 2$ - скважность; $\left\| {{{d}_{{i,n}}}} \right\|_{1}^{N} = {\mathbf{D}}_{{1,N}}^{i}$ – элементы i-й p-парной последовательности.

Комплексная огибающая КДС в векторной форме будет иметь следующий вид:

где ${{{\mathbf{0}}}_{{1,N\left( {q - 1} \right)}}} = \left( {\begin{array}{*{20}{c}} {{{0}_{1}}}&{{{0}_{2}}}&{...}&{{{0}_{n}}}&{...}&{{{0}_{{N\left( {q - 1} \right)}}}} \end{array}} \right)$ – нулевой вектор-строка длиной $N\left( {q - 1} \right)$.

3. КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ ПОЛИФАЗНЫХ КОГЕРЕНТНЫХ ДОПОЛНИТЕЛЬНЫХ СИГНАЛОВ

Анализ корреляционных характеристик КДС проведен в [17, 20].

Апериодическая взаимокорреляционная функция (ВКФ) последовательностей $\left\{ {d_{n}^{i}} \right\}$ и $\left\{ {d_{n}^{j}} \right\}$ определяется по формуле

где $r_{m}^{{i,j}} = 0$ при $m = 0,$ так как комплементарные последовательности, построенные по (5),(6), являются ортогональными.

В векторном виде АКФ полифазного КДС будет иметь вид [17]

где ${{{\mathbf{0}}}_{{1,N\left( {q - 2} \right)}}} = \left( {\begin{array}{*{20}{c}} {{{0}_{1}}}&{{{0}_{2}}}&{...}&{{{0}_{n}}}&{...}&{{{0}_{{N\left( {q - 2} \right)}}}} \end{array}} \right)$ – нулевой вектор-строка длиной $N\left( {q - 2} \right)$;

При $i = j$ получим ${\mathbf{R}}_{{1,2N - 1}}^{{i,j}} = {\mathbf{R}}_{{1,2N - 1}}^{i}$, и согласно (2):

а при $i \ne j$ получим $r_{0}^{{i,j}} = 0$.

Из (11) и (12) следует, что ширина НЗ АКФ (с двух сторон от центрального пика АКФ) полифазного КДС равна

и с учетом длительности дискрета Т₀ получаем

Относительная ширина НЗ АКФ определяется по формуле

где $L = N\left( {\left( {p - 1} \right)q + 1} \right)$ – число дискрет в КДС.

Из (14) следует, что

и при $p = 2$ имеем ${1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3} \leqslant \varepsilon < 1$ [20].

В (1) $M \geqslant N = {{p}^{k}}$ ($k \geqslant 2$ – целое число), поэтому для сигналов, рассмотренных в [6–9], $\varepsilon \ll 1$.

Полифазный КДС можно рассматривать как сигнал, сформированный последовательностью из ансамбля последовательностей с НЗ АКФ [10, 20] с параметрами:

где J = γN/p – число последовательностей в ансамбле.

Набор последовательностей, формирующих p КДС и образованных из смежных наборов p-парных последовательностей D-кода, можно рассматривать как ансамбль последовательностей с нулевой зоной корреляции [20] с параметрами

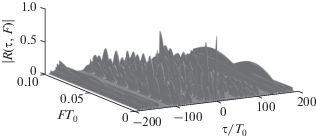
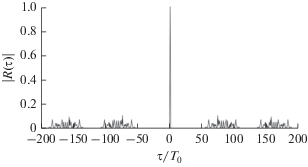
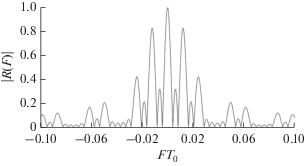
На рис. 1–3 изображены соответственно часть двумерной функции неопределенности $\left| {R\left( {\tau ,F} \right)} \right|$ трехфазного КДС с числом дискрет в импульсе $N = 27$ и скважностью $q = 3$, ее сечение плоскостью $F = 0$, т.е. АКФ КО КДС при полном согласовании фильтра с эхо-сигналом по частоте, а также сечение плоскостью $\tau = 0$ (амплитудно-частотный спектр квадрата КО КДС).

Ширина НЗ АКФ КДС с данными параметрами в относительных единицах равна ${Z \mathord{\left/ {\vphantom {Z {{{T}_{{\text{0}}}}}}} \right. \kern-0em} {{{T}_{{\text{0}}}}}} = 54$. Из рис. 1 видно, что в районе центрального пика функция неопределенности имеет ярко выраженную прямоугольную область нулевой корреляции вдоль всей оси частот F при $N - 1 < \left| {{\tau \mathord{\left/ {\vphantom {\tau {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right| \leqslant N\left( {q - 1} \right)$, что обусловлено наличием вектора ${{{\mathbf{0}}}_{{1,N\left( {q - 2} \right)}}}$ в (11). Размер этой области не зависит от закона манипуляции и рассогласования по частоте, а только от скважности q. Область нулевой корреляции при $0 < \left| {{\tau \mathord{\left/ {\vphantom {\tau {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right| \leqslant N - 1$ вблизи от центрального пика АКФ, обусловленная свойством комплементарных последовательностей (2), наблюдается только при полном согласовании фильтра с эхо-сигналом по частоте.

Сечение функции неопределенности КДС плоскостью $\tau = 0$ (см. рис. 3) имеет огибающую вида $\left| {{{\sin x} \mathord{\left/ {\vphantom {{\sin x} x}} \right. \kern-0em} x}} \right|$ с шириной основного лепестка по нулевому уровню ${2 \mathord{\left/ {\vphantom {2 {\left( {N{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {N{{T}_{0}}} \right)}}$ и внутреннюю гребенчатую структуру. Гребни спектра отстоят друг от друга по F на величину ${1 \mathord{\left/ {\vphantom {1 {\left( {qN{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {qN{{T}_{0}}} \right)}}$. Ширина гребней по нулевому уровню составляет ${2 \mathord{\left/ {\vphantom {2 {\left( {pqN{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {pqN{{T}_{0}}} \right)}}$, а общее число гребней в пределах основного лепестка огибающей амплитудно-частотного спектра квадрата КО КДС равно $2q - 1$. Между гребнями имеют место боковые лепестки шириной ${1 \mathord{\left/ {\vphantom {1 {\left( {pqN{{T}_{0}}} \right)}}} \right. \kern-0em} {\left( {pqN{{T}_{0}}} \right)}}$ по нулевому уровню, общее число которых равно $p - 2$.

Нулевая зона АКФ существует только при полном согласовании фильтра с эхо-сигналом по частоте Доплера [17]. При рассогласовании ΔF по частоте в НЗ АКФ вблизи основного пика АКФ появляются боковые лепестки, максимальный из которых сравнивается по уровню с максимальным боковым лепестком вне НЗ АКФ при $\Delta F = {{0.5} \mathord{\left/ {\vphantom {{0.5} {pqN{{T}_{0}}}}} \right. \kern-0em} {pqN{{T}_{0}}}}$.

Когерентный дополнительный сигнал предполагается использовать при сопровождении радиолокационных целей в режимах разрешения для точного измерения (уточнения) частоты Доплера, когда по предварительному целеуказанию грубая ее оценка уже известна. При этом устройство сжатия КДС должно быть многоканальным по частоте Доплера с необходимой шириной каналов.

4. УСТРОЙСТВО СЖАТИЯ ПОЛИФАЗНЫХ КОГЕРЕНТНЫХ ДОПОЛНИТЕЛЬНЫХ СИГНАЛОВ

Для сжатия когерентной последовательности импульсов обычно используется корреляционно-фильтровая обработка, при которой сначала убирается модуляция отраженного сигнала, а затем с помощью быстрого преобразования Фурье (БПФ) определяется частота Доплера [6, 8].

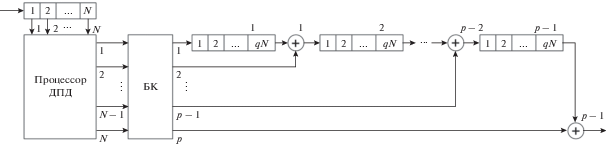
Структурная схема устройства сжатия полифазного КДС изображена на рис. 4 и представляет собой эквивалентную структурную схему согласованного фильтра полифазного КДС при известной частоте Доплера или эквивалентную структурную схему согласованного фильтра в одном частотном канале.

Устройство сжатия состоит из входного регистра на N ячеек памяти, процессора дискретного Д-преобразования с N входами и N выходами, блока коммутации (БК), $p - 1$ одинаковых регистров сдвига на $qN$ ячеек памяти и $p - 1$ одинаковых сумматоров комплексных чисел, где q – скважность, $N = {{p}^{k}}$ – длина D-кода.

При $p = 2$ получим устройство сжатия двухфазного (бинарного) КДС.

Основным элементом данного устройства является процессор дискретного Д-преобразования (процессор ДПД), алгоритм работы которого описывается следующим математическим выражением:

где ${{{\mathbf{S}}}_{{1,N}}}$ – вектор отсчетов входного сигнала дискретного Д-преобразования; T – операция транспонирования вектора.

Подставляя (5) в (16), получим

Известно, что матрицу ВКК можно факторизовать методом Гуда [18, 22], т.е. дискретное Д-преобразование (17) может быть сведено к БПФ в базисе системы функций ВКК (быстрое преобразование Виленкина-Крестенсона, БП ВК), имеющему вид

где $ \otimes $ – операция кронекеровского произведения; ${{{\mathbf{1}}}_{p}}$ – единичная матрица размером $p \times p$; ${{{\mathbf{E}}}_{p}}$ – матрица дискретных экспоненциальных функций (ДЭФ) размером $p \times p$.

Из выражения (18) следует, что процессор ДПД в схеме на рис. 4 может быть заменен на процессор БП ВК с добавлением весовых коэффициентов (матрица ${{{\mathbf{d}}}_{N}}$ в выражении) на входе процессора, являющихся элементами первой строки МДП ${{{\mathbf{D}}}_{N}}$. Тогда структурная схема устройства сжатия полифазного КДС будет иметь вид, изображенный на рис. 5.

Блок коммутации осуществляет соединение p из N его входов с p выходами согласно выражению (4) или (7), т.е. в соответствии с номерами строк, в которых располагаются p-парные или смежные D-коды.

При $p = 2$ алгоритм сжатия полифазных КДС, изображенный в виде структурной схемы на рис. 5, преобразуется в алгоритм сжатия бинарных КДС, а процессор БП ВК – в процессор быстрого преобразования Уолша.

В [23] описано многоканальное устройство сжатия КДС, которое позволяет одновременно убирать манипуляцию полифазных импульсных сигналов, кодированных комплементарными последовательностями, и определять частоту Доплера в ограниченном доплеровском диапазоне частот по предварительному целеуказанию. В состав данного устройства входит процессор быстрого Д-преобразования Фурье (БПДФ_K, K – число используемых частотных каналов), в котором применяется совмещение алгоритмов БПФ в базисах-матрицах дополнительных последовательностей и ДЭФ путем поэлементного перемножения каждой строки МДП размером $N \times N$ на каждую из K строк матрицы ДЭФ размером $N \times N$. Матрица МДП здесь является матрицей импульсных характеристик импульсов КДС. Полученная при этом блочная матрица размером $NK \times N$ представляет собой набор матриц импульсных характеристик на K различных частотах, т.е. строки матрицы ДЭФ играют роль частотных каналов. В алгоритме БПДФ_K факторизуется сама матрица МДП.

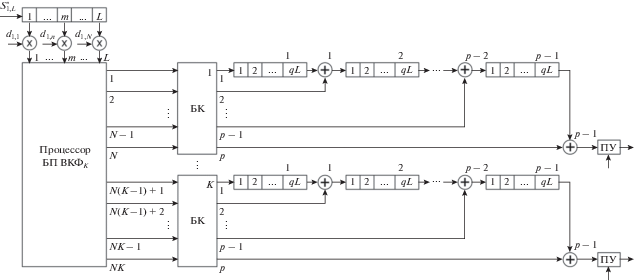
Описанное в [23] многоканальное устройство сжатия КДС можно построить на основе БП ВК, используя выражение (5). Структурная схема такого устройства представлена на рис. 6. Управляемый гетеродин приемного устройства РЛС по грубой оценке частоты Доплера ${{\hat {F}}_{{\text{Д}}}}$, полученной в режиме обнаружения целей, перестраивает свою частоту так, чтобы значение ${{\hat {F}}_{{\text{Д}}}}$ попало в частотный диапазон, перекрытый частотными каналами устройства сжатия КДС. Для сжатия КДС в состав устройства введем процессор быстрого преобразования Виленкина–Крестенсона–Фурье (БП ВКФ_K, K – число используемых частотных каналов), в котором применяется совмещение алгоритмов БПФ в базисах системы функций ВКК и ДЭФ путем поэлементного перемножения каждой строки матрицы ВКК размером $N \times L$, $L = N\left( {\left( {p - 1} \right)q + 1} \right)$ (строки матрицы удлинены повторением каждого элемента или дополнением нулями), на каждую из K строк матрицы ДЭФ размером $L \times L$.

Комплексную огибающую отраженного от цели сигнала можно записать в виде

где $\dot {S}\left( t \right)$ – КО КДС (8). На входной регистр сдвига устройства сжатия сигнал подается с выходов аналого-цифрового преобразователя в квадратурных каналах. Переходя от аналоговых величин к дискретным, т.е. при $t \to {{t}_{n}} = \left( {n - 1} \right){{T}_{0}},$ ${{\hat {F}}_{{\text{Д}}}} \to {{\hat {F}}_{{{{{\text{Д}}}_{k}}}}} = \left( {k - 1} \right)\Delta F,$ $\Delta F = {1 \mathord{\left/ {\vphantom {1 {L{{T}_{0}}}}} \right. \kern-0em} {L{{T}_{0}}}}$ – рассогласование между частотными каналами, $n = 1,2,...,L$, $k = 1,2,...,K$, получим КО эхо-сигнала в дискретном виде:

Следовательно, матрица ДЭФ должна иметь размер $L \times L$.

Так как МДП имеет N столбцов, а число столбцов матриц МДП и ДЭФ должно быть равно, то строки матрицы МДП и импульсы КДС необходимо удлинить, например, за счет повторения каждого отсчета ${L \mathord{\left/ {\vphantom {L {N = }}} \right. \kern-0em} {N = }}\left( {p - 1} \right)q + 1$ раз или дополнением нулями.

Тогда дискретное Д-преобразование Фурье (ДПДФ_K) будет иметь вид

где ${\mathbf{S}}_{{1,L}}^{'}$ – вектор отсчетов удлиненного входного сигнала; $W = \exp \left( { - j{{2\pi } \mathord{\left/ {\vphantom {{2\pi } L}} \right. \kern-0em} L}} \right)$, – диагональная матрица с элементами из k-й строки матрицы ДЭФ, входящая в состав блочной матрицы ${{{\mathbf{E}}}_{{KL,L}}}$; ${\mathbf{D}}_{{N,L}}^{'}$ – МДП с удлиненными строками.

Учитывая (5), из (19) получим дискретное преобразование Виленкина–Крестенсона–Фурье (ДП ВКФ_K):

где ${\mathbf{H}}_{{N,L}}^{'}$ – матрица ВКК с удлиненными строками; ${\mathbf{d}}_{L}^{'} = {\text{diag}}\left\{ {{\mathbf{D}}_{{1,L}}^{{'1}}} \right\}$ – диагональная матрица с элементами из первой строки матрицы ${\mathbf{D}}_{{N,L}}^{'}$.

Из [18] известно, что повторение столбцов матрицы ВКК размером $N \times N$ ($N = {{p}^{k}}$) ${{p}^{l}}$ раз эквивалентно прореживанию строк матрицы ВКК размером $L \times L$ ($L = {{p}^{{k + l}}}$) до прямоугольной матрицы размером $N \times L$. То есть в (20) матрицу ${{{\mathbf{H'}}}_{{N,L}}}$ можно заменить на матрицу ВКК размером $L \times L$, факторизовать ее, а необходимые значения спектра сигнала брать с известных нам прореженных номеров строк.

Таким образом, из (20) получим выражение для БП ВКФ_K:

где ${{{\mathbf{C}}}_{{{{j}_{L}}}}}$ – слабозаполненная матрица из алгоритма факторизации Гуда (18), $j = 1,2,...,k + l.$

При $p = 2$ БП ВКФ_K преобразуется в быстрое преобразование Уолша–Фурье (БП УФ_K) и $L = N\left( {q + 1} \right)$ [10]. Для достижения максимальной эффективности БПФ размер матрицы ДЭФ должен быть равен степени двойки. Для этого введем величину $l = \left\lceil {{{{\log }}_{2}}\left( {q + 1} \right)} \right\rceil $, где $\left\lceil x \right\rceil $ – операция округления числа x к большему. Тогда $L = {{2}^{l}}N = {{2}^{{k + l}}}$.

Прямоугольная матрица в (20)

получена из матрицы Адамара ${{{\mathbf{H}}}_{L}}$ размером $L \times L$ в (21) путем прореживания ее строк, где $\left\| {{{h}_{{i,n}}}} \right\|_{1}^{N} = {{{\mathbf{H}}}_{N}}$ – матрица Адамара размером $N \times N$, $\left\lfloor x \right\rfloor $ – операция выделения целой части числа x.

Диагональная матрица в (20) и (21) имеет вид

где $\left\| {{{d}_{{1,n}}}} \right\|_{1}^{N} = {\mathbf{D}}_{{1,N}}^{1}$. Процессор БП УФ_K имеет NK выходов (прореженные строки). Первые N выходов представляют собой результат перемножения матрицы импульсных характеристик, т.е. МДП, на отсчеты входного сигнала процессора в первом частотном канале, вторые N выходов – во втором частотном канале, и т.д., последние N выходов – в K-м частотном канале. Блок коммутации в каждом частотном канале осуществляет соединение двух из N его входов с двумя выходами в соответствии с номерами строк, в которых располагаются парные или смежные последовательности D-кода. В сумматоре каждого канала выполняется сложение отсчетов АКФ импульсов КДС за счет задержки отсчетов одной из АКФ в регистре сдвига на период следования импульсов qL. По номеру порогового устройства (ПУ) (см. рис. 6) в котором превышен порог, определяется доплеровский сдвиг частоты:

где $k = 1,\,2,\,...,K$ – номер ПУ.

ЗАКЛЮЧЕНИЕ

В данной работе предложен способ формирования полифазного радиолокационного сигнала с НЗ АКФ, при этом данный сигнал представляет собой пачку из p ФКМ-импульсов, кодированных p-ичными комплементарными последовательностями и называется когерентным дополнительным сигналом. НЗ АКФ имеет место только при полном согласовании фильтра с эхо-сигналом по частоте Доплера. При рассогласовании по частоте уменьшается уровень основного пика АКФ и в НЗ АКФ появляются боковые лепестки. Рассмотрено многоканальное устройство сжатия данного сигнала. Показано, что способ формирования D-кода позволяет для сжатия сигнала в согласованном фильтре использовать алгоритмы быстрого преобразования.