Радиотехника и электроника, 2021, T. 66, № 1, стр. 18-26

1. ПОСТАНОВКА ЗАДАЧИ

Волновые эффекты, связанные с формированием в полупрозрачных неоднородных плазменных слоях отраженных и прошедших через слои волн, наиболее просто исследовать в рамках модельной задачи о падении плоской волны на плоскослоистую неоднородную плазму с параболическим профилем распределения электронной плотности. Поэтому рассмотрим параметрическую модель неоднородного по координате x плазменного слоя, квадрат показателя преломления которого задан формулой

Вне слоя будем считать, что ${{n}^{2}}\left( x \right) = 1$. В соотношении (1) $2a$ толщина слоя, β – “плотность” слоя, положительная величина равная отношению плазменной частоты в максимуме электронной плотности слоя к частоте падающего монохроматического излучения, деленная на полутолщину слоя.

Такая модель позволяет провести анализ формирования структуры волнового поля в области значений параметров, соответствующих значимому эффекту полупрозрачности. Реальные ионосферные плазменные слои имеют более сложную структуру, однако в области максимума электронной плотности, где эффект полупрозрачности наиболее существенен, данная модель является достаточной для оценки величины эффекта.

Модель параболического плазменного слоя неоднократно использовалась при исследовании основных эффектов при отражении электромагнитных волн от ионосферной плазмы (см., например, [1] и цитируемую там литературу). Кроме того, данная модель используется в квазиклассическом подходе к описанию эффектов подбарьерного туннелирования и надбарьерного отражения в квантовомеханических задачах (см., например, [2]). Однако в большинстве случаев рассмотрение носит качественный или оценочный характер в предположении почти полностью отражающего или почти прозрачного слоя.

В данной работе мы рассмотрим существенно значимые волновые эффекты, имеющие место именно в переходной области параметров, когда эффекты отражения и прохождения через слой соизмеримы. Такой плазменный слой мы далее будем называть полупрозрачным. Заметим, что именно при условии полупрозрачности нижнего ионосферного слоя происходит дифракционное возбуждение межслоевых волноводных ионосферных каналов. Исследование количественных соотношений для формирующихся отраженной слоем и прошедшей через слой волн имеет большое значение для корректного учета возникающих явлений. Основным математическим методом для решения данной задачи служит построение равномерных и неравномерных асимптотических представлений точного решения. Параметром асимптотических разложений (большим параметром) является отношение толщины слоя к длине волны в свободном пространстве.

2. АСИМПТОТИКИ ТОЧНОГО РЕШЕНИЯ МОДЕЛЬНОЙ ЗАДАЧИ

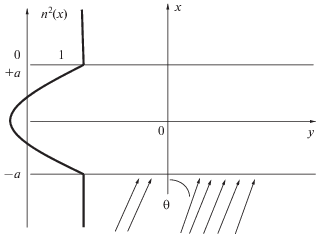
Рассмотрим падение плоской монохроматической волны, направленной под углом θ, снизу на неоднородный слой плазмы (1) (рис. 1). Учитывая однородность задачи по оси $y$, представим решение соответствующего уравнения (уравнения Гельмгольца) в виде

где функция $\psi {\kern 1pt} {}_{x}{\kern 1pt} \left( x \right)$ является решением уравнения внутри слоя – а вне слоя –

В качестве нормировочного условия рассматриваем падение плоской волны единичной амплитуды из области $x \leqslant - a$

и отсутствие волны, падающей на слой сверху, из области $x \geqslant a$.

Общее решение задачи (3) для комплексной амплитуды ψ_x(x) представляется через функции параболического цилиндра (функции Вебера–Эрмита [3], обозначенные далее как $D_{{\nu ,k}}^{ \pm }\left( X \right)$) в виде суперпозиции двух линейно независимых функций [4, 5]:

Здесь и далее используются следующие обозначения [5]:

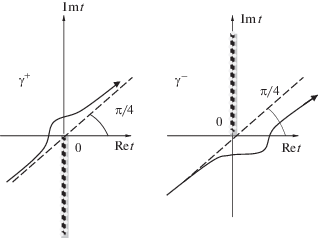
В соотношении (7) контур ${{\gamma }^{ \pm }}$ определен так, что интеграл сходится при любых (конечных) комплекснозначных X и ν: начинается в третьем квадранте комплексной плоскости переменной t и уходит на бесконечность в первом квадранте, огибая сверху (контур ${{\gamma }^{ + }}$), или снизу (контур ${{\gamma }^{ - }}$) точку “0” (рис. 2). Для выделения регулярной ветви логарифмической функции и функции квадратного корня в плоскости переменной t введен разрез от точки “0”, не затрагивающий контур ${{\gamma }^{ \pm }}$, а именно: вдоль отрицательной полуоси {$\operatorname{Im} t \leqslant 0,\operatorname{Re} {\kern 1pt} t = 0$} для контура ${{\gamma }^{ + }}$; или вдоль положительной полуоси {$\operatorname{Im} t \geqslant 0,\operatorname{Re} {\kern 1pt} t = 0$} для контура ${{\gamma }^{ - }}$. Выбор контура ${{\gamma }^{ \pm }}$ (контур ${{\gamma }^{ + }}$, или контур ${{\gamma }^{ - }}$) определяет особенности интеграла (6), значимые для построения асимптотических разложений решения (5) [6].

Анализ решения (5) начнем с определения коэффициентов ${{С}_{ + }}$ и ${{С}_{ - }}$. Для этого в областях $ - a + \varepsilon > x \geqslant - a$ и $ + a - \varepsilon < x \leqslant + a$ (здесь $\varepsilon > 0$ – параметр, задающий некоторую окрестность границ слоя) рассмотрим асимптотики функций $D_{{\nu ,k}}^{ \pm }\left( X \right)$, главный член которых представляет решение (5) в виде квазиплоских волн, идущих к неоднородному слою или от него. При этом структура асимптотических разложений существенно зависит от значения параметра $\nu $. Для $\nu > 0$ имеет место решение, соответствующее “отражающему” (в ГО-приближении) слою, для $\nu < 0$ – “прозрачному” (в ГО-приближении) слою, а для $\nu = 0$ – “полупрозрачному” слою, разделяющему падающую волну на две, отраженную и прошедшую, с равными амплитудами.

Следуя работам [4, 5] и используя результаты работы [6], получим следующую последовательность математических соотношений.

1. Для “отражающего” слоя ($\nu > 0$) имеет место асимптотическое разложение типа Вентцеля–Крамерса–Бриллюэна (ВКБ) (или ГО-асимптотика):

а) в области $ - a \leqslant x < - {{x}_{0}} < 0$,

где а значит, при $x = - а$

В формулах (9)–(12) верхний знак комбинаций $ \pm , \mp $ соответствует индексу “1”, нижний – индексу “2”, а сами индексы означают: “1” – ВКБ-компонента асимптотики функции $D_{{\nu ,k}}^{ + }\left( {X\left( x \right)} \right)$, связанной с падающей на слой волной, а “2” – ВКБ-компонента отраженной слоем волны.

Для амплитудных множителей ${{l}_{{1,2}}}$ (формулы (10) и (12)) здесь и далее приводятся только главные члены асимптотического ряда по ${{\left( {ka} \right)}^{{ - 1}}}$.

б) В области $ + a \geqslant x > {{x}_{0}} > 0$

где а значит, при $x = + а$

При этом ВКБ-асимптотика (13) относится к компоненте волны, падающей на слой сверху.

Используя теперь функциональное соотношение, следующее из определения (7):

из которого вытекают аналогичные соотношения и для асимптотических разложений функций $D_{{\nu ,k}}^{ \pm }\left( X \right)$, и выделяя согласно (8) и (13) в асимптотике представления (5) члены, соответствующие волнам, бегущим к слою и от слоя, получим из граничных условий (4) искомую нормировку:

В частности, для отраженной (отр) слоем и прошедшей (прош) слой волн, представленных в форме ВКБ-асимптотики (квазиплоские волны)

в рассматриваемых областях неоднородного слоя получаем и

Из (23)–(26) при $x = - а$ и $x = + а$ следуют формулы для комплексных коэффициентов отражения и прохождения для условия $\nu > 0$ (см. также [5]):

Отметим также, что падающая (пад) на слой волна, заданная в ВКБ форме (22) в области –a ≤ x < $ < - {{x}_{0}} < 0$, имеет следующие представления для фазовой и амплитудной функций:

2. Для модели “прозрачного” слоя $\left( {\nu < 0} \right)$последовательность соответствующих математических соотношений такова:

а) в области $ - a \leqslant x < 0$

где величины ${{l}_{1}}$ и ${{l}_{2}}$ представлены формулой (10), величина ${{\Theta }_{1}}$ – формулой (9), а величина ${{\Theta }_{2}}$ отличается от соответствующего выражения в (9) только изменением знака в выражении под логарифмом:

Как и в случае “отражающего” слоя, индекс “1” – отвечает ВКБ-компоненте асимптотики (31) функции $D_{{\nu ,k}}^{ + }\left( {X\left( x \right)} \right)$, связанной с падающей на слой волной, а “2” – ВКБ-компоненте отраженной “прозрачным” слоем волны. Особенности ВКБ асимптотических представлений в данном случае имеют место в окрестности точки $x = 0$, т.е. в области максимума слоя, который представляет “границу раздела” областей применимости различных асимптотик ВКБ типа для функции $D_{{\nu ,k}}^{ + }\left( {X\left( x \right)} \right)$. Для “отражающего” слоя, как это видно из формул (9), (10), (14), (15), (23)–(26), (29), (30) такой границей служит критический уровень $x = \pm {{x}_{0}}$.

б) В области $ + a \geqslant x > 0$ справедлива асимптотика (13) с учетом того факта, что теперь $\Gamma > 0$. Для величин l₁ и Θ₁ справедливы формулы (14) и (15). При этом, как и в предыдущем случае, ВКБ-асимптотика (13) относится к компоненте волны, падающей на слой сверху.

Формулы (19)–(21) определяют регулярные по $\nu $выражения для коэффициентов ${{С}_{ + }}$ и ${{С}_{ - }}$ решения (5), поэтому они могут использоваться и для $\nu < 0$, и для $\nu = 0$. В частности, нетрудно показать, что используя функциональное соотношение (18) и выделяя на уровне $x = - a$ компоненты асимптотических представлений решения (5), отвечающие падающей снизу на слой волне единичной амплитуды, а на уровне $x = + a$ компоненты падающей сверху на слой волне (нулевой амплитуды), вновь получаем нормировку (19)–(21).

В отличие от коэффициентов ${{С}_{ + }}$ и ${{С}_{ - }}$, ВКБ-асимптотики точного решения (5) не являются равномерными по $\nu $. Поэтому продолжить формулы (23)–(28) для асимптотики вида (22) из области $\nu > 0$ в область $\nu < 0$ нельзя. В этой области значений параметра $\nu $, используя разложения (31) и (13) для функций $D_{{\nu ,k}}^{ \pm }\left( {X\left( x \right)} \right)$, получим:

а) для $ - a \leqslant x < 0$

б) для $0 < x \leqslant + a$ также Φ_прош(х) задается формулой (25), а

Для падающей на слой волны вида (22) в области $ - a \leqslant x < 0$ остаются справедливыми формулы (29), (30).

Из выражений (25), (33)–(35), определенных при $x = - а$ и $x = + а$ следуют формулы для комплексных коэффициентов отражения и прохождения для случая $\nu < 0$ (см. также [5]):

3. Равномерное по $\nu $ обобщение формул (22)–(28) и (33)–(37) строится на основе асимптотики точного решения с применением в асимптотическом разложении функций $D_{{\nu ,k}}^{ \pm }\left( {X\left( x \right)} \right)$ интегральной функции Бемера–Френеля (или гамма-функции комплексного аргумента) [4, 6]. Такое асимптотическое представление позволяет связать (асимптотически) указанные формулы в области $\nu $ ~ 0, поскольку данная асимптотика справедлива как для положительных, так и для отрицательных значений $\nu $, включая и значение $\nu = 0$. Следуя [6], используем следующее асимптотическое разложение функции $D_{{\nu ,k}}^{ + }\left( {X\left( x \right)} \right)$:

а) в области $ - a \leqslant x < 0$,

где ${{\Theta }_{1}}$ и ${{l}_{1}}$ все также определяются формулами (9) и (10) и соответствующее слагаемое в (38) отвечает квазиплоской волне, падающей снизу на неоднородный слой, а второе слагаемое, содержащее интеграл Бемера–Френеля [3] (контур ${{\gamma }^{ - }}$ для знака “–” проходит, огибая точку “0” сверху, по нижней части комплексной плоскости переменной t с разрезом от точки “0” вдоль отрицательной части мнимой оси), представляет отраженную слоем волну. При этом

Как и ${\text{в}}$ предыдущих асимптотических разложениях, формулами (40) и (41) представлены главные члены асимптотики (38).

б) В области $ + a \geqslant x > 0$ остается справедливой формула (13) с параметрами, определенными в (14) и (15).

Снова используя в (5) соотношение (18), а также найденные ранее константы ${{C}_{ + }}\;{\text{и}}\;{{C}_{ - }}$ (см. (19), (21)), для различных волновых компонент общего решения получим следующие формулы:

в области $ - a \leqslant x < 0$ и в области $ + a \geqslant x > 0$

Естественно, что для падающей на слой волны вида (22) в области $ - a \leqslant x < 0$ остаются справедливыми формулы (29) и (30). Если вместо функции Бемера–Френеля использовать гамма-функцию $\hat {\Gamma }$ комплексного аргумента, для которой справедливо соотношение

то формула (42) примет вид где, соответственно, в области $ - a \leqslant x < 0$и в области $ + a \geqslant x > 0$

Из (42)–(50) при $x = - а$ и $x = + а$ следуют формулы для комплексных коэффициентов отражения и прохождения для условия $\nu $~ 0:

где

Формулы (51), (52), без учета экспоненциального множителя единичной амплитуды с фазовой функцией (53), соответствуют результатам, полученным в [7, 8].

При $\nu = 0$ из (51) и (52) получим

3. СРАВНИТЕЛЬНЫЙ АНАЛИЗ АСИМПТОТИК РЕШЕНИЯ МОДЕЛЬНОЙ ЗАДАЧИ

Рассмотренные выше асимптотические представления решения задачи о падении плоской волны на параболический плазменный слой являются следствиями разложений точного решения (5). Вместе с тем, данная модель многократно исследовалась геометрооптическими методами (соответственно методами ВКБ). Естественен вопрос: насколько полученные выражения совпадают с формулами ГО? Прямой расчет лучевых траекторий, амплитудных и фазовых характеристик квазиплоских волн, вычисленных на основе лучевых построений, и сравнение различных видов асимптотических разложений с точным решением позволяют сделать следующие выводы.

1. В главном члене асимптотических представлений в области применимости формул ГО фазовые функции, определенные через асимптотические разложения точного решения (формулы (23), (25) и (29)), совпадают с результатами прямого расчета эйконала квазиплоских волн.

2. Амплитудные множители, полученные методом ГО, будут совпадать с амплитудными членами (24), (26), (30), (34) и (35) в форме (22), если учесть факторы, выделенные в указанных формулах как дополнительные множители (коэффициенты отражения и прохождения соответствующих волн), в том числе и для “прозрачного” слоя. В последнем случае в качестве уровня отражения лучевых траекторий следует брать уровень $x = 0$, вводить для этого эффективного отражения дополнительный фазовый сдвиг –π/2 , а само отражение рассчитывать, как зеркальное.

3. Формирование волны просачивания через “отражающий” слой можно трактовать как формирование лучевой конгруэнции и соответствующего поля с уровня, симметрично расположенного относительно уровня отражения волны, падающей снизу, т.е. при $x = {{x}_{0}}$. При этом фаза, рассчитанная вдоль падающего луча, переносится на луч волны просачивания без каких-либо дополнительных изменений.

4. Формулы ГО (в областях их применимости) можно использовать для расчета полей и в случае критических значений параметра $\nu $ ~ 0. Для этого необходимо использовать равномерные по $\nu $ асимптотические представления для амплитудных множителей отраженной волны и волны просачивания (формулы (42), (48), (51), (52)).

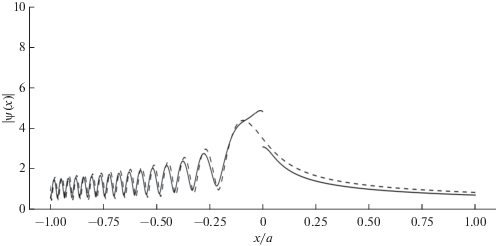
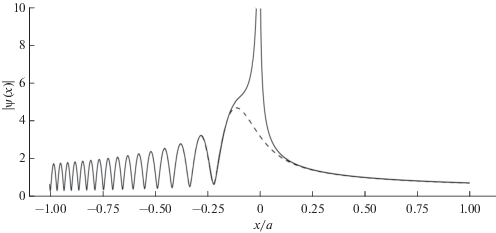
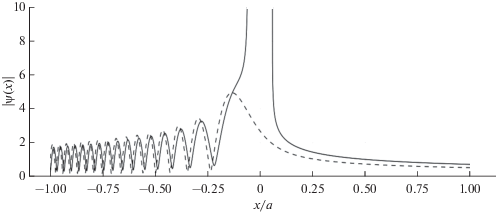
На основе анализа различных асимптотических представлений решения модельной задачи и результатов расчета волнового поля внутри параболического неоднородного слоя с использованием этих асимптотик, представленных на рис. 3–5 соответственно для “прозрачного”, критического и “отражающего” слоя, можно утверждать, что наличие волны просачивания для “отражающего” слоя и волны частичного отражения для “прозрачного” слоя существенно меняет общепринятое в рамках ГО представление о характере волнового поля в задаче отражения волны от слоя конечной толщины. Так, отраженная “прозрачным” (в рамках ГО) слоем волна интерферирует с падающей на слой волной, формируя характерные осцилляции в области, где с позиции ГО имеется только поле падающей волны (см. рис. 3). В области каустической тени (за каустикой отраженных ГО лучей) для случая “отражающего” слоя, волна просачивания имеет не экспоненциальное ослабление, а ослабление чисто геометрооптического характера, связанное с расходимостью лучей, отвечающих волне просачивания (см. рис. 5). То есть в области, близкой к условиям критического отражения, “дифракционное затекание” волнового поля в область каустической тени существенно больше, чем это предсказывает ГО-приближение и его обобщение – волновая теория катастроф [9]. Оценка области углов падения волны на слой, где существенны указанные эффекты, дана в [8].

Отметим также, что при моделировании структуры поля в условиях, близких к критическому отражению, были применены как рассмотренные в работе неравномерные асимптотики для расчета амплитудных множителей квазиплоских волн (сплошные линии с разрывами на рис. 3–5), так и точное решение (5) непосредственно в области отражения, где эти приближения не работают (штриховые линии на рис. 3–5).

Как видно из приведенных графиков, даже при ka = 100 структура волнового поля хорошо воспроизводится асимптотическими формулами вплоть до критической области максимума слоя (порядка X ~ ±0.25 или $x$ ~ $ \pm 0.1{\kern 1pt} {{\beta }^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$). Имеющее место смещение интерференционных максимумов и минимумов на рис. 3 и 5 для “прозрачного” и “отражающего” слоя соответственно, указывает на наличие систематических погрешностей в оценке фазовых соотношений для падающей и отраженной компонент волнового поля при использовании неравномерных по $\nu $ асимптотических формул для коэффициентов отражения и прохождения (просачивания). Последнее может влиять на качество результатов моделирования фазовых и поляризационных характеристик волн, при прохождении и отражении их в неоднородных плазменных слоях. При использовании равномерных асимптотических формул (51)–(53) (при построении рис. 4) такой эффект не наблюдается.