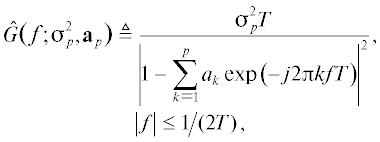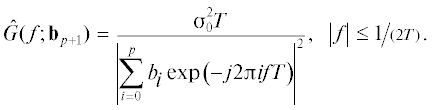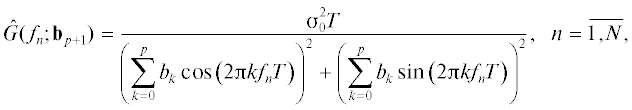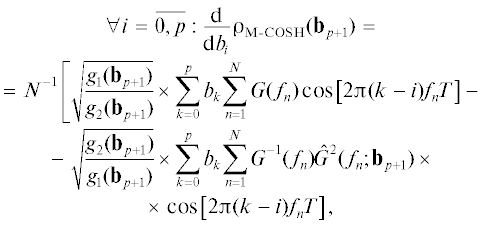1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 66, № 11, 2021

Радиотехника и электроника, 2021, T. 66, № 11, стр. 1100-1108

Метод авторегрессионного моделирования речевого сигнала на основе его дискретного фурье-преобразования и масштабно-инвариантной меры информационного рассогласования

В. В. Савченко a, *, Л. В. Савченко b, **

a Редакция журнала “Радиотехника и электроника”,
125009 Москва, ул. Моховая, 11, корп. 7, Российская Федерация

b Национальный исследовательский университет “Высшая школа экономики”
603155 Нижний Новгород, ул. Большая Печерская, 25/12, Российская Федерация

* E-mail: vvsavchenko@yandex.ru
** E-mail: lsavchenko@hse.ru

Поступила в редакцию 29.09.2020
После доработки 24.02.2021
Принята к публикации 16.04.2021

Полный текст (PDF)

Аннотация

Рассмотрена задача авторегрессионного моделирования речевого сигнала по данным его дискретного фурье-преобразования на интервалах длительностью в один речевой фрейм (миллисекунды). На основе теоретико-информационного подхода разработан новый, двухэтапный метод ее решения, в котором разделяются между собой две вычислительные процедуры: итеративной оптимизации параметров авторегрессии и их автоматического амплитудного масштабирования. Поставлен и проведен натурный эксперимент. Показано, что основным преимуществом нового метода по сравнению с его известными аналогами является чрезвычайно высокая скорость сходимости итераций к оптимальному решению.

ВВЕДЕНИЕ

На протяжении ряда лет авторегрессионная модель (АР-модель) находит широкое применение в системах цифровой обработки и передачи речи в качестве способа кодирования со сжатием речевой информации [1]. Ее объектом служат короткие (миллисекунды) отрезки xm(t), m = 1, 2, …, или фреймы речевого сигнала x(t) в расчете на их приблизительную (квази) стационарность. От точности АР-модели зависит, в частности, узнаваемость диктора по голосу. А это качество наряду с разборчивостью речи [2] является важнейшим требованием действующего государственного стандарта к системам речевой связи.

Интенсивность исследований в данном научном направлении особенно возросла в последние годы в связи с появлением и распространением в мире информационных диалоговых систем с многомодальным пользовательским интерфейсом [3], в которых АР-модель конечного порядка p < ∞ служит математической основой не только автоматического распознавания речи, но и паралингвистического анализа голосовых запросов пользователей в целях оперативного отслеживания их эмоционального состояния в процессе диалога [4]. Проблема состоит в известной вариативности устной речи на выходе речевого тракта диктора [2, 5]. Поэтому используемая АР-модель должна быть непрерывно (фрейм за фреймом [2, 6]) адаптируемой под наблюдаемый в текущем времени сигнал xm(t). Проблема обостряется в условиях малых выборок наблюдений [6, 7].

Особенно остро данная проблема возникает в системах передачи речи по низкоскоростным каналам связи, в которых порядок АР-модели жестко ограничен сверху относительно небольшой величиной p = 8…12. Так, например, рекомендованные Международным союзом электросвязи (ITU) в качестве стандартов G.723.1, G.728 и G.729 алгоритмы речевого кодирования CELP (Code Excited Linear Prediction [8]) основаны на АР-модели 10-го порядка. Их широко применяют в цифровых системах сотовой связи, VoIP, голосовой почты и голосового интерактива. Алгоритмы этого класса обеспечивают сжатие данных в восемь и более раз с задержкой результата на время, не превышающее длительности τ = 10…30 мс стандартного речевого фрейма [9]. Естественной “платой” за указанное сжатие являются потери части полезной информации. Размер потерь в значительной степени определяется точностью настройки АР-модели под наблюдаемый речевой сигнал. Причем из-за естественной ограниченности частотного ресурса актуальность исследований в данном направлении с течением времени отнюдь не ослабевает [10], поэтому актуальной представляется и тема предлагаемой статьи.

Доминирующее положение в области АР-исследований до настоящего времени занимает метод спектрального анализа, разработанный Дж.П. Бергом в 1967 г. В рамках теории линейного предсказания [11] и уравнений Юла–Уолкера [1] данный метод сводит рассматриваемую задачу к корреляционному анализу наблюдаемого сигнала. Проблема малых выборок в этом методе решается с помощью высокоскоростной вычислительной процедуры Левинсона–Дурбина [12]. Ее назначение – оценка вектора АР-параметров сигнала по конечной выборке наблюдений. При этом в целях обеспечения требуемой точности порядок АР-модели определяют на уровне p $ \gg $ 1. Например, равенство p = 10 в алгоритмах класса CELP установлено из расчета четырех-пяти основных формант в спектре звуков речи диктора. Между тем из прикладной лингвистики хорошо известно [6, 13], что оптимальное значение порядка авторегрессии, в частности для сигналов гласных фонем, варьируется в довольно широких пределах, p = 8…20, в зависимости от речевых особенностей конкретного диктора. Однако использование завышенного значения АР-порядка p сопровождается рядом вредных эффектов [14], таких как смещение мод и появление ложных пиков в формируемой статистической оценке спектральной плотности мощности (СПМ). Указанные эффекты особенно ярко выражены для сигналов гласных фонем с характерной для них плохой обусловленностью матриц автоковариаций [15].

1. ПРЕДМЕТ И ЦЕЛЬ ИССЛЕДОВАНИЯ

Альтернативой статистическому подходу может служить алгебраический подход в терминах адаптивного фильтра или дискретного спектрального моделирования (ДСМ) [16, 17]. Его математической основой является спектральная чистополюсная [18] модель речевого сигнала:

(1)

которая может быть представлена в эквивалентном виде

(2)

Здесь введены следующие обозначения: T – период временнóй дискретизации речевого сигнала; ap = {ak} – вектор коэффициентов линейной авторегрессии p-го порядка; ${{\sigma }}_{p}^{2}$ – дисперсия ошибки линейного предсказания [19]; ${{\sigma }}_{0}^{2}$ = const ($ \triangleq $ – символ равенства по определению). Задача в данном случае формулируется как оптимизационная: путем подбора (вариации) (p + 1)-вектора АР-параметров bp+ 1 = {bi} найти наилучшее приближение (2) для СПМ G(f) на конечном множестве ее отсчетов {G(fn)} в пределах конечного набора частот fn, n ≤ N, из ограниченного диапазона |fn| ≤ 0.5F, где F = 1/T – частота дискретизации речевого сигнала. Для ее решения применяют итеративные вычислительные процедуры. Порядок авторегрессии устанавливают при этом на некотором фиксированном уровне, в частности p = 10, а в качестве спектрального эталона {G(fn)} используют дискретную оценку СПМ. Например [17, 18], это может быть мгновенная спектральная оценка [19] на основе дискретного преобразования Фурье (ДПФ) речевого сигнала x(t) в пределах его m-го (наблюдаемого) фрейма xm(t). В пользу такого варианта свидетельствуют следующие соображения [18]. Во-первых, ДПФ-оценки спектра основываются на линейной обработке речевого сигнала и поэтому не связаны с отмеченными выше эффектами смещения и расщепления спектральных мод в условиях малых выборок наблюдений [19]. И, во-вторых, к оценкам СПМ на основе ДПФ применима теорема Парсеваля [20], что упрощает процедуру их последующего амплитудного масштабирования под переменную интенсивность речевого сигнала.

Проблема масштабирования АР-модели речевого сигнала [21] – одна из наиболее острых в области цифровых систем связи [22, 23]. В нашем случае она обусловлена и обостряется большим динамическим диапазоном гласных фонем (десятки децибел) в пределах даже одного потока речи от диктора, а также принципиальной неравноценностью АР-параметров ap и ${{\sigma }}_{p}^{2}$ в рамках рассматриваемой задачи. Если вектор ap согласно выражению (1) оказывает непосредственное влияние на форму СПМ АР-модели (2), то дисперсия ${{\sigma }}_{p}^{2}$ – это только ее масштабный множитель [19]. В задаче ДСМ он играет роль мешающего параметра [15, 18], что объективно усложняет ее решение и ограничивает точность результата. Решению проблемы масштабирования в задаче ДСМ речевого сигнала и посвящена главным образом данная статья.

Цель проведенного исследования – повышение точности АР-модели (2) на основе применения в качестве функции стоимости оптимизационной задачи [16] новой меры: масштабно-инвариантной модификации информационного рассогласования случайных сигналов по Кульбаку–Лейблеру [24]. В отличие от обычной практики ДСМ [18] увеличение размерности поставленной задачи на единицу, с p до p + 1, не привело в новом методе к заметному увеличению сложности вычислений и к ухудшению точности полученного результата, так как авторам удалось разделить между собой две вычислительные процедуры: оптимизации вектора коэффициентов bp+ 1 и масштабирования АР-модели (2).

2. ПОСТАНОВКА ЗАДАЧИ

В работе [24] со ссылкой на симметричную форму информационной метрики Кульбака–Лейблера и определение COSH-расстояния [25]

${{{{\rho }}}_{{{\text{COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}) \triangleq {{(2F)}^{{ - 1}}}\int\limits_{{{ - F} \mathord{\left/ {\vphantom {{ - F} 2}} \right. \kern-0em} 2}}^{{F \mathord{\left/ {\vphantom {F 2}} \right. \kern-0em} 2}} {\left[ {\hat {G}(f;{{{\mathbf{b}}}_{{p + 1}}}){{G}^{{ - 1}}}(f) + G(f){{{\hat {G}}}^{{ - 1}}}(f;{{{\mathbf{b}}}_{{p + 1}}}) - 2} \right]{\text{d}}f \geqslant 0} $

в качестве ее асимптотического эквивалента в частотной области дано обоснование величины

(3)
${{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}) \triangleq \sqrt {\left[ {{{F}^{{ - 1}}}\int\limits_{{{ - F} \mathord{\left/ {\vphantom {{ - F} 2}} \right. \kern-0em} 2}}^{{F \mathord{\left/ {\vphantom {F 2}} \right. \kern-0em} 2}} {\hat {G}(f;{{{\mathbf{b}}}_{{p + 1}}}){{G}^{{ - 1}}}(f)\,{\text{d}}f} } \right] \times \left[ {{{F}^{{ - 1}}}\int\limits_{{{ - F} \mathord{\left/ {\vphantom {{ - F} 2}} \right. \kern-0em} 2}}^{{F \mathord{\left/ {\vphantom {F 2}} \right. \kern-0em} 2}} {G(f){{{\hat {G}}}^{{ - 1}}}(f;{{{\mathbf{b}}}_{{p + 1}}})\,{\text{d}}f} } \right]} - 1 \geqslant 0$

на роль масштабно-инвариантной меры информационного рассогласования речевого сигнала и его АР-модели (2). Причем, учитывая особенности механизма речеобразования [1], а также эффект регуляризации от действия фонового шума в задачах ДСМ [17], из рассмотрения далее исключены возможности равенства нулю как СПМ G(f), так и ее оценки Ĝ(f) по всей области их определения. С использованием (3) поставим следующую оптимизационную задачу: найти оптимальный вектор АР-параметров bp+ 1 по критерию минимума меры ρM-COSH(bp+ 1). Задача в данной постановке представляет очевидный теоретический и практический интерес.

В самом деле, из справедливости тождества

$\begin{gathered} {{\left. {{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}})} \right|}_{{\hat {G}(f;{{{\mathbf{b}}}_{{p + 1}}}) = G{\text{*}}(f)}}} = \\ = {{\left. {{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}})} \right|}_{{\hat {G}(f;{{{\mathbf{b}}}_{{p + 1}}}) = cG{\text{*}}(f)}}} \\ \end{gathered} $

для любых СПМ G*(f) > 0 и константы c > 0, в том числе при равенстве $c = {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{{\sigma }}_{0}^{2}}}} \right. \kern-0em} {{{\sigma }}_{0}^{2}}},$ вытекает инвариантность меры (3) к масштабному множителю ${{\sigma }}_{0}^{2}$ из выражения (2). Отметим при этом, что собственно мера COSH данным свойством не обладает. Как следствие, при ее применении оценка оптимального вектора АР-параметров bp+ 1 будет менять свое значение в зависимости от дисперсии ошибки линейного предсказания ${{\sigma }}_{p}^{2}.$ А это нежелательное явление [18] с точки зрения точности результирующей АР-модели. Поэтому можно утверждать, что в задаче ДСМ традиционная мера COSH-расстояния заведомо проигрывает своей модификации (3) по эффективности.

Конкуренцию новой мере в принципиальном отношении может составить лишь симметричная форма расстояния Итакуры (Symmetric Itakura Distance, SID [25, 26])

(4)
${{{{\rho }}}_{{{\text{SID}}}}}({{{\mathbf{b}}}_{{p + 1}}}) \triangleq \ln \sqrt {\left[ {{{F}^{{ - 1}}}\int\limits_{{{ - F} \mathord{\left/ {\vphantom {{ - F} 2}} \right. \kern-0em} 2}}^{{F \mathord{\left/ {\vphantom {F 2}} \right. \kern-0em} 2}} {\hat {G}(f;{{{\mathbf{b}}}_{{p + 1}}}){{G}^{{ - 1}}}(f){\text{d}}f} } \right] \times \left[ {{{F}^{{ - 1}}}\int\limits_{{{ - F} \mathord{\left/ {\vphantom {{ - F} 2}} \right. \kern-0em} 2}}^{{F \mathord{\left/ {\vphantom {F 2}} \right. \kern-0em} 2}} {G(f){{{\hat {G}}}^{{ - 1}}}(f;{{{\mathbf{b}}}_{{p + 1}}}){\text{d}}f} } \right]} \geqslant 0,$

которая нашла на данный момент довольно широкое применение в задачах медицинской диагностики [27, 28]. Поэтому на ней, вслед за спектральной мерой (3), мы сосредоточим основное внимание.

3. СИНТЕЗ АЛГОРИТМА ВЫЧИСЛЕНИЙ

Учитывая свойства меры ρM-COSH(bp+ 1), перепишем выражения (2) и (3) в дискретном виде:

(5)
(6)
${{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}) = \sqrt {\left[ {{{N}^{{ - 1}}}\sum\limits_{n = 1}^N {\hat {G}({{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}}){{G}^{{ - 1}}}({{f}_{n}})} } \right]\left[ {{{N}^{{ - 1}}}\sum\limits_{n = 1}^N {G({{f}_{n}}){{{\hat {G}}}^{{ - 1}}}({{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}})} } \right]} - 1 \geqslant 0.$

Задача после этого формулируется следующим образом: найти оптимальный вектор АР-параметров bопт из условия минимизации меры (6) при равенстве bp+ 1 = bопт. Константа ${{\sigma }}_{0}^{2}$ в данном случае значения не имеет. Поэтому для определенности далее примем ее (в варианте “gain normalization” [25]) равной единице. Задача в данной формулировке имеет единственное решение [17]. Правда, найти его в явном виде не представляется возможным. Поэтому воспользуемся итеративным методом градиентного спуска [15, 16].

Следуя методологии итеративных вычислений [18], сначала определим градиент целевого функционала

(7)

поставленной задачи, где введены следующие обозначения:

$\begin{gathered} {{g}_{1}}({{{\mathbf{b}}}_{{p + 1}}}) \triangleq {{N}^{{ - 1}}}\sum\limits_{n = 1}^N {\hat {G}({{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}}){{G}^{{ - 1}}}({{f}_{n}})} , \\ {{g}_{2}}({{{\mathbf{b}}}_{{p + 1}}}) \triangleq {{N}^{{ - 1}}}\sum\limits_{n = 1}^N {G({{f}_{n}}){{{\hat {G}}}^{{ - 1}}}({{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}})} . \\ \end{gathered} $

Приравнивая градиент (7) к нулю, получим систему оптимизационных уравнений

$\frac{d}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}) = 0,\,\,\,\,i = \overline {{\text{0,}}p} .$

Искомый вектор bопт = Argmin ρM-COSH(bp+ 1) после этого определим в виде последовательности приближений:

(8)
$\begin{gathered} {{b}_{i}}(l) = {{b}_{i}}(l - 1) - {{{{\gamma }}}_{0}}{{\left. {\frac{{\text{d}}}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{{\mathbf{\hat {b}}}}}_{{p + 1}}})} \right|}_{{{{{{\mathbf{\hat {b}}}}}_{{p + 1}}} = \left\{ {{{b}_{i}}(l - 1)} \right\}}}}, \\ l = 1,2,...{\text{,}} \\ \end{gathered} $

при их инициализации (на нулевом шаге) системой равенств b0(0) = 1 и ${{b}_{i}}(0) = - {{\hat {a}}_{i}}$ $\forall i \geqslant 1.$ Здесь γ0 > 0 – шаг итераций, l – их порядковый номер, ${{\hat {a}}_{i}}$ – выборочная оценка i-го коэффициента авторегрессии p-го порядка, полученная по результатам обработки текущего фрейма данных с использованием, например, метода Берга [19]. При правильно выбранном шаге итераций γ0 ≤ γmax последовательность (8) сходится в асимптотике при l → ∞ в точку минимума bопт дискретной функции стоимости (6). Количество итераций L на практике не превышает нескольких десятков единиц [17, 18] и устанавливается наблюдателем в зависимости от требований к точности приближений.

Финальные значения приближений {bi(L)} определяют согласно (2) форму огибающей дискретной СПМ речевого сигнала {G(fn)} как результат первого этапа ДСМ на основе M-COSH-расстояния. Аналогичным образом определим и метод SID – с той разницей, что выражение для градиента в правой части (8) примет в этом случае иной вид:

(9)

Поскольку в соответствии с (6) выполняется равенство

$\sqrt {{{g}_{1}}({{{\mathbf{b}}}_{{p + 1}}}){{g}_{2}}({{{\mathbf{b}}}_{{p + 1}}})} = {{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}) + 1 \geqslant 1,$

из выражения (9) придем к системе соотношений

$\forall i = \overline {0,p} :\,\,\frac{{\text{d}}}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{SID}}}}}({{{\mathbf{b}}}_{{p + 1}}}) \leqslant \frac{{\text{d}}}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}}).$

Полученный результат имеет большое значение с точки зрения сравнительной динамики итераций (8) при применении двух разных методов ДСМ: у метода, основанного на модифицированном COSH-расстоянии (3), скорость сходимости итераций к оптимуму bопт выше. А это важный довод в пользу предлагаемого метода в расчете на обработку речевого сигнала в режиме реального времени11.

4. ВТОРОЙ ЭТАП ОБРАБОТКИ

Содержанием первого этапа ДСМ в формулировке (5)–(8) была оптимизация вектора АР-параметров bp+ 1. На втором, завершающем этапе обработки речевого сигнала данный вектор должен быть отмасштабирован под наблюдаемый фрейм xm(t). В этой связи отметим важную деталь: вслед за спектральной мерой M-COSH-расстояния (3) ее градиент (7) также инвариантен к масштабу моделируемой СПМ. Это вытекает, в частности, из справедливости равенства

$\begin{gathered} {{\left. {\frac{{\text{d}}}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}})} \right|}_{{G(f) = G{\text{*}}(f)}}} = \\ = {{\left. {\frac{{\text{d}}}{{{\text{d}}{{b}_{i}}}}{{{{\rho }}}_{{{\text{M - COSH}}}}}({{{\mathbf{b}}}_{{p + 1}}})} \right|}_{{G(f) = cG{\text{*}}(f)}}} \\ \end{gathered} $

для любых G*(f) > 0 и c > 0. Как следствие, операция масштабирования в данном случае может быть вынесена за рамки первого этапа. Задача состоит в определении масштабного множителя ${{\sigma }}_{0}^{2}$ в правой части выражения (5) по результатам L-го шага итераций (8). Воспользуемся для ее решения принципом равенства средних мощностей АР-модели (2) и моделируемого фрейма речевого сигнала. При этом в частотной области будем иметь

${{\sigma }}_{0}^{2}(L) \times \sum\limits_{n = 1}^N {{{{\left. {\hat {G}\left( {{{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}}(L)} \right)} \right|}}_{{{{\sigma }}_{{\text{0}}}^{{\text{2}}} = 1}}}} = \sum\limits_{n = 1}^N {G({{f}_{n}})} ,$

откуда получаем

(10)
${{\sigma }}_{0}^{2}(L) = \frac{{\sum\limits_{n = 1}^N {G({{f}_{n}})} }}{{\sum\limits_{n = 1}^N {{{{\left. {\hat {G}\left( {{{f}_{n}};{{{\mathbf{b}}}_{{p + 1}}}(L)} \right)} \right|}}_{{{{\sigma }}_{{\text{0}}}^{{\text{2}}} = 1}}}} }}.$

Полученный результат в совокупности с выражениями (2), (5) и (8) определяет метод авторегрессионного моделирования с масштабированием вектора АР-параметров bp+ 1 под наблюдаемый речевой сигнал. Его эффективность исследуется далее экспериментальным путем.

5. ПРОГРАММА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА

В качестве объекта экспериментального исследования были выбраны сигналы x(t) шести русских гласных фонем в произнесении контрольного диктора как наиболее содержательные в теоретико-информационном смысле [2–6]. Частота дискретизации сигналов F = 8 кГц была согласована с полосой пропускания стандартного телефонного канала связи. Достаточно большая длительность каждого сигнала, Tx = 2…3 с, изначально предполагала его автоматическое членение на последовательность коротких (τ = 16 мс) речевых фреймов x1(t), x2(t), …, xM(t) при их частичном (по 3 мс в начале и в конце) взаимном перекрытии во времени. В результате для каждой фонемы от контрольного диктора предварительно была создана представительная речевая база данных объемом M = 1.6Tx/τ = 200…300 фреймов. После этого по каждому из них методом 128-точечного быстрого преобразования Фурье был сформирован в качестве эталона соответствующий спектральный образец {G(fn)} для всех n ≤ N = = 0.5Fτ = 26.

В качестве предмета экспериментального исследования были рассмотрены АР-модель речевого сигнала фиксированного порядка p = 10 и две спектральные меры ее информационного рассогласования с ДПФ-эталоном {G(fn)}: M-COSH-расстояния (3) и SID (4) в задаче ДСМ (5) на множестве из N = 64 частот fn с шагом 62.5 Гц в полосе 4 кГц. Два соответствующих варианта записи градиента функции стоимости (7) и (9) были использованы при этом для подстановки в правую часть итеративного алгоритма (8). Его сходимость к глобальному минимуму функции стоимости (6) оптимизационной задачи обеспечивалась в ходе эксперимента путем подбора подходящего шага итераций γ0, а также выбором в качестве начального приближения ap(0) заведомо устойчивой [1, 20] спектральной оценки Берга того же порядка p = 10, что и формируемая согласно (2) АР-модель речевого сигнала. Характеристики эффективности алгоритма для каждой из рассматриваемых мер были получены в дальнейшем путем статистического усреднения по каждой отдельной фонеме соответствующих экспериментальных оценок на множестве {xm(t)} из M независимых реализаций речевого сигнала x(t). Погрешность экспериментальных измерений в ее относительном выражении не вышла с доверительной вероятностью 0.9 за пределы δ = 165/√200…300 = 10…11% [29]. В ходе эксперимента были использованы находящиеся в открытом доступе фонетическая база данных контрольного диктора и авторская компьютерная программа Phoneme Training. Они размещены на сайте авторов статьи по ссылке https://sites.google.com/site/frompldcreators/produkty-1/phonemetraining. Полученные результаты отражены на рисунках ниже.

На рис. 1 на примере одного из фреймов фонемы “а” отражена динамика итераций (8) при применении методов авторегрессионного моделирования речевого сигнала на основе M-COSH-расстояния (3) и SID (4). Шаг итераций γ0 в обоих случаях был установлен равным 0.1. Из сравнения двух представленных на рисунке кривых можно сделать вывод о существенном преимуществе предложенного метода по быстродействию и, следовательно, по точности АР-модели (2), если рассматривать случай конечного L < ∞. Так, в нашем примере (см. рис. 1) новому методу потребовалось всего две–четыре итерации для сходимости в окрестности оптимума bопт. Как следует из рассмотрения рис. 2, этого вполне достаточно с точки зрения точности АР-модели (2) по результатам проведенной оптимизации. Причем рассматриваемый выигрыш распространяется на все, без исключения, гласные фонемы в речи контрольного диктора. Это видно, в частности, из рассмотрения гистограммы на рис. 3, где по вертикальной оси отложены значения выигрыша метода M-COSH-расстояния по точности АР-модели (2), определяемого выражением

${{{{\eta }}}_{{{\text{M - COSH}}}}}(L) \triangleq \frac{{{{{{\rho }}}_{{{\text{M - COSH}}}}}\left( {{{{\mathbf{b}}}_{{11}}}(0)} \right) - {{{{\rho }}}_{{{\text{M - COSH}}}}}\left( {{{{\mathbf{b}}}_{{11}}}(L)} \right)}}{{{{{{\rho }}}_{{{\text{M - COSH}}}}}\left( {{{{\mathbf{b}}}_{{11}}}(0)} \right)}} \times 100\% .$
Рис. 1.

Динамика итераций (8) при применении мер M-COSH (кривая 1) и SID (кривая 2) с шагом γ0 = 0.1.

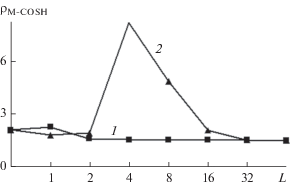
Рис. 2.

Семейство СПМ гласного звука речи “а” по результатам двух этапов вычислений при L = 0 (кривая 1), 2 (кривая 2), 4 (кривая 3) и 32 (кривая 4) в сопоставлении с графиком моделируемого спектрального образца (пунктирная линия).

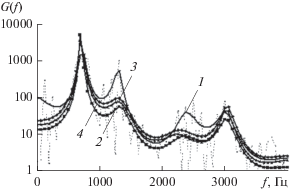
Рис. 3.

Гистограмма выигрыша по точности АР-модели (2) на множестве гласных фонем контрольного диктора в зависимости от числа итераций: L = 2 (светлые столбики), 8 (серые), 32 (черные).

Хотя показатель выигрыша и широко варьируется по своей величине от одной фонемы к другой (по-видимому, это особенность речи конкретного диктора), однако каждый раз (для каждой фонемы) он быстро устремляется к своему максимуму при увеличении числа итераций L.

6. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Как показали результаты проведенного эксперимента, основным преимуществом предложенного метода авторегрессионного моделирования речи являются беспрецедентно высокие динамические свойства итеративной процедуры (8). Их объяснением служит отмеченная выше инвариантность спектральной меры (3) по отношению к масштабному множителю ${{\sigma }}_{p}^{2}$ в правой части выражения (1). Наглядной иллюстрацией сказанного является рис. 4, на котором представлены два графика спектральной АР-оценки (2) сигнала фонемы “а” от контрольного диктора по результатам двух этапов вычислений: до масштабирования и после масштабирования. При этом оба варианта СПМ характеризуются одной и той же величиной рассогласования ρM-COSH = 1.57 по отношению к используемому спектральному ДПФ-образцу {G(fn)}. Отсюда можно сделать вывод, что на этапе итеративной АР-оптимизации (8), а это основная составляющая вычислительного процесса в целом, масштабный множитель ${{\sigma }}_{p}^{2}$ роли не играет. Как следствие, в предложенном методе существенно ослаблены корреляционные связи между отдельными компонентами bi вектора АР-параметров bp+ 1. В итоге был существенно сокращен объем вычислений. (Напомним, именно этим обстоятельством объясняется использование в рамках проведенного выше исследования простейшего в реализации метода градиентного спуска вместо традиционно применяемого [18] метода Ньютона с матричным шагом итераций.) Таким образом, благодаря проведенному исследованию дано обоснование новой меры информационного рассогласования (3) в качестве функции стоимости оптимизационной задачи.

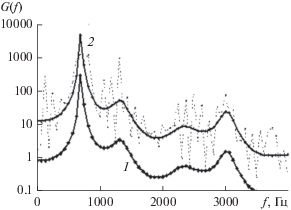
Рис. 4.

График СПМ гласного звука речи “а” по результатам одного (1) и двух (2) этапов вычислений с автоматическим масштабированием под среднюю мощность спектрального образца (пунктирная линия).

Определенные вопросы, правда, вызывает проблема устойчивости, или стабильности [30] АР-модели (2) по результатам ее оптимизации (8). Своими корнями она уходит в проблему устойчивости цифровых рекурсивных фильтров [19]. Однако не следует преувеличивать ее значение в задаче ДСМ. Как справедливо сказано в работе [20], неустойчивый фильтр неработоспособен только в том случае, когда его входной сигнал действует неограниченно долго, так как выходной сигнал фильтра перестает в этом случае зависеть от входного. Но тот же фильтр вполне работоспособен и может быть использован в роли формирователя речевого сигнала с импульсным возбуждением [8, 17] при условии, что его память в конце каждого очередного цикла основного тона принудительно обнуляется.

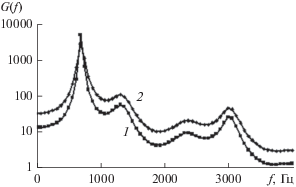
На рис. 5 представлены графики СПМ двух АР-моделей одной и той же фонемы “а” от контрольного диктора. Кривая 1 соответствует исходной, в данном примере – неустойчивой, АР-модели (2) с вектором коэффициентов a10(4) = (0.786787117; –0.33091984; 0.160324858; –0.615996216; 0.275025217; –0.169738362; –0.03057036; –0.09782516; –0.148893196; 0.229581645), полученным согласно процедуре (8) по результатам четырех итераций, а кривая 2 – ее откорректированной, устойчивой модификации. Ее вектор АР-коэффициентов ã10 = (0.770766553; –0.318710928; 0.158034596; –0.573735792; 0.251116841; –0.151925457; –0.023126322; –0.089487844; –0.119269473; 0.191146688) получен методом Берга [13] по реализации сигнала x(t), синтезированного по схеме импульсного возбуждения с частотой основного тона речи контрольного диктора 125 Гц [31]. Как видим, различия в двух представленных СПМ минимальны.

Рис. 5.

График СПМ АР-модели фонемы “а” по результатам оптимизации (8) при L = 4 в первоначальном (кривая 1) и в устойчивом (кривая 2) виде.

Существует еще один, более простой и одновременно радикальный способ преодоления проблемы устойчивости АР-модели (2), а именно [32]: ситуативный отказ от ее использования в целях кодирования информации, если она неустойчива, и ее замена в таких случаях на оценку Берга (1), которая, как известно [1, 14], сохраняет устойчивость при любых обстоятельствах. При таком подходе проблема устойчивости разрешается ценой определенных потерь в потенциально достижимой эффективности АР-моделирования. Соответствующие экспериментальные результаты в виде гистограммы представлены на рис. 6. Под показателем устойчивости здесь понимается относительная частота ΘM формирования устойчивой АР-модели (2) на множестве из M = 200…300 реализаций вектора АР-параметров b11(4) по каждой отдельной фонеме контрольного диктора [2]. Величина погрешности измерений при доверительной вероятности 0.95 составила в данном случае примерно 196/√2000 ≈ 5% [29]. Из анализа гистограммы (см. рис. 6) можно заключить, что, по крайней мере, каждый второй (50%) результат вычислений в рамках процедуры (8) приводит в данном конкретном случае – в расчете на индивидуальные особенности контрольного диктора – к устойчивой АР-модели речевого сигнала.

Рис. 6.

Гистограмма показателей устойчивости АР‑модели (2) гласных звуков речи контрольного диктора при ее оптимизации методом M-COSH-расстояния по результатам четырех итераций (8).

ЗАКЛЮЧЕНИЕ

Если рассматривать ту или иную меру рассогласования речевых сигналов в качестве функции стоимости оптимизационной задачи, то решающее значение с точки зрения эффективности ДСМ будет иметь ее градиент по вектору оптимизируемых параметров bp+ 1. Задача в таком случае сводится к адаптации данного вектора под наблюдаемый спектральный образец {G(fn)} вдоль направления максимума упомянутого градиента. В таком случае разные меры характеризуются разной скоростью достижения и разной степенью обусловленности данного максимума. С указанной точки зрения первостепенный интерес представляют приведенные в данной статье результаты. Наиболее близкой к M-COSH-расстоянию из числа известных спектральных мер является симметричная форма расстояния Итакуры (4). Но она проигрывает предложенной мере (3) в несколько раз по скорости сходимости итеративной вычислительной процедуры (8), а также по точности формируемой АР-модели (2) при любом конечном количестве итераций L < ∞.

Таким образом, полученные в статье результаты открывает качественно новые возможности для исследований и разработок в области автоматической обработки и передачи речи в режиме реального времени.

Список литературы

  1. Rabiner L.R., Schafer R.W. // Foundations and Trends in Signal Processing. 2007. V. 1. № 1–2. P. 1. https://doi.org/10.1561/2000000001

  2. Савченко В.В., Савченко Л.В. // Измерит. техника. 2019. № 9. С. 59. https://doi.org/10.32446/0368-1025it.2019-9-59-64

  3. Perez-Gaspar L.A., Caballero-Morales S.O., Trujillo-Romero F. // Expert Systems with Applications. 2016. V. 66. P. 42. https://doi.org/10.1016/j.eswa.2016.08.047

  4. Stasak B., Epps J., Goecke R. // Computer Speech & Language. 2019. V. 53. P. 140. https://doi.org/10.1016/j.csl.2018.08.001

  5. Kim J., Toutios A., Lee S., Narayanan S. // Computer Speech & Language. 2020. V. 64. Article 101100. https://doi.org/10.1016/j.csl.2020.101100

  6. Савченко В.В., Савченко А.В. // РЭ. 2020. Т. 65. № 11. С. 1101. https://doi.org/10.31857/S0033849420110157

  7. Cui S., Li E., Kang X. // IEEE Int. Conf. Multimedia and Expo (ICME). London. 6–10 Jul. 2020. P. 1. https://doi.org/10.1109/ICME46284.2020.9102765

  8. Chaouch H., Merazka M. // Speech Commun. 2019. V. 108. P. 33. https://doi.org/10.1016/j.specom.2019.02.002

  9. Keser S., Gerek Ö.N., Seke E., Gülmezoğlu M.B. // Speech Commun. 2017. V. 94. P. 50. https://doi.org/10.1016/j.specom.2017.09.002

  10. Sharma G., Umapathy K., Krishnan S. // Appl. Acoustics. 2020. V. 158. Article 107020. https://doi.org/10.1016/j.apacoust.2019.107020

  11. Benesty J., Chen J., Huang Y. / Springer Handbook of Speech Processing. Pt. B. N.Y.: Springer, 2008. P. 111. https://doi.org/10.1007/978-3-540-49127-9_7

  12. Xiao D., Mo F., Zhang Y. et al. // Heliyon. 2018. V. 4. № 11. Article e00948. https://doi.org/10.1016/j.heliyon.2018.e00948

  13. Caвчeнкo B.B. // PЭ. 2019. T. 64. № 6. C. 585. https://doi.org/10.1134/S0033849419060093

  14. Hoon M.L., Van der Hagen T.H., Schoonewelle H., Van Dam H. // Annals of Nuclear Energy. 1996. V. 23. № 15. P. 1219. https://doi.org/10.1016/0306-4549(95)00126-3

  15. Kashani H.B., Sayadiyan A. // Computer Speech & Language. 2018. V. 50. P. 105https://doi.org/10.1016/j.csl.2017.12.008

  16. Chang L., Ming J. // Signal Processing. 2020. V. 168. Article 107348. https://doi.org/10.1016/j.sigpro.2019.107348

  17. Wei B., Gibson J. // IEEE Signal Processing Lett. 2003. V. 10. № 4. P. 101. https://doi.org/10.1109/LSP.2003.808550

  18. Mustiere F., Bouchard M., Bolic M. // IEEE Trans. 2012. V. ASLP-20. № 2. P. 705. https://doi.org/10.1109/TASL.2011.2163511

  19. Marple S.L. Digital Spectral Analysis with Applications. N.Y.: Dover Publications, 2019.

  20. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов: Справочник. М.: Радио и связь, 1985.

  21. Daniels M.L., Rao B.D. // Conf. Record of 46th Asilomar Conf. on Signals Systems and Computers Pacific Grove. 4–7 Nov. 2012. N.Y.: IEEE, 2012. P. 92. https://doi.org/10.1109/ACSSC.2012.6488965

  22. Arun-Sankar M.S., Sathidevi P.S. // Heliyon. 2019. V. 5. № 5. Article e01820. https://doi.org/10.1016/j.heliyon.2019.e01820

  23. Seto K., Ogunfunmi T. // Computer Speech & Language. 2019. V. 54. P. 61. https://doi.org/10.1016/j.csl.2018.09.001

  24. Савченко В.В. // Изв. вузов. Радиоэлектроника. 2020. Т. 63. № 1. С. 55. https://doi.org/10.3103/S0735272720010045

  25. Gray R.M., Buzo A., Gray A., Matsuyama Y. // IEEE Trans. 1980. V. SP-28. № 4. P. 367. https://doi.org/10.1109/TASSP.1980.1163421

  26. Estrada E., Nazeran H., Ebrahimi F., Mikaeili M. // Proc. Amer. Soc. Mechanical Engineering (ASME) 2009 Summer Bioengineering Conf. (SBC 2009) Lake Tahoe. 17–21 Jun. N.Y.: ASME, 2009. Pts. A and B. P. 723. https://doi.org/10.1115/SBC2009-206233

  27. Eva O.D., Lazar A.M. // Int. J. Advanced Computer Sci. Appl. 2017. V. 8. № 8. P. 263. https://doi.org/10.14569/IJACSA.2017.080834

  28. Wang D., Wang D., Yu M. et al. Model-based Health Monitoring of Hybrid Systems. N.Y.: Springer, 2013. https://doi.org/10.1007/978-1-4614-7369-5

  29. Савченко В.В. // Научные ведомости Белгородского гос. ун-та. Сер. История. Политология. Экономика. Информатика. 2015. № 1. Вып. 33/1. С. 74. http://dspace.bsu.edu.ru/handle/123456789/12929.

  30. Kazemipour A., Miran S., Pal P. et al. // IEEE Trans. 2017. V. SP-65. № 9. P. 2333. https://doi.org/10.1109/TSP.2017.2656848

  31. Савченко А.В., Савченко В.В. // Измерит. техника. 2019. № 3. С. 59. https://doi.org/10.32446/0368-1025it.2019-3-59-63

  32. Candan C. // Signal Processing. 2020. V. 166. Article 107256. https://doi.org/10.1016/j.sigpro.2019.107256

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал