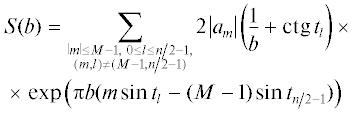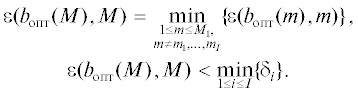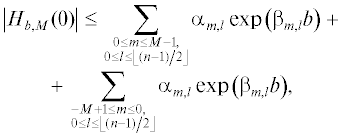Радиотехника и электроника, 2021, T. 66, № 11, стр. 1085-1099
О новом методе аппроксимации квадратов атомарных функций ha(x) неотрицательными рациональными дробями
К. А. Будунова a, *, В. Ф. Кравченко a, b, c, **
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
b Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, ул. 2-я Бауманская, 5, Российская Федерация
c Научно-технологический центр уникального приборостроения РАН
117342 Москва, ул. Бутлерова, 15, Российская Федерация
* E-mail: 1917schw@mail.ru
** E-mail: kvf-ok@mail.ru
Поступила в редакцию 14.04.2021
После доработки 14.04.2021
Принята к публикации 27.05.2021
Аннотация
Впервые рассмотрен метод, позволяющий выполнять синтез устойчивых фильтров с амплитудно-частотными характеристиками, аппроксимирующими атомарные функции ${{h}_{a}}(x)$. Построенные атомарные фильтры могут быть использованы как самостоятельно, так и в качестве прототипов цифровых фильтров с бесконечной импульсной характеристикой. Доказаны три теоремы, лежащие в основе нового метода приближения квадратов атомарных функций рациональными дробями, удовлетворяющими условию неотрицательности. Эти дроби используются далее при синтезе фильтра с амплитудно-частотной характеристикой, являющейся приближением функции ${{h}_{a}}(x).$ Представлен пример восстановления сигнала с применением атомарного фильтра на основе функции ${{h}_{a}}(x)$ в качестве сглаживающего. Описан метод построения фильтров с амплитудно-частотными характеристиками, аппроксимирующими произвольные финитные неотрицательные функции с быстро сходящимся рядом Фурье.
1. АТОМАРНАЯ ФУНКЦИЯ ${{h}_{a}}(x)$ И ЗАДАЧА СИНТЕЗА ФИЛЬТРА НА ЕЕ ОСНОВЕ
Численный метод, предлагаемый в данной работе, был разработан с целью построения фильтров низких частот (ФНЧ) с амплитудно-частотными характеристиками (АЧХ), приближающимися по форме к атомарной функции ${{h}_{a}}(x).$ Финитная бесконечно дифференцируемая функция ${{h}_{a}}(x)$ [1, 2] есть решение уравнения вида
с условием нормировки
Спектр ${{F}_{a}}(t)$ функции ${{h}_{a}}(x)$ определяется выражением
Функция ${{h}_{a}}(x)$ равна нулю вне отрезка $\left[ {\frac{{ - 1}}{{a - 1}},\frac{1}{{a - 1}}} \right],$ а при $a > 2$ обладает следующим свойством:
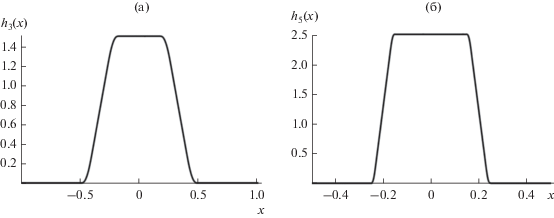
Графики функций ${{h}_{a}}(x)$ для $a = 3$ и $a = 5$ приведены на рис. 1.
Теоретической основой методов фильтрации с применением ${{h}_{a}}(x)$ является ряд Кравченко–Котельникова [3]. Сигнал $f(t)$ с финитным спектром $F[f](\omega ),$ $F[f](\omega ) = 0$ при $\left| \omega \right| > \Omega $ может быть представлен в виде ряда
(1)
$f(t) = \sum\limits_{k = - \infty }^{ + \infty } {f(k\Delta ){{F}_{a}}\left( {\frac{{a\pi }}{\Delta }(t - k\Delta )} \right)} ,$где
Главным преимуществом ряда (1) является быстрое затухание его базисных функций. Благодаря этому свойству ошибка усечения ${{\varepsilon }_{N}}(t)$ ряда (1),
при $N \to \infty $ и $\left| t \right| < \Delta $ удовлетворяет соотношению $\left| {{{\varepsilon }_{N}}(t)} \right| = O({{N}^{{ - {{\alpha }}}}}),$ где $\alpha $ – любое положительное число [4].
Для практического применения ряда (1) в задачах фильтрации сигналов необходимо наличие методов синтеза ФНЧ с АЧХ, аппроксимирующей атомарную функцию ${{h}_{a}}(x).$ Эта задача была успешно решена для цифровых фильтров с конечной импульсной характеристикой (КИХ) [5]. В данной работе рассматривается метод построения аналоговых атомарных фильтров. Они могут быть использованы как самостоятельно, например, в процессе цифро-аналогового преобразования (ЦАП), так и в качестве прототипов цифровых фильтров с бесконечной импульсной характеристикой (БИХ).
Наиболее сложным этапом синтеза атомарного аналогового фильтра является построение дробно-рациональных приближений квадратов функций ${{h}_{a}}(x).$ Впервые такие приближения были получены в [6], однако они имели слишком высокий порядок для практического применения. Далее в работе [7] был предложен метод дробно-рациональной аппроксимации функций $h_{a}^{2}(x)$ с помощью интеграла Коши. В основе данного метода лежит равенство
(3)
$\frac{1}{{2\pi j}}\oint\limits_C {\frac{{\varphi (z)}}{{z - \omega }}dz} = \left\{ {\begin{array}{*{20}{c}} {\varphi (\omega ),}&{ - 1 < \omega < {\text{1,}}} \\ {0,}&{\left| \omega \right| > 1.} \end{array}} \right.$Здесь $\omega $ – вещественная переменная, $C$ – контур, проходящий через точки $z = \pm 1$ и ограничивающий односвязную область D, $\varphi (z)$ – некоторая аналитическая на $D$ функция. В [7] в качестве функций $\varphi (\omega )$ использовались приближения функции $h_{a}^{2}(\omega )$ частичными суммами ряда Фурье. Далее, используя формулы приближенного интегрирования, левую часть (3) можно преобразовать в рациональную дробь и попытаться оптимизировать погрешность приближения этой дробью функции $h_{a}^{2}(\omega ).$
Алгоритм оптимизации из [7] имеет недостаток: найденная дробь может принимать отрицательные значения, а в этом случае она будет непригодной для построения АЧХ устойчивого фильтра. В данной работе впервые предлагается численный метод, позволяющий искать лишь неотрицательные дробно-рациональные аппроксимации $h_{a}^{2}(\omega ).$
2. ПОИСК ДЕЙСТВИТЕЛЬНЫХ ДРОБНО-РАЦИОНАЛЬНЫХ АППРОКСИМАЦИЙ ФУНКЦИИ $h_{a}^{2}(\omega )$
Рассмотрим функцию ${{\varphi }_{a}}(\omega )$ = $\frac{4}{{{{a}^{2}}}}{{\left( {{{{\text{h}}}_{a}}({\omega \mathord{\left/ {\vphantom {\omega {(a - 1)}}} \right. \kern-0em} {(a - 1)}})} \right)}^{2}}$ с носителем ${\text{supp}}{\mkern 1mu} \,{{\varphi }_{a}}(x) = [ - 1,1]$ и ее частичные суммы Фурье $\varphi _{a}^{{(M)}}(\omega ),$
(4)
$\varphi _{a}^{{(M)}}(\omega ) = {{a}_{0}} + \sum\limits_{k = 1}^{M - 1} {{{a}_{k}}} \cos (\pi k\omega ).$Коэффициенты ${{a}_{k}}$ в (4) определяются через коэффициенты ${{c}_{0}},{{c}_{1}},...,{{c}_{k}},...$ ряда Фурье функции $\frac{2}{a}{{{\text{h}}}_{a}}\left( {\frac{\omega }{{a - 1}}} \right){\text{:}}$
по формулам
Поскольку $\varphi _{a}^{{(M)}}(z)$ – целая функция, то ее можно подставить вместо $\varphi (z)$ в формулу (3), причем правая часть (3) в этом случае будет аппроксимацией функции ${{\varphi }_{a}}(\omega ).$
Используем далее формулу приближенного интегрирования. Заменяя интеграл в левой части (3) суммой
(5)
$\frac{1}{{2\pi j}}\sum\limits_{l = 0}^{2n - 1} {\frac{{\varphi _{a}^{{(M)}}(z({{t}_{l}}))z{\kern 1pt} '({{t}_{l}})}}{{z({{t}_{l}}) - \omega }}} \Delta t,$получим рациональную дробь, с некоторой точностью аппроксимирующую функцию ${{\varphi }_{a}}(\omega ).$ Погрешность приближения функции ${{\varphi }_{a}}(\omega )$ дробью (5) зависит от контура C, сетки приближенного интегрирования и числа слагаемых $M$ частичной суммы $\varphi _{a}^{{(M)}}(\omega ).$ Выберем в качестве контура $C$ эллипс ${{C}_{b}}$ с центром в начале координат:
Узлы ${{t}_{l}}$ сетки интегрирования ${{t}_{0}},...,{{t}_{{2n - 1}}}$ положим равными ${{t}_{l}} = \frac{\pi }{{2n}} + l\frac{\pi }{n}.$ Дробь (5) в этом случае примет вид
(6)
$\begin{gathered} {{H}_{{b,M}}}(\omega ) = \frac{1}{{2nj}} \times \\ \times \,\,\sum\limits_{l = 0}^{2n - 1} {\frac{{\varphi _{a}^{{(M)}}(cos{{t}_{l}} + jb\sin {{t}_{l}})( - \sin {{t}_{l}} + jb\cos {{t}_{l}})}}{{cos{{t}_{l}} + jb\sin {{t}_{l}} - \omega }}} . \\ \end{gathered} $Погрешность равномерного приближения $\varepsilon \equiv \varepsilon (b,M)$ функции ${{\varphi }_{a}}(\omega )$ дробью ${{H}_{{b,M}}}(\omega )$ на $\omega \in \mathbb{R}$ определяется формулой
(7)
$\varepsilon = \mathop {\max }\limits_{{{\omega }} \in ( - \infty ,\infty )} \left| {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right|.$Задача минимизации погрешности $\varepsilon (b,M)$ по параметрам $M$ и $b$ равносильна задаче поиска минимума функционала
(9)
$\Phi (b,M) = \mathop {\max }\limits_{{{\omega }} \in ( - \infty ,\infty )} {{\left( {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right)}^{2}}.$Будем считать, что параметр $M$ принимает конечное число значений, $1 \leqslant M \leqslant {{M}_{1}} < \infty .$ Если для каждого фиксированного $M$ найдено решение задачи
то минимум 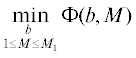 определяется методом перебора.
определяется методом перебора.
О существовании решения задачи (10) при такой постановке (известно лишь, что $b > 0$) ничего сказать нельзя. При фиксированном $M$ можно попробовать применить для поиска оптимального параметра ${{b}_{{опт}}}$ численные методы, например, метод спуска. Далее будут доказаны теоремы, позволяющие выделить конечный отрезок $[{{b}_{0}},{{b}_{1}}],$ на котором ищется решение, что обеспечивает его существование.
3. ТЕОРЕМЫ, ПОЗВОЛЯЮЩИЕ ЗАМЕНИТЬ НЕПРЕРЫВНУЮ ЗАДАЧУ ДИСКРЕТНОЙ
Описанный выше численный метод приближения не может без некоторых изменений быть применен для построения квадратов АЧХ устойчивых фильтров. Решая задачу (8), можно получить аппроксимирующую рациональную дробь, числитель и знаменатель которой являются действительными четными по $\omega $ полиномами, однако эта дробь не обязательно будет неотрицательной. Если функция ${{H}_{{b,M}}}(\omega )$ – квадрат АЧХ устойчивого физически реализуемого фильтра, то она должна удовлетворять также условию
Докажем несколько вспомогательных теорем, определяющих численный метод нахождения неотрицательного решения задачи (8).
Прежде всего при фиксированном $M$ было бы полезно выделить некоторый отрезок $[{{b}_{0}},{{b}_{1}}],$ на котором располагается интересующее нас решение задачи (8) ${{b}_{{опт}}}.$ Поскольку нас интересуют достаточно точные дробно-рациональные аппроксимации функции ${{\varphi }_{a}}(\omega ),$ попробуем хотя бы частично исключить из множества значений $b \in (0, + \infty )$ те точки, в которых выполняется неравенство $\varepsilon > {{\varepsilon }_{1}},$ где ${{\varepsilon }_{1}}$ – некоторая заданная погрешность. В следующих ниже двух теоремах утверждается, что для ${{\varepsilon }_{1}} \in (0,1)$ всегда имеются конечные положительные числа ${{b}_{0}}$ и ${{b}_{1}}$ такие, что $\varepsilon > {{\varepsilon }_{1}}$ при b ∈ $ \in (0,{{b}_{0}}) \cup ({{b}_{1}}, + \infty ).$
Сразу отметим, что в изложенных далее доказательствах учитывается тот факт, что функция $\cos t$ является иррациональной на $\left[ {0,\frac{\pi }{2}} \right]$ во всех $\pi $-рациональных точках, за исключением $t \in \left\{ {0,\frac{\pi }{3},\frac{\pi }{2}} \right\}$ [8]. При этом для любого $n$ и для любого узла дискретизации ${{t}_{l}} \in \left( {0,\frac{\pi }{2}} \right]$ из формулы (6) верно
Отсюда следует, что при ${{t}_{l}} \in (0,2\pi ),$ ${{t}_{l}} \ne {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ ${{t}_{l}} \ne {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$
Теорема 1. Для любого ${{\varepsilon }_{1}} \in (0,1)$ имеется число ${{b}_{0}} = {{b}_{0}}(M,n,{{\varepsilon }_{1}})$ такое, что $\varepsilon > {{\varepsilon }_{1}}$ при $b \in (0,{{b}_{0}})$.
Доказательство. Для доказательства этой теоремы запишем дробь (6) в виде
(12)
${{H}_{{b,M}}}(\omega ) = \frac{1}{n}\sum\limits_{l = 0}^{n - 1} {\sum\limits_{m = 0}^{M - 1} {{{a}_{m}}\frac{{{{A}_{1}}(b,m,{{t}_{l}})\omega + {{A}_{0}}(b,m,{{t}_{l}})}}{{{{{(\omega + \cos {{t}_{l}})}}^{2}} + {{b}^{2}}{{{\sin }}^{2}}{{t}_{l}}}}} } ,$где
Обратим внимание, что $\mathop {\lim }\limits_{b \to 0} {{A}_{1}}(b,m,t)$ = = $\mathop {\lim }\limits_{b \to 0} {{A}_{0}}(b,m,t) = 0.$
Функцию (12) будем рассматривать в точке $\omega = {{\omega }_{0}},$
В этой точке ${{\varphi }_{a}}({{\omega }_{0}}) = 1,$ поэтому
при $\left| {{{H}_{{b,M}}}({{\omega }_{0}})} \right| < 1 - {{\varepsilon }_{1}}.$
Обозначим
и запишем оценки сверху функций $\left| {{{A}_{1}}(b,m,{{t}_{l}})} \right|$ и $\left| {{{A}_{0}}(b,m,{{t}_{l}}) - {{A}_{1}}(b,m,{{t}_{l}})\cos {{t}_{l}}} \right|$ в различных случаях.
1. Пусть $m \geqslant 1,$ $t \ne {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Тогда
2. При $t = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ $m \geqslant 1$ имеем
3. При $m = 0$ выполняются равенства
Введем обозначения
и положим
Тогда при $b < {{b}_{0}},$ где
справедливы оценки
Отсюда
Таким образом, число ${{b}_{0}}$ существует и определяется выражением (13).
Запишем еще одно доказательство этой теоремы, верное в случае, когда
(14)
$\mathop {\max }\limits_l \left| {\varphi _{a}^{{(M)}}(\cos {{t}_{l}})} \right| = \left| {\varphi _{a}^{{(M)}}(\cos {{t}_{{{{l}_{0}}}}})} \right| = K \ne 0.$Положим $\tau = {{t}_{{{{l}_{0}}}}}.$ Тогда в точке $\omega = - \cos \tau $ получим
Первая сумма в правой части (15) равна
При $b < \tilde {b},$ где
справедливо неравенство
Пусть
Тогда
при $b < \tilde {b}.$ Положим
и оценим вторую сумму в правой части (15)
Используя выведенные неравенства$,$ получим, что
при
где
(16)
${{b}_{0}} = \min \left\{ {\tilde {b},\frac{1}{2}\frac{K}{{n(1 + {{\varepsilon }_{1}}) + \Lambda + {\rm X}}}} \right\}.$При выполнении условия (14) число ${{b}_{0}}$ лучше определять по формуле (16). При практических расчетах оценка (14) имела значения на порядок или два меньшие чем (16).
В процессе доказательства теоремы о существовании числа ${{b}_{1}}$ будет использоваться следующая лемма.
Лемма. Пусть $m$ и $t$ фиксированы, $m \in \mathbb{N},$ $t$ – некоторое $\pi $-рациональное число из интервала $\left( {0,\frac{\pi }{2}} \right),$ отличное от $\frac{\pi }{3},$ и для $b > 0$ задана дробь
(17)
$V(b,\omega ) = \frac{{{{p}_{1}}(b){{\omega }^{2}} + {{p}_{0}}(b)}}{{{{\omega }^{4}} + {{q}_{1}}(b){{\omega }^{2}} + {{q}_{0}}(b)}}$с коэффициентами
Тогда наибольшее по модулю значение
дроби (17) ограничено снизу числом ${{\Omega }_{0}} > 0,$
Число ${{\Omega }_{0}}$ можно определить с помощью формулы
где
и
Перейдем к доказательству теоремы.
Теорема 2. Для любого ${{\varepsilon }_{1}} > 0$ существует число ${{b}_{1}} = {{b}_{1}}(M,n,{{\varepsilon }_{1}})$ такое, что $~\varepsilon > {{\varepsilon }_{1}}$ для всех $b > {{b}_{1}}.$
Доказательство. Докажем сначала теорему в случае, когда число $n$ четно.
Запишем дробь ${{H}_{{b,M}}}(\omega )$ в виде
(18)
$\begin{gathered} {{H}_{{b,M}}}(\omega ) = \frac{1}{{2n}}exp\left( {\pi (M - 1)b\sin {{t}_{{{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}}}}} \right) \times \\ \times \,\,\sum\limits_{l = 0}^{{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}} {\sum\limits_{m = 0}^{M - 1} {(S_{{l,m}}^{{(1)}}(b,\omega ) + S_{{l,m}}^{{(2)}}(b,\omega ))} } , \\ \end{gathered} $где
Функции ${{\mu }_{{m,l}}}(b,\omega )$ и ${{\nu }_{{m,l}}}(b,\omega )$ при $l \ne \frac{{n - 1}}{2}$ определяются по формулам
(19)
$\begin{gathered} {{\mu }_{{m,l}}}(b,\omega ) = \frac{{{{C}_{1}}(b,m,{{t}_{l}})\omega + {{C}_{0}}(b,m,{{t}_{l}})}}{{{{{(\omega + \cos {{t}_{l}})}}^{2}} + {{b}^{2}}{{{\sin }}^{2}}({{t}_{l}})}} + \\ + \,\,\frac{{ - {{C}_{1}}(b,m,{{t}_{l}})\omega + {{C}_{0}}(b,m,{{t}_{l}})}}{{{{{(\omega - \cos {{t}_{l}})}}^{2}} + {{b}^{2}}{{{\sin }}^{2}}({{t}_{l}})}}, \\ \end{gathered} $(20)
$\begin{gathered} {{\nu }_{{m,l}}}(b,\omega ) = \frac{{{{C}_{1}}(b,m, - {{t}_{l}})\omega + {{C}_{0}}(b,m, - {{t}_{l}})}}{{{{{(\omega + \cos {{t}_{l}})}}^{2}} + {{b}^{2}}{{{\sin }}^{2}}({{t}_{l}})}} + \\ + \,\,\frac{{ - {{C}_{1}}(b,m, - {{t}_{l}})\omega + {{C}_{0}}(b,m, - {{t}_{l}})}}{{{{{(\omega - \cos {{t}_{l}})}}^{2}} + {{b}^{2}}{{{\sin }}^{2}}({{t}_{l}})}}, \\ \end{gathered} $где
Полагая в лемме $t = {{t}_{{{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}}}},$ $m = M - 1,$ получим оценку снизу максимума модуля функции ${{\mu }_{{M - 1,{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}}}}(b,\omega ){\text{:}}$
(21)
$\mathop {max}\limits_{{{\omega }} \in \mathbb{R}} \left| {{{\mu }_{{M - 1,{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}}}}(b,\omega )} \right| \geqslant {{\Omega }_{0}}.$Для каждого значения параметра $b$ будем рассматривать дробь (18) в точке $\omega = {{\omega }_{0}}(b)$ такой, что
Тогда согласно (21) получим
Можно также показать, что для всех функций ${{\mu }_{{m,l}}}$ и ${{\nu }_{{m,l}}}$ при $l \ne \frac{{n - 1}}{2}$ справедливы оценки
(22)
$\begin{gathered} \left| {{{\mu }_{{m,l}}}(b,\omega )} \right| \leqslant 2\left( {\frac{1}{b} + ctg{{t}_{l}}} \right), \\ \left| {{{\nu }_{{m,l}}}(b,\omega )} \right| \leqslant 2\left( {\frac{1}{b} + ctg{{t}_{l}}} \right). \\ \end{gathered} $Отсюда
Сумма
является монотонно убывающей и затухающей с ростом $b$ функцией, поэтому найдется число ${{\tilde {b}}_{1}}$ такое, что
Таким образом,
Полагая далее
(23)
${{b}_{1}} = \max \left\{ {{{{\tilde {b}}}_{1}},\,\,\frac{{\ln (4n(1 + {{\varepsilon }_{1}})) - \ln ({{\Omega }_{0}}\left| {{{a}_{{M - 1}}}} \right|)}}{{\pi (M - 1)\sin {{t}_{{{n \mathord{\left/ {\vphantom {n {2 - 1}}} \right. \kern-0em} {2 - 1}}}}}}}} \right\},$получим искомое число ${{b}_{1}},$ для которого при $b > {{b}_{1}}$
Пусть теперь число $n$ нечетно. Положим
При $b > {{\tilde {b}}_{1}},$ ${{\tilde {b}}_{1}} = - \frac{3}{{{{\Omega }_{1}}}}W\left( { - \frac{1}{3}} \right)$ ($W(.)$ – $W$-функция Ламберта [9]) выполняется неравенство
Рассмотрим функцию (6) в точке $\omega = 0.$ Запишем ${{H}_{{b,M}}}(0)$ в виде
где
(25)
$\begin{gathered} S_{{m,l}}^{{(1)}}(b) = {{a}_{m}}\exp \left( {\pi b(m\sin {{t}_{l}} - {{\alpha }_{0}})} \right){{\mu }_{{m,l}}}(b,0), \\ S_{{m,l}}^{{(2)}}(b) = {{a}_{m}}\exp \left( { - \pi b(m\sin {{t}_{l}} + {{\alpha }_{0}})} \right){{\nu }_{{m,l}}}(b,0). \\ \end{gathered} $Функции ${{\mu }_{{m,l}}}$ и ${{\nu }_{{m,l}}}$ в (25) при $l < {{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2}$ определяются по формулам (19), (20), а при $l = {{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2}$
(26)
${{\mu }_{{m,{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} 2}} \right. \kern-0em} 2}}}}(b,\omega ) = {{\nu }_{{m,{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} 2}} \right. \kern-0em} 2}}}}(b,\omega ) = \frac{b}{{{{\omega }^{2}} + {{b}^{2}}}}.$Согласно (24)
при $b > {{\tilde {b}}_{1}}.$ Далее используем неравенства (22) и запишем оценку
(27)
$\begin{gathered} \left| {\sum\limits_{m = 0}^{M - 1} {\sum\limits_{l = 0}^{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2}} {\left( {S_{{l,m}}^{{(1)}} + S_{{l,m}}^{{(2)}}} \right)} } } \right| \geqslant \left| {S_{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2},M - 1}}^{{(1)}}} \right| - \\ - \,\,\left| {\sum\limits_{m = 0}^{M - 1} {\sum\limits_{l = 0}^{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2}} {\left( {S_{{l,m}}^{{(1)}} + S_{{l,m}}^{{(2)}}} \right)} } - S_{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0em} 2},M - 1}}^{{(1)}}} \right| \geqslant \left| {{{a}_{m}}} \right|{{\Omega }_{1}} - S(b), \\ \end{gathered} $где
Функция $S(b)$ монотонно убывает и стремится к нулю с ростом b. Выберем ${{\tilde {b}}_{2}}$ так, чтобы
Определяя число ${{b}_{1}}$ по формуле
(28)
${{b}_{1}} = \max \left\{ {{{{\tilde {b}}}_{1}},{{{\tilde {b}}}_{2}},\frac{{\ln (4n(1 + {{\varepsilon }_{1}}) - \ln ({{\Omega }_{1}}\left| {{{a}_{{M - 1}}}} \right|)}}{{\pi (M - 1)}}} \right\},$получим искомое неравенство
Докажем теперь теорему, позволяющую заменить непрерывную задачу (10) дискретной.
Теорема 3$.$ Пусть заданы некоторая погрешность ${{\varepsilon }_{0}},$ фиксированное число $M$ и отрезок $[{{\beta }_{0}},{{\beta }_{1}}].$ Тогда для $b \in [{{\beta }_{0}},{{\beta }_{1}}]$ вместо непрерывной задачи (8) можно без потери точности решать дискретную задачу
(29)
$\mathop {\min }\limits_{0 \leqslant r \leqslant R} \varepsilon \left( {{{\beta }_{0}} + r\Delta ,M} \right),$поскольку шаг $\Delta $ в (30) можно подобрать таким образом, чтобы
(30)
$\left| {\mathop {min}\limits_{b \in \left[ {{{{{\beta }}}_{0}},{{{{\beta }}}_{1}}} \right]} \varepsilon (b,M) - \mathop {\min }\limits_{0 \leqslant r \leqslant R} \varepsilon \left( {{{\beta }_{0}} + r\Delta ,M} \right)} \right| \leqslant \frac{{{{\varepsilon }_{0}}}}{{10}}.$Доказательство. Заметим, что функция
непрерывна вместе со своей частной производной по переменной $b$ при $\omega \in \mathbb{R},$ $b \in [{{\beta }_{0}},{{\beta }_{1}}].$ Поэтому производная по $b$ функционала $\Phi (b,M),$ определяемого формулой (9), существует и равна [10]
где
Для функции $\varepsilon (b,M)$ из формулы (7) справедливо равенство
Функционал $\Phi (b,M)$ никогда не обращается в ноль хотя бы потому, что ни одна рациональная дробь кроме нуля не может быть тождественно равна нулю на $\mathbb{R}\backslash [ - 1,1].$ Отсюда следует, что производная $\frac{{\partial \varepsilon }}{{\partial b}}$ существует и равна
(31)
$\begin{gathered} \frac{{\partial \varepsilon }}{{\partial b}} = \frac{1}{{2\sqrt {\Phi (b,M)} }}\Phi {\kern 1pt} '(b,M) = \\ = \frac{1}{{2\sqrt \Phi }}\mathop {\max }\limits_{{{\omega }} \in \Omega {\kern 1pt} '} \left( {2\left( {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right)\frac{\partial }{{\partial b}}{{H}_{{b,M}}}(\omega )} \right) = \\ = \mathop {\max }\limits_{{{\omega }} \in \Omega {\kern 1pt} '} \left( {sign\left( {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right)\frac{\partial }{{\partial b}}{{H}_{{b,M}}}(\omega )} \right) = \\ = \mathop {\max }\limits_{{{\omega }} \in \Omega {\kern 1pt} '} \left( {\frac{\partial }{{\partial b}}\left| {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right|} \right). \\ \end{gathered} $Производная модуля в последней части цепочки равенств (31) вычисляется для $\omega \in \Omega {\kern 1pt} '(b),$ где
Оценим производную $\left| {\frac{{\partial {{H}_{{b,M}}}(\omega )}}{{\partial b}}} \right|.$ Можно показать, что
(32)
$\left| {\frac{{\partial {{\mu }_{{m,l}}}}}{{\partial b}}} \right| \leqslant {{w}_{{m,l}}}(b),\,\,\,\,\left| {\frac{{\partial {{\nu }_{{m,l}}}}}{{\partial b}}} \right| \leqslant {{w}_{{m,l}}}(b),$где
при $l < \frac{{n - 1}}{2}$ и
при $l = \frac{{n - 1}}{2}.$ Воспользуемся также соотношениями
(33)
${{\mu }_{{m,l}}}(b,\omega ) \leqslant {{{v}}_{{m,l}}}(b),\,\,\,\,{{\nu }_{{m,l}}}(b,\omega ) \leqslant {{{v}}_{{m,l}}}(b),$Учитывая (32) и (33), получим оценку
где
Знаком $\left\lfloor . \right\rfloor $ здесь и далее обозначается целая часть числа. Рассмотрим функции
Нетрудно убедиться, что ${{\Psi }_{1}}(b)$ и ${{\Psi }_{2}}(b)$ выпуклы вниз, поэтому $\left| {\frac{{\partial {{H}_{{b,M}}}(\omega )}}{{\partial b}}} \right|$ можно оценить сверху линейной функцией ${{\Psi }_{0}}(b)$
Поскольку ${{\Psi }_{0}}(b)$ линейна, получим
(34)
$\left| {\frac{{\partial {{H}_{{b,M}}}(\omega )}}{{\partial b}}} \right| \leqslant \max \left\{ {{{\Psi }_{0}}({{\beta }_{0}}),{{\Psi }_{0}}({{\beta }_{1}})} \right\}.$Из теоремы Лагранжа о среднем [10] и неравенства (34) следует
Выбирая число $R$ таким образом, чтобы
(35)
$\frac{{{{\beta }_{1}} - {{\beta }_{0}}}}{R} < \frac{{{{\varepsilon }_{0}}}}{{10}}{{\left( {\max \left\{ {{{\Psi }_{0}}({{\beta }_{0}}),{{\Psi }_{0}}({{\beta }_{1}})} \right\}} \right)}^{{ - 1}}},$получим при $\Delta = {{({{\beta }_{1}} - {{\beta }_{0}})} \mathord{\left/ {\vphantom {{({{\beta }_{1}} - {{\beta }_{0}})} R}} \right. \kern-0em} R}$
4. ЧИСЛЕННЫЙ МЕТОД АППРОКСИМАЦИИ НЕОТРИЦАТЕЛЬНЫМИ РАЦИОНАЛЬНЫМИ ДРОБЯМИ
Опираясь на теоремы 1–3, построим численный метод решения задачи (8) с дополнительным условием (11) неотрицательности аппроксимирующей дроби. Используя результаты предыдущего раздела, можно выделить на интервале $b > 0$ конечное множество точек, в которых ищется решение. Обозначим это множество B. Для каждого фиксированного числа $M$ вместо непрерывной задачи (10) будем теперь рассматривать дискретную задачу:
(36)
$\mathop {\min }\limits_{b \in {{B}_{1}}} \mathop {\max }\limits_{{{\omega }} \in \mathbb{R}} \left| {{{\varphi }_{a}}(\omega ) - {{H}_{{b,M}}}(\omega )} \right|,$где ${{B}_{1}}$ – набор всех точек $b \in B,$ в которых выполняется условие
Предлагаемый в работе метод численного решения задачи (8) с условием (11) состоит из следующих этапов.
1. Сначала для всех $M$ из набора $1 \leqslant M \leqslant {{M}_{1}}$ методом градиентного спуска ищутся решения непрерывной задачи (10) ${{H}_{{{{b}_{{опт}}}(M),M}}}(\omega )$ и их погрешности $\varepsilon ({{b}_{{опт}}}(M),M).$ Далее путем определения корней функций ${{H}_{{{{b}_{{опт}}}(M),M}}}(\omega )$ проверяется их неотрицательность.
2. Выбирается число M, для которого решается задача (36), и задается верхняя оценка погрешности ${{\varepsilon }_{1}}.$
Если (36) решается впервые, то в качестве текущего задается то M, для которого была получена наименьшая ошибка $\varepsilon $ при решении непрерывной задачи. В случае, когда при применении метода спуска для некоторых $M$ были получены неотрицательные решения с погрешностями ${{\gamma }_{M}},$ верхняя оценка погрешности ${{\varepsilon }_{1}}$ полагается равной $min\{ {{\gamma }_{M}}\} ,$ а если ни одно из решений непрерывной задачи не оказалось неотрицательным, задается ${{\varepsilon }_{1}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$
Предположим теперь, что ранее задача (36) решалась для набора чисел $M = {{m}_{i}},$ ${{m}_{i}} \in \left\{ {{{m}_{i}}} \right\}_{{i = 1}}^{I},$ и для некоторых ${{m}_{i}}$ были найдены неотрицательные решения с погрешностью ${{\delta }_{i}}.$ Тогда текущее число $M$ выбирается так, чтобы
Оценка ${{\varepsilon }_{1}}$ полагается равной
Если
то поиск решений завершается.
3. Нижняя оценка погрешности ${{\tilde {\varepsilon }}_{0}}$ решения задачи (10) с условием (11) полагается равной ${{\tilde {\varepsilon }}_{0}} = $ $ = \varepsilon ({{b}_{{опт}}}(M),M).$
4. По формулам (13) или (16) вычисляется число ${{b}_{0}},$ а по формулам (23) или (28) – ${{b}_{1}}.$
5. Число ${{b}_{1}}$ дает достаточно грубую оценку правой границы отрезка, вне которого выполняется неравенство $\varepsilon > {{\varepsilon }_{1}}.$ Имеется возможность получить более точную оценку.
Функция ${{H}_{{b,M}}}(0)$ переменной $b$ удовлетворяет неравенству
где
и
(38)
${{\alpha }_{{m,l}}} = \left\{ {\begin{array}{*{20}{c}} {\left| {{{a}_{m}}} \right|{{\mathop {max}\limits_{b \in [{{b}_{0}},{{b}_{1}}]} {{\mu }_{{m,l}}}(b,0)} \mathord{\left/ {\vphantom {{\mathop {max}\limits_{b \in [{{b}_{0}},{{b}_{1}}]} {{\mu }_{{m,l}}}(b,0)} n}} \right. \kern-0em} n},}&{m \geqslant 0,} \\ {\left| {{{a}_{{ - m}}}} \right|{{\mathop {max}\limits_{b \in [{{b}_{0}},{{b}_{1}}]} {{\nu }_{{m,l}}}(b,0)} \mathord{\left/ {\vphantom {{\mathop {max}\limits_{b \in [{{b}_{0}},{{b}_{1}}]} {{\nu }_{{m,l}}}(b,0)} n}} \right. \kern-0em} n},}&{m < 0} \end{array}} \right.$для $m = 0,...,M - 1,$ $l = 0,...,\left\lfloor {\frac{{n - 1}}{2}} \right\rfloor .$ Функции ${{\mu }_{{m,l}}}(b,\omega )$ и ${{\nu }_{{m,l}}}(b,\omega )$ в (38) определяются формулами (19), (20), (26). Разложим каждую из функций $\exp \left( {{{\beta }_{{m,l}}}b} \right)$ в (37) по формуле Тейлора
выбирая число слагаемых ${{n}_{{m,l}}}$ так, чтобы
при $b \in [{{b}_{0}},{{b}_{1}}].$ Тогда функция
является дробно-рациональным приближением ${{H}_{{b,M}}}(0)$ и отличается от нее на $[{{b}_{0}},{{b}_{1}}]$ не более чем на ${{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {10}}} \right. \kern-0em} {10}}.$ Определяя численно все корни уравнений
лежащие на отрезке $[{{b}_{0}},{{b}_{1}}],$ и выбирая из них наиболее близко располагающийся к ${{b}_{1}},$ получим некоторое число ${{b}_{{10}}}.$ Это число и будет являться новой оценкой правой границы отрезка, на котором ищется решение дискретной задачи.
Для поиска уточнения ${{b}_{{00}}}$ левой границы отрезка используется приближение ${{G}_{M}}(b)$ функции ${{H}_{{b,M}}}(\cos \tau )$ (см. формулу (14)). В остальном процессы определения ${{b}_{{00}}}$ и ${{b}_{{10}}}$ аналогичны.
Еще больше сузить отрезок поиска можно, используя некоторый набор функций ${{H}_{{b,M}}}({{\omega }_{k}}),$ $k = 1,...,N.$
6. При необходимости задаются промежуточные погрешности ${{\tilde {\varepsilon }}_{s}},$ $s = 1,...,q,$ ${{\tilde {\varepsilon }}_{0}} < {{\tilde {\varepsilon }}_{1}} < ... < {{\tilde {\varepsilon }}_{q}} < {{\varepsilon }_{1}},$ и способом, описанным в п. 5, определяются границы отрезков $\left[ {{{b}_{{0s}}},{{b}_{{1s}}}} \right],$ вне которых $\varepsilon > {{\tilde {\varepsilon }}_{{q - s + 1}}}.$
7. Выполняется разбиение каждого из отрезков $[{{b}_{{00}}},{{b}_{{01}}}],$ …, $[{{b}_{{0,q - 1}}},{{b}_{{0,q}}}],$ $[{{b}_{{0,q}}},{{b}_{{1,q}}}],$ $[{{b}_{{1,q}}},{{b}_{{1,q - 1}}}],$…, $[{{b}_{{11}}},{{b}_{{10}}}]$ на меньшие отрезки. Отрезок вида $[{{b}_{{0,k}}},{{b}_{{0,k + 1}}}]$ разбивается на подотрезки ${{L}_{0}}$ узлами ${{b}_{{0,k,l}}},$ $k = 0,...,q - 1,$ $l = 0,...,{{L}_{0}} - 1,$
отрезок $[{{b}_{{1,k}}},{{b}_{{1,k - 1}}}]$ – ${{L}_{1}}$ узлами ${{b}_{{1,k,l}}},$ $k = 1,...,q,$ $l = 0,...,{{L}_{1}} - 1,$
и, наконец, на отрезке $[{{b}_{{0,q}}},{{b}_{{1,q}}}]$ выбирается ${{L}_{{01}}}$ узлов ${{b}_{{0,q,l}}},$ $l = 0,...,{{L}_{{01}}} - 1,$
Описанное разбиение позволяет уменьшить в дальнейшем количество точек дискретизации, в которых ищется неотрицательное решение задачи (10). Теперь на отрезке $[{{b}_{{00}}},{{b}_{{01}}}]$ имеется $S = ({{L}_{0}} + {{L}_{1}})q + {{L}_{{01}}}$ точек вида ${{b}_{{jkl}}}.$ Для определенности отсортируем их в порядке возрастания и будем рассматривать точки $b = {{\tilde {\beta }}_{s}},$ $s = 1,...,S.$
8. Перейдем к определению набора точек дискретизации, в которых ищется решение, задавая на отрезках $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}],$ $s = 1,...,S,$ узлы с шагом Δs = $ = \frac{{{{{\tilde {\beta }}}_{{s + 1}}} - {{{\tilde {\beta }}}_{s}}}}{{R(s)}},$ удовлетворяющим требованию (30). Пусть на $[{{b}_{{00}}},{{b}_{{10}}}]$ выбран некоторый отрезок $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}].$ Для определения шага дискретизации на $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}]$ воспользуемся формулой (35), полагая $R = R(s),$ ${{\beta }_{0}} = {{\tilde {\beta }}_{s}},$ ${{\beta }_{1}} = {{\tilde {\beta }}_{{s + 1}}}.$ При $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}] \subset $ $ \subset \left[ {{{b}_{{0,k}}},{{b}_{{0,k + 1}}}} \right]$ или $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}] \subset \left[ {{{b}_{{1,k + 1}}},{{b}_{{1,k}}}} \right]$ зададим погрешность ${{\varepsilon }_{0}} = {{\tilde {\varepsilon }}_{{q - k}}},$ а если $[{{\tilde {\beta }}_{s}},{{\tilde {\beta }}_{{s + 1}}}] \subset \left[ {{{b}_{{0,q}}},{{b}_{{1,q}}}} \right],$ ${{\varepsilon }_{0}} = {{\tilde {\varepsilon }}_{0}}.$ Неотрицательное решение задачи (8) будем искать на наборе точек B:
Пример 1. Приведем пример применения описанного метода поиска неотрицательного решения задачи (8) для $a = 3,$ $n = 20,$ $1 \leqslant M \leqslant 20.$ Сначала определим для всех указанных $M$ оптимальные параметры ${{b}_{{опт}}},$ используя метод спуска. Найденные параметры вместе с соответствующими погрешностями (7) приведены в табл. 1.
Таблица 1.
Оптимальные параметры ${{b}_{{опт}}}$ и погрешности $\varepsilon ({{b}_{{опт}}},M),$ полученные при решении задач вида (10) методом спуска для различных чисел $M$
| $M$ | ${{b}_{{опт}}}$ | $\varepsilon $ |
|---|---|---|
| 1 | 6.3285 | 4.21 × 10–1 |
| 2 | 1.0000 | 2.29 × 10–1 |
| 3 | 1.0000 | 1.18 × 10–1 |
| 4 | 1.0000 | 6.50 × 10–2 |
| 5 | 0.9401 | 3.60 × 10–2 |
| 6 | 0.6317 | 1.84 × 10–2 |
| 7 | 0.4454 | 1.72 × 10–2 |
| 8 | 0.2841 | 7.42 × 10–3 |
| 9 | 0.4232 | 6.24 × 10–3 |
| 10 | 0.1831 | 2.72 × 10–3 |
| 11 | 0.1767 | 4.09 × 10–3 |
| 12 | 0.1481 | 1.03 × 10–2 |
| 13 | 0.1234 | 2.96 × 10–2 |
| 14 | 0.1435 | 1.21 × 10–2 |
| 15 | 0.1492 | 9.53 × 10–3 |
| 16 | 0.1167 | 3.60 × 10–2 |
| 17 | 0.1031 | 6.15 × 10–2 |
| 18 | 0.1059 | 5.50 × 10–2 |
| 19 | 0.1004 | 7.34 × 10–2 |
| 20 | 0.0991 | 7.72 × 10–2 |
Дробно-рациональная аппроксимация ${{H}_{{{{b}_{{опт}}},M}}}(\omega ),$ приближающая функцию ${{\varphi }_{3}}(\omega )$ с наименьшей погрешностью, получена при $M = 10.$ Далее путем численного определения нулей дробей ${{H}_{{{{b}_{{опт}}},M}}}(\omega ),$ $M = 1,...,20,$ можно обнаружить, что ${{H}_{{{{b}_{{опт}}},M}}}(\omega ) > 0$ при $M = 12,$ а функции ${{H}_{{{{b}_{{опт}}},M}}}(\omega )$ при M = 8, 9, 10, 11 не являются неотрицательными. Для всех остальных ${{H}_{{{{b}_{{опт}}},M}}}(\omega )$ погрешность приближения больше погрешности, полученной при $M = 12,$ поэтому поиск решений (10) будем выполнять для набора чисел $M = 8,9,10,11.$ Текущее $M$ будем выбирать каждый раз по критерию наименьшей погрешности $\varepsilon ,$ т.е. сначала решим задачу (36) для $M = 10,$ задав ${{\varepsilon }_{1}} = 1.03 \times {{10}^{{ - 2}}},$ а далее, если решение не найдено, перейдем к $M = 11.$ Если же неотрицательное решение для $M = 10$ будет найдено с погрешностью $\delta < 1.03 \times {{10}^{{ - 2}}},$ то тогда положим ${{\varepsilon }_{1}} = \delta $ и выберем по табл. 1 $M \in \{ 8,9,11\} $ с наименьшей погрешностью $\varepsilon ,$ удовлетворяющей неравенству $\varepsilon < \delta .$
В табл. 2 представлены результаты решения задачи (8) численным методом, описанным в данном разделе. Приведены значения оценок ${{b}_{0}}$ и ${{b}_{1}}$ границ отрезка, где ищется решение, их уточнения ${{b}_{{00}}}$ и ${{b}_{{10}}},$ а также общее число точек дискретизации ${{N}_{1}}$ на отрезке $[{{b}_{{00}}},{{b}_{{10}}}]$ и количество узлов ${{N}_{2}},$ в которых дробь ${{H}_{{b,M}}}(\omega )$ оказалась неотрицательной.
Таблица 2.
Результаты, полученные при поиске неотрицательных решений путем сведения непрерывной задачи вида (10) для $M = 8,9,10,11$ к дискретной задаче вида (36)
| $M$ | ${{b}_{0}}$ | ${{b}_{1}}$ | ${{b}_{{00}}}$ | ${{b}_{{10}}}$ | ${{N}_{1}}$ | ${{N}_{2}}$ | ${{b}_{{опт}}}$ | $\varepsilon $ |
|---|---|---|---|---|---|---|---|---|
| 8 | 0.009 | 3.57 | 0.1361 | 0.5191 | 37 143 | 16 901 | 0.4702 | 1.07 × 10–2 |
| 9 | 0.0057 | 3.31 | 0.1358 | 0.4811 | 26 870 | 0 | – | – |
| 10 | 0.0068 | 3.16 | 0.1287 | 0.2764 | 10 935 | 0 | – | – |
| 11 | 0.0057 | 3.16 | 0.1291 | 0.2392 | 5582 | 0 | – | – |
Как видно из табл. 2, для $M = 9,10,11$ функция ${{H}_{{b,M}}}(\omega )$ не оказалась неотрицательной ни в одной точке дискретизации. Решение задачи (36) было найдено лишь для $M = 8,$ причем погрешность приближения составила $\varepsilon = 1.07 \times {{10}^{{ - 2}}}.$ Поскольку для $M = 12$ методом спуска была получена ошибка $\varepsilon = 1.03 \times {{10}^{{ - 2}}},$ соответствующая неотрицательной дроби, то оптимальными параметрами оказываются $b = 0.1481,$ $M = 12.$
5. ФИЛЬТРЫ С АЧХ, АППРОКСИМИРУЮЩИМИ АТОМАРНЫЕ ФУНКЦИИ ${{h}_{a}}(\omega )$
Если найдено некоторое неотрицательное дробно-рациональное приближение ${{H}_{{b,M}}}(\omega ) \geqslant 0$ функции ${{\varphi }_{a}}(\omega ),$ то на основе этого приближения можно построить устойчивый фильтр с АЧХ $\left| {H(j\omega )} \right|,$ обладающей следующим свойством:
Определение передаточной функции $H(s)$ такого фильтра выполняется с помощью формулы [11]
Для вычисления $H(j\omega )$ следует найти комплексные нули и полюсы функции ${{H}_{{b,M}}}(\omega )$ и выделить среди них лежащие в верхней полуплоскости. Далее путем замены $s = j\omega $ найдем передаточную функцию фильтра $H(s).$
Выполним моделирование процесса ЦАП и покажем на примере фильтра на основе функции ${{h}_{3}}(\omega ),$ какими преимуществами и недостатками обладают новые атомарные фильтры.
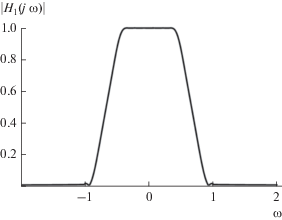
Пример 2. Построим с помощью метода, обсуждавшегося в предыдущем разделе, атомарный фильтр 30-го порядка с АЧХ на основе функции ${{h}_{3}}(\omega ).$ Для $1 \leqslant M \leqslant 20$ оптимальные параметры ${{M}_{{опт}}}$ и ${{b}_{{опт}}}$ функции ${{H}_{{b,M}}}(\omega )$ оказываются равными ${{M}_{{опт}}} = 13,$ ${{b}_{{опт}}} = 0.2974,$ а величина погрешности равномерного приближения (7) составляет $1.14 \times {{10}^{{ - 3}}}.$ Используя далее формулу (39), получим атомарный фильтр ${{h}_{1}}(t)$ с АЧХ $\left| {{{H}_{1}}(j\omega )} \right| = $ $ = \sqrt {{{H}_{{{{b}_{{опт}}},{{M}_{{опт}}}}}}(\omega )} $ (рис. 2). Обратим внимание, что количество полюсов и нулей частотной характеристики фильтра ${{h}_{1}}(t)$ отличается лишь на единицу, поэтому при $\omega \to \infty $ имеем $\left| {{{H}_{1}}(j\omega )} \right| = O\left( {1{\text{/}}\omega } \right).$
Рис. 2.
Амплитудно-частотная характеристика $\left| {{{H}_{1}}(j\omega )} \right|$ фильтра ${{h}_{1}}(t)$ на основе атомарной функции ${{h}_{3}}(\omega ).$
Перейдем к моделированию ЦАП. В качестве модельного выберем сигнал $s(t){\text{:}}$
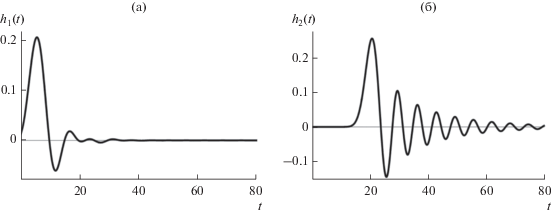
Осуществляя свертку сигнала $s(t)$ с некоторым ФНЧ, получим сигнал ${{s}_{0}}(t).$ В примере ${{s}_{0}}(t)$ имеет спектр с эффективной шириной полосы [12] ${{\Omega }_{{эф}}} = 2.4.$ Обратимся к формуле (2). Полагая $\Omega = {{\Omega }_{{эф}}},$ получим ограничение на шаг дискретизации $\Delta \leqslant \frac{\pi }{{2{{\Omega }_{{эф}}}}} = 0.654.$ Поскольку, как было сказано ранее, АЧХ фильтра ${{h}_{1}}(t)$ затухает достаточно медленно, то с целью снижения эффекта просачивания высокочастотных составляющих выберем шаг несколько меньше чем $0.654,$ $\Delta = 0.422.$ Далее выделим некоторый конечный набор $\{ {{s}_{0}}(k\Delta )\} $ отсчетов сигнала ${{s}_{0}}(t),$ сопоставим ему конечную последовательность модулированных по амплитуде импульсов шириной 0.1 и найдем свертку этой последовательности со сглаживающим ФНЧ. Для сравнения помимо атомарного фильтра ${{h}_{1}}(t)$ будем использовать фильтр Баттерворта 30-го порядка ${{h}_{2}}(t).$ Импульсные характеристики обоих фильтров представлены на рис. 3.
Рис. 3.
Импульсные характеристики фильтров ${{h}_{1}}(t)$ (а) и ${{h}_{2}}(t)$ (б); серой линией показана ось t.
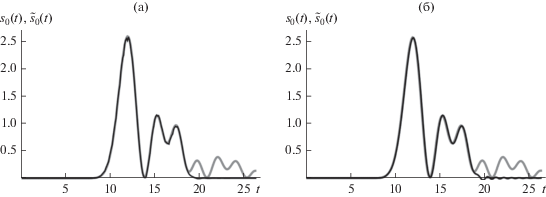
Непосредственно во время фильтрации будем использовать растянутые относительно $t$ фильтры ${{h}_{1}}(7.2t)$ и ${{h}_{2}}\left( {\frac{\pi }{\Delta }t} \right).$ Полоса пропускания фильтра ${{h}_{1}}(7.2t)$ полностью охватывает эффективную ширину полосы спектра сигнала ${{s}_{0}}(t),$ а полоса подавления ${{h}_{1}}(7.2t)$ начинается несколько левее точки $\omega = 2\frac{\pi }{\Delta } - {{\Omega }_{{эф}}},$ где появляются высокочастотные составляющие спектра ${{s}_{0}}(t).$ Результат восстановления сигнала ${{s}_{0}}(t)$ (без учета задержки) по первым 25-ти значимым отсчетам с применением обоих фильтров представлен на рис. 4. Графики рис. 4а и 4б различаются незначительно. На рис. 4а видна возникшая после восстановления небольшая погрешность.
Рис. 4.
Сигнал ${{s}_{0}}(t)$ (серая линия) и результат его восстановления ${{\tilde {s}}_{0}}(t)$ (черная линия) по 25-ти отсчетам с помощью фильтров ${{h}_{1}}(t)$ (а) и ${{h}_{2}}(t)$ (б).
Отбросим теперь первые 10 из 25 использовавшихся ранее отсчетов и вновь восстановим сигнал ${{s}_{0}}(t)$ (рис. 5). Графики на рис. 5 наглядно демонстрируют зависимость эффекта усечения последовательности отсчетов от скорости затухания импульсной характеристики фильтра. Отбрасывание отсчетов практически не повлияло на погрешность восстановления с помощью атомарного фильтра ${{h}_{1}}(t)$ с быстро затухающей импульсной характеристикой, а при использовании фильтра ${{h}_{2}}(t)$ с АЧХ, аппроксимирующей прямоугольный импульс, и медленно затухающей импульсной характеристикой возникла значительная ошибка.
Рис. 5.
Сигнал ${{s}_{0}}(t)$ (серая линия) и результат его восстановления ${{\tilde {s}}_{0}}(t)$ (черная линия) по 15-ти отсчетам с помощью фильтров ${{h}_{1}}(t)$ (а) и ${{h}_{2}}(t)$ (б); серой линией показана ось t.
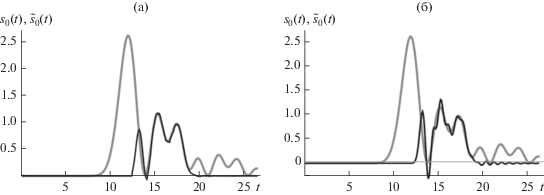
Таким образом, среди недостатков построенного фильтра можно выделить затухание его АЧХ со скоростью $O\left( {{\text{1/}}\omega } \right),$ а среди достоинств – быстрое затухание импульсной характеристики. Последнее свойство позволяет добиться низкой чувствительности к отбрасыванию отсчетов восстанавливаемого сигнала.
6. АМПЛИТУДНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ НА ОСНОВЕ ДРУГИХ ФИНИТНЫХ ФУНКЦИЙ
Описанный в разд. 4 метод можно применять для построения дробно-рациональных аппроксимаций квадратов произвольных неотрицательных финитных функций с достаточно быстро сходящимся рядом Фурье. Пусть ${{\varphi }_{0}}(\omega )$ – неотрицательная функция с носителем $[ - 1,1]$ и преобразованием Фурье $F[\varphi ](t).$ Тогда коэффициенты ${{c}_{k}}$ ряда Фурье
определяются формулой
и функция $\varphi (\omega ) = \varphi _{0}^{2}(\omega )$ представляется в виде
(40)
$\varphi (\omega ) = \sum\limits_{m = - \infty }^{ + \infty } {{{a}_{m}}\exp \left( {jm\pi \omega } \right)} ,$где
Частичные суммы ${{\varphi }^{{(M)}}}(\omega )$ ряда (40),
используются при построении дроби по формуле, подобной (6)
Далее путем определения оптимальных параметров $b = {{b}_{{опт}}}$ и $M = {{M}_{{опт}}}$ с помощью метода из разд. 4 находим неотрицательное дробно-рациональное приближение ${{H}_{{{{b}_{{опт}}},{{M}_{{опт}}}}}}(\omega )$ функции $\varphi (\omega ).$ Применяя формулу (39), можно построить передаточную функцию $H(s)$ фильтра с АЧХ
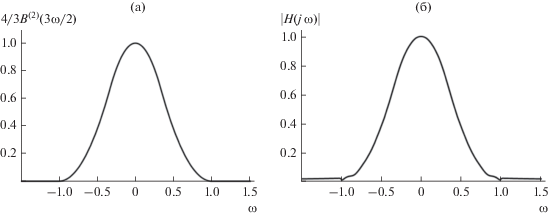
Пример полученной таким образом при $n = 20$ АЧХ на основе B-сплайна ${{B}^{{(2)}}}(\omega )$ [13], нормированного относительно носителя и значения в нуле, представлен на рис. 6б. График функции $\frac{4}{3}{{B}^{{(2)}}}\left( {\frac{3}{2}\omega } \right)$ приведен на рис. 6а. Оптимальные параметры, определенные методом спуска, оказались равными ${{b}_{{опт}}} = 0.3074$ и ${{M}_{{опт}}} = 9,$ погрешность приближения (7) $\varepsilon = 1.9 \times {{10}^{{ - 3}}}.$ Методом поиска неотрицательного дробно-рационального приближения были найдены параметры ${{b}_{{опт}}} = 0.177,$ ${{M}_{{опт}}} = 11$ и погрешность $\varepsilon = 2.79 \times {{10}^{{ - 3}}}.$
ВЫВОДЫ
В работе впервые представлен численный метод построения неотрицательных дробно-рациональных приближений квадратов атомарных функций ${{h}_{a}}(x).$ В качестве основы предложенного метода выступает алгоритм поиска аппроксимирующих ${{h}_{a}}(x)$ действительных рациональных дробей (не обязательно неотрицательных) методом спуска. Доказаны теоремы об оценке границ отрезка, на котором ищется решение и теорема о выборе шага дискретизации, позволяющие перейти от непрерывной задачи минимизации функционала к дискретной. Дано описание численного метода определения конечного множества точек, в которых ищется неотрицательное решение, и приведен пример практического применения этого метода.
Наличие алгоритма поиска неотрицательных рациональных дробей, аппроксимирующих $h_{a}^{2}(\omega ),$ позволяет строить фильтры с АЧХ на основе функции ${{h}_{a}}(\omega ).$ Новые фильтры обладают важным преимуществом – при небольших $a$ их импульсные характеристики быстро затухают. Это свойство дает возможность существенно снизить погрешность усечения в процессе реконструкции сигналов. Предложенные в работе фильтры имеют и недостатки. В частности, количество нулей числителя передаточной функции на основе построенных дробно-рациональных приближений в общем случае отличается от количества нулей знаменателя лишь на единицу, поэтому при больших $\omega $ АЧХ стремится к нулю как $O({\text{1/}}\omega ).$ Построенные атомарные ФНЧ могут быть использованы как самостоятельно, так и в качестве прототипов цифровых БИХ-фильтров.
Приведен пример моделирования ЦАП, в котором продемонстрирована малая чувствительность атомарного фильтра на основе функции ${{h}_{3}}(\omega )$ к отбрасыванию отсчетов восстанавливаемого сигнала. При этом во время восстановления с помощью классического фильтра Баттерворта после отбрасывания отсчетов погрешность оказалась довольно большой.
Может оказаться полезной возможность применения предложенного метода аппроксимации с целью построения дробно-рациональных приближений не только $h_{a}^{2}(\omega ),$ но и других неотрицательных финитных функций с быстро сходящимся рядом Фурье.
Список литературы
Кравченко В.Ф., Кравченко О.В. Конструктивные методы алгебры логики, атомарных функций, вейвлетов, фракталов в физике и технике. М.: Техносфера, 2018.
Кравченко В.Ф., Чуриков Д.В. Цифровая обработка сигналов атомарными функциями и вейвлетами. М.: Техносфера, 2019.
Кравченко В.Ф. Лекции по теории атомарных функций и некоторым их приложениям. М.: Радиотехника, 2003.
Будунова К.А., Кравченко В.Ф., Пустовойт В.И. // РЭ. 2018. Т. 63. № 9. С. 935.
Будунова К.А., Кравченко В.Ф., Пустовойт В.И. // РЭ. 2019. Т. 64. № 10. С. 984.
Будунова К.А. // Матер. 12-й межд. науч.-тех. конф. “Акустооптические и радиолокационные методы измерений и обработки информации”. Москва, 13–16 октября 2019. М.: РНТОРЭС им. А.С. Попова, 2019. Т. 12. С. 23.
Budunova K.A., Kravchenko V.F. // Proc. Conf. 2020 IEEE Ukrainian Microwave Week (UkrMW), Kharkiv, 21–25 Sept. 2020. N.Y.: IEEE, 2020. P. 414.
Niven I. Irrational Numbers. The Carus Mathematical Monographs № 11. Buffalo, N.Y.: The Mathematical Association of America, 1956.
Corless R.M., Gonnet G.H., Hare D.E.G. et al. // Adv. Comp. Maths. 1996. V. 5. P. 329.
Демьянов В.Ф., Малоземов В.Н. Введение в минимакс. М.: Наука, 1972.
Лэм Г. Аналоговые и цифровые фильтры. Расчет и реализация. М.: Мир, 1982.
Свиньин С.Ф., Попов А.И. // Тр. СПИИРАН. 2015. Т. 47. С. 50.
Shikin E.V., Plis A.I. Handbook on Splines for the User. Boca Raton: CRC Press, 1995.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника