1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 66, № 11, 2021

Радиотехника и электроника, 2021, T. 66, № 11, стр. 1061-1065

Электродинамический анализ излучения набора колеблющихся диполей

Г. Ф. Заргано a, *, А. Г. Шеин b, А. В. Харланов b

a Южный федеральный университет
344090 Ростов-на-Дону, ул. Зорге, 5, Российская Федерация

b Волгоградский государственный технический университет
400005 Волгоград, просп. им. Ленина, 28, Российская Федерация

* E-mail: gfzargano@sfedu.ru

Поступила в редакцию 19.02.2021
После доработки 19.02.2021
Принята к публикации 28.02.2021

Полный текст (PDF)

Аннотация

Рассмотрена задача возбуждения электромагнитных полей, генерируемых колеблющимися электрическими диполями, образованными заряженной сферической тонкой пленкой. Приведены зависимости поля от расстояния и времени. Проведено сравнение аналитического и численного решений. Сделано предположение о возможном применении полученных решений для определения параметров сред.

ВВЕДЕНИЕ

Микроволновое излучение как естественных, так и искусственных источников широко применяется для изучения окружающей среды [1], в медицинской диагностике [2]. Поэтому актуальной становится задача нахождения и описания таких источников. Современное развитие радиоэлектроники также связано с вопросами миниатюризации компонентов электронных устройств, их взаимной интеграции и создания новых радиоэлектронных систем и элементов. Особый интерес представляет беспроводная интеграция. Одним из способов решения этих вопросов является использование тонких пленок и происходящих в них физических процессов как отдельных элементов для генерации и преобразования электромагнитных сигналов. В качестве такой пленки можно рассматривать слой фосфолипидов. Будучи помещенными в воду, они образуют сферический бислой. Использование такой пленки в качестве объекта исследования актуально, так как фосфолипидный бислой, несмотря на то что может быть создан искусственно, также является основой мембран большинства биологических клеток. Это позволяет расширить область применения в сторону области электроники, рассматривающей биологические объекты для систем обработки информации и новых устройств – биоэлектроники [3].

1. МОДЕЛЬ КОЛЕБЛЮЩЕЙСЯ ЗАРЯЖЕННОЙ ТОНКОЙ ПЛЕНКИ

На границе пленки с водой возникает двойной электрический слой. Если рассматривать пленку как мембрану, то с внешней и внутренней сторон находятся известные заряды разных знаков [4]. В первом приближении можно считать, что пленка сферическая, а заряды на внутренней и внешней поверхностях пленки распределены равномерно, одинаковы по величине, но разные по знаку. Акустические колебания бислоя и, соответственно, заряда создают переменные поля в соответствии с законами электродинамики [5]. Распространение акустических волн вдоль мембраны вызывает периодические изменения толщины мембраны (рис. 1а). Таким образом, тонкие пленки совершают колебания и, как следствие, будут излучать электромагнитные волны.

Рис. 1.

Сферическая тонкая пленка: а – изменение толщины колеблющейся тонкой пленки, б – пленка в сферических координатах.

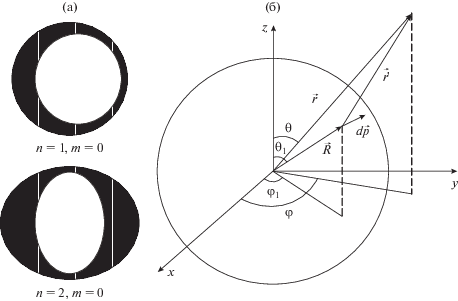
Представим колеблющийся фосфолипидный бислой в виде сферического слоя диполей с переменными дипольными моментами. Элементарный дипольный момент $dp$ в сферических координатах равен

(1)
$dp = h\left( t \right)\sigma dS = h\left( t \right)\sigma {{R}^{2}}\sin {{\theta }_{1}}d{{\theta }_{1}}d{{\varphi }_{1}},$

где $R$ – радиус пленки, $\sigma = {q \mathord{\left/ {\vphantom {q {\left( {4\pi {{R}^{2}}} \right)}}} \right. \kern-0em} {\left( {4\pi {{R}^{2}}} \right)}}$ – поверхностная плотность заряда у поверхности пленки, $q$ – заряд, $\left( {R,{{\theta }_{1}},{{\varphi }_{1}}} \right)$ – координаты элементарного диполя (рис. 1б). Длина диполя меняется со временем по закону:

(2)
$h\left( t \right) = h + {{\eta }_{0}}P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right)\cos \left( {m{{\varphi }_{1}}} \right)\exp \left( { - i\omega t} \right),$

где h – толщина пленки, η0 – амплитуда колебаний пленки, $P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right)$ – присоединенный полином Лежандра, $P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right)\cos \left( {m{{\varphi }_{1}}} \right)$ – собственные функции внутренности полой сферы (по этому закону изменяется амплитуда колебаний пленки) [6], $n = 1,2,3,...,$ $m = 0,1,...,n$ – числа, определяющие вид колебаний набора диполей (см. рис. 1а), $\omega $ – частота акустических колебаний пленки.

Будем рассматривать поля только в ближней зоне, поскольку ввиду малости амплитуды колебаний поля рассматриваемых объектов в дальней зоне предельно малы. Тогда выражение для напряженности электрического и магнитного полей излучения элементарного диполя имеет вид [7]

(3)
$\begin{gathered} d\vec {E}\left( {\vec {r}} \right) = \frac{1}{{4\pi \varepsilon {{\varepsilon }_{0}}}}\left[ {3\vec {n}\left( {\vec {n},d\vec {p}} \right) - d\vec {p}} \right]\frac{1}{{r{{'}^{3}}}}, \\ d\vec {B} = \frac{{\mu {{\mu }_{0}}}}{{4\pi }}\frac{{\left[ {d\dot {\vec {p}},\vec {n}} \right]}}{{{{r}^{{'2}}}}}, \\ \end{gathered} $

где $\vec {r}{\kern 1pt} '$ – радиус-вектор, направленный от элементарного диполя до точки наблюдения, $\vec {n}$ – орт этого вектора, $d\dot {\vec {p}}$ – производная дипольного момента по времени. Подставляя (1) и (2) в (3) и интегрируя эти выражения по всей поверхности сферы, можно найти поле, создаваемое колеблющейся пленкой в произвольной точке пространства. Проще всего это сделать, используя численные методы, однако чем ближе к пленке необходимо измерить поле, тем на меньшие площадки ее необходимо разбивать, что приводит к увеличению объема используемых данных и времени расчета. Поэтому важно найти аналитические подходы к решению данной задачи. В общем случае решение затруднительно, однако задачу можно упростить, рассматривая поле, создаваемое колеблющейся пленкой в направлении $\theta = 0$ рад. Будем искать электрическое поле, так как оно проще для экспериментального обнаружения. Проекции электрического поля, создаваемого элементарным диполем на оси декартовой системы координат, будут иметь вид

(4)
$\begin{gathered} d{{E}_{x}} = \frac{1}{{4\pi \varepsilon {{\varepsilon }_{0}}}}\left[ {\frac{{3R\sin {{\theta }_{1}}\cos {{\varphi }_{1}}\left( {R - r\cos {{\theta }_{1}}} \right)}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} - } \right. \\ \left. { - \,\,\frac{{\sin {{\theta }_{1}}\cos {{\varphi }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{3/2}}}}}} \right] \times \\ \times \,\,\left( {h + {{\eta }_{0}}P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right)\cos } \right.\,\left( {m{{\varphi }_{1}}} \right) \times \\ \left. { \times \,\,\exp \left( { - i\omega t} \right)} \right)\sigma {{R}^{2}}\sin {{\theta }_{1}}d{{\theta }_{1}}d{{\varphi }_{1}}, \\ \end{gathered} $
(5)
$\begin{gathered} d{{E}_{y}} = \frac{1}{{4\pi \varepsilon {{\varepsilon }_{0}}}}\left[ {\frac{{3R\sin {{\theta }_{1}}\sin {{\varphi }_{1}}\left( {R - r\cos {{\theta }_{1}}} \right)}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} - } \right. \\ \left. { - \,\,\frac{{\sin {{\theta }_{1}}\sin {{\varphi }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right]\left( {h + {{\eta }_{0}}P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right) \times } \right. \\ \left. { \times \,\,\cos \left( {m{{\varphi }_{1}}} \right)\,\exp \left( { - i\omega t} \right)} \right)\sigma {{R}^{2}}\sin {{\theta }_{1}}d{{\theta }_{1}}d{{\varphi }_{1}}, \\ \end{gathered} $
(6)
$\begin{gathered} d{{E}_{z}} = \frac{1}{{4\pi \varepsilon {{\varepsilon }_{0}}}}\left[ {\frac{{3\left( {R\cos {{\theta }_{1}} - r} \right)\left( {R - r\cos {{\theta }_{1}}} \right)}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} - } \right. \\ \left. { - \,\,\frac{{\cos {{\theta }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right]\left( {h + {{\eta }_{0}}P_{n}^{m}\left( {\cos {{\theta }_{1}}} \right) \times } \right. \\ \left. { \times \,\,\cos \left( {m{{\varphi }_{1}}} \right)\exp \left( { - i\omega t} \right)} \right)\sigma {{R}^{2}}\sin {{\theta }_{1}}d{{\theta }_{1}}d{{\varphi }_{1}}. \\ \end{gathered} $

Проинтегрируем выражения (4)–(6) сначала по ${{\varphi }_{1}}$ от 0 до $2\pi ,$ а затем по ${{\theta }_{1}}$ от 0 до $\pi .$ Тогда найдем для разных случаев следующие выражения.

При $n = 1,$ $m = 0{\text{:}}$

$dE = d{{E}_{z}} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{2\varepsilon {{\varepsilon }_{0}}}}\frac{{2\left( {{{R}^{2}} + {{r}^{2}}} \right){{{\cos }}^{2}}{{\theta }_{1}} + 3Rr\cos {{\theta }_{1}} - Rr{{{\cos }}^{3}}{{\theta }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\sin {{\theta }_{1}}d{{\theta }_{1}},$
$\begin{gathered} E_{1}^{0} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}} \times \\ \times \,\,\left[ {\frac{{Rr{{{\cos }}^{3}}{{\theta }_{1}} - 3\left( {{{R}^{2}} + {{r}^{2}}} \right){{{\cos }}^{2}}{{\theta }_{1}} + 3Rr\cos {{\theta }_{1}} - 3\left( {{{R}^{2}} + {{r}^{2}}} \right)}}{{3Rr{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} + \frac{{6Rr\left( {{{R}^{4}} + {{r}^{4}}} \right)\cos {{\theta }_{1}} - Rr{{{\cos }}^{3}}{{\theta }_{1}} - 2{{R}^{6}} - 2{{r}^{6}}}}{{3{{R}^{3}}{{r}^{3}}{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right]_{0}^{{{\pi }}}, \\ \end{gathered} $
(7)
$E_{1}^{0}\left( {r,t} \right) = \frac{{2{{\eta }_{0}}\sigma {{R}^{2}}}}{{3\varepsilon {{\varepsilon }_{0}}{{r}^{3}}}}\exp \left( { - i\omega t} \right).$

При $n = 1,$ $m = 1{\text{:}}$

$dE = d{{E}_{x}} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\frac{{\left( {2{{R}^{2}} - {{r}^{2}} - Rr\cos {{\theta }_{1}}} \right)\left( {1 - {{{\cos }}^{2}}{{\theta }_{1}}} \right)}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\sin {{\theta }_{1}}d{{\theta }_{1}},$
$\begin{gathered} E_{1}^{1} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\left[ {\frac{{ - {{R}^{2}}{{r}^{2}}{{{\cos }}^{2}}{{\theta }_{1}} - 2R{{r}^{3}}\cos {{\theta }_{1}} - 2{{R}^{3}}r\cos {{\theta }_{1}} + 2{{r}^{4}} + {{R}^{2}}{{r}^{2}} + 2{{R}^{4}}}}{{3{{R}^{3}}{{r}^{3}}{{{\left( {{{R}^{2}} + {{r}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} - } \right. \\ - \,\,\left. {\frac{{{{R}^{3}}{{{\cos }}^{3}}{{\theta }_{1}} + 3{{R}^{2}}r{{{\cos }}^{2}}{{\theta }_{1}} - 6R{{r}^{2}}\cos {{\theta }_{1}} - 3{{R}^{3}}\cos {{\theta }_{1}} + 2{{r}^{3}} + 3{{R}^{2}}r}}{{{{R}^{3}}{{{\left( {{{R}^{2}} + {{r}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right]_{0}^{{{\pi }}}, \\ \end{gathered} $
(8)
$E_{1}^{1}\left( {r,t} \right) = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}}}{{3\varepsilon {{\varepsilon }_{0}}{{r}^{3}}}}\exp \left( { - i\omega t} \right).$

При $n = 2,$ $m = 0{\text{:}}$

$dE = d{{E}_{z}} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\,\frac{{2\left( {{{R}^{2}} + {{r}^{2}}} \right){{{\cos }}^{2}}{{\theta }_{1}} + 3Rr\cos {{\theta }_{1}} - Rr{{{\cos }}^{3}}{{\theta }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\left( {3{{{\cos }}^{2}}{{\theta }_{1}} - 1} \right)\sin {{\theta }_{1}}d{{\theta }_{1}},$
$\begin{gathered} E_{2}^{0} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\left[ {\frac{{3{{{\cos }}^{4}}{{\theta }_{1}} + 4{{{\cos }}^{2}}{{\theta }_{1}} - 7}}{{5{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right. - \,\,\frac{{6\left( {{{R}^{2}} + {{r}^{2}}} \right)\left( {{{{\cos }}^{3}}{{\theta }_{1}} + 3\cos {{\theta }_{1}}} \right)}}{{5Rr{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} - \\ - \,\,\frac{{18\left( {{{R}^{4}} + {{r}^{4}}} \right)\left( {{{{\cos }}^{2}}{{\theta }_{1}} + 1} \right)}}{{5{{R}^{2}}{{r}^{2}}{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} + \,\,\left. {\frac{{36Rr({{R}^{6}} + {{r}^{6}})\cos {{\theta }_{1}} - 12\left( {{{R}^{8}} + {{r}^{8}}} \right)}}{{5{{R}^{3}}{{r}^{3}}{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right]_{0}^{{{\pi }}}, \\ \end{gathered} $
(9)
$E_{2}^{0}\left( {r,t} \right) = \frac{{6{{\eta }_{0}}\sigma {{R}^{3}}}}{{5\varepsilon {{\varepsilon }_{0}}{{r}^{4}}}}\exp \left( { - i\omega t} \right).$

При $n = 2,$ $m = 1{\text{:}}$

$dE = d{{E}_{x}} = \frac{{3{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\,\frac{{\left( {2{{R}^{2}} - {{r}^{2}} - Rr\cos {{\theta }_{1}}} \right)\left( {1 - {{{\cos }}^{2}}{{\theta }_{1}}} \right)}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\cos {{\theta }_{1}}\sin {{\theta }_{1}}d{{\theta }_{1}},$
(10)
$E_{2}^{1}\left( {r,t} \right) = \frac{{6{{\eta }_{0}}\sigma {{R}^{3}}}}{{5\varepsilon {{\varepsilon }_{0}}{{r}^{4}}}}\exp \left( { - i\omega t} \right).$

При $n = 2,$ $m = 2$ результирующее поле будет равно нулю в силу симметрии колебаний пленки.

При $n = 3,$ $m = 0$ имеем

$dE = d{{E}_{z}} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{4\varepsilon {{\varepsilon }_{0}}}}\frac{{2\left( {{{R}^{2}} + {{r}^{2}}} \right){{{\cos }}^{2}}{{\theta }_{1}} + 3Rr\cos {{\theta }_{1}} - Rr{{{\cos }}^{3}}{{\theta }_{1}}}}{{{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\left( {5{{{\cos }}^{2}}{{\theta }_{1}} - 3} \right)\sin {{\theta }_{1}}d{{\theta }_{1}},$
$\begin{gathered} E_{3}^{0} = \frac{{{{\eta }_{0}}\sigma {{R}^{2}}\exp \left( { - i\omega t} \right)}}{{56\varepsilon {{\varepsilon }_{0}}{{{\left( {{{r}^{2}} + {{R}^{2}} - 2Rr\cos {{\theta }_{1}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left[ {\frac{{5{{{\cos }}^{5}}{{\theta }_{1}} + 35{{{\cos }}^{3}}{{\theta }_{1}}}}{1}} \right. - \\ - \,\,\frac{{7Rr{{{\cos }}^{3}}{{\theta }_{1}} - 21\left( {{{R}^{2}} + {{r}^{2}}} \right){{{\cos }}^{2}}{{\theta }_{1}} + 21Rr\cos {{\theta }_{1}} - 21\left( {{{R}^{2}} + {{r}^{2}}} \right)}}{{Rr}} + \frac{{\left( {{{r}^{2}} + {{R}^{2}}} \right)\left( {9{{{\cos }}^{4}}{{\theta }_{1}} + 105{{{\cos }}^{2}}{{\theta }_{1}} + 30} \right)}}{{Rr}} - \\ - \,\,\frac{{{{{\left( {{{r}^{2}} + {{R}^{2}}} \right)}}^{2}}\left( {12{{{\cos }}^{3}}{{\theta }_{1}} + 210\cos {{\theta }_{1}}} \right)}}{{{{R}^{2}}{{r}^{2}}}} - \frac{{36{{{\cos }}^{2}}{{\theta }_{1}}{{{\left( {{{r}^{2}} + {{R}^{2}}} \right)}}^{3}} + 50\left( {{{r}^{6}} + {{R}^{6}}} \right)}}{{{{R}^{3}}{{r}^{3}}}} + \\ \left. { + \,\,\frac{{72\cos {{\theta }_{1}}{{{\left( {{{r}^{2}} + {{R}^{2}}} \right)}}^{4}}}}{{{{R}^{4}}{{r}^{4}}}} - \frac{{24\left( {{{r}^{{10}}} + {{R}^{{10}}}} \right)}}{{{{R}^{5}}{{r}^{5}}}} - \frac{{42Rr\left( {{{R}^{4}} + {{r}^{4}}} \right)\cos {{\theta }_{1}} - 7Rr{{{\cos }}^{3}}{{\theta }_{1}} - 14{{R}^{6}} - 14{{r}^{6}}}}{{{{R}^{3}}{{r}^{3}}}}} \right]_{0}^{{{\pi }}}, \\ \end{gathered} $
(11)
$E_{3}^{0}\left( {r{\text{,}}t} \right) = \frac{{12{{\eta }_{0}}\sigma {{R}^{4}}}}{{7\varepsilon {{\varepsilon }_{0}}{{r}^{5}}}}\exp \left( { - i\omega t} \right).$

Как видно из формул (7)–(11) поле, создаваемое колеблющейся тонкой пленкой, зависит от расстояния так же, как и поле мультиполя – ${{E}_{n}}\sim {{r}^{{ - n - 2}}}.$ То есть можно предполагать, что различные виды колебаний соответствуют различным видам мультиполей. Особенно наглядно это проявляется для случая $n = 1.$ Тогда $E\sim {{r}^{{ - 3}}},$ что соответствует электрическому диполю. Но при малых амплитудах колебаний сферической тонкой пленки такого типа внутренняя и внешняя стороны пленки колеблются вдоль одного направления в противофазе, не меняя своей кривизны. Они остаются сферами, смещаясь при этом, друг относительно друга. Так как эти сферы заряжены одинаковыми по величине, но разными по знаку зарядами и поле равномерно заряженной сферы совпадает с полем точечного заряда, то такие сферы, по сути, и будут являться колеблющимся электрическим диполем.

2. ПОЛЯ, СОЗДАВАЕМЫЕ НАБОРОМ ДИПОЛЕЙ

Для оценки эффективности такой системы выбраны следующие параметры. Общий заряд системы $q = {{10}^{{ - 13}}}$ Кл [8], толщина пленки $h = {{10}^{{ - 8}}}$ м, амплитуда колебаний пленки $\eta = {{10}^{{ - 9}}}$ м, радиус пленки $R = {{10}^{{ - 5}}}$ м, циклическая частота колебаний $\omega = 2.22 \times {{10}^{8}}$ рад/с для $n = 1$ и $\omega = 3.38 \times {{10}^{8}}$ рад/с для $n = 2$ (частота акустических колебаний [6, 9]).

На рис. 2 представлены графики зависимостей напряженности электрического поля в ближней зоне от расстояния для различных типов колебаний: n = 1, m = 0; n = 1, m = 1; n = 2, m = 0, m = 1.

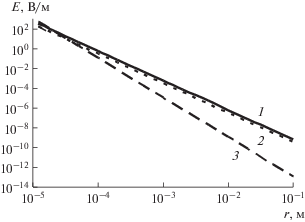
Рис. 2.

Зависимость напряженности электрического поля, создаваемого набором диполей, от расстояния при θ = 0 рад: n = 1, m = 0 (кривая 1); n = 1, m = 1 (кривая 2); n = 2, m = 0, m = 1 (кривая 3).

На рис. 3 представлены зависимости напряженности электрического поля, создаваемого низшими видами колебаний от времени для двух случаев – n = 1 и 2, на расстоянии r = 0.1 мм от центра сферической пленки.

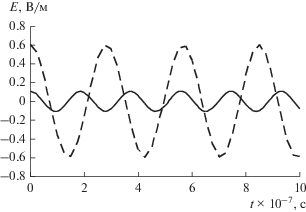
Рис. 3.

Зависимость напряженности электрического поля, создаваемого пленкой, от времени при θ = 0 рад и n = 1 (сплошная линия), n = 2 (пунктирная).

Индукция магнитного поля, создаваемая набором диполей, очень мала по величине (так, например, на расстоянии 1 мм $B\sim {{10}^{{ - 16}}}$ Тл).

Было проведено численное моделирование в среде Turbo Delphi. Интегрирование показало те же результаты, что и аналитическое решение. Чем меньше был шаг интегрирования, тем больше совпадало знаков после запятой. Шаг интегрирования брался из тех соображений, что площадь dS, характеризующая элементарный диполь, должна быть много меньше расстояния от этого диполя до точки наблюдения. То есть должно выполняться неравенство

(12)
${{R}^{2}}\sin \theta d\theta d\varphi \ll {{\left( {\vec {r} - \vec {R}} \right)}^{2}}.$

Это ограничение существенно увеличивает время расчета. Так, например, расчеты полей на расстоянии порядка микрометра от поверхности пленки занимали время порядка часа. Подобные результаты были получены в [11] численными методами.

Данные результаты получены для среды с нулевой проводимостью. Так как вода в общем случае может проводить электрический ток, необходимо обобщить результаты с учетом проводящих свойств вещества. Для этого нужно использовать комплексную диэлектрическую проницаемость:

(13)
$\tilde {\varepsilon } = \varepsilon {{\varepsilon }_{0}} - j\frac{\sigma }{\omega },$

где $\sigma $ – проводимость воды, $j$ – мнимая единица. В этом случае глубина проникновения будет равна [10]:

(14)
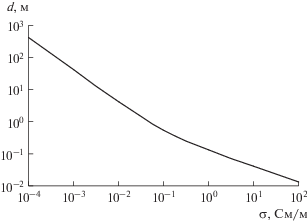
$d = \sqrt {\frac{2}{{{{\omega }^{2}}\mu {{\mu }_{0}}\left[ {\sqrt {{{{\left( {\varepsilon {{\varepsilon }_{0}}} \right)}}^{2}} + {{{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma \omega }} \right. \kern-0em} \omega }} \right)}}^{2}}} - \varepsilon {{\varepsilon }_{0}}} \right]}}} ,$

где относительная диэлектрическая проницаемость $\varepsilon $ и проводимость воды $\sigma $ зависят от частоты электромагнитного поля (14).

Как видно из рис. 4, при значениях проводимости, соответствующих частотам акустических колебаний (~10–1…10–2 См/м [12]), глубина проникновения электромагнитного поля имеет величину порядка 1 м, а на расстоянии 1 мм напряженность электрического поля уменьшается всего на несколько процентов.

Рис. 4.

Зависимость глубины проникновения электромагнитного поля от проводимости среды.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе аналитически и численно найдены поля групп диполей. Показано, что поля, создаваемые колеблющимися тонкими пленками, можно использовать в качестве источника информации о среде и самой пленке, так как от их параметров зависит вид колебаний. Также пленки можно использовать для преобразования сигналов путем возбуждения акустических колебаний пленок внешним сигналом [13] и последующей регистрации генерируемых пленкой полей.

Список литературы

  1. Гуляев Ю.В. Физические поля и излучения человека. Новые неинвазивные методы медицинской диагностики. М.: РБОФ “Знание” им. С.И. Вавилова, 2009.

  2. Гуляев Ю.В., Дмитриев А.С., Ицков В.В. и др. // РЭ. 2018. Т. 63. № 9. С. 947.

  3. Nicolini C. // Biosensors and Bioelectronics. 1995. T. 10. № 1–2. P. 105.

  4. Рубин А.Б. Биофизика: Учеб. для биолог. спец. вузов. В 2-х кн.: М.: Высш. шк., 1987. Кн. 2.

  5. Шеин А.Г., Харланов А.В. // Биомед. технологии и радиоэлектроника. 2007. № 5. С. 15.

  6. Шеин А.Г., Харланов А.В. // Биомед. технологии и радиоэлектроника. 2006. № 4. С. 10.

  7. Федорченко А.М. Теоретическая физика. Классическая электродинамика: Учеб. пособие. Киев: Выща школа, 1988.

  8. Бецкий О.В., Лебедева Н.Н. // Миллиметровые волны в биологии и медицине. 2001. № 3. С. 5.

  9. Харланов А.В. Электромагнитные волны и колебания биологических объектов. Волгоград: ИУНЛ ВолгГТУ, 2012.

  10. Баскаков С.И. Электродинамика и распространение радиоволн. М.: Высш. школа, 1992.

  11. Cifra M. Study of Electromagnetic Oscillations of Yeast Cells in kHz and GHz Region. Ph.D. Thesis Czech Technical University in Prague, 2009.

  12. Artemov V.G., Volkov A.A. // Ferroelectrics. 2014. V. 466. № 1. P. 158.

  13. Kharlanov A.V. // Bioelectromagnetics. 2017. V. 38. № 8. P. 613.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал