Радиотехника и электроника, 2021, T. 66, № 12, стр. 1189-1197

ВВЕДЕНИЕ

Известно, что в системах связи с MIMO-каналом пропускная способность растет пропорционально $\min \left( {{{N}_{{tx}}},{{N}_{{rx}}}} \right)$ [1], где ${{N}_{{tx}}},{{N}_{{rx}}}$ – число передающих и приемных антенн соответственно. При этом также повышается энергетическая эффективность за счет разнесения, так как увеличивается число путей распространения сигнала с некоррелированными замираниями, а также за счет когерентной обработки сигналов, принимаемых разными приемными антеннами. Однако если рассмотреть систему связи с мультиплексированием в MIMO-канале более подробно, то можно отметить, что число путей распространения сигнала с независимыми замираниями равно ${{N}_{{tx}}} \times {{N}_{{rx}}}$, а число путей, по которым передается один символ, равно ${{N}_{{rx}}}$. Поэтому разные символы принимаются с разным качеством.

Для повышения энергетической эффективности в системах MIMO с пространственным мультиплексированием за счет полного разнесения используются алгебраические коды [2–6], среди которых наиболее известным является так называемый код Голден [4]. Так, например, для конфигурации ${{N}_{{rx}}} = {{N}_{{tx}}} = 2$ выигрыш от использования кода Голден составляет 1.5…2 дБ [5]. Однако данные алгебраические коды оптимизированы для оптимального приемника максимального правдоподобия, сложность которого в сочетании с алгебраическим кодированием с полным разнесением растет пропорционально ${{2}^{{{{k}_{b}}{{N}_{{tx}}}{{N}_{{rx}}}}}}$, где ${{k}_{b}}$ – число битов, передаваемых одним модулированным символом. Это обстоятельство делает данные коды непригодными для практического использования при числе передающих антенн ${{N}_{{tx}}} \geqslant 4$.

В данной статье предложен подход, позволяющий достичь эффекта полного разнесения, при котором каждый передаваемый символ распределяется по всем ${{N}_{{tx}}}{{N}_{{rx}}}$ возможным путям распространения и при этом используется линейный приемник, сложность которого практически остается такой же, как и сложность приемника с минимумом средней квадратической ошибки (МСКО) для обычной системы связи с пространственным мультиплексированием.

1. МОДЕЛЬ СИСТЕМЫ

Рассмотрим однопользовательскую MIMO-систему с ${{N}_{{tx}}}$ передающими и ${{N}_{{rx}}}$ приемными антеннами. Для передачи информации по MIMO-каналу используется пространственное мультиплексирование [1], где поток комплексных модулированных символов ${{s}_{i}}$, $i = 1,2, \ldots ,$ разбивается на последовательности векторов:

размером $({{N}_{{tx}}} \times 1)$ каждый, где m-й элемент n-го вектора имеет вид Полагаем, что каждый модулированный символ имеет нулевое математическое ожидание и единичную мощность, т.е. Для простоты последующего изложения рассмотрим передачу блока из ${{N}_{{tx}}}$ векторов, т.е. $n = \overline {1,{{N}_{{tx}}}} $.

Для системы MIMO с пространственным мультиплексированием модель наблюдения описывается следующим выражением [1, 6–10]:

где – $({{N}_{{rx}}} \times 1)$-мерный комплексный вектор наблюдений (индекс T означает операцию транспонирования); – $({{N}_{{rx}}} \times {{N}_{{tx}}})$-мерная матрица комплексных множителей MIMO-канала ${{h}^{{\left( {i,j} \right)}}}$, являющихся некоррелированными гауссовскими случайными величинами с нулевыми средними и дисперсиями $E\left\{ {{{{\left| {{{h}^{{\left( {i,j} \right)}}}} \right|}}^{2}}} \right\} = \frac{1}{{{{N}_{{tx}}}}}$, для всех $i = \overline {1,{{N}_{{rx}}}} $ и $j = \overline {1,{{N}_{{tx}}}} $, что соответствует независимым рэлеевским замираниям; ${{{\mathbf{\eta }}}_{n}}$ – $\left( {{{N}_{{rx}}} \times 1} \right)$-мерный вектор комплексных гауссовских случайных величин с нулевым математическим ожиданием и корреляционной матрицей ${{{\mathbf{R}}}_{{{\eta }}}} = E\left\{ {{{{\mathbf{\eta }}}_{n}}{\mathbf{\eta }}_{n}^{H}~} \right\}$ (индекс H означает операцию эрмитового сопряжения вектора или матрицы), которая в большинстве практических случаев является диагональной ${{{\mathbf{R}}}_{{{\eta }}}} = \frac{1}{\rho }{{{\mathbf{I}}}_{{{{N}_{{rx}}}}}}$ (${{{\mathbf{I}}}_{{{{N}_{{rx}}}}}}$ – единичная матрица, размером $\left( {{{N}_{{rx}}} \times {{N}_{{rx}}}} \right))$, $\rho = \frac{{{{P}_{s}}}}{{2\sigma _{\eta }^{2}}}$ – среднее отношение сигнал/шум (ОСШ) на входе одной приемной антенны, ${{P}_{s}}$ – средняя мощность сигнала на входе приемной антенны, $\sigma _{\eta }^{2}$ – дисперсия мнимой и действительной составляющих отсчета гауссовского шума наблюдений. 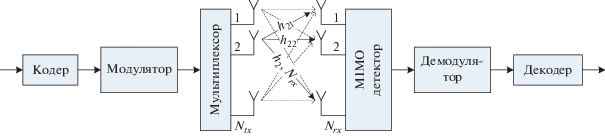Полагаем, что матрица канала ${\mathbf{H}}$ и дисперсия шума $\sigma _{\eta }^{2}$ известны на приемной стороне.

Модель системы показана на рис. 1. Как видно из рисунка, каждый символ, излучаемый одной передающей антенной, поступает на ${{N}_{{rx}}}$ приемных антенн по ${{N}_{{rx}}}$ индивидуальным путям распространения. Всего в модели имеются ${{N}_{{rx}}}{{N}_{{tx}}}$ независимых путей распространения. Это означает, что символы будут приниматься с разным качеством и в данном случае не реализуется полное разнесение. В связи с этим возникает задача обеспечить распределение каждого символа по всем передающим антеннам таким образом, чтобы обеспечить эффект полного разнесения после демодуляции всего сигнала или, по крайней мере, повысить порядок разнесения.

Данную задачу решают пространственные коды на основе алгебраического кодирования, представителем которых для конфигурации ${{N}_{{tx}}} = {{N}_{{rx}}} = 2$ является известный код Голден [4, 5]. Однако полностью реализовать его преимущество возможно только при оптимальном приемнике максимального правдоподобия, сложность которого в данном случае будет пропорциональна ${{2}^{{{{k}_{b}}{{N}_{{tx}}}{{N}_{{rx}}}}}}$. В связи с этим возникает задача использования более простых алгоритмов MIMO-детектирования в сочетании с линейным прекодированием, позволяющим повысить порядок разнесения.

В работе [11] предложено использовать ортогональное преобразование каждого мультиплексированного вектора и индивидуальную задержку каждого сигнала, излучаемого своей антенной. Для его реализации рассматривается приемник, использующий принципы турбообработки [12], основанные на последовательном отказе и последующем учете априорной информации о дискретном распределении и гауссовской аппроксимации [13, 14], который может быть реализован в виде линейного фильтра Калмана. Однако, несмотря на использование более простого, чем оптимальный, алгоритма обработки, его реализация остается сложной при больших значениях числа передающих антенн, так как требуется вычисление обратной матрицы размером $\left( {N_{{tx}}^{2} \times N_{{tx}}^{2}} \right)$.

Рассмотрим использование линейного алгоритма, оптимального по критерию МСКО, для обработки MIMO-сигнала модели (1). Данный алгоритм описывается следующими выражениями [1, 15–17]:

Точность оценивания алгоритма МСКО определяется диагональными элементами корреляционной матрицы или их средним значением где tr – операция вычисления следа матрицы.

2. ОРТОГОНАЛЬНОЕ ПРЕКОДИРОВАНИЕ

Введем расширенный вектор символов

который объединяет блок из N_tx векторов в один вектор размером $\left( {N_{{tx}}^{2} \times 1} \right)$. Для данного вектора можно записать расширенную модель наблюдения где блочно-диагональная матрица расширенного канала, размером $\left( {{{N}_{{rx}}}{{N}_{{tx}}} \times N_{{tx}}^{2}} \right)$.

Для расширенной модели (4), как и для модели (1) можно также применить МСКО-алгоритм (2). Матрица ошибок МСКО-оценивания в данном случае будет блочно-диагональной и определяться следующим выражением:

Нетрудно показать, что

где оценки ${{{\mathbf{\hat {x}}}}_{n}}$ и корреляционная матрица вычисляются с помощью выражений (2) и (3) соответственно.

Очевидно, что значения диагональных элементов корреляционной матрицы для расширенного вектора периодически повторяются

Среднее значение дисперсий для расширенной корреляционной матрицы ошибок оценивания остается прежним, т.е.

Рассмотрим влияние ортогонального преобразования (прекодирования) на корреляционную матрицу ошибок оценивания. Введем матрицу ортогонального преобразования ${\mathbf{\tilde {F}}}$, размером $\left( {N_{{tx}}^{2} \times N_{{tx}}^{2}} \right)$, и используем ее для прекодирования расширенного вектора, т.е. имеем следующее преобразование ${\mathbf{z}} = {\mathbf{\tilde {F}\tilde {x}}}$, где ${\mathbf{\tilde {x}}}$ – расширенный вектор исходных модулированных символов. Модель наблюдения для этого случая может быть записана следующим образом [18–21]:

Вектор оценок МСКО и соответствующая корреляционная матрица ошибок оценивания будут описываться следующими выражениями:

Нетрудно показать, что

Можно доказать, что ${\text{tr}}\left( {{{{{\mathbf{\tilde {F}}}}}^{H}}{{{{\mathbf{\tilde {V}}}}}_{z}}{\mathbf{\tilde {F}}}} \right) = {\text{tr}}{{{\mathbf{\tilde {V}}}}_{z}}$. Это вытекает непосредственно из свойства следа для произведения матриц ${\text{tr}}\left( {{\mathbf{AB}}} \right) = {\text{tr}}\left( {{\mathbf{BA}}} \right)$ [22–25]. Поэтому можно сделать вывод, что прекодирование с использованием ортогонального преобразования не изменяет среднее значение ошибок при МСКО-оценивании. Однако, как показано в [26], на помехоустойчивость линейного приемника влияет не только среднее значение, но и максимальное значение дисперсий ошибок оценивания, а следовательно, и их разброс.

При постоянном среднем значении наименьшее значение максимальной дисперсии может быть достигнуто в том случае, когда все диагональные элементы одинаковы и равны среднему значению. Следовательно, нужно найти такой вид ортогонального преобразования, при котором все диагональные элементы матрицы ${\mathbf{\tilde {V}}}$ будут равны между собой.

Следует отметить, что ошибки оценивания символов, передаваемых на разных тактовых интервалах $n = \overline {1,{{N}_{{tx}}}} $ без прекодирования (6), принадлежат разным векторам и, в соответствии с (5), между собой не коррелированы, т.е. ошибки оценивания символов n-го вектора не коррелированы с ошибками оценивания m-го вектора при $n \ne m$ для любых элементов внутри этого вектора.

Кроме того, ошибки оценивания символов с разными номерами (разным положением внутри векторов) имеют различные дисперсии. Это обстоятельство предполагает возможность распределения символов так, чтобы уменьшить разброс дисперсий относительно среднего значения.

Рассмотрим следующий подход. Пусть имеется уравнение наблюдения:

где $z$ – M-мерный оцениваемый вектор, ${\mathbf{F}}$ – ортогональная матрица, размером $\left( {M \times M} \right)$, ${\mathbf{\mu }}$ – вектор ошибок оценивания с нулевым математическим ожиданием и диагональной корреляционной матрицей с разными диагональными элементами

Корреляционная матрица ошибок оценивания вектора ${\mathbf{z}}$ будет равна:

С учетом того, что матрица ${{{\mathbf{R}}}_{{{\mu }}}}$ является диагональной и на основании соотношения (11) для диагональных элементов корреляционной матрицы ${\mathbf{V}}$ можно записать следующее выражение:

где ${{f}^{{\left( {j,i} \right)}}}$ – (i, j)-й элемент матрицы ${\mathbf{F}}$.

Из выражения (12) следует условие, при котором обеспечивается равенство всех диагональных элементов ${{v}^{{\left( {i,i} \right)}}}$ корреляционной матрицы ошибок оценивания:

В этом случае получим ${{v}^{{\left( {i,i} \right)}}} = {{v}^{{\left( {j,j} \right)}}} = {{\bar {v}}_{d}}$ для всех $i = \overline {1,M} ,\,\,j = \overline {1,M} $. Следовательно, для этого варианта $\mathop {\max }\limits_{i = \overline {1,{{N}_{{tx}}}} } \left( {{{v}^{{\left( {i,i} \right)}}}} \right) = {{\bar {v}}_{d}}$ будет минимально возможным для данных условий.

Таким образом, условие (13) определяет требование к ортогональному преобразованию, при котором обеспечивается равенство всех дисперсий ошибок оценивания. Но это условие не единственное. Другим условием, которое учитывалось при выводе выражения (13), является некоррелированность ошибок оценивания. Это условие обеспечивается тем, что символы каждого преобразованного вектора должны будут передаваться на разных тактовых интервалах. В результате получится ${{N}_{{tx}}}$ векторов, размером $\left( {{{N}_{{tx}}} \times 1} \right)$ каждый, для которых обеспечивается некоррелированность ошибок оценивания. Но и этого условия еще недостаточно. Например, если все символы преобразованного вектора передавать на разных тактах, но через одну антенну, то согласно выражению (6) ошибки оценивания этих символов будут иметь одинаковую дисперсию и в этом случае эффекта разнесения не будет. Поэтому необходимо, чтобы каждый символ преобразованного вектора передавался разными антеннами.

Можно предложить разные способы генерации последовательных номеров антенн и тактов, по которым распределяются прекодированные символы, чтобы обеспечить выполнение всех перечисленных условий. Например, можно использовать простой набор циклических сдвигов, а именно, для первого прекодированного вектора ${\mathbf{F}}{{{\mathbf{x}}}_{1}}$ используется последовательность $\left\{ {1,~2,~ \ldots ,{{N}_{{tx}}}} \right\}$, которая означает, что первый элемент прекодированного вектора передается на первом такте через первый пространственный канал (первую излучающую антенну), второй элемент этого вектора передается на втором такте через второй пространственный канал, и т.д. Следующая последовательность образуется путем циклического сдвига на один элемент, т.е. получается $\left\{ {2,~3,...,{{N}_{{tx}}},1} \right\}$. Она определяет распределение элементов второго прекодированного вектора и показывает, что первый элемент этого вектора передается на первом такте через вторую излучающую антенну, второй элемент – на втором такте через третью излучающую антенну, и так далее.

Такой алгоритм распределения является достаточно простым, но можно предложить и другие, использующие некоторую случайность. Например, можно использовать псевдослучайные числовые последовательности на основе первообразных корней и простых чисел [23]. Для этого сначала выбирается первое простое число, удовлетворяющее условию ${{N}_{s}} > {{N}_{{tx}}}$, и находится первообразный корень $\alpha < {{N}_{{tx}}}$. Последовательность номеров для первого прекодированного вектора будет определяться следующим алгоритмом: ${{I}_{n}} = {{\left[ {\alpha {{I}_{{n - 1}}}} \right]}_{{\bmod {{N}_{s}}}}}$, $n = \overline {1,{{N}_{{tx}}}} $, при начальных условиях ${{I}_{1}} = \alpha $. Так, например, для ${{N}_{{tx}}} = 4$ имеем ${{N}_{s}} = 5,\,\,\alpha = 2$ и генерируемая последовательность будет $\left\{ {2,4,3,1} \right\}$. Для последующих прекодированных векторов последовательность формируют путем циклических сдвигов исходной последовательности.

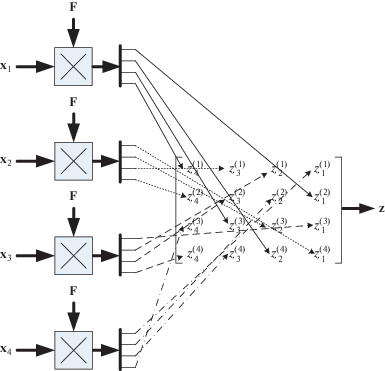
На рис. 2 приведена блок-схема предлагаемого алгоритма ортогонального прекодирования и распределения символов преобразованных векторов по разным тактовым интервалам и разным пространственным каналам.

Использование псевдослучайных последовательностей позволяет избежать закономерностей в общей корреляционной матрице ошибок, которые могут проявиться неожиданным образом, например появлением блоков сильно коррелированных символов. Отметим, что дополнительную рандомизацию можно также ввести путем использования различных ортогональных матриц.

3. ОБРАБОТКА СИГНАЛА НА ПРИЕМНОЙ СТОРОНЕ

Предложенный метод ортогонального прекодирования предназначен для обработки расширенного вектора модулированных символов ${\mathbf{\tilde {x}}}$, размером $\left( {N_{{tx}}^{2} \times 1} \right)$. Для оценивания всех символов используется расширенное наблюдение ${\mathbf{\tilde {y}}}$, размером $\left( {{{N}_{{tx}}}{{N}_{{rx}}} \times 1} \right)$. Оперирование векторами с большой размерностью предполагает увеличение сложности реализации приемника. Рассмотрим, насколько увеличивается сложность обработки при использовании предложенного алгоритма прекодирования.

С учетом приведенных в разд. 2 преобразований модель наблюдения может быть записана в следующем виде:

где расширенная матрица ортогонального прекодирования ${\mathbf{\tilde {F}}}$, размером $\left( {N_{{tx}}^{2} \times N_{{tx}}^{2}} \right)$, является блочно-диагональной:

Матрица перестановок ${\mathbf{\tilde {P}}}$, размером $\left( {N_{{tx}}^{2} \times N_{{tx}}^{2}} \right)$, осуществляет распределение символов после ортогонального преобразования в соответствии с правилами перестановок, описанных в разд. 2. Для этой матрицы справедливо условие ${{{\mathbf{\tilde {P}}}}^{T}}{\mathbf{\tilde {P}}} = {\mathbf{\tilde {P}}}{{{\mathbf{\tilde {P}}}}^{T}} = {{{\mathbf{I}}}_{{N_{{tx}}^{2}}}}$.

Для модели (14) алгоритм оценивания по критерию МСКО описывается выражениями, аналогичными выражениям (9):

Нетрудно показать, что:

где ${{{\mathbf{K}}}_{{{\text{МСКО}}}}} = {{\left( {{{{\mathbf{H}}}^{H}}{\mathbf{H}} + \frac{1}{\rho }{{{\mathbf{I}}}_{{{{N}_{{tx}}}}}}} \right)}^{{ - 1}}}{{{\mathbf{H}}}^{H}}$ – матрица алгоритма МСКО для обычной системы MIMO с пространственным мультиплексированием.

Учитывая блочно-диагональную структуру матрицы ${{{\mathbf{\tilde {K}}}}_{{{\text{МСКО}}}}}$ и матрицы ${\mathbf{\tilde {F}}}$, можно записать алгоритм вычисления оценки вектора ${{{\mathbf{x}}}_{n}}:$

где ${{{\mathbf{P}}}_{n}}$ – $\left( {N_{{tx}}^{2} \times {{N}_{{tx}}}} \right)$ – матрица перестановок элементов n-го преобразованного вектора, состоящая из столбцов матрицы ${\mathbf{\tilde {P}}}$: начиная c $\left( {\left( {n - 1} \right){{N}_{{tx}}} + 1} \right)$-го по $n{{N}_{{tx}}}$-й.

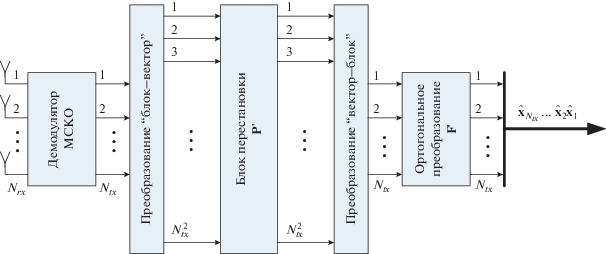
На рис. 3 приведена структурная схема линейного демодулятора МСКО для системы MIMO с ортогональным прекодированием, предложенным в данной статье. Здесь хорошо видно, что по сравнению с обычным приемником МСКО для простой системы с пространственным мультиплексированием среди добавленных блоков, требующих выполнения каких-либо математических операций, можно отметить только блок ортогонального преобразования. Сложность реализации этого блока при использовании быстрых преобразований пропорциональна ${{N}_{{tx}}}{{\log }_{2}}{{N}_{{tx}}}$, что практически не изменит сложность всего приемника, так как реализация обычного алгоритма МСКО требует $ \sim {\kern 1pt} N_{{tx}}^{3}$ операций.

4. МОДЕЛИРОВАНИЕ

Для проверки эффективности предложенного метода было проведено моделирование разработанного алгоритма с ортогональным прекодированием.

Условия моделирования:

1) MIMO-канал с независимыми релеевскими замираниями;

2) модуляция QPSK;

3) турбокодирование со скоростью 3/4;

4) длина кадра 576 бит.

На рис. 4 приведены зависимости вероятности битовой ошибки ${{P}_{{{\text{бит}}}}}$ без кодирования (а) и вероятности ошибки на кадр ${{P}_{{{\text{кадр}}}}}~$ с кодированием (б) для MIMO-системы 4 × 4 с обычным пространственным мультиплексированием (кривая 1) и с предложенным ортогональным прекодированием (кривая 2) при использовании линейных алгоритмов МСКО.

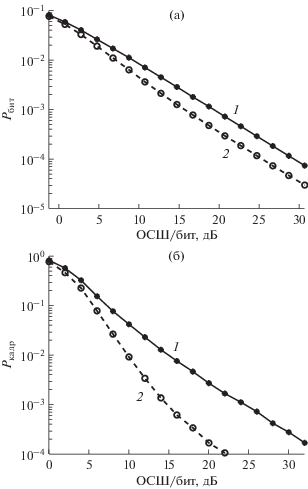
Из приведенных графиков видно, что для случая без кодирования выигрыш предлагаемого варианта с ортогональным прекодированием составляет ~3 дБ, а при кодировании выигрыш при FER = 0.01 (1%) составляет 5 дБ.

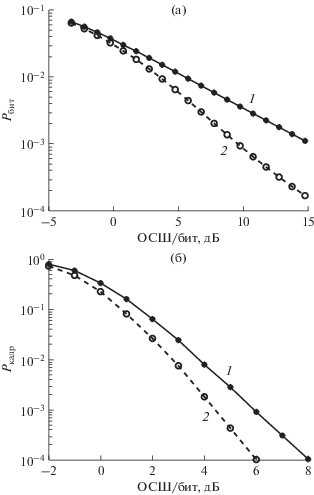
На рис. 5 представлены зависимости вероятности битовой ошибки P_бит без кодирования (а) и вероятности ошибки на кадр P_кадр с кодированием (б) для MIMO-системы 8 × 8: с обычным пространственным мультиплексированием (1) и с предложенным ортогональным прекодированием (2).

На рис. 6 приведены аналогичные кривые для конфигурации MIMO-канала 16 × 16.

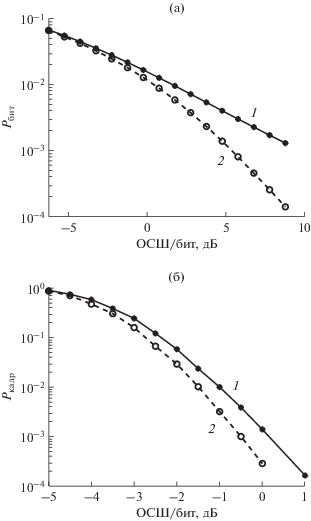
В данном случае выигрыш также наблюдается, но его величина меньше. Это объясняется тем, что при большом числе антенн уже имеется достаточно большое разнесение. Кривые приближаются к предельным характеристикам, определяемыми характеристиками гауссовского канала без замираний, поэтому дальнейшее увеличение порядка разнесения сказывается на помехоустойчивости в меньшей степени.

ЗАКЛЮЧЕНИЕ

Предложен метод ортогонального прекодирования, позволяющий получить дополнительный выигрыш в энергетической эффективности за счет увеличения порядка разнесения. Полученный алгоритм прекодирования оптимизирован для линейных алгоритмов приема пространственно-разнесенных сигналов, например такого, как алгоритм МСКО. При этом сложность обработки сигнала как на передающей, так и на приемной стороне практически не увеличивается.

Путем моделирования системы связи с MIMO-каналом с алгоритмами прекодирования, полученными предложенным методом, показано, что их использование позволяет получить энергетический выигрыш порядка 1.5 дБ при конфигурации MIMO-канала 8 × 8 и порядка 5 дБ при конфигурации 4 × 4.