Радиотехника и электроника, 2021, T. 66, № 4, стр. 345-350

ВВЕДЕНИЕ

Композиционные материалы на основе частиц наполнителя (включений), распределенных в связующей среде (матрице), перспективны для применения в технике СВЧ, в частности, в качестве радиопоглощающих [1, 2]. Взаимодействие таких немагнитных материалов с электромагнитным полем определяется их эффективной диэлектрической проницаемостью (ЭДП). При ее вычислении в приближении Максвелла Гарнетта (МГ) предполагается, что частицы-включения находятся в среде с диэлектрической проницаемостью, равной проницаемости материала матрицы, при этом действующее на включения поле равно объемно усредненному полю в матрице [3]. Такое предположение наиболее соответствует случаю пространственно упорядоченного распределения включений в композите. Адекватность такой трактовки приближения МГ подтверждают результаты работ [4–6]. В [4] на основе точного решения задачи для потенциала показано, что формула МГ для композита со сферическими включениями является первым приближением в формуле для ЭДП кубической решетки, образованной сферическими частицами. В [5] на основе решения задачи дифракции получена приближенная формула для ЭДП композита на основе кубической решетки сферических включений, которая в частном случае отсутствия скин-эффекта переходит в формулу МГ. В [6] показано, что учет упорядочения расположения в композите сферических включений, возникающего при наличии матричного слоя на включениях, приводит к формуле МГ, если все вещество матрицы входит в оболочки включений.

В теории эффективной среды Бруггемана предполагается, что включения погружены в среду, диэлектрическая проницаемость которой равна ЭДП, при этом действующее на включение поле равно среднему полю в композите [3]. Такое предположение наиболее соответствует случаю, когда композит представляет собой идеально перемешанную смесь частиц матрицы и частиц-включений или, в случае сплошной матрицы, предельно разупорядоченному расположению включений в матрице. На адекватность такой трактовки указывает и то, что в формулу Бруггемана для композита со сферическими включениями объемные концентрации и диэлектрические проницаемости включений и матрицы входят симметрично.

Таким образом, теории МГ и Бруггемана следует рассматривать как относящиеся к крайним вариантам расположения включений в композите. В реальности, однако, в композите нет как полного хаоса, так и полного упорядочения. Поэтому в общем случае следует предположить, что частицы композита и матрицы находятся в некотором поле $\tilde {E}$, которое назовем действующим, в общем случае не совпадающем ни со средним полем в матрице, ни со средним полем в композите. При этом частицы матрицы и включения погружены в среду с некоторой диэлектрической проницаемостью ${\tilde {\varepsilon }}$, которую назовем действующей, не совпадающей ни с проницаемостью матрицы (теория МГ), ни с ЭДП (теория Бруггемана).

1. ВЫВОД ФОРМУЛЫ ДЛЯ ЭФФЕКТИВНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Рассмотрим композит, состоящий из смеси эллипсоидальных частиц, главные оси которых направлены вдоль среднего поля в композите (ось $x{\kern 1pt} $). Эффективную диэлектрическую проницаемость $\varepsilon {\kern 1pt} $ зададим обычным образом как отношение усредненной по объему индукции к среднему полю [3]:

где ${{с}_{k}}$ – объемная концентрация компоненты смеси с номером k, ${{\varepsilon }_{k}}$ – диэлектрическая проницаемость частиц этой компоненты, ${{E}_{k}}$ – среднее поле в них. Имеем

где ${{N}_{k}}$ – число частиц компоненты k в единице объема, ${{v}_{k}}$ – объем одной частицы этой компоненты. Формулу (1) запишем в тождественном виде:

Применим формулу для поляризуемости ${{\alpha }_{k}}$ в однородном поле эллипсоида, находящегося в среде с диэлектрической проницаемостью $\tilde {\varepsilon }$ [7]:

где ${{n}_{k}}$ – коэффициент деполяризации вдоль оси $x{\kern 1pt} $. Из (4) получим

Считая эллипсоид находящимся во внешнем поле $\tilde {E}$, для значения поля в эллипсоиде применим формулу [3]

Из (5), (6) находим

Подставляя (5), (7) в (3) и учитывая (2), получим в результате простых преобразований

Установим связь между величинами ${\tilde {\varepsilon }}$ и $\tilde {E}$. С учетом (7) имеем

Левая часть (9) равна среднему полю E в композите. С учетом (2) находим отношение действующего поля к среднему полю:

Пусть композит состоит из непрерывной матрицы с диэлектрической проницаемостью ${{\varepsilon }_{{{\kern 1pt} 1}}}$ и включений. Матрицу можно рассматривать как состоящую из бесконечного множества заполняющих пространство между включениями эллипсоидов, как сплющенных, так и вытянутых, имеющих разные размеры, в том числе предельно малые. Формулы (8), (10) примут вид

где номера ${{m}_{{}}}$ относятся лишь к компонентам из частиц-включений,

Верхний индекс 1 в скобках означает, что данная величина относится к частицам матрицы. В среднем будем считать частицы матрицы сферическими. Полагая $n_{k}^{{(1)}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, $k = 1,\;2,\; \ldots $, получим

где

– объемная концентрация включений.

Если нет оснований считать структуру композита полностью хаотичной или достаточно упорядоченной, то величину $\tilde {\varepsilon }$ можно использовать как подгоночный параметр, например, варьируя ее путем изменения параметра ${{x}_{{}}}$ в формуле

где $\tilde {\varepsilon }(0) = {{\varepsilon }_{{{\kern 1pt} 1}}}$ соответствует приближению МГ, $\tilde {\varepsilon }(1) = {{\varepsilon }_{\operatorname{B} }}$ соответствует теории Бруггемана (${{\varepsilon }_{\operatorname{B} }}$ – значение ЭДП, полученное из (11) при $\tilde {\varepsilon } = \varepsilon $).

При различной ориентации включений примененный подход к нахождению ЭДП остается в силе, но имеет место существенное усложнение формул вследствие необходимости выражать величины через углы ориентации включений по отношении к оси $x{\kern 1pt} $, параллельной среднему полю, по которой вычисляется эффективная проницаемость, а также через коэффициенты деполяризации по трем главным осям эллипсоидальных частиц.

Полученные формулы для вычисления ЭДП очевидным образом применимы для вычисления эффективной магнитной проницаемости композитов на основе магнитодиэлектрических частиц.

2. ЧАСТНЫЕ СЛУЧАИ

Для композита с одним видом включений с проницаемостью ${{\varepsilon }_{2}}$ и коэффициентом деполяризации ${{n}_{{}}}$ формулы (11), (12) имеют вид

где $N$ – число частиц-включений в единице объема,

$v$ – объем одного включения.

Применяя приближение МГ, получим из (17), (15) при $\tilde {\varepsilon } = {{\varepsilon }_{1}}$

Формула (20) совпадает при n = 1/3 с формулой Лорентц–Лоренца, полученной на основе представления о локальном поле, действующем на включения [8]. Учитывая, что $N{\kern 1pt} v = c$, из (20) получим

Применяя приближение Бруггемана, положим в (15), (17), (19) $\tilde {\varepsilon } = \varepsilon $. Получим

Простыми преобразованиями формула (22) приводится к квадратному уравнению относительно $\varepsilon {\kern 1pt} $. При $n = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ (21), (22) переходят в формулы МГ и Бруггемана для композита со сферическими включениями [3].

В случае переменных полей полученные формулы для ЭДП формально применимы лишь в случае слабого скин-эффекта во включениях, поскольку при их выводе применялись статические формулы (4), (6). Однако, как показано в [6], в случае сферических включений подстановка в (20) на место величины $\alpha {\kern 1pt} $ квазистатической поляризуемости сферической частицы в среде с проницаемостью, равной проницаемости матрицы, приводит к известной формуле Левина, полученной путем приближенного решения задачи дифракции на кубической решетке сферических частиц [5]. Такой результат дает основания считать возможным применение формул (11), (17) и в случае существенного скин-эффекта в частицах, если подставить в эти формулы квазистатическую поляризуемость частиц.

Одним из перспективных радиопоглощающих материалов является композит на основе отрезков углеродных волокон-диполей, длина которых на порядки превосходит их толщину. Моделью такого цилиндрического включения служит вытянутый эллипсоид вращения, объем которого равен объему включения [9]. Такой иглообразный эллипсоид эффективно взаимодействует лишь с составляющей электрического поля вдоль его длинной оси. Это позволяет сопоставить композиту с хаотически ориентированными в плоскости иглообразными включениями композит с одинаково ориентированными в направлении поля включениями и применить формулу (17), произведя в ней замену:

где $K$ – фактор ориентации; $K = 1$ при ориентации длинных осей эллипсоидов вдоль поля, $K = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ при хаотической ориентации включений в пространстве и $K = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ при хаотической ориентации в плоскости, параллельной среднему полю в композите [9].

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

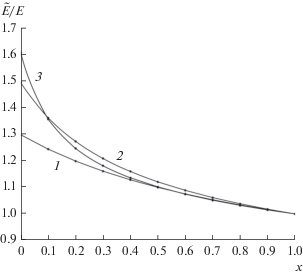
На рис. 1 приведены зависимости ЭДП композита со сферическими включениями от параметра $x{\kern 1pt} $, определяющего величину $\tilde {\varepsilon }$ согласно зависимости (16). При расчетах ЭДП по формулам (17), (19) полагалось ${{{\varepsilon }}_{{{\kern 1pt} 1}}} = 2$, $Nv = c = 0.4$, $n = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$. Значения диэлектрической проницаемости включений ${\kern 1pt} {{\varepsilon }_{2}}$ были равны 10, 20, 100. Соответствующее теории Бруггемана значение ${{\varepsilon }_{\operatorname{B} }}$ эффективной диэлектрической проницаемости вычисляли по формуле (22). Видно, что зависимость ЭДП от действующей диэлектрической проницаемости (параметра $x{\kern 1pt} $) тем сильнее, чем больше проницаемость включений ${{\varepsilon }_{2}}$, при этом ЭДП тем больше, чем ближе значение $\tilde {\varepsilon }$ к величине ${{\varepsilon }_{\operatorname{B} }}$. Соответствующие зависимости отношения действующего поля к среднему полю в композите, вычисленные по формулам (16), (19), приведены на рис. 2.

Рис. 1.

Зависимость эффективной диэлектрической проницаемости композита на основе сферических включений от параметра $x{\kern 1pt} $, определяющего величину $\tilde {\varepsilon }$ при ε₂ = 10 (1), 30 (2) и 100 (3).

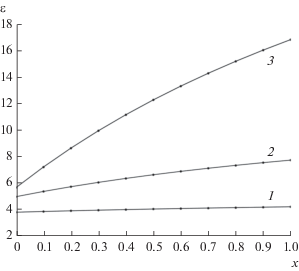
Рис. 2.

Зависимость отношения действующего поля к среднему полю для композита на основе сферических включений от параметра $x{\kern 1pt} $ при ε₂ = 10 (1), 30 (2) и 100 (3).

Расчет ЭДП композита на основе хаотически ориентированных в плоскости цилиндрических диполей проводился на основе сопоставления диполям равнообъемных эллипсоидов с использованием формул (17), (19). Длина диполей $2h = 10$ мм, их радиус $r = 4$ мкм, проводимость ${\sigma } = 71\,429$ См, ${{{\varepsilon }}_{1}} = 1.8$, $с = 0.05\% $. Такие значения параметров соответствуют композиту на основе углеродных волокон, экспериментально исследованному в [9]. Экспериментальные зависимости компонент ЭДП этого композита от частоты $f$ приведены на рис. 3а, 3б (кривые 1).

Рис. 3.

Зависимость вещественной (а) и мнимой (б) части эффективной диэлектрической проницаемости композита на основе отрезков углеродных волокон от частоты: 1 – экспериментальные данные; 2 – расчет по обобщенной формуле; 3 – расчет по модифицированной формуле Оделевского.

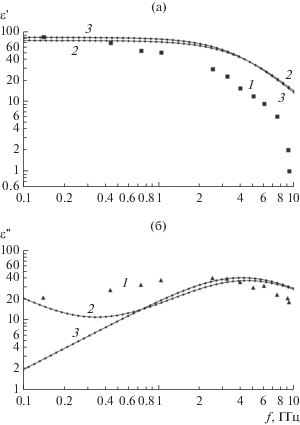
Большая полуось сопоставляемого диполю эллипсоида $a = h$, малая полуось $b = \sqrt {\,\frac{3}{2}} \;r$ определена из условия равенства объемов диполя и эллипсоида. Коэффициент деполяризации вычисляли по известной статической формуле [7]. Допустимость применения статической формулы определяется тем, что в расчетном диапазоне частот $0.1\; \ldots \;10$ ГГц глубина скин-слоя велика по сравнению с радиусом диполей. Диэлектрическую проницаемость ${{{\varepsilon }}_{2}}$ эллипсоида вычисляли по формуле ${{{\varepsilon }}_{2}} = {{({{i{\sigma }} \mathord{\left/ {\vphantom {{i{\sigma }} {\omega }}} \right. \kern-0em} {\omega }}{\text{)}}} \mathord{\left/ {\vphantom {{({{i{\sigma }} \mathord{\left/ {\vphantom {{i{\sigma }} {\omega }}} \right. \kern-0em} {\omega }}{\text{)}}} {{{{\varepsilon }}_{0}}}}} \right. \kern-0em} {{{{\varepsilon }}_{0}}}}$, где $i$ – мнимая единица, $\omega $ – циклическая частота, ${{\varepsilon }_{0}}$ – диэлектрическая проницаемость вакуума [10]. Параметр $x{\kern 1pt} $ в формуле (16) варьировался с целью сближения расчетных и экспериментальных значений ЭДП и оказался равным 0.00035. Результаты расчетов приведены на рис. 3а, 3б (кривые 2).

Представляет интерес сравнение полученных результатов расчета ЭДП с результатами расчетов по известной формуле с подгоночным параметром. В [11] показана удовлетворительная применимость к анализу композита на основе пластинчатых проводящих включений модифицированной формулы Оделевского, которую запишем с учетом различной ориентации диполей в виде

где ${{p}_{c}}$ – параметр, трактуемый как порог перколяции. Условием применимости формулы (24) является выполнение неравенства $c < {{p}_{c}}$. Обоснованное в [9] значение ${{p}_{c}}$ для композитов на основе проводящих цилиндрических включений определяется отношением диаметра диполя к его длине и составляет для рассматриваемого композита 0.0008, что превышает концентрацию включений $c = 0.0005$ в композите. Таким образом, применение формулы (24) достаточно корректно. Варьирование параметра ${{p}_{c}}$ в пределах $c < {{p}_{c}} \leqslant \,\,1$ показало, что его значение, равное 0.0029, обеспечивает оптимальное соответствие расчетных значений $\varepsilon {\kern 1pt} $ экспериментальным, в частности, близость вещественной части $\varepsilon {\kern 1pt} $ на минимальной частоте к ее статическому значению, равному 80 [9]. Результаты расчетов приведены на рис. 3а, 3б (кривые 3). Сравнение кривых 2 и 3 с экспериментальными значениями ЭДП (см. рис. 3а, 3б) показывает, что результаты расчетов вещественной части ЭДП по формуле (24) при частотах ниже 3 ГГц несколько точнее, чем по формуле (17). Расчетные значения мнимой части ЭДП, вычисленные по формуле (17), ближе к экспериментальным значениям на частотах ниже 0.8 ГГц и выше 4 ГГц, чем при использовании формулы (24).

Отметим следующее обстоятельство. Найденное оптимальное значение 0.0029 параметра ${{p}_{c}}$ в формуле (24) существенно отличается от экспериментально обоснованного значения порога перколяции, равного 0.0008. Это указывает на то, что применительно к композиту рассмотренного типа входящий в (24) параметр ${{p}_{c}}$ следует рассматривать не как реальный порог перколяции, а как подгоночный параметр.

Неполное соответствие расчетных значений ЭДП экспериментальным значениям связано с тем, что при расчете не учитывался тот факт, что поляризуемость включений различна в глубине экспериментального образца и на его границах [9]. Возможность учета этого эффекта путем введения зависимости параметра ${\tilde {\varepsilon }}$ и, соответственно, действующего поля от расстояния до границ образца требует отдельного исследования.

ЗАКЛЮЧЕНИЕ

Рассмотрен композит на основе ориентированных эллипсоидальных частиц. Введено понятие действующей диэлектрической проницаемости среды, в которую погружены частицы матрицы и включения, а также понятие действующего на частицы поля. Получена формула для эффективной диэлектрической проницаемости композита, переходящая в частных случаях в формулы Лорентца и Лоренца, Максвелла Гарнетта и Бруггемана. При выводе формулы не была использована гипотеза о локальном поле. На примере композита со сферическими включениями показана возможность применения полученной формулы в случае сильного скин-эффекта в материале включений. Для композита на основе отрезков углеродных волокон показана путем сравнения результатов расчетов с экспериментом возможность применения действующей диэлектрической проницаемости как подгоночного параметра.