Радиотехника и электроника, 2021, T. 66, № 5, стр. 483-489

1. ПОСТАНОВКА ЗАДАЧИ

В работах [1, 2] автором были предложены формулы для коллекторного тока усилителя с общим эмиттером (при возможном наличии стабилизирующего резистора в эмиттерной цепи):

Функции D₀₁ и D₂₂ выражаются через специальную математическую функцию Ламберта и имеют следующий вид:

Здесь U_in – это напряжение входного усиливаемого сигнала, R – внутреннее сопротивление p–n-переходов n–p–n-транзистора (предполагается одинаковым для обоих переходов), α – коэффициент передачи тока, R_n – нагрузочное сопротивление в цепи коллектора, R_ne – стабилизирующее сопротивление в цепи эмиттера, E – напряжение источника питания (включенного в коллекторную цепь), φ – температурный потенциал, I_s – ток насыщения. W(z) – специальная функция Ламберта (ее теорию можно посмотреть в [3]). В работе [1] было показано, что расчетные данные (при расчетах использовалась формула (1)) близки к экспериментальным данным, а также к результатам компьютерного моделирования в приложении Orcad.

Напряжение коллектор-эмиттер U_ce в рассмотренном усилителе определяется следующей формулой:

Если подставить в нее выражение (1), мы получим “усилительную” функцию U_ce = F(U_in), которая при нулевом значении R_ne имеет вид достаточно резкого перепада от напряжения питания к почти нулевому значению.

Цель статьи – использовать данную функцию (а также другие функции подобного рода) при выводе дифференциальных уравнений для двух симметричных схем, скомпонованных из пары усилителей с общим эмиттером (триггер и мультивибратор). Среди материалов, приведенных в открытых источниках, аналогичных уравнений для транзисторных схем автором не найдено (исследовались лишь уравнения для ламповых приборов, имеющие другую форму – см., например, [4]).

2. МЕТОДЫ И РЕЗУЛЬТАТЫ

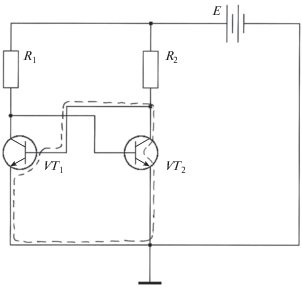
Рассмотрим симметричный триггер, содержащий два биполярных транзистора (рис. 1). Пусть величины сопротивлений одинаковы: R₁= R₂= R. Коллекторные цепи обоих транзисторов аналогичны коллекторной цепи усилителя с общим эмиттером (без стабилизации). Будем считать, что присутствие первого усилителя с высоким входным сопротивлением не влияет на режим работы второго усилителя (и наоборот), поэтому расчеты “выходных” функций, произведенные для усилителя с общим эмиттером (в работах [1, 2]), остаются верными. Если пренебречь током базы, “усилительную” функцию можно выразить через “токовую” функцию для коллекторного тока i_c(U_be), определяемую формулой (1):

Если применить закон Кирхгофа к контуру, выделенному на рис. 1 пунктиром (см. также работу [5], в которой рассматривалась статическая задача для триггера), можно получить соотношение

Рассмотрев аналогично другую часть симметричной схемы, мы придем к выводу, что

По своей форме это есть трансцендентное или алгебраическое (все зависит от вида функции F) уравнение, решив которое, мы найдем несколько значений для напряжения база-эмиттер. Ясно, что уравнение (5) может быть применено не только к триггеру на биполярных транзисторах, но и к другим физическим системам с похожим поведением, и выражение для усилительной функции, имеющей характер нисходящего перепада между двумя стационарными состояниями, может быть аппроксимировано посредством выражений, отличающихся от (4). Для удобства дальнейшей графической иллюстрации решения данного уравнения рассмотрим пример, когда усилительная функция аппроксимируется не формулой (4), а следующим выражением:

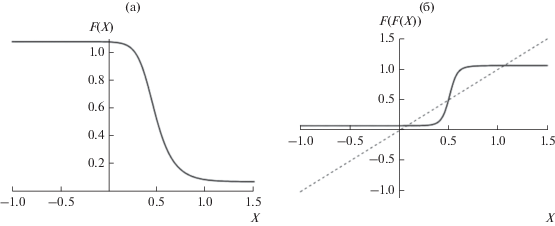
Графики для функции F(x) и для результата ее повторного действия F(F(x)) приведены на рис. 2а, 2б (см. [5], в нашем случае E = 0.02, G = 10, B = = 0.004). Из рис. 2б видно, что имеются три решения уравнения (5). Двум крайним решениям соответствуют устойчивые равновесные значения напряжения триггера. Среднее решение – неустойчивое, система при малейшем отклонении от этой точки “сваливается” в одно из крайних состояний равновесия.

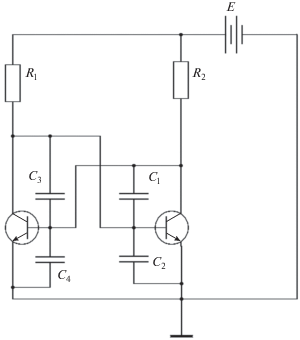
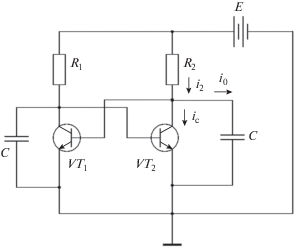
Чтобы обосновать утверждения об устойчивости состояний равновесия, рассмотрим динамическую задачу. Для этого необходимо учесть емкости p–n-переходов в биполярных транзисторах. Расчетная схема триггера должна принять вид, изображенный на рис. 3. Если пренебречь токами базы, схему с емкостями можно упростить (рис. 4), заменив пару емкостей C₁ и C₂ на емкость C = C₁C₂/(C₁+ C₂) (аналогично – для C₃,C₄).

Для транзистора, изображенного на рис. 4 справа, выполняется соотношение, следующее из закона Кирхгофа:

(мы помним, что величина сопротивления резистора R₂ равна R).

Так как (в пренебрежении током базы первого транзистора)

то можно записать

Ток, проходящий через конденсатор, зависит от производной напряжения коллектор–эмиттер:

Поэтому получаем

Выражение в скобках является введенной нами выше усилительной функцией F(U_be2) (напомню: мы считаем, что подключение “симметричного” усилителя с большим входным сопротивлением оставляет в силе формулы для коллекторного тока исходного усилителя). Вследствие этого последнее уравнение можно записать в виде

Из закона Кирхгофа следует, что U_be1= U_ce2. Аналогично U_be2= U_ce1. Поэтому имеем

Если рассмотреть первый транзистор (слева на рис. 4), мы получим такое же выражение:

Итак, если обозначить напряжения коллектор-эмиттер как y₁ и y₂, мы имеем для них следующую симметричную систему дифференциальных уравнений:

Стационарные состояния данной системы определяются уже рассмотренным выше уравнением (5):

Остановимся на значениях емкости C, входящей в уравнения (8). Как известно (см. [6] и [7]), емкости p–n-переходов зависят от напряжения, причем полная емкость перехода равна сумме двух емкостей: барьерной и диффузионной. При обратных и небольших прямых напряжениях доминирует барьерная емкость, а при достаточно больших прямых напряжениях – диффузионная емкость (пропорциональная току через переход, который растет при увеличении прямого напряжения). В данной работе мы имеем дело с составной емкостью C, состоящей из последовательно соединенных емкостей коллекторного и эмиттерного перехода. Предположим, что эта емкость в исследуемом нами триггере является функцией напряжения коллектор–эмиттер и что нам известна соответствующая вольт-фарадная характеристика. Следует ожидать, что при малых значениях U_ce, когда оба транзисторных перехода открыты, емкость будет иметь диффузионный характер. При больших же значениях U_ce, когда оба перехода закрыты, емкость будет барьерной (и ее величина будет существенно меньшей). Обозначим явно зависимость емкости от напряжения в полученных уравнениях:

Если емкость C не принимает бесконечно больших значений, то стационарные состояния такой усложненной системы будут определяться тем же уравнением (5). Пусть y₁₀ и y₂₀ – одно из стационарных состояний. Для определения его типа используем общую теорию динамических систем, изложенную, например, в [4]. Обозначим правую часть первого уравнения (9) как P(y₁, y₂), а правую часть второго уравнения – как Q(y₁, y₂). Из общей теории следует, что типы состояний равновесия определяются корнями λ следующего характеристического уравнения:

Здесь

В нашем случае

Характеристическое уравнение имеет следующий вид:

Его решения:

Так как функция F имеет “квазиступенчатый” вид (вид перепада от величины, близкой к напряжению питания, к почти нулевой величине), в области крайних стационарных точек производные, стоящие под знаком квадратного корня, близки к нулю (если края функции F достаточно плоские). В центральной же стационарной точке эти производные, напротив, велики (если перепад достаточно крутой). Поэтому, если функция F достаточно близка к идеальной “ступеньке”, двум крайним стационарным состояниям соответствуют действительные отрицательные значения λ, а центральному состоянию – действительные значения, одно из которых отрицательно, а другое – положительно. Из общей теории следует, что крайние стационарные состояния будут устойчивыми узлами, а центральное – седлом (неустойчивым состоянием равновесия).

При численном решении дифференциальных уравнений (9) для начальных оценок разумно использовать одно из постоянных значений емкости в одной из стационарных точек или некоторое среднее постоянное значение. При уточнении расчетов нужно использовать более сложные модели.

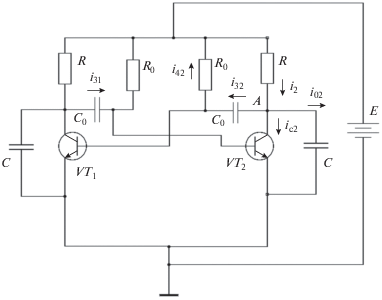
Далее рассмотрим схему симметричного мультивибратора (рис. 5). Такое устройство можно рассматривать в качестве “наследника” симметричного триггера – схема рис. 4 дополнена парой конденсаторов и парой сопротивлений с номиналами C₀ и R₀. Конденсаторы включены в разрыв проводников, соединяющих коллекторы и базы транзисторов. Дополнительные сопротивления соединяют противоположные от коллекторов выводы этих конденсаторов с полюсом питания. Так же как и в триггере, мы учитываем присутствие емкостей p–n-переходов транзистора (пренебрегая токами базы).

Важную роль в этой задаче будет играть напряжение на дополнительных конденсаторах C₀. Уточним, что под данным напряжением мы будем понимать разность между потенциалом того вывода конденсатора, который ближе к краю схемы (к правому краю для правого конденсатора или к левому краю для левого), и потенциалом другого вывода (того, который ближе к центру). В соответствии с этим на рисунке выбрано направление токов i₃₂ и i₃₁.

Так же как и в случае триггера, мы будем составлять уравнения для правого транзистора (обозначенного индексом “2”). Рассмотрим контур, проходящий через источник питания E, резистор R в правой части схемы, коллектор второго транзистора и его эмиттер (контур направим против часовой стрелки). Тогда имеем

В узле A

С учетом этого предыдущее соотношение (10) записывается в виде

Теперь рассмотрим контур, проходящий через базу и эмиттер первого транзистора, источник питания E и правый резистор R₀ (контур также направим против часовой стрелки). Из законов Кирхгофа следует:

Так как в пренебрежении током базы (для первого транзистора) i₄₂= i₃₂, то соотношение (11) можно записать так:

Первые два слагаемых в правой части соотношения (12) представляют собой уже рассмотренную ранее усилительную функцию (замечания, касающиеся высокого входного сопротивления, здесь сохраняют свою силу):

Используем контур, проходящий через правый конденсатор C₀, через коллектор и эмиттер второго транзистора и через базу и эмиттер первого (тоже против часовой стрелки), чтобы выразить U_be1 в выражении (12) через “правые” параметры:

где V₂ – напряжение на правом конденсаторе C₀.

Далее рассмотрим контур, проходящий по часовой стрелке через левый конденсатор C₀, через коллектор и эмиттер первого транзистора и через базу и эмиттер второго, чтобы выразить U_be2 через более удобные для нас величины (для этого можно воспользоваться и симметрией схемы):

В итоге получим уравнение

Используем контур, проходящий через источник питания, правый резистор R₀, правый конденсатор C₀ и через коллектор и эмиттер правого транзистора (против часовой стрелки), чтоб записать еще одно уравнение

Аналогичные уравнения можно записать и для другой половины схемы (они будут выглядеть точно так же, с точностью до замены индекса “2” на “1”). Приведем все четыре уравнения для величин V₁, V₂, U_ce1, U_ce2:

В этих уравнениях, как и в уравнениях для триггера, емкость C зависит от напряжения (в первом уравнении системы (13) C зависит от U_ce1, в третьем – от U_ce2). Для начальных оценок можно использовать одно из постоянных значений емкости в одной из стационарных точек задачи о триггере, в который мультивибратор превратится, если конденсаторы C₀ замкнуть накоротко, а резисторы R₀ убрать, или же, как и в задаче о триггере, использовать некоторое среднее постоянное значение емкости.

Рассматриваемая система (13) является системой с двумя степенями свободы (и с четырехмерным фазовым пространством). Отметим, что схожая задача для лампового мультивибратора рассматривалась еще в [4] (но там были не только другие активные элементы, но и другая конфигурация соединительных проводников). В процессе решения авторы [4] перешли к системе с одной степенью свободы (с двумя неизвестными функциями). Здесь мы останемся в рамках модели с двумя степенями свободы и проведем по возможности более простое рассмотрение движений исследуемой нами системы без сокращения числа переменных.

Если R₀$ \gg $ R, то уравнения записываются в виде

С целью упрощения вида уравнений рассмотрим возможный предельный случай. Если внутренняя емкость транзистора C (в [4] ее аналогом является внутренняя паразитная емкость лампы) стремится к нулю, то первое уравнение становится не дифференциальным, а конечным трансцендентным (или алгебраическим – в зависимости от вида функции F):

Функция f₁ задает фазовую поверхность “вырожденной” системы (как и аналогичная ей функция f₂). Именно по этим фазовым поверхностям проходят “медленные” движения системы. При этом уравнения “быстрых” движений можно записать так:

Если рассматривать точки фазового пространства с конечными величинами функций f₁ и f₂, то при стремлении C к нулю производные величин U_ce1 и U_ce2 должны стремиться к бесконечности. Ясно, что линии движения при этом почти параллельны плоскости V₁V₂ фазового пространства. Это означает, что V₁ и V₂ (напряжения на конденсаторах) при таких движениях (скачках) не меняются.

Исследуем “медленные” движения. Выразим U_ce1 из уравнения (15) и подставим во второе уравнение (14):

Вспомним, что усилительная функция F для усилителя с общим эмиттером имеет вид резкого перепада от напряжения питания E к почти нулевому значению (в несколько десятых долей вольта). Допустим, что медленные движения нашей системы происходят на почти постоянных “хвостах” усилительной функции (а “быстрые” – при перепаде ее значения). Пусть для определенности F в формуле (16) равно E. Тогда

Решение этого уравнения:

Здесь A – произвольная константа. Данное решение соответствует разрядке конденсатора.

Если F = 0, то вместо (17) мы будем иметь уравнение

Его решение

Конденсатор при этом находится в процессе зарядки.

Дифференциальные уравнения (13) имеют решение в виде незатухающих колебаний не для всех значений параметров. В заключение работы мы приведем численное решение, полученное средствами пакета Wolfram Mathematica 9.0 (рис. 6). Усилительная функция F при этом определяется формулой (6), параметры задачи следующие: E₀= 0.02, G = 5, B = 0.0004, R₀= 1.1, C₀= = 100, R = 0.01, C = 0.0033, E = 1 + E₀.

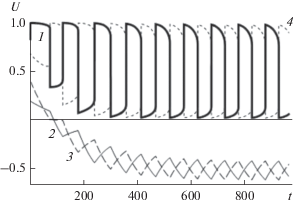
Из графиков видно, что при данных значениях параметров предположение о постоянстве U_ce1(t) (и U_ce2(t)) в пределах полупериода колебаний (фактически сделанное ранее) является чересчур грубым приближением. Но движения все равно подразделяются на “быстрые” и “медленные”.

Численное решение уравнений с усилительной функцией, которая записывается через формулу (1), имеет похожий вид.

ВЫВОДЫ

В работе получены дифференциальные уравнения для симметричного транзисторного триггера и мультивибратора. При этом использовалось полученное ранее автором выражение для токовой характеристики транзисторного усилителя с общим эмиттером (хотя можно использовать и выражения другого вида – в работе приведен пример подобной аппроксимации). Уравнения триггера в общем виде могут быть записаны следующим образом (для неизвестных функций y₁, y₂):

Здесь g – числовой параметр (равный 1/RC) или же функция, зависящая от y₁ в первом уравнении и от y₂ во втором уравнении, а F(y) – “квазиступенчатая” функция, график которой выглядит как достаточно резкий перепад от большего значения к меньшему.

Уравнения мультивибратора (для неизвестных функций y₁, y₂, z₁, z₂) имеют следующий вид:

Здесь g₀= 1/R₀C₀, R, R₀ и E – числовые параметры.

Для дифференциальных уравнений триггера проведено исследование характера состояний равновесия. Для дифференциальных уравнений мультивибратора проведено исследование “медленных” и “быстрых” движений. Приведен пример численного решения.