Радиотехника и электроника, 2022, T. 67, № 1, стр. 68-77

ВВЕДЕНИЕ

В практике современной хозяйственной и военной деятельности все большее применение находят беспилотные летательные аппараты (БПЛА), использование которых позволяет повысить экономичность решения целого ряда транспортных и других задач [1–3]. При этом все больше находит групповое применение БПЛА, позволяющее решать целый ряд сложных технических задач. К таким задачам прежде всего относятся групповые действия как средств нападения [4], так и защиты самого различного назначения [5, 6].

Необходимо отметить, что в этой области существует обширный класс задач группового управления, в рамках которого требуется длительный согласованный полет группы по маршруту с заданной пространственной топологией участников. К таким задачам относятся: мобильный мониторинг больших объемов воздушного пространства и земной поверхности [7], ликвидация последствий различного рода катастроф и т.д.

Весьма специфическим вариантом группового использования БПЛА является формирование на их основе нестационарных антенных фазированных решеток [8], обладающих по сравнению с традиционными стационарными антеннами целым рядом преимуществ, связанных прежде всего с возможностью управления их параметрами за счет изменения числа и взаимного пространственного расположения приемо-передающих модулей, размещенных на отдельных летательных аппаратах.

Следует отметить, что решение задачи синтеза согласованного управления объектами группы всегда сложнее, чем управление одиночным объектом [9]. Общие подходы к решению задачи группового управления рассмотрены в [9, 10]. Возрастание сложности задачи обусловлено несколькими причинами [11]:

– сложностью описания групповых действий с формулировкой коллективного интереса, который должен реализовать каждый из участников группы;

– возрастанием сложности формирования сигнала управления, одновременно обеспечивающего и выполнение целевого назначения, и обеспечение требуемого положения участников в общей топологии группы с предотвращением их столкновения [12–16];

– значительным возрастанием размерности решаемой задачи одновременного управления всеми участниками группы;

– увеличением сложности информационного обеспечения процедуры формирования сигналов управления.

В зависимости от способов учета этих сложностей на практике применяют различные подходы, основанные на использовании алгоритмов оптимизации роя частиц [17, 18], генетических алгоритмов [19], теории игр [20] и иерархического управления [21]. Каждый из этих подходов имеет свои достоинства. Вместе с тем необходимо отметить, что в общем случае они ориентированы на конкретный способ управления (централизованный, с лидером, сетевой) [10], достаточно сложны в реализации, не обеспечивают стабильного управления, требуют высокой вычислительной производительности и не дают возможности проведения анализа связи сигналов управления с параметрами БПЛА и условиями их применения.

В связи с этим весьма востребованным является синтез группового управления, в котором будут снижены перечисленные недостатки.

Цель статьи – разработать упрощенные варианты синтеза универсального группового управления с длительным сохранением заданной топологии участников со сниженными требованиями к вычислительной производительности и оценить возможность их использования в алгоритмах формирования топологии приемо-передающих модулей нестационарных антенн на базе БПЛА. Снижение размерности решаемой задачи можно обеспечить за счет ее декомпозиции, основанной на синтезе управления для отдельного объекта с учетом пространственного положения других участников.

1. ПОСТАНОВКА ЗАДАЧИ

Решение задачи синтеза управления отдельными объектами с учетом состояния всех участников будет выполняться на основе математического аппарата статистической теории оптимального управления в модифицированном варианте решения задачи Летова–Калмана, позволяющем снизить требования к вычислительной производительности системы управления.

При этом будем полагать, что выполняются следующие допущения:

– каждый объект самостоятельно формирует свое управление для текущей ситуации на основе информации о цели, стоящей перед группой, о своем состоянии и состоянии других объектов;

– в оптимизируемом функционале должны учитываться как требования обеспечения маршрута группы, так и требования обеспечения заданной топологии участников;

– информационный обмен между участниками осуществляется в составе локальной сети по принципу “каждый с каждым” [10];

– в качестве оптимального для группы понимается такое управление каждым объектом в текущей ситуации, которое вносит максимально возможный вклад в достижение общей цели, т.е. обеспечивает максимальное приращение общего функционала при переходе группы из текущего состояния в конечное [22–24].

При таком подходе функционал качества функционирования всей группы ${{I}_{\Sigma }}$ может быть представлен в виде суммы отдельных функционалов ${{I}_{i}}$, характеризующих оптимальность управления каждым участником группы:

где $N$ – число участников группы. Отсюда следует, что минимизация каждого ${{I}_{i}}$ приводит к уменьшению ${{I}_{\Sigma }}$. Правомочность такого подхода далее будет продемонстрирована на примере конкретных функционалов качества.

В математическом плане задача формулируется следующим образом. Пусть поведение группы, состоящей из $N$ однотипных объектов, динамика каждого из которых определяется линейной стохастической моделью

где – составной вектор, в котором $n$-мерный вектор

определяет требуемые координаты состояния (программу движения группы), а $n$-мерный вектор

отображает текущее (управляемое) состояние объекта, контролируется $m$-мерным ($m \leqslant 2n$) измерением

Здесь и далее ^T обозначает операцию транспонирования.

Необходимо найти $r$-мерный ($r \leqslant n$) вектор ${{{\mathbf{u}}}_{i}}$ сигналов управления одним $i$‑м объектом, оптимальный по минимуму функционала

В (1)–(6) ${{{\mathbf{F}}}_{{{\text{т}}i}}}$ и ${{{\mathbf{F}}}_{{{\text{у}}i}}}$ – в общем случае нестационарные динамические матрицы, учитывающие внутренние связи процессов (3) и (4), при этом ${{{\mathbf{F}}}_{{{\text{т}}i}}}$, как правило, определяет программу движения группы; ${{{\mathbf{B}}}_{{{\text{y}}i}}}$ – матрица эффективности сигналов управления ${{{\mathbf{u}}}_{i}}$; ${{{\mathbf{Н}}}_{i}}$ – матрица связи ${{{\mathbf{x}}}_{i}}$ и ${{{\mathbf{z}}}_{i}}$; ${{{\mathbf{\xi }}}_{{{\text{y}}i}}}$ и ${{{\mathbf{\xi }}}_{{{\text{и}}i}}}$ – независимые центрированные гауссовские шумы состояния и измерений с известными матрицами спектральных плотностей; $\Delta {{{\mathbf{x}}}_{{ij}}} = {{{\mathbf{x}}}_{i}} - {{{\mathbf{x}}}_{j}}$ – вектор разности координат $i$-го и $j$-го объектов; ${{{\mathbf{K}}}_{i}}$ – положительно определенная матрица размером $r \times r$ штрафов за величину сигналов управления; ${{M}_{{\text{y}}}}$ – знак математического ожидания при условии наличия измерений (5);

где ${{{\mathbf{O}}}_{1}}$, ${{{\mathbf{O}}}_{2}}$, ${{{\mathbf{O}}}_{3}}$, ${{{\mathbf{O}}}_{4}}$ – нулевые матрицы соответствующих размеров, L и Q – неотрицательно определенные матрицы размером $n \times n$-штрафов за точность приближения ${{{\mathbf{x}}}_{{{\text{у}}i}}}$ к ${{{\mathbf{x}}}_{{{\text{т}}i}}}$ в текущий момент времени $t$ и конечный момент времени ${{t}_{{\text{к}}}}$, ${\mathbf{M}}$ и ${\mathbf{G}}$ – неотрицательно определенные матрицы размером $n \times n$-штрафов за нарушение требуемого соотношения между ${{{\mathbf{x}}}_{i}}$ и ${{{\mathbf{x}}}_{j}}$ в текущий и конечный моменты времени. При формировании (7) было учтено, что объекты управления однотипные, поэтому матрицы ${\mathbf{M}}$, ${\mathbf{Q}}$ и ${\mathbf{G}}$ одинаковы для всех объектов.

Спецификой функционала (6) является то, что в рамках решения общей задачи он учитывает и требования к формированию желаемой траектории, определяемые первым и четвертым слагаемыми, и требования обеспечения заданной топологии группы, определяемые вторым и пятым слагаемыми.

2. РЕШЕНИЕ ЗАДАЧИ

Поскольку исходные модели (1)–(5) линейные, функционал качества – квадратичный, а возмущения – гауссовские, то в соответствии с теоремой разделения [25] задачи синтеза управления и фильтрации могут решаться раздельно. При этом синтез управления может выполняться в детерминированной постановке (${{{\mathbf{\xi }}}_{{xi}}} = 0$) в предположении точного знания состояния при условии, что в полученном алгоритме координаты состояния ${{{\mathbf{x}}}_{i}}$ и ${{{\mathbf{x}}}_{j}}$ будут заменены их оптимальными оценками ${{{\mathbf{\hat {x}}}}_{i}}$ и ${{{\mathbf{\hat {x}}}}_{j}}$.

В условиях линейно-квадратично-гауссовской (ЛКГ) задачи для отыскания управления каждым объектом может быть использован детерминированный вариант уравнения Беллмана [26]:

при $j \ne i$. Здесь ${{S}_{i}}$ – функция Беллмана; ${{\Phi }_{{\text{т}}}}\left[ \cdot \right]$ – подынтегральная часть используемого функционала (6); ${{{\mathbf{\dot {x}}}}_{i}}$ – задается моделью (1) при ${{{\mathbf{\xi }}}_{{xi}}} = 0$, ${{\Phi }_{{\text{к}}}}\left[ \cdot \right]$ – терминальная часть функционала, определяющая граничные условия для ${{S}_{i}}$, ${\mathbf{U}}$ – евклидово пространство возможных значений ${{{\mathbf{u}}}_{i}}$.

Используя (1) и (6) в (8), (9), получим

где все слагаемые, не зависящие от ${{{\mathbf{u}}}_{i}}$, вынесены за знак операции минимума.

Управление ${{{\mathbf{u}}}_{i}}$ для каждого объекта ($i = \overline {1,N} $), минимизирующее (6), можно найти, приравняв в (10) нулю результат дифференцирования по ${\mathbf{u}}_{i}^{T}$ слагаемых в фигурных скобках:

Подставив (12) в (10), получим

Решение этого уравнения в частных производных будем искать в классе квадратичных форм:

Используя (15) в (12), будем иметь

Для вычисления симметричных матриц ${{{\mathbf{R}}}_{{i1}}}$ и ${{{\mathbf{P}}}_{{j1}}}$, используемых в (17), подставим (15) и (16) в (13). Тогда

Поскольку в общем случае матрица ${\mathbf{F}}$ не симметричная, то для обеспечения симметричности матрицы ${\mathbf{R}}$ необходимо применять специальные меры по ее симметрированию [26]. С учетом этого получим

Граничные условия для (18) и (19) определяются по результатам сравнения (11) и (14) при $t = {{t}_{{\text{к}}}}$:

Поскольку рассматривалась ЛКГ-задача, то на основании принципа статистической эквивалентности [25] можно утверждать, что статистический закон управления будет адекватен детерминированному при условии замены в нем координат состояния ${{{\mathbf{x}}}_{i}}$, ${{{\mathbf{x}}}_{j}}$ и $\Delta {{{\mathbf{x}}}_{{ij}}}$ их оптимальными оценками ${{{\mathbf{\hat {x}}}}_{i}}$, ${{{\mathbf{\hat {x}}}}_{j}}$ и $\Delta {{{\mathbf{\hat {x}}}}_{{ij}}}$, т.е.

Анализ (18)–(21) позволяет сделать следующие заключения.

В общем случае, в систему коллективного управления с сетевым информационным обменом должны входить: оптимальные регуляторы, вычисляющие на каждом объекте сигналы управления ${{{\mathbf{u}}}_{i}}$, оптимальные фильтры, формирующие оценки ${{{\mathbf{\hat {x}}}}_{i}}$ и $\Delta {{{\mathbf{\hat {x}}}}_{{ij}}}$,$j = \overline {1,N} $,$j \ne i$, и система обмена оценками координат состояния каждого объекта.

Сигнал управления, формируемый на каждом объекте, зависит от его параметров ${{{\mathbf{F}}}_{{{\text{y}}i}}}$ и ${{{\mathbf{B}}}_{{{\text{y}}i}}}$, требуемого закона управления ${{{\mathbf{F}}}_{{{\text{т}}i}}}$, состояния самого объекта ${{{\mathbf{\hat {x}}}}_{i}}$ и состояния других объектов, определяющих топологию $\Delta {\mathbf{\hat {x}}}_{{ij}}^{{}}$.

Коэффициенты матриц ${{{\mathbf{R}}}_{{i1}}}$ и ${{{\mathbf{P}}}_{{j1}}}$, вычисляемые по правилам (18) и (19), совокупным образом учитывают в (21) параметры объекта ${{{\mathbf{F}}}_{i}}$ и ${{{\mathbf{B}}}_{i}}$, требования к точности ${{{\mathbf{L}}}_{{i1}}}$ и экономичности управления ${{{\mathbf{K}}}_{i}}$, а также степень соответствия требуемым состояниям $i$-го и j-го объектов, определяемую коэффициентами матрицы ${{{\mathbf{M}}}_{{j1}}}$.

Использование (21) позволяет обеспечить не только движение каждого объекта по требуемой траектории за счет учета ${{{\mathbf{x}}}_{i}}$, но и предотвратить столкновения между ними в процессе совместного движения за счет учета $\Delta {{{\mathbf{x}}}_{{ij}}}$.

Спецификой функционирования по правилу (18)–(21) является необходимость решения так называемой двухточечной краевой задачи [26]. Суть этой задачи состоит в том, что уравнения (18), (19) решаются в обратном времени от известного момента времени ${{t}_{{\text{к}}}}$ окончания управления при граничных условиях (20) до текущего момента времени $t$, в то время как управление системой (1), вычисление сигнала управления и формирование оптимальных оценок ${{{\mathbf{\hat {x}}}}_{i}}$ и $\Delta {{{\mathbf{\hat {x}}}}_{{ij}}}$ выполняются в прямом времени от $t$ к ${{t}_{{\text{к}}}}$.

Кроме того, следует отметить, что необходимость решения уравнений (18) и (19) предопределяет проявление “проклятия размерности” [26], обусловленное тем, что процедура формирования управления (21), определяемая размерностью $8{{n}^{2}}$ их решения, намного превышает сложность управляемой системы (1) размерностью $2n$.

Эта особенность затрудняет применение алгоритма (18)–(21) для систем высокой размерности, делает ее практически невозможной при оптимизации общего управления для всей группы БПЛА.

Например, для синтеза группового управления десятью БПЛА, каждый их которых определяется стандартной моделью 6-го порядка (три угловых и три линейных перемещения) для управляемых координат (4) и 6-го порядка для требуемых (3), необходимо в процессе вычисления (18), (19) решить ${{N}_{{10}}} = 2{{(12 \times 10)}^{2}} = 28\,800$ уравнений, что делает этот способ неприемлемым для использования.

“Проклятие размерности” предопределяет необходимость декомпозиции задачи синтеза общего группового управления на задачи управления отдельными БЛА. Кроме того, при решении ряда групповых задач достаточно сложно определить время окончания работы ${{t}_{{\text{к}}}}$.

3. ЛОКАЛЬНО-ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

Процедуру коллективного управления можно существенно упростить, если использовать оптимизацию по минимуму локального функционала качества [1], при которой в (6) ${{{\mathbf{L}}}_{{i1}}} = 0$, ${{{\mathbf{M}}}_{{j1}}} = 0$, а каждый момент времени рассматривается как момент возможного окончания управления, т.е. ${{t}_{{\text{к}}}} = t$. Тогда из (6) и (20) следует

Используя (2), (7), (23) в (21), получаем

где $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{т}}ij}}} = {{{\mathbf{\hat {x}}}}_{{{\text{т}}i}}} - {{{\mathbf{\hat {x}}}}_{{{\text{т}}j}}}$, $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{у}}ij}}} = {{{\mathbf{\hat {x}}}}_{{{\text{у}}i}}} - {{{\mathbf{\hat {x}}}}_{{{\text{у}}j}}}$, $j = \overline {1,N} $, $j \ne i$.

Несомненным преимуществом (24) является возможность формирования сигнала группового управления без решения высокоразмерной двухточечной краевой задачи с использованием уравнений (18)–(20). При этом не требуется знания времени ${{t}_{{\text{к}}}}$ окончания управления.

Кроме того, полученная система коллективного управления характеризуется наличием отрицательных обратных связей по всем координатам в каждом объекте. Это свидетельствует о ее высокой устойчивости и низкой чувствительности к точности выдерживания параметров. При этом сигнал управления в ней зависит от ошибок управления ${{{\mathbf{\hat {x}}}}_{{{\text{т}}i}}} - {{{\mathbf{\hat {x}}}}_{{{\text{у}}i}}}$ и $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{т}}ij}}} - \Delta {{{\mathbf{\hat {x}}}}_{{{\text{у}}ij}}}$. Эта особенность позволяет в два раза снизить требования к пропускной способности линий передач, поскольку достаточно обмениваться только ошибками $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{т}}ij}}}$ и $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{у}}ij}}}$.

Более того, из (24) отчетливо прослеживается его возможность обеспечить не только движение каждого объекта по требуемой траектории за счет учета ${{{\mathbf{\hat {x}}}}_{{{\text{т}}i}}} - {{{\mathbf{\hat {x}}}}_{{{\text{у}}i}}}$, но и предотвращать их взаимные столкновения за счет учета $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{т}}ij}}} - \Delta {{{\mathbf{\hat {x}}}}_{{{\text{у}}ij}}}$. Эта особенность дает возможность еще более упростить процедуру группового управления и его информационного обеспечения за счет перехода к централизованному управлению или управлению “с лидером” [10], которые могут быть получены как частные случаи управления (24).

Для реализации централизованного управления достаточно для каждого БПЛА использовать первое слагаемое, для которого ${{{\mathbf{x}}}_{{{\text{т}}i}}}$ задается центром управления.

При управлении с лидером, формирующим траекторию полета, для него достаточно формировать управление, учитывающее в (24) только первое слагаемое, в то время как взаимное расположение других элементов группы определяется использованием только второго слагаемого.

При использовании группы БПЛА в качестве элементов активной фазированной антенной решетки (АФАР) первое слагаемое обеспечивает лишь вывод носителей приемо-передающих модулей в требуемую точку пространства. После этого работают только вторые слагаемые.

Таким образом, предложенный вариант управления позволяет реализовать различные способы совместного функционирования объектов, обеспечивающие движение по заданным траекториям и предотвращение столкновений между ними при минимальных требованиях к вычислительной производительности цифровых вычислительных машин (ЦВМ) беспилотных летательных аппаратов, и получить более простые варианты группового управления.

Приведем результаты исследования эффективности рассмотренного способа синтеза группового управления.

Пример. Проверку работоспособности предложенного способа оптимизации группового управления выполняли на примере синтеза совместного управления группой из трех БПЛА в процессе их совместного полета с заданными интервалами [11] как по прямолинейным, так и по сложным, криволинейным траекториям при условии, что управление для них формируется как по закону (24), так и по закону

в котором не учитывается влияние других участников группы.

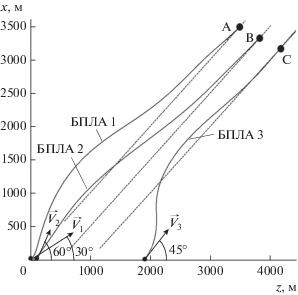
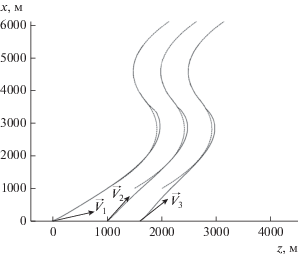
Начальные положения БПЛА принимались следующие: для первого – $z = 0\,\,{\text{м}}$, $x = 0\,\,{\text{м}}$, для второго – $z = 50\,\,{\text{м}}$, $x = 0\,\,{\text{м}}$ и для третьего – $z = 1900\,\,{\text{м}}$, $x = 0\,\,{\text{м}}$. Требуемые траектории полета представляют три параллельные линии под углом ${{\psi }_{{{\text{т}}i}}} = 45^\circ $ к оси $oz$ прямоугольной системы координат, расположенных на удалении друг от друга на $550\,\,{\text{м}}$, по которым БПЛА перемещаются со скоростями ${{V}_{i}} = 42\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Начальные курсы БПЛА: для первого – ${{\psi }_{1}} = 30^\circ $, для второго ${{\psi }_{2}} = 60^\circ $ и третьего – ${{\psi }_{3}} = 45^\circ $ (рис. 1).

Необходимо проверить способность выхода группы в требуемые точки пространства $A$, $B$, $С$ с требуемым курсом, выдерживая требуемые интервалы в горизонтальной плоскости, независимо от начальных курсов каждого БПЛА и первоначальных расстояний между ними.

В качестве показателей эффективности были использованы: линейные ошибки вывода БПЛА в требуемые точки, ошибки управления по угловым координатам, а также время регулирования и реализуемые перегрузки. Следует отметить, что расчет управления БПЛА производился в полярной системе координат, а построение траекторий – в прямоугольной.

Для расчета сигналов управления необходимо иметь модели состояния (3), (4), в качестве которых целесообразно использовать кинематические уравнения [26]:

при условии, что где ${{\varphi }_{{{\text{т}}i}}}$ и ${{\varphi }_{{{\text{г}}i}}}$ – требуемый и текущий пеленги желаемых точек $A$, $B$, $С$ выхода БЛА в горизонтальной плоскости; ${{\omega }_{{{\text{т}}i}}}$ и ${{\omega }_{{{\text{г}}i}}}$ – требуемая и текущая угловые скорости линий визирования этих точек с БПЛА (см. рис. 1), ${{j}_{{{\text{г}}i}}}$ – мгновенное поперечное ускорение (сигнал управления), ${{D}_{i}}$ – дальность до требуемой точки, а ${{\dot {D}}_{i}}$ – скорость ее изменения.

Соотношениям (3), (4), (22) и (26), (27) соответствуют векторно-матричные представления:

Используя (28) в (24), получим законы управления для каждого БПЛА:

Раскрыв это соотношение, получим

Анализ (29) позволяет сделать следующие выводы.

Сигнал управления каждым БПЛА содержит три слагаемых, среди которых первое слагаемое в квадратных скобках определяет маршрутную составляющую, обеспечивающую полет по маршруту, в то время как второе и третье слагаемые отвечают за их взаимное пространственное положение. Соотношение между маршрутной и топологической составляющими управления определяется выбором соответствующих коэффициентов ${{{{q}_{{\varphi i}}}} \mathord{\left/ {\vphantom {{{{q}_{{\varphi i}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$, ${{{{q}_{{\omega i}}}} \mathord{\left/ {\vphantom {{{{q}_{{\omega i}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$ и ${{{{g}_{{\varphi j}}}} \mathord{\left/ {\vphantom {{{{g}_{{\varphi j}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$, ${{{{g}_{{\omega j}}}} \mathord{\left/ {\vphantom {{{{g}_{{\omega j}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$.

Рациональные значения соотношений ${{{{q}_{{\varphi i}}}} \mathord{\left/ {\vphantom {{{{q}_{{\varphi i}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$, ${{{{q}_{{\omega i}}}} \mathord{\left/ {\vphantom {{{{q}_{{\omega i}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$ и ${{{{g}_{{\varphi j}}}} \mathord{\left/ {\vphantom {{{{g}_{{\varphi j}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$, ${{{{g}_{{\omega j}}}} \mathord{\left/ {\vphantom {{{{g}_{{\omega j}}}} {{{k}_{i}}}}} \right. \kern-0em} {{{k}_{i}}}}$ коэффициентов матриц ${\mathbf{Q}}$, ${\mathbf{G}}$ и ${{{\mathbf{K}}}_{i}}$, отвечающие за точность и экономичность управления, выбираются по известным правилам [27] с учетом ограничений на величину сигнала управления, время переходных процессов и допустимую ошибку управления в установившемся режиме. Кроме того, для их вычисления может быть использован и более простой так называемый принцип равнопрочности [28], суть которого состоит в предположении, что произведения всех весовых коэффициентов ошибок на квадраты (дисперсии) этих ошибок для всех координат состояния полагаются одинаковыми. Однако такой подход является приближенным и требует уточнения за счет вариации коэффициентов ошибок по результатам моделирования и вычисления конкретных значений функционалов качества.

Ошибки формирования требуемой топологии группы, определяемые взаимным расположением i-го и j-го БПЛА, совпадают друг с другом, отличаясь только знаком. Эта особенность дает возможность еще более упростить информационное обеспечение группы за счет обмена этими ошибками.

Исследование эффективности полученного алгоритма будет проводиться в детерминированной постановке.

Сначала исследуем случай управления по закону (25), в котором не учитываются изменения состояний других объектов. В соотношениях (29) им соответствуют слагаемые в квадратных скобках. Следует отметить, что такой закон может быть применен для централизованного управления и управления ведущим БЛА при использовании управления с лидером.

Траектории полета для этого управления представлены на рис. 1. Из рисунка видно, что все три БПЛА могут выйти на требуемый курс, однако траектории полета первого и второго БПЛА пересекаются на начальном участке, что свидетельствует об их столкновении.

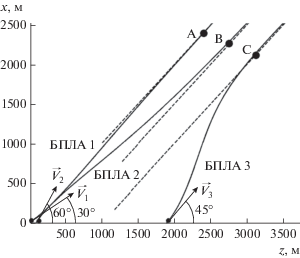
Для сравнения на рис. 2 представлены траектории полета трех БПЛА при тех же условиях, полученные с использованием коллективного управления (29). Из рисунка видно, что время регулирования, характеризующее время выхода группы на требуемые курсы, несколько увеличилось, однако полет обеспечивается без пересечения траекторий, что исключает их столкновение. Более того, группа стремится сохранять требуемые расстояния между БПЛА в течение всего полета.

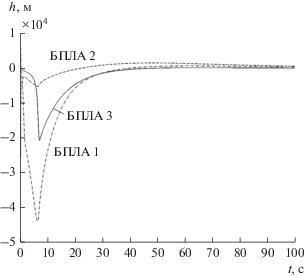
Для оценивания линейных ошибок управления воспользуемся соотношением, определяющим линейный промах БПЛА в горизонтальной плоскости [26]:

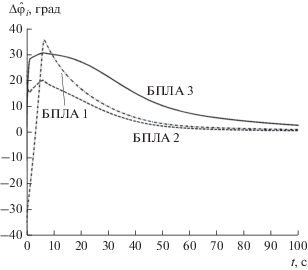
где ${{D}_{i}}$ – текущая дальность до требуемых точек $A$, $B$, $С$ (рис. 2); ${{{{\omega }}}_{i}}$ – угловая скорость линии визирования этих точек с БЛА; ${{V}_{i}}$ – скорость БПЛА в данный момент времени.

На рис. 3 представлены зависимости текущих линейных промахов каждого БПЛА от времени. На рис. 4 приведены зависимости угловых ошибок ${{\varphi }_{{{\text{т}}i}}} - {{\varphi }_{{{\text{у}}i}}}$ управления от времени. Из рис. 3 и 4 следует, что коллективное управление по предложенному закону (29) реализует устранение как линейных, так и угловых ошибок, что является необходимым условием построения нестационарных антенных решеток. Причем время устранения ошибок по линейным и угловым координатам будет зависеть от начальных условий: от наличия пересекающихся курсов между ЛА, расстояний между БПЛА и расстояний между требуемыми точками выхода группы.

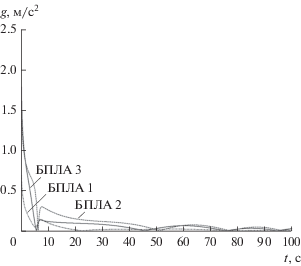
Результаты исследования закона группового управления (29) при движении по более сложным траекториям приведены на рис. 5–8. На рис. 5 показаны траектории полета группы при обходе опасной зоны, а на рис. 6 – соответствующие такой ситуации модули поперечных ускорений.

Из рис. 6 видно, что максимальное значение перегрузок, действующих на БЛА, не превышает $2.5g$, что свидетельствует об отсутствии принципиальных ограничений на возможность реализации предложенного закона управления. В последнем случае первое слагаемое в (29) используется только до момента вывода БЛА в нужные точки пространства.

На рис. 7 и 8 проиллюстрирована способность сигналов управления (29) обеспечивать полет и по расходящимся, и по наиболее сложным траекториям синусоидального характера.

ЗАКЛЮЧЕНИЕ

По итогам выполненной работы можно сказать, что в систему группового управления с сетевым информационным обменом должны входить: оптимальные регуляторы, реализующие для каждого объекта сигналы управления; оптимальные фильтры, формирующие оценки ${{{\mathbf{\hat {x}}}}_{i}}$ и ${{{\mathbf{\hat {x}}}}_{j}}$, $\Delta {{{\mathbf{\hat {x}}}}_{{ij}}}$, $j = \overline {1,N} $, $j \ne i$, и система обмена оценками координат состояния каждого объекта.

Синтезированный алгоритм коллективного управления обеспечивает адекватное управление группой как по линейным, так и по угловым координатам при минимальных вычислительных затратах, реализуя высокую безопасность совместного движения, в том числе и при использовании сложных траекторий. Эта особенность предопределяет потенциальную возможность использования (29) для формирования нестационарных фазированных решеток как движущихся, так и “неподвижных” на базе мультикоптеров.

Обмен ошибками $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{т}}ij}}}$, $\Delta {{{\mathbf{\hat {x}}}}_{{{\text{y}}ij}}}$ между объектами позволяет сохранять требуемую топологию в течение всего полета.

Следует отметить, что предложенный вариант группового управления на базе (24), (29) обладает высокой универсальностью. На его основе, в частности, можно в установившемся режиме реализовать и другие виды группового управления [10]. При централизованном управлении достаточно использовать из (29) для каждого объекта слагаемые, заключенные в квадратные скобки. В случае управления с лидером для него достаточно применять слагаемые в квадратных скобках, в то время как для всех остальных – слагаемые в фигурных скобках.

В целом рассмотренный алгоритм согласно проведенным исследованиям не накладывает принципиальных ограничений на возможность его реализации.