Радиотехника и электроника, 2022, T. 67, № 10, стр. 1006-1014
Влияние подложки на электрофизические свойства пленок из тонких однослойных углеродных нанотрубок: in silico исследования
О. Е. Глухова a, М. М. Слепченков a, А. А. Петрунин a, *
a Саратовский национальный исследовательский государственный университет им. Н.Г. Чернышевского
410012 Саратов, ул. Астраханская, 83, Российская Федерация
* E-mail: sacha.petrynin@gmail.com
Поступила в редакцию 30.03.2022
После доработки 30.03.2022
Принята к публикации 25.04.2022
- EDN: JBXGGY
- DOI: 10.31857/S0033849422100035
Аннотация
Исследованы электронные и электрофизические свойства моно- и бислойных пленок одностенных углеродных нанотрубок (ОУНТ), расположенных на подложках различных типов, включая подложки в виде пленок из кристаллического диоксида кремния SiO2 с пространственными группами симметрии P42/mnm и P3121. Установлено, что подложка играет важную роль в формировании профиля плотности электронных состояний пленок из ОУНТ. Выявлено, что за счет подложки квантовая емкость пленок из ОУНТ увеличивается в 1.6…2.2 раза при приложении напряжения более 1 В. Показано, что наличие подложки приводит к изменению электрического сопротивления монослойных пленок от 2 до 17%. Электрическое сопротивление бислойной пленки при наличии подложки практически не изменяется в обоих направлениях токопереноса и составляет минимально допустимое для ОУНТ значение ~6.4 кОм.
ВВЕДЕНИЕ
Одной из наиболее актуальных тем современной науки и техники является поиск материала для создания тонких гибких проводящих пленок, востребованных в различных приложениях электроники. В настоящее время одним из наиболее перспективных материалов для этих целей являются углеродные нанотрубки (УНТ) [1–10]. Тонкие пленки на основе УНТ толщиной 1…100 нм обладают высокой электропроводностью, прозрачностью, гибкостью и растяжимостью [2], а также проще и дешевле в изготовлении по сравнению с тонкими пленками из других современных материалов, в частности пленок оксида индия и оксида олова [11, 12]. Современные технологии синтеза позволяют изготавливать пленки из УНТ как с хаотично ориентированными трубками [6–10], так и с упорядоченным расположением трубок в составе пленки [13, 14]. Широко применяются методы печати одностенных УНТ и композитов на их основе с использованием недорогих чернил [7–9, 15]. Уже получены экспериментальные образцы пленок из УНТ металлического типа проводимости, прозрачность которых в видимом диапазоне может достигать 40…70% при толщине пленки 0.1…1 мкм [2]. В работе [6] путем осаждения нанотрубок на подложку методом погружения с использованием длинных УНТ (~10 мкм) были синтезированы однородные пленки с поверхностным сопротивлением ~100 Ом/кв при величине прозрачности ~90% в видимой области. На базе сравнительно дешевых и производимых в макрообъемах пленок из УНТ созданы первые образцы высоко растяжимых электрохимических сенсоров [16–18]. Пленки с функционализированными УНТ используются при разработке нательных датчиков движения, растяжимых на десятки процентов [19, 20]. Нанотрубки, декорированные наночастицами оксида железа, признаны перспективным материалом для анода литий-ионных батарей нового поколения [21].
Прогнозируется, что технология создания электронных компонентов на основе пленок из УНТ является потенциальным кандидатом на замену кремниевой комплементарной технологии металл–оксид–полупроводник (КМОП), традиционно используемой для изготовления элементов электронных схем [18, 22–25]. Одним из наиболее подходящих материалов для высокопроизводительной электроники на основе УНТ является пленка с матрицей из одностенных углеродных нанотрубок (ОУНТ) [26]. Уже разрабатываются интегральные схемы гигагерцового диапазона на основе пленок ОУНТ [27–29]. В частности, на основе ОУНТ разработан полевой транзистор с высокой плотностью тока, 0.55 мА/мкм, и крутизной характеристики 0.46 мСм/мкм при напряжении питания 0.8 В, а также многокаскадные кольцевые генераторы на полевых транзисторах с частотой до 5.54 ГГц [27]. Предложена технология трехмерных интегральных схем, которая повышает скорость работы полевых транзисторов на основе ОУНТ. Используя эту технологию, исследователи создали трехмерные схемы многокаскадного кольцевого генератора с частотой генерации до 680 МГц и временной задержкой 0.15 нс [28].
В то же время малоизученными по-прежнему остаются закономерности влияния на электронные и электрофизические свойства пленок из ОУНТ подложек, традиционно используемых при разработке элементной базы современных электронных наноустройств. В данной работе методами in silico исследуются электронные и электрофизические свойства моно- и бислойных пленок из ОУНТ типа “кресло”, расположенных на подложке оксида кремния SiO2. Этот тип подложки был выбран в связи с тем, что диоксид кремния SiO2 широко используется в производстве электронных устройств, в том числе устройств на основе углеродных наноструктур [30–33]. Выбор трубок “кресло” обусловлен наличием у них ахиральной структуры и присущим им металлическим типом проводимости. Ахиральная структура позволяет согласовать вектор трансляции нанотрубки с вектором трансляции подложки, в отличие от хиральных нанотрубок. Металлический тип проводимости ОУНТ выбран в связи с тем, чтобы наглядно продемонстрировать закономерности влияния подложки на электропроводимость пленки из нанотрубок. Исследование проводили для атомистических моделей тонких пленок, построенных на основе ОУНТ типа (m, m), где m = 4, 5, 6 и 7, диаметр 5…10 Å, т.е. трубок суб- и нанометрового диаметра.
1. МЕТОДЫ И ПОДХОДЫ ИССЛЕДОВАНИЯ
Для исследования электронных свойств, в частности зонной структуры пленок из ОУНТ, использован метод SCC-DFTB (метод функционала плотности в приближении сильной связи с самосогласованием заряда) [34–37]. Этот метод ранее хорошо зарекомендовал себя при прогностических исследованиях электронных свойств новых композитных материалов, в том числе углеродных композитных материалов [38]. Полная энергия системы в рамках этого подхода определяется выражением вида
(1)
${{E}_{{{\text{tot}}}}} = \mathop \sum \limits_{i\mu v} c_{\mu }^{i}c_{v}^{i}H_{{\mu v}}^{0} + \frac{1}{2}\mathop \sum \limits_{\alpha \beta } {{\gamma }_{{\alpha \beta }}}\Delta {{q}_{\alpha }}\Delta {{q}_{\beta }} + {{E}_{{{\text{отт}}}}} + {{E}_{{{\text{вдв}}}}},$Квантовую емкость рассчитывали по формуле вида [41]
(2)
${{C}_{q}}\left( U \right) = \frac{1}{{mU}}\mathop \smallint \limits_0^V e{\text{DOS}}\left( {{{E}_{{\text{F}}}} - eU{\kern 1pt} '} \right)dU{\kern 1pt} ',$Для расчета электропроводности был применен формализм Ландауэра–Буттикера [42], определяющий величину тока, протекающего через данную структуру, по величине коэффициента прозрачности барьера $T\left( E \right)$. Для ее вычисления решается нестационарное уравнение Шредингера с применением аппарата неравновесных функций Грина–Келдыша. Таким образом, электропроводность пленок из ОУНТ рассчитывали по формуле
(3)
$G = \frac{I}{V} = \frac{{{{e}^{2}}}}{h}\mathop \smallint \limits_{ - \infty }^\infty T\left( E \right){{F}_{T}}\left( {E - {{\mu }}} \right)dE,~$(4)
$\begin{gathered} {{F}_{T}} = \frac{1}{{4{{k}_{{\text{B}}}}T}}{\text{sec}}{{{\text{h}}}^{2}}\left( {\frac{E}{{2{{k}_{{\text{B}}}}T}}} \right), \\ T\left( E \right) = \frac{1}{N}\mathop \sum \limits_{k = 1}^N {\text{Tr}}\left[ {{{{\mathbf{\Gamma }}}_{s}}\left( E \right){\mathbf{G}}_{C}^{A}\left( E \right){{{\mathbf{\Gamma }}}_{d}}\left( E \right){\mathbf{G}}_{C}^{R}\left( E \right)} \right]. \\ \end{gathered} $2. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Были исследованы два типа пленок ОУНТ: монослойные и бислойные. Монослойные пленки представляют собой слой из ОУНТ с расстоянием между трубками $\sim \,3.4\,~{\text{{\AA}}}$, что соответствует расстоянию между ОУНТ в пучках, образующихся в процессе синтеза нанотрубок. Такое же расстояние соблюдается и в бислойных пленках, где трубки соседних слоев взаимно перпендикулярны. Фрагменты тонких моно- и бислойных пленок показаны на рис. 1а. Отметим, что для построения суперъячейки 2D-модели “пленка ОУНТ + подложка” необходимо, чтобы трансляционный шаг периодической ячейки ОУНТ совпадал полностью с трансляционным шагом подложки. Также необходимо обеспечить совпадение шага дистанцирования ОУНТ-ОУНТ с шагом трансляции подложки в направлении, перпендикулярном оси трубки.
Рис. 1.
Атомистические модели моно- и бислойной пленок: а – фрагменты моно- и бислойной пленок на основе ОУНТ (5,5); б – суперъячейки монослойных пленок; в – суперъячейка бислойной пленки.
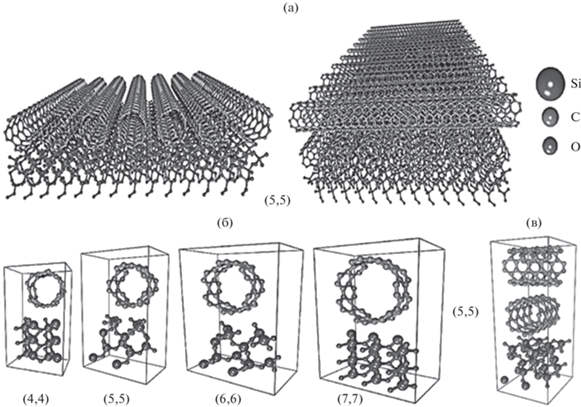
Для монослойных пленок из трубок (4,4) и (7,7) это условие построения суперъячейки 2D-модели обеспечивается использованием топологической модели подложки в виде диоксида кремния – структуры с пространственной группой P42/mnm, которая характеризуется наличием энергетической щели зонной структуры Eщель. В качестве топологии поверхности подложки выбрана поверхность (100) в соответствии с известными экспериментальными данными о широко применяемых подложках для ОУНТ. Толщина слоя подложки составила три элементарных ячейки по оси z и равна 7.2 Å. При такой субнанометровой толщине пленка диоксида кремния сохраняет свои диэлектрические свойства, как и в случае 3D-образцов, и позволяет в ходе проведения in silico исследований применять высокоточные квантовые методы. Рассчитанные энергетические параметры для подложки с поверхностью (100) составили: ${{E}_{{{\text{щель}}}}}{\text{\;}}$ = 2.30 эВ, энергия Ферми ${{E}_{{\text{F}}}}$ = –6.29 эВ.
Для монослойных пленок из трубок (5,5) и (6,6) применялась другая топологическая модель диоксида кремния – структура с пространственной группой P3121 с поверхностью (110). Толщина пленки подложки также является субнанометровой и составляет 7.4 Å. Энергетические характеристики подложки с поверхностью (110) также отвечают диэлектрическим свойствам: ${{E}_{{{\text{щель}}}}}{\text{\;}}$ = 3.87 эВ, энергия Ферми ${{E}_{{\text{F}}}}$ = –6.29 эВ. На рис. 1а показан фрагмент 2D-модели “монослойная пленка ОУНТ + + подложка” на примере пленки из трубок (5,5). Там же представлена модель фрагмента бислойной пленки из ОУНТ (5,5) на подложке. Как и в случае монослойной пленки, бислойная пленка располагается на подложке типа P3121 с поверхностью (110) той же толщины. Из всех рассматриваемых ОУНТ трубка (5,5) является единственной, для которой в рамках проведенного исследования удалось построить энергетически выгодную суперъячейку 2D-модели “пленка ОУНТ + подложка” с межтрубным расстоянием 3.4 Å для обоих слоев. Суперъячейки моно- и бислойной пленок показаны на рис. 1б, 1в. Метрические и энергетические параметры суперъячеек приведены для всех моделей пленок в табл. 1. Заряд Qтрубки рассчитывали согласно процедуре Малликена. Расстояние трубка-подложка во всех моделях составляет ~2.9…3.1 Å. Все расчеты проводили при температуре 300 K.
Таблица 1.
Метрические и энергетические параметры моно/бислойных пленок
| Параметры | ${{L}_{x}},\,~{\text{A}}$ | ${{L}_{y}},~\,\,{\text{A}}$ | Qтрубка, |e| | ${{E}_{{\text{F}}}},{\text{эВ}}$ | N | N(SiO2) |
|---|---|---|---|---|---|---|
| Монослой | ||||||
| (4,4) | 8.82 | 4.92 | –0.0021 | –4.28 | 68 | 36 |
| (5,5) | 10.18 | 4.92 | –0.0034 | –3.86 | 76 | 36 |
| (6,6) | 11.54 | 4.92 | –0.0023 | –4.09 | 84 | 36 |
| (7,7) | 12.9 | 4.92 | –0.0079 | –4.37 | 110 | 54 |
| Бислой | ||||||
| (5,5) | 10.18 | 10.18 | –0.0229 | –3.98 | 232 | 72 |
В табл. 1 не приводятся данные об энергетической щели, поскольку во всех случаях углеродные пленки демонстрируют металлический тип проводимости. Из данных таблицы видно, что во всех случаях трубки “забирают” на себя заряд от подложки. Величина этого заряда небольшая, но, тем не менее, она вносит определенные коррективы в закономерности электронных свойств пленок на основе ОУНТ. Наибольший перенос заряда наблюдается с подложки на бислойную пленку, причем на первый слой трубок, непосредственно контактирующий с подложкой, перешел заряд величиной –0.0213е. Второй слой трубок принял гораздо меньший заряд, и избыточный заряд составил всего лишь –0.0016е. Все атомы нанотрубок вблизи подложки несут на себе отрицательный заряд. На основе полученных расчетов можно предположить, что электронный заряд через нижний слой нанотрубок перетекает на верхний слой. Это может быть обусловлено π-электронами нанотрубок, которые ведут себя достаточно активно в трубках субнанометрового диаметра. Как известно, в тонких ОУНТ наблюдается явление регибридизации электронных σ- и π-облаков, что приводит к увеличению химической активности атомов подобных трубок. Ионизация трубок приводит, как следствие, к заметным изменениям электронного строения.
Распределения плотности электронных состояний для монослойных пленок показаны на рис. 2а, для бислойной пленки – на рис. 3а. Во всех случаях приведены графики DOS системы “пленка + + подложка” и парциальные DOS для углерода, кремния и кислорода. На рис. 2а показаны пленки с трубками (4,4) и (7,7), располагающиеся на одинаковых подложках P42/mnm с поверхностью (100). Графики DOS кислорода и кремния демонстрируют большую энергетическую щель. Плотность состояний кислорода характеризуется высоким пиком интенсивности у потолка валентной зоны. Вклад углерода становится заметным в зоне проводимости (интервал –3…–2.5 эВ). Именно углерод обеспечивает ненулевую DOS на уровне Ферми. Графики DOS для пленок трубок (5,5) и (6,6) на подложке P3121 с поверхностью (110) представлены на рис. 2б. Пик интенсивности DOS кислорода у потолка валентной зоны в этом случае в четыре раза меньше по сравнению с DOS для другого типа подложки. Интересным является тот факт, что не только подложка оказывает влияние на профиль DOS пленок ОУНТ, формируя его в большой степени, но и электронная структура нанотрубок влияет на электронное строение подложки. Это четко видно на рис. 2б при сравнении DOS кислорода и кремния. Подложка у пленок с ОУНТ (5,5) и (6,6) одна и та же, но в первом случае графики DOS кислорода и кремния имеют пик на уровне энергии –1.7 эВ, а во втором случае этот пик отсутствует. Зона проводимости системы “пленка из трубок (6,6) + подложка” вблизи уровня Ферми полностью сформирована углеродом, т.е. нанотрубками (полный DOS пленки и парциальный DOS углерода на рис. 2б полностью сливаются выше уровня Ферми). Можно сделать вывод, что подложка играет важную роль в формировании DOS, а топология поверхности определяет степень и характер взаимного влияния трубки и подложки.
Рис. 2.
Плотности электронных состояний монослойных пленок: а – на подложке P42/mnm с поверхностью (100); б – P3121 с поверхностью (110); вертикальная линия – уровень Ферми; общий DOS (1), парциальные DOS углерода (2), кислорода (3) и кремния (4).

Рис. 3.
Электронные и электрофизические характеристики бислойной пленки (5,5) на подложке: а – плотность электронных состояний (общий DOS (1); парциальные DOS углерода (2), кислорода (3) и кремния (4); б – интегральные функции пропускания бислойной пленки вдоль осей x (1) и y (2).
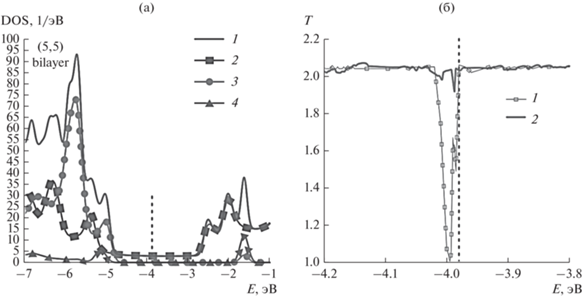
Профиль DOS системы “бислойная пленка + + подложка” представлен на рис. 3а. Как и ожидалось, профиль DOS в этом случае практически полностью совпадает с профилем DOS монослойной пленки, показанном на рис. 2б. Увеличилась лишь интенсивность пиков и значений DOS вблизи уровня Ферми.
Из данных табл. 1 и рис. 2, 3 видно, что подложка оказывает влияние и на положения уровня Ферми пленок из ОУНТ. Ранее было установлено, что пленки из ОУНТ без подложки характеризуются уровнем Ферми –4.5 ± 0.4 эВ. При наличии подложки типа P42/mnm уровень Ферми сдвигается в сторону увеличения до значения ~–4.3 эВ, при наличии подложки P3121 уровень Ферми сдвигается более заметно до отметки ~–4.0 эВ, причем и для моно-, и для бислойной пленки. Это очень важный момент, поскольку, с одной стороны, подложка не снижает проводимости пленки, а с другой – уменьшает работу выхода электронов, сдвигая уровень Ферми по оси энергий в направлении 0 эВ. Этот факт очень важен для применения ОУНТ в эмиссионной электронике.
На основе рассчитанных распределений DOS была проведена численная оценка квантовой емкости для пленок ОУНТ и системы “пленка ОУНТ + + подложка” по формуле (2) при изменении напряжения от –3 до 3 В (рис. 4). Из графиков видно, что в области напряжений от –1 до 1 В квантовая емкость принимает минимальные значения для всех исследуемых структур, причем согласно проведенному анализу DOS (см. рис. 2 и 3а) для системы “пленка ОУНТ + подложка” практически весь вклад в квантовую емкость вносит DOS ОУНТ. При напряжении менее –1 В квантовая емкость выходит на насыщению, вплоть до значений 1400 и 1280 Ф/г для пленок ОУНТ с подложками типа P42/mnm и P3121 соответственно. Бислойная пленка за счет большего содержания ОУНТ демонстрирует в интервале напряжений от –1 до 3 В наибольшее значение квантовой емкости среди всех рассматриваемых структур, а в интервале от –3 до –1 квантовая емкость ее значения не превышает 1200 Ф/г.
Рис. 4.
Квантовая емкость тонких пленок из ОУНТ: а – без подложки; б – на подложке. Кривая 1 отвечает бислойной пленке из ОУНТ (5,5), кривые 2, 3, 4, 5 отвечают монослойным пленкам из ОУНТ (4,4), (5,5), (6,6) и (7,7), соответственно.

Следующим важным этапом наших исследований было выявление закономерности влияния подложки на электропроводность пленок. Первым шагом в этом направлении был расчет функции пропускания электронов T(E), зависящей от энергии первой зоны Бриллюэна. На рис. 5 представлены рассчитанные функции Т(Е), значения которых приведены в квантах проводимости e2/h (где h – постоянная Планка). Для монослойных пленок электропроводность рассчитывали только для направления токопереноса вдоль оси трубок, т.е. вдоль оси x. Как известно, ОУНТ типа “кресло” имеют два канала (два кванта) проводимости на уровне Ферми. Вследствие отмеченного ранее перераспределения заряда между ОУНТ и подложкой количество квантов проводимости системы “пленка ОУНТ + подложка” будет снижено, что скажется и на величине сопротивления исследуемых структур.
Рис. 5.
Интегральные функции пропускания монослойных пленок ОУНТ (4,4), (5,5), (6,6) и (7,7); вертикальная линия – уровень Ферми.

В отличие от монослойных пленок, бислойные структуры обладают электропроводностью в обоих направлениях, x и y, поэтому функции пропускания рассчитывали для двух направлений. Результаты расчетов представлены на рис. 3б. Наличие двух слоев нанотрубок приводит к повышенным значениям функции пропускания по сравнению с монослойной пленкой. Функция T(E) принимает значение 2.1 на уровне Ферми EF и справа от него. Можно прогнозировать для этого типа пленки повышенное значение электропроводности.
Заключительном этапом исследования был расчет электропроводности и электрического сопротивления пленок ОУНТ на подложке. В табл. 2 приведены полученные расчетные значения этих электрофизических параметров для пленок ОУНТ на подложке и без нее. Как известно, минимальное сопротивление для индивидуальной ОУНТ составляет 6.4 кОм при наличии двух каналов проводимости на уровне Ферми. Однако при объединении ОУНТ в плотно упакованные моно/бислойные пленки сопротивление пленки заметно отличается от значения 6.4 кОм, что объясняется перекрыванием π-электронных облаков соседних трубок. Как видно из данных табл. 2, все монослойные нанотрубные пленки характеризуются гораздо большим сопротивлением, ~7…8 кОм, по сравнению с эталонной величиной 6.4 кОм, установленной экспериментально [44]. Минимальное значение сопротивления монослойной пленки составляет 6.867 кОм. Такая особенность поведения сопротивления объясняется естественными причинами перераспределения электронного заряда между пленкой и подложкой. Однако ситуация заметно меняется для пленки из двух слоев нанотрубок. Без подложки сопротивление каждого из слоев пленки было близко к идеальному и составляло ~6.43 кОм, а при наличии подложки оно практически не изменилось. Сопротивление верхнего слоя трубок бислойной пленки составило 6.438 кОм, что почти не отличается от значений сопротивления для пленки без подложки.
Таблица 2.
Электрофизические параметры пленок на подложке и без нее
| Параметры | (4,4) | (5,5) | (6,6) | (7,7) | (5,5)-X бислой | (5,5)-Y бислой |
|---|---|---|---|---|---|---|
| Пленки на подложке | ||||||
| G, мкСм | 123.824 | 132.686 | 144.638 | 123.528 | 148.005 | 155.312 |
| R, кОм | 8.076 | 7.537 | 6.913 | 8.095 | 6.800 | 6.438 |
| Пленки без подложки | ||||||
| G, мкСм | 121.045 | 145.619 | 134.027 | 144.914 | 155.312 | 155.312 |
| R, кОм | 8.261 | 6.867 | 7.461 | 6.900 | 6.438 | 6.431 |
ЗАКЛЮЧЕНИЕ
Проведено in silico исследование влияния подложки в виде тонкой пленки из диоксида кремния толщиной 7.2 Å на электронное строение и электропроводность моно- и бислойных пленок из ОУНТ типа “кресло”. Равновесные конфигурации суперъячеек монослойных пленок на подложке были найдены для всех рассмотренных ОУНТ (4,4), (5,5), (6,6) и (7,7) типа “кресло” диаметром 0.5…1 нм, в то время как для бислойных пленок равновесная конфигурация была найдена только для пленки из ОУНТ (5,5). На основе результатов расчетов распределений DOS и квантовой емкости установлена закономерности влияния подложки на электронное строение тонких пленок из ОУНТ типа “кресло”. Варьируя топологию поверхности подложки из диоксида кремния, можно добиться увеличения квантовой емкости пленок из ОУНТ в 1.6…2.2 раза за счет трансфера заряда с атомов подложки на атомы нанотрубок в составе пленки.
Диэлектрическая подложка из диоксида кремния существенным образом оказывает влияние и на электропроводящие свойства монослойных пленок из ОУНТ. В зависимости от выбора топологии поверхности подложки электрическое сопротивление пленки можно увеличивать в пределах 10…17%, либо уменьшать в пределах 2…7%. Основываясь на результатах расчетов, полученных для единственной равновесной конфигурации суперъячейки бислойной пленки, можно сказать, что подложка практически не оказывает влияние на ее электропроводность и сопротивление в обоих направлениях токопереноса. Сопротивление каждого из слоев бислойной пленки хорошо коррелируют с минимально возможным значением сопротивления ~6.4 кОм, установленным для отдельной ОУНТ типа “кресло”. Таким образом, можно предположить, что решающую роль в определении электронного строения и электрофизических характеристик пленок из ОУНТ типа “кресло” оказывает кристаллическая фаза подложки.
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Jiang S., Hou P.X., Chen M.L. et al. // Sci. Adv. 2018. V. 4. № 5. P. eaap9264. https://doi.org/10.1126/sciadv.aap9264
Devaraju S., Lee T., Mohanty A.K. et al. // RSC Adv. 2017. V. 7. № 31. P. 19267. https://doi.org/10.1039/C7RA01180F
Siwal S.S., Saini A.K., Rarotra S. et al. // J. Nanostruct. Chem. 2021. V. 11. № 1. P. 93. https://doi.org/10.1007/s40097-020-00378-2
Qu S., Dai Y., Zhang D. et al. // Funct. Compos. Struct. 2020. V. 2. № 2. P. 022002. https://doi.org/10.1088/2631-6331/ab9752
Zhang Q., Zhou W., Xia X. et al. // Adv. Mater. 2020. V. 32. P. 2004277. https://doi.org/10.1002/adma.202004277
Mirri F., Ma A.W., Hsu T.T. et al. // ACS Nano. 2012. V. 6. № 11. P. 9737. https://doi.org/10.1021/nn303201g
Shimoni A., Azoubel S., Magdassi S. // Nanoscale. 2014. V. 6. № 19. P. 11084. https://doi.org/10.1039/C4NR02133A
Yu W., Zhou H., Li B.Q., Ding S. // ACS Appl. Mater. Interfaces. 2017. V. 9. № 5. P. 4597. https://doi.org/10.1021/acsami.6b13904
Sweeney C.B., Lackey B.A., Pospisil M.J. et al. // Sci. Adv. 2017. V. 3. № 6. P. e1700262. https://doi.org/10.1126/sciadv.1700262
Mustonen K., Nasibulin A.G., Pudas M. et al. // Carbon. 2013. V. 62. P. 513. https://doi.org/10.1016/j.carbon.2013.05.072
Bu Q., Zhan Y., He F. et al. // J. Appl. Polym. Sci. 2016. V. 133. P. 43243. https://doi.org/10.1002/app.43243
De Volder M.F., Tawfick S.H., Baughman R.H., Hart A.J. // Science. 2013. V. 339. № 6119. P. 535. https://doi.org/10.1126/science.1222453
Zhou Y., Azumi R. // Sci. Technol. Adv. Mater. 2016. V. 17. № 1. P. 493. https://doi.org/10.1080/14686996.2016.1214526
Dong C., Hao J. // Colloids Surf. A Physicochem. Eng. Asp. 2019. V. 566. P. 207. https://doi.org/10.1016/j.colsurfa.2019.01.020
Sajed F., Rutherglen C. // Appl. Phys. Lett. 2013. V. 103. № 14. P. 185_1. https://doi.org/10.1063/1.4824475
Bandodkar A.J., Jeerapan I., You J.M. et al. // Nano Lett. 2016. V. 16. № 1. P. 721. https://doi.org/10.1021/acs.nanolett.5b04549
Wang C., Takei, K., Takahashi T., Javey A. // Chem. Soc. Rev. 2013. V. 42. № 7. P. 2592. https://doi.org/10.1039/C2CS35325C
Cai L., Wang C. // Nanoscale Res. Lett. 2015. V. 10. № 1. P. 1. https://doi.org/10.1186/s11671-015-1013-1
Cai L., Song L., Luan P. et al. // Sci. Rep. 2013. V. 3. № 1. P. 1. https://doi.org/10.1038/srep03048
Dinh T., Phan H.P., Nguyen T.K. et al. // J. Mater. Chem. C. 2016. V. 4. № 42. P. 10061. https://doi.org/10.1039/C6TC02708C
Lv X., Deng J., Wang B. et al. // Chem. Mater. 2017. V. 29. № 8. P. 3499. https://doi.org/10.1021/acs.chemmater.6b05356
Franklin A.D., Chen Z.H. // Nat. Nanotech. 2010. V. 5. № 12. P. 858. https://doi.org/10.1038/nnano.2010.220
Franklin A.D., Luisier M., Han S.J. et al. // Nano. Lett. 2012. V. 12. № 2. P. 758. https://doi.org/10.1021/nl203701g
Qiu C., Zhang Z., Xiao M. et al. // Science. 2017. V. 355. № 6322. P. 271. https://doi.org/10.1126/science.aaj1628
Xu L., Qiu C., Peng L.-M., Zhang Z. // Nano Res. 2021. V. 14. № 4. P. 976. https://doi.org/10.1007/s12274-020-3135-8
Franklin A.D. // Nature. 2013. V. 498. № 7455. P. 443. https://doi.org/10.1038/498443a
Zhong D., Zhang Z., Ding L. et al. // Nat. Electron. 2018. V. 1. № 1. P. 40. https://doi.org/10.1038/s41928-017-0003-y
Xie Y., Zhang Z., Zhong D., Peng L. // Nano Res. 2019. V. 12. № 8. P. 1810. https://doi.org/10.1007/s12274-019-2436-2
Liu L., Ding L., Zhong D. et al. // ACS Nano. 2019. V. 13. № 2. P. 2526. https://doi.org/10.1021/acsnano.8b09488
Liu Z., Zhao J., Xu W. et al. // ACS Appl. Mater. Interfaces. 2014. V. 6. № 13. P. 9997. https://doi.org/10.1021/am502168x
Xiang L., Zhang H., Dong G. et al. // Nat. Electron. 2018. V. 1. № 4. P. 237. https://doi.org/10.1038/s41928-018-0056-6
Li X., Zhu Y., Cai W. et al. // Nano Lett. 2009. V. 9. № 12. P. 4359. https://doi.org/10.1021/nl902623y
Liu S., Guo X. // NPG Asia Mater. 2012. V. 4. № 8. P. e23. https://doi.org/10.1038/am.2012.42
Elstner M., Porezag D., Jungnickel G. et al. // Phys. Rev. B 1998. V. 58. № 11. P. 7260. https://doi.org/10.1103/PhysRevB.58.7260
Elstner M., Seifert G. // Phil. Trans. R. Soc. A. 2014. V. 372. № 2011. P. 20120483. https://doi.org/10.1098/rsta.2012.0483
Ghorbani-Asl M., Bristowe P.D., Koziol K. // Phys. Chem. Chem. Phys. 2015. V. 17. № 28. P. 18273. https://doi.org/10.1039/C5CP01470K
Naumov V.S., Loginova A.S., Avdoshin A.A. et al. // Int. J. Quantum Chem. 2021. V. 121. № 2. P. e26427. https://doi.org/10.1002/qua.26427
Slepchenkov M.M., Shmygin D.S., Zhang G., Glukhova O.E. // Carbon. 2020. V. 165. P. 139. https://doi.org/10.1016/j.carbon.2020.04.069
Rappe A.K., Casewit C.J., Colwell K.S. et al. // J. Am. Chem. Soc. 1992. V. 114. №125. P. 10024. https://doi.org/10.1021/ja00051a040
Hourahine B., Aradi B., Blum V. et al. // J. Chem. Phys. 2020. V. 152. № 12. P. 124101. https://doi.org/10.1063/1.5143190
Mousavi-Khoshdel S.M., Jahanbakhshbonab P., Targholib E. // Phys. Lett. A. 2016. V. 380. № 41. P. 3378. https://doi.org/10.1016/j.physleta.2016.07.067
Datta S. Quantum Transport: Atom to Transistor. Cambridge: Univ. Press, 2005. P. 217. https://doi.org/10.1017/CBO9781139164313
Glukhova O.E., Shmygin D.S. // Beilstein. J. Nanotechnol. 2018. V. 9. № 1. P. 1254. https://doi.org/10.3762/bjnano.9.117
Dresselhaus G., Dresselhaus M.S., Saito R. Physical properties of carbon nanotubes. Singapore: World Scientific, 1998.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


