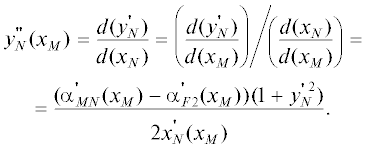Радиотехника и электроника, 2022, T. 67, № 2, стр. 140-148

ВВЕДЕНИЕ

Бифокальные двухзеркальные системы позволяют расширить угол зрения по сравнению с однозеркальными и апланатическими двухзеркальными системами. В связи с этим синтезу бифокальных систем посвящено большое количество работ [1–14].

В работе [14] на основе известного подхода [1–6] развита методика точного решения задачи синтеза цилиндрических бифокальных двухзеркальных систем в приближении геометрической оптики. В рамках развитой методики осуществлен выбор начальных участков зеркал и обеспечена непрерывность функций, описывающих форму зеркал, и их производных. Непрерывность вторых производных этих функций, которая обеспечивает непрерывность отраженных полей в первом приближении геометрической оптики, была реализована приближенно. Форма начальных участков зеркал при этом задавалась в виде отрезков парабол, один из коэффициентов которых был найден путем численной минимизации скачка второй производной на границах соседних участков зеркал. При этом вопрос о том, обеспечивают ли найденные решения задачи синтеза двухзеркальной системы для заданного угла зрения минимальную среднеквадратическую аберрацию (СКА) остался открытым.

Цель данной работы – дальнейшее развитие методики синтеза и оптимизации цилиндрических бифокальных двухзеркальных систем с целью реализации минимальной СКА в заданном угле зрения. При этом в процессе синтеза задается начальный участок только одного из зеркал.

1. МЕТОДИКА СИНТЕЗА БИФОКАЛЬНОЙ ДВУХЗЕРКАЛЬНОЙ СИСТЕМЫ

Рассмотрим задачу синтеза цилиндрической бифокальной двухзеркальной системы, с одной стороны которой расположены два симметричных относительно оси y (рис. 1) фокуса (точки идеальной фокусировки F₁ и F₂) с декартовыми координатами (${{x}_{{{{F}_{1}}}}},{{y}_{{{{F}_{1}}}}}$) и (${{x}_{{{{F}_{2}}}}},{{y}_{{{{F}_{2}}}}}$). При положении источника цилиндрической волны в каждом из этих фокусов с другой стороны бифокальной системы формируются два симметричных относительно оси y плоских фронта.

Пусть форма вспомогательного (первого) и основного (второго) зеркала описываются неизвестными четными фунциями y₁(x) и y₂(x) соответственно, а функция y₁₀(x), описываюшая начальный участок вспомогательного зеркала, задана, т.е. на интервале [–x₀, x₀] функция y₁(x) = y₁₀(x) известна. При этом поверхности первого и второго зеркал пересекают ось y в точках (0, b) и (0, 0) соответственно (рис. 1). Потребуем, чтобы лучи из источника, расположенного в точке F₀ с координатами (0, –f₀) после двух отражений от зеркал формировали плоский фронт y = h, где h – произвольная постоянная. При этом луч, идущий вдоль оси y, падает на первое зеркало в точке (0, b), отражается от него, падает на второе зеркало в точке (0, 0), снова отражается и снова идет вдоль оси y. Эйконал от источника до фронта этого (осевого) луча имеет вид

Пусть другой луч, выходящий из точки F₀, падает на первое зеркало в точке P с координатами (x_P, y_P), отражается от него, падает на второе зеркало в точке Q с координатами (x_Q, y_Q) и отражается от него параллельно оси y. При этом его эйконал определяется формулой

где ${{\alpha }_{{PQ}}} = {{\alpha }_{{FP}}} - 2{{\gamma }_{p}}$ – угол межу осью y и отрезком PQ; ${{\alpha }_{{FP}}} = {\text{arctg}}\,({{{{x}_{P}}} \mathord{\left/ {\vphantom {{{{x}_{P}}} {({{y}_{P}} - {{y}_{F}})}}} \right. \kern-0em} {({{y}_{P}} - {{y}_{F}})}})$ – угол межу осью y и падающим лучом в точке P; ${{\gamma }_{P}} = {\text{arctg}}(y_{{10}}^{'}({{x}_{P}}))$ – угол между осью y и нормалью первому зеркалу в точке P; PQ – расстояние от точки P до точки Q.

Потребуем, чтобы все лучи, выходящие из точки F после двух отражений от зеркал, были параллельно оси y и формировали плоский фронт на выходе системы. Для этого необходимо равенство эйконалов всех лучей (от источника до фронта). Потребуем, чтобы эйконалы всех лучей были равны эйконалу центрального луча:

Решение этого уравнения имеет вид

Зная расстояние от точки P до точки Q и угол ${{\alpha }_{{PQ}}}$, нетрудно найти координаты точки Q:

Множество точек Q образует начальный участок второго зеркала.

Для реализации на стыках начальных участков с соседними непрерывности функций, описывающих форму поверхности зеркал и их производных, необходимо, чтобы луч плоской волны, падающей на зеркало под углом к оси yпосле отражения в точке D попадал в точку A, а после отражения в точке A – в фокус F₁. Из геометрии, представленной на рис. 2, нетрудно найти координаты этого фокуса, а также фокуса F₂, учитывая, что он симметричен фокусу F₁ относительно оси y:

где x_A = –x₀; y_A = y(–x₀); ${{\alpha }_{{A{{F}_{1}}}}} = $ $ = \operatorname{arctg} \left( {{{({{x}_{D}} - {{x}_{A}})} \mathord{\left/ {\vphantom {{({{x}_{D}} - {{x}_{A}})} {({{y}_{D}} - {{y}_{A}})}}} \right. \kern-0em} {({{y}_{D}} - {{y}_{A}})}}} \right)$ + $2~\operatorname{arctg} (y{\kern 1pt} '({{x}_{A}}))$ – угол между осью y и линией, соединяющей фокус F₁ с краем (точка A) начального участка вспомогательного зеркала; $f$ – расстояние от края начального участка до фокуса.

Рассмотрим луч, который из фокуса F₁ падает на первое зеркало в точке A, отражается и падает на второе зеркало в точке D. Из геометриина рис. 1 следует, что угол выхода луча из системы определяется формулой

где $y_{2}^{'}({{x}_{D}})$ – первая производная функции y₂(x) в точке D.

Для определения нового участка второго зеркала предложим, что луч из фокуса ${{F}_{1}}$ падает на начальный участок первого зеркала, отражается от него в точке S с координатами (x_S, y_S), падает на второе зеркало в точке T с координатами (x_T, y_T) и отражается под углом $\delta $ (см. рис. 2). Отсюда получаем угол между осью y и падающим от точки ${{F}_{1}}$ в точку S лучом ${{\alpha }_{{{{F}_{1}}S}}} = {\text{arctg}}({{({{x}_{S}} - {{x}_{{{{F}_{1}}}}})} \mathord{\left/ {\vphantom {{({{x}_{S}} - {{x}_{{{{F}_{1}}}}})} {({{y}_{S}} - {{y}_{{{{F}_{1}}}}})}}} \right. \kern-0em} {({{y}_{S}} - {{y}_{{{{F}_{1}}}}})}})$ и угол ${{\alpha }_{{ST}}} = {{\alpha }_{{{{F}_{1}}S}}} - 2{{\gamma }_{S}}$ между осью y и лучом, отраженным от зеркала в точке S.

Для того чтобы двухзеркальная система формировала на выходе плоский фронт, необходимо равенство эйконалов всех лучей, которые выходят из фокуса ${{F}_{1}}$ и после отражения от зеркал идут параллельно (под углом $\delta $ к оси Y). Отсюда получаем уравнение

где ${{l}_{0}} = \sqrt {{{{({{x}_{C}} - {{x}_{B}})}}^{2}} + {{{({{y}_{C}} - {{y}_{B}})}}^{2}}} $; ST – расстояние от точки S до точки T.

Решение этого уравнения имеет вид

Зная длину ST и угол α_ST, можно определять координаты точки T по формулам

Множество точек T образует новый участок второго зеркала. При этом функция y₂(x) и ее первая производная также непрерывны на стыке начального участка второго зеркала с его новым (соседним) участком.

Для определения нового участка первого зеркала рассмотрим падение плоской волны на второе зеркало. Пусть луч, который падает на начальный участок второго зеркала в точке M с координатами (x_M, y_M) под углом δ к оси y, отражается от второго зеркала и падает на первое зеркало в точке N с координатами (x_N, y_N), снова отражается и проходит через фокус ${{F}_{2}}$ (см. рис. 2). Угол между осью y и отраженным лучом в точке М равен ${{\alpha }_{{MN}}} = \delta - 2{{\gamma }_{M}}$.

Приравнивая эйконалы лучей, отраженных от разных точек M зеркала, получим уравнение

где d_M – расстояние от точки M до фронта волны; d_C – расстояние от точки C до фронта волны.

Решение этого уравнения имеет вид

где $A = {{l}_{0}} + f + 2({{x}_{C}} - {{x}_{M}})\sin (\delta ) + $ $ + \,\,2({{y}_{C}} - {{y}_{M}})\cos (\delta ).$

Зная расстояние MN и угол α_MN, координаты точки N можно найти по формулам

Множество точек N образует новый участок первого зеркала. При этом фунция y₁(x) и ее первая производная непрерывны на стыке начального отрезка с новым.

Для обеспечения непрерывности амплитудного распределения отраженных волн в первом приближении геометрической оптики необходимо,чтобы вторые производные функций, описываюших поверхности зеркал, были непрерывными. Первая производная функции y₁(x) в точке N имеет вид

Так как координаты точки$N$определяются через координаты точки $M$, вторую производную второго отрезка первого зеркала в точке $N$ определяем дифференцированием его первой производной в точке N по координате ${{x}_{M}}$:

Для того чтобы вторая производная первого зеркала на стыках была непрерывной, значение второй производной первого участка в точке В должно равняться значению второй производной в точке N, когда точки M и C совпадают. Заменим x_M  на –x₀ в выражении для второй производной (15) и приравняем его значению второй производной начального отрезка первого зеркала в точке B. В результате получим уравнение

где ${{y}_{0}} = {{y}_{1}}({{x}_{0}})$, $y_{0}^{'} = y_{1}^{'}({{x}_{0}})$; – значения функции y₁(x), ее первой и второй производной соответствено в точке B с координатами (x₀, y₀).

2. СИНТЕЗ И ОПТИМИЗАЦИЯ БИФОКАЛЬНЫХ ДВУХЗЕРКАЛЬНЫХ СИСТЕМ

Задача синтеза и оптимизации состоит в нахождении формы зеркал и фокальной кривой, обеспечивающие минимальную величину СКА эйконала на выходе двухзеркальной системы, которую будем определять по формуле

где ${{L}_{i}}$ – эйконал луча с номером i; n – количество учтенных лучей, D – размер апертуры системы; ${{L}_{0}}$ – эйконал луча, относительно которого СКА имеет минимальное значение (этот луч будем называть опорным).

Зададим исходные параметры системы: расстояние между зеркалами b, полуразмер начального отрезка x₀, расстояние f от конца начального отрезка до фокуса F₁, расстояние p от первого зеркала до фокуса F₀ начальной системы, и используем изложенный выше алгоритм синтеза бифокальной системы с начальным отрезком первого зеркала в виде полинома второго порядка $y(x) = a{{x}^{2}} + b$ и четвертого $y(x) = {{a}_{4}}{{x}^{4}} + {{a}_{2}}{{x}^{2}} + b$. Один из коэффициентов полинома находим из условия непрерывности второй производной функций, описывающих форму зеркал (16). В первом случае, подставляя ${{y}_{0}} = ax_{0}^{2} + b$;$y_{0}^{'} = 2a{{x}_{0}}$; 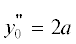в уравнение (16), находим a. Во втором случае аналогично находим a₄ при заданном значении a₂, которое в данном случае является дополнительной степенью свободы для оптимизации. Реализуя описанный выше алгоритм синтезирования отрезков зеркал m раз, находим форму зеркал, которые состоят из 2m + 1 отрезков.

Проведем анализ СКА двухзеркальной системы, синтезированной для фиксированного значения угла зрения в зависимости от ее параметров. Для вычисления СКА системы по формуле (17) необходимо найти эйконалы лучей, для определения которых, в свою очередь, необходимо знать направление фронта и величину эйконала ${{L}_{0}}$ опорного луча, относительно которого будет рассчитываться СКА. Если источник находится в фокусе, углы выхода всех лучей из системы одинаковы и определяются формулой (7). При смещенном положении источника углы выхода лучей будут разные. Найдем k таких лучей и выберем из них несколько опорных, проходящих вблизи центра двухзеркальной системы. По формуле (17) найдем СКА для каждого опорного луча с соответствующим (ортогональным) фронтом (рис. 3) и выберем из полученных величин СКА минимальное значение. Полученное приближенное значение СКА уточняем, меняя угол выхода опорного луча и находя минимум СКА.

Для определения фокальной кривой найдем геометрическое место положений источника (см. рис. 3), которые обеспечивают наименьшую величину СКА. Декартовые и полярные координаты источника связаны формулами x_Fj = $ = - {{R}_{j}}{\text{sin}}\left( {{{\theta }_{j}}} \right)$, ${{y}_{{Fj}}} = - {{R}_{j}}{\text{cos}}\left( {{{\theta }_{j}}} \right)$. Задача состоит в том, чтобы найти оптимальную функцию ${{R}_{j}}\left( {{{\theta }_{j}}} \right)$. Для 20 значений угла ${{\theta }_{j}}$ находим ${{R}_{j}}~~$с использованием стандартной численной процедуры нахождения минимума. Применяя сплайн-итерполяцию, находим функцию ${{R}_{j}}\left( {{{\theta }_{j}}} \right)$ и таким образом получаем фокальную кривую.

Проведем исследование зависимости величины СКА от параметров бифокальной системы. На рис. 4 представлены зависимости СКА от угла зрения системы c разным размером начального участка 2x₀ в виде параболы, разными расстояниями между зеркалами b₁ и разным числом синтезированных отрезков m. Видно, что СКА медленно уменьшается при увеличении x₀. Это объясняется тем, что только система из начальных участков имеет фокус в точке F(0, –f₀) на оси x. Новые синтезированные участки уже не обеспечивают точную фокусировку при положении источника в этой точке, их число при заданной апертуре системы увеличивается при уменьшении x₀ и это, соответственно, приводит к увеличению СКА.

При увеличении числа синтезированных отрезков зеркал их края приближаются друг к другу. В результате зеркала либо пересекаются (рис. 5а), либо у них появляются точки возврата (рис. 5б). Параметры системы, при которых у зеркала при построении первого нового участка возникают точки возврата или решение задачи синтеза перестает существовать, будем называть критическими.

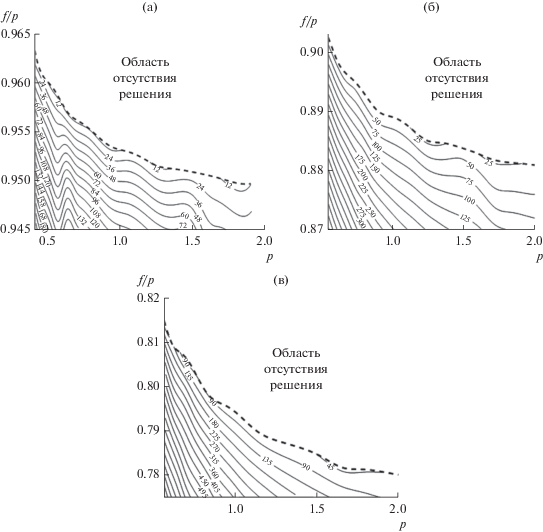
Далее исследуем СКА бифокальной системы в зависимости от параметров f и p = f₀ + b для трех наборов фиксированных параметров: расстояния b между зеркалами и x₀ (отношение b/x₀ определяет угол зрения). Линии уровня СКА для трех наборов фиксированных параметров, соответствующих значениям угла зрения 50, 70 и 105 град в зависимости от параметров f и p, показаны на рис. 6а–6в. На рисунках видны границы областей существования решения, а также уменьшение величины СКА по мере приближения параметров системы к этим границам. При этом линии уровней СКА идут почти параллельно границе.

На рис. 7 представлены зависимости СКА от параметра p системы при движении вдоль границы (при критической величине f) для тех же трех наборов фиксированных параметров. Из рисунка видно, что зависимость СКА от p имеет колебательный характер, при этом для больших углов зрения средная величина СКА при уменьшении p уменьшается. Минимальные величины СКА для исследованного интервала (p < 2.5) и углов зрения 50, 70 и 105 град равны $8.0 \times {{10}^{{ - 6}}}$, $2.2 \times {{10}^{{ - 5}}}~$ и $4.1 \times {{10}^{{ - 5}}}$ соответственно.

На рис. 8 приведены зависимости СКА бифокальной двухзеркальной системы от угла зрения для трех оптимальных наборов параметров, которые соответствуют трем углам зрения 50, 70 и 105 град. Как видно из рисунка, при увеличении угла зрения примерно в два раза СКА увеличивается в пять раз. При этом полученные в результате минимальные величины СКА в 60 раз меньше СКА двухзеркальных бифокальных систем, синтезированных в работе [13], и близки к СКА трехфокальных систем [14, 15].

Велчина апертуры D для разных наборов параметров получается разной. Для анализа полученных результатов удобно считать все величины относительно апертуры системы. Для этого достаточно умножить все геометрические размеры на множитель, равный обратной величине D. В результате для систем с D = 1 и углами зрения 50, 70 и 105 град величина p равна 1.30, 1.14 и 1.41, а растояние между зеркалами b равно соответственно 0.073, 0.089 и 0.061.

На рис. 9 показаны фокальные кривые синтезированных систем с оптимальными параметрами для углов зрения 50, 70 и 105 град. Видно, что с увеличением угла зрения в два раза угловой размер фокальной кривой увеличивается также в два раза, при этом фокальный размер меняется немонотонно, а различие между минимальным и максимальным размерами составляет 23%.

Дальнейшее исследование показало, что использование дополнительной степени свободы при задании формы первого участка вспомогательного зеркала в виде полинома четвертого порядка не приводит к дополнительному уменьшению СКА.

ЗАКЛЮЧЕНИЕ

На основе полученных результатов можно сделать следующие выводы.

1. Разработанная методика позволяет синтезировать и оптимизировать двухзеркальные бифокальные цилиндрические системы по минимуму СКА.

2. Синтезированные и оптимизированные в результате разработанной методики бифокальные двухзеркальные системы имеют СКА в десятки раз меньшие, чем известные.

3. Увеличение угла зрения в два раза приводит к увеличению СКА в пять раз, при этом различие между минимальным и максимальным продольным размером составляет 23%.

4. Задание формы начального участка вспомогательного зеркала в виде полинома четвертого порядка вместо полинома второго порядка и использование дополнительной степени свободы не приводит к дополнительному уменьшению СКА.