Радиотехника и электроника, 2022, T. 67, № 2, стр. 149-156

ВВЕДЕНИЕ

Оценка спектральных параметров метеообразований (МО) является важнейшей задачей, возлагаемой на доплеровские метеорадиолокаторы (ДМРЛ) [1, 2]. Она решается на этапе межпериодной обработки (МПО) эхо-сигналов, отраженных от МО. При наличии мешающих отражений от местных предметов (МП) в виде отдельно стоящих объектов (здания, вышки, трубы и т.д.) или неровностей местности (горы, холмы, земля, леса) результаты оценки спектров МО могут оказаться существенно искаженными, в особенности на малых углах места.

Таким образом, на систему МПО ДМРЛ накладывается дополнительная задача – скомпенсировать или ослабить влияние отражений от МП на результаты доплеровской (спектральной) обработки и тем самым повысить качество информации, выдаваемой ДМРЛ. Одним из возможных вариантов ее решения является применение режекторных фильтров, использующих отличия в частотных свойствах МО и МП, обусловленных различием их радиальных скоростей $~{{V}_{r}}$ и характером межпериодных флюктуаций, определяющим ширину доплеровского спектра $~{{\Delta }}{{F}_{{\text{д}}}}$.

Цель данной работы – статистический синтез и исследования режекторных фильтров с различной глубиной и шириной зон режекции для эффективной компенсации отражений от МП при условии минимальных искажений спектров МО.

1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ МО В ПРИСУТСТВИИ ПОМЕХ

Известно [3, 4], что оптимальной оценкой вектора параметров ${\mathbf{\hat {\Theta }}}~$ = $~\left\{ {{{{{{\hat {\Theta }}}}}_{l}}} \right\}_{{l = 1}}^{L}$ является оценка, максимизирующая отношение правдоподобия $l$ или функционал $f\left( l \right)$ от него:

где ${{p}_{{{\text{сп}}}}}\left( {{\mathbf{u}},{\mathbf{\Theta }}} \right)$ и ${{p}_{{\text{п}}}}\left( {\mathbf{u}} \right)$ – плотности распределений M-мерного вектора входных воздействий ${\mathbf{u}} = \left\{ {{{u}_{i}}} \right\}_{{i = 1}}^{M}$ по гипотезам наличия H₁ в смеси эхо-сигналов от МО или его отсутствия H₀, т.е. наличие только шума и, возможно, отражений от МП соответственно.

Надо отметить, что в качестве функционала обычно выбирается функция, монотонно зависящая от $l$, чаще всего логарифм (${\text{ln}}$). Для анализа уравнения (1) целесообразно воспользоваться наиболее распространенной в практике метеорадиолокации гауссовской аппроксимацией входных воздействий: ${\mathbf{u}}\sim CN\left( {0,{{{\mathbf{\Phi }}}_{1}}\left( {\mathbf{\Theta }} \right)} \right)$ и $~~{\mathbf{u}}\sim CN\left( {0,{{{\mathbf{\Phi }}}_{0}}} \right)$ для гипотез ${{H}_{1}}$ и ${{H}_{0}}$ соответственно. Эта запись означает, что векторы ${\mathbf{u}}$ являются комплексными $C$, нормальными $N$ с нулевым средним и корреляционной матрицей (КМ) $~{\mathbf{\Phi }}$. В этом случае отношение правдоподобия можно представить в виде

а в роли максимизированной может выступать скалярный функционал векторного аргумента Θ: где с – постоянный коэффициент, ${{{\mathbf{\Psi }}}_{{0,1}}} = {\mathbf{\Phi }}_{{0,1}}^{{ - 1}}$ – матрицы, обратные КМ для гипотез ${{H}_{0}}$ и ${{H}_{1}}$ соответственно.

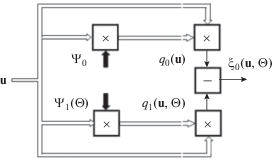
На рис. 1 представлена структурная схема получения функции ${{\xi }}\left( {{\mathbf{u}},{\mathbf{\Theta }}} \right)$, подлежащей максимизации в процессе поиска. Она представляет собой разность двух квадратичных форм вектора входных воздействий с матрицами ${{{\mathbf{\Psi }}}_{0}}\left( {\mathbf{u}} \right)$ и ${{{\mathbf{\Psi }}}_{1}}\left( {{\mathbf{u}},{\mathbf{\Theta }}} \right)$, обратными КМ ${{{\mathbf{\Phi }}}_{0}}$ и ${{{\mathbf{\Phi }}}_{1}}$(Θ). Априори эти матрицы неизвестны и поэтому подлежат оцениванию на этапе адаптации. Вместе с тем известно, что КМ интенсивных отражений от МП имеют достаточно узкий спектр $~\Delta {{F}_{{\text{д}}}} < 1{\text{\;}}\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ (даже в Х-диапазоне) и в смеси со спектром шума сосредоточены в окрестности нулевой доплеровской частоты ${{F}_{{\text{Д}}}} = 0$ (скорость ${{V}_{r}} = 0$). В этой ситуации их можно представить действительными КМ авторегрессионных случайных процессов высокого порядка р с унимодальными спектрами [5, 6].

Учтем, что оптимальное решение поставленной задачи для произвольных КМ ${{{\mathbf{\Phi }}}_{0}}$ и ей обратной ${{{\mathbf{\Psi }}}_{0}}$ сложно, особенно, если доплеровские спектры отражений от МП достаточно широкие. Поэтому предположения, указанные выше и практически доказанные в [6], позволяют свести ее решение к использованию режекторного фильтра на первом этапе МПО в подавляющем большинстве практических случаев. Структуры и параметры режекторных фильтров могут быть различными, а их выбор – неоднозначен и, как правило, продиктован представлением о свойствах отражений от МП или базироваться на ранее полученных экспериментальных данных.

2. СТАТИСТИЧЕСКИЙ СИНТЕЗ РЕЖЕКТОРНЫХ ФИЛЬТРОВ

В качестве базового решения для синтеза режекторных фильтров можно использовать известные из литературы [7] фильтры с конечной импульсной характеристикой (КИХ) произвольного m-го порядка. Они обладают важным свойством, которое заключается в том, что на его выходе обеспечивается минимум мощности помехи, если его дискретная импульсная характеристика пропорциональна первой или последней строке$~~z \times z$-мерной матрице ${{{\mathbf{\Psi }}}^{{\left( z \right)}}} = {{{\mathbf{\Phi }}}^{{\left( z \right) - 1}}}$, где ${{{\mathbf{\Phi }}}^{{\left( z \right)}}}$ – КМ z-мерного вектора помехи на его входе. При этом порядок КИХ-фильтра будет удовлетворять условию $m = z - 1$. Фильтры с такими свойствами в литературе называются фильтрами линейного предсказания с минимальной среднеквадратической ошибкой [8, 9]. Рассмотрим методику синтеза режекторных фильтров на этой основе для произвольного закона зондирования (вобуляции).

Пусть нормированный спектр помехи ${{s}_{{{\text{норм}}}}}\left( f \right)$, подлежащий подавлению, удовлетворяет условию

где $f = {{{{F}_{{\text{Д}}}}} \mathord{\left/ {\vphantom {{{{F}_{{\text{Д}}}}} {{{F}_{{{\text{ср}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{ср}}}}}}}$ − доплеровская частота, нормированная к средней частоте зондирования ${{F}_{{{\text{ср}}}}}$, ${{\rho }_{{pp}}}$ − диагональный элемент нормированной КМ-помехи.

Тогда нормированная $M \times M$ корреляционная матрица помехи ρ = $\left\{ {{{\rho }_{{pq}}}} \right\}_{{p,q = 1}}^{M}$ может быть получена по формуле Винера–Хинчина:

где ${\mathbf{x}}\left( f \right) = \left\{ {{\text{exp}}\left( {j2\pi f{{\gamma }_{l}}} \right)} \right\}_{{l = 1}}^{M}$, ${{\gamma }_{l}} = \sum\nolimits_{i = 1}^{l - 1} {{{{{T}_{i}}} \mathord{\left/ {\vphantom {{{{T}_{i}}} {{{T}_{{{\text{ср}}}}}}}} \right. \kern-0em} {{{T}_{{{\text{ср}}}}}}}} $ – нормированный к среднему интервалу зондирования ${{T}_{{{\text{ср}}}}} = {1 \mathord{\left/ {\vphantom {1 {{{F}_{{{\text{ср}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{ср}}}}}}}$ временной интервал между первым и l‑м импульсами M-элементной пачки.

Если помеха аппроксимируется процессом авторегрессии высокого порядка$~p~$ с известной КМ, то вычислений по формуле (5) не требуется. Для спектров гауссовской формы при $p \to \infty $ можно полагать

где ρ₁ − коэффициент корреляции (КК) отсчетов помехи, следующих с интервалом ${{T}_{{{\text{ср}}}}}$.

Тогда КМ аддитивной смеси шума приемника и помехи с относительной интенсивностью $\kappa $ будет иметь вид

где ${{I}_{M}}$ – единичная $M \times M$ диагональная матрица.

Воспользуемся разложением матрицы, обратной КМ (7), на треугольные сомножители Холецкого ${{{\mathbf{\Psi }}}_{0}} = {\mathbf{\Phi }}_{0}^{{ - 1}} = {\mathbf{H}}{\text{*}}{\mathbf{H}}$, где ${\mathbf{H}} = \left\{ {{{h}_{j}}} \right\}_{{j = 1}}^{z}$ – правый сомножитель нижне-верхнего разложения [10]. Тогда z‑мерные строки матрицы ${\mathbf{H}}$ будут представлять собой импульсные характеристики (ИХ) трансверсального КИХ-фильтра m-го порядка. В частности, такой режекторный фильтр может быть также представлен как каскадное соединение элементарных решетчатых фильтров (ЭРФ) [11–13], как показано на рис. 2 для режекторных фильтров 3-го порядка при $z = 4$. Алгоритм определения параметров его настройки сводится к выбору коэффициентов ${{{{\alpha }}}_{m}}$ и ${{S}_{m}}$. Физический смысл параметра ${{{{\alpha }}}_{m}}$ заключается в нормировании мощности помехи m-й ступени к единице, а параметр ${{S}_{m}}$ должен декоррелировать выходной процесс $m$-й ступени с входным.

3. РЕЖЕКТОРНЫЙ ФИЛЬТР ПОМЕХ С БЛИЗКОЙ К НУЛЕВОЙ ШИРИНОЙ СПЕКТРА

В ходе экспериментов, проведенных на первых отечественных ДМРЛ [6, 14], было показано, что коэффициент корреляции отражений от близко стоящих местных предметов (типа труб и мерзлой земли) стремится к единице ${{\rho }_{1}} \to 1$, если приемопередающие тракты обладают достаточно высокой стабильностью. Поэтому ширина спектра межпериодных флуктуаций таких МП достаточно мала [6]. В пределе можно полагать, что она имеет нулевую ширину: ${{s}_{{{\text{норм}}}}}\left( f \right) = {{\delta }}\left( {f{\text{\;}}} \right)~$ – дельта-функция. Тогда согласно (5) для нормированной корреляционной матрицы можно записать

где ${\mathbf{E}} = \left\{ {{{e}_{i}}} \right\}_{{i = 1}}^{M}$, ${\mathbf{E}}$ – матрица единичного ранга со всеми элементами, равными единице при любом законе зондирования.

В этом случае КМ (7) преобразуется к виду ${{{\mathbf{\Phi }}}_{0}} = {{{\mathbf{I}}}_{M}} + \kappa {\mathbf{EE}}{\text{*}}$, а обратная ей матрица равна

Тогда треугольную матрицу ${\mathbf{H}}$ можно представить суммой

Для элементов диагональных матриц ${\mathbf{D}}1$ и ${\mathbf{D}}2$ справедливы соотношения

а ${\mathbf{G}}$ – нижняя треугольная матрица с нулевой диагональю и единичными поддиагональными элементами.

Согласно этим соотношениям можно показать, что диагональные элементы весового вектора оптимального КИХ-фильтра при $\kappa \gg 1$ и $z \geqslant 2$ имеют следующий вид:

а поддиагональные элементы ${{h}_{{z,~j}}}$ любой строки матрицы ${\mathbf{H}}$ равны z-му диагональному элементу матрицы ${\mathbf{D}}2$.

Свойства матрицы ${\mathbf{H}}$ заключаются в следующем [10, 14]. Сумма ее диагональных и поддиагональных элементов $\sum\nolimits_{i = 1}^z {{{h}_{{z,~j}}}} \approx 0$ при $\kappa \gg 1$ и $z \geqslant 2$, а квадрат нормы при тех же условиях – ${\mathbf{h}}_{z}^{*}{{{\mathbf{h}}}_{z}} = \sum\nolimits_{i = 1}^z {h_{{z,~j}}^{2}} \approx 1$. Эти соотношения позволяют считать, что квадрат модуля частотной характеристики имеет вид

и в точке $f = 0$ близок к нулю. Это условие выполняется для фильтров всех порядков $z \gg 2$ c ИХ ${\mathbf{h}}_{{zz}}^{*} = \left\{ {{{h}_{{z,j}}}} \right\}_{{j = 1}}^{z}$ при $z \in 2,M$ и тем точнее, чем выше порядок фильтра.

При этом свойства нормы ${\mathbf{h}}_{z}^{*}{{{\mathbf{h}}}_{z}}$ означают, что мощность шума на выходе каждого фильтра практически совпадает с мощностью входного некоррелированного шума в смежных z-каналах приема.

На рис. 3а показана 40-элементная вобулированная пачка импульсов, а на рис. 3б – соответствующая ей скоростная характеристика (СХ) ${{K}_{z}}\left( {{{V}_{r}}} \right)$ (для фильтра четвертого порядка) при $\kappa = {{10}^{7}}$, полученная из (12) заменой аргумента $f$ на ${{2{{V}_{r}}{{T}_{{{\text{ср}}}}}} \mathord{\left/ {\vphantom {{2{{V}_{r}}{{T}_{{{\text{ср}}}}}} {{\lambda }}}} \right. \kern-0em} {{\lambda }}}$, где ${{\lambda }}$ – длина волны, ${{T}_{{{\text{ср}}}}}$ – средний период повторения в вобулированной пачке импульсов. На рис. 3в показана та же самая СХ, что и на рис. 3б, но в более широком диапазоне. Из рисунка видно, что в точке ${{V}_{r}} = 0$ СХ имеет очень “глубокий” провал, который подавляет неподвижную компоненту любого МП, практически не трогая даже края спектров отражений от МО.

Однако в ряде случаев, например для МП в виде лиственных лесных массивов или травяного покрова земли в летний период, спектр межпериодных флуктуаций может быть достаточно широким, в частности, за счет ветра. Поэтому в этом случае приемлемы режекторные фильтры с большей шириной провала при ${{V}_{r}} = 0$, чем показано на рис. 3.

4. ФИЛЬТРЫ С РАСШИРЕННОЙ ЗОНОЙ РЕЖЕКЦИИ ПОМЕХ

Синтез фильтра с расширенной зоной режекции также можно осуществить по приведенной выше методике. Простейший способ расширения – это использовать спектр, составленный из $N$ спектров нулевой ширины

где ${{f}_{n}}$ – частота n-й компоненты спектра помехи.

Для такой модели спектра нормированная КМ имеет вид

Соответственно, корреляционная матрица ${{{\mathbf{\Phi }}}_{0}}$ смеси помехи и шума и матрица, обратная ей ${{{\mathbf{\Psi }}}_{0}}$, вычисляются по формулам

Здесь z-мерные подвекторы строки ${{{\mathbf{h}}}_{z}} = \left\{ {{{h}_{{z,j}}}} \right\}_{{j = 1}}^{z}$ нижней треугольной $M \times M$ матрицы ${\mathbf{H}}$ представляют собой импульсные характеристики трансверсальных КИХ-фильтров порядка $m = z - 1$. Эти фильтры должны обеспечить подавление отражений от указанных МП.

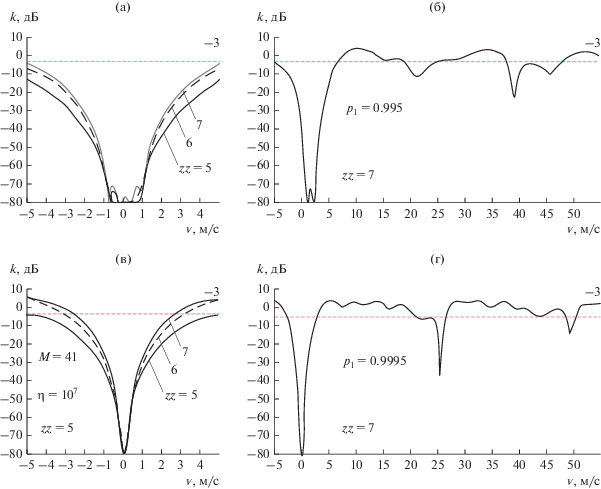
На рис. 4 для пачки импульсов с законом вобуляции (см. рис. 3а) представлены скоростные характеристики режекторных фильтров подавления помех со спектром вида (13). При моделировании были приняты следующие параметры: $N = 3,$ ${{V}_{r}} = {{{{f}_{1}}{{\lambda }}} \mathord{\left/ {\vphantom {{{{f}_{1}}{{\lambda }}} 2}} \right. \kern-0em} 2}$, ${{V}_{2}} = 0$, ${{V}_{3}} = {{ - {{f}_{1}}{{\lambda }}} \mathord{\left/ {\vphantom {{ - {{f}_{1}}{{\lambda }}} 2}} \right. \kern-0em} 2}$ − для рис. 4а; $N = 3,$ ${{V}_{1}} = {{ - 2{{f}_{1}}{{\lambda }}} \mathord{\left/ {\vphantom {{ - 2{{f}_{1}}{{\lambda }}} 2}} \right. \kern-0em} 2}$, ${{V}_{2}} = 0$, ${{V}_{3}} = {{2{{f}_{1}}{{\lambda }}} \mathord{\left/ {\vphantom {{2{{f}_{1}}{{\lambda }}} 2}} \right. \kern-0em} 2}$ – для рис. 4в. При этом было выбрано: ${{{{f}_{1}}{{\lambda }}} \mathord{\left/ {\vphantom {{{{f}_{1}}{{\lambda }}} 2}} \right. \kern-0em} 2} = \Delta {{V}_{r}} = 15{\text{\;}}{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и $\kappa = {{10}^{7}}$. На рис. 4б и 4г показаны те же самые СХ, что и на рис. 4а и 4в соответственно, но в увеличенном масштабе.

Из рис. 4 видно, что, как и в предыдущем случае, в скоростной характеристике этих фильтров имеются достаточно глубокие “провалы” в окрестности нулевой скорости, но при этом наблюдается существенно более широкая зона режекции по сравнению с рис. 3б. Ширина этой зоны эффективно регулируется значениями $\Delta {{V}_{r}}$, порядком фильтра $m = z - 1$, а также задаваемой интенсивностью помехи $\kappa $.

Очевидно, что в качестве исходных здесь могут использоваться не только дискретные спектры вида (13), но и непрерывные спектры. На рис. 5 представлены скоростные характеристики фильтров подавления помех с нормированной КМ вида (6) при ${{\rho }_{1}} = 0.995$ (рис. 5а, 5б) и ${{\rho }_{1}} = 0.9995$, (рис. 5в, 5г), $\kappa = {{10}^{7}}$.

Видно, что в этих случаях также формируется глубокий провал в окрестности ${{V}_{r}} = 0$, ширина и глубина которого могут эффективно регулироваться выбором значения коэффициента корреляции. Причем чем больше значение ${{\rho }_{1}}$, тем ýже и глубже провал в скоростной характеристике.

На рис. 6а показано одно из экспериментальных конических сечений пространства, иллюстрирующее отражаемость обстановки на малых углах места без использования режекторного фильтра. Видно, что в ближней зоне доплеровского метеорадиолокатора (окрашено темным цветом) из-за влияния местных предметов оценка характеристик МО практически невозможна. После введения КИХ-фильтра 8-го порядка (рис. 6б) отражения от МП в основном подавлены, что создает условия получения корректных оценок параметров МО.

ЗАКЛЮЧЕНИЕ

$1.{\text{\;}}$ Показано, что задача оценивания параметров метеообразований при наличии отражений от местных предметов сводится к максимизации функционала от отношения правдоподобия. При этом можно сделать обоснованное предположение о гауссовом характере входных воздействий, в которых смесь шума и отражений от местных предметов является помехой, а отражения от метеообразований играют роль полезного сигнала.

$2.{\text{\;}}$ Методика синтеза межпериодной обработки, оптимальной в статистическом смысле, сводится к отысканию матрицы, обратной корреляционной матрице входного процесса, а оптимальный весовой вектор обработки определяется как строка (столбец) ее треугольного сомножителя разложения Холецкого. В предположении о высокой интенсивности и узком доплеровском спектре флуктуации местных предметов (при высоком значении коэффициента корреляции) задача упрощается и сводится к выбору параметров неадаптивного режекторного фильтра (КИХ-фильтра).

$3.{\text{\;}}$ Проведен синтез фильтра с близкой к нулю широкой зоной режекции и определены его импульсная и частотная характеристики. Для 40-элементной вобулированной пачки импульсов представлен конкретный пример частотной характеристики фильтра с глубоким провалом в области нулевой скорости.

4. Синтез фильтра с расширенной зоной режекции проведен на основе представления спектра помехи в виде суммы спектров ${{\delta }}$-образной формы. Для тех же условий, что и в п. 3, представлены примеры частотных характеристик с различной шириной зоны режекции и определены параметры, которые могут управлять шириной и глубиной “провала” в зоне воздействия помех.

Полученные результаты были использованы в первых отечественных доплеровских метеорадиолокаторах C- и Х-диапазонов, где за счет применения режекторных фильтров удалось повысить качество выдаваемой информации.