Радиотехника и электроника, 2022, T. 67, № 3, стр. 249-258

Синтез бифокальных зеркально-линзовых цилиндрических систем с минимальными аберрациями

В. А. Калошин^a, *, Ви Ут Нам^b

^a Институт радиотехники и электроники им. В.А. Котельникова РАН
125007 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

^b Московский физико-технический институт (национальный исследовательский университет)
141700 Долгопрудный, Московской обл., Институтский пер. 9, Российская Федерация

^* E-mail: vak@cplire.ru

Поступила в редакцию 10.03.2021
После доработки 10.03.2021
Принята к публикации 28.03.2021

EDN: NRDWPX
DOI: 10.31857/S0033849422020061

Полный текст (PDF)

Аннотация

Развита методика синтеза и оптимизации бифокальных зеркально-линзовых цилиндрических систем с использованием последовательного нахождения участков первой поверхности диэлектрической линзы и зеркала, примыкающего ко второй поверхности линзы. При этом начальный участок первой поверхности линзы задается в виде полинома второго порядка, параметры которого определяются в результате решения найденного в работе уравнения в общем случае обеспечивающего непрерывность вторых производных функций, описывающих поверхности линзы и зеркала. Начальный участок зеркала находится в результате решения задачи синтеза плоского фронта для центрального положения источника. Определены параметры оптимизации с целью минимизации величины средне-квадратической аберрации при фиксированной толщине линзы, коэффициенте преломления и угле зрения бифокальной системы. На плоскости этих параметров для углов зрения 50, 70 и 100 градусов найдены области существования решения задачи синтеза, зависимости величины средне-квадратической аберрации от параметров оптимизации и набор параметров, обеспечивающих ее минимальное значение.

ВВЕДЕНИЕ

Цилиндрические зеркальные, линзовые и зеркально-линзовые фокусирующие системы применяются в качестве планарных диаграммо-образующих систем (ДОС) многолучевых антенных решеток [1–6] и антенн с главным зеркалом в виде параболического цилиндра [7].

Цилиндрические зеркально-линзовые ДОС можно реализовать в виде двухслойной конструкции [1, 3, 5, 6, 8], что является преимуществом перед трехслойной конструкцией двухзеркальных ДОС [6, 9]. Апланатические и бифокальные зеркально-линзовые ДОС позволяют обеспечить более широкий угол зрения по сравнению с однозеркальными ДОС [2]. При этом зеркально-линзовые ДОС на основе диэлектрических линз имеют меньшие потери и более простую конструкцию по сравнению с ДОС на основе линз с принудительным преломлением [1, 3].

В работе [10] была синтезирована зеркально-линзовая апланатическая система на основе диэлектрической линзы и проведены исследования зависимости средне-квадратической аберрации (СКА) от параметров системы.

В работе [5] с использованием последовательного нахождения участков первой поверхности диэлектрической линзы и зеркала, примыкающего ко второй поверхности линзы, была синтезирована и исследована бифокальная ДОС, которая обеспечивает меньшую величину СКА в заданном угле зрения, чем апланатическая. При этом вопрос об оптимальных параметрах такой системы, обеспечивающих минимальную величину СКА, остался открытым.

Следует отметить, что можно реализовать бифокальную волноводно-щелевую решетку с использованием двухслойной однозеркальной ДОС [4], а трехфокальную волноводно-щелевую антенную решетку – с использованием зеркально-линзовой ДОС на основе диэлектрической линзы [6]. Однако в процессе синтеза в этих работах в качестве дополнительной степени свободы использовалось определенное положение щелей в волноводах решеток, что ограничивает ширину рабочей полосы частот и область применения ДОС.

Цель данной работы – развитие методики синтеза и оптимизации цилиндрических бифокальных зеркально-линзовых ДОС на основе диэлектрической линзы с целью реализации минимальной СКА в заданном угле зрения и ее апробация на конкретных примерах.

1. МЕТОДИКА СИНТЕЗА БИФОКАЛЬНОЙ ЗЕРКАЛЬНО-ЛИНЗОВОЙ СИСТЕМЫ

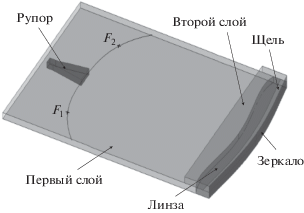
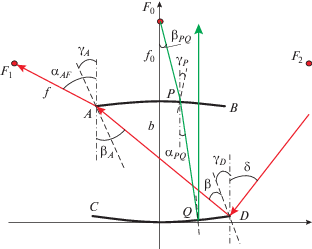
Рассмотрим задачу синтеза зеркально-линзовой бифокальной системы, которая фокусирует поле источника цилиндрической волны, расположенного в любом из двух фокусов (F₁, F₂) в первом слое (рис. 1) в плоскую волну во втором слое. Система содержит цилиндрическую диэлектрическую линзу и зеркало, поверхность которого совпадает со второй поверхностью линзы. Первый и второй слои связаны через щель, форма которой совпадает с формой зеркала (металлизированной второй поверхностью линзы). Предположим, что задан коэффициент преломления линзы n, а форма первой поверхности линзы (далее – поверхность линзы) и зеркала описываются четными функциями y₁(x) и y₂(x), соответственно. При этом поверхности линзы и зеркала симметричны относительно оси y и пересекают ее в точках с декартовыми координатами (0, b) и (0, 0) соответственно (рис. 2). Задача синтеза заключается в нахождении этих функций.

Рис. 1.

Конструкция двухслойной зеркально-линзовой бифокальной системы.

Рис. 2.

Начальные участки зеркала и линзы.

Для решения задачи применим, как и в работе [5], методику последовательного нахождения участков поверхности линзы и зеркала. Предложим, что форма начального участка поверхности линзы (между точками A и B) известна, т.е. функция y₁(x) = y₁₀(x) на интервале [–x₀, x₀], где y₁₀(x) – известная функция.

Осевой луч, выходящий из точки F₀ с декартовыми координатами (0, b + f₀), идет вдоль оси y и не преломляется линзой. Эйконал этого луча от точки F₀ до плоского фронта (y = b + f₀) определяется формулой L₀ = 2f₀ + (n + 1)b, где f₀ – расстояние от точки F₀ до поверхности линзы.

Рассмотрим другой луч, выходящий из фокуса F₀ и падающий на поверхность линзы в точке P с координатами (x_P, y_P). Луч преломляется линзой, падает на зеркало в точке Q с координатами (x_Q, y_Q) и отражается от него. Эйконал этого луча определяется формулой

(1)

$\begin{gathered} L = \sqrt {x_{P}^{2} + {{{({{f}_{0}} + b - {{y}_{P}})}}^{2}}} + n{{l}_{{PQ}}} + {{f}_{0}} + \\ + \,\,b - {{y}_{P}} - {{l}_{{PQ}}}\frac{{\sqrt {{{n}^{2}} + S_{{FP}}^{2}} - {{S}_{{FP}}}y_{P}^{'}}}{{n\sqrt {(1 + y_{P}^{{'2}})} }}, \\ \end{gathered} $

где

$\begin{gathered} y_{P}^{'} = \left. {{{d{{y}_{1}}} \mathord{\left/ {\vphantom {{d{{y}_{1}}} {dx}}} \right. \kern-0em} {dx}}} \right|x = {{x}_{P}}; \\ {{S}_{{FP}}} = \frac{{{{x}_{P}} - y_{P}^{'}(b + {{f}_{0}} - {{y}_{P}})}}{{\sqrt {{{{({{x}_{P}} - y_{P}^{'}(b + {{f}_{0}} - {{y}_{P}}))}}^{2}} + ({{x}_{P}}y_{P}^{'} + b + {{f}_{0}} - {{y}_{P}}){{)}^{2}}} }}; \\ \end{gathered} $

l_PQ – расстояние от точки P до точки Q (рис. 2).

Потребуем, чтобы все лучи, выходящие из точки F₀, после преломления линзой и отражения от зеркала были параллельны оси y. Для этого необходимо равенство эйконалов всех лучей от источника до фронта. Приравняем эйконал произвольного луча эйконалу осевого луча:

$\sqrt {x_{P}^{2} + {{{({{f}_{0}} + b - {{y}_{P}})}}^{2}}} + n{{l}_{{PQ}}} + {{f}_{0}} + b - {{y}_{P}} - \,\,{{l}_{{PQ}}}\frac{{\sqrt {{{n}^{2}} + S_{{FP}}^{2}} - {{S}_{{FP}}}y_{P}^{'}}}{{n\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} }} = 2{{f}_{0}} + (1 + n)b{\kern 1pt} .$

Решение этого уравнения имеет вид

(3)

${{l}_{{PQ}}} = n\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} \frac{{{{f}_{0}} + nb + {{y}_{P}} - \sqrt {x_{P}^{2} + {{{({{f}_{0}} + b - {{y}_{P}})}}^{2}}} }}{{\left( {{{n}^{2}}\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} + \sqrt {{{n}^{2}} + S_{{FP}}^{2}} - {{S}_{{FP}}}y_{P}^{'}} \right)}}.$

Координаты точки Q определяются формулой

(4)

$\begin{gathered} {{x}_{Q}} = {{x}_{P}} + \frac{{{{f}_{0}} + nb + {{y}_{P}} - \sqrt {x_{P}^{2} + {{{({{f}_{0}} + b - {{y}_{P}})}}^{2}}} }}{{\left( {{{n}^{2}}\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} + \sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} - {{S}_{{FP}}}y_{P}^{'}} \right)}} \times \\ \times \,\,\left( {y_{P}^{'}\sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} + {{S}_{{FP}}}} \right), \\ {{y}_{Q}} = {{y}_{P}} + \frac{{{{f}_{0}} + nb + {{y}_{P}} - \sqrt {{{x}_{P}}^{2} + {{{({{f}_{0}} + b - {{y}_{P}})}}^{2}}} }}{{\left( {{{n}^{2}}\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} + \sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} - {{S}_{{FP}}}y_{P}^{'}} \right)}} \times \\ \times \,\,\left( {\sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} - {{S}_{{FP}}}y_{P}^{'}} \right). \\ \end{gathered} $

Множество точек Q образует начальный участок зеркала.

Первая производная функции y₂(x) = y_Q(x_Q), описывающей поверхность начального участка зеркала, определяется формулой

(5)

$\begin{gathered} y_{Q}^{'}({{x}_{Q}}) = \frac{{n\sin ({{\alpha }_{{PQ}}})}}{{1 + n\cos ({{\alpha }_{{PQ}}})}} = \\ = \frac{{y_{P}^{'}\sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} + {{S}_{{FP}}}}}{{\sqrt {(1 + y_{P}^{{'{\kern 1pt} 2}})} + \sqrt {{{n}^{2}} + {{S}_{{FP}}}^{2}} - {{S}_{{FP}}}y_{P}^{'}}}. \\ \end{gathered} $

Для реализации непрерывности функций, описывающих форму поверхности зеркала и линзы, и их производных на стыках (A, D) начальных участков с соседними необходимо, чтобы луч плоской волны, падающей на зеркало под углом δ к оси y, после отражения в точке D попадал в точку A, а после преломления в точке A – в фокус F₁. Из геометрии на рис. 2 нетрудно найти координаты этого фокуса, а также фокуса F₂, учитывая, что он симметричен фокусу F₁ относительно оси y:

(6)

$\begin{gathered} {{x}_{{{{F}_{1}}}}} = - {{x}_{0}} - f\frac{{n{{S}_{{AD}}} - y_{0}^{'}\sqrt {1 - {{n}^{2}}S_{{AD}}^{2}} }}{{\sqrt {(1 + y{{{_{0}^{'}}}^{2}})} }};\,\,\,{{x}_{{{{F}_{2}}}}} = - {{x}_{{{{F}_{1}}}}}; \\ {{y}_{{{{F}_{1}}}}} = {{y}_{0}} - f\frac{{n{{S}_{{AD}}}y_{0}^{'} + \sqrt {1 - {{n}^{2}}S_{{AD}}^{2}} }}{{\sqrt {(1 + y{{{_{0}^{'}}}^{2}})} }};\,\,\,\,{{y}_{{{{F}_{2}}}}} = {{y}_{{{{F}_{1}}}}}; \\ \end{gathered} $

где

${{S}_{{AD}}} = \frac{{({{x}_{D}} - {{x}_{A}}) + y_{A}^{'}({{y}_{D}} - {{y}_{A}})}}{{\sqrt {{{{(({{x}_{D}} - {{x}_{A}}) + y_{A}^{'}({{y}_{D}} - {{y}_{A}}))}}^{2}} + {{{(({{x}_{D}} - {{x}_{A}})y_{A}^{'} - ({{y}_{D}} - {{y}_{A}}))}}^{2}}} }};$

y₀ = y₁₀(–x₀); $y_{A}^{'} = \left. {{{d{{y}_{1}}} \mathord{\left/ {\vphantom {{d{{y}_{1}}} {dx}}} \right. \kern-0em} {dx}}} \right|x = {{x}_{A}}$, а f – расстояние от края начального участка линзы до фокуса.

Рассмотрим луч, который выходит из фокуса F₁, падает на линзу в точке A, преломляется, падает в точку D, отражается от зеркала и выходит под углом δ к оси Y. Этот угол определяется формулой

(7)

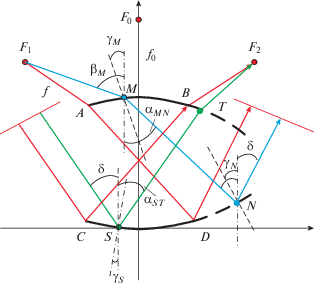
$\delta = \arcsin \left( {\frac{{n(({{x}_{D}} - {{x}_{A}}) - y_{D}^{'}({{y}_{D}} - {{y}_{A}}))}}{{\sqrt {{{{(({{x}_{D}} - {{x}_{A}}) - y_{D}^{'}({{y}_{D}} - {{y}_{A}}))}}^{2}} + {{{(({{x}_{D}} - {{x}_{A}})y_{D}^{'} + ({{y}_{D}} - {{y}_{A}}))}}^{2}}} }}} \right) + \operatorname{arctg} (y_{D}^{'}),$

где $y_{D}^{'} = \left. {{{d{{y}_{2}}} \mathord{\left/ {\vphantom {{d{{y}_{2}}} {dx}}} \right. \kern-0em} {dx}}} \right|x = {{x}_{D}}$.

Для определения нового участка зеркала предположим, что луч из фокуса ${{F}_{1}}$ падает на начальный участок линзы в точке M с координатами (x_M, y_M), $( - {{x}_{0}} \leqslant {{x}_{M}} \leqslant {{x}_{0}})$, преломляется, падает на зеркало в точке N с координатами (x_N, y_N) и отражается под углом $\delta $ к оси y (рис. 3). Отсюда для угла между осью y и падающим из точки ${{F}_{1}}$ в точку M лучом получаем ${{\beta }_{M}} = \operatorname{arctg} ({{({{x}_{M}} - {{x}_{{F1}}})} \mathord{\left/ {\vphantom {{({{x}_{M}} - {{x}_{{F1}}})} {({{y}_{{F1}}} - {{y}_{M}})}}} \right. \kern-0em} {({{y}_{{F1}}} - {{y}_{M}})}})$. Угол между осью y и лучом, проходящим через линзу от точки M до точки N, определяется формулой

(8)

${{\alpha }_{{MN}}} = {\text{arcsin}}\left( {\frac{{({{x}_{M}} - {{x}_{{F1}}}) - y_{M}^{'}({{y}_{M}} - {{y}_{F}})}}{{n\sqrt {{{{(({{x}_{M}} - {{x}_{{F1}}}) - y_{M}^{'}({{y}_{M}} - {{y}_{F}}))}}^{2}} + {{{(({{x}_{M}} - {{x}_{{F1}}})y_{M}^{'} + ({{y}_{M}} - {{y}_{F}}))}}^{2}}} }}} \right) + \operatorname{arctg} ( - y_{M}^{'}),$

где $y_{M}^{'} = \left. {{{d{{y}_{1}}} \mathord{\left/ {\vphantom {{d{{y}_{1}}} {dx}}} \right. \kern-0em} {dx}}} \right|x = {{x}_{M}}$.

Рис. 3.

К определению нового участка зеркала.

Из условия равенства эйконалов всех лучей, которые выходят из фокуса, после преломления линзой и отражения от зеркала, получаем уравнение

(9)

$\sqrt {{{{({{x}_{M}} - {{x}_{{{{F}_{1}}}}})}}^{2}} + {{{({{y}_{M}} - {{y}_{{{{F}_{1}}}}})}}^{2}}} + n{{l}_{{MN}}} - {{x}_{N}}\sin (\delta ) - \,{{y}_{N}}\cos (\delta ) = f + n{{l}_{0}} - {{x}_{D}}\sin (\delta ) - {{y}_{D}}\cos (\delta ),$

где ${{l}_{0}} = \sqrt {{{{({{x}_{D}} - {{x}_{A}})}}^{2}} + {{{({{y}_{D}} - {{y}_{A}})}}^{2}}} $; l_MN – расстояние от точки M до точки N, δ – угол между выходящими лучами и осью y.

Решение уравнения (9) имеет вид

(10)

${{l}_{{MN}}} = \frac{{f - \sqrt {{{{({{x}_{M}} - {{x}_{{{{F}_{1}}}}})}}^{2}} + {{{({{y}_{M}} - {{y}_{{{{F}_{1}}}}})}}^{2}}} + n{{l}_{0}} + ({{x}_{M}} - {{x}_{A}})\sin (\delta ) + ({{y}_{M}} - {{y}_{A}})\cos (\delta )}}{{n - \sin ({{\alpha }_{{MN}}})\sin (\delta ) + \cos ({{\alpha }_{{NM}}})\cos (\delta )}}.$

Зная длину l_MN и угол α_MN, можно определить координаты точки N по формулам

(11)

$\begin{gathered} {{x}_{N}} = {{x}_{M}} + {{l}_{{MN}}}\sin ({{\alpha }_{{MN}}}), \\ {{y}_{N}} = {{y}_{M}} - {{l}_{{MN}}}\cos ({{\alpha }_{{MN}}}). \\ \end{gathered} $

Множество точек N образует новый участок зеркала. При этом функции y₂(x) и ее первая производная непрерывны в точке D стыка начального участка зеркала с новым (соседним) участком.

Из законов преломления и отражения в точке N получим

(12)

$y_{N}^{'}({{x}_{N}}) = \frac{{n\sin ({{\alpha }_{{MN}}}) - \sin (\delta )}}{{n\cos ({{\alpha }_{{MN}}}) + \cos (\delta )}}.$

Для определения нового участка линзы рассмотрим падение плоской волны на начальный участок зеркала. Пусть один из лучей падает на зеркало в точке S с координатами (x_S, y_S) под углом δ к оси y. Этот луч отражается от зеркала, проходит через линзу, после преломления выходит из точки T с координатами (x_T, y_T) и проходит через фокус ${{F}_{2}}$ (см. рис. 2). Угол между осью Y и отрезком ST определяется формулой

(13)

$\begin{gathered} {{\alpha }_{{ST}}} = \arcsin \left( {\frac{{W(1 + y_{D}^{'}y_{S}^{'}) + (y_{D}^{'} - y_{S}^{'})\sqrt {1 - {{W}^{2}}} }}{{\sqrt {{{{(y_{D}^{'} - y_{S}^{'})}}^{2}} + {{{(1 + y_{D}^{'}y_{S}^{'})}}^{2}}} }}} \right) - \\ - \,\,\operatorname{arctg} (y_{S}^{'}), \\ \end{gathered} $

где $y_{S}^{'} = \left. {{{dy} \mathord{\left/ {\vphantom {{dy} {dx}}} \right. \kern-0em} {dx}}} \right|x = {{x}_{S}}$;

$W = \frac{{(({{x}_{D}} - {{x}_{A}}) - y_{D}^{'}({{y}_{D}} - {{y}_{A}}))}}{{\sqrt {{{{(({{x}_{D}} - {{x}_{A}}) - y_{D}^{'}({{y}_{D}} - {{y}_{A}}))}}^{2}} + {{{(({{x}_{D}} - {{x}_{A}})y_{D}^{'} + ({{y}_{D}} - {{y}_{A}}))}}^{2}}} }}.$

Из условия равенства эйконалов лучей получаем уравнение

(14)

${{d}_{{SC}}} + n{{l}_{{ST}}} + \sqrt {{{{({{x}_{S}} + {{l}_{{ST}}}\sin ({{\alpha }_{{ST}}}) - {{x}_{{{{F}_{2}}}}})}}^{2}} + {{{({{y}_{S}} + {{l}_{{ST}}}\cos ({{\alpha }_{{ST}}}) - {{y}_{{{{F}_{2}}}}})}}^{2}}} = n{{l}_{0}} + f,$

где ${{d}_{{SC}}} = ({{x}_{S}} - {{x}_{C}})\sin (\delta ) - ({{y}_{S}} - {{y}_{C}})\cos (\delta )$.

Решение уравнения (14) имеет вид

(15)

${{l}_{{PQ}}} = \frac{{ - B - \sqrt {{{B}^{2}} - AC} }}{A},$

где $A = {{n}^{2}} - 1$; $B = ({{x}_{{{{F}_{2}}}}} - {{x}_{S}})\sin ({{\alpha }_{{ST}}}) + ({{y}_{{{{F}_{2}}}}} - {{y}_{S}}) \times $ $ \times \,\,\cos ({{\alpha }_{{ST}}})\,\,\, + $ $n({{d}_{{SC}}} - f - {{l}_{0}})$; $C = {{({{d}_{{SC}}} - f - {{l}_{0}})}^{2}} + $ $ + \,\,{{({{x}_{S}} - {{x}_{{{{F}_{2}}}}})}^{2}} - {{({{y}_{S}} - {{y}_{{{{F}_{2}}}}})}^{2}}$.

Координаты точки T нового отрезка линзы рассчитываются по формулам

(16)

$\begin{gathered} {{x}_{T}} = {{x}_{S}} + {{l}_{{ST}}}\sin ({{\alpha }_{{ST}}}), \\ {{y}_{T}} = {{y}_{S}} + {{l}_{{ST}}}\cos ({{\alpha }_{{ST}}}). \\ \end{gathered} $

Из закона преломления находим первую производную функции, описывающую новый участок линзы:

(17)

$y_{T}^{'}({{x}_{T}}) = \frac{{\sin ({{\beta }_{T}}) - n\sin ({{\alpha }_{{ST}}})}}{{\cos ({{\beta }_{T}}) - n\cos ({{\alpha }_{{ST}}})}},$

где ${{\beta }_{T}} = {\text{arctg}}({{({{x}_{{{{F}_{2}}}}} - {{x}_{T}})} \mathord{\left/ {\vphantom {{({{x}_{{{{F}_{2}}}}} - {{x}_{T}})} {({{y}_{{{{F}_{2}}}}} - {{y}_{T}})}}} \right. \kern-0em} {({{y}_{{{{F}_{2}}}}} - {{y}_{T}})}})$.

Множество точек T образует новый участок линзы. При этом функции y₁(x) и ее первая производная также непрерывны на стыке B начального участка зеркала с новым (соседним) участком.

Непрерывность функций, описывающих поверхности линзы и зеркала и их первых производных, обеспечивает непрерывность фазового распределения поля на выходе системы в приближении геометрической оптики. Для обеспечения непрерывности амплитудного распределения необходимо, чтобы вторые производные функций, описывающих поверхности линзы и зеркала в местах стыков соседних участков также были непрерывными. Для этого необходимо и достаточно удовлетворить этому условию для точек стыков с начальным участком зеркала. Непрерывность вторых производных в остальных точках поверхности линзы и зеркала обеспечивается автоматически.

Вторую производную функций y_Q(x_Q), y_N(x_N), описывающих начальный и второй участок поверхности зеркала, можно получить дифференцированием (5) и (12) по x_P и x_M соответственно. При совпадении точек Q и D, D и N заменим x_P на – x₀, а x_M на x₀. В результате, получим уравнение, решение которого обеспечивает непрерывность вторых производных функции y₁(x):

(18)

$\frac{{\alpha _{M}^{'}(q{{S}_{l}} - n\sqrt {{{q}^{2}} + 1} - {{C}_{l}}){{v}_{0}}^{2}({{q}^{2}} + 1)}}{{{{{(n + {{C}_{l}} + \sqrt {{{q}^{2}} + 1} )}}^{2}}({{v}_{0}}^{2}\sqrt {{{q}^{2}} + 1} + (u_{0}^{'}{{v}_{0}} - {{u}_{0}}v_{0}^{'})q + \alpha _{M}^{'})}} + \frac{{\alpha _{G}^{'}(n + {{C}_{p}})}}{{{{{(n + {{C}_{p}} + 1)}}^{2}}(1 + l{\kern 1pt} '{{C}_{p}} + l{{C}_{p}}\alpha _{G}^{'})}} = 0,$

где

$\begin{gathered} u_{0}^{'} = {{S}_{l}} - {{S}_{e}} - y_{0}^{'}({{C}_{l}} + {{C}_{e}});\,\,\,\,\,{{u}_{0}} = n\sqrt {{{{(2{{x}_{0}} + l{{S}_{p}})}}^{2}} + {{{(l{{C}_{p}})}}^{2}}} + (2{{x}_{0}} + l{{S}_{p}}){{S}_{l}} + l{{C}_{p}}{{C}_{l}}; \\ {{v}_{0}} = n - {{((2{{x}_{0}} + l{{S}_{p}}){{S}_{l}} + l{{C}_{p}}{{C}_{l}})} \mathord{\left/ {\vphantom {{((2{{x}_{0}} + l{{S}_{p}}){{S}_{l}} + l{{C}_{p}}{{C}_{l}})} {(l{{C}_{p}}\sqrt {{{q}^{2}} + 1} )}}} \right. \kern-0em} {(l{{C}_{p}}\sqrt {{{q}^{2}} + 1} )}};\,\,\,\,\,\,\,v_{0}^{'} = {{ - \alpha _{M}^{'}(q{{C}_{l}} + {{S}_{l}})} \mathord{\left/ {\vphantom {{ - \alpha _{M}^{'}(q{{C}_{l}} + {{S}_{l}})} {\sqrt {{{q}^{2}} + 1} }}} \right. \kern-0em} {\sqrt {{{q}^{2}} + 1} }}; \\ \alpha _{M}^{'} = \frac{{y_{0}^{{''}}}}{{1 + y_{0}^{{'2}}}} + \frac{{({{C}_{e}} - {{S}_{e}}y_{0}^{'})(\beta _{M}^{'}(1 + y_{0}^{{'2}}) + y_{0}^{{''}})}}{{(1 + y_{0}^{{'2}})\sqrt {{{n}^{2}}(1 + y_{0}^{{'2}}) - ({{S}_{e}} + {{C}_{e}}y_{0}^{'})} }}; \\ \end{gathered} $

$\begin{gathered} \beta _{M}^{'} = \frac{{{{C}_{e}} - y_{0}^{'}{{S}_{e}}}}{{f(C_{e}^{2} - S_{e}^{2})}};\,\,\,\,{{S}_{e}} = \frac{{n{{S}_{b}} - y_{0}^{'}\sqrt {1 - {{n}^{2}}S_{b}^{2}} }}{{\sqrt {(1 + y{{{_{0}^{'}}}^{2}})} }};\,\,\,\,{{C}_{e}} = \frac{{n{{S}_{b}}y_{0}^{'} + \sqrt {1 - {{n}^{2}}{{S}_{b}}^{2}} }}{{\sqrt {(1 + y_{0}^{{'2}})} }};\,\,\,\,{{S}_{b}} = \frac{{2{{x}_{0}} + l(y_{0}^{'}{{C}_{p}} + {{S}_{p}})}}{{\sqrt {(1 + y_{0}^{{'2}})} }}; \\ q = \frac{{2{{x}_{0}} + l{{S}_{p}}}}{{l{{C}_{p}}}};\,\,\,\,{{S}_{l}} = \frac{{n{{S}_{r}}(n{{C}_{p}} + 1) - n{{S}_{p}}\sqrt {1 - {{n}^{2}}S_{r}^{2}} }}{{\sqrt {{{n}^{2}}S_{r}^{2} + {{{(n{{C}_{p}} + 1)}}^{2}}} }};\,\,\,\,\,{{C}_{l}} = \frac{{{{n}^{2}}{{S}_{r}}{{S}_{p}} + (n{{C}_{p}} + 1)\sqrt {1 - {{n}^{2}}S_{r}^{2}} }}{{\sqrt {{{n}^{2}}S_{r}^{2} + {{{(n{{C}_{p}} + 1)}}^{2}}} }};\,\,\,\,h = \frac{{n{{S}_{p}}}}{{n{{C}_{p}} + 1}}; \\ \end{gathered} $

$\begin{gathered} {{S}_{r}} = \frac{{q - h}}{{\sqrt {{{{(q - h)}}^{2}} + {{{(1 + qh)}}^{2}}} }}; \\ l = \frac{{{{f}_{0}} + {{y}_{0}} + nb - \sqrt {x_{0}^{2} + {{{(b + {{f}_{0}} - {{y}_{0}})}}^{2}}} }}{{n + {{C}_{p}}}}; \\ l{\kern 1pt} ' = \frac{{(y_{0}^{'} - {{F}_{P}} + l{{S}_{p}}{{\alpha }_{G}})}}{{n + {{C}_{p}}}};\,\,\,\,{{F}_{P}} = \frac{{{{x}_{0}} - y_{0}^{'}(b + {{f}_{0}} - {{y}_{0}})}}{{\sqrt {x_{0}^{2} + {{{(b + {{f}_{0}} - {{y}_{0}})}}^{2}}} }}; \\ {{\alpha }_{G}} = \frac{{y_{0}^{{''}}}}{{1 + y_{0}^{{'2}}}} + \frac{{{{C}_{x}}}}{{\sqrt {{{n}^{2}} - S_{x}^{2}} }}\left( {\beta _{P}^{'} - \frac{{y_{0}^{{''}}}}{{1 + y_{0}^{{'2}}}}} \right); \\ {{C}_{x}} = \frac{{b + {{f}_{0}} - {{y}_{0}} + {{x}_{0}}y_{0}^{'}}}{{\sqrt {{{{({{x}_{0}} - (b + {{f}_{0}} - {{y}_{0}})y_{0}^{'})}}^{2}} + {{{(b + {{f}_{0}} - {{y}_{0}} + {{x}_{0}}y_{0}^{'})}}^{2}}} }}; \\ {{S}_{x}} = \frac{{{{x}_{0}} - (b + {{f}_{0}} - {{y}_{0}})y_{0}^{'}}}{{\sqrt {{{{({{x}_{0}} - (b + {{f}_{0}} - {{y}_{0}})y_{0}^{'})}}^{2}} + {{{(b + {{f}_{0}} - {{y}_{0}} + {{x}_{0}}y_{0}^{'})}}^{2}}} }}; \\ \end{gathered} $

$\begin{gathered} {{C}_{p}} = \frac{{\sqrt {{{n}^{2}} + S_{t}^{2}} - {{S}_{t}}y_{0}^{'}}}{{n\sqrt {(1 + y_{0}^{{'2}})} }};\,\,\,\,{{S}_{p}} = \frac{{y_{0}^{'}\sqrt {{{n}^{2}} + {{S}_{t}}^{2}} + {{S}_{t}}}}{{n\sqrt {(1 + y_{0}^{{'2}})} }}; \\ {{S}_{t}} = \frac{{{{x}_{0}} - y_{0}^{'}(b + {{f}_{0}} - {{y}_{0}})}}{{\sqrt {{{{({{x}_{0}} - y_{0}^{'}(b + {{f}_{0}} - {{y}_{0}}))}}^{2}} + ({{x}_{0}}y_{0}^{'} + b + {{f}_{0}} - {{y}_{0}}){{)}^{2}}} }}; \\ \beta _{P}^{'} = \frac{{{{x}_{0}}y_{0}^{'} + b + {{f}_{0}} - {{y}_{0}}}}{{\sqrt {x_{0}^{2} + {{{(b + {{f}_{0}} - {{y}_{0}})}}^{2}}} }}; \\ \end{gathered} $

${{y}_{0}}$, $y_{0}^{'}$, $y_{0}^{{''}}$ – значения соответственно функции y₁(x), ее первой и второй производной в точке B с координатами (x₀, y₀).

2. СИНТЕЗ И ОПТИМИЗАЦИЯ ЗЕРКАЛЬНО-ЛИНЗОВОЙ СИСТЕМЫ

Для синтеза зеркально-линзовой бифокальной системы зададим исходные параметры: расстояние b между центральными точками наповерхности линзы и зеркала (толщина линзы), полуразмер x₀ начального отрезка поверхности линзы, расстояние f от конца начального отрезка поверхности линзы до фокуса F₁, расстояние f₀ от центральной точки поверхности линзы до фокуса начальной системы F₀. Будем синтезировать бифокальную систему с начальным отрезком зеркала в виде полинома второго порядка y₁₀(x) = ax²+ b.

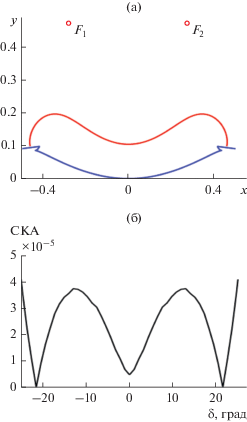
Подставляя y₀= $ax_{0}^{2}$ + b, $y_{0}^{'}$ = 2ax₀, 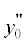= 2a в уравнение (18) и решая его с использованием стандартной численной процедуры, находим параметр a. Реализуя описанный выше алгоритм синтеза новых отрезков m раз, находим форму поверхности линзы и зеркала, которые имеют непрерывные первые и вторые производные.

Задача оптимизации состоит в нахождении геометрических параметров системы, а также формы фокальной кривой, обеспечивающих минимальную средне-квадратическую аберрацию (СКА) эйконала на выходе ДОС, которую будем определять по формуле

(19)

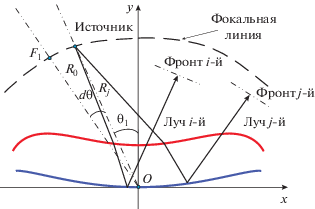
$\sigma = \frac{1}{D}\sqrt {\frac{1}{k}\sum\limits_{i = 1}^k {{{{({{L}_{i}} - {{L}_{0}})}}^{2}}} } ,$

где L_i – эйконал луча с номером i; k – количество учтенных лучей, D – размер апертуры системы; L₀ – эйконал луча, относительно которого СКА имеет минимальное значение (далее – опорный луч).

Для вычисления СКА системы по формуле (19) необходимо найти направление фронта и величину эйконала L₀ опорного луча, а также отличие эйконалов всех остальных лучей от эйконала этого луча. Если источник находится в фокусе, то углы выхода всех лучей одинаковые и определяются формулой (7). При смещении положения источника углы выхода лучей будут разные. Для каждого положения источника найдем k лучей, которые выходят из источника, преломляются линзой и отражаются от зеркала. Далее выбирая каждый из этих лучей в качестве опорного по формуле (19) найдем СКА относительно каждого из опорных лучей с соответствующим (ортогональным) фронтом (рис. 4). Выберем из полученных величин СКА минимальное значение и определим соответствующее направление излучения. Полученное приближенное значение СКА можно уточнить, меняя угол выхода опорного луча вблизи найденного значения и определяя минимум СКА.

Рис. 4.

Геометрия лучей в зеркально-линзовой системе.

Для определения фокальной кривой найдем геометрическое место положений источника (см. рис. 4), которые обеспечивают наименьшую величину СКА. Декартовые и полярные координаты источника связаны формулами $~{{x}_{{Fj}}} = {{R}_{j}}\sin \left( {{{\theta }_{j}}} \right)$, $~{{y}_{{Fj}}} = {{R}_{j}}{\text{cos}}\left( {{{\theta }_{j}}} \right)$. Задача состоит в нахождении оптимальной функции R(θ). Для угла ${{\theta }_{j}}$, соответствующего положению фокуса, эта величина известна (${{R}_{0}}$ = $\sqrt {x_{{{{F}_{1}}}}^{2} + ~y_{{{{F}_{1}}}}^{2}} $). Далее, уменьшая угол ${{\theta }_{j}}$ на некоторое малое значение $~\xi $, находим в окрестности ${{R}_{0}}$ значение ${{R}_{{j + 1}}}$$({{\theta }_{0}} - \xi )$ с использованием стандартной процедуры нахождения минимума. Применяя описанный алгоритм многократно, находим значения $~{{R}_{j}}\left( {{{\theta }_{j}}} \right)$ для 20 точек. Далее повторяем процедуру в сторону увеличения ${{\theta }_{j}}$ до необходимой величины, которая определяется углом зрения системы. Используя сплайн-интерполяцию определяем искомую функцию R(θ).

При решении задачи синтеза бифокальной зеркально-линзовой системы было замечено, что описанный выше алгоритм позволяет получить аналитическое решение не для всех наборов исходных параметров. Решение перестает существовать в двух случаях: в первом алгоритм перестает работать из-за того, что уравнение (18) не имеет действительного корня, а во втором – когда в процессе синтеза у зеркала появляется точка возврата (рис. 5а). В последнем случае бифокальной системы зависимость СКА от угла зрения имеет вид, соответствующий трехфокальной системе (рис. 5б).

Рис. 5.

Бифокальная зеркально-линзовая система с параметрами n = 1.5, f = 0.6201, f₀ = 0.683, x₀ = 0.01295, b = 0.1024: а) геометрия системы, б) зависимость СКА от угла зрения.

Набор параметров, при котором алгоритм перестает работать, будем называть критическим. При увеличении числа синтезированных отрезков у зеркала всегда появляются точки возврата, которые и определяют предельный размер апертуры системы.

Будем оптимизировать систему с фиксированным углом зрения, толщиной линзы b = 0.102 и коэффициентом преломления n = 1.5. Угол зрения определяется отношением x₀/b, поэтому будем фиксировать параметр x₀. В результате параметрами оптимизации являются: расстояние f от края начального участка линзы до фокуса F₁ и расстояние f₀ от фокуса начальной системы F₀ до поверхности линзы. Проведем исследование величины СКА в зависимости от этих двух параметров.

Линии уровня величины 10⁵σ в зависимости от величин f₀ и f/f₀ при фиксированных значениях n и b показаны на рис. 6а–6в для углов зрения 50, 70 и 100 град при x₀ = 0.0129, 0.0181 и 0.0265 соответственно. Видно, что минимальная величина СКА достигается при следующих наборах параметров: f₀ = 0.722, f/f₀ = 0.923 (для угла зрения 50 град), f₀ = = 0.794, f/f₀ = 0.863 (для угла зрения 70 град) и f₀ = = 0.951, f/f₀ = 0.719 (для угла зрения 100 град), которые в отличие от бифокальной двухзеркальной системы [11] находятся достаточно далеко от границы области существования решения.

Рис. 6.

Линии уровня 10⁵ σ бифокальной зеркально-линзовой системы с коэффициентом преломления n = 1.5 и толщиной b = 0.102 при x₀ = 0.0129 (а), 0.0181 (б) и 0.0265 (в).

На рис. 7а–7в показаны зависимости СКА синтезированных систем с оптимальными параметрами от угла зрения. Как видно из рисунков, максимальная величина СКА зеркально-линзовых систем с оптимальными параметрами для углов зрения 50, 70 и 100 град составляет соответственно 2.1 × 10^–5, 5.2 × 10^–5 и 1.3 × 10^–4. При этом величина апертуры D бифокальных систем равна соответственно 0.707, 0.789 и 0.850.

Рис. 7.

Зависимость 10⁵ σ от угла зрения оптимальной бифокальной зеркально-линзовой системы с n = 1.5, b = 0.1024 и тремя наборами параметров: а) f = 0.666, f₀ = 0.722, x₀ = 0.0129; б) f = 0.685, f₀ = 0.794, x₀ = 0.01812; в) f = 0.683, f₀ = = 0.951, x₀ = 0.0265.

Для анализа полученных результатов удобно считать все размеры относительно апертуры системы. Для этого достаточно умножить все размерные параметры на множитель, равный обратной величине D. В результате для систем с D = 1 и углами зрения 50, 70 и 100 град величина f₀ равна, соответственно, 1.02, 1.01 и 1.12, а толщина линзы b – 0.145, 0.130 и 0.120.

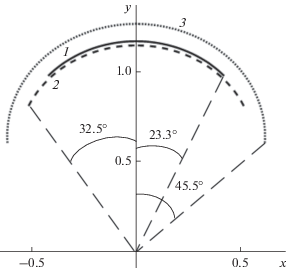
На рис. 8 показаны фокальные кривые синтезированных систем с оптимальными параметрами для углов зрения 50, 70 и 100 град.

Рис. 8.

Фокальные кривые синтезированных систем с углами зрения 50 (1), 70 (2) и 100 град (3).

Отметим, что полученные величины СКА в два-три раза превышают соответствующие величины для двухзеркальных бифокальных систем синтезированных и оптимизированных в [11], но при этом для угла зрения 70° – в девять раз меньше аналогичной величины для бифокальной зеркально-линзовой системы, синтезированной в работе [5].

С увеличением угла зрения от 50 до 100 град величина СКА увеличивается в пять раз, угловой размер фокальной линии – примерно в два раза, толщина линзы уменьшается на 17%, а продольный размер системы (f₀ + b) увеличивается на 6%.

ЗАКЛЮЧЕНИЕ

На основе полученных результатов можно сделать следующие выводы:

1. Развитая в работе методика позволяет синтезировать и оптимизировать бифокальные зеркально-линзовые цилиндрические системы по минимуму СКА.

2. Синтезированная и оптимизированнаяв работе система имеют на порядок меньшую величину СКА, чем известная бифокальная зеркально-линзовая система с аналогичным углом зрения.

3. Продольный размер бифокальных зеркально-линзовых систем с оптимальными параметрами слабо зависит от угла зрения и близок к размеру апертуры.

Список литературы

Калошин В.А. // Тр. 13-й Междунар. Крымской конф. СВЧ техника и телекоммуникационные технологии, Crimico-2003. 8–12 сент. 2003. Севастополь: Вебер, 2003. С. 383.
Ettorre M., Gandini E., Sauleau R. // Proc. 5th Europ. Conf. on Antennas and Propagation (EUCAP). Rome. 11–15 Sept. 2011. N.Y.: IEEE, 2011. P. 2947.
Tekkouk K., Ettorre M., Le Coq L., Sauleau R. // IEEE Trans. 2016. V. AP-64. № 2. P. 504.
Калошин В.А., Ле Д.Т., Фролова Е.В. // РЭ. 2019. Т. 64. № 8. С. 768.
Калошин В.А., Ле Д.Т., Ви У.Н. // Журн. радиоэлектроники. 2020. № 3. http://jre.cplire.ru/jre/ mar20/13/text.pdf.
Калошин В.А., Ле Д.Т. // Журн. радиоэлектроники 2020. № 4. http://jre.cplire.ru/jre/apr20/4/text.pdf.
Калошин В.А., Нгуен К.Т. // Журн. радиоэлектроники. 2020. № 7. http://jre.cplire.ru/jre/jul20/9/ text.pdf.
Калошин В.А., Нгием Х.Д., Фролова Е.В. // Журн. радиоэлектроники. 2018. № 1. http://jre.cplire.ru/ jre/jan18/3/text.pdf.
Банков С.Е., Фролова Е.В. // РЭ. 2017. Т. 62. № 5. С. 463.
Калошин В.А., Фролова Е.В. // Журн. радиоэлектроники. 2015. № 12. http://jre.cplire.ru/jre/dec15/19/ text.pdf.
Калошин В.А., Ви Ут Нам // РЭ. 2022. Т. 67. № 2. С. 140.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал