Радиотехника и электроника, 2022, T. 67, № 3, стр. 234-243
Исследование характеристик распространения ультракоротких радиоволн в неоднородной тропосфере для трилинейной модели индекса преломления. Результаты моделирования
В. А. Светличный a, О. В. Смирнова a, *
a СПИИРАН-Научно-техническое Бюро Высоких Технологий
199178 Санкт-Петербург, 14 линия Васильевского острова, 39, Российская Федерация
* E-mail: sov@oogis.ru
Поступила в редакцию 23.03.2021
После доработки 19.07.2021
Принята к публикации 07.09.2021
- EDN: KXEWOT
- DOI: 10.31857/S0033849422030159
Аннотация
На основе приведенного нами ранее аналитического решения задачи с использованием разработанной авторами программы для ЭВМ выполнено численное исследование спектра нормальных волн, высотных множителей модов горизонтальной и вертикальной ветви спектра, а также характерных особенностей формирования поля дипольных источников для трилинейной модели тропосферы в зависимости от длины радиоволны, параметров модели тропосферы и высоты расположения источника.
Данная статья является продолжением работы [1] и посвящена численному исследованию спектра нормальных волн в задаче о поле источника в неоднородной тропосфере для трилинейной модели вертикального профиля индекса преломления, а также – в рамках этой модели – особенностей формирования поля и характеристик распространения УКВ в зависимости от длины радиоволны, высоты расположения источника и параметров тропосферы.
Одним из затруднений метода нормальных волн является нахождение корней характеристического уравнения задачи, поскольку удобных и достаточно универсальных методов вычисления комплексных корней высших трансцендентных функций и их комбинаций до сих пор не создано. Авторами был разработан численный метод нахождения корней в задачах распространения радиоволн в тропосфере с кусочно-линейным профилем индекса преломления [2], который используется и в данной работе. В левой части характеристического уравнения задачи (см. [1, формула (18)]) стоит целая трансцендентная функция $D\left( t \right)$ спектральной переменной $t$, которую можно представить в виде ряда Тейлора по степеням $t - {{t}_{0}}$ вокруг выбранной точки ${{t}_{0}}$, сходящегося на всей комплексной плоскости. Эта функция удовлетворяет обыкновенному дифференциальному уравнению с полиномиальными коэффициентами, поэтому его решение в виде ряда Тейлора можно построить стандартным методом, причем для коэффициентов ряда получаются удобные рекуррентные формулы. Несколько первых коэффициентов вычисляются по точным формулам для функции и ее производных. Однако дифференциальное уравнение имеет высокий порядок, что создает трудности в реализации такого подхода. Поэтому приходится строить такие решения для отдельных частей функции $D\left( t \right)$ и затем полученные ряды перемножать. Нетрудно убедиться, что, например, функции $F_{{nm}}^{{\left( {1,2} \right)}}\left( t \right)$ удовлетворяют дифференциальным уравнениям четвертого порядка, а $F_{{1,2}}^{{\left( 0 \right)}}\left( t \right)$ – уравнению второго порядка.
Таким путем получается аппроксимирующий полином для функции $D\left( t \right)$, корни которого находятся с помощью стандартных программ для ЭВМ. Ложные корни из числа найденных отсеиваются путем подстановки всех корней в формулу для $D\left( t \right)$. Если ${{t}_{s}}$ – истинное значение простого корня функции $D\left( t \right)$, а ${{\tilde {t}}_{s}}$ – найденное приближенное значение этого корня, то при достаточной близости их имеем $D\left( {{{{\tilde {t}}}_{s}}} \right) \approx {{\left( {{{dD} \mathord{\left/ {\vphantom {{dD} {dt}}} \right. \kern-0em} {dt}}} \right)}_{{{{{\tilde {t}}}_{s}}}}}\left( {{{{\tilde {t}}}_{s}} - {{t}_{s}}} \right)$. Отсюда получаем количественный критерий для отсеивания ложных корней: $\left| {D\left( {{{{\tilde {t}}}_{s}}} \right)\left( {{{dD} \mathord{\left/ {\vphantom {{dD} {dt}}} \right. \kern-0em} {dt}}} \right)_{{{{{\tilde {t}}}_{s}}}}^{{ - 1}}} \right| < {\text{ne}}{{{\text{v}}}_{{{\text{пор}}}}}$, где ${\text{ne}}{{{\text{v}}}_{{{\text{пор}}}}}$– задаваемое пороговое значение параметра (невязки), определяющее точность нахождения корней. В наших исследованиях обычно считалось ${\text{ne}}{{{\text{v}}}_{{{\text{пор}}}}} = {{10}^{{ - 3}}}$. Используя найденное приближенное значение корня, при необходимости можно уточнить его, полагая ${{t}_{0}} = {{\tilde {t}}_{s}}$ и повторяя описанную процедуру. Обследуя выбранную область комплексной плоскости $t$ путем перебора с заданным шагом значений ${{t}_{0}}$, находим все корни в ней.
Аналитическое решение задачи было построено в работе [1] с использованием традиционной [3] пары линейно независимых решений ${{w}_{{1,2}}}\left( {\tilde {z}} \right)$ уравнения Стокса–Эйри, удобных для преобразования и анализа полученных формул. Однако численная реализация расчетных формул и создание соответствующей программы для ЭВМ требует перехода от функций Эйри ${{w}_{{1,2}}}\left( {\tilde {z}} \right)$ к другой паре линейно независимых решений. В качестве таких функций в работе используются ${\text{Ai}}\left( {\tilde {z}} \right)$ и ${\text{Ai}}\left[ {\tilde {z}\exp \left( {{{ - 2\pi i} \mathord{\left/ {\vphantom {{ - 2\pi i} 3}} \right. \kern-0em} 3}} \right)} \right]$, которые образуют численно удовлетворительную пару во всей верхней полуплоскости $\operatorname{Im} \tilde {z} \geqslant 0$, т.е. одна из них является доминирующей, а другая – подчиненной, что позволяет сохранить точность при вычислении билинейных комбинаций этих функций (типа вронскиана) для комплексных значений аргумента [4]. Следует, однако, отметить, что в характеристическое уравнение входят функции Эйри различных аргументов
В ходе исследований был создан программный комплекс для ПЭВМ в среде MatLab, который позволяет находить корни характеристического уравнения (результаты представляются таблицей и в виде графического изображения спектра на комплексной плоскости $\left( t \right)$), рассчитывать дистанционные и высотные зависимости функции ослабления поля для заданных высот точек наблюдения, представляемые в виде графиков. Кроме того, предусмотрено построение графиков модулей высотных множителей ${{f}_{s}}\left( t \right)$, а также траекторий корней характеристического уравнения на комплексной плоскости $\left( t \right)$ в зависимости от какого-либо параметра.
Аналитическое решение задачи, изложенное в [1], прошло несколько проверок, однако численные расчеты на ЭВМ также требуют определенного тестирования, что достигается сравнением с какими-либо результатами, известными ранее. В этих целях было выполнено сравнение результатов расчета спектров, высотных множителей и дистанционных зависимостей функции ослабления для трилинейной модели профиля $N\left( z \right)$ и ранее использованной модели в виде “ступеньки” [2]. В численных расчетах невозможно устремить толщину ${{h}_{2}} - {{h}_{1}}$ переходного слоя к нулю (см. [1, формулы (2)]), поэтому расчеты выполнялись для малой толщины.
Проиллюстрируем полученные результаты на частном примере. В дальнейшем значения индекса преломления N будем задавать в N-ед. (1 N-ед. = = 10–6). Параметры тропосферы для трилинейной модели: $N\left( 0 \right) = 10$, $N\left( {100} \right) = 10$, $N\left( {100.3} \right) = 0$ N‑ед., ${{\tilde {g}}_{3}} = 0$, длина радиоволны 0.3 м (т.е. ширина переходной области в профиле $N\left( z \right)$ равна длине волны), поляризация поля вертикальная, параметры подстилающей поверхности $\varepsilon = 80$, $\sigma = 3$ См/м. Высота расположения источника ${{z}_{0}} = 25$ м. В модели “ступенька” скачок индекса преломления $N\left( z \right)$ на высоте 100 м также составлял 10 N-ед. Небольшие значения $N\left( z \right)$ не должны удивлять, так как для характеристик распространения радиоволн важны только относительные изменения этой величины по высоте $z$. При этом степень аппроксимирующего полинома равнялась 70, окно поиска корней определялось изменением ${{t}_{0}}$ в пределах прямоугольника $\left| {\operatorname{Re} {{t}_{0}}} \right| \leqslant 20$, $0 \leqslant \operatorname{Im} {{t}_{0}} \leqslant 20$, уточнение значений корней путем повторного выбора значений параметра ${{t}_{0}} = {{\tilde {t}}_{s}}$ не проводилось. На рис. 1 приведен полученный спектр нормальных волн для трилинейной модели тропосферы, а в табл. 1 – численные значения нескольких комплексных постоянных распространения ${{t}_{s}}$, занумерованных в порядке возрастания их мнимых частей как для модели “ступенька”, так и для трилинейной модели с указанием полученных значений невязки ${\text{nev}}$. Картина спектра для “ступеньки” в точности такая же, как и для трилинейной модели: одинаковое количество выявленных точек спектра – 34, четкое разделение их на две ветви (горизонтальную и вертикальную), наличие трех наиболее слабозатухающих нормальных волн.
Рис. 1.
Спектр нормальных волн, полученный методом скользящего окна в заданной области комплексной плоскости (t): 1 – точки спектра для однородной тропосферы, 2 – точки спектра для трилинейной модели с параметрами $N\left( 0 \right) = 10$, $N\left( {100} \right) = 10$, $N\left( {100.3} \right) = 0$ N-ед.

Таблица 1.
Сравнение значений комплексных постоянных распространения и их невязок для модели “ступенька” и трилинейной модели
| $s$ | Модель “ступенька” | Трилинейная модель | ||
|---|---|---|---|---|
| ${{t}_{s}}$ | ${\text{nev}}$ | ${{t}_{s}}$ | ${\text{nev}}$ | |
| 1 | 6.78411 + 0.02149i | 0.00044 | 6.79201 + 0.02136i | 0.00010 |
| 2 | 5.10460 + 0.19000i | 0.00017 | 5.11252 + 0.18998i | 0.00011 |
| 3 | 3.44148 + 0.41317i | 0.00004 | 3.45160 + 0.41189i | 0.00011 |
| 4 | 1.30749 + 0.78811i | 0.00001 | 1.32390 + 0.78498i | 0.000002 |
| 5 | –1.57555 + 1.27093i | 0.00007 | –1.55041 + 1.26591i | 0.00019 |
| 6 | –5.22272 + 1.81910i | 0.00001 | –5.18629 + 1.81210i | 0.00008 |
| 7 | –9.62445 + 2.41869i | 0.000062 | –9.57477 + 2.41005i | 0.00004 |
| 8 | 6.26253 + 2.59184i | 0.000007 | 6.27029 + 2.59187i | 0.00032 |
| 9 | –14.77602 + 3.06325i | 0.00009 | –14.71064 + 3.05258i | 0.00067 |
| 19 | 11.39113 + 11.53518i | 0.97 × 10–6 | 11.39893 + 11.53522i | 0.78 × 10–4 |
| 31 | 15.92290 + 9.32714i | 0.00075 | 15.93084 + 9.32755i | 0.00003 |
| 32 | 16.25629 + 19.90096i | 0.00002 | 16.2641 + 19.90102i | 0.00001 |
| 33 | 16.58474 + 20.46621i | 1.54 × 10–6 | 16.59257 + 20.46626i | 0.00099 |
| 34 | 16.90864 + 21.02367i | 0.00001 | 16.91647 + 21.02373i | 0.00033 |
Как видно из таблицы, соответствующие корни ${{t}_{s}}$ близки для обеих моделей $N\left( z \right)$, причем наименьшие отличия имеют место как раз для первых трех-четырех слабозатухающих нормальных волн, представляющих интерес на больших загоризонтных расстояниях от источника. При этом различие вещественных частей корней, как правило, составляет порядка 0.01, а мнимых – заметно меньше. Для горизонтальной ветви отличия корней ${{t}_{s}}$ несколько большие, чем для вертикальной, и это можно объяснить тем, что волноводные моды лучше “чувствуют” характеристики верхней стенки волноводного канала. Скачок $N\left( z \right)$ в модели “ступенька” должен сильнее отражать радиоволны, чем два скачка производной $N\left( z \right)$ в переходном слое трилинейной модели, поэтому, казалось бы, мнимые части корней горизонтальной ветви должны быть меньше в модели “ступенька”, тогда как из табл. 1 следует обратное.
Построение графиков высотных множителей ${{f}_{s}}\left( y \right)$ позволяет провести более детальную классификацию типов нормальных волн. На рис. 2 приведены графики нескольких из них для трилинейной модели M-профиля (практически совпадающие с графиками для модели “ступенька”). Напомним, что согласно принятому правилу [3] ${{f}_{s}}\left( 0 \right) = 1$.
Рис. 2.
Графики высотных множителей: а – первых четырех модов при s = 1 (1), 2 (2), 3 (3) и 4 (4), б – волноводных модов при s = 5 (1), 6 (2), 7 (3) и 9 (4), в – дифракционных модов при $s = 8$ (1), 10 (2), 11 (3) и 12 (4).

Представленные графики показывают, что в данном примере спектр нормальных волн содержит наряду с дифракционными волнами соскальзывания и волноводными модами также волны типа “шепчущей” галереи (ВШГ), включающие как собственно волну шепчущей галереи (см. рис. 2а, $s = 1$), так и волны промежуточного типа ($s = 2,3,4$), поле которых в нижней части волноводной области резко убывает по мере уменьшения координаты $z$. Фактически их можно рассматривать как нормальные волны приподнятого волновода, возникающего из-за роста модифицированного индекса преломления $M\left( z \right)$ в первой области высот $0 < z < {{h}_{1}}$ для данной модели среды, за которой следует область инверсии. Кривые на рис. 2а,2б демонстрируют постепенный переход вертикальной структуры поля первых модов от ВШГ к волнам волноводного типа с ростом номера $s$. Выбранная модель тропосферы по общепринятой классификации [5] соответствует приподнятому волноводу в интервале высот 36.6…100.3 м, однако осциллирующий характер высотной зависимости волноводных модов на рис. 2б сохраняется и в области меньших высот, т.е. в спектре есть нормальные волны как приподнятого волновода, так и приводного. По-видимому, это объясняется наличием изломов в профиле $N\left( z \right)$ для трилинейной модели.
Следует отметить еще одну особенность высотных множителей нормальных волн горизонтальной ветви спектра (см. рис. 2а, 2б): за исключением волн типа шепчущей галереи ($s = 1,{\text{ }}2$), функции $\left| {{{f}_{s}}\left( y \right)} \right|$ растут не только в области высот $z > {{h}_{2}}$, но и (в среднем) в интервале высот волноводной области. Такой рост характерен для волн вертикальной ветви (см. рис. 2в) и объясняется дифракционным просачиванием энергии поля из освещенной области вниз в зону тени. Это свидетельствует о таких же дифракционных свойствах и волноводных модов горизонтальной ветви, причем не только в области $z > {{h}_{2}}$, но и в нижележащей области.
На рис. 3 приведены результаты сравнения дистанционных зависимостей функции ослабления, рассчитанных для трех значений высоты $z$, точки наблюдения и указанных выше параметров моделей $N\left( z \right)$. На графиках также приведена соответствующая зависимость для однородной тропосферы ($z = 150$ м). Графики свидетельствуют о хорошем соответствии этих зависимостей для обеих моделей $N\left( z \right)$, в том числе для различных высот $z$ (отличия отсчетов в интерференционных минимумах объясняется невозможностью точного попадания в них в ходе расчетов). В дифракционной области поле имеет четко выраженный двухмодовый характер – при выбранной высоте расположения источника оно формируется двумя наименее затухающими нормальными волнами. Более быстрое, в среднем, затухание поля с ростом дальности от источника для трилинейной модели $N\left( z \right)$ объясняется несколько большими значениями мнимых частей постоянных распространения этих волн, что уже обсуждалось выше.
Рис. 3.
Дистанционные зависимости функции ослабления для модели “ступенька” (а) и для трилинейной модели (б) при z = 25 (1), 50 (2) и 150 м (3), сплошные линии – случай однородной тропосферы при z = 150.
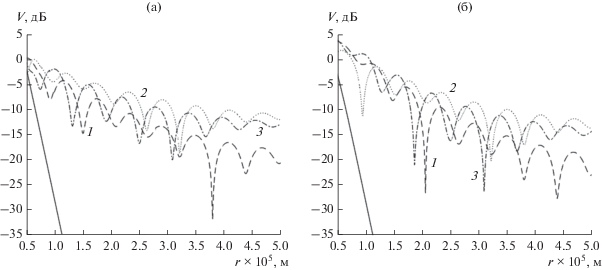
Таким образом, сравнение результатов расчетов по двум разработанным программам, использующим различные модели вертикального профиля индекса преломления тропосферы, показывает их хорошее качественное и количественное согласие при условии близости параметров тропосферы.
Проследим теперь за изменениями спектра нормальных волн и характеристик распространения радиоволн в зависимости от длины волны при наличии инверсии в профиле индекса преломления $N\left( z \right)$. Общая закономерность состоит в том, что при достаточно большом значении М‑дефицита затухание радиоволн снижается по мере уменьшения длины волны, и, в конце концов, радиоволны захватываются в тропосферный волновод. На рис. 4,5 иллюстрируются результаты расчета дистанционных зависимостей функции ослабления поля на разных высотах $z$ для ряда значений длины радиоволны. Поляризация поля – вертикальная, параметры тропосферы $N\left( 0 \right) = 340$, $N\left( {100} \right) = 345$, $N\left( {120} \right) = 335$ N-ед., ${{\tilde {g}}_{3}} = 0.039$ N-ед./м соответствуют наличию приподнятого волновода в области высот 66.9…120 м с М-дефицитом 6.86 N-ед., высота источника ${{z}_{0}} = 50$ м, параметры подстилающей поверхности $\varepsilon = 80$, $\sigma = 3$ См/м.
Рис. 4.
Дистанционные зависимости функции ослабления при наличии инверсии для $\lambda = 1$ м (а), 0.5 (б) и 0.3 (в) при z = 50 (1), 110 (2) и 150 м (3), сплошные линии – случай однородной тропосферы при z = 150.
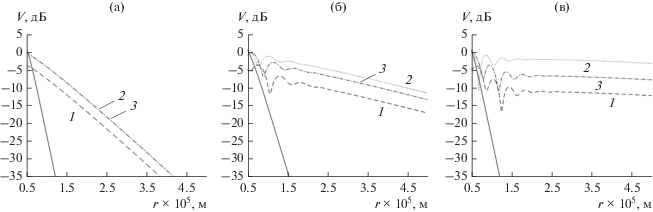
Рис. 5.
Дистанционные зависимости функции ослабления при наличии инверсии для значений длины волны $\lambda = 0.2$ м (а), $\lambda = 0.1$ м (б), при z = 50 (1), 110 (2) и 150 м (3), сплошные линии – случай однородной тропосферы при z = 150.
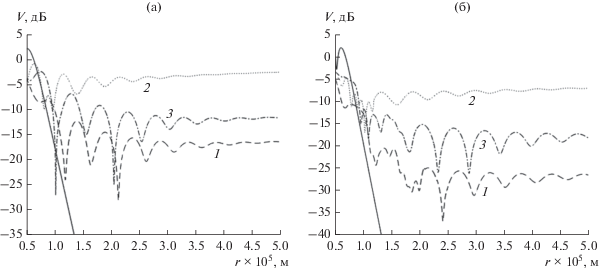
Хотя источник расположен несколько ниже инверсии, наибольший уровень поля имеет место в интервале высот инверсии, а наименьший – ниже нее, причем уровень поля на высоте 150 м заметно превышает уровень поля на высоте 50 м. Для небольших длин радиоволн 0.1…0.3 м функция ослабления в загоризонтной области сначала убывает довольно быстро (в среднем), а затем скорость ее убывания значительно уменьшается (и даже сменяется медленным ростом из-за общего множителя $2\sqrt {i\pi x} $, см. [1]):
(1)
$V\left( {x;y,{{y}_{0}}} \right) = 2\sqrt {i\pi x} \sum\limits_{s = 1}^\infty {{{\Lambda }_{s}}\exp \left( {i{{t}_{s}}x} \right){{f}_{s}}\left( y \right){{f}_{s}}\left( {{{y}_{0}}} \right)} .$Это объясняется появлением в спектре слабозатухающих ВШГ, поле которых сосредоточено в основном в области высот инверсии (см. рис. 2а). Поскольку источник расположен довольно низко, он слабо возбуждает эти нормальные волны, и их поле доминирует в общей функции ослабления только начиная с достаточно больших расстояний, когда другие нормальные волны уже затухли. Распределение полного поля по высоте на больших дальностях как раз и связано со структурой этих нормальных волн по вертикальной координате.
В условиях наличия приподнятого волновода высота расположения источника также влияет на пространственную структуру поля в загоризонтной области. На рис. 6, 7 представлены результаты расчетов для высоты источника ${{z}_{0}} = 25$ м, на рис. 8 – 175 м, на рис. 9 – 250 м. Длина радиоволны 0.3 м, поляризация горизонтальная, параметры тропосферы $N\left( 0 \right) = 320$, $N\left( {150} \right) = 330$, $N\left( {200} \right) = 310$ N-ед., ${{\tilde {g}}_{3}} = 0.039$ N-ед./м соответствуют приподнятому волноводу в области высот 95.7…200 м с М-дефицитом 12.15 N-ед., параметры подстилающей поверхности $\varepsilon = 80$, $\sigma = 3$ См/м. Дистанционные зависимости функции ослабления даны для – высот 10, 25, 100, 175, 220 и 400 м.
Рис. 6.
Дистанционные зависимости функции ослабления поля для значения ${{z}_{0}} = 25$ м (а): 1 – z = 10 м, 2 – z = 25 м, 3 – z = 100 м, 4 – z = 175 м, 5 – z = 220 м, 6 – z = 400 м; спектр нормальных волн (б): 1 – для однородной тропосферы, 2 – для трилинейной модели с параметрами $N\left( 0 \right) = 320$, $N\left( {150} \right) = 330$, $N\left( {200} \right) = 310$ N-ед.
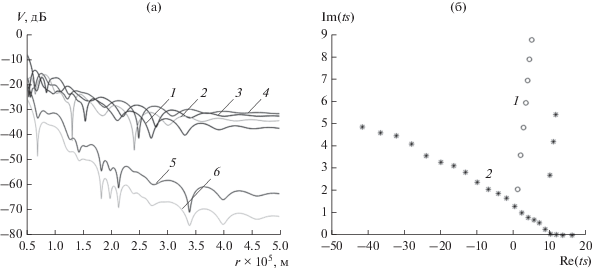
Рис. 7.
Высотные зависимости функции ослабления поля при ${{z}_{0}} = 25$ м на разных дальностях (а): r = 200 (1), 300 (2), 400 (3) и 500 км (4), а также высотные множители первых четырех модов (б): ${{t}_{1}} = 12.623 + 2.2 \times {{10}^{{ - 6}}}i$, ${{t}_{2}} = 10.575 + 0.011i$, ${{t}_{3}} = 9.188 + 0.211i$, ${{t}_{4}} = 7.575 + 0.516i$ при s = 1 (1), 2 (2), 3 (3), 4 (4).
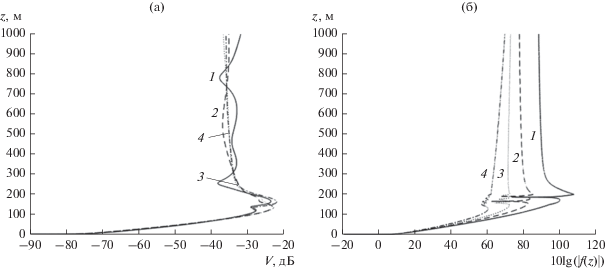
Рис. 8.
Дистанционные зависимости функции ослабления поля для высоты расположения источника ${{z}_{0}} = 175$ м (а): 1 – z = 10 м, 2 – z = 25 м, 3 – z = 100 м, 4 – z = 175 м, 5 – z = 220 м, 6 – z = 400 м; высотные разрезы функции ослабления поля на дальностях (б): 1 – r = 200 км, 2 – r = 300 км, 3 – r = 400 км, 4 – r = 500 км.
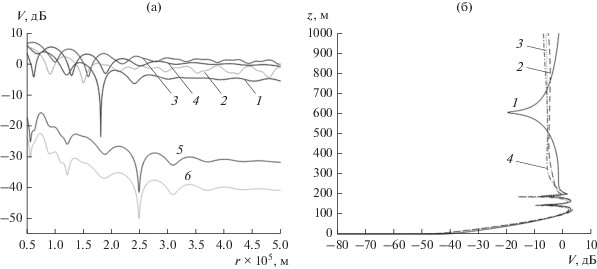
Рис. 9.
Дистанционные зависимости функции ослабления поля для высоты расположения источника ${{z}_{0}} = 250$ м (а): 1 – z = 10 м, 2 – z = 25 м, 3 – z = 100 м, 4 – z = 175 м, 5 – z = 220 м, 6 – z = 400 м; высотные разрезы функции ослабления поля на дальностях (б): 1 – r = 200 км, 2 – r = 300 км, 3 – r = 400 км, 4 – r = 500 км.

Как видно из рис. 6, наибольший уровень поля имеется в области инверсии и в некоторой области выше нее, хотя источник расположен существенно ниже инверсии, причем скорость убывания функции ослабления на небольших высотах резко снижается практически до нуля на дальностях более 300 км. Эти особенности поля опять-таки объясняются наличием в спектре модов типа ВШГ с очень малым затуханием и характерной структурой их поля по вертикали.
Волны шепчущей галереи существенно изменяют вид высотной зависимости функции ослабления поля на больших расстояниях от источника в интервале высот геометрической тени (см. рис. 7): вместо глубокого минимума в области выше инверсии расчет дает примерно постоянное значение и только при выходе в освещенную область уровень ее будет возрастать.
Если источник находится в области высот инверсии, то уровень поля значительно возрастает на всех высотах точки наблюдения 10…400 м (см. рис. 8), что объясняется ростом множителей ${{f}_{s}}\left( {{{y}_{0}}} \right)$ для ВШГ (1). Аномально высокий уровень поля на больших расстояниях в области высот инверсии (см. рис. 8 кривые 3, 4) связан с множителем $2\sqrt {i\pi x} $ (1) и очень малым затуханием ВШГ. Наконец, когда источник поля находится выше области инверсии, уровень поля снижается, но по-прежнему остается более высоким в области инверсии и выше нее, чем на небольших высотах (см. рис. 9а).
Наконец, рассмотрим случай монотонно убывающего N-профиля (рис. 10) с параметрами $N\left( 0 \right) = 332$, $N\left( {150} \right) = 310$, $N\left( {200} \right) = 300$ N-ед., соответствующего приводному волноводу с M-дефицитом 11.85 N-ед. (Длина волны, высота источника и другие параметры те же, что и на рис. 6, 7). В этом случае уровень функции ослабления остается высоким во всем интервале дальностей и высот 10…400 м (см. рис. 10а), но спектр (см. рис. 10б) существенно отличается как по составу, так и по виду высотных множителей (рис. 11б, 11в). Графики первых трех высотных множителей заметно отличаются ${\text{от}}$ таковых для ВШГ на рис. 2а и 7, причем, несмотря на быстрый рост высотных множителей интервале высот 0…200 м (прирост более 100 дБ), функция ослабления в высотных разрезах (см. рис. 11а) изменяется в небольших пределах и четко демонстрирует характерное усиление поля в волноводной области. Отсутствие больших изменений функции ослабления в высотных разрезах объясняется очень малыми значениями коэффициентов возбуждения первых модов ${{\Lambda }_{s}} \approx {{10}^{{ - 9}}}$.
Рис. 10.
Дистанционные зависимости функции ослабления поля для значения M-дефицита равного 11.85 N-ед. (а): 1 – z = 10 м, 2 – z = 25 м, 3 – z = 100 м, 4 – z = 175 м, 5 – z = 220 м, 6 – z = 400 м; спектр нормальных волн для приводного волновода (б): 1 – для однородной тропосферы, 2 – для трилийнейной модели с параметрами $N\left( 0 \right) = 332$, $N\left( {150} \right) = 310$, $N\left( {200} \right) = 300$ N-ед.

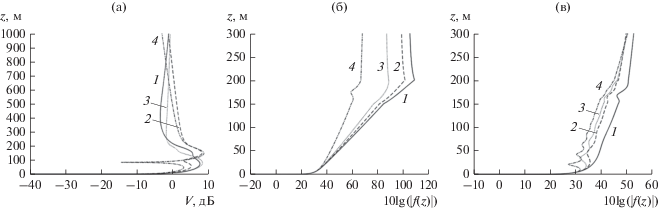
Рис. 11.
Высотные разрезы функции ослабления (а) и графики высотных множителей (б, в) (первые корни ${{t}_{1}} = 9.956 + 0.0066i$, ${{t}_{2}} = 9.555 + 0.028i$, ${{t}_{3}} = 9.033 + 0.111i$) для приводного волновода: а) r = 200 (1), 300 (2), 400 (3) и 500 км (4), б) s = 1 (1), 2 (2), 3 (3), 4 (4), в) s = 5 (1), 6 (2), 7 (3), 8 (4).
Численные расчеты подтверждают наличие горизонтальной ветви в спектре нормальных волн для трилинейной модели профиля $N\left( z \right)$ и в условиях отсутствия инверсии, установленное в работе [1], в результате асимптотического исследования характеристического уравнения. В качестве примера на рис. 12 приведены дистанционные зависимости функции ослабления и спектр для параметров тропосферы $N\left( 0 \right) = 340$, $N\left( {100} \right) = 345$, $N\left( {150} \right) = 345$ N-ед. Длина волны 30 см, поляризация поля – горизонтальная, высота расположения источника 25 м, параметры подстилающей поверхности, значения высоты точки наблюдения – как в предыдущих случаях. Несмотря на монотонное возрастание модифицированного индекса преломления $M\left( 0 \right) = 340$, $M\left( {100} \right) = 355.7$, $N\left( {150} \right) = 368.55$ N-ед. в спектре явно выделяется горизонтальная ветвь. Однако графики модулей высотных множителей первых восьми модов (см. рис. 13а, 13б) показывают, что все они относятся к типу дифракционных волн соскальзывания, поэтому дистанционные зависимости функции ослабления по своему характеру такие же, как для стандартной тропосферы.
Рис. 12.
Дистанционные зависимости функции ослабления (а): 1 – z = 10 м, 2 – z = 25 м, 3 – z = 100 м, 4 – z = 175 м, 5 – z = 220 м, 6 – z = 400 м и спектр нормальных волн (б): 1 – для однородной тропосферы, 2 – для трилийнейной модели с параметрами $N\left( 0 \right) = 340$, $N\left( {100} \right) = 345$, $N\left( {150} \right) = 345$ N-ед., в условиях отсутствия инверсии в профиле N(z).
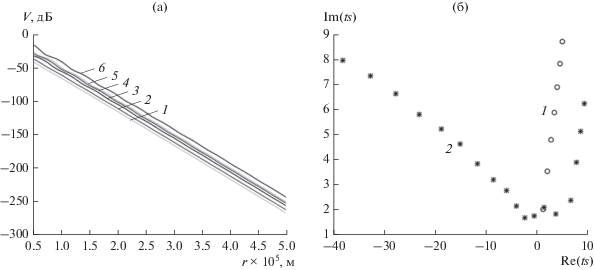
Рис. 13.
Графики модулей высотных множителей: а) ${{t}_{1}} = - 2.393 + 1.691i$ (кривая 1), ${{t}_{2}} = - 0.502 + 1.766i$ (кривая 2), ${{t}_{3}} = 3.660 + + 1.833i$ (кривая 3), ${{t}_{4}} = 1.379 + 2.093i$ (кривая 4); б) ${{t}_{5}} = - 4.088 + 2.144i$ (кривая 1), ${{t}_{6}} = 6.668 + 2.375i$ (кривая 2), ${{t}_{7}} = - 5.990 + 2.766i$ (кривая 3), ${{t}_{8}} = - 8.531 + 3.2i$ (кривая 4).

Выполненное исследование демонстрирует большие возможности метода нормальных волн не только в плане расчетов характеристик распространения радиоволн в неоднородной тропосфере, но, самое главное, в интерпретации полученных результатов, выявления закономерностей формирования поля и его пространственной структуры в дифракционной области. Анализ высотных множителей позволяет выполнять более детальную классификацию нормальных волн, чем простое деление на волны горизонтальной и вертикальной ветвей. Численное моделирование показывает, что ВШГ могут оказать существенное влияние на структуру поля по высоте выше волновода в области геометрической тени, а также значительно уменьшить скорость убывания функции ослабления на больших расстояниях, начиная с некоторых дальностей.
Асимптотическое исследование характеристического уравнения, выполненное в предыдущей, теоретической части работы, и численное моделирование показывают, что из-за наличия изломов в трилинейной модели профиля N(z) горизонтальная ветвь спектра существует всегда, притом что по виду высотных множителей моды горизонтальная ветвь ближе к дифракционным волнам соскальзывания. В этом плане представляет интерес исследование динамики “горизонтальной” ветви спектра при изменении степени гладкости модели M-профиля.
Список литературы
Светличный В.А., Смирнова О.В. // РЭ. 2022. Т. 67. № 3. С. 225.
Светличный В.А., Смирнова О.В. // РЭ. 2018. Т. 63. № 7. С. 682.
Фок В.А. Проблемы дифракции и распространения электромагнитных волн. М.: Сов. радио, 1970.
Олвер Ф. Асимптотика и специальные функции. М.: Наука, 1990.
Кукушкин А.В., Фрейлихер В.Д., Фукс И.М. // Изв. вузов. Радиофизика. 1987. Т. 30. № 7. С. 811.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


