Радиотехника и электроника, 2022, T. 67, № 3, стр. 225-233

Данная работа продолжает исследование характеристик распространения УКВ-радиоволн в неоднородной по высоте тропосфере на основе метода нормальных волн и нового метода численного нахождения корней характеристического уравнения, начатое в работе [1]. В ней использована более сложная трилинейная модель вертикального профиля индекса преломления тропосферы. Ранее она была применена в работах [2–4], однако в них аналитическая часть решения граничной задачи не была доведена до расчетных формул в той форме, которая является канонической для поля в слоистой тропосфере [5], и в указанных публикациях недостаточно информации о результатах исследования спектра нормальных волн, а также особенностей формирования поля в данной задаче. Необходимость подобного исследования, на наш взгляд, обусловлена тем, что, несмотря на большое количество публикаций, посвященных изучению характеристик распространения радиоволн в неоднородной тропосфере, закономерности формирования поля в различных условиях выяснены далеко не в полной мере. Метод нормальных волн подходит для этой цели в большей степени, чем широко применяющиеся для расчета поля численные пошаговые методы решения волнового параболического уравнения [6, 7].

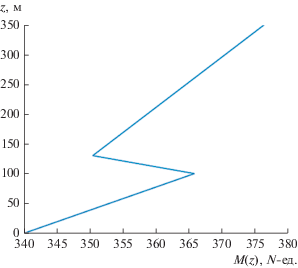
В работе использована декартова система координат с осью $z$, направленной вертикально вверх, кривизна земного шара учитывается в параболическом приближении линейно растущей с высотой $z$ добавкой к обычному индексу преломления $N\left( z \right)$. Соответственно, вертикальный профиль модифицированного индекса преломления тропосферы описывается выражением

где $a$ – радиус Земли, $ - {{\tilde {g}}_{3}}$ – градиент индекса преломления тропосферы $N\left( z \right)$ в области $z > {{h}_{2}}$ (в модели стандартной тропосферы принимается ${{\tilde {g}}_{3}} = 0.039 \times {{10}^{{ - 6}}}$ м^–1). Как видно из (2), в профиль $M\left( z \right)$ введен отрицательный сдвиг на $N\left( {{{h}_{2}}} \right) + {{\tilde {g}}_{3}}{{h}_{2}}$, удобный с точки зрения численных расчетов на ЭВМ. Сдвиг приводит к несущественной перенормировке волнового числа ${{k}_{0}} = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$. Схематически трилинейный М-профиль показан на рис. 1. Задаваемыми параметрами являются значения индекса преломления на трех высотах: $N\left( 0 \right)$, $N\left( {{{h}_{{1,2}}}} \right)$ и градиент индекса преломления $ - {{\tilde {g}}_{3}}$ в области $z > {{h}_{2}}$.

В качестве источника поля выбраны точечный вертикальный электрический или магнитный диполь, расположенный на высоте ${{z}_{0}}$, зависимость поля от времени – гармоническая exp(–iωt), поле описывается при помощи однокомпонентного векторного потенциала Герца $\Pi \left( {\vec {r},z} \right)$, который удовлетворяет уравнению Гельмгольца

где ${{M}_{{ст\,0}}}$ – комплексная амплитуда магнитного момента в случае магнитного диполя (для электрического диполя ${{M}_{{ст\,0}}}$ следует заменить на ${{{{P}_{{ст\,0}}}} \mathord{\left/ {\vphantom {{{{P}_{{ст\,0}}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}$ – комплексную амплитуду электрического дипольного момента, деленную на электрическую постоянную). На подстилающей (морской) поверхности $\left( {z = 0} \right)$ для $\Pi \left( {\vec {r},z} \right)$ задается импедансное граничное условие, а при $z \to \infty $ – условие излучения в трактовке В.А. Фока [5].

Для решения поставленной граничной задачи применим преобразование Фурье по горизонтальным координатам:

введем приведенную высоту $y = {{{{k}_{0}}z} \mathord{\left/ {\vphantom {{{{k}_{0}}z} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$, где ${{m}_{e}} = \sqrt[3]{{{{{{k}_{0}}{{a}_{e}}} \mathord{\left/ {\vphantom {{{{k}_{0}}{{a}_{e}}} 2}} \right. \kern-0em} 2}}}$, ${{a}_{e}} = g_{3}^{{ - 1}}$, и вместо волнового числа $\kappa $ используем обычную спектральную переменную t = = ${{m_{e}^{2}\left( {{{\kappa }^{2}} - k_{0}^{2}} \right)} \mathord{\left/ {\vphantom {{m_{e}^{2}\left( {{{\kappa }^{2}} - k_{0}^{2}} \right)} {k_{0}^{2}}}} \right. \kern-0em} {k_{0}^{2}}}$ [5]. Будем считать для определенности, что источник поля находится в интервале высот $0 < {{z}_{0}} < {{h}_{1}}$. Тогда дифференциальные уравнения для образа Фурье потенциала Герца в каждой из трех областей $0 \leqslant z \leqslant {{h}_{1}}$, ${{h}_{1}} \leqslant z \leqslant {{h}_{2}}$, $z \geqslant {{h}_{2}}$ примут вид где ${{y}_{{1,2}}} = 2{{N}_{{1,2}}}m_{e}^{2}$, ${{p}_{{1,2}}} = \sqrt[3]{{{{{{g}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{g}_{{1,2}}}} {{{g}_{3}}}}} \right. \kern-0em} {{{g}_{3}}}}}}$. Их решения выражаются через линейные комбинации функций Эйри ${{w}_{{1,2}}}\left( {\tilde {z}} \right)$ различных аргументов с произвольными коэффициентами. Подчиняя полученные решения вместе с их производными по $y$ условиям непрерывности на границах $z = {{h}_{{1,2}}}$, импедансному граничному условию на морской поверхности ($q = i{{m}_{e}}\delta $, $\delta $ – приведенный поверхностный импеданс подстилающей поверхности) и условию излучения ${{\tilde {\Pi }}^{{\left( 3 \right)}}}\left( {t;y;{{y}_{0}}} \right) \approx $ ${{w}_{1}}\left( {t - y} \right)$ при $y \to \infty $, определяем эти коэффициенты и приходим после ряда преобразований к выражениям для потенциала Герца в виде двукратных интегралов Фурье в указанных трех областях изменения высоты: где причем ${{\tilde {t}}_{0}} = \frac{{t - {{y}_{1}}}}{{p_{1}^{2}}}$; ${{\tilde {t}}_{1}} = {{\tilde {t}}_{0}} - {{p}_{1}}{{y}_{{h1}}}$; ${{\tilde {t}}_{{2,3}}} = \frac{{t - {{y}_{2}}}}{{p_{2}^{2}}} - $ $ - \,\,{{p}_{2}}{{y}_{{h1,2}}}$; ${{\tilde {t}}_{4}} = t - {{y}_{{h2}}}$. Нижние индексы у функций в (10) принимают значения $n,m = 1,2$, ${{y}_{ > }}$ и ${{y}_{ < }}$ – большая и меньшая из величин $y$, ${{y}_{0}}$, а ${{y}_{0}} = {{{{k}_{0}}{{z}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}{{z}_{0}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$, ${{y}_{{h1,2}}} = {{{{k}_{0}}{{h}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{k}_{0}}{{h}_{{1,2}}}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$ – приведенные высоты расположения источника и границ слоев тропосферы.

Интегралы в (6)–(8) сводятся к однократным, поскольку те части подынтегральных функций, которые являются функциями спектральной переменной $t$, не зависят от угловой переменной на плоскости двумерных волновых векторов $\vec {\kappa }$:

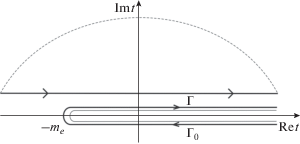
После этого переходим к переменной интегрирования $t = {{m_{e}^{2}\left( {{{\kappa }^{2}} - k_{0}^{2}} \right)} \mathord{\left/ {\vphantom {{m_{e}^{2}\left( {{{\kappa }^{2}} - k_{0}^{2}} \right)} {k_{0}^{2}}}} \right. \kern-0em} {k_{0}^{2}}}$. Ветвь корня в обратном преобразовании $\kappa = {{k}_{0}}\sqrt {1 + {t \mathord{\left/ {\vphantom {t {m_{e}^{2}}}} \right. \kern-0em} {m_{e}^{2}}}} $ фиксируем условием $\operatorname{Im} \sqrt {t + m_{e}^{2}} \geqslant 0$, для чего на комплексной плоскости $\left( t \right)$ проведем разрез так, как показано на рис. 2. Исходный контур интегрирования ${{\Gamma }_{0}}$ охватывает разрез и обходит его по часовой стрелке. Поскольку при такой фиксации ветви корня мнимая часть аргумента функции Ганкеля на всей комплексной плоскости $\left( t \right)$ больше нуля и эта функция стремится к нулю при $t \to \infty $, то возникает идея “разогнуть” исходный контур в прямую $\left( { - \infty + i0,\infty + i0} \right)$, а затем вычислить интеграл с помощью леммы Жордана, замкнув его полуокружностью бесконечно большого радиуса в верхней полуплоскости. Каких-либо других точек ветвления подынтегральная функция не имеет; из физических соображений ясно, что полюсов в нижней полуплоскости (т.е. корней характеристического уравнения $1 - {{R}_{1}}\left( t \right){{R}_{2}}\left( t \right) = 0$) не может быть (см. ниже). Однако при этом остальная часть подынтегральной функции должна обеспечить возможность указанной деформации исходного контура и замыкания его в верхней полуплоскости. Для этого было исследовано ее поведение при $t \to \infty $ как в нижней, так и верхней полуплоскости $\left( t \right)$ с использованием асимптотических разложений для функций Эйри. Поскольку это исследование довольно громоздко, соответствующие результаты вынесены в Приложение. В итоге было установлено, что рассматриваемые части подынтегральных функций в (6)–(8) не препятствуют описанной выше деформации исходного контура интегрирования в нижней полуплоскости $\operatorname{Im} t < 0$, так как они быстро убывают при $t \to \infty $. Иное положение имеет место в верхней полуплоскости $\operatorname{Im} t > 0$. Здесь функции ${{\tilde {\Pi }}^{{\left( {1,2} \right)}}}\left( {t;y,{{y}_{0}}} \right)$ стремятся к нулю при $t \to \infty $, тогда как ${{\tilde {\Pi }}^{{\left( 3 \right)}}}\left( {t;y,{{y}_{0}}} \right)$ стремится к нулю только в секторе $0 \leqslant \arg t \leqslant {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ и растет в секторе ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3} < \arg t \leqslant \pi $ при достаточно больших $y$ как $t\exp \left[ {\left( {y + {{y}_{0}} - 2{{y}_{{h2}}}} \right)\sqrt t } \right]$ (см. Приложение, формула (П.6)). Заметим, однако, что интеграл по развернутому контуру $\left( { - \infty + i0,\infty + i0} \right)$ сходится, в том числе на левом конце интервала интегрирования, где функции ${{\tilde {\Pi }}^{{\left( {1,2,3} \right)}}}\left( {t;y,{{y}_{0}}} \right)$ убывают как ${{t}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Тем не менее из-за стремления к нулю функции Ганкеля при $t \to \infty $

применить лемму Жордана все же можно, если $\operatorname{Re} \left[ {{{k}_{0}}\left( {z + {{z}_{0}} - 2{{h}_{2}} + ir} \right)\sqrt t } \right] < 0$ – тогда произведение функции Ганкеля на растущую экспоненту быстро стремится к нулю и в секторе ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3} < \arg t \leqslant \pi $. Фактически достаточно, чтобы это неравенство выполнялось на луче $\arg t = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$, что дает $r > \sqrt 3 \left( {z + {{z}_{0}} - 2{{h}_{2}}} \right)$. Данное условие не является сколько-нибудь существенным ограничением, поскольку в прикладных задачах обычно горизонтальные расстояния от источника до точки наблюдения гораздо больше, чем размер области расчета поля по вертикали.

Следует отметить, что выявленное ограничение возможности применения леммы Жордана характерно уже для задачи о поле источника над сферической подстилающей поверхностью в однородной тропосфере, если ее решать в рассматриваемом приближении. В конечном счете, это связано с ограниченной применимостью метода учета кривизны Земли в параболическом приближении – строго говоря, необходимо решать задачу в сферической системе координат, и лишь на последнем этапе асимптотически упрощать полученные расчетные формулы для того, чтобы легче было находить корни характеристического уравнения и получать другие численные результаты. В случае однородной тропосферы можно обосновать возможность применения леммы Жордана при решении задачи в сферической системе координат, используя асимптотики Дебая для функций Риккати–Бесселя, но при этом нужно учитывать явление Стокса. Однако возможности построения аналитического решения задачи в сферической системе координат для различных профилей $N\left( z \right)$ весьма ограничены, а в то же время рассматриваемый подход имеет широкую область применимости, позволяющую решать различные прикладные вопросы.

После вычисления интегралов по вычетам аргумент функции Ганкеля в подынтегральных выражениях упрощается:

поскольку корни характеристического уравнения считаются удовлетворяющими условию ${t \mathord{\left/ {\vphantom {t {m_{e}^{2}}}} \right. \kern-0em} {m_{e}^{2}}} \ll 1$, и эта функция заменяется ее асимптотикой при ${{k}_{0}}r \gg 1$. Затем полученные выражения для потенциала Герца преобразуются к стандартной форме где $V\left( {x;y,{{y}_{0}}} \right)$ – функция ослабления поля, которая имеет вид Здесь ${{t}_{s}}$ – корни характеристического уравнения, $x = {{{{k}_{0}}r} \mathord{\left/ {\vphantom {{{{k}_{0}}r} {2m_{e}^{2}}}} \right. \kern-0em} {2m_{e}^{2}}}$ – приведенное горизонтальное расстояние от источника, ${{f}_{s}}\left( y \right)$ – высотные множители нормальных волн, которые описываются в различных интервалах изменения высоты такими формулами ${{\Lambda }_{s}}$ – коэффициенты возбуждения нормальных волн,

Штрихи у высотных множителей в (15) означают производную по полным аргументам тех функций Эйри в них, которые зависят от переменной высоты $y$. Попутно отметим, что высотные множители непрерывны вместе с первой производной по переменной $y$ при переходе через границы слоев $y = {{y}_{{h1,2}}}$.

Вид представления (13) функции ослабления в данной задаче полностью соответствует общей записи этой функции для поля в слоистой среде в работе В.А. Фока [5]. Более того, оказалось, что выражение (15) для коэффициентов возбуждения нормальных волн, которое сначала было получено в данной работе в результате описанного хода решения задачи и преобразований полученных выражений, может быть выведено гораздо проще с помощью формулы, которая следует из [5, с. 305, формула (6.27)]:

причем интеграл в (16) легко вычисляется, поскольку где $W\left( {\tilde {y}} \right)$ – любое решение однородного уравнения Эйри, каковыми и являются высотные множители (14). Приведение функции ослабления к стандартной форме (13) имеет еще и тот смысл, что при этом достаточно рассмотреть случай, когда источник поля расположен в области высот $0 < z < {{h}_{1}}$, и нет необходимости заново решать задачу для случаев, когда он расположен в других областях, поскольку в силу известной теоремы взаимности $V\left( {x;y,{{y}_{0}}} \right) = V\left( {x;{{y}_{0}},y} \right)$.

Характеристическое уравнение 1 – R₁(t)R₂(t) = 0 данной задачи, которое служит для нахождения комплексных постоянных распространения нормальных волн (спектра), целесообразно записать в следующем виде:

Нетрудно убедиться, что при $N\left( z \right) \equiv 0$ полученное решение переходит в известную формулу [5] для функции ослабления поля над сферической Землей в случае однородной среды (вакуума). Действительно, при этом параметры в выражениях (14)–(15) равны: ${{y}_{{1,2}}} = 0$, ${{g}_{{1,2,3}}} = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$, ${{p}_{{1,2}}} = 1$, ${{\tilde {t}}_{0}} = t$, ${{\tilde {t}}_{{1,2}}} = t - {{y}_{{h1}}}$, ${{\tilde {t}}_{{3,4}}} = t - {{y}_{{h2}}}$, соответственно, находим поэтому во всех трех областях высотные множители равны ${{f}_{s}}\left( y \right) = {{{{w}_{1}}\left( {{{t}_{s}} - y} \right)} \mathord{\left/ {\vphantom {{{{w}_{1}}\left( {{{t}_{s}} - y} \right)} {{{w}_{1}}\left( {{{t}_{s}}} \right)}}} \right. \kern-0em} {{{w}_{1}}\left( {{{t}_{s}}} \right)}}$ и Λ_s = 1/(t_s – q²), а характеристическое уравнение приобретает вид $F_{1}^{{\left( 0 \right)}}\left( t \right) = 0$.

В Приложении выводятся асимптотические формулы для подынтегральных функций ${{\tilde {\Pi }}^{{\left( j \right)}}}\left( {t;y,{{y}_{0}}} \right)$ и выполняется асимптотический анализ корней характеристического уравнения задачи при $\left| t \right| \gg 1$.

Вторая часть работы будет посвящена численному исследованию спектра нормальных волн в данной задаче, а также особенностей формирования поля в зависимости от длины радиоволны, высоты расположения источника и параметров тропосферы.