1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 67, № 4, 2022

Радиотехника и электроника, 2022, T. 67, № 4, стр. 361-368

Межобзорное накопление отраженных радиолокационных сигналов на фоне негауссовских коррелированных помех

В. И. Кошелев a, В. А. Белокуров a, *

a Рязанский государственный радиотехнический университет им. В.Ф. Уткина
390005 Рязань, ул. Гагарина, 59/1, Российская Федерация

* E-mail: belokurov.v.a@rsreu.ru

Поступила в редакцию 23.03.2021
После доработки 26.10.2021
Принята к публикации 10.11.2021

Полный текст (PDF)

Аннотация

Изложены результаты синтеза алгоритма межобзорного накопления отраженных радиолокационных сигналов на фоне негауссовских коррелированных помех инвариантного к закону распределения помехи. Предложен алгоритм аналитического расчета порога обнаружения синтезированного алгоритма. Проведено тестирование и сравнение синтезированного алгоритма с известным на основе обработки реальных данных.

ВВЕДЕНИЕ

В настоящее время перспективным направлением повышения энергетической дальности радиолокационных станций (РЛС) является межобзорное накопление отраженных радиолокационных сигналов.

Для решения данной задачи предложено несколько подходов. В отечественной литературе можно отметить направление, связанное с использованием оценочно-корреляционного подхода [1], предложенного Ю.Г. Сосулиным. Данный подход основан на рекуррентном вычислении отношения правдоподобия с учетом апостериорной плотности распределения вероятностей вектора оцениваемых параметров.

Другой подход [2, 3] к решению задачи межобзорного накопления отраженных радиолокационных сигналов заключается в формировании обобщенного отношения правдоподобия по возможным траекториям движения цели и сравнении с порогом максимального значения обобщенного отношения правдоподобия. При этом, как правило, авторы [4] ограничиваются рассмотрением случая гауссовского некоррелированного шума.

Вопросы межобзорного накопления на фоне негауссовского некоррелированного шума рассмотрены в работах [5–8]. Законы распределения шума следующие: Вейбулла, К-распределение, логнормальное, экспоненциальное. В работе [9] рассмотрен синтез алгоритма межобзорного накопления на фоне коррелированных помех с К‑распределением. Особенностью данных работ является то, что авторы предполагают закон распределения помех априорно известным.

В работах [1, 10] рассмотрено применение оценочно-корреляционного подхода при обнаружении сигнала на фоне негауссовских шумов. При этом описанный подход требует априорного знания не только закона распределения шума, но и переходной плотности распределения вероятностей и ряда других параметров, что несколько ограничивает применение данного подхода на практике.

Вопросам обнаружения на фоне негауссовских помех посвящено большое количество работ. В их числе работы [10–12], в которых рассмотрен синтез локально оптимального обнаружителя при обнаружении пачки импульсов на фоне негауссовских коррелированных помех и который заключается в предварительной обработке квадратурных составляющих отраженной пачки импульсов с помощью безынерционного преобразователя, реализующего нормализацию входной негауссовской помехи.

Анализу законов распределения отраженных сигналов от морской поверхности посвящено большое количество работ как в отечественной литературе [13], так и зарубежной [14]. В данных работах показано, что в зависимости от разрешения РЛС, закон распределения амплитуды помехи могут иметь следующие распределения: релеевское, логнормальное, K-распределение, обобщенное K‑распределение и др. Кроме того, анализ экспериментальных данных РЛС IPIX, выполненный авторами в данной работе показывает, что закон распределения может меняться между каналами по дальности при высоком разрешении по дальности. Поэтому одним из перспективных направлений синтеза обнаружителей, инвариантных к закону распределения помехи, является описание распределения помех с помощью сферических инвариантных процессов [15].

В литературе [16–18] рассмотрены различные алгоритмы обнаружения малоразмерных целей с использованием сферических инвариантных процессов. Общим для представленных в работах алгоритмах является обнаружение цели по данным одного обзора, при этом вопрос использования подобных алгоритмов с целью межобзорного накопления не рассмотрен.

Цель данной работы – синтезировать алгоритм межобзорного накопления отраженных радиолокационных сигналов на фоне негауссовских коррелированных помех инвариантного к закону распределения помехи, а также алгоритм вычисления порога обнаружения.

Полученные в результате синтеза алгоритмы обнаружения и вычисления порога обнаружения тестируются на реальных данных, полученных с помощью РЛС IPIX [http://soma.mcmaster.ca/ipix/ dartmouth/datasets.html]. В качестве цели использовался 1.5-метровый пенопластовый буй, обтянутый металлической проволокой и расположенный на морской поверхности. Дальность от РЛС до буя составляла около 2 км. Учитывая, что радиальная скорость относительно РЛС данной цели близка к нулю, то вопросы устранения неоднозначности измерения скорости не рассматривались.

1. ФОРМИРОВАНИЕ ТРАЕКТОРИЙ ДВИЖЕНИЯ ЦЕЛИ

Перед синтезом алгоритма межобзорного накопления необходимо ввести ряд обозначений, связанных с возможными траекториями движения цели.

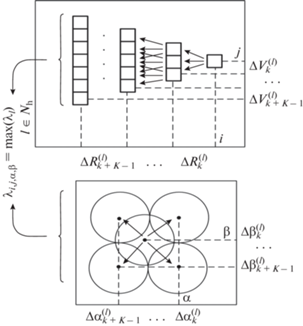
На рис. 1 иллюстрируется принцип формирования траекторий в координатах “дальность–скорость–азимут–угол места”, на котором введены следующие обозначения: $i,j,\beta ,\alpha $ – номера каналов по дальности, скорости, азимуту и углу места соответственно. Диапазоны значений каналов определяются числом каналов по дальности NR, по скорости N, по азимуту ${{N}_{\alpha }}$, угол места ${{N}_{\beta }}$. Обозначим $\Delta R_{k}^{{(l)}}$ – смещение по дальности между k-м и (k + 1)-м обзорами в l-й гипотезе движения цели, выраженное в номере канала по дальности; $\Delta V_{k}^{{(l)}}$ – смещение по скорости между k-м и (k + 1)-м обзорами в l-й гипотезе движения цели; $\Delta \alpha _{k}^{{(l)}}$ – смещение по азимуту между k-м и (k + 1)-м обзорами в l-й гипотезе движения цели; $\Delta \beta _{k}^{{(l)}}$ – смещение по углу места между k-м и (k + 1)-м обзорами в l-й гипотезе движения цели. Переменная l обозначает одну из Nh возможных гипотез движения цели.

Рис. 1.

Формирование возможных траекторий движения цели в координатах “дальность–скорость”.

Одна из Nh возможных гипотез движения цели за K обзоров может быть записана в виде

$\left\{ {\begin{array}{*{20}{c}} {i + k\Delta R_{k}^{{(l)}}}&{j + k\Delta V_{k}^{{(l)}}}&{\alpha + k\Delta \alpha _{k}^{{(l)}}}&{\beta + k\Delta \beta _{k}^{{(l)}}} \end{array}} \right\}_{{k = 0}}^{{K - 1}}.$
Смещение по дальности $\Delta R_{k}^{{(l)}}$ определяется в виде $\operatorname{int} ({{(j + k\Delta V_{k}^{{(l)}})\delta V{{T}_{{{\text{обз}}}}}} \mathord{\left/ {\vphantom {{(j + k\Delta V_{k}^{{(l)}})\delta V{{T}_{{{\text{обз}}}}}} {\delta R}}} \right. \kern-0em} {\delta R}})$, где $\delta R$ – ширина канала по дальности; int() – целая часть числа. Максимальное значение, на которое может переместиться цель между обзорами при движении цели со скоростью ${{V}_{{\max }}}$, определяется как $\operatorname{int} ({{{{V}_{{\max }}}{{T}_{{{\text{обз}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\max }}}{{T}_{{{\text{обз}}}}}} {\delta R}}} \right. \kern-0em} {\delta R}})$. Аналогичным образом определяются смещения по скорости и угловым координатам. Максимальное значение изменения скорости между обзорами $\Delta V_{{\max }}^{{}}$ определяется в соответствии с выражением $\operatorname{int} ({{{{a}_{{\max }}}{{T}_{{{\text{обз}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{\max }}}{{T}_{{{\text{обз}}}}}} {\delta V}}} \right. \kern-0em} {\delta V}})$, где ${{a}_{{\max }}}$ – максимальное значение ускорения цели между обзорами, $\delta V$ – величина разрешающей способности по скорости.

Рассмотрим принцип формирования траекторий движения цели при использовании линейной модели движения в лучевой системе координат [19]. Предположим, что РЛС неподвижна. Обработка радиолокационной информации строится по корреляционно-фильтровой схеме [20].

В соответствии с линейной моделью движения дальность до цели R между k-м и k – 1-м обзорами меняется в соответствии с выражением

${{R}_{k}} = {{R}_{{k - 1}}} \pm V{{T}_{{{\text{обз}}}}},$
где $V$ – скорость цели, которая выбирается исходя из номера канала по скорости, входящего в l‑ю ячейку, Tобз – период обзора РЛС. Аналогичным образом в рамках линейной модели движения определяются смещения по угловым координатам.

Номера каналов по дальности, скорости и угловым координатам соответствующих каждой Nh возможной гипотезе движения необходимы для формирования решающего правила, обеспечивающего межобзорное накопление отраженных сигналов, синтез которого приведен в следующем разделе.

2. СИНТЕЗ АЛГОРИТМА МЕЖОБЗОРНОГО НАКОПЛЕНИЯ ОТРАЖЕННЫХ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ НА ФОНЕ НЕГАУССОВСКИХ КОРРЕЛИРОВАННЫХ ПОМЕХ

Обозначим ${\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ массив данных, формируемых на выходах аналого-цифровых преобразователей двух квадратурных каналов и соответствующих i-му каналу по дальности, $\alpha $-му каналу по азимуту и $\beta $-му каналу по углу места на k-м обзоре и входящий в l-ю гипотезу движения.

Представим принятую пачку импульсов ${\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ в i-м канале по дальности, $\alpha $-м канале по азимуту и $\beta $-м канале по углу места на k-м обзоре в виде

${\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} = \left\{ \begin{gathered} A_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}{\mathbf{s}}_{j}^{{(l)}} + {\mathbf{y}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}},\,\,\,\,{\text{гипотеза}}\,\,\,{{{\text{H}}}_{1}} \hfill \\ {\mathbf{y}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}},\,\,\,\,{\text{гипотеза}}\,\,\,{{{\text{H}}}_{0}} \hfill \\ \end{gathered} \right.,$
где
${\mathbf{s}}_{j}^{{(l)}} = \left[ {\begin{array}{*{20}{c}} 1&{\exp (\operatorname{i} (j + k\Delta V_{k}^{{(l)}}))}&{...}&{\exp (\operatorname{i} (N - 1)(j + k\Delta V_{k}^{{(l)}}))} \end{array}} \right]$
– модель опорного сигнала, соответствующая настройке $\left( {j + k\Delta V_{k}^{{(l)}}} \right)$-го канала по скорости; $A_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}$ – амплитуда отраженного сигнала на k-м обзоре в $i + k\Delta R_{k}^{{(l)}}$-м канале по дальности; $\alpha + k\Delta \alpha _{k}^{{(l)}}$-м канале по азимуту; $\beta + k\Delta \beta _{k}^{{(l)}}$-м канале по углу места; i – мнимая единица.

Вектор ${\mathbf{y}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ в i-м канале по дальности представим в виде составного гауссовского случайного вектора [15]:

${\mathbf{y}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} = \sqrt {{{\tau }_{i}}} {\mathbf{x}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}},$
где ${{\tau }_{i}}$ – скалярная случайная величина с известной плотностью распределения вероятностей $p({{\tau }_{i}})$; ${\mathbf{x}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ – векторная комплексная случайная величина, размерностью $N \times 1$, с гауссовским законом распределения с нулевым математическим ожиданием и корреляционной матрицей ${\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ в $i + k\Delta R_{k}^{{(l)}}$-м канале по дальности, $\alpha + k\Delta \alpha _{k}^{{(l)}}$-м канале по азимуту, $\beta + k\Delta \beta _{k}^{{(l)}}$-м канале по углу места. Матрица ${\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ имеет размерность $N \times N$ (N – количество импульсов в пачке). Случайные величины ${{\tau }_{i}}$ в различных каналах дальности статистически независимы.

Плотность распределения вектора ${\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ при гипотезе H1 имеет вид

$p({\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}\left| {{{{\text{H}}}_{1}}} \right.) = \int\limits_0^\infty {\frac{1}{{{{{(\pi {{\tau }_{i}})}}^{N}}\det ({\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}})}}} \exp \left( { - \frac{{{{{\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} - A_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} - A_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}{\mathbf{s}}_{j}^{{(l)}}} \right)}}{{{{\tau }_{i}}}}} \right)p({{\tau }_{i}}){\text{d}}{{\tau }_{i}},$
где индекс H – символ комплексного сопряжения и транспонирования; det() – определитель матрицы.

Плотность распределения вектора ${\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ при гипотезе H0 имеет вид

$p({\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}\left| {{{{\text{H}}}_{0}}} \right.) = \int\limits_0^\infty {\frac{1}{{{{{(\pi {{\tau }_{i}})}}^{N}}\det ({\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}})}}} \exp \left( { - \frac{{{{{\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}{{{{\tau }_{i}}}}} \right)p({{\tau }_{i}}){\text{d}}{{\tau }_{i}}.$

Отношение правдоподобия для i-го канала по дальности, $\alpha $-го канала по азимуту и $\beta $-го канала по углу места на k-м обзоре имеет вид

(1)
$\lambda _{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} = \frac{{p({\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}\left| {{{{\text{H}}}_{1}}} \right.)}}{{p({\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}\left| {{{{\text{H}}}_{0}}} \right.)}}.$

С учетом выражения (1) отношение правдоподобия для l-й возможной гипотезы движения цели при накоплении данных с K обзоров имеет вид

(2)
${{\lambda }_{l}} = \prod\limits_{k = 0}^{K - 1} {\frac{{{{h}_{N}}\left( {{{{\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} - A_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} - A_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}{\mathbf{s}}_{j}^{{(l)}}} \right)} \right)}}{{{{h}_{N}}\left( {{{{\left( {{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}} ,$
где
${{h}_{N}}(x) = \int\limits_0^\infty {\frac{1}{{{{{\left( {\pi \tau } \right)}}^{N}}}}\exp \left( { - \frac{x}{\tau }} \right)p(\tau )\,} {\text{d}}\tau $
– монотонная функция.

Так как амплитуда отраженного сигнала неизвестна, то подставим в выражение (2) ее оценку [21], которая может быть представлена в виде

$\hat {A}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}\,\,{\text{ = }}\,\,\frac{{{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}}}{{{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{s}}_{j}^{{(l)}}}}.$

Возможная гипотеза движения цели априорно неизвестна, поэтому максимизируем выражение (2) по всем возможным гипотезам движения цели, начинающим движение из $\left( {i,j,\alpha ,\beta } \right)$-го канала:

(3)
${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \left( {{{\lambda }_{l}}} \right) = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \prod\limits_{k = 0}^{K - 1} {\frac{{{{h}_{N}}\left( {{{{\left( {{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}} - \frac{{{{{\left| {{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right|}}^{2}}}}{{{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{s}}_{j}^{{(l)}}}}} \right)}}{{{{h}_{N}}\left( {{{{\left( {{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}.} $

Представить в явном виде числитель и знаменатель в выражении (3) невозможно [22], в связи с чем введем аппроксимацию функции ${{h}_{N}}(x)$ в виде

${{h}_{N}}(x) \approx \frac{{\Gamma (N)}}{{2\sqrt N }}{{x}^{{ - N + 0.5}}}p\left( {\sqrt {\frac{x}{N}} } \right).$

Подставим последнее выражение в формулу (3) и, проведя преобразование отношения правдоподобия, получим:

(4)
${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \left( {{{\lambda }_{l}}} \right) = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \prod\limits_{k = 0}^{K - 1} {\left( {{{{\left( {1 - \frac{{{{{\left| {{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right|}}^{2}}}}{{{{{\left( {{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{s}}_{j}^{{(l)}}}}} \right)}}^{{ - 1}}}} \right)} .$

Одним из достоинств использования математического аппарата сферических инвариантных процессов является то, что данные процессы включают в себя большой набор различных законов распределения: Релея, экспоненциальный, K-распределение, обобщенное K-распределение, Вейбулла, инверсное гамма-распределение и другие, за исключением логнормального [15]. Каждый закон распределения в рамках сферических инвариантных процессов описывается своей функцией ${{h}_{N}}(x)$.

Учитывая, что корреляционная матрица ${\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ априорно неизвестна, то в соответствии с адаптивным байесовским подходом подставим в выражение (4) оценку корреляционной матрицы [23], не зависящую от мощности помехи:

(5)
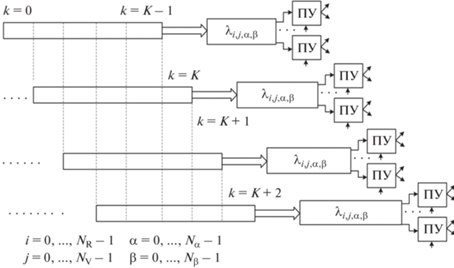
${\mathbf{\hat {C}}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}} = \frac{N}{{{{N}_{C}}}}\sum\limits_{m = 0}^{{{N}_{C}} - 1} {\frac{{{\mathbf{Z}}_{{{{{\left( {i + m,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}{{{\left( {{\mathbf{Z}}_{{{{{\left( {i + m,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}}}{{{{{\left( {{\mathbf{Z}}_{{{{{\left( {i + m,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{\mathbf{Z}}_{{{{{\left( {i + m,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}}}} ,$
где ${{N}_{C}}$ – объем обучающей выборки, используемой для оценки корреляционной матрицы ${{{\mathbf{C}}}_{l}}$.

В соответствии с выражением (4) необходимо в “скользящем окне” из K-обзоров формировать все возможные траектории движения цели для всех каналов $i,j,\alpha ,\beta $ и для каждой l-й возможной траектории движения цели вычислить отношение правдоподобия в соответствии с выражением (4). После этого выбрать максимальное значение

${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \left( {{{\lambda }_{l}}} \right)$
и сравнить его с порогом обнаружения
${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \left( {{{\lambda }_{l}}} \right) \geqslant {{\lambda }_{{{\text{th}}}}},$
где ${{\lambda }_{{{\text{th}}}}}$ – порог (от англ. threshold) обнаружения, вычисленный на основе критерия Неймана–Пирсона.

Процесс формирования “скользящего окна” показан на рис. 2.

Рис. 2.

Формирование “скользящего” окна по обзорам.

Предложенный алгоритм межобзорного накопления может быть использован как дополнительный канал обработки в существующих РЛС.

3. ВЫЧИСЛЕНИЯ ПОРОГА ОБНАРУЖЕНИЯ

В известных работах [5, 24], посвященных межобзорному накоплению на фоне негауссовского некоррелированного шума порог выбирается с помощью метода Монте-Карло. В связи с этим актуальным является вопрос вычисления порога обнаружения при формировании решающего правила (4), который в соответствии с критерием Неймана–Пирсона обеспечит заданную вероятность ложной тревоги. Для этого необходимо найти плотность распределения вероятностей статистики ${{\lambda }_{l}}$ после чего определить закон распределения

${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{\operatorname{h} }}} \left( {{{\lambda }_{l}}} \right).$

Воспользуемся асимптотическим свойством статистики

$\frac{{{{{\left| {{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right|}}^{2}}}}{{{{{\left( {{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{s}}_{j}^{{(l)}}}},$
входящей в выражение (5). В работе [25] доказано, что плотность распределения данной статистики при использовании оценки корреляционной матрицы ${\mathbf{\hat {C}}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$ в виде (5) описывается выражением
(6)
$\begin{gathered} p(x\left| {{{{\text{H}}}_{0}}} \right.) = \frac{{(N - {{N}_{C}} + 1)({{N}_{C}} - 1)}}{{({{N}_{C}} - 1)}}{{(1 - x)}^{{N - {{N}_{C}}}}} \times \\ \times \,\,{}_{2}{{{\text{F}}}_{1}}((N - {{N}_{C}} + 2),(N - {{N}_{C}} + 2),(N + 2),x), \\ \end{gathered} $
где ${}_{2}{{{\text{F}}}_{1}}()$ – гипергеометрическая функция Гаусса.

Используя данное асимптотическое свойство, вычислим порог обнаружения. Для этого, используя плотность распределения (6), сформируем Ns случайных величин $\left\{ {{{x}_{i}}} \right\}_{{i = 0}}^{{{{N}_{S}} - 1}}$. После этого над отсчетами $\left\{ {{{x}_{i}}} \right\}_{{i = 0}}^{{{{N}_{S}} - 1}}$ выполним преобразование $\left\{ {{1 \mathord{\left/ {\vphantom {1 {(1 - {{x}_{i}})}}} \right. \kern-0em} {(1 - {{x}_{i}})}}} \right\}_{{i = 0}}^{{{{N}_{S}} - 1}}$, которое соответствует решающему правилу (4).

С точки зрения вычисления порога обнаружения необходимо знание “хвоста” плотности распределения статистики, соответствующей решающему правила (4) при гипотезе H0. Использование аппроксимации плотности распределения вероятности отсчетов полиномами на основе различных ортогональных многочленов [10], например полиномами Лежандра и Лагерра, нецелесообразно. Результаты аппроксимации плотности распределения в логарифмическом масштабе представлены на рис. 3.

Рис. 3.

Результат аппроксимации гистограммы (кривая 1) отсчетов на входе порогового устройства при гипотезе H0 полиномом Лежандра порядка 30 (кривая 2) и полиномом Лагерра порядка 60 (кривая 3), описывающей решающее правило (4).

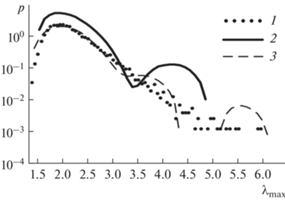
При увеличении порядка полиномов наблюдаются выраженные колебания в области “хвоста” распределения, что затрудняет использование данных аппроксимаций для вычислении порога обнаружения.

В работе [26] показано, что “хвост” любого распределения может быть аппроксимирован обобщенным распределением Парето, параметры которого можно определить методом максимального правдоподобия:

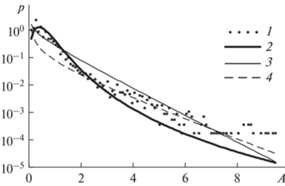
$F(y) = 1 - \frac{{{{M}_{1}}}}{{{{N}_{S}}}}{{\left( {1 + {{с}_{{{\text{Par}}}}}\frac{{y - u}}{{{{a}_{{{\text{Par}}}}}}}} \right)}^{{ - \frac{1}{{c{{{\kern 1pt} }_{{{\text{Par}}}}}}}}}},$
где ${{a}_{{{\text{Par}}}}},{{c}_{{{\text{Par}}}}}$ – параметры обобщенного распределения Парето; u – порог, фиксирующий выбросы случайной величины; M1 – число отсчетов случайных величин, превысивших порог u.

Результат аппроксимации распределением Парето эмпирической функции распределения отсчетов $\left\{ {{1 \mathord{\left/ {\vphantom {1 {(1 - {{x}_{i}})}}} \right. \kern-0em} {(1 - {{x}_{i}})}}} \right\}_{{i = 0}}^{{{{N}_{S}} - 1}}$ показан на рис. 4. Параметры обобщенного распределения Парето вычислены методом максимального правдоподобия.

Рис. 4.

Результат аппроксимации эмпирической функции распределения отсчетов на входе порогового устройства (кривая 1) обобщенным распределением Парето (кривая 2).

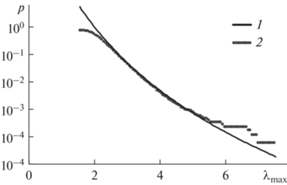
Зависимости на рис. 4 построены при числе отсчетов NS = 100 000. Порог u выбирается таким образом, чтобы его значение превысило M1 отсчетов. Отношение числа превышение порога u к числу отсчетов ${{{{M}_{1}}} \mathord{\left/ {\vphantom {{{{M}_{1}}} {{{N}_{S}}}}} \right. \kern-0em} {{{N}_{S}}}} = 0.1$. Порог обнаружения вычисляется на основе выражения

$u + \frac{{{{{\hat {a}}}_{{{\text{Par}}}}}}}{{{{{\hat {c}}}_{{{\text{Par}}}}}}}\left( {{{{\left( {F\frac{{{{N}_{S}}}}{{{{M}_{1}}}}} \right)}}^{{ - \hat {c}{{{\kern 1pt} }_{{{\text{Par}}}}}}}} - 1} \right),$
где F – заданная вероятность ложной тревоги.

Вычисленная для заданного значения F, числа импульсов в пачке N, числа пачек, используемых для оценки ${\mathbf{\hat {C}}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}$, величина порога обнаружения загружается в память обнаружителя и используется в дальнейшем в процессе обнаружения.

4. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

Тестирование синтезированного алгоритма проводилось на экспериментальных данных, полученных с помощью РЛС IPIX. Параметры РЛС: несущая частота 9.39 ГГц; мощность излучения 8 кВт; период повторения импульсов от 0 до 20 мс; разрешение по дальности может изменяться в диапазоне 30…150 м. Режим работы – разрешение по дальности 30 м, период повторения импульсов 1 мс. Данные в каждом файле сгруппированы по 14 каналов дальности. Число зондирующих импульсов 131072. Для анализа синтезированного в данной работе алгоритма межобзорного накопления использованы данные следующих файлов [http:// soma.mcmaster.ca/ipix/dartmouth/datasets.html] 19931107_135603_starea.cdf; 19931107_141630_starea.cdf; 19931107_145028_starea.cdf; 19931108_213827_starea.cdf; 19931108_220902_starea.cdf.

На первом этапе анализировали законы распределения помех в каналах по дальности. Были рассмотрены следующие виды законов распределения: К-распределение, инверсное гамма-распределение, обобщенное К-распределение. Кроме того, рассмотрено логнормальное распределение.

На рис. 5 для примера показаны гистограмма, а также плотности распределения вероятностей, соответствующие распределениям: К-распределение, инверсное гамма-распределение, обобщенное К-распределение, логнормальное распределение. Данные взяты из файла 19931108_213827_starea.cdf. Разрешение по дальности 30 м.

Рис. 5.

Результаты аппроксимации гистограммы отсчетов амплитуды помехи в одном из каналов по дальности (кривая 1) плотностью инверсного гамма распределения (кривая 2); плотностью K-распределения (кривая 3); плотностью обобщенного K-распределения (кривая 4).

Параметры распределений вычислялись на основе метода моментов. В табл. 1 показаны статистики критерия “Хи-квадрат” для различных распределений в зависимости от номера канала по дальности (19931108_213827_starea.cdf).

Таблица 1.

Статистики критерия “Хи-квадрат”

Распределение Номер канала
1 2 3 4 5 6 7
K распределение 223.1 118.6 238.9 273.7 227.3 399.4 549.3
Обобщенное K распределение 672.2 282.8 516.1 698.4 555.8 748.1 944.3
Инверсное гамма-распределение 137.8 57.2 97.5 120 109.5 402.4 630.4
Логнормальное распределение 305.4 88.9 244.2 220.5 215.3 517.9 570.3

Примечание. Полужирным шрифтом выделены минимальные значения статистик критерия “Хи-квадрат” для соответствующего канала по дальности.

Анализ данных табл. 1 показывает, что в каналах по дальности с 1 по 5 из рассмотренных распределений наиболее близким является инверсное гамма-распределение, в каналах по дальности с 6 по 7 наиболее близким является K-распределение.

Учитывая, что отношение сигнал-помеха в экспериментальных данных известно, для анализа эффективности были построены зависимости D(F), где D – вероятность правильного обнаружения.

В работе [27] авторы приводят выражение для решающей статистики при межобзорном накоплении в виде

(7)
${{\lambda }_{{i,j,\alpha ,\beta }}} = \mathop {\max }\limits_{l \in {{N}_{{\text{h}}}}} \left( {{{\lambda }_{l}}} \right) = \mathop {\max }\limits_{j \in {{N}_{\operatorname{h} }}} \prod\limits_{k = 0}^{K - 1} {\frac{{{{{\left| {{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right|}}^{2}}}}{{{{{\left( {{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{Z}}_{{{{{\left( {i,\alpha ,\beta } \right)}}_{k}}}}^{{(l)}}{{{\left( {{\mathbf{s}}_{j}^{{(l)}}} \right)}}^{H}}{{{\left( {{\mathbf{C}}_{{{{{(i,\alpha ,\beta )}}_{k}}}}^{{(l)}}} \right)}}^{{ - 1}}}{\mathbf{s}}_{j}^{{(l)}}}}} .$
Решающее правило (7) использовано для сравнения с синтезированным в данной работе межобзорным алгоритмом накопления (4). Особенность радара IPIX заключается в том, что сканирование в пространстве не осуществляется. Данные снимаются при одном значении азимута и угла места. В связи с этим из выражения для решающего правила (4) исключены гипотезы возможного движения по азимуту и углу места. Движение цели рассматривается только в координатах “дальность–скорость”.

Результаты обработки экспериментальных данных, взятых из файла 19931107_135603_starea.cdf, приведены на рис. 6. Число импульсов в пачке N = 16. Число обзоров K = 1.2. Число пачек, используемых для вычисления оценки корреляционной матрицы NC = 8N. В проведенном эксперименте цель находилась в 9-м канале по дальности, а отношение сигнал-помеха лежит в диапазоне 0…6 дБ.

Рис. 6.

Характеристики обнаружения межобзорного алгоритма обнаружения (4) (кривая 1) и алгоритма (7) (кривая 2) при K = 2, межобзорного алгоритма обнаружения (4) (кривая 3) и алгоритма (7) (кривая 4) при K = 1.

Рис. 7.

Характеристики обнаружения межобзорного алгоритма обнаружения (4) (кривая 1) и алгоритма (7) (кривая 2) при K = 3, межобзорного алгоритма обнаружения (4) (кривая 3) и алгоритма (7) (кривая 4) при K = 1.

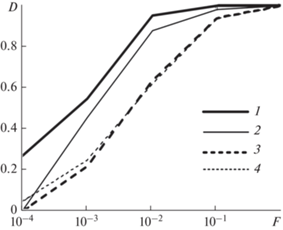
Совпадение эффективности алгоритмов (4) и (7) при K = 1 подтверждает результаты работы [21]. При увеличении количества обзоров вероятность правильного обнаружения алгоритмов (4) и (7) также увеличивается. При вероятностях F больше 10–2 эффективность алгоритмов (4) и (7) также практически совпадает.

При увеличении количества обзоров с K = 2 до K = 3 алгоритм (4) обеспечивает более высокую вероятность правильного обнаружения по сравнению с алгоритмом (4). При F = 10–2 выигрыш составляет 0.1 по вероятности правильного обнаружения при сравнении с известным алгоритмом (7).

ЗАКЛЮЧЕНИЕ

Таким образом, в работе синтезирован алгоритм межобзорного накопления отраженных радиолокационных сигналов на фоне негауссовских коррелированных помех и получен инвариантный относительно закона распределения помехи алгоритм вычисления порога обнаружения, использующий асимптотические свойства статистики, входящей в решающее правило (4). Обработка экспериментальных данных с РЛС IPIX показала, что предлагаемый алгоритм межобзорного накопления при трех и более обзорах обеспечивает повышение вероятности правильного обнаружения цели не менее чем на 0.1 при вероятности ложной тревоги 10–2.

Список литературы

  1. Сосулин Ю.Г. Теория обнаружения и оценивания стохастических сигналов. М.: Советское радио, 1978.

  2. Bussy S., Lops M., Venturino L. // IEEE Trans. 2005. V. AES-41. № 7. P. 937.

  3. Barniv Y., Kella O. // IEEE Trans. 1985. V. AES-21. № 1. P. 144.

  4. Arnold J., Shaw S.W., Pasternack H. // IEEE Trans. 1993. V. AES-29. № 1. P. 44.

  5. Daikun Z., Shouyong W., Xing Q. // Chinese J. Electronics. 2016. V. 25. № 3. P. 583.

  6. Jiang H., Wei Y., Kirubarajab T. et al. // IEEE Trans. 2017. V. AES-53. № 2. P. 736.

  7. Белокуров В.А., Кошелев В.И. // Радиотехника. 2019. Т. 83. № 11(18). С. 41.

  8. Белокуров В.А., Кошелев В.И. // Радиотехника. 2019. Т. 83. № 5-2. С. 161.

  9. Abramovich Y., Besson O. // IEEE Signal Processing Lett. 2015. V. 22. № 10. P. 1791.

  10. Акимов П.С., Бакут П.А., Богданович В.А. и др. Теория обнаружения сигналов. М.: Радио и связь, 1984.

  11. Шелухин О.И. Негауссовские процессы в радиотехнике. М.: Радио и связь, 1998.

  12. Валеев В.Г. Нелинейная обработка сигналов. М.: Радиотехника, 2013.

  13. Винокуров В.И. Морская радиолокация. М.: Судостроение, 1986.

  14. Ward K., Tougth R., Watts S. Sea Clutter: Scattering, the K Distribution and Radar Performance. L.: The Institution of Engineering and Technology, 2006.

  15. Weiner M. Adaptive Antennas and Receivers. N.Y.: Taylor and Francis group, 2006.

  16. Sangston K.J., Gini F., Greco M.S. // IEEE Trans. 2012. V. AES-48. № 1. P. 64.

  17. Gini F., Greco M. S. // IEEE Trans. 1999. V. AES-35. № 7. P. 1095.

  18. Jay E., Ovarlez J.P., Declercq D., Duvaut P. // Signal Processing. 2003. V. 83. № 6. P. 1151.

  19. Меркулов В.И., Верба В.С., Ильчук А.Р. и др. Автоматическое сопровождение целей в РЛС интегрированных авиационных комплексов. Сопровождение одиночных целей. М.: Радиотехника, 2018.

  20. Ширман Я.Д., Манжос В.Н. Теория и техника обработки радиолокационной информации на фоне помех. М.: Радио и связь, 1981.

  21. Kay S. Fundamental of Statistical Signal Processing. Detection Theory. N.Y.: SpringerLink, 1993.

  22. Conte E., Lops M., Ricci G. // IEEE Trans. 1995. V. AES-31. № 2. P. 617.

  23. Conte E., De Maio A., Ricci G. // IEEE Trans. 2002. V. AES-38. № 2. P.415.

  24. Liu S., Chen X., Zeng T. // IET Radar, Sonar and Navigation. 2013. V. 7. № 8. P. 773.

  25. Pascal F., Ovarlez J-P., Forster P. et al. // Proc. 12th Europ. Signal Processing Conf. Vienna. 6–10 Sept. 2004. N.Y.: IEEE, 2004. P. 2143.

  26. Franke J., Härdle W.K., Hafner C.M. Statistics of Financial Markets. An Introduction. Berlin: Springer-Verlag, 2008.

  27. Xu S.-W., Shui P.-L., Yan X.-Y // Circuits, Systems and Signal Processing, 2017. V. 36. № 6. P. 2360.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал