Радиотехника и электроника, 2022, T. 67, № 5, стр. 440-446

ВВЕДЕНИЕ

Как известно, в таких одиночных рассеивателях, как наноцилиндр из серебра или золота, в оптическом диапазоне волн $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$ ($\lambda $ – длина волны) существуют не только поверхностные волны (плазмон-поляритоны) с высокой степенью локализации поля вблизи поверхности цилиндра, но и их резонансы [1]. Эффект локализации и существовааание резонансов поля используется в спектроскопии, а также при создании сенсоров волн оптического диапазона [1]. Отметим, что спектры рассеяния и поглощения на одиночных цилиндрах с круглой, эллиптической и прямоугольной формой поперечного сечения анализировались в работах [2–6]. Оптические резонаторы из двух серебряных цилиндров прямоугольного сечения исследовались в [3, 4], а для случая двух эллиптических цилиндров – в [7]. Достоинством таких резонаторов является возможность управлять резонансной частотой путем изменения расстояния между цилиндрами. Случаи линейных кластеров, образованных двумя одинаковыми сплошными сферами из карбида кремния, (полыми) цилиндрами из метаматериала, а также двух (трех) одинаковых наноцилиндров или цилиндров разного диаметра из серебра рассматривались в [1, 8–12].

Цель данной работы состоит в строгом электродинамическом исследовании особенностей связанных резонансов плазмонов, образующихся при рассеянии плоской волны светового диапазона длин волн треугольным кластером, образованным тремя одинаковыми цилиндрами из реального серебра, расположенных в углах равностороннего треугольника.

1. ФОРМУЛИРОВКА ЗАДАЧИ. МЕТОД РЕШЕНИЯ

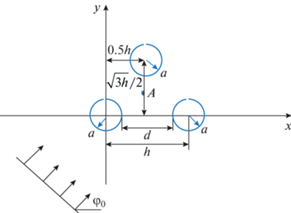
Рассмотрена двумерная задача дифракции плоской электромагнитной волны на кластере (структуре), состоящем из трех одинаковых серебряных наноцилиндров, расположенных в углах равностороннего треугольника. Считается, что все цилиндры имеют одинаковый радиус ${{a}_{l}} = a$ ($l = 1,2,3$) и одинаковое расстояние h = 2a + d $ \equiv $ $ \equiv 2a + \chi a$ между их центрами ($d = \chi a$ – расстояние между их поверхностями, рис. 1). Предполагается, что длина волны $\lambda $ падающей электромагнитной принадлежит световому диапазону длин волн $\lambda \approx 300...900\,\,нм$.

Геометрия исследуемой задачи представлена на рис. 1. Относительная диэлектрическая проницаемость серебра 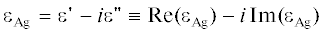в световом длин волн определялась путем аппроксимации кубичными сплайнами экспериментальных данных работы [13]. Отметим, что использование результатов работы [13], так же как и теории Друде [1], накладывает ограничение на минимальный диаметр $2{{a}_{{}}}$ серебряных цилиндров $2a \geqslant 10$ нм, так как при $2a < 10$ нм необходимо учитывать явления пространственной дисперсии [1].

Таким образом, с точки зрения классической электродинамики речь идет о решении задачи дифракции плоской электромагнитной волны на трех однородных диэлектрических цилиндрах.

Исследован случай ТМ-поляризации, когда в электромагнитном поле присутствуют компоненты ${{H}_{z}}(x,y),$ ${{E}_{x}}(x,y),$ ${{E}_{y}}(x,y)$. Задача дифракции в этом случае сводится к нахождению скалярной функции $U(x,y) = {{H}_{z}}(x,y)$, а волновое поле падающей плоской волны задается выражением

где угол ${{\varphi }_{0}}$ определяет направление распространения волны. Использована гауссовская система физических единиц, зависимость от времени выбрана в виде $\exp (i\omega t)$, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda } = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число вакуума, $\omega $ – круговая частота, $с$ – скорость света в вакууме.

Полное поле $U(x,y)$ в кусочно-однородной среде удовлетворяет уравнению Гельмгольца

где диэлектрическая проницаемость $\varepsilon (x,y)$ среды определяется выражением ${{\varepsilon }_{{{\text{Ag}}}}}$ – относительная диэлектрическая проницаемость серебра.

Уравнение (2) необходимо дополнить условием непрерывности величин

на границах цилиндров, где $N$ обозначает нормаль к границам цилиндров.

Полное поле вне цилиндров состоит из падающего ${{U}^{0}}$ и рассеянного ${{U}^{s}}$ полей

где рассеянное поле ${{U}^{s}}$ представляет собой сумму полей, рассеянных каждым цилиндром:

Численное исследование сформулированной дифракционной задачи удобнее проводить в цилиндрической системе координат ($x = r\cos \varphi ,$ y = $ = r\sin \varphi $). В такой системе координат падающее поле (1) имеет вид

При этом рассеянное поле (6) должно удовлетворять в дальней зоне условию излучения

где $\Phi (\varphi )$ – диаграмма рассеяния кластера.

Полное сечение рассеяния кластера ${{\sigma }_{S}}$ выражается через решение сформулированной выше краевой задачи по формуле

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение краевой задачи проводили методом дискретных источников [14–18]. Точность численного решения оценивалась невязкой граничных условий $\Delta $ в линейной норме на цилиндрах и во всех расчетах была не хуже чем $\Delta = {{10}^{{ - 3}}}$.

Рассмотрим сначала случай, когда плоская волна с углом падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ рассеивается треугольным кластером, в котором фиксировано расстояние $d = 0.1а$ ($\chi = 0.1$) между цилиндрами.

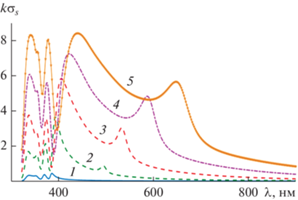
На рис. 2 представлены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{s}}$ для пяти различных значений радиусов цилиндров: a = 10, 20, 30, 40, 50 нм. Из рис. 2 следует, что каждая кривая содержит несколько максимумов (резонансов). При этом увеличение радиусов цилиндров сопровождается как увеличением значений нормированного поперечника рассеяния $k{{\sigma }_{s}}$, так и смещением его резонансов в сторону больших значений длин волн.

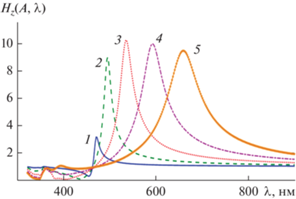
На рис. 3 представлена зависимость модуля поля ${{H}_{z}}(А,\lambda )$ от длины волны в пространственной точке А с координатами $x = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2},$ $y = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 4}} \right. \kern-0em} 4}$, соответствующей центральной точке внутренней области кластера (см. рис. 1). Значения радиусов цилиндров $a = 10,\,\,20,\,\,30,\,\,40,\,\,50\,\,{\text{нм}}$. Из рис. 3 видно, что каждая кривая имеет ярко выраженный максимум, расположение которого совпадает с расположением первого (правого) максимума нормированного поперечника рассеяния (см. рис. 2). При этом изменение радиуса цилиндров в пределах $20\,\,{\text{нм}} < a < 50\,\,{\text{нм}}$ приводит к изменению значений максимума поля ${{H}_{z}}(А,\lambda )$ в пределах $9 < {{H}_{z}}(А,\lambda ) < 10$, в то время как при $a = 10\,\,{\text{нм}}$ максимум поля ${{H}_{z}}(А,\lambda )$ принимает значение ${{H}_{z}}(А,\lambda ) \approx 3$, т.е. в три раза меньшее.

На рис. 4а–4г представлены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{s}}$ для кластеров, у которых расстояние между цилиндрами $d = \chi а$ равнялось соответственно $d = \chi а = 0.2a,0.5a,1.0a,2.0a$ при пяти различных значениях радиусов цилиндров: a = 10, 20, 30, 40, 50 нм. Из результатов, представленных на этих рисунках, следует, что увеличение расстояние между цилиндрами $d = \chi а$ приводит к смещению максимумов (резонансов) нормированного поперечника рассеяния $k{{\sigma }_{s}}$ в сторону меньших значений длин волн и слиянию (уменьшению числа резонансов) максимумов (резонансов) поперечника рассеяния $k{{\sigma }_{s}}$. Отметим, что процессу слияния максимумов поперечника рассеяния $k{{\sigma }_{s}}$ соответствует процесс вырождения резонансов плазмонов.

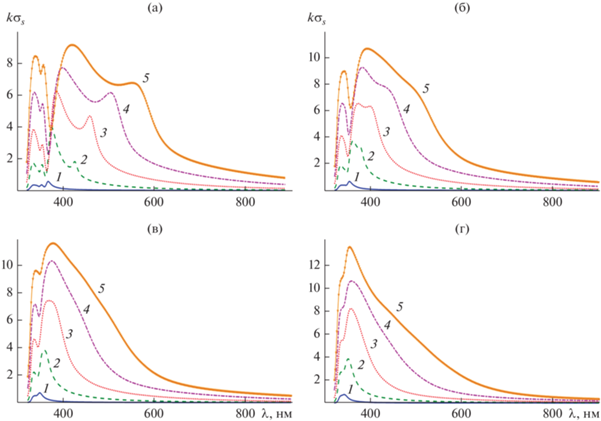
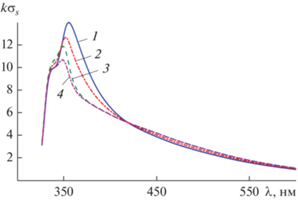
Рисунок 5 посвящен исследованию влияния угла падения ${{\varphi }_{0}}$ плоской волны на нормированный поперечник рассеяния $k{{\sigma }_{s}}$. Кластер характеризовался следующими параметрами: $\chi = 2.0$, $a = 40\,\,{\text{нм}}$, а угол падения ${{\varphi }_{0}}$ плоской волны принимал значения 0, π/6, π/4 и π/2. Из рисунка видно, что изменение угла падения ${{\varphi }_{0}}$ в пределах $0 < {{\varphi }_{0}} < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ слабо сказывается на положении максимума (резонанса) нормированного поперечника рассеяния $k{{\sigma }_{s}}$. Отметим, что при меньших расстояниях между цилиндрами $\chi < 2.0$ изменение угла падения ${{\varphi }_{0}}$ в пределах $0 < {{\varphi }_{0}} < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ сказывается еще меньше (результаты мы не приводим).

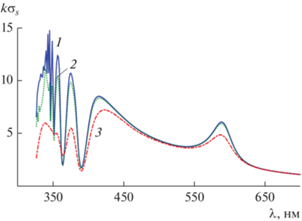
Исследовано также влияние потерь серебра $\operatorname{Im} (\varepsilon )$ цилиндров кластера на значения нормированного поперечника рассеяния $k{{\sigma }_{s}}$ (рис. 6). Кластер имел следующие параметры: $\chi = 0.1$, $a = 40\,\,{\text{нм}}$, угол падения ${{\varphi }_{0}}$ плоской волны был равен φ₀ = π/6, потери серебра Im(ε_Ag) = 0, 0.1Im(ε_Ag) и Im(ε_Ag). Из данных, представленных на рис. 6, следует что потери наиболее сильно сказываются в области длин волн λ < 400 нм, соответствующей мультипольным резонансам плазмонов. Отметим, что в случае реальных потерь резонансы поперечника рассеяния kσ_s области длин волн λ $ \ll $ 360 нм сливаются, приводя к общему увеличению значений поперечника рассеяния.

Рассмотрим случай, когда плоская волна с углом падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$ рассеивается треугольным кластером, в котором фиксирован радиус цилиндров $а = 40\,\,{\text{нм}}$ (или $а = 10\,\,{\text{нм}}$), а параметр $\chi $, определяющий расстояние между ними, изменяется, принимая значения χ = 0.05, 0.1, 0.25, 0.5, 1.0, 3.0. На рис. 7а представлены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{s}}$ в случае радиуса цилиндра $а = 40\,\,{\text{нм}}$ и указанных шести значений параметра $\chi $. Случай цилиндра радиусом $а = 10\,\,{\text{нм}}$ изображен на рис. 7б.

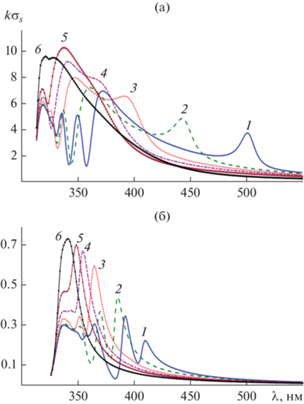
Из этих рисунков видно, что увеличение расстояния между цилиндрами, как и уменьшение радиуса цилиндра, приводит к уменьшению числа резонансных максимумов спектра нормированного поперечника рассеяния $k{{\sigma }_{s}}$.

Теперь рассмотрим структуру ближнего поля ${{H}_{z}}$ вблизи кластера, которая имеет место в случае резонансов поперечника рассеяния $k{{\sigma }_{s}}$.

На рис. 8а, 8б представлено пространственное распределение линий равных амплитуд компоненты поля ${{H}_{z}}$ вблизи треугольного кластера с параметрами $а = 40\,\,{\text{нм}}$, χ = 0.1, углом падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$ и двух резонансных длинах волн λ = 386.623 (а), 422.525 нм (б) (см. кривую 2 на рис. 7а). Как видим, при резонансной длине волны λ = 386.623 нм связанные резонансы поверхностных волн (плазмонов) фактически приводят к резонансу всей области между цилиндрами (см. рис. 8а), в случае резонансной длины волны λ = 422.525 нм (б) связанные резонансы поля наблюдаются только между соседними частями двух цилиндров (см. рис. 8б)!

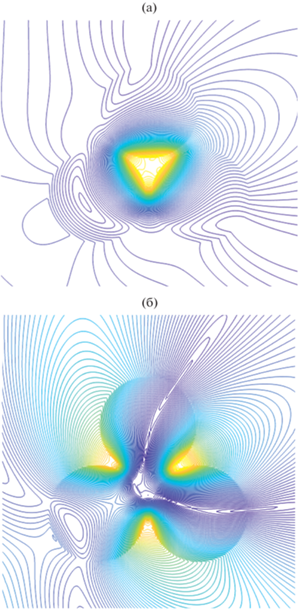
Аналогичные явления наблюдаются и при увеличении расстояния между цилиндрами до значений χ = 0.25 и длинах волн λ = 500 (а), 360 нм (б) (см. кривую 3 на рис. 7а). Эти случаи пространственного распределения линий равных амплитуд компоненты поля ${{H}_{z}}$ изображены на рис. 9а, 9б.

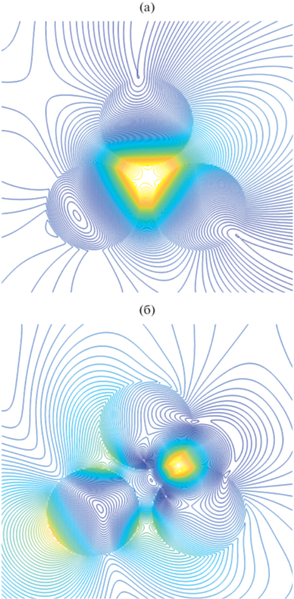
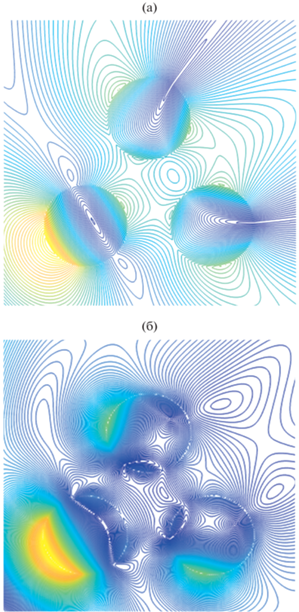
Дальнейшее увеличение расстояния между цилиндрами приводит к исчезновению резонанса во внутренней области между цилиндрами и появлению резонансов на частях каждого цилиндра. Это можно увидеть на рис. 10а, 10б, где представлены картины пространственного распределения линий равных амплитуд компоненты поля ${{H}_{z}}$ для кластера с параметрами $а = 40\,\,{\text{нм}}$, χ = 1, углом падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$ и двух резонансных длинах волн λ = 375 (а), 340 нм (б) (см. кривую 5 на рис. 7а).

ЗАКЛЮЧЕНИЕ

Численно исследована двумерная задача дифракции ТМ-поляризованной плоской волны на треугольном кластере, состоящем из трех одинаковых серебряных круговых цилиндров. Показано слабое влияние угла падения плоской волы на положение максимумов относительного поперечника рассеяния. Установлено, что реальные потери серебра относительно слабо влияют в области дипольного резонанса и сильно сказываются на мультипольных резонансах, что приводит к слиянию полей мультипольных резонансов в один общий резонанс. Обнаружены эффекты “вырождения” резонансов в кластере, образования локальных и связанных резонансов плазмонов, а также перехода резонанса плазмона в резонанс внутренней области кластера.

Автор заявляет об отсутствии конфликта интересов.