1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 67, № 5, 2022

Радиотехника и электроника, 2022, T. 67, № 5, стр. 447-453

Исследование геодезических линз с плавным переходом

А. С. Венецкий a, В. А. Калошин a, *, Т. Т. Чан b

a Институт радиотехники и электроники им. В.А. Котелгьникова РАН
125007 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

b Московский физико-технический институт (Национальный исследовательский университет)
141700 Долгопрудный, Московской обл., Институтский пер., 9, Российская Федерация

* E-mail: vak@cplire.ru

Поступила в редакцию 17.05.2021
После доработки 17.05.2021
Принята к публикации 25.06.2021

Полный текст (PDF)

Аннотация

Рассмотрены задачи синтеза и анализа геодезических линз с осевой симметрией и плавным переходом к планарному волноводу, ортогональному оси линзы. В приближении геометрической оптики найдено аналитическое решение для образующей поверхности геодезической линзы с кусочно-линейной образующей поверхности плавного перехода. Проведен анализ фазовых аберраций и электродинамическое моделирование метало-воздушных геодезических линз с различными формами плавного перехода с использованием приближения Кирхгофа и метода конечных элементов.

ВВЕДЕНИЕ

Впервые задача о синтезе волноводной линзы в виде двух параллельных искривленных проводящих поверхностей была поставлена в статье [1]. Задача синтеза такой линзы заключается в нахождении формы ее поверхности, обеспечивающего преобразование поля источника цилиндрической волны в основную моду планарного волновода с заданным двумерным фазовым фронтом. В работе [2] было найдено явное геометрооптическое решение задачи синтеза образующей поверхности линзы, являющейся телом вращения и преобразующей цилиндрический фронт источника на границе линзы в линейный фронт в планарном волноводе, ортогональном ее оси. Синтезированная поверхность линзы при этом ортогональна планарному волноводу в точках стыка.

Поскольку лучи в такой линзе совпадают с геодезическими линиями, такие линзы получили название геодезические.

В работе [3] решение [2] было обобщено на случай источника, расположенного в планарном волноводе на расстоянии от границы линзы. В работе [4] предложена металло-воздушная геодезическая линза с плавным согласующим переходом к планарному волноводу.

В работах [5–8] исследовались диэлектрические геодезические линзы с плавным переходом, в которых наличие ортогонального соединения с планарным волноводом приводит не только к появлению отраженной моды, как в металло-воздушных линзах, но и к существенным потерям на излучение. Наличие у линзы плавного перехода в этих работах приводит к фазовым аберрациям, т.е. искажению выходного фронта по сравнению с заданным.

В работах [9, 10] описаны методики численного решения задачи синтеза геодезической линзы с плавным переходом, обеспечивающие точную фокусировку лучей основной частью линзы (за исключением плавного перехода). В работах [11‒13] найдены аналитические решения задачи синтеза геодезической линзы с плавным переходом частного вида и получены формулы для образующей поверхности линзы в виде однократного интеграла.

Цель данной работы – найти образующую осесимметричной геодезической линзы, которая обеспечивает точную фокусировку цилиндрической волны источника, расположенного внутри планарного волновода, ортогонального оси линзы, в линейный фронт при наличии между линзой и планарным волноводом перехода с кусочно-линейной образующей, а также провести электродинамический анализ металло-воздушных геодезических линз с различными плавными переходами и сопоставить результаты моделирования.

1. СИНТЕЗ ГЕОДЕЗИЧЕСКОЙ ЛИНЗЫ С ПОЛИКОНИЧЕСКИМ ПЕРЕХОДОМ

В приближении геометрической оптики задача синтеза металло-воздушной линзы сводится к нахождению образующей поверхности, расположенной посередине между двумя металлическими поверхностями линзы. Для луча, распространяющегося вдоль этой (средней) поверхности, справедлив принцип Ферма, т.е. эйконал (оптический путь) луча, соединяющего две точки поверхности, должен быть минимален по сравнению со всеми другими кривыми, соединяющими эти точки, и лучи, таким образом, являются геодезическими линиями данной поверхности.

Используя принцип Ферма, нетрудно получить уравнение z = f(ρ) геодезической кривой на поверхности тела вращения в цилиндрической системе координат (ρ, φ, z). Учитывая, что элемент дуги произвольной кривой на поверхности тела вращения в цилиндрической системе координат имеет вид

(1)
$d{{s}^{2}} = {{\rho }^{2}}d{{\varphi }^{2}} + [1 + {{(\rho {\kern 1pt} '(z))}^{2}}]d{{z}^{2}}$
и с учетом принципа Ферма, можно получить
(2)
$\frac{d}{{ds}}\left( {\frac{{\partial L}}{{\partial{ \dot {\varphi }}}}} \right) - \frac{{\partial L}}{{\partial \varphi }} = 0,$
(3)
$\frac{d}{{ds}}\left( {\frac{{\partial L}}{{\partial{ \dot {z}}}}} \right) - \frac{{\partial L}}{{\partial z}} = 0,$
где $L = \sqrt {{{\rho }^{2}}{{{\dot {\varphi }}}^{2}} + [1 + {{{(\rho {\kern 1pt} '(z))}}^{2}}]{\kern 1pt} {{{\dot {z}}}^{2}}} $ – эйконал луча, $\dot {\varphi } = {{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {ds}}} \right. \kern-0em} {ds}}$, $\dot {z} = {{dz} \mathord{\left/ {\vphantom {{dz} {ds}}} \right. \kern-0em} {ds}}$.

В силу осевой симметрии задачи ∂L/∂φ = 0 и из уравнения (2) с учетом (1) следует:

(4)
${{\rho }^{2}}\frac{{d\varphi }}{{ds}} = \gamma \,\,({\text{const}}).$

С учетом (4) уравнение (1) можно свести к уравнению

(5)
${{\left( {\frac{{dz}}{{ds}}} \right)}^{2}} = \frac{{{{\rho }^{2}} - {{\gamma }^{2}}}}{{{{\rho }^{2}}[1 + {{{(\rho {\kern 1pt} '(z))}}^{2}}]}}.$

Дифференциальные уравнения первого порядка (4), (5) описывают семейство лучей (геодезических кривых), где γ – лучевой параметр.

Для определения константы γ найдем угол пересечения соответствующего луча с линией меридиана в произвольной точке поверхности. Используя уравнения (4), (5), можно привести компоненты касательного вектора к траектории луча $\vec {\tau } = \left( {\frac{{dx}}{{ds}},\frac{{dy}}{{ds}},\frac{{dz}}{{ds}}} \right)$ к виду

(6)
$\begin{gathered} \frac{{dx}}{{ds}} = \rho {\kern 1pt} '(z)Q\cos \varphi - \sin \varphi \frac{\gamma }{\rho }, \\ \frac{{dy}}{{ds}} = \rho {\kern 1pt} '(z)Q\sin \varphi + \cos \varphi \frac{\gamma }{\rho },\,\,\,\frac{{dz}}{{ds}} = Q, \\ \end{gathered} $
где $Q = \frac{1}{\rho }\sqrt {\frac{{{{\rho }^{2}} - {{\gamma }^{2}}}}{{1 + {{{[\rho {\kern 1pt} '(z)]}}^{2}}}}} .$

Искомый угол пересечения β можно найти из соотношения

(7)
$(\vec {\tau },\vec {l}) = \cos \beta ,$

где $\vec {l} = (\cos \mu \cos \varphi ,\cos \mu \sin \varphi ,\sin \mu )$ – единичный вектор, касательный к меридиану в точке пересечения с траекторией луча,

$\cos \mu = \frac{{\rho {\kern 1pt} '(z)}}{{\sqrt {1 + \rho {\kern 1pt} {{'}^{2}}} }},\,\,\,\,\sin \mu = \frac{1}{{\sqrt {1 + \rho {\kern 1pt} {{'}^{2}}} }},$

Из (7) следует, что $\cos \beta = {{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} } \rho }} \right. \kern-0em} \rho },$

(8)
$\gamma = \rho \sin \beta {\kern 1pt} .$

Соотношение (8) для геодезических линий на поверхностях вращения известно как теорема Клеро [17]. Из этого соотношения в частности следует, что в точке, где геодезическая кривая ортогональна меридиану (β = π/2), значение ρ минимально и, следовательно, $\gamma = {{\rho }_{{\min }}}$.

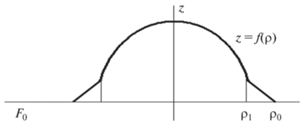
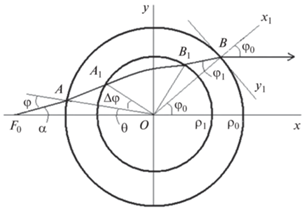
Выведем уравнение, которому должна удовлетворять поверхность с коническим согласующим переходом (рис. 1), чтобы лучи, выходящие из точки F0 с декартовыми координатами x = –F0, y = 0, z = 0 (рис. 2) после прохождения линзы были параллельны оси x.

Рис. 1.

Образующая линзы с коническим переходом.

Рис. 2.

Проекция луча на плоскость z = 0.

Рассмотрим луч, выходящий из источника в точке F0 (рис. 2), который идет в плоскости XOY до точки А, преломляется, проходит вдоль плавного перехода до точки А1, преломляется , проходит вдоль поверхности линзы до точки В1, преломляется, проходит вдоль плавного перехода до точки В, снова преломляется и идет в плоскости XOY параллельно оси х. При этом поверхность перехода (${{\rho }_{1}} \leqslant \rho \leqslant {{\rho }_{0}}$) является частью поверхности конуса, а поверхность линзы ($0 \leqslant \rho \leqslant {{\rho }_{1}}$) подлежит определению.

Из (8) для угла φ0 входа и выхода луча следует

(9)
$\sin {{\varphi }_{0}} = {\gamma \mathord{\left/ {\vphantom {\gamma {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}.$

Из уравнений (4), (5) для функции z = f(ρ) следует

$\frac{{d\varphi }}{{d\rho }} = \frac{\gamma }{\rho }\frac{{\sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}.$

Интегрируя последнее уравнение и используя симметрию луча, можно найти приращение угла φ = = 2ΔΦ для луча между точками А1 и В1 (см. рис. 2):

$2\Delta \Phi = 2\int\limits_\gamma ^{{{\rho }_{1}}} {\frac{\gamma }{\rho }} \frac{{\sqrt {1 + z{\kern 1pt} {{'}^{2}}} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}d\rho .$

Для каждого луча, исходящего из фокуса в точке F0 и выходящего из линзы в точке В параллельно оси x, можно записать

(10)
$\theta + 2\Delta \varphi + 2\Delta \Phi + {{\varphi }_{0}} = \pi .$

Зададим образующую на отрезке ${{\rho }_{1}} \leqslant \rho \leqslant {{\rho }_{0}}$ линейной функцией $z = A({{\rho }_{0}} - \rho )$ и тогда получим

(11)
$\begin{gathered} \Delta \varphi = \int\limits_{{{\rho }_{1}}}^{{{\rho }_{0}}} {\frac{\gamma }{\rho }} \frac{{\sqrt {1 + z{\kern 1pt} {{'}^{2}}} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}d\rho = \\ = k\left( {\arcsin \frac{\gamma }{{{{\rho }_{1}}}} - \arcsin \frac{\gamma }{{{{\rho }_{0}}}}} \right), \\ \end{gathered} $
где $k = \sqrt {1 + {{A}^{2}}} $.

Из теоремы синусов для треугольника F0AO (см. рис. 2) следует

$\frac{{\sin \alpha }}{{{{\rho }_{0}}}} = \frac{{\sin \varphi }}{{{{f}_{0}}}},\,\,\,\,{{f}_{0}} = \left| {O{{F}_{0}}} \right|,$
откуда с учетом (9) получаем $\alpha = \arcsin \frac{\gamma }{{{{f}_{0}}}}$.

Уравнение (10) может быть записано в виде

$\begin{gathered} \int\limits_\gamma ^{{{\rho }_{1}}} {\frac{1}{\rho }} \frac{{\sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}d\rho = \\ = \frac{1}{{2\gamma }}\left( {\pi - 2\arcsin \frac{\gamma }{{{{\rho }_{0}}}} + \arcsin \frac{\gamma }{{{{f}_{0}}}} - 2\Delta \varphi } \right). \\ \end{gathered} $

Заменой переменных t = 1/ρ, G = 1/γ, a1 = 1/ρ1, a0 = 1/ρ0, $u(t) = \sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} $ это уравнение приводится к виду

(12)
$\int\limits_{{{a}_{1}}}^G {\frac{{u(t)dt}}{{\sqrt {{{G}^{2}} - {{t}^{2}}} }}} = F(G),$
где $F(G)\, = \,\frac{\pi }{2} - \arcsin {\kern 1pt} \frac{{{{a}_{0}}}}{G} + \frac{1}{2}\arcsin {\kern 1pt} \frac{1}{{{{f}_{0}}G}} - k\left( {\arcsin {\kern 1pt} \frac{{{{a}_{1}}}}{G} - } \right.$ $\left. { - \,\,\arcsin \frac{{{{a}_{0}}}}{G}} \right)$.

Уравнение (12) сводится к интегральному уравнению Абеля. Его решение имеет вид [18]

(13)
$u(x) = \frac{2}{\pi }\frac{d}{{dx}}\int\limits_{{{a}_{1}}}^x {\frac{{sF(s)ds}}{{\sqrt {{{x}^{2}} - {{s}^{2}}} }}} .$

Интегрируя (13) по частям, дифференцируя по х и полагая х = 1/ρ, a1 = 1/ρ1, a0 = 1/ρ0, получаем

(14)
$\begin{gathered} u(\rho ) = \frac{{{{\rho }_{1}}}}{{\sqrt {\rho _{1}^{2} - {{\rho }^{2}}} }}\left( {1 - \frac{2}{\pi }\arcsin \frac{{{{\rho }_{1}}}}{{{{\rho }_{0}}}} + \frac{1}{\pi }\arcsin \frac{{{{\rho }_{1}}}}{{{{f}_{0}}}}} \right) + \\ + \,\,\frac{1}{4} - \frac{1}{\pi }\arcsin \frac{{{{\rho }^{2}} + \rho _{0}^{2} - 2\rho _{1}^{2}}}{{\rho _{0}^{2} - {{\rho }^{2}}}} + \\ + \,\,\frac{1}{{2\pi }}\arcsin \frac{{{{\rho }^{2}} + f_{0}^{2} - 2\rho _{1}^{2}}}{{f_{0}^{2} - {{\rho }^{2}}}} + \\ + \,\,k\left( {\frac{2}{\pi }\frac{{{{\rho }_{1}}}}{{\sqrt {\rho _{1}^{2} - {{\rho }^{2}}} }}\arcsin \frac{{{{\rho }_{1}}}}{{{{\rho }_{0}}}} - \frac{1}{2}} \right. + \\ \left. { + \,\,\frac{1}{\pi }\arcsin \frac{{{{\rho }^{2}} + \rho _{0}^{2} - 2\rho _{1}^{2}}}{{\rho _{0}^{2} - {{\rho }^{2}}}}} \right) - k\left( {\frac{{{{\rho }_{1}}}}{{\sqrt {\rho _{1}^{2} - {{\rho }^{2}}} }} - 1} \right). \\ \end{gathered} $

Полученное решение задачи синтеза нетрудно обобщить на случай кусочно-линейной образующей плавного перехода: $z = {{z}_{{i - 1}}} + {{A}_{i}}(\rho - {{\rho }_{{i - 1}}})$, где i = 1,…, N, ${{\rho }_{N}} \leqslant \rho \leqslant {{\rho }_{0}}$. В этом случае выражение для Δφ в (12) принимает вид

$\begin{gathered} \Delta \varphi = \sum\limits_{i = 1}^N {{{k}_{i}}\left( {\arcsin \frac{\gamma }{{{{\rho }_{i}}}} - \arcsin \frac{\gamma }{{{{\rho }_{{i - 1}}}}}} \right)} , \\ {{k}_{i}} = \sqrt {1 + A_{i}^{2}} . \\ \end{gathered} $

При этом вместо формулы (14) имеем

(15)
$\begin{gathered} u(\rho ) = \frac{{{{\rho }_{N}}}}{{\sqrt {\rho _{N}^{2} - {{\rho }^{2}}} }}\left( {1 - \frac{2}{\pi }\arcsin \frac{{{{\rho }_{N}}}}{{{{\rho }_{0}}}} + \frac{1}{\pi }\arcsin \frac{{{{\rho }_{N}}}}{{{{f}_{0}}}}} \right) + \\ + \,\,\frac{1}{4} - \frac{1}{\pi }\arcsin \frac{{{{\rho }^{2}} + \rho _{0}^{2} - 2\rho _{N}^{2}}}{{\rho _{0}^{2} - {{\rho }^{2}}}} + \\ + \,\,\frac{1}{{2\pi }}\arcsin \frac{{{{\rho }^{2}} + f_{0}^{2} - 2\rho _{N}^{2}}}{{f_{0}^{2} - {{\rho }^{2}}}} + \\ + \,\,\sum\limits_{i = 0}^{N - 1} {{{b}_{i}}\left( {\frac{2}{\pi }\frac{{{{\rho }_{N}}}}{{\sqrt {\rho _{N}^{2} - {{\rho }^{2}}} }}\arcsin \frac{{{{\rho }_{N}}}}{{{{\rho }_{i}}}} - \frac{1}{2}} \right. + } \\ + \,\left. {\,\frac{1}{\pi }\arcsin \frac{{{{\rho }^{2}} + \rho _{i}^{2} - 2\rho _{N}^{2}}}{{\rho _{i}^{2} - {{\rho }^{2}}}}} \right) + {{b}_{N}}\left( {\frac{{{{\rho }_{N}}}}{{\sqrt {\rho _{N}^{2} - {{\rho }^{2}}} }} - 1} \right), \\ \end{gathered} $
где ${{b}_{i}} = {{k}_{{i + 1}}} - {{k}_{i}}$ при $0 < i < N$, ${{b}_{0}} = {{k}_{1}}$, ${{b}_{N}} = - {{k}_{N}}$.

Так как $u(\rho ) = \sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} $, то при выполнении условия $u(\rho ) \geqslant 1$ в области $0 \leqslant \rho < {{\rho }_{N}}$, образующая описывается формулой

$f(\rho ) = - \int\limits_0^\rho {\sqrt {{{u}^{2}}(\rho ) - 1} d\rho } + {{C}_{0}},$
а константа С0 находится из уравнения
$ - \int\limits_0^{{{\rho }_{N}}} {\sqrt {{{u}^{2}}(\rho ) - 1} {\kern 1pt} d\rho } + {{C}_{0}} = {{z}_{N}},$
где zN – значение координаты поверхности на границе линзы и плавного перехода.

Полагая ρ1 = ρ0 в формуле (14), получаем известное [3] уравнение образующей геодезической линзы без согласующего перехода:

(16)
$\begin{gathered} u{\kern 1pt} (\rho ) = \frac{1}{\pi }\frac{{{{\rho }_{0}}}}{{\sqrt {\rho _{0}^{2} - {{\rho }^{2}}} }}\arcsin \left( {\frac{{{{\rho }_{0}}}}{{{{f}_{0}}}}} \right) + \frac{3}{4} + \\ + \,\,\frac{1}{{2\pi }}\arcsin \left( {\frac{{{{\rho }^{2}} + f_{0}^{2} - 2\rho _{0}^{2}}}{{f_{0}^{2} - {{\rho }^{2}}}}} \right), \\ u{\kern 1pt} (\rho ) = \sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} ,\,\,\,f(\rho ) = - \int\limits_0^\rho {\sqrt {{{u}^{2}}(\rho ) - 1} } + {{C}_{0}}, \\ \end{gathered} $
где константа С0 находится из уравнения

$\int\limits_0^{{{\rho }_{0}}} {\sqrt {{{u}^{2}}(\rho ) - 1} {\kern 1pt} d\rho } = {{C}_{0}}.$

Из формулы (16) следует, что $f'({{\rho }_{0}}) = \infty $. Это означает, что поверхность линзы пересекает плоскость XOY под прямым углом. Для реализации плавного перехода от линзы к планарному волноводу можно использовать различные варианты образующей: рассмотренную выше линейно-ломаную, в виде окружности или описываемую интегралом [10, 13].

2. АНАЛИЗ ГЕОДЕЗИЧЕСКИХ ЛИНЗ С ПЛАВНЫМ ПЕРЕХОДОМ

Проведем исследование аберраций эйконала для пяти вариантов линз с радиусом ρ0 = 1.05 и фокусным расстоянием f0 = 1.5, содержащих плавный переход с внутренним радиусом а = 1.

1. Линза с поликоническим переходом (из трех конусов), синтезированная выше. Образующая представляет собой кусочно-ломаную непрерывную линию с тремя отрезками равной длины, аппроксимирующими четверть окружности.

2. Линза, синтезированная в [3], с образующей плавного перехода в виде дуги окружности

$z(\rho ) = - \sqrt {z_{2}^{2} - {{{(\rho - {{\rho }_{2}})}}^{2}}} + {{z}_{2}},$
где
$\begin{gathered} {{z}_{2}} = \frac{{d\sqrt {{{d}^{2}}{{c}^{2}} - {{b}^{2}}{{c}^{2}} + {{c}^{2}}} - bc + c + c{{d}^{2}}}}{{{{b}^{2}} - 2b + 1}}, \\ {{\rho }_{2}} = \frac{{b{{z}_{2}} - {{z}_{2}} + c}}{d} + a. \\ \end{gathered} $
– координаты центра окружности, найденные из условия совпадения образующих линзы и плавного перехода в точке М с координатами (ρ2, z2), $d = f{\kern 1pt} '(a)$, с = f(a), $b = \sqrt {1 + f{\kern 1pt} {{'}^{2}}(a)} $.

3. Линза, синтезированная в [3], с образующей плавного перехода в виде четверти окружности.

4. Линза с плавным переходом, синтезированная в работе [13], образующая которой определяется формулами

$\begin{gathered} z(\rho ) = \frac{1}{\pi }\int\limits_0^\rho {\sqrt {{{{\left( {\arccos \left( {\sqrt {\frac{{{{a}^{2}} - {{\rho }^{2}}}}{{f_{0}^{2} - {{\rho }^{2}}}}} } \right) + \frac{\pi }{2} + a\frac{{\arcsin \left( {\frac{a}{{{{f}_{0}}}}} \right)}}{{\sqrt {{{a}^{2}} - {{\rho }^{2}}} }} + \Omega (\rho ,a)} \right)}}^{2}} - {{\pi }^{2}}} d\rho } , \\ \Omega (\rho ,a) = 2{\kern 1pt} \rho \frac{d}{{d\rho }}\left[ {\int\limits_a^{{{\rho }_{0}}} {\frac{{({{\rho }_{0}} - R)}}{{R{{h}^{2}}}}\arcsin \left( {\sqrt {\frac{{{{a}^{2}} - {{\rho }^{2}}}}{{{{R}^{2}} - {{\rho }^{2}}}}} } \right)dR} } \right],\,\,\,\,0 \leqslant \rho \leqslant a, \\ \end{gathered} $
$\begin{gathered} z(\rho ) = z(a) + \frac{1}{2}\left\{ {{{h}^{2}}\ln \left( {\frac{{\sqrt {{{{\left( {{{\rho }_{0}} - \rho } \right)}}^{2}} + 2{{h}^{2}}\left( {{{\rho }_{0}} - \rho } \right)} + {{\rho }_{0}} + {{h}^{2}} - \rho }}{{\sqrt {{{{\left( {{{\rho }_{0}} - a} \right)}}^{2}} + 2{{h}^{2}}\left( {{{\rho }_{0}} - a} \right)} + {{\rho }_{0}} + {{h}^{2}} - a}} + \Phi (\rho ,a)} \right)} \right\}, \\ \Phi (\rho ,a) = - \frac{{{{\rho }_{0}} + {{h}^{2}} - \rho }}{{{{h}^{2}}}}\sqrt {{{{\left( {{{\rho }_{0}} - \rho } \right)}}^{2}} + 2{{h}^{2}}\left( {{{\rho }_{0}} - \rho } \right)} + \frac{{{{\rho }_{0}} + {{h}^{2}} - a}}{{{{h}^{2}}}}\sqrt {{{{\left( {{{\rho }_{0}} - a} \right)}}^{2}} + 2{{h}^{2}}\left( {{{\rho }_{0}} - a} \right)} , \\ \end{gathered} $
${{h}^{2}} = \frac{{2\left[ {\arccos \left( {\frac{a}{{{{\rho }_{0}}}}} \right) - \frac{a}{{{{\rho }_{0}}}}\ln \left( {\frac{{{{\rho }_{0}} + \sqrt {\rho _{0}^{2} - {{a}^{2}}} }}{a}} \right)} \right]}}{{\arcsin ({a \mathord{\left/ {\vphantom {a {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}})}},\,\,\,\,a \leqslant \rho \leqslant {{\rho }_{0}}.$

5. Линза с плавным переходом, синтезированная в работе [10], формула образующей которой имеет вид

$\begin{gathered} z(\rho ) = \int\limits_0^\rho {\left\{ {\left[ { - \frac{1}{2}\left( {1 + \frac{{\rho _{0}^{2} - {{\rho }^{2}}}}{{{{h}^{2}}}}} \right) + \frac{2}{{\pi {{h}^{2}}}}} \right.} \right.} \times \\ \times \,\,\sqrt {{{a}^{2}} - {{\rho }^{2}}} \sqrt {\rho _{0}^{2} - {{a}^{2}}} - \frac{1}{{2\pi }}\arcsin \left( {\frac{{{{\rho }^{2}} + {{f}_{0}}^{2} - 2{{a}^{2}}}}{{{{f}_{0}}^{2} - {{\rho }^{2}}}}} \right) - \\ {{\left. {{{{\left. { - \,\,\frac{1}{4} + \frac{{({{\rho }^{2}} - \rho _{0}^{2})}}{{{{h}^{2}}}}\arcsin \left( {\frac{{{{\rho }^{2}} + \rho _{0}^{2} - 2{{a}^{2}}}}{{\rho _{0}^{2} - {{\rho }^{2}}}}} \right)} \right]}}^{2}} - 1} \right\}}^{{\frac{1}{2}}}}d\rho , \\ 0 \leqslant \rho \leqslant a, \\ \end{gathered} $
$\begin{gathered} z(\rho ) = z(a) + \int\limits_a^\rho {\sqrt {{{{\left( {\frac{{\rho _{0}^{2} - {{\rho }^{2}}}}{{{{h}^{2}}}}} \right)}}^{2}} + 2\frac{{\rho _{0}^{2} - {{\rho }^{2}}}}{{{{h}^{2}}}}} \,\,d\rho } , \\ a \leqslant \rho \leqslant {{\rho }_{0}}, \\ \end{gathered} $
$\begin{gathered} h = \sqrt {{{\rho }_{0}}\left( {\frac{{\pi - {{\gamma }_{{12}}} - \sin 2{{\gamma }_{{12}}}}}{{{{\gamma }_{{13}}}}}} \right),} \,\,\,\,\frac{a}{{{{\rho }_{0}}}} = \sin {{\gamma }_{{12}}}, \\ \frac{a}{{{{f}_{0}}}} = \sin {{\gamma }_{{13}}},\,\,\,\,{{f}_{0}} = 1.5,\,\,\,\,{{r}_{0}} = 1.05,\,\,\,\,a = 1. \\ \end{gathered} $

Перейдем к вычислению величины эйконала на выходе линз, которая определяются формулой

(17)
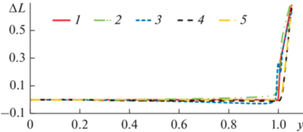
$\begin{gathered} L = \left| {FA} \right| + 2\int\limits_\gamma ^a \rho \frac{{\sqrt {1 + f{\kern 1pt} {{'}^{2}}(\rho )} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}d\rho + \\ + \,\,2\int\limits_a^{{{\rho }_{0}}} \rho \frac{{\sqrt {1 + z{\kern 1pt} {{'}^{2}}(\rho )} }}{{\sqrt {{{\rho }^{2}} - {{\gamma }^{2}}} }}d\rho + \left| {BC} \right|, \\ \end{gathered} $
где $\left| {FA} \right| = \sqrt {{{\rho }_{0}}^{2} + f_{0}^{2} - 2{{\rho }_{0}}{{f}_{0}}\cos \theta } $, $\left| {BC} \right| = {{\rho }_{0}} - $ $ - \,\,{{\rho }_{0}}\cos {{\varphi }_{0}}$, первый интеграл выражает оптический путь луча в линзе, а второй – в плавном переходе.

На рис. 3 приведены рассчитанные по формуле (17) аберрации эйконала на выходе линзы (отличие эйконала произвольного луча от эйконала центрального луча) для описанных выше вариантов 1–5 геодезических линз с плавным переходом. Как видно из рисунка, величина аберрации существенна только в части выходной апертуры, соответствующей плавному переходу (1 < y < 1.05). При этом величина аберрации строго равна нулю при y < 1 только для вариантов 1 и 5.

Рис. 3.

Аберрации эйконала в линзах с образующей плавного перехода: 1 – кусочно-линейной, 2 – в виде сопряженной части окружности, 3 – в виде четверти окружности, 4 – из работы [13], 5 – из работы [11].

Для анализа исследуемых геодезических линз было проведено электродинамическое моделирование характеристик излучения соответствующих линзовых антенн в приближении Кирхгофа и методом конечных элементов (МКЭ) с использованием программного продукта Ansys HFSS.

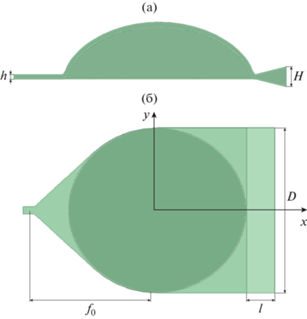
На рис. 4 приведены сечение и вид сверху линзовых антенн радиусом ρ0 = 79.125 мм с возбуждающим Н-секториальным рупором в горизонтальной плоскости и излучающим Е-секториальным рупором в вертикальной плоскости. Высота вертикальных стенок Е-секториального рупора h = 3.5 мм совпадает с расстоянием между проводящими поверхностями линзы. Внутренний радиус плавного перехода линзы равен 75 мм, фокусное расстояние f0 = 112.5 мм. Длина Е-секториального рупора l = 25 мм.

Рис. 4.

Геодезическая линза с плавным переходом: а) сечение, б) вид сверху.

Угол раствора Н-секториального рупора равен α = 86°, угол раствора Е-секториального рупора β = = 26°, размер его апертуры в Н-плоскости H = 15 мм.

Диаграмма направленности (ДН) плоской апертуры в приближении Кирхгофа имеет вид [19]

(18)
$\begin{gathered} D = \frac{{4\pi }}{{{{\lambda }^{2}}}} \times \\ \times \,\,\frac{{{{{\left| {\int\limits_A {{{E}_{y}}\left( {y,z} \right)\exp \left[ {(jk\sin \theta (y\cos \varphi + z\sin \varphi )} \right]dxdy} } \right|}}^{2}}}}{{\int\limits_A {{{{\left| {{{E}_{y}}\left( {y,z} \right)} \right|}}^{2}}dxdy} }}, \\ \end{gathered} $
где ${{E}_{y}}\left( {y,z} \right) = \left| {{{E}_{y}}\left( {y,z} \right)} \right|\exp \left[ {j\Phi (y,z)} \right] = \left| {{{E}_{y}}\left( {y,z} \right)} \right| \times $ $ \times \,\,\exp (jkL(y,z))$.

В нашем случае

$\left| {{{E}_{y}}\left( {y,z} \right)} \right| = \frac{{\cos \left( {\frac{{\pi \alpha (y)}}{{2{{\alpha }_{0}}}}} \right)}}{{\sqrt {\cos \alpha (y)} }}$

– амплитудное распределение (изменением амплитуды в Н-плоскости мы пренебрегаем), $\alpha (y) = \arcsin ({y \mathord{\left/ {\vphantom {y {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}})$, а Ф(y,z) = kL(y, z) = k(L(y) + + L(z) – фазовое распределение поля на выходе, где L(y) определяется формулой (17), а L(z) = $ = \sqrt {{{{(l + \Delta l)}}^{2}} + {{z}^{2}}} $, где$\Delta l = \frac{{{h \mathord{\left/ {\vphantom {h H}} \right. \kern-0em} H}}}{{1 - {h \mathord{\left/ {\vphantom {h H}} \right. \kern-0em} H}}}l$.

На рис. 5а, 5б соответственно приведены ДН, рассчитанные на частоте 30 ГГц по формуле (18) и с использованием МКЭ. (Номер кривой соответствует номеру варианта линзы.)

Рис. 5.

Диаграммы направленности линзовой антенны при φ = 0: а) приближение Кирхгофа; б) МКЭ; номера кривых соответствуют номеру варианта 1–5.

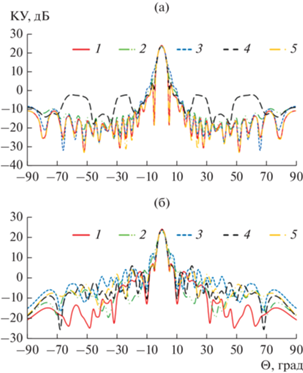
Видно, что результаты расчета ДН в приближении Кирхгофа вблизи главного лепестка близки к результатам, полученным с использованием МКЭ.

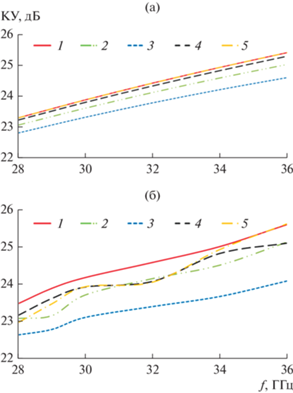
На рис. 6а, 6б в тех же обозначениях, что и на рис. 5, приведены частотные зависимости коэффициента усиления (КУ), рассчитанные по формуле (18) и с использованием МКЭ. Видно, что при расчете обоими методами наибольшее усиление обеспечивает антенна на базе геодезической линзы с поликоническим плавным переходом (вариант 1), а наименьшая величина КУ у антенны на базе линзы с образующей плавного перехода в виде четверти окружности (вариант 3). При расчете разных вариантов линз в приближении Кирхгофа отличия КУ меньше, чем при моделировании с использованием МКЭ. При этом максимальные отличия величины КУ, рассчитанные двумя методами, наблюдаются у антенны с вариантом линзы 3 на высоких частотах (более 0.8 дБ).

Рис. 6.

Зависимости КУ от частоты при φ = 0, θ = 0: а) приближение Кирхгофа; б) МКЭ; номера кривых соответствуют номеру варианта 1–5.

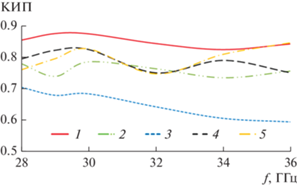
На рис. 7 в тех же обозначениях приведены частотные зависимости величины КИП, рассчитанные с использованием результатов КУ, полученных МКЭ (см. рис. 5б). Как видно из рисунка, величина КИП максимальная у варианта линзы 1, минимальная – у варианта 3. При этом все линзы обеспечивают уровень КИП выше 0.6.

Рис. 7.

Зависимости КИП от частоты, номера кривых соответствуют номеру варианта 1–5.

ЗАКЛЮЧЕНИЕ

На основании полученных результатов можно сделать следующие выводы:

1. Все металло-воздушные линзы с различными вариантами плавного перехода к планарному волноводу в исследованном частотном диапазоне (28…36 ГГц) обеспечивают уровень КИП антенны более 0.6.

2. Максимальный КИП (более 0.8) обеспечивает синтезированная в работе линза с поликоническим плавным переходом, минимальный – линза с образующей плавного перехода в виде четверти окружности.

3. Приближение Кирхгофа дает завышенную (до 0.6 дБ) величину коэффициента усиления, что можно объяснить отсутствием учета отражения.

Авторы заявляют об отсутствии конфликта интересов.

Список литературы

  1. Myers S.B. // J. Appl. Phys. 1947. V. 18. № 2. P. 221.

  2. Rinehart R.F. // J. Appl. Phys. 1948. V. 19. № 9. P. 860.

  3. Rinehart R.F. // Proc. IRE. 1952. V. 40. № 6. P. 686.

  4. Kunz K.S. // J. Appl. Phys. 1954. V. 25. № 5. P. 642.

  5. Toraldo di Francia G. // Optica Acta. 1955. V. 1. № 4. P.157.

  6. Spiller E., Harper J.S. // Appl. Opt. 1974. V. 13. № 9. P. 2105.

  7. Wood V. E. // Appl. Opt. 1976. V. 15. № 11. P. 2817.

  8. Southwell W.H. // J. Opt. Soc. Amer. 1977. V. 67. № 10. P. 1293.

  9. Kassai D., Marom E. // J. Opt. Soc. Amer. 1979.V. 69. № 9. P. 1242.

  10. Jiang W.Y., Dubois G.R., Ristic V.M. // Can. Elec. Eng. J. 1984. V. 9. № 4. P. 160.

  11. Sottini S., Russo V., Righini G.C. // J. Opt. Soc. Amer. 1979. V. 69. № 9. 1248.

  12. Sottini S., Giorgetti E. // J. Opt. Soc. Amer. A. 1987. V. 4. № 2. P. 346.

  13. Sochacki J. // Appl. Optics. 1986. V. 25. № 2. P. 235.

  14. Shimano T., Arimoto A., Muraoka K. // Appl. Optics. 1990. V. 29. № 34. P. 5062.

  15. Miñano J.C., Benítez P., Parkyn B. et al. // Int. Optical Design Conf. 2006. SPIE-OSA. V. 6342. P. 634214.

  16. Nelson J., Fonseca G., Qingbi Liao, Quevedo-Teruel O. // IEEE Trans. 2020. V. AP-68. № 5. P.3410.

  17. Мохов О.И. Классическая дифференциальная геометрия, Курс лекций, МГУ им. М.В. Ломоносова. https://teach_in.ru>differential-geometry-M.pdf.

  18. Забрейко П.П., Кошелев А.И., Красносельский М.А. и др. Интегральные уравнения. М.: Наука, 1968.

  19. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. школа, 1988.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал