Радиотехника и электроника, 2022, T. 67, № 5, стр. 485-492
Оптимальное комплексирование измерителей в условиях противодействия среды
А. Н. Детков *
Государственный научно-исследовательский институт авиационных систем
125319 Москва, ул. Викторенко, 7, Российская Федерация
* E-mail: detkov@gosniias.ru
Поступила в редакцию 01.12.2021
После доработки 02.12.2021
Принята к публикации 25.12.2021
- EDN: TIGRBR
- DOI: 10.31857/S0033849422050047
Аннотация
Методами марковской теории оценивания случайных процессов решена задача синтеза оптимальных и квазиоптимальных алгоритмов комплексной обработки информации при двухканальном векторном наблюдении с нарушениями в условиях противодействия среды. Задача решена применительно к дискретно-непрерывному марковскому процессу для случая, когда его непрерывная часть представляет собой векторную марковскую последовательность, а дискретная часть характеризуется двухкомпонентным дискретным марковским процессом, каждая компонента которого описывается цепью Маркова на несколько положений. Приведена структурная схема квазиоптимальной комплексной обработки информации. На простом примере методом имитационного моделирования показана эффективность комплексирования активного и пассивного угломерных каналов бортовой радиолокационной станции в условиях противодействия среды.
ВВЕДЕНИЕ
Наблюдения в различных физических полях расширяют возможности информационно-управляющих систем (ИУС) бортовых радиоэлектронных комплексов навигации и прицеливания, повышают их живучесть, эффективность навигации и наведения летательного аппарата (ЛА) на цель. В связи с этим актуальным является использование информации о пространственно энергетических характеристиках целей и фонов, получаемой как различными способами при наблюдении собственных и/или отраженных излучений цели, так и в различных участках спектра электромагнитного излучения – оптическом и радиоволновом [1–3].
При работе в условиях противодействия среды [4], под которыми понимаются интенсивные естественные и искусственные помехи, велика вероятность перерывов в поступлении информации о цели. Причины их возникновения могут быть весьма разнообразными [5]:
– прекращение излучения целей или резкое внезапное изменение характеристик излучения;
– подавление приемного устройства средством противодействия;
– наличие облаков, дымов и аэрозолей как искусственного, так и естественного происхождения;
– перенацеливание на “ложные цели” и т.д.
Возникающие при этом перерывы информации носят случайный скачкообразный характер. При синтезе помехоустойчивых алгоритмов обработки информации в ИУС необходимо предусматривать защиту от информационных “отказов” измерителей, поэтому для повышения достоверности и надежности обработки информации особенно эффективно их комплексирование в условиях противодействия среды [4, 6].
Развитие средств вычислительной техники позволяет реализовать комплексную обработку информации (КОИ) в цифровой форме при достаточно большом числе уровней квантования аналого-цифровых преобразователей и разрядов для представления чисел [7]. Оптимальность работы алгоритма предполагает наилучшее использование априорной и апостериорной информации о вероятности пропадания и восстановления полезного сигнала и оптимизацию оценок признаков различия цели и помех [6].
Потребность в одновременном измерении одних и тех же параметров с помощью устройств и систем, работающих на различных физических принципах, обусловлена тем, что каждый измеритель в отдельности не удовлетворяет всем требованиям, которые предъявляются к измерению этих параметров. Целью комплексирования оборудования является объединение различных измерителей в единый комплекс, обладающий существенно более высокими характеристиками точности, помехоустойчивости и надежности измерений по сравнению с отдельными измерителями. Максимального выигрыша от комплексирования можно достичь, решив задачу синтеза, что позволяет определить оптимальную структуру и характеристики системы комплексной обработки информации.
Для решения задачи КОИ в условиях противодействия среды может быть использован математический аппарат дискретно-непрерывных марковских процессов (ДНМП) в дискретном времени, адекватный решаемой задаче при реализации синтезированных алгоритмов на ЭВМ.
1. ПОСТАНОВКА ЗАДАЧИ ОЦЕНИВАНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА В ДИСКРЕТНОМ ВРЕМЕНИ
Пусть в дискретные моменты времени tk = $ = {{t}_{0}} + k\Delta $, k = 1, 2, …, разделенные постоянным интервалом $\Delta = {{t}_{k}} - {{t}_{{k - 1}}}$, ${{t}_{k}} \in \left[ {{{t}_{0}},{{T}_{{\text{н}}}}} \right)$, разностное уравнение вектора состояния ${\mathbf{x}}({{t}_{k}}) = {\mathbf{x}}(k)$ и уравнения измерений ${\mathbf{y}}({{t}_{k}}) = {\mathbf{y}}(k)$ имеют вид
(1)
$\begin{gathered} {\mathbf{x}}(k) = {{{\mathbf{\Phi }}}_{{xx}}}(k,k - 1){\mathbf{x}}(k - 1) + {{{\mathbf{\Gamma }}}_{{xx}}}(k,k - 1){\mathbf{\xi }}(k - 1), \\ {\mathbf{x}}\left( 0 \right) = {{{\mathbf{x}}}_{0}}, \\ \end{gathered} $(2)
$\begin{gathered} {\mathbf{y}}(k) = {\mathbf{h}}\left( {{{a}_{j}}(k),{{b}_{m}}(k)} \right){\mathbf{x}}(k) + \\ + \,\,{{{\mathbf{\Gamma }}}_{{yy}}}\left( {{{a}_{j}}(k),{{b}_{m}}(k)} \right){\mathbf{\zeta }}(k), \\ \end{gathered} $Применительно к решаемой задаче синтеза вектор состояния представляет собой ДНМП ${{\left[ {{{{\mathbf{x}}}^{T}}(k),{{a}_{j}}(k),{{b}_{m}}(k)} \right]}^{T}}$, где ${\mathbf{x}}(k)$ – непрерывная ${{n}_{x}}$-мерная компонента ДНМП, описывающий в пространстве состояний динамику фазовых координат объекта (например, ЛА на котором установлены измерители), ${\mathbf{s}}(k) = {{\left[ {{{a}_{j}}(k),{{b}_{m}}(k)} \right]}^{T}}$ – дискретная компонента ДНМП – двухкомпонентный дискретный марковский процесс, каждая компонента которого описывается цепью Маркова на ${{M}_{1}}$ и ${{M}_{2}}$ положений соответственно, с матрицами вероятностей переходов
По условию задачи известны матрицы ${{{\mathbf{\Phi }}}_{{xx}}}$, ${{{\mathbf{\Gamma }}}_{{xx}}}$, ${\mathbf{h}}$, ${{{\mathbf{\Gamma }}}_{{yy}}}$, а также начальные распределения марковского вектора, причем компоненты марковской цепи ${{a}_{j}}(k)$ и ${{b}_{m}}(k)$, характеризующие нарушения в каналах измерений, не зависит друг от друга.
Цель работы – на основе марковской теории оценивания случайных процессов [8–13] разработать оптимальные (квазиоптимальные) алгоритмы комплексной обработки ДНМП [xT(k), aj(k), bm(k)]T по наблюдаемым в дискретном времени выходным сигналам измерителей y(k) = $ = {{\left[ {{\mathbf{y}}_{1}^{T}(k),{\mathbf{y}}_{2}^{T}(k)} \right]}^{T}}$ в условиях противодействия среды.
2. ЗАКОН РАСПРЕДЕЛЕНИЯ СМЕШАННОГО ВЕКТОРА СОСТОЯНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА
На основании свойств марковских процессов в дискретном времени запишем рекуррентные уравнения, описывающие апостериорное распределение ДНМП по наблюдаемой последовательности измерений ${\mathbf{Y}}_{1}^{k} \triangleq {\mathbf{y}}\left( 1 \right),{\mathbf{y}}\left( 2 \right),...,{\mathbf{y}}\left( k \right)$:
(3)
$\begin{gathered} f\left( {{\mathbf{x}}\left( k \right),{{a}_{j}},{{b}_{m}}\left| {{\mathbf{Y}}_{1}^{k}} \right.} \right) = f{\text{*}}\left( {{\mathbf{x}}\left( k \right),{{a}_{j}},{{b}_{m}}} \right) = \\ = \frac{{f\left( {{\mathbf{y}}\left( k \right)|{\mathbf{x}}\left( k \right),{\mathbf{s}}\left( k \right)} \right)}}{{f\left( {{\mathbf{y}}\left( k \right)\left| {{\mathbf{Y}}_{1}^{{k - 1}}} \right.} \right)}}\sum\limits_i {\sum\limits_n {\pi _{{ij}}^{a}\pi _{{nm}}^{b}} } \,\int {f\left( {{\mathbf{x}}\left. {\left( k \right)} \right|{\mathbf{x}}\left( {k - 1} \right)} \right)} f{\text{*}}\left( {{\mathbf{x}}\left( {k - 1} \right),{{a}_{i}}\left( {{{t}_{{k - 1}}}} \right),{{b}_{n}}\left( {{{t}_{{k - 1}}}} \right)} \right)d{\mathbf{x}}\left( {k - 1} \right), \\ \end{gathered} $Представим апостериорную плотность вероятности вектора непрерывных компонент ДНМП $f{\text{*}}\left( {{\mathbf{x}}\left( k \right),{{a}_{j}},{{b}_{m}}} \right)$ (3) в виде системы рекуррентных уравнений
(4)
$\begin{gathered} f_{{jm}}^{*}\left( {{\mathbf{x}}\left( k \right)} \right) = f{\text{*}}\left( {{\mathbf{x}}\left( k \right),{{a}_{j}},{{b}_{m}}} \right) = \\ = \frac{{f\left( {{\mathbf{y}}\left. {(k)} \right|{\mathbf{x}}\left( k \right),{\mathbf{s}}\left( k \right)} \right)}}{{f\left( {{\mathbf{y}}\left. {(k)} \right|{\mathbf{Y}}_{1}^{{k - 1}}} \right)}}{{{\tilde {f}}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right), \\ \end{gathered} $(5)
$\begin{gathered} {{{\tilde {f}}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right) = \sum\limits_i {\sum\limits_n {\pi _{{ij}}^{a}} } \pi _{{nm}}^{b}P_{{in}}^{*}(k - 1) \times \\ \times \,\,\int {f\left( {{\mathbf{x}}\left( k \right)\left| {{\mathbf{x}}\left( {k - 1} \right),{{a}_{j}},{{b}_{m}}} \right.} \right)} f_{{in}}^{*}\left( {{\mathbf{x}}\left( {k - 1} \right)} \right)d{\mathbf{x}}\left( {k - 1} \right), \\ \end{gathered} $Апостериорная вероятность дискретной компоненты ДНМП $P_{{jm}}^{*}\left( k \right)$ описывается системой рекуррентных уравнений:
(6)
$\begin{gathered} P_{{jm}}^{*}\left( k \right) = P{\text{*}}\left( {{{a}_{j}}\left( k \right),{{b}_{m}}\left( k \right)} \right) = \\ = \frac{{f\left( {{\mathbf{y}}\left( k \right)|{\mathbf{x}}\left( k \right),{\mathbf{s}}\left( k \right),{\mathbf{Y}}_{1}^{{k - 1}}} \right)}}{{f\left( {{\mathbf{y}}\left( k \right)\left| {{\mathbf{Y}}_{1}^{{k - 1}}} \right.} \right)}}{{{\tilde {P}}}_{{jm}}}\left( k \right), \\ \end{gathered} $(7)
${{\tilde {P}}_{{jm}}}(k) = \sum\limits_i {\sum\limits_n {{{\pi }}_{{ij}}^{a}} } {{\pi }}_{{nm}}^{b}P_{{in}}^{*}\left( {k - 1} \right),$3. КВАЗИОПТИМАЛЬНЫЙ АЛГОРИТМ ОЦЕНИВАНИЯ ВЕКТОРА СОСТОЯНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА ПРИ КОМПЛЕКСИРОВАНИИ ИЗМЕРИТЕЛЕЙ
Большие вычислительные затраты при практической реализации оптимального алгоритма (3)–(5) вынуждают ограничиться приближенным нахождением компонент ДНМП. Для этого необходимо выполнить двухмоментную параметрическую гауссовскую аппроксимацию условной плотности вероятности ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right)$. Эта аппроксимация состоит в замене неизвестных функций ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right)$ некоторыми известными функциями, в частности ${\mathbf{\tilde {x}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\tilde {R}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}})$ – математического ожидания и корреляционной функции условной плотности вероятности ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right)$ соответственно [14]. Применяя, таким образом, на каждом k-м шаге гауссовскую аппроксимацию для условной плотности вероятности ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{x}}\left( k \right)} \right)$, можно показать, что квазиоптимальный алгоритм фильтрации непрерывного компонента ДНМП описывается системой рекуррентных уравнений:
– вектор оценки ${\mathbf{x}}{\kern 1pt} *{\kern 1pt} \left( {k,{{a}_{j}},{{b}_{m}}} \right)$ и корреляционная матрица погрешностей оценки ${\mathbf{R}}_{{xx}}^{*}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$ непрерывных компонентов ДНМП при условии $A\left( k \right) = {{a}_{j}}$, $B\left( k \right) = {{b}_{m}}$ определяются по результатам измерений ${{{\mathbf{y}}}_{1}}\left( k \right)$ и ${{{\mathbf{y}}}_{2}}\left( k \right)$:
(8)
$\begin{gathered} {\mathbf{x}}{\text{*}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = {\mathbf{\tilde {x}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) + {{{\mathbf{K}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) \times \\ \times \,\,\left( {{{{\mathbf{y}}}_{1}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right) + \\ + \,\,{{{\mathbf{K}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)\left( {{{{\mathbf{y}}}_{2}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right), \\ \end{gathered} $(9)
$\begin{gathered} {\mathbf{R}}_{{xx}}^{*}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = {{{{\mathbf{\tilde {R}}}}}_{{xx}}}\left( {{{a}_{j}},{{b}_{m}}} \right) - \\ - \,\,\left[ {\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{1}^{T}\left( {{{a}_{j}}} \right)}&{{{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{2}^{T}\left( {{{b}_{m}}} \right)} \end{array}} \right] \times \\ \times \,\,{{\left[ {\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {R}}}}}_{{11}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{12}}}(k,{{a}_{j}},{{b}_{m}})} \\ {{{{{\mathbf{\tilde {R}}}}}_{{21}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{22}}}(k,{{a}_{j}},{{b}_{m}})} \end{array}} \right]}^{{ - 1}}} \times \\ \times \,\,\left[ {\begin{array}{*{20}{c}} {{\mathbf{h}}_{1}^{{}}\left( {{{a}_{j}}} \right){{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}})} \\ {{\mathbf{h}}_{2}^{{}}\left( {{{b}_{m}}} \right){{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}})} \end{array}} \right], \\ \end{gathered} $${{{\mathbf{K}}}_{1}}(k,{{a}_{j}},{{b}_{m}})$ и ${{{\mathbf{K}}}_{1}}(k,{{a}_{j}},{{b}_{m}})$ – оптимальные коэффициенты передачи:
(10)
$\begin{gathered} {{{\mathbf{K}}}_{1}}(k,{{a}_{j}},{{b}_{m}}) = {{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{1}^{T}\left( {{{a}_{j}}} \right) \times \\ \times \,\,\left( {{{{{\mathbf{\tilde {R}}}}}_{{11}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - {{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right.{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) \times \\ {{\left. { \times \,\,{{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right)}^{{ - 1}}} - {{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{2}^{T}\left( {{{b}_{m}}} \right) \times \\ \times \,\,\left( {{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)\left( {{{{{\mathbf{\tilde {R}}}}}_{{11}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - } \right.} \right. \\ - \,\,{{\left. {{{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right)}^{{ - 1}}}, \\ \end{gathered} $(11)
$\begin{gathered} {{{\mathbf{K}}}_{2}}(k,{{a}_{j}},{{b}_{m}}) = - {{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{1}^{T}\left( {{{a}_{j}}} \right) \times \\ \times \,\,\left( {{{{{\mathbf{\tilde {R}}}}}_{{11}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - {{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right.{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) \times \\ {{\left. { \times \,\,{{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right)}^{{ - 1}}}{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) + \\ + \,\,{{{{\mathbf{\tilde {R}}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}}){\mathbf{h}}_{2}^{T}\left( {{{b}_{m}}} \right)\left( {{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right. + \\ + \,\,{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) \times \\ \times \,\,\left( {\left( {{{{{\mathbf{\tilde {R}}}}}_{{11}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - } \right.{{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right.{\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) \times \\ \times \,\,{{\left. {{{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right)}^{{ - 1}}}{{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right){\mathbf{\tilde {R}}}_{{22}}^{{ - 1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right); \\ \end{gathered} $(12)
$\begin{gathered} {\mathbf{\tilde {x}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \,\,{{{\mathbf{\Phi }}}_{{xx}}}(k,k - 1){\mathbf{x}}{\text{*}}(k - 1,{{a}_{i}},{{b}_{n}}), \\ \end{gathered} $(13)
$\begin{gathered} {{{{\mathbf{\tilde {R}}}}}_{{xx}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \hfill \\ \times \,\,\left\{ {{{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{R}}{\text{*}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right){\mathbf{\Phi }}_{{xx}}^{T} + {{{\mathbf{\Gamma }}}_{{xx}}}{\mathbf{\Gamma }}_{{xx}}^{T} + } \right. \hfill \\ + \,\,{{\left[ {{{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right) - {\mathbf{\tilde {x}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}^{{}}} \times \hfill \\ \times \left. {\,\,{{{\left[ {{{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right) - {\mathbf{\tilde {x}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}}^{T}}} \right\}, \hfill \\ \end{gathered} $(14)
$\begin{gathered} {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \,\,{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}(k - 1,{{a}_{i}},{{b}_{n}}), \\ \end{gathered} $(15)
$\begin{gathered} {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \,\,{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right), \\ \end{gathered} $(16)
${{{\mathbf{\tilde {R}}}}_{{yy}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \left[ {\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {R}}}}}_{{11}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{12}}}(k,{{a}_{j}},{{b}_{m}})} \\ {{{{{\mathbf{\tilde {R}}}}}_{{21}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{22}}}(k,{{a}_{j}},{{b}_{m}})} \end{array}} \right];$(17)
$\begin{gathered} {{{{\mathbf{\tilde {R}}}}}_{{11}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \left\{ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{R}}_{{xx}}^{*}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right){\mathbf{\Phi }}_{{xx}}^{T}{\mathbf{h}}_{1}^{T}\left( {{{a}_{j}}} \right)} \right. + \\ + \,\,{{{\mathbf{\Gamma }}}_{{yy1}}}\left( {{{a}_{j}}} \right){\mathbf{\Gamma }}_{{yy1}}^{T}\left( {{{a}_{j}}} \right) + \\ + \,\,\left[ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]\,\, \times \\ \times \,\,\left. {{{{\left[ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}}^{T}}} \right\}, \\ \end{gathered} $(18)
$\begin{gathered} {{{{\mathbf{\tilde {R}}}}}_{{12}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \,\,\left\{ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{R}}_{{xx}}^{*}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right){\mathbf{\Phi }}_{{xx}}^{T}{\mathbf{h}}_{2}^{T}\left( {{{b}_{m}}} \right) + } \right. \\ + \,\,\left[ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right] \times \\ \times \,\,\left. {{{{\left[ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}}^{T}}} \right\}, \\ \end{gathered} $(19)
$\begin{gathered} {{{{\mathbf{\tilde {R}}}}}_{{21}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \left\{ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{R}}_{{xx}}^{*}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right){\mathbf{\Phi }}_{{xx}}^{T}{\mathbf{h}}_{1}^{T}\left( {{{a}_{j}}} \right) + } \right. \\ + \left[ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right] \times \\ \times \,\,\left. {{{{\left[ {{{{\mathbf{h}}}_{1}}\left( {{{a}_{j}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}}^{T}}} \right\}, \\ \end{gathered} $(20)
$\begin{gathered} {{{{\mathbf{\tilde {R}}}}}_{{22}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) = \sum\limits_i {\sum\limits_n {\frac{{{{\pi }}_{{ij}}^{a}{{\pi }}_{{nm}}^{b}P_{{in}}^{*}(k - 1)}}{{{{{\tilde {P}}}_{{jm}}}(k)}}} } \times \\ \times \,\,\left\{ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{R}}_{{xx}}^{*}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right){\mathbf{\Phi }}_{{xx}}^{T}{\mathbf{h}}_{2}^{T}\left( {{{b}_{m}}} \right)} \right. + \\ + \,\,{{{\mathbf{\Gamma }}}_{{yy2}}}\left( {{{b}_{m}}} \right){\mathbf{\Gamma }}_{{yy2}}^{T}\left( {{{b}_{m}}} \right) + \\ + \,\,\left[ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right] \times \\ \times \,\,\left. {{{{\left[ {{{{\mathbf{h}}}_{2}}\left( {{{b}_{m}}} \right){{{\mathbf{\Phi }}}_{{xx}}}{\mathbf{x}}{\text{*}}\left( {{{a}_{i}},{{b}_{n}}} \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \right]}}^{T}}} \right\}. \\ \end{gathered} $При этом начальные условия для квазиоптимального алгоритма КОИ (6)–(20):
Уравнения оценивания апостериорной вероятности дискретной компоненты ДНМП (6), (7) остаются без изменения, ${\text{a}}$ условная плотность вероятности одношагового предсказания наблюдаемых сигналов имеет вид [15]
(21)
$\begin{gathered} f\left( {\left. {{\mathbf{y}}\left( k \right)} \right|{\mathbf{x}}\left( k \right),{\mathbf{s}}\left( k \right),{\mathbf{Y}}_{1}^{{k - 1}}} \right) = \frac{1}{{\sqrt {{{{\left( {2\pi } \right)}}^{{\left( {{{n}_{{y1}}} + {{n}_{{y2}}}} \right)}}}\det \left\{ {{{{{\mathbf{\tilde {R}}}}}_{{yy}}}} \right\}} }} \times \\ \times \,\,\exp \left\{ { - \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{y}}}_{1}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \\ {{{{\mathbf{y}}}_{2}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \end{array}} \right]} \right. \times \\ \times \,\,{{\left[ {\begin{array}{*{20}{c}} {{{{{\mathbf{\tilde {R}}}}}_{{11}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{12}}}(k,{{a}_{j}},{{b}_{m}})} \\ {{{{{\mathbf{\tilde {R}}}}}_{{21}}}(k,{{a}_{j}},{{b}_{m}})}&{{{{{\mathbf{\tilde {R}}}}}_{{22}}}(k,{{a}_{j}},{{b}_{m}})} \end{array}} \right]}^{{ - 1}}} \times \\ \times \,\,\left. {{{{\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{y}}}_{1}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \\ {{{{\mathbf{y}}}_{2}}\left( k \right) - {{{{\mathbf{\tilde {y}}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)} \end{array}} \right]}}^{T}}} \right\}. \\ \end{gathered} $Задача фильтрации считается решенной, если на выходе оптимального фильтра на каждом k-м шаге формируется оптимальная оценка, соответствующая определенному критерию оптимальности. Байесовское решение может быть получено на основе минимизации апостериорного риска [11], который применительно к решаемой задаче имеет вид
(22)
$\begin{gathered} \gamma \left( {{\mathbf{u}}{\text{*}}\left( k \right),{\mathbf{Y}}\left( k \right)} \right) = \mathop {\min }\limits_{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} }}\left( k \right)} \sum\limits_{\mu = 1}^{{{M}_{1}}} {\sum\limits_{\nu = 1}^{{{M}_{2}}} {\int\limits_{ - \infty }^\infty {{{g}_{{jm\mu \nu }}}\left( {{\mathbf{x}}\left( k \right),{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }}\left( k \right)} \right)} } } \times \\ \times \,\,f\left( {{\mathbf{x}}\left( k \right),A\left( k \right) = {{a}_{\mu }},B\left( k \right) = {{b}_{\nu }}} \right)d{\mathbf{x}}\left( k \right), \\ \end{gathered} $При решении многих практических задач малым ошибкам непрерывного компонента соответствуют меньшие потери. В таких случаях применяется функция потерь [11], простая по дискретному и квадратичная по непрерывному компонентам
(23)
$\begin{gathered} {{g}_{{jm\mu \nu }}}\left( {{\mathbf{x}}\left( k \right),{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }}\left( k \right)} \right) = \alpha \left( {1 - {{{{\delta }}}_{{jm\mu \nu }}}} \right) + \\ + \,\,\beta {{{{\delta }}}_{{jm\mu \nu }}}{{\left( {{\mathbf{x}}\left( k \right) - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }}\left( k \right)} \right)}^{T}}\left( {{\mathbf{x}}\left( k \right) - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} }}\left( k \right)} \right), \\ \end{gathered} $Функция потерь (23) означает, что при любом неправильном определении значений дискретного компонента потери равны коэффициенту $\alpha $, а при правильном принятии решения потери пропорциональны сумме квадратов ошибок оценки непрерывного компонента. Подставляя выражение (23) в (22) и выполняя минимизацию апостериорного риска, можно показать, что решающее правило имеет вид [16]
(24)
$\begin{gathered} {\text{если}}\,\,P_{{jm}}^{*}(k)\left\{ {\alpha + } \right.\beta {\text{Tr}}\left\{ {{\mathbf{R}}{\text{*}}(k,{{a}_{j}},{{b}_{m}})} \right\} \geqslant P_{{\mu \nu }}^{*}(k) \\ \times \,\,\left\{ {\alpha + } \right.\beta {\text{Tr}}\left\{ {{\mathbf{R}}{\text{*}}(k,{{a}_{\mu }},{{b}_{\nu }})} \right\}, \\ {\text{то}}\,\,{\mathbf{x}}{\text{*}}\left( k \right) = {\mathbf{x}}{\text{*}}(k,{{a}_{j}},{{b}_{m}}),A\left( k \right) = a_{j}^{*},B\left( k \right) = b_{m}^{*}, \\ \end{gathered} $Таким образом, в качестве безусловной оценки непрерывного компонента ДНМП выступает условное апостериорное математическое ожидание ${\mathbf{x}}_{{jm}}^{*}\left( k \right)$. Из (24) следует, что принятие решения сводится к максимизации взвешенных апостериорных вероятностей дискретных компонент ДНМП. При этом следует отметить, что с увеличением погрешности оценки непрерывного компонента ДНМП уменьшаются веса погрешностей оценки дискретных компонент ДНМП. В результате может приниматься гипотеза с меньшей апостериорной вероятностью, но и с меньшими погрешностями оценки непрерывного компонента ДНМП, т.е. может отвергаться гипотеза с большей апостериорной вероятностью.
Условная корреляционная матрица ${\mathbf{R}}{\text{*}}(k,{{a}_{j}},{{b}_{m}})$ характеризует качество оценки при правильном определении значений дискретных компонент ${{a}_{j}}$ и ${{b}_{m}}$. Безусловная корреляционная матрица ${\mathbf{R}}{\text{*}}(k)$ погрешностей оценки непрерывного компонента ДНМП определяется по формуле
(25)
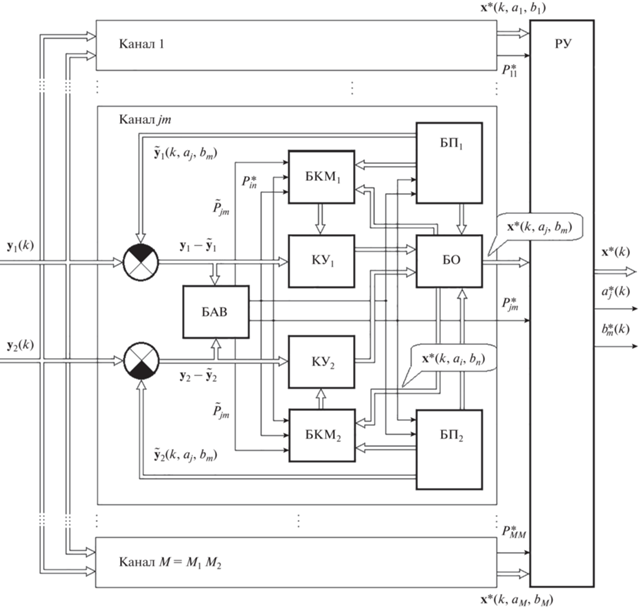
$\begin{gathered} {\mathbf{R}}{\text{*}}(k) = \sum\limits_{j = 1}^{{{M}_{1}}} {\sum\limits_{m = 1}^{{{M}_{2}}} {P_{{jm}}^{*}(k)} \left( {{\mathbf{R}}{\text{*}}(k,{{a}_{j}},{{b}_{m}}) + } \right.} \\ + \,\,\left( {{\mathbf{x}}{\text{*}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - {\mathbf{x}}{\text{*}}\left( k \right)} \right) \times \\ \times \,\,\left. {{{{\left( {{\mathbf{x}}{\text{*}}\left( {k,{{a}_{j}},{{b}_{m}}} \right) - {\mathbf{x}}{\text{*}}\left( k \right)} \right)}}^{T}}} \right). \\ \end{gathered} $Квазиоптимальный цифровой фильтр КОИ (рис. 1), реализующий алгоритм (6)–(21), (23)–(25), является многоканальным с числом каналов $M = {{M}_{1}} \times {{M}_{2}}$ и в основном сохраняет структуру и все обратные связи, присущие оптимальному устройству. Каждый канал состоит из многоканальных блоков вычисления коэффициента усиления КУ1 и КУ2: ${{{\mathbf{K}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${{{\mathbf{K}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$; блока оценки БО, в котором вычисляются ${\mathbf{x}}{\text{*}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${\mathbf{x}}{\text{*}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right)$; блоков прогноза БП1 и БП2, в которых вычисляются ${\mathbf{\tilde {x}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${{{\mathbf{\tilde {y}}}}_{1}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${{{\mathbf{\tilde {y}}}}_{2}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$; блока апостериорных вероятностей БАВ, в котором вычисляются $P_{{jm}}^{*}(k)$, $P_{{in}}^{*}(k - 1)$, ${{\tilde {P}}_{{jm}}}(k)$, и блоков вычисления корреляционных матриц БКМ1 и БКМ2, в которых вычисляются ${{{\mathbf{\tilde {R}}}}_{{xx}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${{{\mathbf{\tilde {R}}}}_{{xy}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${{{\mathbf{\tilde {R}}}}_{{yy}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$, ${\mathbf{R}}_{{xx}}^{*}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$ и ${\mathbf{R}}_{{xx}}^{*}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right)$. Окончательное решение о принятии безусловных оценок ${\mathbf{x}}{\text{*}}(k)$, $a_{j}^{*}(k)$, $b_{m}^{*}(k)$ производится в решающем устройстве РУ.
Пример. В качестве примера использования синтезированного квазиоптимального алгоритма КОИ рассмотрим задачу наведения ЛА на цель в горизонтальной плоскости в условиях нарушений в каналах измерений. При этом исходные вектор состояния и матрицы априорных уравнений (1), (2) имеют вид
(26)
$\begin{gathered} {\mathbf{x}}(k) = \left[ {\begin{array}{*{20}{c}} \varphi \\ \omega \end{array}} \right],\,\,\,\,{{{\mathbf{\Phi }}}_{{xx}}}(\Delta ) = \exp \left\{ { - \alpha \Delta } \right\}\,\left[ {\begin{array}{*{20}{c}} {\cos \mu \Delta + \frac{\alpha }{\mu }\sin \mu \Delta }&{\frac{1}{\mu }\sin \mu \Delta } \\ { - \mu \sin \mu \Delta }&{\cos \mu \Delta - \frac{\alpha }{\mu }\sin \mu \Delta } \end{array}} \right], \\ {{{\mathbf{\Gamma }}}_{{xx}}}(\Delta ) = \sqrt {{{D}_{x}}\left( {1 - \exp \left\{ { - 2\alpha \Delta } \right\}} \right)} \left[ {\begin{array}{*{20}{c}} 1&0 \\ { - \alpha }&{\sqrt {{{\mu }^{2}} - {{\alpha }^{2}}} } \end{array}} \right], \\ {\mathbf{\xi }} = \left[ {\begin{array}{*{20}{c}} {{{\xi }_{1}}} \\ {{{\xi }_{2}}} \end{array}} \right],\,\,\,\,{\mathbf{h}}\left( {{{a}_{j}}(k),{{b}_{m}}(k)} \right) = \left[ {\begin{array}{*{20}{c}} 1&0 \\ {{{b}_{m}}(k)}&0 \end{array}} \right],\,\,\,\,{{{\mathbf{\Gamma }}}_{{yy}}}\left( {{{a}_{j}}(k)} \right) = \left[ {\begin{array}{*{20}{c}} {\sqrt {{{a}_{j}}(k){{D}_{{y1}}}} }&0 \\ 0&{\sqrt {{{D}_{{y2}}}} } \end{array}} \right]; \\ \end{gathered} $Проверка качества квазиоптимального алгоритма проведена с помощью статистического моделирования на ЭВМ для случая, когда параметры уравнений (26) имеют значения: $\mu $ = 0.16 рад/с, $\Delta $ = = 1 с, $\sqrt {{{{{D}_{x}}} \mathord{\left/ {\vphantom {{{{D}_{x}}} {{{D}_{{y1}}}}}} \right. \kern-0em} {{{D}_{{y1}}}}}} $ =1; $\sqrt {{{{{D}_{x}}} \mathord{\left/ {\vphantom {{{{D}_{x}}} {{{D}_{{y2}}}}}} \right. \kern-0em} {{{D}_{{y2}}}}}} $ = 0.5; а цепи Маркова принимают значения ${{a}_{1}}$ = 1, ${{a}_{2}}$ = 100; ${{b}_{1}}$ = 1, ${{b}_{2}}$ = 0. Вероятности перехода $\pi _{{11}}^{1}$ = $\pi _{{11}}^{2}$ = 0.8; $\pi _{{12}}^{1}$ = $\pi _{{12}}^{2}$ = = 0.2. В целях повышения наглядности функционирования алгоритма была сформирована тестовая реализация для дискретных компонент A(k), B(k). При этом было принято, что длина реализации $k = \overline {1,350} $, а цепь Маркова принимает значения
Определение статистических характеристик квазиоптимальных алгоритмов КОИ проводили методом Монте-Карло, при этом тестовая реализация дискретной цепи Маркова $A\left( k \right)$ сохранялась неизменной, а независимые гауссовские последовательности ${{\xi }_{1}}(k)$, ${{\xi }_{2}}(k)$, ${{\zeta }_{1}}(k)$, ${{\zeta }_{2}}(k)$ сформированы с помощью датчика случайных чисел [14]. Для определения оценок дискретного и непрерывного компонентов было использовано решающее правило (23)–(24), в котором $\alpha = 1$, $\beta = 0$.
Результаты моделирования приведены на рис. 2 и в табл. 1.
Рис. 2.
Результаты моделирования и оценивания в дискретном времени: а) измерения угла пеленга активным каналом РЛС; б) измерения угла пеленга пассивным каналом РЛС; в) зависимость угла пеленга φ (1) и оценки угла пеленга $\varphi {\text{*}}$ (2) от дискретного времени наведения k; г) зависимость угловой скорости линии визирования $\omega $ (1) и оценки угловой скорости линии визирования $\omega {\text{*}}$ (2) от дискретного времени наведения k; д) – зависимость вероятности отсутствия нарушений в каналах измерений $P_{1}^{*}$ (1) и $P_{2}^{*}$ (2) от дискретного времени наведения k.
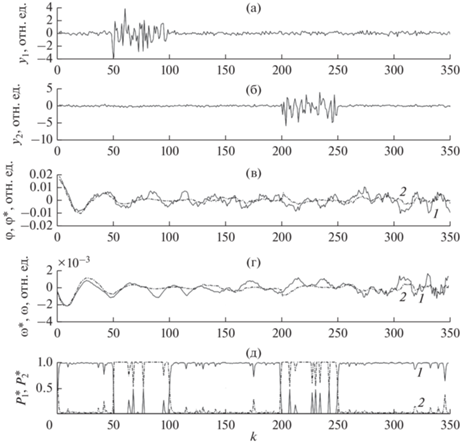
Таблица 1.
Среднеквадратическое отклонение (СКО) погрешности оценивания угла пеленга в условиях нарушения измерений
| Алгоритм оценки | Оценка по измерениям только ${{y}_{1}}$ | Оценка по измерениям только ${{y}_{2}}$ | КОИ
по измерениям ${{y}_{1}}$ и ${{y}_{2}}$ |
|---|---|---|---|
| Квазиоптимальный алгоритм (6)–(22) | 0.14 | 0.22 | 0.09 |
| Квазиоптимальный алгоритм по методу переприсвоения параметров условных АПВ вектора ${\mathbf{x}}(k)$ [5] | 0.23 | 0.28 | 0.19 |
| Псевдобайесовский алгоритм 2-го порядка [6] | 0.92 | 1.06 | 0.79 |
Данные табл. 1 показывают эффективность комплексирования активного и пассивного радиолокационных угломерных каналов на основе квазиоптимального алгоритма (6)–(21), (23)–(25) в условиях скачкообразных нарушений в каналах измерений. Необходимо отметить, что при реализации квазиоптимального алгоритма отсутствует рост числа каналов фильтра, как в случае байесовского алгоритма адаптивного оценивания [6], что обусловлено марковским свойством ДНМП.
ЗАКЛЮЧЕНИЕ
Методами теории условных марковских процессов решена задача оптимального оценивания ненаблюдаемых компонент векторной марковской последовательности дискретно-непрерывного марковского процесса при двухканальном векторном наблюдении. Синтезированные алгоритмы основаны на разложении смешанной апостериорной плотности вероятности вектора состояния ${{\left[ {{{{\mathbf{x}}}^{T}}(k),{{a}_{j}}(k),{{b}_{m}}(k)} \right]}^{T}}$ и являются алгоритмами с обратными связями по дискретному процессу ${\mathbf{s}}(k) = {{\left[ {{{a}_{j}}(k),{{b}_{m}}(k)} \right]}^{T}}$. На основе квазиоптимального алгоритма разработана соответствующая структурная схема цифрового фильтра КОИ.
Особенность синтезированного квазиоптимального алгоритма комплексирования состоит в неразрывной связанности уравнений фильтрации и экстраполяции дискретного и непрерывного компонентов ДНМП между собой, что потребует дополнительных вычислительных затрат по сравнению с известными алгоритмами. Однако современная высокопроизводительная вычислительная техника позволяет построить практически реализуемый цифровой фильтр КОИ в условиях противодействия среды.
Список литературы
Ярлыков М.С., Богачев А.С., Меркулов В.И., Дрогалин В.В. Радиоэлектронные комплексы навигации, прицеливания и управления вооружением. Т. 1. Теоретические основы. М.: Радиотехника, 2012.
Верба В.С., Меркулов В.И., Попов Е.В., Чернов В.С. // Информационно-измерительные и управляющие системы. 2014. Т. 12. № 2. С. 32.
Верба В.С., Меркулов В.И., Миляков Д.А., Чернов В.С. // Журн. радиоэлектроники. 2015. № 4. http://jre.cplire.ru/koi/apr15/7/ text.pdf.
Федосов Е.А., Инсаров В.В., Селивохин О.С. Системы управления ко-нечным положением в условиях противодействия среды. М.: Наука, 1989.
Бухалёв В.А., Скрынников А.А., Болдинов В.А. Алгоритмическая помехозащита беспилотных летательных аппаратов. М.: Физматлит, 2018.
Гришин Ю.П., Казаринов Ю.М. Динамические системы, устойчивые к отказам. М.: Радио и связь, 1985.
Евланов П.А., Жук С.Я. // Изв. вузов СССР. Радиоэлектроника. 1990. Т. 33. № 7. С. 49.
Mиpoнoв M.A. // PЭ. 1985. T. 30. № 5. C. 973.
Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов. радио, 1977.
Тихонов В.И., Кульман Н.К. Нелинейная фильтрация и квазикогерентный приём сигналов. М.: Сов. радио, 1975.
Сосулин Ю.Г. Теория обнаружения и оценивания стохастических сигналов. М.: Сов. радио, 1978.
Ярлыков М.С. Применение марковской теории нелинейной фильтрации в радиотехнике. М.: Сов. радио, 1980.
Ярлыков М.С., Миронов М.А. Марковская теория оценивания случайных процессов. М.: Радио и связь, 1993.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991.
Дeткoв A.H. // PЭ. 2021. T. 66. № 8. C. 748.
Репин В.Г., Тартаковский Г.П. Статистический синтез при априорной неопределенности и адаптация информационных систем. М.: Сов. радио, 1978.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника