Радиотехника и электроника, 2022, T. 67, № 7, стр. 645-650
Плоская синфазная решетка нерегулярных ТЕМ-рупоров с металлизацией межрупорного пространства
М. Д. Дупленкова a, *, В. А. Калошин a
a Институт радиотехники и электроники им. В.А. Котельникова РАНул. Моховая, 11, стр. 7
125009 Москва, Российская Федерация
* E-mail: vak@cplire.ru
Поступила в редакцию 26.06.2021
После доработки 12.08.2021
Принята к публикации 25.09.2021
- EDN: BUKUDU
- DOI: 10.31857/S0033849422070099
Аннотация
Исследовано влияние геометрии ТЕМ-рупора в составе бесконечной синфазной решетки нерегулярных рупоров с металлизацией межрупорного пространства на полосу согласования решетки. Анализ частотных зависимостей коэффициента отражения проведен в рамках модели плавного перехода в канале Флоке для разных законов изменения волнового сопротивления с использованием двух методов теории волноводов: поперечных сечений и матриц рассеяния, а также численного моделирования с использованием метода конечных элементов.
ВВЕДЕНИЕ
Регулярный (линейный) ТЕМ-рупор является одним из наиболее широко используемых сверхширокополосных (СШП) излучателей [1–5]. Это объясняется, с одной стороны, простотой его конструкции, а с другой – возможностью согласования с питающей линией в очень широкой полосе частот. Последнее обстоятельство объясняется тем, что волновое сопротивление (импеданс) регулярного ТЕМ-рупора в квазистатическом приближении зависит только от двух угловых параметров [6] и не меняется вдоль его длины. Однако при увеличении размера поперечного сечения одиночного регулярного ТЕМ-рупора за счет связи с окружающим пространством, а в составе решетки – за счет связи между излучателями происходит постепенное изменение его импеданса, что необходимо учитывать при оптимизации геометрии ТЕМ-рупоров, в том числе в составе антенных решеток.
Известно, что при использовании ТЕМ-рупора в качестве элемента антенной СШП-решетки возникает сильное заднее излучение [7, 8], а при подавлении его путем использования экрана – резонансы в частотной характеристике коэффициента отражения [9]. В работе [10] предложены и исследованы решетки регулярных ТЕМ-рупоров с металлизацией межрупорного пространства. Наличие экрана в таких решетках позволяет подавить заднее излучение, не приводя при этом к появлению частотных резонансов и в результате в конечной решетке регулярных ТЕМ с металлизацией межрупорного пространства удалось реализовать полосу согласования более 15 : 1 [11]. Наилучшие результаты по согласованию синфазной решетки щелевых рупоров (полоса частот 12 : 1) были получены в работе [12].
Для увеличения полосы согласования при заданных габаритах антенны или антенной решетки можно использовать нерегулярные ТЕМ-рупоры [4, 5], в том числе симметричные [13] или несимметричные [14, 15] петлевые ТЕМ-рупоры, проводники которых образуют, соответственно, две или одну петлю, замыкаясь на задний экран (авторы [13] называют их “комбинированными рупорами”).
Следует отметить, что задача оптимизации закона изменения импеданса за счет изменения геометрии ТЕМ-рупора вдоль его длины рассматривалась только для одиночного нерегулярного ТЕМ-рупора [1–5] и ТЕМ-рупора в составе кольцевой решетки [14, 15].
Таким образом, несмотря на большое количество работ, задача поиска оптимальной геометрии нерегулярного ТЕМ-рупора в составе плоской двумерно-периодической антенной решетки, обеспечивающей максимальную полосу согласования при заданной длине рупора, не рассматривалась. Решению этой задачи в рамках модели бесконечной синфазной решетки посвящена данная работа.
1. ЧИСЛЕННО-АНАЛИТИЧЕСКИЕ МОДЕЛИ
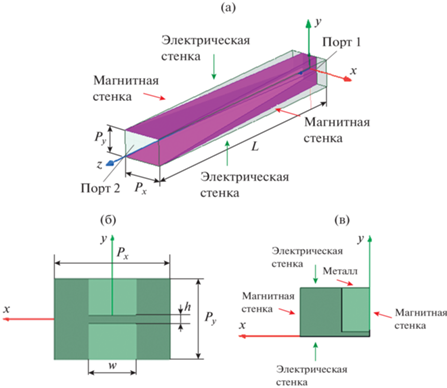
В квазипериодическом режиме возбуждения анализ бесконечной антенной решетки сводится к анализу одного периода (канала Флоке), на границах которого установлены условия периодичности [16, 17]. В синфазной решетке из элементов с двумя плоскостями симметрии вместо условий периодичности на границах канала Флоке в зависимости от ориентации векторов поля могут быть установлены электрические или магнитные стенки [17] (рис. 1). Канал Флоке в этом случае и его входной порт показаны на рис. 1а, 1б соответственно. С учетом двух плоскостей симметрии канала Флоке его анализ сводится к анализу волновода с эквивалентным поперечным сечением (рис. 1в).
Таким образом, задача анализа бесконечной решетки ТЕМ-рупоров сводится к анализу нерегулярногого волновода с поперечным сечением, равным четверти сечения канала Флоке, в котором распространяется ТЕМ-мода. Следует отметить, что в отличие от работы [10] в данной работе волновод возбуждается полубесконечной щелевой линией из проводников конечной толщины (см. рис. 1б).
Для анализа нерегулярного одномодового волновода с ТЕМ-модой будем использовать два известных в теории волноводов метода: поперечных сечений (МПС) для линии с медленно меняющимся импедансом и матриц рассеяния (ММР) для линии со ступенчатым изменением импеданса.
В приближении МПС коэффициент отражения определяется известной [18] формулой
(1)
$\begin{gathered} \rho = {{\rho }_{1}} + {{\rho }_{2}}{\text{exp}}\left( { - 2j\beta L} \right) + \\ + \,\,\mathop \smallint \limits_0^L \frac{{Z_{c}^{'}\left( t \right)}}{{2{{Z}_{c}}~\left( t \right)}}{\text{exp}}\left( { - 2j\beta L} \right)dt, \\ \end{gathered} $Пусть импеданс входного сечения волновода равен импедансу питающей щелевой линии Zc1 = = 25 Ом, длина волновода L = 180 мм, а величины периодов решетки в Е- и Н-плоскости равны соответственно Py = 20 мм и Pх = 30 мм. Импеданс пустого канала (волновода Флоке) при этом Zс2 = = ${{120\pi {{P}_{y}}} \mathord{\left/ {\vphantom {{120\pi {{P}_{y}}} {{{P}_{x}}}}} \right. \kern-0em} {{{P}_{x}}}}$ = 251 Ом.
Рассмотрим четыре закона изменения импеданса вдоль длины нерегулярного ТЕМ-рупора (формулы (2)–(5) соответственно): линейный, косинусоидальный, экспоненциальный и закон Клопфенштейна, описывающий предельный по малости величины скачков импеданса чебышевский переход [19]:
(3)
$Z\left( z \right) = - \cos \left( {\frac{{\pi z}}{L}} \right)\left( {\frac{{{{Z}_{{c2}}} - {{Z}_{{c1}}}}}{2}} \right) + \left( {\frac{{{{Z}_{{c2}}} + {{Z}_{{c1}}}}}{2}} \right),$(4)
$\begin{gathered} Z\left( z \right) = a + b{{e}^{{cz}}},\,\,\,\,\,~~a = {{Z}_{{c1}}} - b, \\ b = \frac{{{{Z}_{{c2}}} - {{Z}_{{c1}}}}}{{{{e}^{{cL}}} - 1}},\,\,\,\,\,c = 0.015, \\ \end{gathered} $(5)
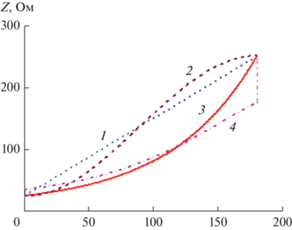
$\begin{gathered} \ln \left[ {Z\left( z \right)} \right] = \frac{1}{2}\ln \left( {{{Z}_{{c1}}}{{Z}_{{c2}}}} \right) + \frac{{{{Z}_{{c2}}} - {{Z}_{{c1}}}}}{{\left( {{{Z}_{{c2}}} + {{Z}_{{c1}}}} \right){\text{ch}}\left( A \right)}} \times \\ \times \,\left\{ {{{A}^{2}}\mathop \smallint \limits_0^L \frac{{{{I}_{1}}(A\sqrt {1 - {{y}^{2}})} }}{{(A\sqrt {1 - {{y}^{2}})} }}dy + U\left( z \right) + U\left( {z - L} \right)} \right\}, \\ \end{gathered} $Рис. 2.
Зависимости импеданса от продольной координаты, найденные в соответствии с законами: линейным (1), косинусоидальным (2), экспоненциальным (3), Клопфенштейна (4).
При использовании ММР заменим непрерывный закон изменения импеданса ступенчатым. Элементы матрицы рассеяния i-й ступеньки с малым перепадом импеданса длиной ∆l имеют вид [18]
(6)
$\begin{gathered} S{{11}_{i}} = \frac{{{{Z}_{{c\left( {i + 1} \right)}}} - {{Z}_{{ci}}}}}{{{{Z}_{{c\left( {i + 1} \right)}}} + {{Z}_{{ci}}}}}, \\ S{{22}_{i}} = - {{e}^{{ - 2j\beta \Delta l}}}\frac{{{{Z}_{{c\left( {i + 1} \right)}}} - {{Z}_{{ci}}}}}{{{{Z}_{{c\left( {i + 1} \right)}}} + {{Z}_{{ci}}}}}, \\ ~S{{12}_{i}} = S{{21}_{i}} = {{e}^{{ - j\beta \Delta l}}}\frac{{2\sqrt {{{Z}_{{c\left( {i + 1} \right)}}}{{Z}_{{ci}}}} }}{{{{Z}_{{c\left( {i + 1} \right)}}} + {{Z}_{{ci}}}}}. \\ \end{gathered} $По матрицам рассеяния известным образом, например в соответствии с [18], определяем волновые матрицы передачи ступенек:
(7)
$\begin{gathered} T{{11}_{i}} = S{{12}_{i}} - \frac{{S{{{11}}_{i}}S{{{22}}_{i}}}}{{S{{{12}}_{i}}}},\,\,\,\,\,T{{22}_{i}} = \frac{1}{{S{{{12}}_{i}}}}, \\ T{{12}_{i}} = \frac{{S{{{11}}_{i}}}}{{S{{{12}}_{i}}}},\,\,\,\,T{{21}_{i}} = \frac{{S{{{22}}_{i}}}}{{S{{{12}}_{i}}}}, \\ \end{gathered} $Для определения геометрии ТЕМ-рупора по зависимости его импеданса от продольной координаты воспользуемся результатами работы [8], в которой эта связь была найдена методом Галеркина. Отметим, что каждому значению импеданса соответствует континуум значений взаимосвязанных параметров – ширины проводников w(z) и величина зазора между ними h(z), т.е. каждому значению импеданса соответствует бесконечное число вариантов геометрии рупора. Далее для каждого закона изменения импеданса будем исследовать вариант 1 и 2 геометрии рупоров. У всех рупоров входная ширина проводника w(0) = 12.5 мм, т.е. равна ширине проводника питающей линии. Входной зазор h(0) = 1 мм также равен зазору между проводниками питающей линии с импедансом Zc1 = 25 Ом. В варианте 1 ширина проводников ТЕМ-рупора линейно растет с ростом z от 12.5 до 30 мм, а в варианте 2 (щелевого рупора) – остается постоянной. Рассчитанные зависимости h(z) для четырех описанных выше законов изменения импеданса показаны на рис. 3а, 3б для вариантов 1 и 2 ТЕМ-рупора соответственно.
Рис. 3.
Изменение величины зазора между проводниками h(z) для варианта 1 (а) и 2 (б) геометрии рупора, определенное для линейного закона изменения импеданса (1), косинусоидального (2), экспоненциального (3) и закона Клопфенштейна (4).
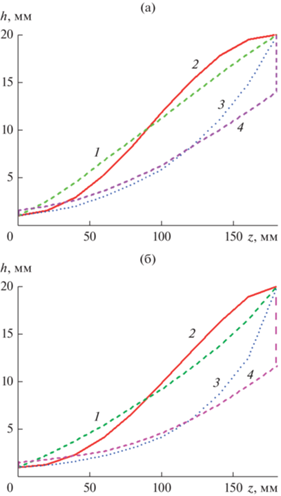
Для линейного закона изменения импеданса в варианте 1 зависимость h(z) близка к линейной (см. рис. 3а, кривая 1), откуда следует, что импеданс регулярного ТЕМ-рупора в решетке меняется по закону, близкому к линейному. При этом реализация линейного закона изменения импеданса в варианте 2 приводит к нелинейной зависимости h(z) (см. рис. 3б, кривая 1).
Далее тремя методами: МПС, ММР и конечных элементов (МКЭ) в программной среде ANSYS HFSS было проведено численное моделирование частотных зависимостей коэффициента отражения для восьми решеток ТЕМ-рупоров (с четырьмя законами изменения импеданса, каждому из которых соответствовали два варианта геометрии рупора). Результаты моделирования приведены на рис. 4.
Рис. 4.
Зависимости коэффициента отражения от частоты для рупора длиной L = 180 мм при численном моделировании по методам МПС (1), ММР (2) и МКЭ вариант 1 (3), вариант 2 (4): а – линейный закон, б – косинусоидальный, в – экспоненциальный, г – Клопфенштейна.
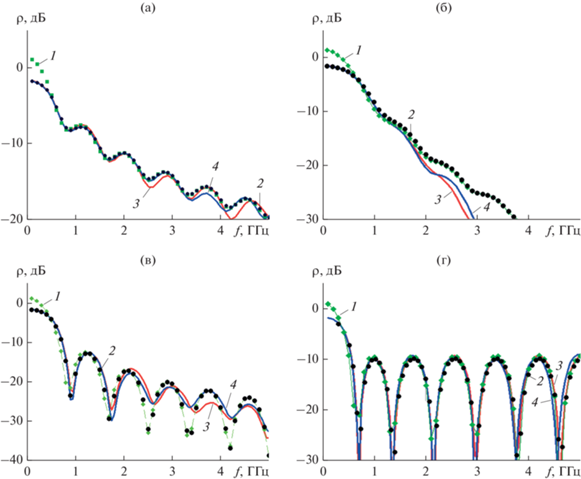
Как видно из рис. 4а–4г, кривые 3 и 4 практически совпадают, т.е. коэффициент отражения в исследованном диапазоне частот определяется законом изменения импеданса и практически не зависит от конкретных геометрических параметров ТЕМ-рупора. При этом наибольшую ширину полосы согласования по уровню –10 дБ обеспечивает закон Клопфенштейна, а наименьшую – линейный закон. Следует также отметить, что МПС и ММР хорошо описывают коэффициент отражения от нижней границы полосы согласования до уровня –20 дБ, а ММР – также и области более низких частот. При этом ММР более сложен при использовании по сравнению с МПС.
Разница в нижней частоте полосы согласования на рис. 4 для экспоненциального закона (0.7 МГц) и закона Клопфенштейна (0.55 МГц) небольшая, однако она увеличивается с уменьшением уровня отражения (например, до уровня –13 дБ) путем увеличении длины рупоров, когда нижняя частота для экспоненциального закона (кривая 2) определяется первым частотным максимумом (рис. 5).
Рис. 5.
Зависимости коэффициента отражения от частоты рупора длиной L = 220 мм: регулярный рупор (1), с экспоненциальным законом (2), с законом Клопфенштейна (3).
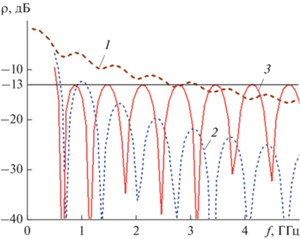
На рис. 5 приведена также частотная зависимость коэффициента отражения регулярного (линейного) рупора (кривая 1). Как и следовало ожидать, его полоса согласования серьезно уступает рупору с экспоненциальным законом изменения импеданса и, тем более, с законом Клопфенштейна.
ЗАКЛЮЧЕНИЕ
На основании полученных результатов можно сделать следующие выводы.
1. Методы поперечных сечений и матриц рассеяния в импедансном приближении можно применять для оценки нижней частоты согласования по уровню –10 дБ для решеток ТЕМ-рупоров с металлизацией межрупорного пространства вне зависимости от геометрии рупора.
2. Метод матриц рассеяния более трудоемок, чем метод поперечных сечений, однако позволяет более точно вычислять величину коэффициента отражения на частотах ниже полосы согласования.
3. Наибольшую ширину полосы согласования решетки ТЕМ-рупоров при заданных габаритах элемента обеспечивает ТЕМ-рупор с законом изменения импеданса Клопфенштейна, а наименьшую – с законом, близким к линейному, в частности, регулярный ТЕМ-рупор.
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Jamali A.A., Marklein R. // XXX URSI General Assembly and Scientific Symposium, 2011. P. 1.
Wang Z.P., Hall P.S., Kelly J., Gardner P. // Electron. Lett. 2011. V. 47. № 25. P. 1357.
Ascama H.D.O., Hiramatsu R.K., de Oliveira A.M. et al. // J. Microwaves, Optoelectronics and Electromagnetic Appl. 2013. V. 12. № 2. P. 655.
Bassam S., Rashed-Mohassel J. // Progress in Electromagnetics Research Symposium Online. 2006. V. 2. № 6. P. 474.
Ефимова Н.А., Калошин В.А. // РЭ. 2014. Т. 59. № 1. С. 60.
Maloney J.G., Smith G.S. // IEEE Antennas Propag. Soc. Int. Symp. 1995. V. 1. P. 182.
Калошин В.А., Нгуен К.З. // Журн. радиоэлектроники. 2017. № 5. http://jre.cplire.ru/jre/may17/ 14/text.pdf.
Банков С.Е., Калошин В.А., Нгуен К.З.// РЭ. 2018. Т. 63. № 7. С. 702.
McGrath D.T. // IEEE Antennas Propag. Soc. Int. Symp. 1998. Atlanta. 21–26 Jun. V. 2 P. 1024.
Банков С.Е., Калошин В.А, Ле Н.Т. // РЭ. 2018. Т. 63. № 12. С. 1263.
Калошин В.А., Ле Н.Т. // Журн. радиоэлектроники. 2020. № 3. http://jre.cplire.ru/jre/mar20/8/text.pdf.
Kindt R.W., Pickles W. R. // IEEE Trans. 2010. V. AP-58. № 11.P. 3568.
Koshelev V.I., Plisko V.V. // J. Phys.: Conf. Ser. 2021. V. 1843. № 1. P. 012002.
Бирюков В.Л., Ефимова Н.А., Калиничев В.И. и др. // Журн. радиоэлектроники. 2013. № 1. http://jre.cplire.ru/jre/jan13/20/text.pdf.
Elmansouri M.A., Ha J., Filipovic D.S. // IEEE Trans. 2017. AP-65. № 3. P. 1374.
Банков С.Е., Курушин В.Д., Гутцайт Э.М. Решение оптических и СВЧ задач с помощью HFSS. М.: Оркада, 2012.
Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. М.: Мир, 1974.
Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. школа, 1988.
Klopfenstein R.W. // Proc. IRE. 1956. № 1. P. 31.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника