Радиотехника и электроника, 2022, T. 67, № 7, стр. 651-659
Расчет токов на многоэлементных излучающих структурах итерационным методом
Д. П. Табаков a, *, Б. М. А. Аль-Нозайли b
a Поволжский государственный университет телекоммуникаций и информатики
443010 Самара, ул. Л. Толстого, 23, Российская Федерация
b Самарский национальный исследовательский университет им. ак. С.П. Королева
443086 Самара, Московское шос., 34, Российская Федерация
* E-mail: illuminator84@yandex.ru
Поступила в редакцию 07.10.2021
После доработки 07.10.2021
Принята к публикации 25.11.2021
- EDN: GOZDVS
- DOI: 10.31857/S0033849422070142
Аннотация
Рассмотрен строгий метод электродинамического анализа многоэлементной излучающей структуры, в котором использованы классические итерационные методы, применяемые к блочной системе линейных алгебраических уравнений (СЛАУ). Приведены выражения для элементов СЛАУ в случае тонкопроволочной излучающей структуры при различных вариантах проекционных функций. Представлена математическая модель директорной антенны, для которой проведено численное моделирование. Исследована сходимость итерационного процесса при вычислении распределений токов, входного сопротивления и диаграммы направленности. Показано, что в отсутствие сильных межэлементных связей метод обладает высокой эффективностью.
ВВЕДЕНИЕ
Моделирование распределения токов на многоэлементных излучающих структурах имеет особое значение в теории антенн. При проектировании таких излучающих структур необходимо учитывать взаимодействие между их отдельными элементами, что является довольно сложной задачей. Долгое время в инженерной практике для расчета взаимодействия использовался метод наведенных электродвижущих сил (ЭДС). Основные принципы этого метода изложены в работе [1]. Метод наведенных ЭДС позволяет находить наведенные и собственные сопротивления элементов антенны, а также амплитуды и фазы токов в пассивных элементах. Из недостатков метода отметим, что он накладывает определенные ограничения на длину и расстояние между элементами из-за использования приближенных распределений тока. Наиболее полно учесть взаимодействие между элементами излучающих структур позволяют строгие математические модели, сводящиеся к системам интегральных уравнений [2].
В настоящее время для решения таких задач применяют системы автоматизированного проектирования, в которых используют метод моментов [3], метод конечных элементов и метод конечных разностей [4]. К недостаткам такого подхода можно отнести высокие требования к ЭВМ, высокую стоимость программного обеспечения, отсутствие математической модели в явном виде.
Таким образом, разработка универсальных методов расчета межэлементного взаимодействия является актуальной задачей. В [5] рассмотрен итерационный подход к решению интегральных уравнений теории проволочных антенн на основе многошагового метода минимальных невязок. Здесь метод применялся непосредственно к общей матрице системы линейных алгебраических уравнений (СЛАУ). В [6] в качестве основы для расчета взаимодействия было предложено использовать модификацию метода Гаусса–Зейделя [7] для случая блочной матрицы СЛАУ. Сделан вывод о том, что предложенный метод может быть эффективен для расчета метаструктур, имеющих конечные размеры [8]. Результаты работы [6] были дополнены в [9] алгоритмами расчета элементов блочной матрицы СЛАУ для случая построения структуры из однотипных элементов, обладающих различными видами симметрий. Показано, что данные алгоритмы позволяют существенно сокращать время расчета.
В данной статье рассмотрен вопрос использования метода [6] для расчета многоэлементных излучающих структур. В качестве примера рассмотрена директорная антенна [10], математическая модель для которой была построена на основе тонкопроволочных интегральных представлений электромагнитного поля [11]. Для случая различных систем проекционных функций (СПФ) проведено исследование сходимости результатов вычисления токов, входного сопротивления и диаграмм направленности.
1. АЛГОРИТМ ИТЕРАЦИОННОГО РЕШЕНИЯ ВНУТРЕННЕЙ ЭЛЕКТРОДИНАМИЧЕСКОЙ ЗАДАЧИ
Внутренняя электродинамическая задача для многоэлементных излучающих структур сводится к операторной системе вида
(1)
$\sum\limits_{j = 1}^N {{{l}_{{i,j}}}} \begin{array}{*{20}{l}} {\left( {{{f}_{j}}} \right) = {{g}_{i}},} \end{array}\,\,\,\,i = 1, \ldots ,N,$К системе (1) была применена схема метода моментов [3]: на $i$-м элементе введены системы базисных $b_{p}^{{\left( i \right)}}$ и тестовых $t_{p}^{{\left( i \right)}}$ функций (здесь и далее индексы $p = {{p}_{{i\left( j \right)}}} = 1, \ldots ,{{P}_{{i\left( j \right)}}}$ и $q = {{q}_{{i\left( j \right)}}} = 1, \ldots ,{{P}_{{i\left( j \right)}}}$ обозначают проекционные функции на соответствующем элементе структуры), определен оператор скалярного произведения $S$ функций. По системе базисных функций $b_{q}^{{\left( j \right)}}$произведено разложение неизвестных функций ${{f}_{j}}$:
Подставляя (2) в (1) и определяя последовательно скалярные произведения с тестовыми функциями для правой и левой частей получающихся уравнений, приходим к СЛАУ вида
где ${\mathbf{Z}}$ – блочная матрица, ${\mathbf{I}}$, ${\mathbf{E}}$ – соответственно блочные векторы неизвестных и правой части. Будем считать, что(4)
$\begin{gathered} {{{\mathbf{z}}}_{{i,j}}} \in {\mathbf{Z}},\,\,\,\,{{{\mathbf{i}}}_{j}} \in {\mathbf{I}},\,\,\,\,{{{\mathbf{e}}}_{j}} \in {\mathbf{E}}; \\ Z_{{p,q}}^{{\left( {i,j} \right)}} = S\left( {t_{p}^{{\left( i \right)}},{{l}_{{ij}}}\left( {b_{q}^{{\left( j \right)}}} \right)} \right) \in {{{\mathbf{z}}}_{{i,j}}},\,\,\,\,I_{q}^{{\left( j \right)}} \in {{{\mathbf{i}}}_{j}}, \\ E_{p}^{{\left( i \right)}} = S\left( {t_{p}^{{\left( i \right)}},{{g}_{i}}} \right) \in {{{\mathbf{e}}}_{j}}. \\ \end{gathered} $Неизвестные коэффициенты $I_{q}^{{\left( j \right)}}$ входят в (2). Общее число скалярных элементов матрицы ${\mathbf{Z}}$ можно определить как $\bar {P} \times \bar {P}$, где $\bar {P} = \sum\nolimits_{j = 1}^N {{{P}_{j}}} $.
Решать СЛАУ прямым методом в случае использования базисных и тестовых функций универсального вида нецелесообразно, так как даже для структур, содержащих не более ста элементов, число $\bar {P}$ будет довольно большим. Здесь возникают две проблемы. Первая заключается собственно в выборе метода решения СЛАУ. Известно, что точные методы могут применяться для СЛАУ относительно небольших размеров вследствие сложности решения, пропорциональной $O({{\bar {P}}^{3}})$ и, что гораздо важнее, вследствие накопления погрешностей округления [7]. Вместе с тем возникает вторая проблема – хранение таких матриц в памяти ЭВМ. Непосредственное применение итерационных методов, основанных на расщеплении матрицы (методы типа последовательной верхней релаксации), может привести к негативному результату, если отсутствует диагональное преобладание в матрице ${\mathbf{Z}}$.
Достичь сходимости классических итерационных методов можно, рассматривая именно блочную СЛАУ (3) в предположении, что между элементами структуры отсутствует достаточно сильная связь. Под сильной будем понимать кондуктивную связь или такую связь по полю, при которой найдется элемент, энергия наведенных полей на котором превышает энергию излучаемого им поля. Сильная связь по полю возможна, например, в резонансных случаях. Практически пригодность метода можно определить по наличию или отсутствию сходимости решения.
Применяя процедуру Гаусса–Зейделя [7] к блочной СЛАУ, можно записать следующую форму ее решения:
(5)
${\mathbf{i}}_{i}^{{\left( {k + 1} \right)}} = {{{\mathbf{p}}}_{i}}{{{\mathbf{e}}}_{i}} - \sum\limits_{j > i} {{{{\mathbf{w}}}_{{i,j}}}{\mathbf{i}}_{j}^{{\left( k \right)}}} - \sum\limits_{j < i} {{{{\mathbf{w}}}_{{i,j}}}{\mathbf{i}}_{j}^{{\left( {k + 1} \right)}}} ,$(6)
${{{\mathbf{p}}}_{i}} = {\mathbf{z}}_{{ii}}^{{ - 1}},\,\,\,\,{{{\mathbf{w}}}_{{i,j}}} = {{{\mathbf{p}}}_{i}}{{{\mathbf{z}}}_{{i,j}}}$(8)
$\xi \leqslant {{{{\delta }}}_{k}} = \mathop {{\text{max}}}\limits_j \left( {{{\left| {{\mathbf{i}}_{j}^{{\left( {k + 1} \right)}} - {\mathbf{i}}_{j}^{{\left( k \right)}}} \right|} \mathord{\left/ {\vphantom {{\left| {{\mathbf{i}}_{j}^{{\left( {k + 1} \right)}} - {\mathbf{i}}_{j}^{{\left( k \right)}}} \right|} {\left| {{\mathbf{i}}_{j}^{{\left( {k + 1} \right)}}} \right|}}} \right. \kern-0em} {\left| {{\mathbf{i}}_{j}^{{\left( {k + 1} \right)}}} \right|}}} \right),$Обсудим теперь общие и частные преимущества данной формы решения внутренней задачи. Общих преимуществ здесь два. Первое заключается в отсутствии необходимости решения полной СЛАУ, второе – в том, что в случае (6) обратить нужно только $N$ матриц ${{{\mathbf{z}}}_{{ii}}}$, имеющих относительно небольшой размер и допускающих применение прямых методов, основанных, например, на $LU$-факторизации, в случае (7) процедура обращения сводится к поиску обратных диагональных элементов. Но наиболее важные преимущества появляются при решении внутренней задачи для структур, состоящих из однотипных элементов. В этом случае собственные матрицы ${{{\mathbf{z}}}_{{ii}}}$ будут равны между собой. Таким образом, обратить нужно будет только одну матрицу. Если элементы структуры одинаково ориентированы в пространстве и (или) имеют плоскости либо оси симметрии, то множество весовых матриц также будут иметь одинаковый вид, что позволяет существенно снизить затраты памяти ЭВМ на хранение полной матрицы СЛАУ.
2. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ТОНКОПРОВОЛОЧНОЙ МНОГОЭЛЕМЕНТНОЙ СТРУКТУРЫ
Многоэлементная тонкопроволочная структура $L$ представляет собой совокупность $N$ тонких проводников ${{L}_{1}},{{L}_{2}}, \ldots ,{{L}_{N}}$ произвольной формы, расположенных в свободном пространстве с характеристическим сопротивлением ${{W}_{m}}$. Для простоты предположим, что радиус всех проводников одинаков и равен $\epsilon $. Каждый проводник можно описать векторным уравнением, зависящим от натурального параметра $l$:
(9)
${\mathbf{F}}\left( {\mathbf{r}} \right) = \sum\limits_{j = 1}^N {\int\limits_{{{L}_{j}}} {{{I}_{j}}\left( {l{\kern 1pt} '} \right){{{\mathbf{K}}}^{{\left( F \right)}}}} } \left( {{\mathbf{r}},{{{\mathbf{r}}}_{j}}\left( {l{\kern 1pt} {\text{'}}} \right)} \right)dl{\kern 1pt} {\text{'}},\,\,\,\,F \equiv E,H;$Для ${{I}_{j}}\left( {l{\kern 1pt} {\text{'}}} \right)$ целесообразно представление в виде рядов:
(10)
$\begin{gathered} {\mathbf{F}}({\mathbf{r}}) = \sum\limits_{j = 1}^N {\sum\limits_{q = 1}^{{{P}_{j}}} {I_{q}^{{(j)}}} } \int\limits_{{{L}_{j}}} {b_{q}^{{(j)}}} (l{\kern 1pt} '){{{\mathbf{K}}}^{{\left( F \right)}}}\left( {{\mathbf{r}},{{{\mathbf{r}}}_{j}}\left( {l{\kern 1pt} '} \right)} \right)dl{\kern 1pt} ', \\ F \equiv E,H. \\ \end{gathered} $На каждой образующей справедливо граничное условие для идеального проводника:
(11)
$\left( {{{{\mathbf{E}}}^{{\left( {{\text{ext}}} \right)}}}\left( {{{{\mathbf{r}}}_{i}}\left( l \right)} \right) + {\mathbf{E}}\left( {{{{\mathbf{r}}}_{i}}\left( l \right)} \right)} \right) \cdot {\mathbf{\hat {l}}}{{{\kern 1pt} }_{i}}{\kern 1pt} \left( l \right) = 0.$Здесь и далее оператор “$ \cdot $” использован для обозначения скалярного произведения векторов. Умножая поочередно (11) на тестовые функции $t_{p}^{{\left( i \right)}}\left( l \right)$ и интегрируя по $l$, получаем СЛАУ для вычисления $I_{q}^{{\left( j \right)}}$, по форме совпадающую с (3), в которой:
(12)
$\begin{gathered} Z_{{p,q}}^{{\left( {i,j} \right)}} = \int\limits_{{{L}_{i}}} {\int\limits_{{{L}_{j}}} {t_{p}^{{(i)}}} } \left( l \right)b_{q}^{{\left( j \right)}}\left( {l{\kern 1pt} {\text{'}}} \right){{{{\mathbf{\hat {l}}}}}_{i}}\left( l \right) \cdot {{{\mathbf{K}}}^{{\left( E \right)}}}\left( {{{{\mathbf{r}}}_{i}}\left( l \right),{{{\mathbf{r}}}_{j}}\left( {l{\kern 1pt} {\text{'}}} \right)} \right)dl{\kern 1pt} {\text{'}}dl, \\ E_{p}^{{\left( i \right)}} = \mathop \smallint \limits_{{{L}_{i}}} t_{p}^{{(i)}}\left( l \right){{{{\mathbf{\hat {l}}}}}_{i}}\left( l \right) \cdot {{{\mathbf{E}}}^{{\left( {{\text{ext}}} \right)}}}\left( {{{{\mathbf{r}}}_{i}}\left( l \right)} \right)dl. \\ \end{gathered} $Конкретизируем способ вычисления интегралов в (12) с помощью процедуры сегментации проводников, предполагающей представление i-го проводника в виде совокупности ${{S}_{i}} + 1$ узлов $L_{i}^{{\left( {{{S}_{i}}} \right)}}$: ${{{\mathbf{r}}}_{{i,1}}},{{{\mathbf{r}}}_{{i,2}}}, \ldots ,{{{\mathbf{r}}}_{{i,{{S}_{i}} + 1}}}$. Между узлами с номерами $m$ и $~m + 1$ находится $m$-й сегмент ri,m(l), уравнение которого может быть записано в следующем виде:
Здесь ${\mathbf{r}}_{{i,m}}^{{\text{*}}} = {{\left( {{{{\mathbf{r}}}_{{i,m}}} + {{{\mathbf{r}}}_{{i,m + 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\mathbf{r}}}_{{i,m}}} + {{{\mathbf{r}}}_{{i,m + 1}}}} \right)} {2{\text{\;}}}}} \right. \kern-0em} {2{\text{\;}}}}$ – центр сегмента, ${{\Delta }_{{i,m}}} = \left| {{{{\mathbf{r}}}_{{i,m + 1}}} - {{{\mathbf{r}}}_{{i,m}}}} \right|$ – длина сегмента, ${{{\mathbf{\hat {l}}}}_{{i,m}}} = $ $ = {{\left( {{{{\mathbf{r}}}_{{i,m + 1}}} - {{{\mathbf{r}}}_{{i,m}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\mathbf{r}}}_{{i,m + 1}}} - {{{\mathbf{r}}}_{{i,m}}}} \right)} {{{\Delta }_{{i,m}}}}}} \right. \kern-0em} {{{\Delta }_{{i,m}}}}}$ – единичный вектор касательной на сегменте. Здесь и далее индексы m = mi(j) = $ = 1, \ldots ,{{S}_{{i\left( j \right)}}}$ и $n = {{n}_{{i\left( j \right)}}} = 1, \ldots ,{{S}_{{i\left( j \right)}}}$ означают сегменты на соответствующем элементе структуры.
В качестве базисных будем использовать взвешенные суммы функций, кусочно-постоянных в пределах каждого сегмента:
(13)
$b_{q}^{{\left( {j,{{S}_{j}}} \right)}}\left( {l{\kern 1pt} {\text{'}}} \right) = \sum\limits_{n = 1}^{{{S}_{j}}} {b_{q}^{{(j)}}} \left( {{{{\dot {l}}}_{{j,n}}}} \right){{\sigma }}\left( {l{\kern 1pt} {\text{'}},{{{\dot {l}}}_{{j,n}}},{{\Delta }_{{j,n}}}} \right),$(14)
$t_{p}^{{\left( {i,{{S}_{i}}} \right)}}\left( l \right) = \sum\limits_{m = 1}^{{{S}_{i}}} {t_{p}^{{(i)}}} \left( {{{{\dot {l}}}_{{i,m}}}} \right){{\delta }}\left( {l - {{{\dot {l}}}_{{i,m}}}} \right).$Такой подход можно рассматривать как обобщенный метод коллокаций [12]. Из представленных выражений видно, что в случае (13) роль весовых коэффициентов играют значения функций $b_{q}^{{\left( j \right)}}\left( l \right)$, вычисленные в точках коллокации ${{\dot {l}}_{{j,n}}}$, а в случае (14) аналогичная роль принадлежит функциям $t_{p}^{{\left( i \right)}}\left( l \right)$.
Применяя приведенные выражения в (12) с учетом свойств дельта-функции, получаем формулы для расчета матричных коэффициентов и коэффициентов правой части СЛАУ с помощью конечных сумм:
(15)
$\begin{gathered} Z_{{p,q}}^{{\left( {i,j} \right)}} \approx \sum\limits_{m = 1}^{{{S}_{i}}} {\sum\limits_{n = 1}^{{{S}_{j}}} {t_{p}^{{(i)}}} } \left( {{{{\dot {l}}}_{{i,m}}}} \right)b_{q}^{{\left( j \right)}}\left( {{{{\dot {l}}}_{{j,n}}}} \right)W_{{m,n}}^{{\left( {i,j} \right)}}, \\ E_{p}^{{\left( i \right)}} \approx \sum\limits_{m = 1}^{{{S}_{i}}} {t_{p}^{{(i)}}} \left( {{{{\dot {l}}}_{{i,m}}}} \right)Q_{m}^{{\left( i \right)}}, \\ \end{gathered} $(16)
$\begin{gathered} W_{{m,n}}^{{\left( {i,j} \right)}} = \int\limits_{{{L}_{{j,n}}}} {{{{{\mathbf{\hat {l}}}}}_{{i,m}}} \cdot {{{\mathbf{K}}}^{{\left( E \right)}}}} ({\mathbf{r}}_{{i,m}}^{{\text{*}}},{{{\mathbf{r}}}_{{j,n}}}\left( {l{\kern 1pt} {\text{'}}} \right))dl{\kern 1pt} {\text{'}}, \\ Q_{m}^{{\left( i \right)}} = {{{{\mathbf{\hat {l}}}}}_{{i,m}}} \cdot {{{\mathbf{E}}}^{{\left( {{\text{ext}}} \right)}}}({\mathbf{r}}_{{i,m}}^{{\text{*}}}). \\ \end{gathered} $Традиционному методу коллокаций соответствует выбор:
(17)
$b_{q}^{{\left( j \right)}}\left( l \right) = {{\delta }_{{l,{{{\dot {l}}}_{{j,q}}}}}},\,\,\,\,t_{p}^{{\left( i \right)}}\left( l \right) = {{{{\delta }}}_{{l,{{{\dot {l}}}_{{i,p}}}}}},\,\,\,\,{{P}_{{i\left( j \right)}}} = {{S}_{{i\left( j \right)}}},$Следует отметить, что в данном разделе приведен один из наиболее простых с вычислительной точки зрения вариантов построения СЛАУ для определения неизвестных токов на элементах излучающей структуры, предполагающий использование упрощенных с учетом тонкопроволочного приближения ядер ${{{\mathbf{K}}}^{{\left( F \right)}}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} '} \right)$ в (9), (10), (12). В отсутствие данного приближения возникает необходимость решения систем интегральных уравнений (ИУ) с логарифмическими и гиперсингулярными особенностями в ядрах, что существенно усложняет процедуру построения СЛАУ. В качестве альтернативы также можно использовать варианты, предполагающие обращение дифференциального оператора, приводящие к системам ИУ со слабыми (логарифмическими) особенностями. Подобный подход использован в [14, 15]. В [14] для системы тонких параллельно расположенных прямолинейных вибраторов, возбуждаемых точечными источниками, получена система ИУ Фредгольма второго рода и обоснован выбор параметра регуляризации исходной задачи, а также представлены выражения для расчета нормированной диаграммы направленности излучающей системы. В [15] представлено решение обобщенной задачи для системы тонких прямолинейных проводников, произвольно расположенных в пространстве. В рамках данной задачи имеются более широкие возможности выбора вида функции стороннего поля. Подробно рассмотрены ядра системы ИУ, приведен метод получения СЛАУ.
При использовании тонкопроволочного приближения необходимо оценить погрешность, с которой осевой ток на конкретном проводнике аппроксимирует реальный азимутально-независимый поверхностный ток. Способ вычисления данной погрешности будет рассмотрен далее.
3. АНАЛИЗИРУЕМАЯ ИЗЛУЧАЮЩАЯ СТРУКТУРА
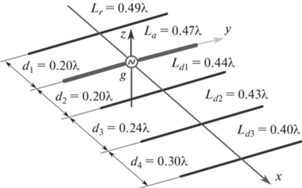
В качестве структуры для тестирования предложенных алгоритмов решения внутренней задачи была выбрана директорная антенна (ДА). Она состоит из пяти элементов – тонких идеально проводящих прямолинейных цилиндрических вибраторов, имеющих диаметр $2\epsilon \ll \lambda $, лежащих в плоскости $xOy$ симметрично плоскости $zOx$. Вибратор ${{L}_{a}}$ является активным и содержит в центре разрыв длиной $d \ll \lambda $, в который помещен генератор сторонней ЭДС $g$. Здесь и далее названия вибраторов также будут использоваться для обозначения их длины. Вибратор ${{L}_{r}}$ играет роль рефлектора, а вибраторы ${{L}_{{di}}}$ ($i = 1,2,3$) – роль директоров.
Распределения токов обозначим в соответствии с обозначениями самих вибраторов: ${{I}_{1}}\left( l \right) = {{I}_{r}}\left( l \right)$, ${{I}_{2}}\left( l \right) = {{I}_{a}}\left( l \right)$, ${{I}_{{j + 2}}}\left( l \right) = {{I}_{{dj}}}\left( l \right)$, $j = 1,2,3$. Уравнения образующих имеют общую форму:
Значения ${{s}_{j}}$ (смещение вдоль оси $Ox$) ${{L}_{j}}$ несложно определить из рис. 1.
Под действием генератора сторонней ЭДС, имеющего амплитуду, равную $U$, на активном вибраторе возникает касательная компонента стороннего электрического поля ${{E}^{{\left( {{\text{ст}}} \right)}}}\left( l \right)$, равная нулю всюду за исключением области зазора, где она равна ${U \mathord{\left/ {\vphantom {U d}} \right. \kern-0em} d}$. Эта компонента создает на активном вибраторе распределение тока ${{I}_{a}}\left( l \right)$, который, в свою очередь, создает токи на пассивных элементах антенны.
После сегментации такой структуры к ней в полной мере становятся применимы выражения (3) и (15). Сегментацию будем осуществлять так, чтобы длины сегментов в пределах отдельного элемента были равны (${{{{\Delta }}}_{{i,m}}} = {{{{\Delta }}}_{i}}$). Число сегментов выбирается в соответствии с (18). С учетом симметрии структуры относительно плоскости $zOx$ целесообразным является четное число сегментов на элементе ${{S}_{i}} = 2S_{i}^{'}$. В этом случае конец сегмента с индексом $S_{j}^{'}$ будет началом сегмента с индексом ${{S}_{j}} + 1$, а соответствующая точка будет принадлежать плоскости симметрии. Ширину зазора $d$, в который помещается генератор $g$, после сегментации можно принять равной $2{{{{\Delta }}}_{2}}$. Далее при моделировании будем использовать СПФ, построенные на основе (15) и соответствующие различным вариантам метода коллокаций.
Вариант 1. СПФ типа (17). Выражения (15) при этом приобретают простой вид:
(19)
$Z_{{p,q}}^{{\left( {i,j} \right)}} = W_{{p,q}}^{{\left( {i,j} \right)}},\,\,\,\,E_{p}^{{\left( i \right)}} = Q_{p}^{{\left( i \right)}}.$Вариант 2. СПФ, учитывающие симметрию и способ возбуждения структуры:
(20)
$\begin{gathered} b_{q}^{{\left( j \right)}}\left( l \right) = {{{{\delta }}}_{{l,{{{\dot {l}}}_{{j,q}}}}}} + {{{{\delta }}}_{{l,{{{\dot {l}}}_{{j,q{\kern 1pt} '}}}}}}, \\ t_{p}^{{\left( i \right)}}\left( l \right) = b_{p}^{{\left( i \right)}}\left( l \right),\,\,\,\,{{P}_{{i\left( j \right)}}} = S_{{i\left( j \right)}}^{'}; \\ \end{gathered} $Выражения (15) при этом приобретают вид
(21)
$\begin{gathered} Z_{{p,q}}^{{\left( {i,j} \right)}} = W_{{p,q}}^{{\left( {i,j} \right)}} + W_{{p,q{\kern 1pt} {\text{'}}}}^{{\left( {i,j} \right)}} + W_{{p{\kern 1pt} {\text{'}},q}}^{{\left( {i,j} \right)}} + W_{{p{\kern 1pt} {\text{'}},q{\kern 1pt} {\text{'}}}}^{{\left( {i,j} \right)}}, \\ E_{p}^{{\left( i \right)}} = Q_{p}^{{\left( i \right)}} + Q_{{p{\kern 1pt} {\text{'}}}}^{{\left( i \right)}}. \\ \end{gathered} $В выражениях (20) и (21) $p{\kern 1pt} {\text{'}} = 2S_{i}^{'} + 1 - p$, q' = $ = 2S_{i}^{'} + 1 - q$.
Вариант 3. СПФ, учитывающие симметрию и способ возбуждения структуры, а также вид собственных функций на ее отдельных элементах [16]:
(22)
$\begin{gathered} b_{q}^{{\left( j \right)}}\left( l \right) = \sqrt 2 \cos \left( {\left( {2q - 1} \right){{рl} \mathord{\left/ {\vphantom {{рl} {\left( {2{{L}_{j}}} \right)}}} \right. \kern-0em} {\left( {2{{L}_{j}}} \right)}}} \right), \\ t_{p}^{{\left( i \right)}}\left( l \right) = b_{p}^{{\left( i \right)}}\left( l \right). \\ \end{gathered} $Число проекционных функций ${{P}_{j}} \leqslant S_{j}^{'}$, его можно определить, анализируя сходимость решения при максимальном соотношении ${{{{L}_{a}}} \mathord{\left/ {\vphantom {{{{L}_{a}}} {{\lambda }}}} \right. \kern-0em} {{\lambda }}} = {{\gamma }}$.
Предварительный анализ показал, что в первых двух случаях сходимости итерационного процесса (5) можно достичь только с использованием полного обращения собственных матриц ${{{\mathbf{z}}}_{{i,i}}}$ (первое выражение (6)), а в третьем случае можно использовать как полное обращение, так и простые обратные матрицы (7). Поэтому будем считать, что вариант 3 использует полное обращение собственных матриц, а также введем еще один вариант:
Вариант 4. СПФ вида (22) с использованием в итерационном процессе (5) простых обратных матриц (7).
4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
При проведении численного моделирования половинное число сегментов $S_{j}^{'}$ ($j = 1 \ldots 5$) на различных элементах антенны предполагалось равным $S{\kern 1pt} ' = 75$, что соответствовало условию (18) при ${\epsilon \mathord{\left/ {\vphantom {\epsilon {{{L}_{a}}}}} \right. \kern-0em} {{{L}_{a}}}} = 7 \times {{10}^{{ - 4}}}$. Число проекционных функций для вариантов 3 и 4 было равно 25 на активном вибраторе и 5 на пассивных вибраторах. Амплитуда $U$ генератора ЭДС полагалась равной 1В. Моделирование проводилось в диапазоне ${{\gamma }} = 0.35 \ldots 1.35$. Отметим, что нормированная ширина зазора ${d \mathord{\left/ {\vphantom {d {{{L}_{a}}}}} \right. \kern-0em} {{{L}_{a}}}}$ оказалась равной ${1 \mathord{\left/ {\vphantom {1 {75}}} \right. \kern-0em} {75}}$. При исследовании сходимости итерационных процессов в (8) предполагалось, что $\xi = {{10}^{{ - 6}}}$.
На первом этапе была проведена оценка сходимости решения внутренней задачи. На рис. 2 приведены результаты расчета распределения тока на активном вибраторе (здесь и далее $t = {l \mathord{\left/ {\vphantom {l L}} \right. \kern-0em} L} \in \left[ { - 1;1} \right]$ – нормированная координата на образующей соответствующего вибратора), полученные для варианта 3 ИП при различном числе сегментов, ${{\gamma }} = 0.47$. Из рисунка видно, что $S{\kern 1pt} ' = 75$ можно считать достаточным для проведения дальнейших исследований. На рис. 3 приведены результаты расчета амплитудных распределений тока на всех вибраторах антенны, полученных с помощью вариантов 1 и 3 ИП, ${{\gamma }} = 0.47$. Здесь можно видеть достаточно хорошее совпадение результатов, полученных с помощью разных СПФ.
Рис. 2.
Распределения тока на активном вибраторе, полученные для ${{\gamma }} = 0.47{\text{\;}}$в рамках варианта 3 при различном числе сегментов: $S{\kern 1pt} ' = 25$ (1), $75$ (2) и $150$ (3).

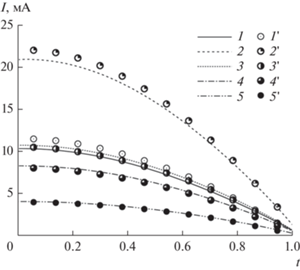
Рис. 3.
Распределения тока на элементах вибратора, полученные для ${{\gamma }} = 0.47{\text{\;}}$ в рамках варианта 1 (1–5) и варианта 3 (1 '–5 ') для вибраторов 1, …, 5 (кривые 1–5 соответственно).
Погрешность, с которой осевой ток $I\left( l \right)$ на проводнике $L$ аппроксимирует реальный азимутально-независимый поверхностный ток ${{I}_{S}}\left( l \right)$, можно оценить, используя выражение для магнитного поля ${\text{на}}$ поверхности прямолинейного проводника [13]:
(23)
$\begin{gathered} {{I}_{S}}\left( l \right) = \frac{{{{k}^{3}}{{\epsilon }^{2}}}}{2}\int\limits_L I \left( {l{\kern 1pt} '} \right)\frac{{ix + 1}}{{{{x}^{3}}}}{\text{exp}}\left( { - ix} \right)dl{\kern 1pt} '\,\, + O\left( {{{{\left( {k\epsilon } \right)}}^{2}}} \right),~ \\ ~x = k\sqrt {{{{\left( {l - l{\kern 1pt} '} \right)}}^{2}} + {{\epsilon }^{2}}} .{\text{\;}} \\ \end{gathered} $Слагаемое $O\left( {{{{\left( {k\epsilon } \right)}}^{2}}} \right)$ обусловлено влиянием соседних проводников. С практической точки зрения удобно использовать величину ${{\delta }_{{\mathbf{i}}}} = {{\left| {{{{\mathbf{i}}}_{S}} - {\mathbf{i}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{{\mathbf{i}}}_{S}} - {\mathbf{i}}} \right|} {\left| {{{{\mathbf{i}}}_{S}}} \right|}}} \right. \kern-0em} {\left| {{{{\mathbf{i}}}_{S}}} \right|}}$, в которой токи ${{{\mathbf{i}}}_{S}}~$ и ${\mathbf{i}}$ – векторы, составленные из значений соответствующих токов в точках коллокации. При выбранных параметрах моделирования для ${{\gamma }} = 0.47$ на активном вибраторе ${{\delta }_{{\mathbf{i}}}} \approx {{10}^{{ - 5}}}$, что позволяет считать корректным используемое приближение для ядра ИУ.
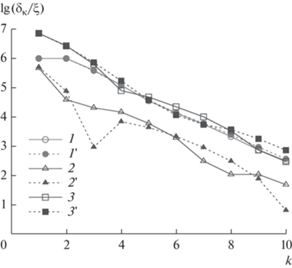
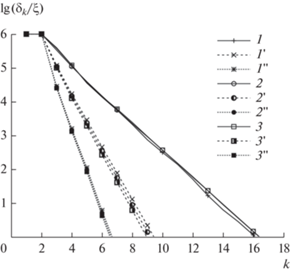
На рис. 4 показаны результаты исследования сходимости итерационных процессов для различных ${{\gamma }}$. В целом сходимость можно оценить как очень хорошую. Видно, что кривые сходимости для различных вариантов ИП ведут себя примерно одинаково. Кривые для варианта 1 не показаны, так как они полностью идентичны кривым варианта 2. Вариант 2 является более предпочтительным, так как уменьшает количество элементов блочной СЛАУ по сравнению с вариантом 1 в четыре раза, а также существенно снижает сложность обращения собственных матриц ${{{\mathbf{z}}}_{{i,i}}}$. Здесь будет уместен вывод о том, что для достижения быстрой сходимости проекционные функции необходимо выбирать с учетом формы собственных функций для отдельных элементов излучающей структуры. Сходимость ухудшается для всех вариантов в области первого резонанса, когда между элементами антенны усиливается связь по полю. Таким образом, ухудшение сходимости является косвенным свидетельством наличия резонансов в излучающей системе. Важным моментом здесь также является асимптотическая линейность зависимости ${\text{lg}}\left( {{{{\delta }} \mathord{\left/ {\vphantom {{{\delta }} \xi }} \right. \kern-0em} \xi }} \right)$ от $k$, которая позволяет прогнозировать число итераций, необходимых для достижения заданной точности.
Рис. 4.
Сходимость решения СЛАУ с различными вариантами итерационных процедур 2–4 (кривые 1–3 соответственно) при ${{\gamma }} = 0.47$ (1–3), $0.41$ (1 '–3 ') и $0.36{\text{\;}}$ (1 "–3 ").
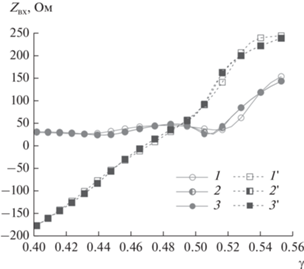
На рис. 5 приведена зависимость сходимости результатов по входному сопротивлению антенны от ${{\gamma }}$ для варианта 4. Наихудшая сходимость наблюдается при ${{\gamma }} \approx 0.5$. На рис. 6 приведены результаты расчета зависимости входного сопротивления от ${{\gamma }}$, полученной в рамках варианта 4 для различного числа итераций. Результаты, полученные для пяти и десяти итераций, практически не имеют визуальных отличий.
Рис. 5.
Оценка сходимости входного сопротивления для варианта 4 при различном числе итераций: $k$ = 1 (1), 3 (2), 6 (3) и 9 (4).
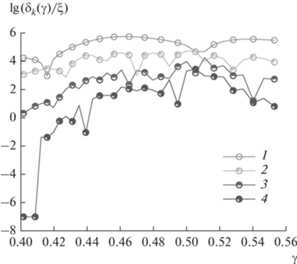
Рис. 6.
Зависимость входного сопротивления ${\text{Re}}{{Z}_{{{\text{вх}}}}}{\text{\;}}$(1–3), ${\text{Im}}{{Z}_{{{\text{вх}}}}}{\text{\;}}$(1 '–3 ') от ${{\gamma }}$ для варианта 4 при различном числе итераций $k = 2$ (1), $5$ (2) и 10 (3).
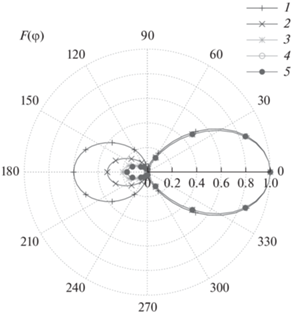
На рис. 7 приведен результат расчета нормированной азимутальной диаграммы направленности (ДН) в рамках варианта 1 для ${{\gamma }} = 0.47$ при различных значениях числа итераций $k$. Наибольшие отличия здесь наблюдаются в области обратного лепестка ДН. Форма главного лепестка ДН при изменении числа итераций практически не меняется. На рис. 8 приведено сравнение сходимости по току, входному сопротивлению и нормированной ДН для различных вариантов при ${{\gamma }} = 0.47$. Можно видеть, что лучшая сходимость в данном случае наблюдается для входного сопротивления, а кривые сходимости по току и нормированной ДН ведут себя примерно одинаково.
ЗАКЛЮЧЕНИЕ
Таким образом, изложены основные принципы электродинамического анализа многоэлементных излучающих структур, имеющих конечные размеры, с помощью итерационных процедур типа Гаусса–Зейделя, реализуемых для блочной матрицы СЛАУ. Приведена подробная реализация предложенного метода для тонкопроволочных многоэлементных излучающих структур, на основе которой построены четыре варианта математической модели, описывающей решение внутренней задачи электродинамики для директорной антенны. Для всех вариантов проведено численное моделирование.
Показано, что предложенный подход может быть очень эффективен в случае отсутствия сильных связей между элементами и в случае наличия ярко выраженных резонансных явлений в излучающей системе. Кроме решения внутренней электродинамической задачи было проведено исследование сходимости для наиболее важных характеристик излучающей структуры: входного сопротивления и диаграммы направленности.
Также представленные результаты подтверждают важность правильного выбора системы проекционных функций для описания распределений токов по элементам структуры. Можно сделать вывод о том, что в случае отсутствия сильных связей между элементами целесообразно выбирать эти системы исходя из их близости к собственным функциям отдельных элементов.
В качестве актуальной задачи здесь можно обозначить расширение границ применения предложенного метода. Так, ранее уже было показано [6], что в случае сильных связей между элементами, а также при наличии ярко выраженных резонансов, сходимость итерационного процесса может резко ухудшаться, а иногда и вообще отсутствовать. Также метод неприменим к структурам с кондуктивными связями в случае построения блочной СЛАУ на основе метода коллокаций. В настоящий момент авторы связывают решение этих проблем с правильным выбором систем проекционных функций.
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Schelkunoff S.A., Friis H.T. Antennas Theory and Practice. N.Y.: Wiley, 1952.
Ильинcкий A.C. // PЭ. 2019. T. 64. № 11. C. 1096. https://doi.org/10.1134/S003384941911010X
Harrington R.F. Field Computation by Moment Method. N.Y.:Macmillan, 1968.
Gallagher R.H. Finite element analysis: fundamentals. New Jersey: Prentice-Hall, 1974.
Ильинский А.С., Перфилов О.Ю., Самохин А.Б. // Матем. моделирование. 1994. Т. 6. № 3. С. 52.
Неганов В.А., Марсаков И.Ю., Табаков Д.П. // Физика волновых процессов и радиотехнические системы. 2013. Т. 16. № 3. С. 7.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория базовых знаний, 2000.
Веселаго В.Г. // Успехи физ. наук. 1967. Т. 92. № 3. С. 517.
Табаков Д.П. // Радиотехника. 2015. № 7. С. 86.
Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. М.: Сов. радио, 1974.
Капитонов В.А., Неганов В.А., Марсаков И.Ю., Табаков Д.П. // Физика волновых процессов и радиотехнические системы. 2012. Т. 15. № 4. С. 6.
Митра Р. Вычислительные методы в электродинамике. М.: Мир, 1977.
Стрижков В.А. // Матем. моделирование. 1989. Т. 1. № 8. С. 127.
Тихонов А.Н., Дмитриев В.И. // Вычислительные методы и программирование: Сб. вычислит. центра Моск. ун-та. 1968. Т. 10. С. 3.
Il’inskii A.S., Berezhnaya I.V. // Computational Mathematics and Modeling. 1990. V. 1. № 3. P. 301.
Табаков Д.П., Майоров А.Г. // Труды учебных заведений связи. 2019. Т. 5. № 4. С. 36. https://elibrary.ru/ item.asp?id=41664174.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника