1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 68, № 10, 2023

Радиотехника и электроника, 2023, T. 68, № 10, стр. 1003-1007

Проектирование сверхпроводниковых интегральных согласующих структур

Ф. В. Хан a, b, *, А. А. Атепалихин a, b, Л. В. Филиппенко a, В. П. Кошелец a

a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

b Московский физико-технический институт (национальный исследовательский университет)
141701 Долгопрудный, Московская область, Институтский пер., 9, Российская Федерация

* E-mail: khanfv@hitech.cplire.ru

Поступила в редакцию 17.05.2023
После доработки 17.05.2023
Принята к публикации 25.05.2023

Полный текст (PDF)

Аннотация

Разработаны и исследованы сверхпроводниковые интегральные структуры, предназначенные для согласования импедансов генератора на основе распределенного джозефсоновского перехода и детектора на основе туннельного перехода сверхпроводник–изолятор–сверхпроводник в субтерагерцовом диапазоне частот. Проведено моделирование структур с помощью метода матриц передачи. Выполнен расчет дизайнов в программе численного трехмерного моделирования. Найдено качественное соответствие результатов, полученных двумя методами. Спроектированы три дизайна с различными топологиями, покрывающие частотный диапазон 250…680 ГГц по уровню –2 дБ.

ВВЕДЕНИЕ

На сегодняшний день устройства сверхпроводниковой электроники получили широкое распространение благодаря набору уникальных характеристик, недостижимых для приборов, работающих на других принципах. Низкая шумовая температура [1, 2], сильная нелинейность, рабочие частоты в терагерцовой (ТГц) области, а также возможность интеграции сверхпроводниковых элементов, – все это обусловливает использование приборов на основе туннельных джозефсоновских переходов типа сверхпроводник–изолятор–сверхпроводник (СИС) в качестве источников ТГц-излучения и приемников с высокой чувствительностью. Подобные устройства применяются в различных областях науки и техники – начиная от исследования состава веществ [3] и заканчивая радиоастрономическими приложениями, такими как система радиотелескопов ALMA (https://almaobservatory.org) и проект Миллиметрон (https://millimetron.ru/).

Сверхпроводниковые устройства обычно имеют топологию планарных интегральных структур, выполненных на одной подложке вместе с антенной и включающих в себя помимо туннельных джозефсоновских контактов микрополосковые линии со сверхпроводящими электродами, по которым распространяется сигнал и с помощью которых осуществляется согласование между элементами схемы.

Наилучшие характеристики генераторов и приемных элементов достигаются, с одной стороны, путем совершенствования технологии изготовления образцов [4]: так современные методы электронной и оптической литографии, ионного травления и магнетронного напыления позволяют получить переходы высокого качества и достичь значений шумовой температуры приемника всего в несколько значений стандартного квантового предела в ТГц-диапазоне частот (Tкв = hf/kБ, где f – рабочая частота). С другой стороны, работоспособность устройств существенным образом зависит от дизайна структуры. Как показано в работе [5], многократные отражения от СИС-детектора, возникающие в результате рассогласования элементов, приводят к повышению шумовой температуры и уменьшению рабочей полосы на промежуточной частоте.

В данной работе проводится расчет, исследование и оптимизация ниобиевых интегральных согласующих структур в частотном диапазоне 250…700 ГГц для обеспечения наилучшего согласования. Структуры были рассчитаны с помощью полуаналитической модели, основанной на методе матриц передачи, и в программе численного трехмерного моделирования Ansys HFSS. Результаты расчетов сравниваются между собой и с экспериментальными данными для ранее изготовленных образцов.

1. ОПИСАНИЕ ИССЛЕДУЕМЫХ ОБРАЗЦОВ

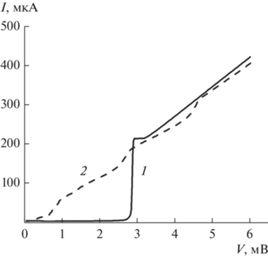
Изображение сверхпроводниковой линии передачи СВЧ-сигнала показано на рис. 1. В качестве генератора ТГц-сигнала используется распределенный джозефсоновский переход (РДП), частота генерации f которого связана с приложенным напряжением V известным соотношением: hf = 2eV [6]. Детектор в схеме выполнен на основе сосредоточенного СИС-перехода, в котором под действием внешнего переменного сигнала резко повышается вероятность туннелирования квазичастиц и, как следствие, возрастает ток при напряжениях ниже щелевого (возникают так называемые квазичастичные ступени) [7]; этот эффект используется в экспериментальных образцах для оценки приходящей мощности. Вольтамперная характеристика (ВАХ) СИС-перехода под действием внешнего сигнала частотой 400 ГГц и автономная ВАХ показаны на рис. 2. Для обеспечения независимого подключения РДП и СИС-детектора по постоянному току и возможности передачи СВЧ-сигнала в широкой полосе частот в линии присутствует разрыв по постоянному току, выполненный в виде щелевой антенны.

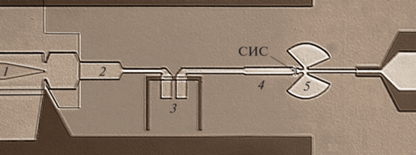
Рис. 1.

Характерное изображение одной из сверхпроводниковых интегральных структур, полученное с помощью оптического микроскопа. Цифрами обозначены: 1 – генератор на РДП, 2, 4 – ступенчатые трансформаторы импеданса, 3 – разрыв по постоянному току в виде щелевой антенны, 5 – радиальный замыкатель, предназначенный для отстройки емкости СИС-детектора. Образцы, спроектированные в данной работе, отличаются геометрическими размерами элементов внутри каждого из блоков 1–5.

Рис. 2.

Экспериментально измеренные ВАХ СИС-перехода, используемого в качестве детектора излучения: 1 – автономная ВАХ; 2 – ВАХ под воздействием переменного внешнего сигнала частотой 400 ГГц.

2. МЕТОДЫ МОДЕЛИРОВАНИЯ СВЕРХПРОВОДНИКОВЫХ ИНТЕГРАЛЬНЫХ СТРУКТУР

При проектировании сверхпроводниковых интегральных согласующих структур были использованы две модели, описанные в работе [8]. Обе модели находятся в хорошем согласии друг с другом и экспериментальными данными для ранее изготовленных образцов (рис. 3).

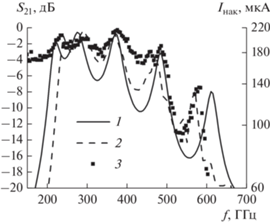
Рис. 3.

Сравнение результатов моделирования с экспериментальными данными для образца, изготовленного ранее: 1 – частотная зависимость коэффициента S21, полученная с помощью полуаналитического расчета, 2 – результаты численного расчета; 3 – экспериментально измеренные значения тока накачки Iнак СИС-детектора в зависимости от частоты РДП.

2.1. Полуаналитический метод

При моделировании первым способом используется метод матриц передачи (или ABCD-матриц) и рассчитывается доля приходящей от генератора к детектору мощности [9, 10]. Каждый элемент структуры представлен в расчете в виде четырехполюсника с соответствующей матрицей. При перемножении матриц в порядке следования элементов от детектора к генератору получается результирующая матрица всей структуры, из которой после преобразований можно вычислить коэффициент S21.

По сравнению с обычной микрополосковой линией в сверхпроводниковой линии возникают дополнительные эффекты: частичное проникновение магнитного поля в электроды линии передачи и обусловленное этим изменение фазовой скорости [11], а также возникновение сильного затухания волн на частотах, близких к щели. Данные эффекты учитываются с помощью рассчитанного отдельно импеданса на квадрат поверхности верхнего и нижнего электродов по формулам из теории Маттиса–Бардина [12].

Разработанная программа позволяет относительно быстро производить расчет структуры при изменении геометрического размера или другого параметра отдельных элементов схемы (например, толщины слоя изоляции), что значительно ускоряет процесс проектирования и оптимизации. В связи с этим разработку новых топологий сверхпроводниковых интегральных схем проводили с помощью данного метода.

2.2. Численный расчет в программе трехмерного моделирования

Дополнительно к расчету с помощью ABCD-матриц было проведено моделирование всех спроектированных структур в программе Ansys HFSS; в HFSS производится решение уравнений Максвелла во всей моделируемой структуре с помощью метода конечных элементов, а после находится коэффициент S21, соответствующий отношению амплитуды сигнала на выходном порте к амплитуде сигнала на входе, что можно интерпретировать (с точностью до возведения в квадрат) как мощность, приходящую от генератора к детектору. Моделирование сверхпроводящих элементов и постановка соответствующих граничных условий обсуждались в работах [13, 14].

Моделирование новых образцов позволило, с одной стороны, верифицировать результаты расчетов, полученные полуаналитическим методом, а с другой – показать, что обе модели приводят к одним и тем же результатам для широкого класса структур.

3. ПРОЕКТИРОВАНИЕ ЛИНИЙ ПЕРЕДАЧИ

Для согласования РДП и СИС-детектора через разрыв по постоянному току используются многоступенчатые трансформаторы импеданса, выполненные в виде отрезков микрополосковых линий длиной λ/4, где λ – длина волны распространяющегося по линии излучения в центре полосы согласования (λ ~ 100…300 мкм).

В простейшем случае одноступенчатого трансформатора наилучшее согласование между генератором с импедансом Zген и нагрузкой с импедансом Zн получается, если характеристический импеданс линии равен Z = (ZвхZн)1/2. Для обеспечения согласования между СИС-детектором, генератором (абсолютные значения порядка нескольких долей ома) и разрывом по постоянному току (десятки ом) в широкой полосе частот требуется использовать трансформаторы, состоящие из нескольких секций; выражения для характеристического импеданса каждой секции можно найти, например, в [9]. При постоянной толщине слоя изолятора и электродов характеристический импеданс взаимно однозначно связан с шириной микрополоска. Значение ширины выбирается на этапе проектирования.

Ранее было установлено, что ширина полосы согласования импеданса СИС-перехода с внешней структурой зависит от параметра χ, который показывает степень шунтирования СИС-перехода [15]:

$\chi = 2\pi f{{R}_{{{\text{ВЧ}}}}}CS,$
где f – частота излучения, RВЧ – высокочастотный импеданс перехода (зависящий от напряжения в рабочей точке), C – емкость перехода на единицу площади (~0.08…0.09 пФ/мкм2), S – площадь перехода.

Характерное значение параметра χ для СИС-перехода с нормальным сопротивлением 13 Ом и площадью 1 мкм2 на частоте 400 ГГц составляет примерно 2.8. Ширина полосы согласования импеданса детектора на СИС-переходе со структурой обратно пропорциональна параметру χ: Δf ~ 1/χ. Это мотивирует уменьшать его значение, расширяя тем самым рабочий диапазон согласования по частоте. Одним из способов достижения малых значений χ является повышение плотности туннельного тока джозефсоновского перехода путем уменьшения толщины барьера d. Поскольку зависимость R(d) имеет экспоненциальный характер, а зависимость C(d) – линейный, то значительное уменьшение сопротивления приведет к незначительному возрастанию емкости, и произведение RВЧC уменьшится.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

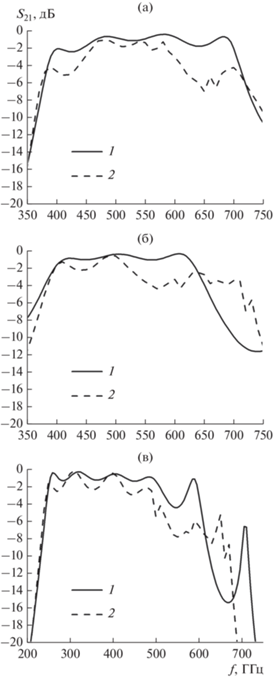
На рис. 4 показаны расчеты трех дизайнов сверхпроводниковых линий передачи, покрывающих диапазон 250…680 ГГц по уровню не хуже ‒2 дБ. Высокочастотная линия с характеристикой, показанной на рис. 4а, выполнена с двухсекционным трансформатором между разрывом по постоянному току и СИС-детектором (см. рис. 1, позиция 4). В другой высокочастотной линии (рис. 4б) используется односекционный трансформатор. Зависимость параметра S21 от частоты, показанная на рис. 4в, соответствует низкочастотной линии. Результаты полуаналитического расчета и численного моделирования находятся в качественном соответствии друг с другом.

Рис. 4.

Зависимости параметра S21 от частоты: 1 – полуаналитический расчет; 2 – численное моделирование; а – дизайн высокочастотной линии с двухсекционным трансформатором между СИС-детектором и разрывом по постоянному току; б – высокочастотная линия с односекционным трансформатором; в – низкочастотная линия.

ЗАКЛЮЧЕНИЕ

Разработанные и апробированные на экспериментальных образцах методы моделирования сверхпроводниковых линий передачи позволили оптимизировать топологию согласующих структур. Спроектированы три дизайна с полосой согласования 360…680, 400…610 и 250…550 ГГц по уровню –2 дБ. Получено качественное соответствие между результатами численного моделирования и полуаналитического расчета.

Авторы заявляют об отсутствии конфликта интересов.

Список литературы

  1. De Lange G., Boersma D., Dercksen J. et al. // Superconductor Sci. Technol. 2010. V. 23. № 4. P. 045016. https://doi.org/10.1088/0953-2048/23/4/045016

  2. Billade B., Pavolotsky A., Belitsky V. // IEEE Trans. 2013. V. TST-3. № 4. P. 416. https://doi.org/10.1109/TTHZ.2013.2255734

  3. Kinev N.V., Rudakov K.I., Filippenko L.V., Koshelets V.P. // Phys. Solid State. 2021. V. 63. P. 1414. https://doi.org/10.1134/S1063783421090171

  4. Fominsky M.Yu., Filippenko L.V., Chekushkin A.M. et al. // Electronic 2021. V. 10. № 23. P. 2944. https://doi.org/10.3390/electronics10232944

  5. Chenu J.Y., Navarrini A., Bortolotti Y. et al. // IEEE Trans. 2016. V. TST-6. № 2. P. 223. https://doi.org/10.1109/TTHZ.2016.2525762

  6. Шмидт В.В. Введение в физику сверхпроводников. М.: МЦНМО, 2000.

  7. Tucker J.R., Feldman M.J. // Rev. Mod. Phys. 1985. V. 57. № 4. P. 1055. https://doi.org/10.1103/RevModPhys.57.1055

  8. Хан Ф.В., Атепалихин А.А., Филиппенко Л.В., Кошелец В.П. // РЭ. 2023. Т. 68. № 9. С. 904.

  9. Фуско В. СВЧ цепи. М.: Радио и связь, 1990.

  10. Frickey D.A. // IEEE Trans. 1994. V. MTT-42. № 2. P. 205. https://doi.org/10.1109/22.275248

  11. Swihart J.C. // J. Appl. Phys. 1961.V. 32. № 3. P. 461. https://doi.org/10.1063/1.1736025

  12. Mattis D.C., Bardeen J. // Phys. Rev. 1958. V. 111. № 2. P. 412. https://doi.org/10.1103/PhysRev.111.412

  13. Kerr A.R., Pan S.K. // Int. J. Infrared Millimeter Waves. 1990. V. 11. № 10. P. 1169. https://doi.org/10.1007/BF01014738

  14. Belitsky V., Risacher C., Pantaleev M., Vassilev V. // Intern. J. Infrared Millimeter Waves. 2006. V. 27. № 1. P. 809. https://doi.org/10.1007/s10762-006-9116-5

  15. Likharev K.K. Dynamics of Josephson Junctions and Circuits. Amsterdam: OPA, 1986.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал