Радиотехника и электроника, 2023, T. 68, № 2, стр. 107-120

1. ПОСТАНОВКА ЗАДАЧИ

Планарные квазиоптические устройства активно используются в антенной технике и технике СВЧ для формирования заданного распределения поля. Среди них мы можем отметить планарное зеркало [1] и линзу [2], предложенные в середине ХХ в.

Интерес к планарным квазиоптическим структурам повысился в последние десятилетия благодаря развитию технологии печатных схем СВЧ. Комбинация этой технологии с оптическими принципами преобразования поля порождает новые типы планарных линз, зеркал, фильтров и т.д. [3]. Можно отметить ряд планарных рефлекторов на основе технологии substrate integrated waveguides (SIW) [4–6]. Офсетное параболическое зеркало этого типа было рассмотрено в [4]. Более сложная двухзеркальная планарная система Грегори представлена в [5]. Перспективным решением является применение многослойных структур, таких как исследованное в работе [6] двухслойное зеркало типа пиллбокс.

В последнее время печатные планарные линзы с метаповерхностями являются объектом интенсивного исследования. Интерес к ним обусловлен возможностью создания эффективных и технологичных планарных линз. Теоретические исследования и практические разработки планарных линз с метаповерхностями, среди которых можно отметить интересные для практических применений линзы Люнебурга, представлены в работах [7–12].

Как отмечено выше, популярность структур с метаповерхностями обусловлена их технологичностью. Однако мы должны также отметить большие успехи в области 3D-печати [13], существенно расширяющие класс интересных для практики объектов. Многие структуры, которые ранее оценивались как неперспективные из-за их низкой технологичности, сейчас находят применение. Следует отметить, что параметры поверхностных волн могут контролироваться не только при помощи метаповерхностей, но также путем изменения толщины и проницаемости диэлектрической пластины, в которой они распространяются. Такие способы управления полностью соответствуют возможностям трехмерной печати. Линзы данного типа имеют большие преимущества в силу существенно меньших тепловых потерь по сравнению с линзами на метаповерхностях.

Среди квазиоптических структур, перспективных для 3D-печати, можно отметить анизотропную линзу Люнебурга [14], которая традиционно используется в качестве базового элемента для построения многолучевых антенн (МА). Благодаря своей симметрии она не имеет оптических аберраций, что потенциально позволяет создавать МА с сектором обзора в 360°, а это весьма важно для систем связи с пространственным разделением сигналов. Однако возможности традиционных градиентных линз (линза Люнебурга – это частный случай градиентной линзы) существенно ограничены эффектом затенения. Кроме линзы, МА содержит систему облучателей, которая препятствуют нормальному излучению в свободное пространство, когда облучатели заполняют сектор углов в 360°. Во многих случаях для устранения эффекта затенения сектор обзора приходится уменьшать до 90°. Таким образом, возможности градиентных линз используются далеко не полностью.

Применение двух одинаковых градиентных линз, соединенных при помощи системы направленных трехдецибельных ответвителей было предложено в работе [15]. Эта структура получила название двухлинзовой МА. В такой антенне линзы изолированы друг от друга, а связь между ними обеспечивается при помощи кольцевой решетки направленных ответвителей. Двухлинзовая МА преобразует цилиндрическую волну, создаваемую облучателем в одной из линз, например в нижней, в волну с плоским фазовым фронтом в верхней линзе, из которой происходит излучение в свободное пространство. По этой причине облучатели МА не мешают излучению и, таким образом, устраняется эффект затенения. Потенциально двухлинзовая МА обеспечивает одновременный обзор пространства в полном секторе азимутальных углов, равном 360°.

Двухслойная линза Люнебурга, предложенная в работе [16], является развитием двухлинзовой МА [15]. Планарные линзы в этой структуре имеют распределенную связь, которая обеспечивает передачу электромагнитной энергии с одного слоя структуры на другой. В результате необходимость в использовании решетки направленных 3дБ-ответвителей отпадает, что значительно упрощает конструкцию МА.

Идея двухслойной линзы была развита в работе [17], в которой рассмотрен синтез двухслойной линзы Моргана. Линза Моргана является обобщением линзы Люнебурга, синтез которой описан в [18]. В работе [17] показано, что с точки зрения удобства практической реализации линза Моргана имеет ряд преимуществ перед линзой Люнебурга, а также показано, что двухслойная линза Моргана обеспечивает точное выполнение фазовых условий синтеза для поля излучения. Условие полной передачи энергии с одного слоя на другой выполняется приближенно. Однако возникающие при этом потери могут быть уменьшены до пренебрежимо малых значений в 0.2 дБ.

В работе [19] путем электродинамического моделирования исследуется двухслойная линза Моргана на основе двух связанных радиально неоднородных планарных диэлектрических волноводов с переменными толщиной и расстоянием между ними. Такая структура может быть изготовлена методами 3D-печати. Ее достоинством является простота организации распределенной связи, которая в случае открытых диэлектрических волноводов не требует использования специальных элементов. Она возникает при простом сближении волноводов. Показано [19], что применение двухслойной конструкции позволяет существенно ослабить эффект затенения линзы облучателями и расширить сектор обзора в азимутальной плоскости до 360°.

Данная работа продолжает исследования, представленные в [17, 19]. В ней рассматривается двухслойная линза Моргана на основе двух связанных плоских волноводов (ПВ). Под ПВ мы понимаем волноведущую структуру, образованную двумя параллельными металлическими экранами. Внутри ПВ расположен радиально неоднородный диэлектрический диск, который выполняет функцию линзы Моргана. Таким образом, в общем случае ПВ имеет частичное заполнение диэлектриком, которое выбирается таким образом, чтобы эффективная проницаемость ПВ ε_e в каждой точке пространства совпадала с синтезированным согласно [18] значением. Распределенная связь между ПВ образуется за счет того, что они имеют общий экран, выполненный в виде двумерной ленточной решетки с малым относительно длины волны периодом.

Строго говоря, толщина диска должна изменяться непрерывно. Однако на практике удобно изготовить такой диск в виде набора тонких диэлектрических слоев. Для этого возможно использовать стандартные диэлектрические подложки, например Rogers Duroid 5880 толщиной 0.125 (здесь и далее все размеры приводятся в миллиметрах). Поэтому в данной работе мы ограничимся анализом структуры с дискретным изменением толщины диска.

Практика показала, что использование стандартных средств электродинамического моделирования для расчета параметров антенны данного типа крайне затруднительно. Проблема состоит в том, что в отличие от работы [19] данная линза имеет не только большой электрический размер, но и состоит из множества электрически малых ячеек – периодов решетки. Каждый из них представляет собой достаточно сложный объект, описание которого с высокой точностью требует использования сеток с ячейками, много меньшими периода решетки. В результате общее число ячеек, необходимых для анализа всей антенны данного типа, в целом многократно превосходит число ячеек, использованных в [19]. Такой рост размерности решаемой задачи создает не только количественные трудности, связанные с ростом времени решения, но и часто делает его невозможным в принципе, так как даже просто создание геометрии объекта требует слишком большого объема оперативной памяти компьютера.

Цель данной работы – создать специализированный метод электродинамического моделирования структур, аналогичных обсуждаемой линзе Моргана.

2. ОБЪЕКТ ИССЛЕДОВАНИЯ

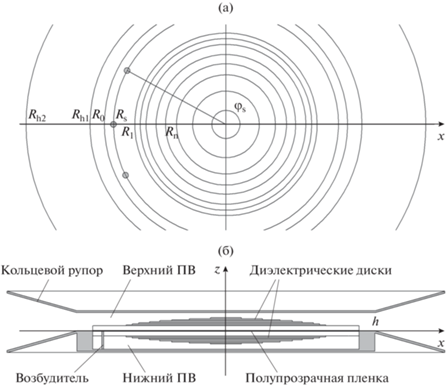
Анализируемая в данной работе структура (рис. 1а, 1б) состоит из двух планарных линз, расположенных симметрично относительно плоскости XOY внутри нижнего и верхнего плоских волноводов (ПВ). Высота ПВ – h. Каждая линза формируется системой соосных диэлектрических дисков, имеющих одинаковую толщину ${{d}_{0}}$. Диски характеризуются радиусами ${{R}_{n}}$, $n = 0,1,...,N$. Внешняя граница линзы имеет радиус ${{R}_{0}}$. Как отмечалось в работе [19], для применения в двухслойной линзе лучше подходит линза Моргана [18], имеющая оболочку с постоянным коэффициентом преломления. Она располагается в области ${{R}_{1}} < r < {{R}_{0}}$, где r – радиальная координата. В области оболочки диск имеет толщину ${{d}_{с}}$, большую ${{d}_{0}}$. Здесь индекс с означает, что величина относится к оболочке линзы. Для простоты считаем, что ${{d}_{с}} = m{{d}_{0}}$, где m – целое число. В этом случае оболочка может быть сформирована в виде набора дисков стандартной толщины радиусом ${{R}_{0}}$.

Верхний и нижний ПВ разделены полупрозрачной пленкой в виде двумерной периодической решетки (рис. 2). Решетка является изотропной в плоскости XOY структурой, так как она имеет одинаковые периоды Р по обоим осям координат и образована металлическими лентами шириной w.

В нижнем ПВ располагаются возбудители линзы в виде металлических штырей с радиусом $\rho $. Положение их центров характеризуется радиусом ${{R}_{s}}$ и угловой координатой ${{\varphi }_{s}}$. Здесь индекс s означает, что величина относится к возбудителям. Возбуждающий штырь является продолжением центрального проводника коаксиальной линии, расположенной с внешней стороны ПВ. Присутствие коаксиальной линии будем описывать с помощью сосредоточенного источника, включенного между штырем и нижним экраном нижнего ПВ.

В нижнем ПВ при $r = {{R}_{0}}$ расположена металлическая стенка, которая делает невозможным излучение во внешнее пространство из нижнего ПВ. Связь с внешним пространством осуществляется в верхнем ПВ через кольцевой рупор. Необходимость в использовании кольцевого рупора обусловлена тем, что двухслойная линза формирует требуемое распределение источников и, следовательно, диаграмму направленности (ДН) только в азимутальной плоскости XOY. При этом ДН в угломестной плоскости без использования дополнительных средств имеет, как правило, недопустимо большую ширину. Для ее сужения используем кольцевой рупор.

3. СИНТЕЗ ДВУХСЛОЙНОЙ ЛИНЗЫ

Метод синтеза двухслойной линзы Моргана описан в работе [18]. Он состоит из двух этапов. На первом определяются обобщенные параметры структуры, к которым относятся коэффициенты преломления или эффективные диэлектрические проницаемости четной и нечетной линз как функции радиальной координаты r. Алгоритм решения данной задачи универсален и не зависит от конструкции двухслойной линзы. Мы не будем подробно его описывать, отметим только, что в качестве исходных данных используются коэффициенты преломления n_{сe, co} четной и нечетной линз и коэффициенты преломления сред, окружающих четную и нечетную линзы n_ve,vo. Индекс v означает, что величина относится к среде, окружающей линзу, индексы е и о – соответственно четные и нечетные линзы, а также четные и нечетные волны, о которых мы скажем ниже.

Напомним, что в соответствии с работой [18] под четной и нечетной линзами понимаются виртуальные структуры, получающиеся при размещении в плоскости симметрии (XOY) соответственно магнитной и электрической стенок. Параметр $\Delta n$ определяет уровень связи между слоями линзы. Его выбирают по результатам численных расчетов, исходя из условия минимизации потерь, обусловленных неполной передачей энергии с нижнего слоя на верхний.

Второй этап синтеза связан с определением геометрических параметров структуры. Для его выполнения необходимо задать конструкцию линзы и построить ее математическую модель. Нетрудно заметить, что линзу можно представить в виде множества частично заполненных диэлектриком ПВ. В пределах каждой области параметры ПВ неизменны. В таком ПВ (рис. 3а) основной является ТМ-волна, не имеющая продольных компонент магнитного поля.

В соответствии с методом симметрии [20] задача для симметричной структуры (см. рис. 3а) сводится к анализу двух парциальных структур (см. рис. 3б), которые получаются из исходной размещением в плоскости симметрии магнитной и электрической стенок. Волны в волноводе с магнитной стенкой принято называть четными, а с электрической стенкой – нечетными [20], что объясняет смысл использованных ранее терминов четная и нечетная линзы.

Основная волна ПВ при ее распространении вдоль оси 0х характеризуется коэффициентом замедления U и полем, имеющим три компоненты E_x, H_y, E_z. Известно [3], что волны в однородном ПВ распространяются, так же как волны в однородной двумерной среде. При этом коэффициент преломления среды n равен коэффициенту замедления волны U. Поскольку функцию n_e,o(r) определяют на первом этапе синтеза, то для выполнения второго этапа необходимо найти параметры структуры, обеспечивающие равенство

где U_e,o – коэффициенты замедления четной и нечетной волн.

Определение коэффициентов замедления связано с решением задачи о собственных волнах парциальных структур (см. рис. 3б). Полное решение, учитывающее периодичность решетки, может быть получено только численно. Известен упрощенный подход, когда решетка описывается как однородная пленка, на ее поверхностях установлены двухсторонние эквивалентные граничные условия (ЭГУ) [3, 21]. Мы будем применять этот метод для моделирования всей линзы в целом. Численное решение было получено с помощью системы электродинамического моделирования HFSS. Оно используется для верификации приближенной модели.

Анализ, основанный на применении граничных условий [21], показывает, что для нечетных волн граничные условия на плоскости z = 0 совпадают с условиями на идеальной электрической стенке. В случае четных волн они имеют более сложную импедансную форму:

где ${{\beta }_{{0,p}}},{{X}_{0}}$ – параметры, зависящие от коэффициента заполнения решетки $q = {w \mathord{\left/ {\vphantom {w P}} \right. \kern-0em} P}$ и относительной диэлектрической проницаемости заполнения ПВ $\varepsilon $. ЭГУ (3) записаны для двумерной задачи, в которой поле не зависит от координаты у. В силу изотропии рассматриваемого ПВ в плоскости XOY достаточно анализировать только волны, распространяющиеся вдоль оси 0х, которым соответствует указанная выше двумерная задача. Выражения для функций ${{\beta }_{{0,p}}}(q,\varepsilon ),{{X}_{0}}(q,\varepsilon )$ могут быть найдены в работах [3, 21].

Вывод дисперсионных уравнений относительно неизвестных U_e,o, а также выражений для полей собственных волн ведется по стандартной схеме частичных областей, на которой не будем останавливаться подробно, а приведем окончательные результаты:

где ${{A}_{{e,o}}} = \frac{{i\varepsilon {{Z}_{{e,o}}}}}{{{{W}_{0}}{{q}_{{e,o}}}}}$, ${{p}_{{e,o}}} = k\sqrt {U_{{e,o}}^{2} - 1} $, ${{q}_{{e,o}}} = k\sqrt {\varepsilon - U_{{e,o}}^{2}} $;

где $a = h - d$.

Здесь соотношения (4) – это искомые дисперсионные уравнения для четных и нечетных волн, выражения для импедансов даются соотношением (5), а поле собственных волн описывается формулой (6), k и W₀ – волновое число и волновое сопротивление свободного пространства. Верхняя строка в (5) соответствует четным волнам, а нижняя нечетным. Выражение (6) описывает поперечную относительно направления распространения компоненту магнитного поля волны. Поперечная компонента электрического поля находится с помощью уравнений Максвелла.

Нетрудно увидеть, что поскольку Z_o = 0, уравнение (4) для нечетных волн совпадает с уравнением частично заполненного ПВ с идеально проводящими экранами [3]. Таким образом, коэффициент замедления U_o не зависит от параметров полупрозрачной пленки, которые влияют только на величину U_е.

Решая уравнения (4) относительно неизвестных U_е, о, находим их искомые зависимости от параметров линзы. Следует отметить, что модель, основанная на ЭГУ (3), в случае четных волн является приближенной. Для ее проверки в системе HFSS в режиме собственных волн было получено численное решение.

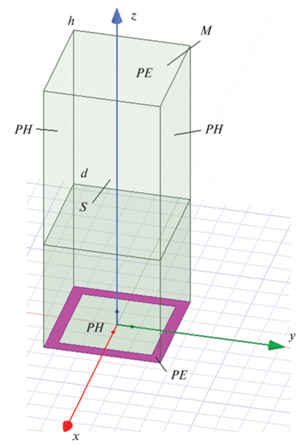
Использованная для этого модель (рис. 4) включает параллелепипед, охватывающий один период решетки. Его высота совпадает с высотой ПВ h. Также внутри параллелепипеда имеется диэлектрическое заполнение, высота которого d. На поверхностях параллелепипеда установлены граничные условия, соответствующие электрической PE и магнитной PH стенкам. На поверхностях при x = ±P/2 установлены периодические граничные условия, которые обозначены как М (master) и S (slave). Поле на поверхности S связано с полем на поверхности М через фазовый сдвиг Δφ = –kU. В режиме собственных волн задается величина Δφ, а также остальные параметры структуры. По этим параметрам программа находит частоту f, на которой поле удовлетворяет периодическим граничным условиям. Выполняя расчет частоты для разных значений коэффициента замедления U, получаем массив данных, используя который методами аппроксимации можно получить функциональные зависимости коэффициента замедления от частоты и других параметров.

На рис. 5 представлена зависимость коэффициента замедления четной волны от коэффициента заполнения решетки, полученная по приближенной модели при h = 2.5, P = 1, ε = 2.2, f = 10 ГГц и d = = 0.5, 1.0, 1.5, 2.0. Точки получены с помощью HFSS. Здесь и далее все размеры приводятся в миллиметрах. Из рис. 5 видна достаточно высокая точность расчетов по приближенной модели, что свидетельствует о возможности ее корректного использования в более сложных ситуациях, в которых численное решение либо невозможно, либо нецелесообразно из-за больших затрат компьютерных ресурсов.

Описанная выше приближенная модель использовалась для синтеза геометрических параметров двухслойной линзы. Как сказано выше, сначала выполнялся первый этап синтеза, на котором задавались параметры Δn и n_сe, co, по которым находились функции n_e,o(r). Отметим, что функции n_e, o(r) связаны простым соотношением:

Поэтому нам достаточно задать только коэффициент преломления оболочки нечетной линзы. Аналогичный параметр для четной линзы задается автоматически при заданной величине Δn.

На втором этапе мы сначала фиксировали высоту ПВ h, частоту f и диэлектрическую проницаемость ε и находили толщину диэлектрического слоя d(r) из уравнения

Как отмечено выше, параметр U_o не зависит от параметров полупрозрачной пленки. Поэтому толщина диэлектрика может быть найдена независимо от параметров решетки.

Далее мы фиксировали найденные значения толщины d(r) и период решетки Р и, решая уравнение

находили функцию q(r).

На заключительном этапе синтеза мы должны учесть дискретное изменение толщины диэлектрического слоя с шагом d₀. На рис. 6 показан пример зависимости синтезированных значений коэффициентов преломления четной и нечетной линз от нормированного радиуса ρ. Радиус нормирован так, что на внешней границе линзы он равен единице. (Кривые) Зависимости на рис. 6 получены при h = 2.5, ε = 2.2, d₀ = 0.125, m = 4 (см. разд. 2), Δn = 0.045, P = 1, f = 10 ГГц. Отметим, что, задавая с помощью параметра m толщину диэлектрика в оболочке линзы, мы автоматически задаем коэффициент преломления n_сo.

На рис. 7 представлена синтезированная зависимость коэффициента заполнения решетки от радиальной координаты, полученная с учетом дискретного изменения толщины линзы. Принимая во внимание, что период решетки Р = 1, нетрудно увидеть, что ширина металлических лент w близка к 0.2, т.е. имеет реализуемое в рамках стандартной технологии печатных схем значение.

4. ЭЛЕКТРОДИНАМИЧЕСКИЙ АНАЛИЗ ЛИНЗЫ

Как отмечено выше, полный анализ двухслойной линзы требует больших затрат вычислительных ресурсов. Первый шаг к более простой постановке задачи состоит в представлении решетки в виде полупрозрачной пленки с ЭГУ на ее поверхностях. Второе приближение связано с особенностями взаимодействия электромагнитных волн на скачках толщины диэлектрического слоя. Нетрудно заметить, что четная и нечетная линзы могут рассматриваться как совокупность однородных ПВ с диэлектрическим заполнением разной толщины. Распространение волн в однородном ПВ описывается известным достаточно простым способом [3]. Основной проблемой оказывается построение модели рассеяния волн однородных ПВ на их стыках.

Следует отметить следующие важные факторы. Для анализируемой структуры характерны достаточно малые скачки толщины (d₀ = 0.125), вызывающие незначительные возмущения падающих на них волн. Границы ПВ имеют кольцевую форму. При этом для них характерны большие электрические радиусы кривизны. По этой причине их можно считать локально плоскими и допустить, что характер взаимодействия волн на изогнутых границах мало отличается от аналогичного взаимодействия на прямолинейных границах.

Нами была рассмотрена тестовая структура (рис. 8), которая позволяет анализировать наклонное падение волн ПВ на прямолинейную границу их раздела. Данная структура представляет собой стык двух ПВ с диэлектрическими заполнения разной толщины d_{1, 2}. На ее боковых поверхностях установлены периодические граничные условия, которые, так же как и на рис. 4, обозначены M и S. Торцевые поверхности – это порты 1 и 2. Верхняя и нижняя поверхности – это идеальные электрические стенки. Поля на границах M и S связаны через фазовый сдвиг φ = –βD, где D – размер тестовой структуры вдоль оси 0y, а β имеет смысл проекции волнового вектора волны ПВ на ось 0у (рис. 9).

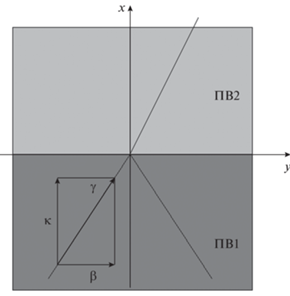
На рис. 9 γ = kU – волновой вектор волны ПВ, а κ, β – его проекции на оси координат. Модуль волнового вектора волны задается параметрами ПВ. Видно, что угол падения φ_i определяется параметром граничных условий φ или постоянной β:

Структуру на рис. 8 анализировали в системе HFSS, которая рассчитывала ее параметры рассеяния. Для нас наибольший интерес представляла зависимость от волнового числа β фазы коэффициента передачи со входа 1 на вход 2 – S₂₁. Необходимо отметить, что синтез линзы проводился без учета фазовых сдвигов на скачках толщины диэлектрического заполнения, которые полагаются равными нулю. Поэтому отличие фазы коэффициента передачи от нуля вносит ошибку в наиболее важное для формирования ДН фазовое распределение поля на выходе линзы. Оценка этой погрешности важна как для определения точности синтеза линзы, так и для рационального построения ее электродинамической модели.

На рис. 10 показана зависимость фазы коэффициента передачи φ₂₁ от параметра β/k. Отметим, что отсчетные плоскости портов совпадают с плоскостью YOZ. Зависимости получены при h = = 2.5, ε = 2.2, f =10 ГГц и трех сочетаний толщин d_1,2: d₁ = 0, d₂ = 0.5; d₁ = 0.5, d₂ = 0.625; d₁ = 1, d₂ = = 1.125. Таким образом, кривая 1 соответствует скачку на внешней границе линзы, а кривые 2, 3 – на внутренних стыках ПВ.

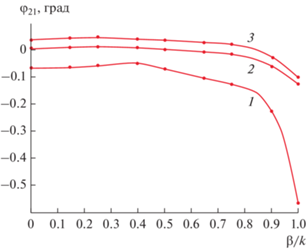
Видно, что фазовые сдвиги на внутренних стыках ПВ крайне незначительны и не превышают 0.1°. Таким образом, даже с учетом того, что волна в линзе может проходить до тридцати стыков, обусловленная ими фазовая ошибка оказывается около 3°, и ею вполне обоснованно можно пренебречь. Фазовый сдвиг на внешней границе линзы превышает сдвиги на внутренних стыках, особенно при больших значениях параметра β/k. Однако эта граница пересекается волной однократно, и она не может существенно изменить распределение поля.

Незначительное отличие фазы φ₂₁ от нуля свидетельствует о том, что реактивные, нераспространяющиеся волны ПВ высших типов слабо возбуждаются на их стыках и для построения адекватной модели достаточно учитывать только распространяющиеся волны. Поскольку высоту ПВ, как правило, выбирают так, что в ПВ с диэлектриком выполняются условия одноволнового режима, то отсюда следует, что мы можем с необходимой точностью описывать поле в ПВ полем основной ТМ-волны.

В отсутствие диэлектрического заполнения эта волна переходит в поперечную Т-волну. Однако даже в случае неоднородного заполнения при достаточно малой высоте ПВ свойства основной ТМ-волны незначительно отличаются от свойств Т-волны. Традиционным подходом, применяющимся для описания структур с Т- и квази-Т-волнами является использование их интегральных характеристик, таких как ток, напряжение, характеристическое сопротивление. Мы воспользуемся этим подходом для анализа стыков ПВ, образующих линзу.

Линза состоит из N областей (см. рис. 1а). Обозначим их номерами n = 1, …, N. При этом оболочке соответствует область с нулевым номером (${{R}_{1}} < r < {{R}_{0}}$, ${{R}_{0}} = 1$). Область с номером N расположена при $0 < r < {{R}_{{N - 1}}}$. Границы областей характеризуются радиусами ${{R}_{n}}$, n = 0, …, N – 1. Оболочку целесообразно разделить на две подобласти 1' и 1'', расположенные при ${{R}_{s}} < r < {{R}_{0}}$ и ${{R}_{1}} < r < {{R}_{s}}$ соответственно.

Нетрудно заметить, что антенна, показанная на рис. 1, имеет симметричную часть, расположенную при r < R₁, и несимметричную часть, включающую оболочку с возбудителем, короткозамыкатель в нижнем ПВ и кольцевой рупор, соединенный с верхним ПВ. На первом этапе мы заменим возбудитель нитью электрического тока $I_{{z0}}^{{}}$:

где

Введем симметричные четный и нечетный токи $I_{z}^{{e,o}}(z)$:

Тогда ток $I_{{z0}}^{{}}$, отличный от нуля при z < 0, представляется суммой четной и нечетной составляющих:

Представление (13) позволяет нам расширить симметричную часть линзы, включив в нее оболочку, и отдельно решать задачи о возбуждении четной и нечетной волн токами $I_{z}^{{e,o}}$. На следующем этапе учтем наличие несимметричных элементов в виде короткозамыкателя, металлического штыря возбудителя и кольцевого рупора.

Запишем поле в регулярном ПВ:

где J_m и Y_m – функции Бесселя и Неймана. Выражение (14) записано в цилиндрической системе координат с центром, совпадающим с центром линзы. Функция ${{e}_{z}}(z)$ определяется выражением (6). Она описывает распределение поля основной волны ПВ с диэлектрическим заполнением. Коэффициенты A_m, B_m в общем случае неизвестны. Они находятся из решения граничной задачи. Интересующие нас компоненты магнитного поля находятся из (14) с использованием соотношений из [22]:

Введем теперь упомянутые ранее токи и напряжения:

Как можно увидеть из соотношений (16), использование тока и напряжения в ПВ позволяет избавиться от зависимости поля от координаты z, т.е. свести задачу к двумерной.

Выражения вида (14) можно записать для всех N областей, формирующих линзу. В области n = N надо положить B_m = 0, чтобы исключить появление поля, стремящегося к бесконечности. В области n = 1 (оболочка) к полю (14) надо добавить первичное поле, которое создает нить тока в бесконечном ПВ. Его можно найти, используя теорию возбуждения направляемых волн [23] и выражение для функции Грина свободного пространства в цилиндрических координатах [22]:

где $H_{m}^{{(2)}}$ – функция Ганкеля второго рода.

Нетрудно заметить, что соотношения (14) и (17) представляют собой разложения в ряд Фурье по азимутальной координате. Ортогональность экспоненциальных функций дает нам возможность анализировать возбуждение линзы азимутальными гармониками независимо друг от друга. Таким образом, двумерная задача сводится к набору одномерных задач, что существенно упрощает общее решение.

Для анализа несимметричной части линзы и всей структуры в целом нам потребуется представление поля в выходном ПВ, т.е. в области ${{R}_{0}} < r < {{R}_{{h1}}}$:

Поскольку в этой области мы имеем незаполненный ПВ, то поле его основной волны не зависит от координаты z, а ее коэффициент замедления U = 1.

При r = r_n, n = 1, …, N – 1 должны выполняться граничные условия непрерывности напряжения и продольного тока J_r:

Отметим, что соотношения вида (19) для четной и для нечетной линз отличаются только индексами е, о, которые на данном этапе не приводим.

Следует сказать, что система уравнений (19) недостаточна для однозначного определения всех коэффициентов разложений, так как число неизвестных превышает число уравнений. Она позволяет только найти соотношение между коэффициентами A₁,B₁ для напряжений в оболочках четной и нечетной линз. Окончательное определение всех неизвестных связано с выполнением граничных условий в нижнем ПВ на короткозамыкателе, в верхнем ПВ на стыке с незаполненным ПВ и в нижнем ПВ на цилиндре возбудителя.

Для удовлетворения указанных граничных условий необходимо перейти от напряжений и токов в четной и нечетной линзах к напряжениям и токам в нижнем и верхнем ПВ. Для этого воспользуемся следующими соотношениями:

Здесь верхний и нижний знаки соответствуют индексам 1,2, которые, в свою очередь, соответствуют нижнему и верхнему ПВ.

На стыке выходного ПВ и оболочки должны выполняться условия равенства напряжений ${{V}_{2}},{{V}^{o}}$ и токов ${{J}_{2}},{{J}^{o}}$, где ${{J}^{o}},{{V}^{o}}$ – ток и напряжение в выходном ПВ. Напряжение на короткозамыкающей стенке при z < 0, r = R₀ должно обращаться в нуль: V₁(R₀) = 0.

Наиболее сложный вид имеют граничные условия, описывающие возбудитель. Они – типичные для структур, содержащих тонкие металлические цилиндры. Электрическое поле, возбуждаемое таким цилиндром, слабо зависит от азимутальной координаты в системе координат с центром на оси цилиндра, поэтому его можно заменить полем нити тока и вычислять в любой точке на поверхности цилиндра, например при r = R_s + ρ. Аналогичный вывод следует для напряжения. Полный ток, текущий по цилиндру, равен i₀ (см. формулу (11)). Потребуем для тока и напряжения выполнения закона Ома:

где V_s – напряжение на цилиндре, R_s – внутреннее сопротивление источника, подключенного к цилиндру, ${\rm E}$ – его ЭДС. Под источником обычно понимается коаксиальная линия, центральным проводником которой является анализируемый металлический цилиндр. В этом случае ЭДС источника равна удвоенной амплитуде падающей по линии передачи волны. Отметим, что напряжение на возбудителе равно сумме напряжений всех азимутальных гармоник.

Перечисленные выше граничные условия вместе с соотношениями (19) образуют полную систему, позволяющую найти все практически важные параметры линзы. Для вычисления ДН воспользуемся упрощенным подходом. Вообще говоря, для ее определения необходимо рассмотреть прохождение волн через кольцевой рупор. Однако, как показывают численные расчеты, кольцевой рупор оказывает влияние преимущественно на ДН в угломестной плоскости. В то же время наиболее интересная ДН в азимутальной плоскости почти полностью совпадает с ДН излучения в выходной ПВ, поэтому для ее вычисления нам достаточно устремить радиус в соотношении (18) к бесконечности и получить искомую ДН $F(\varphi )$:

Входное сопротивление антенны находится как отношение напряжения V_s к току i₀. Через него не составляет труда выразить коэффициент отражения от входа возбудителя.

Выше была изложена схема решения граничной задачи для случая одного возбудителя. Ее можно без труда обобщить для линзы с несколькими источниками питания.

5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Рассмотрим численные результаты для структуры с двумя возбудителями. Анализ численных результатов, полученных с помощью описанной выше модели, начнем с расчета входного сопротивления и настройки возбудителя. На рис. 11 показаны частотные зависимости действительной и мнимой частей входного импеданса, рассчитанные для следующих параметров: ε = 2.2, h = 2.5, d₀ = 0.125, m = 4, R₀ = 100, Δn = 0.045, L = R₀ – R_s = = 3.5, 5, 6.5.

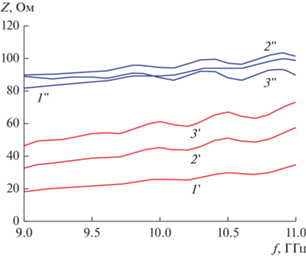
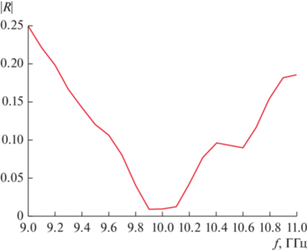
Видно, что действительная часть сопротивления (кривые 1 '–3 ') монотонно уменьшается при приближении возбудителя к короткозамыкателю. При этом мнимая часть близка к 90 Ом и характер ее изменения выражен слабее. Такое поведение входного сопротивления ожидаемо. Наличие индуктивной положительной мнимой части связано с индуктивностью металлического цилиндра. Ее присутствие отмечается во многих возбудителях штыревого типа. Традиционным методом улучшения согласования является последовательное включение сосредоточенного конденсатора, компенсирующего индуктивность. С точки зрения наилучшего согласования оптимальным является выбор параметра L = 5. При этом значении расстояния от штыря до короткозамыкателя действительная часть входного сопротивления близка в центре рабочего диапазона частот 9…11 ГГц к сопротивлению стандартного кабеля в 50 Ом. Частотная зависимость модуля коэффициента отражения для указанного выше значения параметра L и последовательного конденсатора с реактивным сопротивлением на частоте 10 ГГц в 95 Ом показана на рис. 12.

Важным фактором, характеризующим достоверность полученного решения, является погрешность выполнения закона сохранения энергии. Она описывается следующим параметром:

где P_i – мощность волны, падающей на вход антенны. Численные расчеты показывают, что параметр Δ не превышает 10^–14, т.е. закон сохранения энергии выполняется с очень хорошей точностью.

Перейдем к выбору параметра Δn. Для решения данной задачи разместим два возбудителя в точках ${{\varphi }_{{s1,2}}} = 0^\circ ,\,\,\,180^\circ $ и рассчитаем коэффициент передачи Т из одного возбудителя в другой при разных значениях Δn. Оптимальный выбор параметра Δn должен обеспечивать минимум коэффициента передачи.

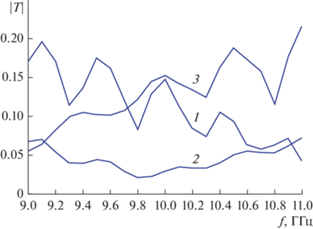
На рис. 13 представлена частотная зависимость модуля коэффициента передачи, рассчитанная при параметрах, приведенных выше и для Δn = 0.035, 0.045, 0.055. Видно, что наилучший результат получается при Δn = 0.045. В этом случае в центре частотного диапазона коэффициент передачи близок к –30 дБ, это свидетельствует о том, что большая часть энергии, поступившей в возбудитель, расположенный в нижнем ПВ, перешла за счет связи через полупрозрачную решетку в верхний ПВ и излучилась из него.

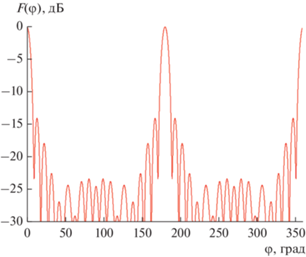
На рис. 14а–14в представлены ДН в азимутальной плоскости, рассчитанные при возбуждении линзы одиночным возбудителем на частотах f = 9, 10, 11 ГГц. Обращает на себя внимание довольно высокий уровень первых боковых лепестков и заднего излучения. Боковые лепестки колеблются в диапазоне –(12…16) дБ, что характерно для апертурной антенны с распределением в раскрыве, близком к равномерному. Отсюда можно сделать вывод, что одиночный возбудитель не обеспечивает оптимальное облучение линзы с необходимым уменьшением поля на ее границах. Поэтому интересно рассмотреть возможность использования сдвоенного возбудителя, состоящего из двух синфазных одиночных возбудителей. Такой облучатель должен иметь суженную ДН, что в результате должно уменьшить боковое и заднее излучение линзы.

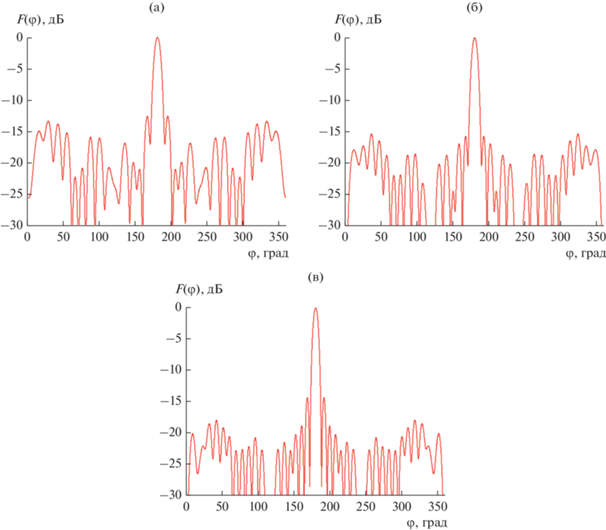
На рис. 15а–15в показаны ДН, полученные для сдвоенного возбудителя (${{\varphi }_{{s1,2}}} = \pm 5^\circ $) на частотах f = 9, 10, 11 ГГц. Они характеризуются расширенным главным лепестком и существенно сниженным уровнем бокового и заднего излучения. Боковые лепестки находятся на уровне, близком к –20 дБ, характерному для амплитудного распределения с нулями на краях апертуры. Таким образом, использование сдвоенного возбудителя дало ожидаемый эффект коррекции формы ДН линзы.

Приведем также рассчитанную ДН линзы с двумя одиночными возбудителями, расположенными при ${{\varphi }_{{s1,2}}} = 0^\circ ,\,\,180^\circ $ (рис. 16). На их входы падают волны одинаковой амплитуды. Видно, что ДН имеет два главных лепестка, соответствующих двум независимым каналам. Лепестки ориентированы в противоположных направлениях и слабо искажены присутствием второго возбудителя.

ЗАКЛЮЧЕНИЕ

Приведенные выше результаты позволяют сделать следующие выводы. Предложена приближенная электродинамическая модель двухслойной градиентной линзы, позволяющая оперативно оценивать основные параметры устройства. Ряд приближений, положенных в основу модели проверены путем численных расчетов в системе HFSS. Количественные результаты, получаемые предложенным методом, отвечают известным физическим представлениям и закону сохранения энергии.

Полученные характеристики двухслойной линзы показывают, что она может служить основой для построения многолучевой антенны с улучшенными показателями качества, в частности с расширенным сектором обзора пространства в азимутальной плоскости.

Авторы заявляют об отсутствии конфликта интересов.