Радиотехника и электроника, 2023, T. 68, № 2, стр. 157-164

ВВЕДЕНИЕ

Железоиттриевый феррит со структурой граната обладает рекордными как магнитными, так и упругими свойствами [1]. Ширина линии ферромагнитного резонанса (ФМР) для этого материла составляет менее 1 Э, что на один-два порядка меньше ширины линии для других ферритов. Упругая добротность почти на порядок превышает упругую добротность кварца. Столь высокие эксплуатационные характеристики железоиттриевого граната (ЖИГ) являются основой для создания многочисленных устройств аналоговой обработки информации в СВЧ-диапазоне [2, 3]. В числе таких устройств можно упомянуть фильтры, фазовращатели, линии задержки, невзаимные вентили, циркуляторы и др. [4, 5]. Новые перспективы обеспечивает применение в устройствах тонких эпитаксиальных пленок [6, 7]. Широкие дополнительные возможности открывает комплексное использование магнитоупругих свойств ЖИГ [8]. Особо следует отметить широко развернувшиеся в последнее время работы по активации магнитных свойств магнитоупругих сред упругими импульсами, возбуждаемыми интенсивным воздействием света от фемтосекундного лазера [9–11].

Используемые в перечисленных применениях пленки ЖИГ (иногда с замещением) формируются, как правило, методом жидкофазной эпитаксии на подложках из гадолиний-галлиевого граната. Упругие свойства таких подложек близки к свойствам ЖИГ, т.е. имеют практически столь же низкие упругие потери.

В ряде работ [12–15] выявлено заметное влияние упругих свойств подложки на формирование линии ФМР собственно ЖИГ. Показано, что в определенных условиях локального возбуждения пленки СВЧ магнитным полем на линию ФМР накладывается сетка линий упругих резонансов подложки. Такие линии являются стоячими модами упругих колебаний, возбуждаемых по толщине подложки, причем число возбуждаемых мод может достигать пятисот и более. Так, в работе [14, рис. 2] на линию ФМР, имеющую частоту около 200 МГц, наложена сетка линий упругих резонансов с периодом 3.8 МГц. В работе [13, рис. 5 ] на линию ФМР, соответствующую частоте 1860 МГц, наложена сетка упругих мод с шагом 3.8 МГц. В работе [12, рис. 2] на частоту ФМР около 5550 МГц наложена сетка с шагом 3.5 МГц.

В более ранних работах [16–18] сообщалось о наблюдении осцилляций на амплитудно-частотных характеристиках прошедших через структуру “пленка–подложка” объемных магнитостатических волн. В качестве причины осцилляций было предложено взаимодействие магнитостатических волн с упругими волнами, распространяющимися вдоль плоскости подложки. В более современной работе [19] подобные осцилляции наблюдались на частотных зависимостях коэффициента передачи поверхностных магнитостатических волн в структуре “пленка–подложка”, возбуждаемой копланарными преобразователями.

Во всех перечисленных работах констатировалось соответствие частотного интервала между осцилляциями резонансным частотам упругих колебаний подложки, однако теоретическое рассмотрение отсутствовало. Для интерпретации наблюдаемых явлений в работах [12, 14, 15] была использована модель связанных осцилляторов – одного магнитного и множества упругих, соответствующих модам стоячих упругих колебаний по толщине подложки (например, формула (6) в работе [15]). Подробный вывод предложенной системы уравнений, в том числе и в приведенной в [12] ссылке на работу [20], отсутствовал. Рассмотрение в такой модели нелинейного характера колебаний намагниченности (например, отмеченного в эксперименте, описанном в работе [13]), по-видимому, может вызвать некоторые трудности, поэтому в данной работе предложена модель, основанная на заведомо нелинейной прецессии намагниченности, связанной с поперечными компонентами упругих колебаний по толщине подложки.

1. ГЕОМЕТРИЯ ЗАДАЧИ

Будем рассматривать геометрию, сходную с принятой в работе [21] для решения задачи о возбуждении гиперзвуковых упругих колебаний в нормально намагниченной ферритовой пластине. Отмеченные далее некоторые отличия вызваны конкретной спецификой решаемой задачи.

Принятая здесь геометрия задачи показана на рис. 1. В основе геометрии лежит пластина, состоящая из пленки на подложке, общей толщиной $d$, из которой на пленку приходится толщина ${{d}_{0}}$, на подложку – ${{d}_{s}}$. Пленка обладает магнитными, упругими и магнитоупругими свойствами, подложка является немагнитной, однако упругие и кристаллографические свойства пленки и подложки совпадают. Материал пластины в целом имеет кубическую кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью пластины. Внешнее постоянное магнитное поле ${{\vec {H}}_{0}}$ приложено перпендикулярно плоскости пластины, в плоскости которой действует переменное магнитное поле $\vec {h}$.

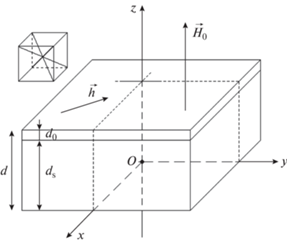
Задача решается в декартовой системе координат $Oxyz$, плоскость Oxy которой совпадает с плоскостью пластины, а оси Ox, Oy и Oz параллельны ребрам куба кристаллографической ячейки. Центр системы координат O находится на нижней по рисунку поверхности пластины, так что ее верхняя поверхность соответствует координате $z = d$.

2. ПОСТАНОВКА ЗАДАЧИ

Приведем общую постановку задачи. Уравнения колебаний для намагниченности и упругого смещения подобны полученным в работе [21]. Приведем их здесь без подробного вывода.

Уравнения для намагниченности:

Здесь ${{m}_{{x,\,y,z}}}$ – динамические компоненты намагниченности, нормированные на намагниченность насыщения материала ${{M}_{0}}$, $\alpha $ – параметр затухания Гильберта, ${{H}_{{ex,\,ey,\,ez}}}$ – эффективные поля, определяемые выражениями

где ${{u}_{{x,\,y,\,z}}}$ – компоненты упругого смещения, ${{B}_{2}}$ – константа магнитоупругого взаимодействия, а поле ${{h}_{{x,\,y}}}$ имеет гармоническую зависимость от времени следующего вида:

где ${{h}_{{0x,\,0y}}}$ – постоянные.

Уравнения для компонент упругого смещения имеют вид

где $\beta $ – параметр упругого затухания, ${{{\text{c}}}_{{44}}}$ – компонента модуля упругости, $\rho $ – плотность материала пластины.

Граничные условия возьмем отличными от принятых в работе [21]. Там рассматривались условия, симметричные относительно центральной плоскости пластины, что диктовалось требованием максимизации связи намагниченности с упругим смещением для повышения мощности возбуждаемого гиперзвука. По той же причине толщина пластины выбиралась из условия совпадения частоты упругого резонанса пластины с частотой ее ФМР. Такие требования заставили в работе [21] ограничить возбуждение только первой упругой моды по толщине пластины, что дало следующий результат – значительное повышение мощности возбуждаемого гиперзвука в нелинейном режиме. Благодаря такому выбору толщины пластины последующие ее резонансные моды выходили далеко за частоту ФМР и не оказывали заметного влияния на колебания намагниченности.

Однако в работах [12–15] наблюдались многократные “расщепления” линии ФМР, обусловленные наложением на эту линию сетки упругих мод высоких порядков, вплоть до пятисотого. При этом упругие колебания возбуждались не в ферритовой пленке, как таковой, а в ее подложке, не обладавшей магнитными свойствами. То есть здесь имело место резко несимметричное возбуждение упругих колебаний, происходящее только на одной поверхности подложки, тогда как вторая оставалась свободной. Благодаря единству упругих свойств пленки и подложки, можно полагать, что упругие колебания по-прежнему присутствуют по всей толщине пластины, но связаны они с прецессией намагниченности только на одной ее поверхности, например с той, координата z которой равна $d$. Таким образом, граничные условия принимают вид

При этом толщину пластины $d$ будем считать значительно превышающей толщину, резонанс на которой соответствовал бы частоте ферромагнитного резонанса.

3. ВОЗБУЖДЕНИЕ УПРУГИХ КОЛЕБАНИЙ

Как показано выше, упругие колебания возбуждаются в пластине за счет того, что на одной из ее поверхностей действует упругое смещение, определяемое состоянием намагниченности на этой поверхности. Предположим, что это состояние, т.е. компоненты ${{m}_{{x,\,y,\,z}}}$ вблизи поверхности заданы, и рассмотрим возбуждаемые при этом упругие колебания.

Задача для упругости состоит из уравнений (9), (10) и граничных условий (11)–(14). Благодаря единообразию уравнений и граничных условий для компонент ${{u}_{x}}$ и ${{u}_{y}}$, переходящих друг в друга при замене $x$ на $y$ и обратно, ограничимся рассмотрением задачи только для ${{u}_{x}}$.

Введем обозначения для скорости упругой волны

Положим далее, что компонента намагниченности ${{m}_{x}}$ имеет зависимость от времени вида $\exp \left( {i\omega t} \right)$, т.е.

а компонента ${{m}_{z}}$ во времени остается постоянной, что имеет место при круговой прецессии намагниченности:

При этом граничное условие (11) принимает вид

где величины $m_{x}^{{\left( 0 \right)}}$ и $m_{z}^{{\left( 0 \right)}}$ на данном этапе рассмотрения положим постоянными.

Введем обозначение

С этим обозначением задача (9), (11), (13) принимает вид уравнения

со следующими граничными условиями:

Предположим, что в установившемся режиме упругая волна, определяемая уравнением (20), имеет чисто гармонический характер с амплитудой, не зависящей от времени. В такой постановке (20)–(22) можно рассматривать как “задачу о распространении периодического граничного режима” [22, с. 107]. То есть режим, задаваемый условием (21) при координате $z = d$, имеющий зависимость от времени вида $\exp \,\left( {i\omega t} \right)$, распространяется далее по всей пластине до ее свободной поверхности при $z\,\, = \,\,0$.

Будем искать решение в виде

где частоту $\omega $ полагаем заданной возбуждающим полем $h$.

Подставляя (23) в (20), сокращая на $\exp \,\left( {i\omega t} \right)$ и выделяя зависящую от координаты часть $Z\left( z \right)$, получаем граничную задачу для $Z$ в виде уравнения

и граничных условий

где волновое число $k$ определяется формулой

Представляя $k$ в виде суммы действительной и мнимой частей

получае${\text{м}}$

Возвращаясь к задаче (24)–(26), будем искать решение уравнения (24) в виде

Подставляя (31) в (24) и учитывая граничные условия (25), (26), где $A$ определяется выражением (19), получаем

Учитывая (23), получаем компоненту смещения ${{u}_{x}}$ в виде

При этом в соответствии с (16) и (17) можно записать

Компоненту смещения ${{u}_{y}}$ получаем заменой индекса $x$ на $y$:

В этих выражениях k определяется формулами (27)–(30).

4. ЭФФЕКТИВНЫЕ ПОЛЯ

Для подстановки в эффективные поля (4)–(6), входящие в уравнения движения для намагниченности (1)–(3), требуются не упругие смещения ${{u}_{{x,\,y}}}$, а их производные ${{\partial {{u}_{{x,\,y}}}} \mathord{\left/ {\vphantom {{\partial {{u}_{{x,\,y}}}} {\partial z}}} \right. \kern-0em} {\partial z}}$. Дифференцируя (34), (35) по $z$, получаем

Подставляя (36), (37) в (4)–(6), получаем эффективные поля в виде

Введем вспомогательный параметр:

С этим параметром поля (38)–(40) принимают вид

Параметр $P\,\left( {k,z,d} \right)$ содержит волновое число k, имеющее комплексный характер (28), действительная и мнимая составляющие которого определяются выражениями (29), (30), содержащими частоту $\omega $, скорость упругой волны v и параметр затухания $\beta $. Подставим (28) в (41) и воспользуемся формулами тригонометрических функций от комплексного аргумента [23, с. 76, ф-лы 408.16, 408.17]:

В результате получаем

Введем вспомогательные обозначения:

С этими обозначениями выражения (47), (48) принимают вид

Подставляя (53), (54) в (41) и выделяя действительную и мнимую части, получаем

Введем обозначения:

С этими обозначениями (55) принимает вид

Модуль параметра $P$ принимает вид

Здесь параметры g и h через посредство (56), (57), (49)–(52), (29), (30) содержат частоту $\omega $, скорость упругой волны $v$ и параметр затухания $\beta $. Получаемые при этом выражения являются довольно громоздкими, поэтому при машинном счете авторы рекомендуют их вычислять последовательно в обратном порядке, т.е. сначала (29), (30), затем (49)–(52) и после (56), (57).

5. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ

Получаемая полная система уравнений для трех компонент намагниченности ${{m}_{x}}$, ${{m}_{y}}$, ${{m}_{z}}$ и двух компонент упругого смещения ${{u}_{x}}$ и ${{u}_{y}}$ при заданном значении $z$ имеет вид:

три уравнения для намагниченности (1)–(3):

два уравнения для упругого смещения (36), (37):

При этом входящие в уравнения для намагниченности (60)–(62) эффективные поля имеют вид (38)–(40):

В рамках настоящей работы система (60)–(64) с учетом (65)–(67) решалась численно методом Рунге–Кутты четвертого порядка [24, с. 702, вариант “с”]. В результате решения получалось развитие колебаний во времени. Условием решения аналитической части задачи было принято предположение о стационарности режима, поэтому амплитуда колебаний регистрировалась только по прошествии времени, значительно превышающего время релаксации магнитной и упругой систем. Упругие колебания регистрировались при заданном значении координаты z по толщине пластины. Осуществлялась пошаговая развертка по частоте, так что в результате получали амплитудно-частотные характеристики магнитных и упругих колебаний в установившемся режиме. Результаты расчетов представлены далее.

6. АМПЛИТУДНО-ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

Предметом настоящего рассмотрения являются амплитудно-частотные характеристики магнитных колебаний, представляющие собой резонансные кривые ФМР по частоте. Для расчета использовались типичные параметры пленки ЖИГ на подложке из гадолиний-галлиевого граната, подобные принятым в работе [21]: намагниченность насыщения $4\,\pi \,{{M}_{0}}$ = 1750 Гс, константа упругости ${{c}_{{44}}} = 7.64 \times {{10}^{{11}}}$ эрг см^–3, константа магнитоупругого взаимодействия ${{B}_{2}} = 6.96 \times {{10}^{6}}$ эрг см^–3, плотность $\rho $ = 5.17 г см^–3. При этих параметрах скорость упругой волны равна

Постоянное поле ${{H}_{0}}$ задавалось равным 2750 Э, что при $\gamma $ = 2.8 МГц Э^–1 обеспечивало частоту ФМР равной 2800 МГц. Подобно [21] для удобства развертки по времени параметры магнитного и упругого затухания были выбраны несколько большими (примерно на порядок) реальных: $\alpha $ = = 0.02, $\beta $= ${{10}^{8}}$ с^–1. При принятых значениях параметров действительная часть волнового числа $k$ (28) превышала мнимую более чем на два порядка, что позволило для параметра $P$ (58) ограничиться действительной частью (56), т.е. значительно упростить вычисления.

Толщина пленки ЖИГ принималась равной ${{d}_{0}}$ = 0.6865 мкм, что при заданных выше параметрах материала соответствовало частоте упругого резонанса 2800 МГц, т.е. равнялась частоте ФМР. Толщина пластины, т.е. структуры в целом, была в 200 раз больше толщины пленки, т.е. $d$ = 137.3 мкм. Координата $z$, на уровне которой регистрировалось упругое смещение, равнялась 0.6865 мкм, т.е. находилась вблизи поверхности структуры, противоположной местонахождению пленки.

Отметим, что в реальных экспериментах, например описанных в работах [12–19], толщина подложки превышала толщину пленки на два-три порядка и более, так что частота упругого резонанса подложки составляла единицы МГц. Именно такая частота соответствовала осцилляциям, наблюдаемым на амплитудно-частотных характеристиках.

На рис. 2 представлены резонансные кривые ФМР по частоте при низком уровне возбуждения ${{h}_{0}}$ = 0.01 Э, так что колебания намагниченности являются чисто линейными. Кривые построены при двух различных значениях константы магнитоупругого взаимодействия: В₂ = 0 и 6.96 × 10⁶ эрг см^–3.

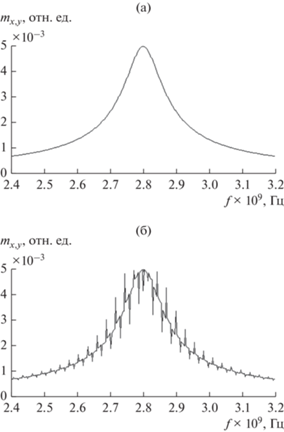
На рис. 2а магнитоупругая связь отсутствует, так что кривая имеет чистый вид, соответствующий линейному ферромагнитному резонансу. Кривая совершенно чистая, какие-либо осцилляции полностью отсутствуют.

Однако из рис. 2б, где магнитоупругая связь имеет место, видно, что в этом случае на резонансной кривой наблюдаются сильные осцилляции.

Толщина пластины выбрана в 200 раз больше толщины пленки, т.е. 137.3 мкм. Учитывая, что при резонансе первой моды на толщине пластины в целом укладывается половина длины упругой волны, получаем частоту этой моды 14 МГц. Полагая, что резонансы последующих мод соответствуют укладыванию на полной толщине нечетного числа полуволн, получаем, что расстояние по частоте между модами должно составлять 28 МГц.

Из рис. 2б видно, что расстояние по частоте между пиками осцилляций как раз соответствует 28 МГц. Такое совпадение свидетельствует в пользу предложенной модели.

На рис. 3 показаны резонансные кривые ферромагнитного резонанса по частоте при высоком уровне возбуждения ${{h}_{0}}$ = 10 Э, так что колебания намагниченности являются сильно нелинейными. Кривые построены при тех же значениях параметров, что на рис. 2.

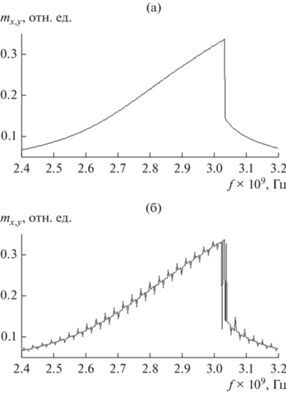
Представленная на рис. 3а резонансная кривая имеет вид “скошенного треугольника”, типичный для нелинейного резонанса при расстроечном механизме ограничения амплитуды [13, 25]. Магнитоупругое взаимодействие отсутствует, так что кривая совершенно гладкая, осцилляции отсутствуют.

На рис. 3б представлена та же кривая при наличии магнитоупругого взаимодействия. Видно сильное проявление осцилляций, таких же, как на рис. 2б. Расстояние по частоте между пиками осцилляций равно тем же 28 МГц.

Таким образом, можно полагать, что предложенная модель применима для описания нелинейных колебаний намагниченности также в достаточной степени.

ЗАКЛЮЧЕНИЕ

В работе рассмотрено влияние упругих резонансов подложки на ферромагнитный резонанс в пленках ЖИГ. В условиях малости толщины пленки по сравнению с толщиной подложки предложена модель, рассматривающая возбуждение упругих колебаний как задачу о распространении периодического граничного режима. Получена система связанных уравнений для намагниченности и упругого смещения с граничными условиями, отражающими возбуждение упругих колебаний на той поверхности подложки, где находится пленка. Получены эффективные поля, отражающие воздействие упругой системы на магнитную, что позволило свести задачу к системе из пяти уравнений первого порядка – для трех компонент намагниченности и двух компонент упругого смещения. Решение полученной системы методом Рунге–Кутты с последующим выделением стационарной амплитуды позволило получить амплитудно-частотные характеристики ферромагнитного резонанса. Выявлен сильно осциллирующий характер резонансной характеристики, обусловленный наложением на основную резонансную кривую эквидистантной сетки резонансных линий, соответствующих модам упругих резонансов высоких порядков по толщине подложки. Показано, что осциллирующий характер резонансной кривой имеет место как в линейном, так и в сильно нелинейном режиме, причем эквидистантный характер осцилляций сохраняется.