Сенсорные системы, 2019, T. 33, № 1, стр. 60-64

ВВЕДЕНИЕ

Проективная геометрия возникла в XVII веке благодаря творчеству художников и архитекторов, стремившихся верно изобразить окружающий мир на их картинах и чертежах. Позже трудами Дезарга, Понселе и многих других ученых она превратилась в самостоятельную область математики, которая в наше время нашла практическое применение в техническом зрении и компьютерной графике.

Задачи представления объемного объекта в виде дискретного изображения, сопоставления нескольких кадров, полученных в результате съемки одного и того же объекта с разных ракурсов, или исправления искажений цифровых фотографий крайне важны для медицины (рентгенографии и компьютерной томографии (Cabral et al., 1994)), зрительных систем в автопилотах (Xu et al., 2000), компьютерной графики (McMillan, 1997), дополненной реальности (Tuceryan et al., 2002) и других областей. В решении всех этих задач важную роль играет проективное преобразование изображений. Поскольку многие из этих задач представляют не только теоретический, но и практический интерес, на время работы алгоритмов, а значит, и на их вычислительную сложность, могут накладываться значительные ограничения. В частности, многие системы распознавания, такие как в работах (Skoryukina et al., 2015, 2017) или алгоритмы в работах (Fedorenko, Usilin, 2017; Kuznetsova et al., 2015) должны находиться в режиме реального времени. Поэтому вычислительно эффективные алгоритмы проективного преобразования, работающие с заданной точностью, представляют немалый интерес. Например, в работе (Musin, 1991) описана реализация, действующая быстро за счет уменьшения числа операций умножения и деления, составляющих основную вычислительную сложность алгоритма.

В этой работе рассматривается определенное геометрическое преобразование, так называемое проективное – переводящее прямые в прямые. Преобразование, обратное к проективному, так же является проективным, что легко позволяет использовать обратный метод (Hartshorne, 1967).

В работе предложено решение, которое в ряде случаев ускоряет работу алгоритма за счет уменьшения числа пикселей, требующих специальной обработки. Для пикселей, прообразы которых целиком лежат внутри исходного изображения, не нужно проверять граничные условия. Для пикселей, прообразы которых целиком лежат вне исходного изображения, при определенных граничных условиях можно вообще никаких вычислений не производить. Кроме того, большая часть современных процессоров поддерживают SIMD (Single Instruction Multiple Data) принцип вычислений, который позволяет выполнять одну и ту же операцию над несколькими элементами данных одновременно, реализуя таким образом параллелизм на уровне данных. Предложенный метод может эффективно задействовать SIMD-инструкции, что позволяет дополнительно повысить вычислительную эффективность проективного преобразования.

АЛГОРИТМ ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ

Обратный метод. Задача проективного преобразования изображения является частным случаем задачи повторной дискретизации – преобразования дискретного изображения из одной системы координат в другую (Wolberg, 1994). Существуют два основных метода решения этой задачи: прямой и обратный. В первом случае для каждого пикселя исходного изображения выполняется поиск соответствующего ему положения на конечном изображении. В случае обратного преобразования каждый пиксель конечного изображения сопоставляется с пикселями исходного изображения с использованием обратного преобразования. В отличие от прямого, обратный метод гарантирует, что будет вычислено значение для каждого пикселя конечного изображения и поэтому чаще используется на практике.

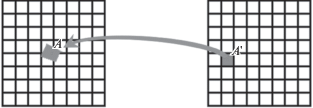
Рассмотрим обратный метод решения задачи повторной дискретизации изображения. В этом методе для центра каждого пикселя конечного изображения $A{\text{'}}$ с применением обратного преобразования находится соответствующая ему точка на исходном изображении $A$, и ее значение берется в качестве значения пикселя конечного изображения. Поскольку точка $A$ может не совпадать с центром какого-либо пикселя исходного изображения, значение в ней или восстанавливается по ближайшему пикселю, или интерполируется по близлежащим пикселям (линейным, квадратичным сплайновым или другим методом). Этот алгоритм и будет применяться в нашем решении (рис. 1).

Этот метод не совсем точен, поскольку используя его, мы приближаем значение пикселя конечного изображения значением в некоторой конкретной точке, в то время как в область пикселя конечного изображения могут отобразиться несколько пикселей исходного. Эту неточность можно снизить, вычисляя значение каждого пикселя конечного изображения по нескольким точкам внутри него (Wolberg, 1994).

Свойства проективного преобразования. Как было отмечено выше, проективное преобразование – это преобразование плоскости, переводящее прямые в прямые. В матричном виде оно задается как

где $T = \left( {{{t}_{{ij}}}} \right),$ $i \in \left\{ {1,2,3} \right\},$ $j \in \left\{ {1,2,3} \right\}$ – матрица проективного преобразования, $\bar {x}$ и $\bar {u}$ – однородные координаты в плоскости исходного и конечного изображений соответственно. В координатном виде оно задается следующей формулой: где $\left( {x,y} \right)$ – координаты точки в плоскости исходного изображения, $\left( {u,v} \right)$ – координаты ее образа в плоскости конечного изображения, при этом $\det \left( T \right) \ne 0$. В обратном методе используется обратное проективное преобразование. Обозначим его матрицу как $P = {{T}^{{ - 1}}}$, тогда выполняется равенство

В плоскости исходного изображения лежит прямая

образом которой является бесконечно удаленная прямая. Если она не пересекает выпуклый четырехугольник, то этот четырехугольник переходит в выпуклый четырехугольник в плоскости конечного изображения.

Получается, что если прямая (4) не пересекает исходное изображение, то его образом будет выпуклый четырехугольник в плоскости конечного изображения (рис. 2).

Граничные условия проективного преобразования. Как видно из рис. 2, некоторым пикселям на конечном изображении могут соответствовать области, выходящие за границы исходного. Значения таких пикселей определяются граничными условиями задачи. Например, это может быть циклическое или симметричное повторение пикселей изображения за пределами его границ. Также может использоваться постоянное значение, т.е. считаться, что за пределами исходного изображения бесконечно много пикселей с одним постоянным значением (черный в примере на рис. 3) или значение ближайшего определенного пикселя изображения.

Эти условия достаточно сильно различаются между собой и могут потребовать дополнительных вычислений (например, в случае симметричного или цикличного повторения значений), поэтому их проверка для каждого конкретного пикселя может быть достаточно вычислительно затратной.

Базовый алгоритм. В соответствии с предыдущими пунктами получаем базовый алгоритм проективного преобразования изображения.

Для каждого пикселя конечного изображения:

– находим координаты прообраза центра этого пикселя;

– находим значение в точке прообраза при помощи интерполяции и с учетом граничных условий.

Вычислительная оптимизация алгоритма проективного преобразования. Рассмотрим частный случай, при котором в плоскости исходного изображения прямая (4) не пересекает прямоугольник:

где M – длина изображения, N – его высота, s – отступ, и координатные оси направлены вдоль сторон исходного изображения. Величина отступа определяется используемым методом интерполяции и в наиболее простых случаях (линейный метод или интерполяция по ближайшему пикселю) равна одному пикселю.

Рассмотрим еще один прямоугольник в плоскости исходного изображения

Поскольку прямая (4) не пересекает (5), образами (5) и (6) являются выпуклые четырехугольники (5') и (6'),

при этом (6') лежит внутри (5') в силу непрерывности преобразования (2) внутри прямоугольника (5).

Тогда все пиксели конечного изображения можно разделить на три класса:

– целиком лежит вне (5'). Если граничное условие постоянное значение, то для этих пикселей не нужно вычислять координаты прообразов центров.

– лежит на границе (5'), или (6'), или между ними. Для такого пикселя нужно производить точные вычисления, согласно базовому алгоритму:

– целиком лежит внутри (6'). Для таких пикселей нет необходимости производить проверки, связанные с граничными условиями.

Таким образом, любая строка пикселей конечного изображения состоит не более чем из пяти отрезков пикселей одного из выше указанных типов (рис. 3).

ПРЕДЛОЖЕННЫЙ АЛГОРИТМ

Входными данными алгоритма являются матрица обратного преобразования (3), исходное изображение, а также набор параметров, таких как используемый метод интерполяции, граничные условия, информация о размерах конечного изображения. Выходными – конечное изображение.

Сам алгоритм состоит из следующих шагов:

1. Проверим, что преобразование (3) не вырождено и прямая (4) не пересекает прямоугольник (5). Если одно из этих условий нарушено, используем базовый алгоритм.

2. С применением прямого преобразования (2) находим координаты вершин четырехугольников (5') и (6').

3. Для каждой строки:

(a) вычисляем границы отрезков пикселей одного типа по точкам пересечения строки с (5') и (6');

(b) на отрезках внешних пикселей: в зависимости от граничных условий или задаем указанное значение пикселям, или выполняем вычисления, согласно базовому алгоритму с учетом граничных условий;

(c) на отрезках граничных пикселей вычисляем значения пикселей, согласно базовому алгоритму с учетом граничных условий;

(d) на отрезке внутренних пикселей вычисляем значения пикселей, согласно базовому алгоритму без учета граничных условий.

Для получения большего ускорения вычисления на отрезке внутренних пикселей могут быть использованы SIMD-инструкции. Их использование упрощается, поскольку знаменатель преобразования (3) заведомо не обращается в 0, а значит, отсутствует необходимость в этой проверке. Таким образом, операции для соседних пикселей становятся однотипными и легко выполняются при помощи SIMD.

РЕЗУЛЬТАТЫ

Для получения экспериментальных данных было использовано изображение (рис. 3) размером 3264 на 2448 пикселей и набором из 700 матриц проективного преобразования, таких, что существенную часть конечного изображения составляют пиксели исходного. Для каждой матрицы время работы предложенного алгоритма определялось как медианное среднее по 21 эксперименту. В качестве базового метода использовался обратный метод вычисления проективного преобразования из пункта “Базовый алгоритм” без SIMD-инструкций. Было рассмотрено два варианта вычислительной оптимизации: алгоритм из пункта “Предложенный алгоритм” без и с использованием SIMD-инструкций внутри (6'). Ускорение посчитано как отношение времени работы оптимизированного алгоритма ко времени работы базового алгоритма.

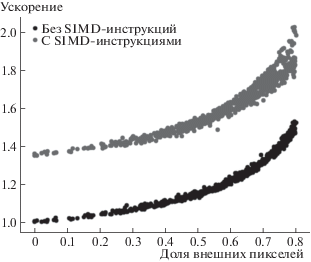
В качестве граничного условия использовалось постоянное значение, поэтому время вычислений зависело от доли внешних пикселей. Результаты эксперимента представлены на рис. 4. Измерения проводились на процессоре Intel Core i7-7700HQ.

С использованием предложенного алгоритма (раздел “Предложенный алгоритм”) было получено ускорение в 1.4 раза при 80% внешних пикселей и практически никакого ускорения при их отсутствии. Ускорение на 5% было достигнуто при 20% внешних пикселей, что уже является значимым результатом для индустриальных распознающих систем. Использование SIMD-инструкций еще сильнее ускорило работу алгоритма: в 1.35 раза при отсутствии внешних пикселей и в 1.7–2 раза при 80%.

ЗАКЛЮЧЕНИЕ

В этой работе предложен метод повышения вычислительной эффективности алгоритма проективного преобразования изображения, основанный на предварительном вычислении границ образа исходного изображения, который можно применить в том случае, если этот образ конечен. Было экспериментально показано, что в сочетании с использованием SIMD-инструкций и постоянным граничным условием, он позволяет снизить время вычислений в 1.4–2 раза, в зависимости от числа внешних пикселей на конечном изображении.

Работа выполнена при частичной финансовой поддержке грантов РФФИ 17-29-03297 и 16-29-09508.