Сенсорные системы, 2019, T. 33, № 3, стр. 238-266

ВВЕДЕНИЕ

Данная статья продолжает развитие темы, отраженной в цикле авторских работ по распознаванию формы объекта по плоской центральной его проекции инвариантно к группе дробно линейных (проективных) преобразований картинной плоскости в 3D пространстве. Объектами исследования были и остаются плоские гладкие фигуры с минимумом особенностей (не включающие обычно используемых опорных элементов из списка: точки излома, перегиба, спрямления, ветвления и прочая). Поскольку дисциплина “Обработка изображений” давно приобрела статус фундаментальной науки с мощной алгоритмической базой методов обнаружения, подчеркивания и сглаживания границ, нет необходимости в обсуждении приемов получения “продукта анализа” для данного исследования: собственно границы овала, как геометрической характеристики объекта, поставляемого “практической задачей опознания”. В рамках этой работы нас будет интересовать исключительно теоретический аспект соотнесения аналитического описания кривой, задающей (либо приближающей) границу овала, с теми способами его обработки, что в конечном итоге должны вывести к инвариантному его представлению, т.е. к возможности классифицировать разнообразные гладкие фигуры, относя их к проективно эквивалентным семействам, либо к формированию “эталонного образа” данного овала для последующих нужд в практических задачах распознавания. Данная работа продолжает тему исследований проективно инвариантных свойств фигур семейства овалов. Учет данных теоретического плана, полученных в последние годы (Савчик, Николаев, 2016, теорема1; Балицкий и др., 2017, теорема2), в сочетании с детально изученными особенностями T-поляры (носителя проективно инвариантных свойств геометрии овала), позволил по-новому взглянуть на процедуру поиска ЭТ на ней (а заодно и на схемы детекции ЭС овала со скрытыми симметриями), что и привело в конечном итоге к построению системы универсальных процедур обработки плоских геометрических объектов, представляющих собой композицию овальной кривой с фиксированной точкой P, привлекающих для этой цели триаду (нелинейно зависимых и быстро формируемых в едином вычислительном цикле) вурф-функций w1(n), w2(n), w3(n). Предложенная триада функций (в силу целенаправленно избранной их структуры) связала характерные особенности ЭТ и ДТ, ранее предполагавшихся подчиняющимися ничем не связанным закономерностям рода необходимых признаков их существования (теорема1 и теорема2). Новый подход с объединением вычисления ЭТ и ДТ оказался осуществимым благодаря исследованным в предшествующей работе цикла (Николаев, 2019) свойствам T-поляры в качестве носителя ДТ (тем самым на эмпирическом модельном материале был расширен за пределы объекта еxtL список уже не обязательно прямолинейных носителей ДТ, гарантировавших их наличие согласно теореме2 на прямой произвольного внешнего расположения). Теперь уже нет необходимости декларировать обязательным выполнение условие коллинеарности для триады ЭТ, чтобы именно с этой инцидентной ЭТ прямой еxtL связывать поиск ДТ: квартет ДТ (две дуальных пары независимого положения) принадлежат T-поляре, т.е. наличие единственной особой внутренней точки P у фигуры порождает и саму T-поляру, и вхождение (в цепь ее вершин, совпадающих с числом n вершин аппроксимации самого овала) дискретных носителей инвариантных свойств ЭТ и ДТ (в количестве не менее трех для ЭТ и в большинстве случаев – четырех для ДТ).

Поясним механизм генерации T-поляры. Любая текущая точка A_i контура овала позволяет вычислить положение точки B_i, лежащей на прямой A_i-P по другую сторону от тестовой P и принадлежащей контуру. T-полярой будем называть геометрическое место точек пересечения пары касательных к овалу в A_i и B_i, т.е. “дискретное вращение” хорды A_i-B_i вокруг полюса P порождает (при сменах номера i вершины контура) цепь вершин криволинейной T-поляры (всегда расположенной целиком по одну сторону от асимптоты, проходящей через P), терминально уходящей в “область бесконечных значений координат” и обладающей свойством двойного самопокрытия (поскольку смена A_i позицией B_i по ходу последовательного обхода вершин не меняет локализацию вершины T_i у T-поляры). Если для каждой T_i производить оценку численного значения вурфа (чаще называемого двойным отношением коллинеарного квартета точек), то необходимым и достаточным признаком наличия ЭТ в некой T_j будет условие гармоничности квартета для нее. Квартет образуют T_j, C_j, P и D_j (C_j и D_j принадлежат контуру в пересечениях с прямой T_j-P), а условие гармоничности может быть численно выражено “в длинах отрезков” |ab| согласно правилу: W(T_j, C_j, P, D_j) = |T_jC_j|*|PD_j|/(|C_jP|*|T_jD_j|) = 1. Итак, совершая для каждой i-й вершины T-поляры оценку вурфа W(T_i, C_i, P, D_i), мы сформируем тем самым вурф-функцию w1(i), которая не менее трех раз (согласно теореме1) принимает значение, равное 1, помечая при этом каждую позицию ЭТ. Таким образом, инициирующая пара A_i, B_i контура детерминирует на нем пару C_i, D_i , входящую в квартет для функции w1(i) (в точках, не принадлежащих к разряду гармонических, w1(i) будет принимать значения, не равные 1). Вторая и третья вурф-функции (w2(i) и w3(i)) “в комплекте описания для текущей A_i” обязательной особенностью структуры также имеют вхождение пары T_i, P, только вторая и четвертая точки квартета (однотипным образом принадлежащие контуру овала с P) выбираются для них по другому правилу. На модельном примере овала общего вида (т.е. не имеющего свойств явной либо скрытой симметрии) покажем в разделе 1 схему вычисления триады функций w1(i), w2(i), w3(i) и процедуру локализации на их основе сетов ЭТ и ДТ.

Завершая вводную часть, отметим, что данное исследование адресуется читателям, в том числе не сведущим в языке и задачах современной математики; для понимания существа излагаемых проблем и результатов вполне достаточно иметь область интересов естественнонаучного плана (психология, физиология сенсорных систем). Авторские декларации (эвристической природы и теоремного характера) преподносятся в образной геометрической форме: исчерпывающее понимание смысла приводимых далее формул, численных схем и приемов обработки вовсе не обязательно для уяснения содержательной логики выносимых на обсуждение тезисов. По той же причине статья не включает описания алгоритмов и реализующих их вычислительных программ, а текст ее обильно иллюстрирован примерами результатов компьютерного моделирования (предлагаемых методов и численных схем), снабженных подробными комментариями.

1. ОВАЛ ОБЩЕГО ВИДА С ПОЛЮСОМ P И СВОЙСТВА ТРИАДЫ ВУРФ-ФУНКЦИЙ ДЛЯ T-ПОЛЯРЫ

Для возможности визуального сравнения порождаемых структур обработки овала в зависимости от положения на нем тестового полюса P наш модельный пример включает тройку тестовых полюсов P1, P2 и P3, каждый из которых детерминирует свою T-поляру, помеченную на рис. 1 в виде набора {T1-поляра, T2-поляра, T3-поляра} и представляющую лишь фрагмент таковых в непосредственной близости к фигуре. Сеты ЭТ k-й Tk-поляры фигурируют на рисунке в виде {E1k, E2k, E3k} (при том, что для T2-поляры не было возможности изобразить позицию ЭТ E32 по причине ее удаленного расположения). Для облегчения понимания читателем структурных деталей и правил формирования триады вурф-функций для некой точки A при тестовом полюсе P2 и его T2-поляре пунктирными прямыми показана схема вычисления текущих инвариантных позиций T, F и E12 (в методических целях положение A избрано на прямой с ЭТ E12) на ней и на контуре овала (это точки A, B, C, D и A', B'), а также некоторых правил и структурных свойств, в поле рис. вынесенных в рамки врезок. Хорда AB задает позицию T, что при вычислении C и D на пересечении с прямой T-P2 образует квартет позиций, достаточный для оценки вурфа w1 = = W(T, D, P2, C). Найденная пара C, D дает возможность вычисления координат F (на пересечении касательных для пары, что обеспечивает на прямой F-P2 оценку позиций A', B', комплектующую квартет второй вурф-функции w2 = W(F, A', P2, B'). Третья функция w3 доопределяет свой квартет по тройке A, P2, B позицией пересечения прямой A-P2 со своей T-полярой (в иллюстративном случае это ЭТ E12), что задает w3 = W(E12, A, P2, B).

Рис. 1.

Овал общего вида с тестовыми полюсами P1, P2, P3 и задаваемые ими T-поляры. Показаны позиции дуальных пар вершин D1j, D2j и d1j, d2j, а также правила образования (квартетов опорных точек) вурф-функций w1(n), w2(n), w3(n) полюса P2 (для т. A контура овала).

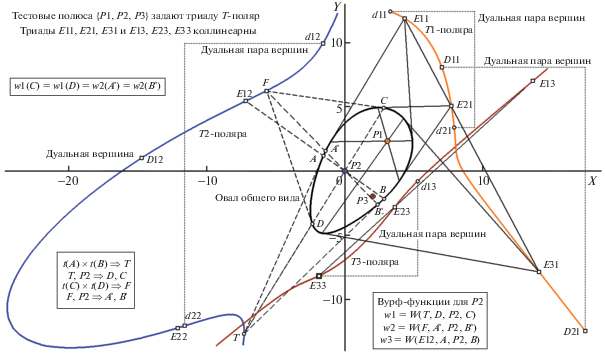
В теореме1 говорится о том, что овал общего вида с заданным в его поле тестовым полюсом P (в произвольной позиции, не принадлежащей границе контура) порождает вовне его (в местах взаимопересечения криволинейных T-поляры и H-поляры, о которой мы не будем рассказывать в рамках данного повествования; оба этих инструмента проективно инвариантного анализа гладких выпуклых кривых введены в работе (Николаев, 2011 а)) не менее трех стабильных точек, названных эллиптическими (ЭТ). Заметим, что любая ЭТ Ek T-поляры детерминирует на контуре овала квартет проективно инвариантных позиций (на рис. 1 для E12 таковыми являются “гармонические” A и B и “тангенциальные” C ' и D ' – в местах прикосновения к контуру внешних касательных из E12; на рисунке они не показаны). Ранее нами описаны конкретные случаи, когда овал, обладая свойством скрытой осевой симметрии и имея позицию тестового полюса P, принадлежащую оси, образует сеты ЭТ в три, пять или семь точек, при том, что сетом может оказаться либо точно коллинеарная триада, либо структура в виде проективного пучка двух или трех прямолинейных носителей (по триаде ЭТ на каждом) с общим центром пучка в точке E1, являющейся плюккеровым полюсом для поляры (Акимова и др., 2014), тождественной неявной оси симметрии данного овала (Николаев, 2011б; 2012). К рассмотрению случаев обработки осесимметричного овала (и новой схемы итеративного поиска позиции оси посредством привлечения выявленных свойств триады w1, w2, w3) мы вернемся в следующем разделе статьи, а сейчас на материале того же рис. 1 рассмотрим особенности поведения проективно инвариантных ДТ.

Теорема2 декларирует наличие у композиции “овал + extL” минимального набора проективно стабильных точек, инцидентных прямой L (их должно быть не менее четырех) и контуру самого овала (на овальной кривой удается детектировать как минимум октет таковых, детерминируемых вышеуказанным квартетом на L). Заметим, что подобная проективно инвариантная конфигурация в минимальном виде включает на L и на контуре овала дюжину стабильных позиций, а сами эти 12 вершин и соединяющие их прямые воспроизводят на языке плюккеровых полюсов и поляр удвоенную диспозицию известной для коник (квадратичных кривых, где частным случаем овала выступает эллипс) теоремы взаимности (Моденов, 1969; Акимова и др., 2014)), в своей “тангенциальной части” заявляющей о симметричном вхождении пары полюсов и соответствующих им поляр в диспозицию дуального соответствия: “поляра первого полюса включает второй полюс, тогда как поляра второго проходит через первый полюс”. При перенесении подобного дуализма полюсов из мира эллипсов в царство овалов утрачивается универсальный характер выполнения этого правила: свойство симметричного включения полюса в поляру “дуального оппонента” становится уникальным, т.е. подлежит целевому поиску, что и осуществляется в “обобщенном” случае не на прямолинейном носителе extL неизвестного генезиса (что гарантирует теорема2), а на цепи вершин T-поляры, полученной для P. И, что характерно именно для теоремы взаимности, поиск дуальных полюсов на T-поляре не предполагает коллинеарности квартета детектируемых стабильных точек (двух дуальных пар на L), а каждая пара ищется независимо на криволинейном носителе, что существенным образом облегчается благодаря особенностям вурф-функций w2 и w3. Вернемся к рис. 1.

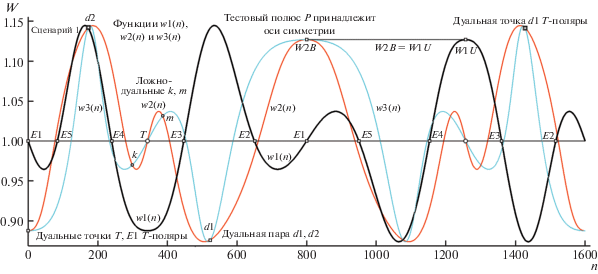
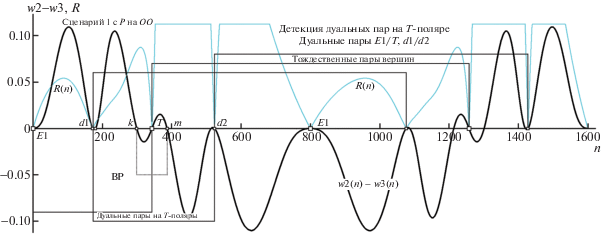
На T1-поляре отмечена кружками дуальная пара вершин d11, d21, а вторая пара ДТ D11, D21 помечена на ней квадратиками. Какие же тангенциальные свойства связывают, например, пару d11, d21? Если вычислить позиции прикосновения к овалу касательных из d11, то прямая, соединяющая точки касания, пройдет через d21, и наоборот: прямая точек касания из d21 непременно включит вершину d11. На T2-поляре удалось показать позиции только одной пары ДТ: d12 и d22 (парная для D12 вершина не попала в поле рис. 1). Врезка внизу справа для текущей A (при P2 и T2-поляре) расшифровывает литерной структурой, как устроены вурф-квартеты для w2 и w3. В проиллюстрированном случае пара A, B не совпадает с A', B'. Их полное совмещение (A с A' и B с B') привело бы к слиянию F и E12, гипотетические F ' и T ' стали бы тогда парой ДТ, а на языке структурных формул новая особенность расположения теперь уже “ДТ” выражалась бы условием w2 = w3. Отметим, что равенство вурф-функций w2(m) и w3(m) для некоторой (из числа последовательно анализируемых) m-й вершины T-поляры еще не означает “победы в задаче поиска ДТ”, так как оценка вида w2(m)–w3(m) = 0 выражает “арифметическую, но не структурную часть признака ДТ”. Необходимое условие детекции ДТ требует добавления достаточного условия их локализации: “вершины на T-поляре для w2(m) и w3(m) должны позиционно совпасть” (что в деталях рис. 1 выразилось бы для гипотетической пары F ', T ' оценкой: “расстояние между вершинами F и E12 равно 0”). Детальнее связь между необходимым и достаточным признаками ДТ отражена на рис. 2, где на общей шкале номеров вершин n показаны ординаты разности вурф-функций w2(n)–w3(n), комплектуемые кривой (тонкие линии) оценки R(n) расстояния между вершинами квартетов w2(n) и w3(n) на T1-поляре. На рис. 2 большими квадратиками отмечена пара ДТ D21 и D11, тогда как номера вершин второй пары d21, d11 помечены малыми. Поскольку любая T-поляра при полном обходе ее порождающего контура обладает самопокрытием (так как ее координаты совпадают для пары касательных по разные стороны от P на общей хорде, соединяющей точки касания), то дальнейшее чередование малых и больших квадратов на шкале n не добавляет новых пар ДТ – это те же две пары, только идентифицируемые номером касательной, идущей в ту же вершину T-поляры из “точки-напарницы” по другую сторону от полюса P. Как выглядит триада вурф-функций wj(n) (j = 1, 2, 3) на модельном примере овала общего вида (того же, что и на рис. 1) с тестовым полюсом P1, демонстрирует рис. 3. Сводная эта диаграмма дает убедиться в целевом предназначении избранных нами вурф-функций: кривая w1(n) в местах пересечения ею “гармонического плато W = 1” фиксирует номера всех ЭТ композиции; места взаимопересечений кривых w2(n) и w3(n) отвечают номерам “пар=кандидатов на роль ДТ” (для них срабатывает “необходимый, но недостаточный” признак ДТ: w2(n) = w3(n)), что требует дополнительного отсева кандидатов согласно критерию R(n) = 0 (показано на рис. 2). Заметим, что аттестация операции вычленения истинных ДТ категорией “отсев” не вполне корректна. Фактически эта процедура создает расширенную таксономию проективно инвариантных элементов (ИЭ) T-поляры: список успешно локализованных ДТ “по технической необходимости в более разнообразном ассортименте ИЭ” можно дополнить набором пар вершин, не реализующих структурного признака A ≡ A', B ≡ B', а обладающих лишь свойством равенства численных значений w2(n) = w3(n). Назовем эти новые ИЭ “w-равными” (ВР), и чуть более детально коснемся их “целевой эксплуатации” в следующем разделе. Подведем текущий итог: благодаря предложенной триаде вурф-функций (формируемых и анализируемых в общем быстром цикле вычислений) T-поляра поставляет (в качестве списков инвариантных вершин) три типа ИЭ: соответственно ЭТ (всегда не менее трех), ДТ (не менее четырех в подавляющем большинстве случаев, а в “уникальных ситуациях”, к чему мы еще дважды вернемся, – не менее одной пары ДТ) и ВР (эмпирический модельный факт – не менее двух).

Рис. 2.

Модельная диаграмма классификации вершин T1-поляры (в сцене рис. 1) по типам ДТ и ВР привлечением функций R(n) и w2(n)–w3(n). Остальные пояснения в тексте.

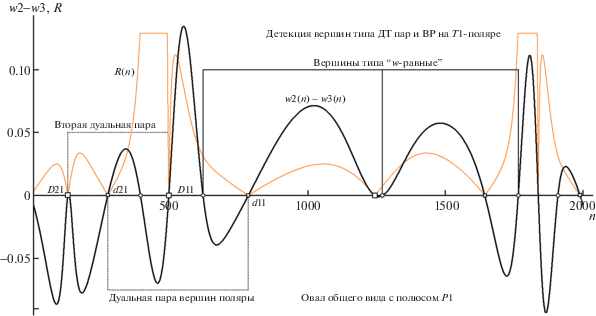
Рис. 3.

Вид триады вурф-функций (сцена рис. 1) для полюса P1 с разметкой номеров вершин T1-поляры по типам ЭТ, ДТ и ВР. Остальные пояснения в тексте.

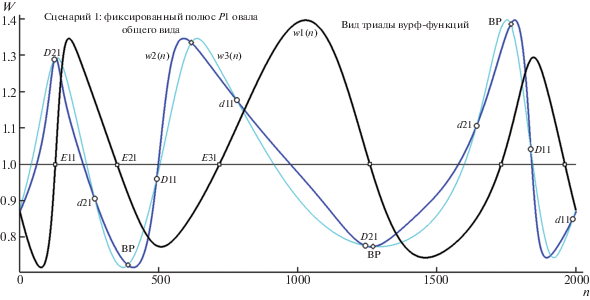
Другая немаловажная особенность получаемых вурф-распределений, привлекаемая в без труда реализуемых целях оптимизации программ обработки (с использованием свойств симметрии формируемой триады функций wj), связана с поведением w-функций, при котором их вершина на T-поляре пересекает зону несобственных значений (“уходит в бесконечность” и возвращается из нее у другого конца асимптоты). Этот “прыжок через бесконечность” меняет упорядоченную структуру вурф-квартета, в итоге чего некоторое численное значение “w” заменяется на “1/w”. Поэтому для гармонического уровня w ≡ 1 (в роли оси симметрии для “волн” wj(n) по разные ее стороны) локальные экстремумы функций w(n) > 1 и w(n) < 1, соответствующие одной и той же паре A, B, не равны по абсолютной величине (например: 1 – 9/10 ≠ 10/9 – 1). Симметрия амплитуд волн w(n) устанавливается (в новом масштабе теперь уже относительно нулевой абсциссы “n”) в результате логарифмирования вурф-функции (так как справедливо ln(a/b) + ln(b/a) = 0). Нелинейная зависимость триады w1(n), w2(n) и w3(n) имеет по сути ту же природу, что довольно необычным образом сказывается на свойствах симметрии вурф-отображений, требуемых в нашей задаче для описания (и распознавания) композиций “Овал + P”. На рис. 4 показан для композиции “овал общего вида + P1” вид прологарифмированных W-отображений ln(w1(n))(ln(w3(n))) и ln(w2(n))(ln(w1(n))). Их замечательная особенность выражается в том, что всякое W-отображение строится по законам описания в декартовой прямоугольной системе, для которой кривая отображения в каждой своей точке обладает парой координат, равных значениям двух независимых вурф-функций, связанных общим номером n текущей вершины T-поляры. Следствием подобного способа формирования кривой вурф-отображения оказывается полная утеря зависимости от произвола нумерации вершин T-поляры для ее 2D W-координат: проективное (перспективное) преобразование исходной композиции не меняет ее “инвариантного портрета”. Свойства нелинейной зависимости, связывающей члены триады wj(n) таковы, что замена знака одного из аргументов отображения на противоположный делает два отображения тождественными (исходно они осесимметричны относительно ординаты декартовой системы ln(Wi), ln(Wj)). На врезке рис. 4 показана одна из возможных трансформаций W-отображения ln(w1)(ln(w3)), “тождественно совмещающая” его с ln(w2)(ln(w1)): ln(w2(n))(ln(w1(n))) ≡ ≡ ln(w1(n))(–ln(w3(n))). Исчерпывающе информативной для детекции ЭТ (при сохраненной связи с номерами “гармонических” вершин в распределении w1(n)) оказываются позиции пересечения ветвями W-отображения (рис. 4) ординаты на вурф-плоскости (три в верхней части картины и три тождественные им и симметричные относительно абсциссы в нижней части). Вкратце коснемся информационной природы второго “полезного” W-отображения w2(n)(w3(n)), дающего полную картину распределения ДТ и ВР (рис. 5, где представлены совместно W-отображения w2(n)(w3(n)) для “Сценария 1 и 2”, соответствующие позициям тестовых полюсов P1 и P2). Для того, чтобы яснее представить различие распределений ДТ и ВР в ситуации “Сценария 2”, на рис. 6 (аналогично рис. 2 для “Сценария 1”) показан классификационный анализ вершин, проведенный привлечением критерия R(n). Сходным образом (как на рис. 3) на рис. 7 продемонстрирован вид триады функций w1(n), w2(n) и w3(n) для “Сценария 2” (т.е. для случая, когда тестовый полюс занимает позицию P2).

Рис. 4.

Вид композиции двух радиально симметричных W-отображений (для полюса P1 в сцене рис. 1) вида ln(w2(n))(ln(w1(n))), ln(w1(n))(ln(w3(n))). Остальные пояснения в тексте.

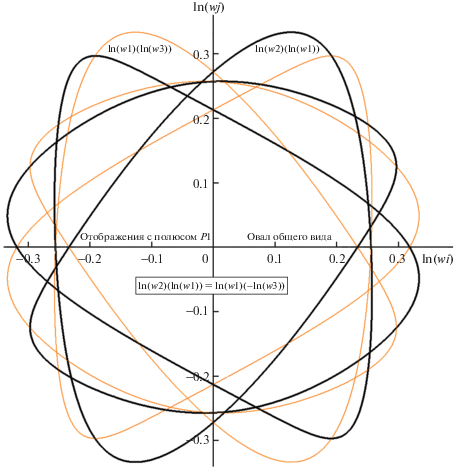
Рис. 5.

Совместная диаграмма двух W-отображений (для полюсов P1 и P2 в сцене рис. 1) ln(w3(n))(ln(w2(n))) с показом позиций P1 и P2 на овале. Остальные пояснения в тексте.

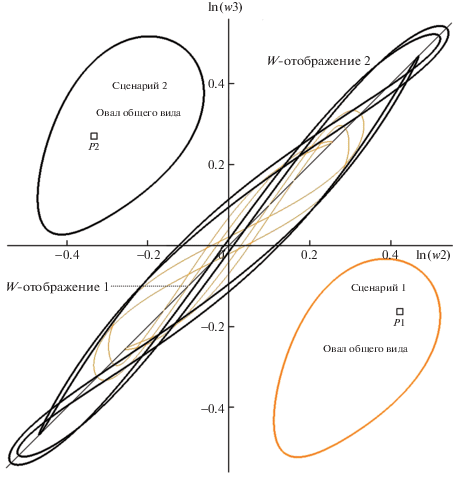
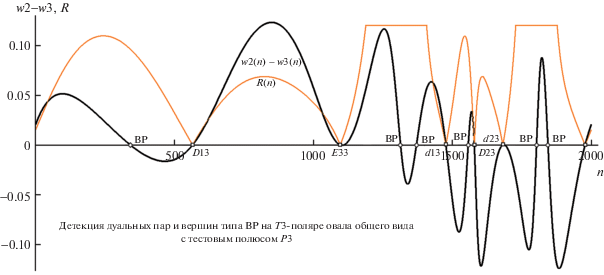
Рис. 6.

Диаграмма детекции вершин D12, D22 и d12, d22 T2-поляры (тип ДТ, сцена рис. 1) с привлечением функций R(n) и w2(n)–w3(n). Остальные пояснения в тексте.

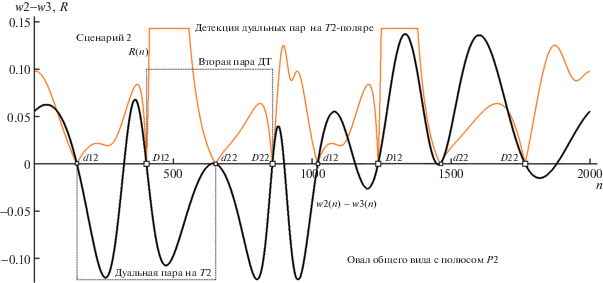
Рис. 7.

Вид триады вурф-функций w1(n), w2(n) и w3(n) (сцена рис. 1) для полюса P2 с разметкой номеров вершин T2-поляры по типам ЭТ и ДТ. Остальные пояснения в тексте.

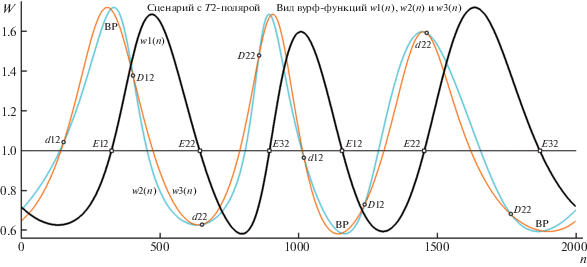
Нетрудно понять, что необходимый признак наличия на T-поляре вершин типа ДТ и ВР (неразличимых без привлечения критерия R(n) = 0) в виде условия w2(m) = w3(m) на дополнительном W-отображении выразится (для способа локализации вершин ДТ и ВР) геометрическим правилом: “кривая w2(n)(w3(n)) фиксирует позиции инвариантных ДТ и ВР в точках пересечения диагональю положительного квадранта плоскости отображения”. Отметим, что для задачи создания малоразмерных дескрипторов входной композиции (реализуемой либо глобальной разметкой контура овала инвариантными позициями всех трех типов, либо путем сепаратного формирования дескрипторов согласно классификации “ЭТ”, “ДТ” с возможным добавлением сета “ВР”) технически проще осуществлять не по структуре W-отображений, а на этапе вычисления триады вурф-функций. W-отображения обоих типов “ценны сами по себе” (вне рамок привлечения технологии дескрипторов), в качестве проективно инвариантного интегрального портрета опознаваемой конфигурации, и связь их структуры с сетами инвариантных точек того или иного типа рассмотрена нами выше в чисто методических целях. Не перегружая текст однотипным комментарием к иллюстративному материалу, приведем карту вурф-функций wj(n) для “Сценария 3” (рис. 8, тестовый полюс в положении P3), обратив внимание читателя на особенность этого случая, выразившуюся на рис. 1 в “совмещении функциональных нагрузок” вершины E33, оказавшейся не только “эллиптической” (тип ЭТ), но и имеющей дуальную ей пару в виде d13 (тип ДТ; из разряда “случайных событий” этот феномен перейдет в “теоретически закономерный факт” в работе с осесимметричными овалами – при условии, что тестовый полюс P принадлежит оси, что будет обсуждено в разд. 2). Детали “объединения” E33 в дуальную пару с d13 помогают мотивировать рис. 9, где сравнительная картина поведения диаграмм w2(n)–w3(n) и R(n) описывает для “Сценария 3” закономерности членения инвариантных вершин T-поляры по типам ЭТ, ДТ и ВР.

Рис. 8.

Вид вурф-функций w1(n), w2(n) и w3(n) (сцена рис. 1) для полюса P3 с разметкой вершин T3-поляры на типы ЭТ и ДТ (D13, D23 и d13, d23). Остальные пояснения в тексте.

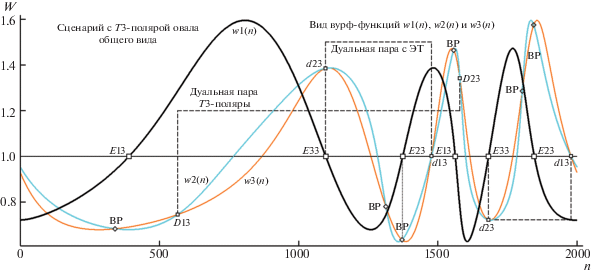
Рис. 9.

Диаграмма детекции вершин D13, D23 и d13, d23 на T3-поляре (тип ДТ, полюс P3, сцена рис. 1) с привлечением функций R(n) и w2(n)–w3(n). Показан случай позиционной “кооперации” ЭТ E33 в роли дуальной с вершиной d13. Остальные пояснения в тексте.

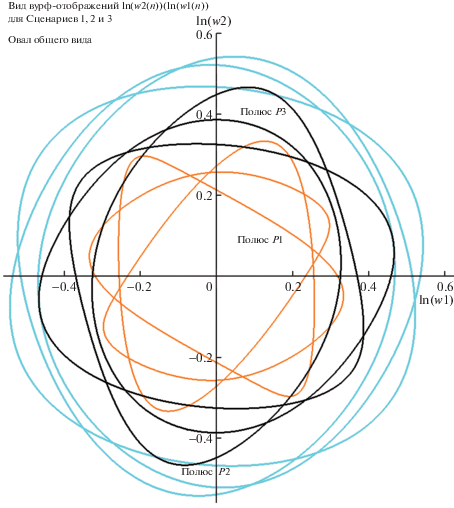
Завершая раздел, посвященный гладким выпуклым фигурам общего вида (не обладающим признаками симметрии), ограничимся демонстрацией W-отображений вида w1(n)(w2(n)) для “Сценариев 1, 2 и 3” (рис. 10). Вывод, который можно сделать на основании сопоставления отображений вида ln(w1(n))(ln(w2(n))) (если сравнить рис. 4 и 10) таков: поскольку диаграммы этого вида обладают точной центральной (радиальной) симметрией, то их исчерпывающий анализ (например, для задачи детекции ЭТ) возможен по любой полуплоскости W-отображения (а с учетом дублирования вершин ЭТ номерами “смежных” касательных, порождающих ту же самую позицию на T-поляре, всю полноту информации уже содержит произвольно взятый квадрант отображения).

Рис. 10.

Объединенная диаграмма трех вурф-отображений вида ln(w2(n))(ln(w1(n))) для полюсов P1, P2, P3 (каждое выделено своим цветовым тоном) по сценариям “1”, “2” и “3” в модельной ситуации овала общего вида (см. рис. 1). Остальные пояснения в тексте.

Далее перейдем к описанию новых результатов, полученных привлечением той же триады вурф-функций, но уже для ситуаций, когда входным объектом является “Овал”, обладающий свойствами скрытой осевой симметрии, а “тестовый полюс P” фигурирует в качестве случайным образом выбранной позиции на поле фигуры, целенаправленной цепью итераций сближаемой с осью симметрии априори неизвестного расположения (достижение этой цели необходимо для решения задачи).

2. СЛУЧАЙ ОСЕСИММЕТРИЧНОГО ОВАЛА С ПОЛЮСОМ P НА НЕЯВНОЙ ОСИ

Сделаем разъяснение, какие особенности геометрии овала, о котором пойдет речь в данном разделе, относятся при его типизации к категории осесимметричного, но могут быть дополнительно подразделены на имеющих явную либо скрытую симметрию. Явная симметрия (будем называть подобные фигуры ортоформой овала) проявляется известным школьнику набором декартовых свойств кривой: “хорды, перпендикулярные оси, делятся ею пополам”; “пара касательных в точках пересечения контура осью паралельна этим хордам”. Под влиянием априори неизвестного проективного преобразования (оно хорошо приближает математически возможные трансформации оптической проекции объекта при сменах ракурса его регистрации сенсором=камерой), совершенного над некой ортоформой осесимметричного овала, перечисленные выше “свойства явной симметрии” утрачивают свою истинность, и с переходом в разряд скрытых (или неявных) требуют “обобщенных дефиниций” – теперь уже в качестве проективно инвариантных признаков осевой симметрии. Объект нашего рассмотрения не обязан следовать условию равенства частей хорд (соединяющих произвольные пары симметричных точек овала), рассекаемых осью и ей перпендикулярных. Не истинны для него и аффинные модификации свойств осевой симметрии. Следовательно, и признак параллельности тех же самых хорд, но уже не под прямым углом рассекаемых осью, при постоянстве отношения их длин, также не может быть гарантированно выполняемым для нашего объекта. Таким образом, перечисленные свойства ортоформы нельзя использовать в процедурах поиска положения неявной оси (станем далее называть искомую прямую образом оси, обозначая сокращенно – ОО) по причине их выполнения лишь в сугубо частных случаях реализации, т.е. в силу не универсальной их природы. При оценке позиции ОО можно опираться исключительно на проективно инвариантные свойства симметрии, список которых мы формулируем ниже.

Свойство 1: все пары i симметричных точек контура овала принадлежат прямым L_i, пересекающимся в общей точке полюса симметрии PS (точке собственной либо в частном случае его ортоформы – несобственной, т.е. бесконечно удаленной).

Свойство 2: две касательные к контуру овала в точках пересечения с ним прямой ОО, также пересекаются в PS.

Свойство 3: для любой прямой L_i и четверки точек, принадлежащей этой прямой, две из которых C_i и D_i проективно симметричны, третья P_i образована пересечением данной L_i с ОО, а четвертая есть PS, численное значение W (PS, C_i, P_i, D_i) всегда равно 1. Иными словами, любая пара C_i, D_i симметричных точек овала разделяется парой P_i, PS в гармоническом отношении. Легко убедиться, что декартовы признаки осевой симметрии у ортоформы полностью удовлетворяют триаде обобщенных свойств (для этого достаточно “мысленно перенести” полюс PS в несобственную область). Но вернемся к нашей задаче.

Рассмотрим, какие особенности поведения введенной нами триады вурф-функций проявятся в сопоставлении двух положений тестового полюса P: при его принадлежности ОО и для позиции вне оси (т.е. будет описан вариант общего случая скрытой симметрии). Начнем с первого случая (наименовав композицию “Сценарий 1”). С целью напоминания правил построения wj(A) на рис. 11 для текущей точки A и для B, парной ей относительно полюса P, показаны структуры квартетов, образующих вурфы каждой wj(A) (структурные правила приведены во врезке наверху слева, а сами квартеты выделены каждый своим цветовым тоном, причем тем же тоном размечены и вершины T-поляры, входящие в квартет). Функция w1(A) требует знания позиций для четверки {J, P, S, c}, где c является плюккеровым полюсом поляры A-B (каковой расположен на T-поляре в пересечении касательных у A и B, что зафиксировано на врезке справа в виде правила t(A) × t(B) $ \Rightarrow $ c), а J и S принадлежат контуру на пересечениях с прямой c-P. Функцию w2(A) компонует квартет {b, P, a, r}, где r плюккеров полюс поляры J-S (вычислен по правилу t(J) × t(S) $ \Rightarrow $ r), а пара b, a лежит на контуре в пересечениях с r-P. Для оценки w3(A) необходимо знание координат четверки {B, P, A, d}, где d принадлежит T-поляре на ее пересечении с прямой A-P. Для того, чтобы показать, что A не относится к типу ДТ, для d изображена ее плюккерова поляра U-D (t(U) × × t(D) $ \Rightarrow $ d), не совпадающая с хордой J-S. Пунктирными прямыми показаны на T-поляре структурные свойства d1 – одной из ДТ (дуальная ей d2 – за пределами поля рис.11, на пересечении касательных в K и G, т.е. t(K) × t(G) $ \Rightarrow $ d2, а сами K и G лежат на контуре в пересечениях с d1-P, при этом d2 инцидентна плюккеровой поляре a1–b1 полюса d1). Есть тут еще одна особая ДТ T – на пересечении ОО (продолжение хорды L–R) с T-полярой, ей дуален полюс симметрии PS (будет показано на следующем рис. 12 с более детальным обсуждением – ниже).

Рис. 11.

Правила формирования триады вурф-функций овала неявной осевой симметрии в ситуации вычисления T-поляры для тестового полюса P на хорде оси LR (“Сценарий 1”). Структура (квартеты опорных точек) этих функций показана для вершин A, a1, a2 контура овала. На T-поляре отмечены позиции T и d1 (тип ДТ). Остальные пояснения в тексте.

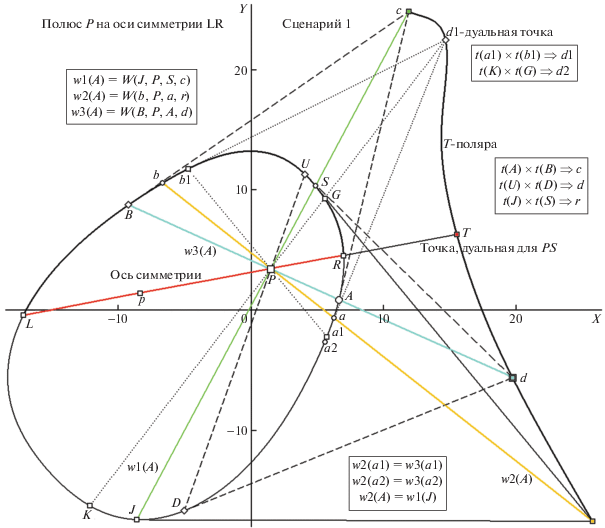
Рис. 12.

Картина объектов “Сценария 1” (осесимметричный овал с полюсом P на оси AB) с показом особенностей формирования пяти “эллиптических точек” (ЭТ с коллинеарными триадами вершин {E1, E3, E4} и {E1, E2, E5} на пересечениях T- и H-поляр), дуальной пары PS, T и точек k, m контура, задающих вершины ВР. Остальные пояснения в тексте.

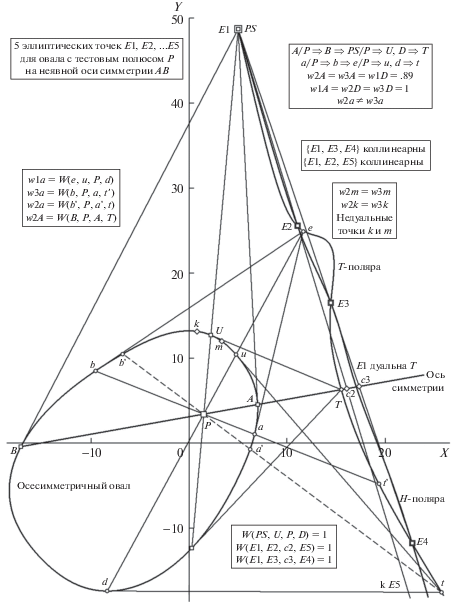
Взаимосвязь вурф-функций обусловлена их сходной структурой, где в квартете сложного отношения обязательно присутствуют P и одна из вершин T-поляры (а разнятся они парами позиций контура). В качестве примеров этих связей (рис. 11, врезка внизу справа) показано, что связи могут быть универсальными (w2(A) = w1(J)), дуальными (w2(a1) = w3(a1)) либо “ложно-дуальными” (w2(a2) = w3(a2), соответствующими типу ВР). Обозрев структурные черты триады вурф-функций, на примере того же “Сценария 1”, рассмотрим, какие нюансы добавляет поиск ЭТ с их особенностями в случае превышения минимального количества таковых, гарантированного теоремой1 (рис. 12). В нашем случае число ЭТ равно пяти, при этом они образуют проективный пучок из двух коллинеарных троек ({E1, E3, E4} и {E1, E2, E5}) с центром пучка в PS, который будем считать “главной” ЭТ E1. Процедура последовательного вычисления вспомогательных позиций для вурф-функций стандартна (врезка справа вверху): A, P $ \Rightarrow $ B; A, B $ \Rightarrow $ PS; PS, P $ \Rightarrow $ U, D; U, D $ \Rightarrow $ T… (что идентично на врезке справа в записи строчными литерами для некоторой другой текущей точки a, цепь вычислений для которой приводит к позиции t и далее позволяет сформировать вурф-функции w1(a) = W(d, P, u, e), w2(a) = = W(b', P, a', t)) и w3(a) = W(b, P, a, t')).

Сводный рис. 12 изображает вид овала совместно с участком пересекающихся T-поляры и H-поляры, ЭТ которых образуют на пересечениях описанную выше структуру пучка с их общей ЭТ E1 (в роли центра пучка для прямых-носителей триад и по сути – плюккерова полюса симметрии PS для поляры-оси ОО с хордой A–B). В силу того, что PS является ЭТ, w1(A) = w2(D) = w3(D) = = W(PS, U, P, D) ≡ 1 (в то время как W(T, A, P, B) = = w1(D) = w2(A) = w3(A) = .89 ≠ 1). Это обстоятельство вносит нюанс: вершина E1 оказывается носителем “двойной природы”, являясь не только ЭТ, но и образуя совместно с T пару ДТ, что для “Сценария 1” (при любом положении P в границах хорды A-B), не влияя на вид W-отображений, уменьшает число проективно инвариантных позиций на контуре (подобная ситуация в случае гарантированного минимума ЭТ согласно теореме1 может привести при некоторых положениях P на хорде A–B к “неполному комплекту” инвариантных точек контура, – вместо 20 их окажется лишь 16). Для технологии описания осесимметричного овала дескрипторами по сетам вершин контура это вероятное событие не очень критично, поскольку позиция P должна будет подвергнуться дополнительному сдвигу вдоль A–B до финального уникального положения Pm (ведь текущая позиция P случайна, ничем не примечательна по части “устойчивой единственности” на хорде ОО), которое и будет детерминировать финальную Tm-поляру со всеми ее перевычисленными (“окончательно локализованными”) вершинами ЭТ, ДТ и ВР (координаты которых станут данными для дескрипторов – по алгоритмической схеме плоскостного вурфа (Депутатов, 1926; Глаголев, 1963), когда по “скользящей” пятерке соседних инвариантных вершин контура вычисляются 2D вурф-координаты шаблона, реализующего конечноразностную модель производной Шварца (Овсиенко, Табачников, 2008)). Безусловно, это интересный факт: полюс PS “отнимает ресурс” у сета ДТ. Переходя к рассмотрению карт w-функций, добавим реплику о “вурф-равных” точках ВР – в качестве новых проективно инвариантных вершин T-поляры (типизация каковых возможна при совместном анализе признаков w2(n) = w3(n) и R(n) ≠ 0).

На рис. 13 для “Сценария 1” показан вид триады w1(n), w2(n) w3(n), где отмечены и позиции “особой” пары E1, T, относящейся одновременно к типу ДТ, “традиционной” пары ДТ d1, d2, а также (общие с показанными на рис. 10) вершины k, m, фиксированные на пересечениях w2(n) и w3(n) (и удовлетворяющие лишь “арифметическому” признаку ДТ w2(k) = w3(k), w2(m) = w3(m)), окончательно типизируемые как ВР – по причине их неподчинению структурному критерию R(k) = 0, R(m) = 0), что и демонстрирует рис. 12. Рисунок 14 позволяет понять ключевую роль функции R(n) для однозначной классификации вершин T-поляры по типам ДТ и ВР (там же дополнительно показаны и “дублирующие” позиции вершин контура овала при полном его обходе, названные “тождественными”, каковые относятся к общей точке T-поляры, порождаемой парой касательных на концах хорды через P в ее роли плюккровой поляры для этой точки, как “полюса”). В общих чертах обсудив связь поведения триады вурф-функций для ситуации “Сценария 1” – в рамках задачи поиска проективно инвариантных вершин T-поляры и задаваемых на их основе сетов ЭТ и ДТ контура овала, перейдем к иллюстрируемому сопоставлению карт W-отображений для “Сценария 1” и “Сценариев 2 и 3” (случаи, когда P не принадлежит ОО), содержащих эмпирические признаки сближения тестового полюса P с искомой ОО, что и послужит построению итерационной схемы “сдвига P на ОО”. Заметим, что на большом материале сделанных модельных тестов не выявлено особенностей триады wj(n), помогающих (для любых сценариев “Овал + P”), решению задачи детекции ОО, поэтому в следующем разделе основное наше внимание будет уделено свойствам W-отображений w1(n)(w2(n)) либо ln(w1(n))(ln(w2(n))) – с их “эмпирическим признаком сближения с ОО”.

Рис. 13.

Вурф-функции w1(n), w2(n), w3(n) (“Сценарий 1”, P принадлежит “образу оси” ОО) с отмеченными номерами вершин пяти ЭТ, дуальных пар d1, d2 и T, E1, а также позиций ВР (k, m на контуре овала), названных “ложнодуальными”. Остальные пояснения в тексте.

Рис. 14.

Метод классификации вершин T-поляры (“Сценарий 1”, тип ДТ и ВР) при помощи инвариантных свойств функций w2(n)–w3(n) и R(n), с показом номеров вершин контура (названы “тождественными”), задающих общую вершину поляры. Комментарии в тексте.

3. СВОЙСТВА ОТОБРАЖЕНИЙ ОСЕСИММЕТРИЧНЫХ ФИГУР, ИТЕРАЦИОННАЯ СХЕМА ПОИСКА ОО

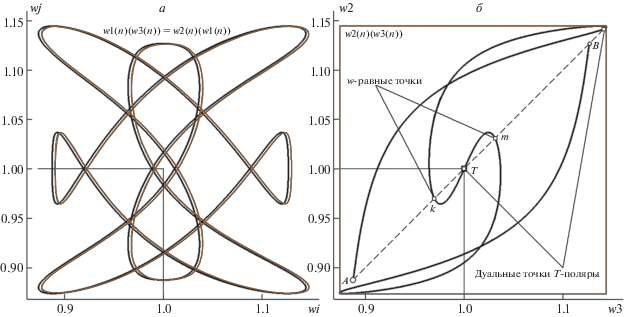
Прежде чем начать обзор “Сценариев 2 и 3”, завершим описание “Сценария 1” демонстрацией ключевых W-отображний вида w2(n)(w1(n)) и w2(n)(w3(n)) (рис. 15, первое (а) позволяет идентифицировать сет ЭТ, второе (б) – фиксировать ДТ и ВР на диагонали декартовой вурф-плоскости (W3, W2)). Напомним, что на врезке рис. 4 для овала общего вида (в композиции с внутренним полюсом P) показана модификация W-отображения ln(w1)(ln(w3)), точно совмещающая его с картой ln(w2)(ln(w1)) посредством операции смены знака при аргументе ln(w3(n)): ln(w2(n))(ln(w1(n))) ≡ ln(w1(n))(–ln(w3(n))). Свойства симметрии W-отображений для случая осесимметричного овала (с P на ОО) в сравнении с ситуацией овала общего вида выражены более впечатляюще, – не прологарифмированные и без какой-либо смены знака у аргумента отображения две карты полностью совпадают: w1(n)(w3(n)) ≡ w2(n)(w1(n)) (и это – при любом положении P на хорде ОО!). Поскольку на настоящий момент мы не можем привести убедительных теоретических обоснований тому факту, что сдвиг тестового полюса с ОО (в любом его положении на ней) приводит к однотипным изменениям в картине W-отображений вида w1(n)(w3(n)) и w2(n)(w1(n)) (о которых – речь пойдет далее), в конце этого раздела будут предъявлены аналогичные модельные примеры для сдвига p из другого положения на ОО (на рис. 11 позиция p на ОО показана без комментариев) с теми же “новыми признаками удаленности P от ОО”.

Рис. 15.

Вид вурф-отображений для “Сценария 1”: w2(n)(w1(n)), полностью идентичного карте w1(n)(w3(n)) (а; кривая, изображенная тонкой линией, сдвинута по абсциссе) и карты w2(n)(w3(n)) (б; на диагонали, образованной штриховой прямой, показаны позиции пары ВР k, m и дуальной пары PS, T, включающей ЭТ). Остальные пояснения в тексте.

Для “протокола” (и не описывая деталей – в силу стандартности всех приводимых диаграмм на рис. 16 и 17) дадим выкладки для “Сценария 2” с его весьма малым уходом P с хорды ОО, демонстрирующие для этого случая вид вурф-функций w1(n), w2(n) и w3(n) (рис. 17), а также сепарацию инвариантных вершин T-поляры по типам ЭТ, ДТ и ВР (рис. 16) с привлечением критерия R(n) = 0. Оба рис. дают возможность проследить, что ЭТ E1 – в качестве полюса симметрии PS – более не “мигрирует” в сет ДТ “на правах дуальной” к особой точке T (на пересечении OO c T-полярой), т.е. набор ДТ оказывается теперь “каноническим” – в две пары вершин, среди которых ЭТ более не фигурируют. Для более детального ознакомления с существом этой “метаморфозы” на рис. 18 показано, каким образом инвариантные вершины T-поляры E1 и D (типизируемые как ЭТ и ДТ в паре с D') при смене сценария к “1-му от 2-го” (криволинейная поляра для случая “1”, задаваемая полюсом на оси, обозначена как Ta-поляра и изображена другим цветом) сближаются до тождественного слияния в позиции PS, “передавая ей присущие им типы” ЭТ и ДТ. На врезке рис. 18 вверху справа выписаны конкретные литерные переобозначения для d, E2, E3 и E4 T-поляры, смещение которых при переходе в вершины Ta-поляры ad, e2, e3, e4 изображается “оператором перехода” P → AB (т.е. полюс P смещается на хорду AB ОО).

Рис. 16.

Классификация вершин T-поляры вида ДТ и ВР (метки “малый квадрат” для ВР, “большой” – для парных вершин ДТ) согласно “Сценарию 2” (тестовый полюс P сдвинут с хорды ОО) посредством функций w2(n)–w3(n) и R(n). Остальные пояснения в тексте.

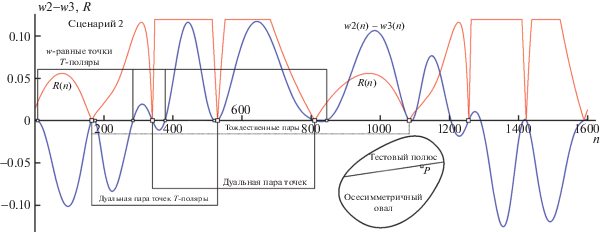
Рис. 17.

Вид триады вурф-функций w1(n), w2(n), w3(n) для “Сценария 2” с показом позиций сета пяти ЭТ (E1÷E5) и двух пар ДТ D1, D2 и d1, d2. Остальные пояснения в тексте.

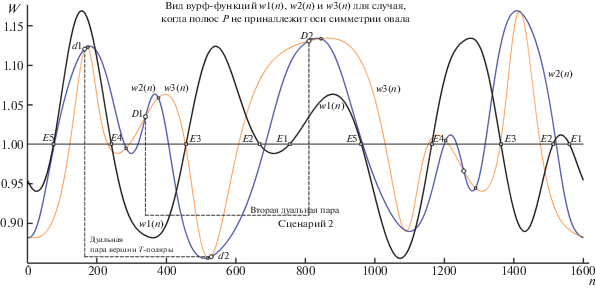
Рис. 18.

Картина “захвата” одной из ДТ (D) в пару к ЭТ (полюсу PS) при переходе от “Сценария 2” к “Сценарию 1” (оранжевыми прямыми показано, как происходит слияние вершин D и E1 в позицию PS в результате сдвига тестового P на хорду ОО). Остальные пояснения в тексте.

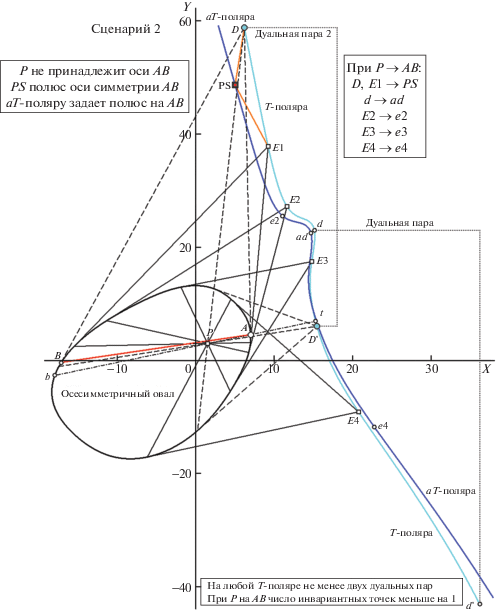
Рисунок 19 поясняет, какие трансформации произошли с W-отображениями (а и б) в итоге сдвига тестового полюса P с прямой ОО по “Сценарию 2” (целесообразно вернуться к диаграммам рис. 15, а и б, где показаны те же отображения, но согласно “Сценарию 1”). Абсолютное совпадение карт w1(n)(w3(n)) и w2(n)(w1(n)) (рис. 15, а) сменяет относительно ординаты декартовой плоскости вурфов (рис. 19, а) осесимметричное их “расхождение – с поворотом в противоположных направлениях”. Угловой разворот картин, отмеченный на рис. 19, а параметром v, в серии проведенных модельных испытаний был избран (оказался функционально пригодным) в качестве “градуальной меры сближения P с ОО”. Картина w2(n)(w3(n)) (от рис. 15, б к 18, б) также претерпевает кардинальные изменения: по виду разомкнутая кривая (в действительности – замкнутая двойного самопокрытия, с точками возврата A и B) расщепляется в петлеобразную структуру той же топологии “в среднем”.

Рис. 19.

Трансформация W-отображений с переходом к “Сценарию 2”: кривые w2(n)(w1(n)) (утолщенная линия) и w1(n)(w3(n)) (тонкая линия) совершают симметричный поворот в противоположных направлениях на суммарный угол v (он избран мерой сближения P с ОО) (a). Карта w2(n)(w3(n)) утрачивает свойство самопокрытия (б). Комментарии в тексте.

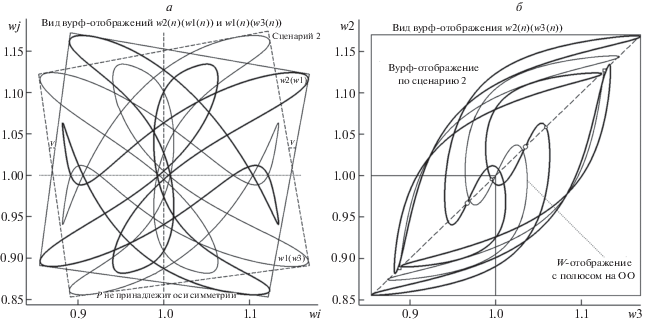
Серия иллюстраций рис. 20–22 по своему содержанию (классификация ДТ и ВР, вид триады вурф-функций и W-отображенй) идентична сету рис. 16–18 при единственном отличии: серия соответствует “Сценарию 3”, когда тестовый полюс P отодвинут от ОО еще дальше (врезка рис. 20), чем по “Сценарию 2”. Рисунок 22 дает представление о симметричном развороте отображений w2(w1) и w1(w3), позволяющем получить оценку параметра v (а), и виде отображения w2(w3) с фиксацией позиций ДТ и ВР на диагонали W-плоскости (б).

Рис. 20.

Классификация вершин T-поляры вида ДТ и ВР (аналогично рис. 16) согласно “Сценарию 3” (с еще большим сдвигом P от хорды ОО) посредством функций w2(n)–w3(n), R(n) и разметка номеров “тождественных пар” для нее. Остальные пояснения в тексте.

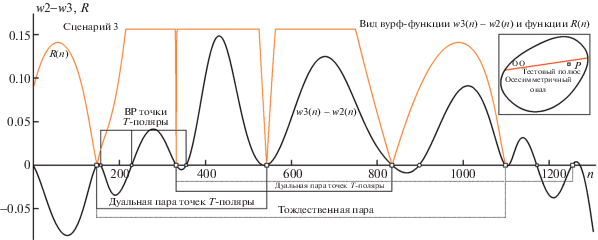
Рис. 21.

Вид вурф-функций w1(n), w2(n) и w3(n) для “Сценария 3” с показом позиций ВР и двух пар ДТ D1, D2 и d1, d2 в пересечениях w2(n) и w3(n). Остальные пояснения в тексте.

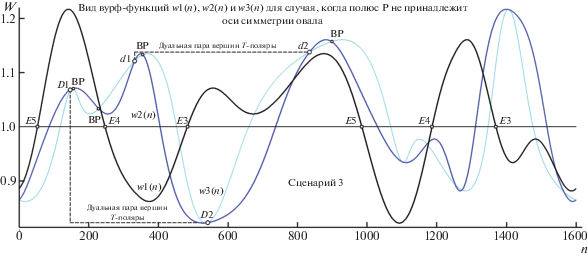
Рис. 22.

Отображения для “Сценария 3”: сет ЭТ и симметричный поворот карт w2(n)(w1(n)) и w1(n))(w3(n)) с оценкой меры v (а); карта w2(n)(w3(n)) несет информацию о ДТ и ВР (б).

Справедливость тезиса об угловом расхождении W-отображений w1(n)(w3(n)) и w2(n)(w1(n)) (из исходно слитного в ситуации инцидентности P хорде ОО) при сдвиге P с ОО дополнительно иллюстрируют рис. 23–26 (где показываются последствия перехода от “Сценария 4” к “Сценарию 5” для полюса p, сдвигаемого из иной, нежели P, позиции). Рисунок 23 для “Сценария 4” показывает вид функций w1(n), w3(n), abs(w3(n)–w2(n)) и R(n) с итогами классификации инвариантных вершин T-поляры по типам ЭТ, ДТ и ВР. Рисунок 24 для этого же сценария показывает структурные особенности тангенциальных свойств пар E1, T и d1, d2, воспроизводя на врезках вид отображений w2(n)(w3(n)) (слева вверху) и ln(w2(n)) (ln(w1(n))), радиально симметричная кривая которого (справа внизу) идентична карте ln(w1(n))(ln(w3(n))). Рисунок 25, демонстрирующий типизацию вершин, – аналог рис. 23, только теперь это диаграммы для “Сценария 5”. Итоговый рис. 26 иллюстрирует, каким образом “параметр сдвига” $v$ может быть “считан” с двойной карты “расщепления” отображений ln(w2(n))(ln(w1(n))) и ln(w1(n))(ln(w3(n))) (справа дана нелогарифмированная их картина, не обладающая радиальной симметрией и мало пригодная для оценки $v$).

Рис. 23.

Аналог карты вурф-функций рис. 13 и 14 по “Сценарию 4” (полюс p у другого края ОО; кривые w2(n), w3(n) заменены на abs(w2(n)–w3(n)). Остальные пояснения в тексте.

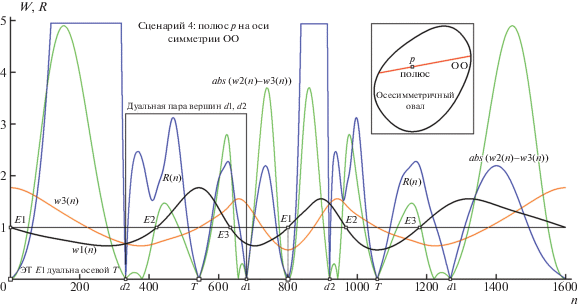
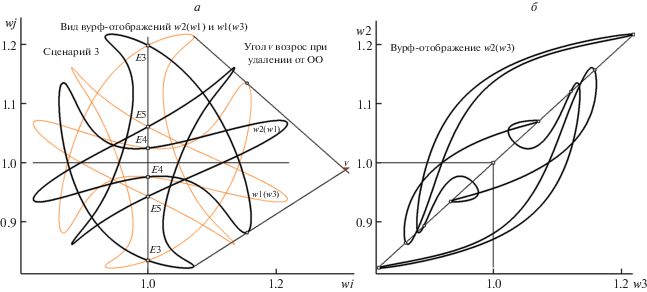
Рис. 24.

Схема диспозиции пар ДТ d1, d2 и E1, T для “Сценария 4”; вид отображений w2(w3) и ln(w2)(ln(w1)) ≡ ≡ ln(w1)(ln(w3) (на диагональных врезках). Остальные пояснения в тексте.

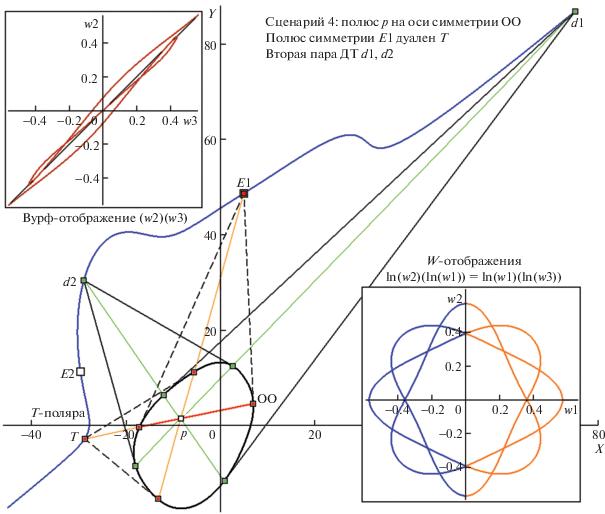
Рис. 25.

Аналог картины функций рис. 23 для “Сценария 5” (полюс p выдвинут с хорды ОО) с показом вершин ЭТ (метка “большой квадрат”) и ДТ (“малый”). Комментарии в тексте.

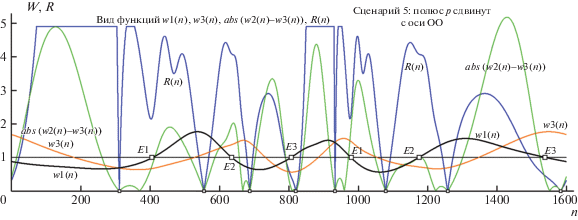
Рис. 26.

Разворот W-отображений ln(w2)(ln(w1)) и ln(w1)(ln(w3) (“Сценарий 5”), задающий оценку $v$ (слева); пара w2(w1), w1(w3) не годна для оценки (справа). Разъяснения в тексте.

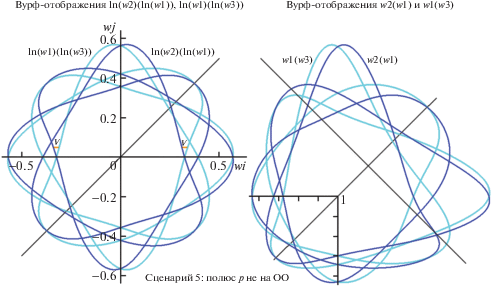
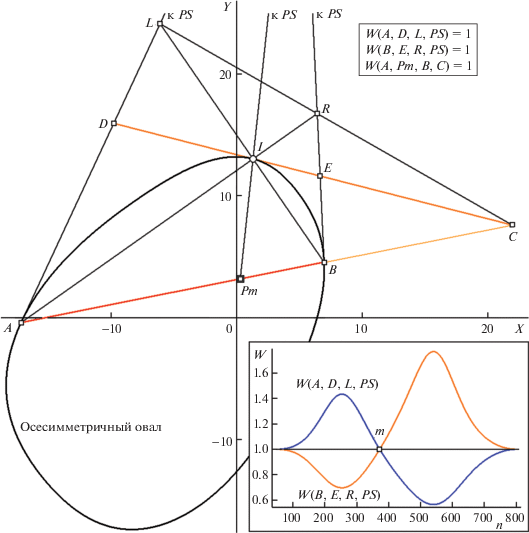
Осталось обсудить два вопроса: как переместить на хорду ОО полюс P из случайно выбранной его позиции и при помощи какой процедуры однозначно определить ему на ОО проективно инвариантное (финальное) положение? Ответ на первый вопрос чрезвычайно прост: пара случайных “стартовых точек” для P с разными значениями $v$ задает вектор его смещения (в направлении уменьшения оценки $v$). По трем таким прямолинейным сдвигам (с одинаковым шагом) можно аппроксимировать (используя монотонность $v$(r), где r –расстояние до хорды ОО по прямой первых сдвигов) четвертый шаг, перемещающий P на ОО. Алгоритмы поиска уникальной инвариантной точки Pm на хорде ОО обсуждались нами в предшествующих публикациях цикла. Вкратце рассмотрим самый простой из них. На рис. 27 показано положение Pm, удовлетворяющее оценкам вурфов, вынесенным во врезку. Так как к этой стадии позиция неявной оси уже найдена, следовательно известно и положение полюса симметрии PS. Вычисляя положения касательной в последовательно перебираемых вершинах I контура (на дуге от A до B, ближайшей к PS), можно получить координатные оценки для пересечений D, E, L, R. Нетрудно показать, что вурф-функции w1(A, D(n), L(n), PS) и w2(B, E(n), R(n), PS) имеют противофазную динамику (вынесено во врезку внизу справа), пересекаясь при гармоническом значении, что и задает искомый номер вершины I(m) контура, детерминирующий позицию Pm. При этом должны быть выполнены проверочные условия: касательная в I(m) пересекает ОО в той же точке C(m), что и прямая L(m)-R(m). Завершая рассмотрение вычислительных методов проективно инвариантного описания осесимметричных овалов, отметим, что схемы, предложенные для решения этой задачи, имеют асимптотику вычислительной сложности алгоритмов – со значительным ростом скорости обработки – в сравнении с универсальными переборными схемами для аналогичных сценариев, разработанных нами ранее (Николаев, 2015).

Рис. 27.

Метод детекции уникальной позиции Pm на хорде ОО сообразно противофазному ходу по n (на врезке) вурфов W(A, D, L, PS), W(B, E, R, PS). Остальные пояснения в тексте.

4. ОБРАБОТКА ОВАЛОВ РАДИАЛЬНОЙ СИММЕТРИИ И МЕТОД ПОИСКА НЕЯВНОГО ЕЕ ЦЕНТРА

Аналогично осесимметричному случаю – ортоформа кривой центрального (или иначе – радиального) типа симметрии определяется свойством хорд (проходящих через ее центр) делиться им пополам, что и соответствует явным признакам, не универсальным для форм скрытого типа. Для овалов неявного типа симметрии требуются более сложные ее признаки, привлекающие категории несобственных элементов плоскости у ортоформы, для общего случая трансформируемых с использованием понятия линии горизонта. Именно в эту собственную прямую переходит проективная прямая ортоформы при произвольных оптических искажениях, присущих сенсору сообразно сменам ракурса регистрации объекта. Проективно инвариантному описанию (и распознаванию) овалов, обладающих скрытой центральной симметрией, в рамках много лет ведущегося нами исследования – посвящено уже немало работ. Следует уточнить, что докладываемый здесь новый подход к задаче поиска “неявного центра C симметрии” относится не ко всей цепочке процедур обработки, а к тому ее первоначальному этапу, когда из случайным образом выбранной “стартовой” точки (ею и будет исходный тестовый полюс P) череда итерационных шагов=сдвигов должна привести в окрестность центра. Из “окрестности” – “точно в центр” полюс P “доставляет сверхбыстрый алгоритм”, основанный на свойстве гармонического контура для P, принадлежащего центру, находиться в проективной связи с контуром овала, и эту финальную схему незачем (и невозможно) “улучшать” (Николаев, 2014; алгоритм не зависит от количества n вершин аппроксимации овала, требуя на его контуре октета “примерно оппозитно распределенных краевых точек”, вурфы которых образуют “как бы сеть четырех пружинок для P”, задающую итоговый вектор сдвига для следующего шага итерации). Из-за неудач в выборе стартовой позиции полюса P и плохо сбалансированного октета на контуре алгоритм “идеальный – для окрестности” требует оптимизации вдали от нее (неблагоприятный выбор координат старта может “выбросить” итерируемый полюс на контур, неудачный октет – дать в итоге циклическую траекторию, приводящую в C по спирали за неудовлетворительно большое число шагов). В новой постановке “счастливо сошлись” несколько априори ясных обстоятельств. Отображения, получаемые из предложенной триады вурф-функций, на финальной стадии поиска центра C малопригодны, так как при полном совмещении P с центром симметрии поляры (T и H типа) “выпрямляются, сливаясь с линией горизонта” (а набор ЭТ становится непрерывно бесконечным). Зато теоретически понятна геометрическая тенденция для W-отображений, вычисляемых по ходу сближения с центром C: их декартов “размер” должен “стремиться к 0” (что и может послужить в качестве “азимута на центр”). Наконец, как-то вычислимая (вдали от C) триада ЭТ (по теореме 1) позволяет фиксировать на контуре 12 стабильных позиций (шесть “тангенциальных” и шесть “гармонических”, а необходим – октет), тогда как две пары ДТ (“модернизация” теоремы 2) на T-поляре детерминируют на контуре требуемые восемь фиксированных позиций (циклический “сэндвич” из двух четверок, где вершины одной четверки не сближаются с точками квартета другой). Проиллюстрируем эту схему (кратко – в силу отсутствия принципиально сложных моментов) на модельных примерах.

На рис. 28 показан вид овала неявной радиальной симметрии с размеченными позициями центра C и трех квазиколлинеарных тестовых полюсов p1, p2 и p3 с примерной азимутальной направленностью “к центру”. Там же изображена триада T-поляр, этими полюсами порождаемая, и линия горизонта HL. Модельные вычисления для этой сцены обеспечили координатные оценки квартетов ДТ на T-полярах (“обобщенная” теорема 2) и на HL (гарантии “исходной” теоремы 2): в виде дуальных пар D1, D2 и d1, d2, визуальная упорядоченность каковых (следствие квазиколлинеарности полюсов) “от одной T-поляры к соседней” вполне явственна. Итак, показано, что с “краевыми октетами на контуре овала проблем не возникает” (от T3-поляры до HL). На верхней врезке показан и совместный облик W-отображений w3(n)(w2(n)) для p1 и p2 (не актуальных в решении стоящей задачи, тем не менее следующих теоретическому тезису: “полюс, более близкий к C, порождает более компактное отображение”). Рисунок 29 (а, б, в) детально информирует о типизации вершин каждой из T-поляр (ВР литерно не размечены, но их легко отождествить на пересечениях функций w2(n) и w3(n)), объединяя пунктиром пары ДТ и фиксируя триады ЭТ. Итоговый рис. 30 демонстрирует “градуальную меру s сближения тестового полюса с центром C” на материале радиально симметричных прологарифмированных отображений ln(w2(n))(ln(w1(n))). Мерой s избран поперечный размер квадрата, вмещающего каждую из карт (карты выделены цветами: от самой мелкой – для p1 до наибольшей – для p3, а ограничивающие квадраты очерчены). Технических вариантов проведения итерационной процедуры “сдвиг полюса в окрестность C” в силу их простоты можно предложить “не один”. Например, получить сет s для квадратной решетки полюсов (либо для правильного пятиточечника случайной диспозиции), избрав азимут первого шага по паре “от полюса с maxs к полюсу с mins”. Процедура оценки s быстрая, с целью – достичь окрестности C, после чего эстафета передается “сверхбыстрому алгоритму поиска C”.

Рис. 28.

Картина динамики квартетов ДТ для триады T-поляр и прямой HL в соответствии с расположением тестовых полюсов p1÷p3 и центра C. Комментарии для врезки в тексте.

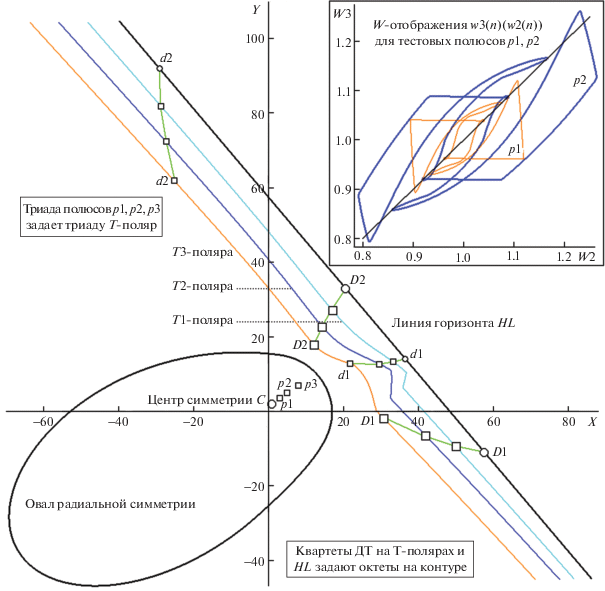
Рис. 29.

Вид вурф-функций w1(n), w2(n), w3(n) для полюсов p1 (а), p2 (б), p3 (в) с показом вершин T-поляр для сетов ЭТ и пар ДТ (D1, D2 и d1, d2). Остальные пояснения в тексте.

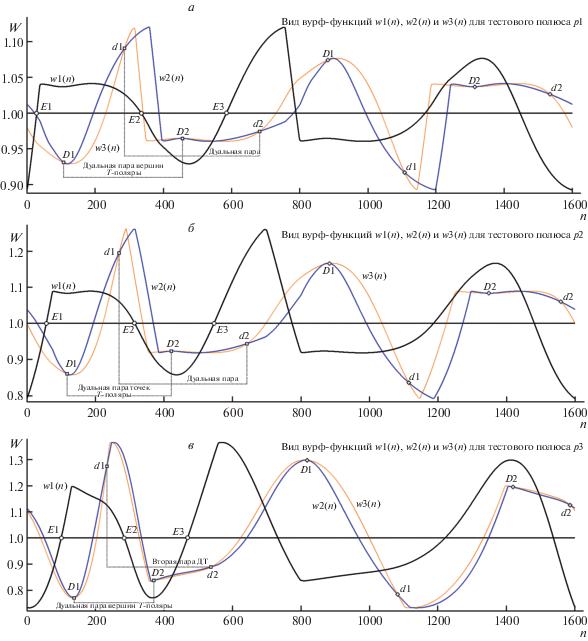
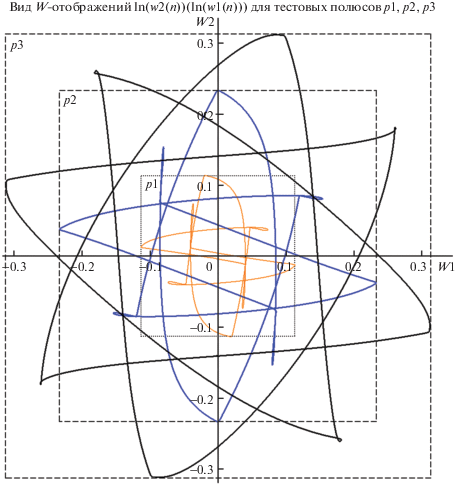
Рис. 30.

Сводная карта W-отображений ln(w2(n))(ln(w1(n))) для полюсов p1, p2 и p3 овала радиальной симметрии (рис. 28), показывающая смену оценок s в согласии с изменениями дистанции между p и C (каждая кривая вписана в рамку=квадрат). Комментарии в тексте.

ЗАКЛЮЧЕНИЕ

Не имея на сегодня строго доказанного положения о T-поляре, как универсальном носителе квартета инвариантных позиций ДТ (аналог теоремы 2 для нее еще не построен; при том, что не получено и численных примеров его опровержения), тезисы процедур, изложенных нами выше, следует охарактеризовать эвристическими схемами. Косвенным свидетельством в его пользу может послужить гипотеза, вытекающая из “обстоятельств, не использованных в доказательстве теоремы 2”: свойством дуальности может обладать не только прямая L, заданная извне при овале, но и кривая S, обладающая свойством – “всякая прямая, пересекающая овал, пересекает extS ровно в одной точке”. Нетрудно показать, что этому ограничению для extS удовлетворяет любая T-поляра, порождаемая полюсом intP (она имеет асимптоту, проходящую через P, и лежит по одну сторону от нее, не содержа петель). Подведем главные итоги изложенной работы (на фоне ее бэкграунда) по актуальной технической теме – “Проективно инвариантное опознание плоских фигур”.

Во Введении была сформулирована постановка одной из задач проективно инвариантного описания гладких выпуклых фигур, регистрируемых (оптика камер задана плоской центральной проекцией) в произвольной композиции совместно с intP. Такая постановка подразумевает быструю дискретную реализацию проективно инвариантного описания входного объекта в виде W-отображения (интерес к вурфу, по сути ключевому элементу производной Шварца, рассмотренной более века назад, до сих пор не угас у математиков (Овсиенко, Табачников, 2008)). Элемент новизны доложенного материала – в том, что вурф-отображения не только единообразно и быстро могут быть вычислены на основе исключительно T-поляр (с целью проективно инвариантной репрезентации фигур общего вида “Овал + intP”), но и оказались источником “меры сближения с элементами скрытой симметрии” гладкой выпуклой кривой (хордой ОО либо центром C – в виде параметров v и s) в важной задаче поиска этих элементов (также реализуемой быстрыми алгоритмами). Процесс получения W-отображений входного объекта (дающего реальный шанс решать задачи распознавания овалов по схеме Фреше (Alt, Godau, 1995) на базе методов оптимизации (Гилл, Мюррей, 1985)), разработанный и успешно испытанный нами на численных моделях, не единственный в пуле новых результатов работы. Привлечение оценки R(n) в работе с функциями w2(n) и w3(n) (в едином вычислительном цикле) открыло возможность использования нового вида инвариантных вершин T-поляры, названого нами “вурф-равными” (ВР), что может пригодиться в качестве замены сетам ЭТ (либо для расширения списка стабильных точек контура в схемах с переопределенными системами уравнений при формировании эталонных описаний кривой в условиях высоких шумов ее позиционного квантования). Нами описаны технически перспективные методы привлечения выявленных дуальных свойств T-поляры, следствием чего может стать отказ от опоры на ЭТ в роли источника данных для получения малоразмерных дескрипторов объекта и вычислительно более оптимальные приемы формирования W-отображений, не требующие поиска ЭТ в качeстве исходной посылки для вычисления дополнительного сета стабильных ДТ (на основе не универсальных признаков коллинеарности триад ЭТ), “не нуждаясь в предварительном анализе композиций ЭТ, их поставляет сама T-поляра”. В случае технической необходимости нет проблем и с получением сета ЭТ: вурф-функция w1(n) “безотказно и быстро” указывает все соответствующие им вершины на T-поляре.

В качестве альтернативы “избыточным” инвариантным описаниям опознаваемого объекта (рода его интегральной репрезентации вурф-отображениями; в виде циклического графа дескриптора по сету стабильных вершин контура либо по схеме “проекция на эталонный четырехвершинник”) в случае технических требований к скорости процедур распознавания можно использовать предельно компактные описания в виде “стэка инвариантных позиций”. Примером могут послужить “выборки из карт W-отображений” (их носитель – ортогональная декартова плоскость, а потому расстояния на ней между “характерными точками” – проективно инвариантны) следующего вида: вертикальный набор квазисимметричных пересечений сдвоенной карты w1(n)(w3(n)) и w2(n)(w1(n) (рис. 22, а) содержит инвариантное описание сета ЭТ; биссектриса отображения w2(n)(w1(n)) – информирует о распределении вершин T-поляры типа ДТ и ВР (рис. 22, б).

В завершение темы не один год идущего исследования свойств кривых семейства овалов (и инструментов проективного их анализа, к числу которых относится T-поляра) следует упомянуть, что классические дифференциальные методы оценки инвариантов для них (Картан, 1933; Faugeras, 1993) не приложимы в рамках задач технического зрения (по причинам практически не реализуемых требований к точности вычисления производных высокого порядка на дискретных сетках для гладкой кривой). Однако растущая актуальность подобного класса задач автоматического распознавания побуждает искать компромиссные подходы (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009). Следует добавить, что П. Олвер с коллегами продолжают искать полуэмпирические подходы к производимому численными методами анализу гладкой плоской кривой, – к приемлемой для технических задач оценке ее дифференциальных инвариантов и “полуинвариантов” (Olver, 2011; Hoff, Olver, 2013), но и в этих работах схемы и методы обнаружения проективно устойчивых свойств симметрии выпуклого замкнутого контура не рассматриваются. Свойства симметрии гладких фигур если и исследуются, то, как правило, это относится к кривым фиксированного аналитического порядка (в качестве примера можно привести работу (Brugalle, 2007), где изложены свойства и особенности кривых седьмого порядка). Продолжается изучение аспектов симметрии и для алгебраических объектов шестого порядка на вещественной проективной плоскости (Itenberg, Itenberg, 2004).

Итоговое заключение по изложенной выше теме “новые функции и приложения старого инструмента” (T-поляры) сформулируем так: разработанные численные методы и схемы для задач проективно инвариантной репрезентации кривых семейства овалов и полученные по ним модельные результаты оригинальны и, можно полагать, технически перспективны (прямые и косвенные аналоги обсуждавшихся здесь аспектов привлечения вурф-функций и W-отображений не обнаружены нами в доступных базах цитирования).