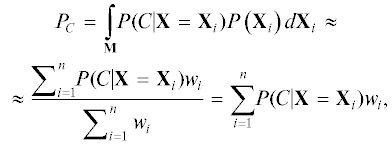Сенсорные системы, 2019, T. 33, № 3, стр. 222-237
Безопасное управление скоростью наземного беспилотного транспортного средства в условиях неопределенности собственного положения
В. И. Кибалов 1, *, О. С. Шипитько 1, Н. С. Коробов 1, 2, А. С. Григорьев 1
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д.19, Россия
2 Московский физико-технический институт (государственный университет)
141701 Московская обл., Долгопрудный, Институтский пер., д. 9, Россия
* E-mail: kibalov@visillect.com
Поступила в редакцию 17.01.2019
После доработки 04.03.2019
Принята к публикации 28.03.2019
Аннотация
В данной работе предложена система управления скоростью беспилотного наземного транспортного средства (БПНТС), основанная на математической модели БПНТС, системе траекторного управления движением и алгоритме локализации Монте-Карло. Планируемая траектория движения преобразуется системой управления в управляющие сигналы, которые поступают на вход математической модели. Выход модели – предсказанная траектория транспортного средства. Рассчитанная в режиме реального времени опережающая траектория движения применяется к каждой частице – гипотезе системы позиционирования о текущем положении транспортного средства. На основе предсказаний траекторий частиц также рассчитывается вероятность столкновения для опережающего отрезка траектории и принимается решение о максимальной допустимой скорости движения. Предлагаемый алгоритм был протестирован на реальном БПНТС. Результаты экспериментов демонстрируют, что разработанная математическая модель позволяет точно прогнозировать траекторию движения БПНТС, а система управления скоростью движения снижает скорость БПНТС до безопасного значения при выполнении маневров и проезде узких проемов. Наблюдаемое поведение системы аналогично снижению скорости водителем при управлении транспортным средством в сложных и неоднозначных дорожных ситуациях.
ВВЕДЕНИЕ
Активное развитие беспилотных наземных транспортных средств (БПНТС) неуклонно приближает их внедрение в транспортную систему городов. В качестве одного из главных преимуществ БПНТС перед традиционным автомобилем, управляемым человеком, зачастую приводится увеличение безопасности передвижения (Harper et al., 2016; Liu et al., 2018) или, другими словами, уменьшение количества дорожно-транспортных происшествий. Однако в действительности существует множество технических и научных задач, решение которых необходимо для гарантии безопасности движения автономных транспортных средств. Одной из таких задач является безопасное управление транспортным средством, включающее в себя оценку вероятности столкновения при движении по заданной траектории и выбор сигналов управления, минимизирующих эту вероятность (Lambert et al., 2008a).
Множество существующих подходов к планированию траектории и оценке вероятности столкновения делают допущение в том, что текущее положение транспортного средства (ТС) достоверно известно (Hu et al., 2018; Kuffner, LaValle, 2000). Однако при работе в реальном окружении неизбежно возникает необходимость учета неопределенности, вызванной непредсказуемыми девиациями движения ТС, неточностями измерений датчиков, изменяющимися условиями окружающей среды и другими факторами. Таким образом, актуальна задача оценки безопасности траектории движения в условиях неопределенности собственного положения, что подтверждается работами, посвященными изучению этой проблемы (Bopardikar et al., 2015; Du Toit, Burdick, 2011).
Распространенный подход к планированию пути и оценке вероятности столкновения – планирование Монте-Карло (Monte Carlo Motion Planning, MCMP), который позволяет оценить вероятность столкновения путем многократной симуляции движения по траектории (Janson et al., 2018; Schmerling, Pavone, 2016; Broadhurst et al., 2005). Вероятность столкновения вычисляется как отношение числа симуляций, в которых был зафиксирован факт столкновения, к общему числу симуляций. Такой подход требует проведения большого числа экспериментов для получения надежной оценки вероятности, и, как следствие, вычислительно сложен. Кроме того, метод является приближенным – не гарантирует оптимальности полученной оценки.
Альтернативный подход к оценке вероятности столкновения – оценка на основе распространения априорного распределения вероятностей пространства состояний ТС вдоль траектории движения (Liu, Ang, 2014; Van Den Berg et al., 2011; Vitus, Tomlin, 2011; Houénou et al., 2014; Lambert et al., 2008b). Такой подход является аналитическим – возможно точное вычисление за конечное количество операций. В работе (Patil et al., 2012) авторы предлагают расширение такого подхода, учитывающее, что распределение состояний в каждый момент времени зависит от того, были ли распределения в предыдущие моменты времени свободны от столкновений. Учет осуществляется через усечение распределения на каждом шаге алгоритма – отбрасывание гипотез, для которых наблюдаются столкновение и аппроксимация усеченного гауссового распределения. Такой подход позволяет распространять усеченное априорное распределение вероятностей вперед вдоль траектории движения и, как следствие, позволяет более точно рассчитать вероятность столкновения. Недостаток всех алгоритмов, основанных на распространении априорного распределения – аппроксимация моделей ошибок измерения сенсоров и неопределенности передвижения ТС нормальным распределением. Такая аппроксимация позволяет вычислять вероятность столкновения аналитически, однако редко реализуется в прикладных задачах.
Известны также работы, рассматривающие задачу оценки безопасности траектории движения не только с учетом статических препятствий, но и учитывающих возможные траектории движения других участников дорожного движения (Schreier et al., 2016; Mehta et al., 2018; Annel et al., 2016). Несмотря на то что задачи планирования траектории движения и оценки вероятности столкновения широко изучены, большинство существующих подходов не учитывает неопределенность собственного положения в момент планирования. Оценка текущего собственного положения ТС считается точной, а будущая неопределенность, как правило, моделируется нормальным распределением с центром в точках желаемой траектории, что не всегда отражает реальную неопределенность при движении и оценке собственного положения ТС.
В данной работе предложен метод оценки безопасности траектории движения ТС в условиях неопределенности собственного положения. Система включает в себя математическую модель ТС и фильтр частиц (в робототехнике более известный как алгоритм локализации Монте-Карло (Thrun, 2002)). В отличие от других работ, метод Монте-Карло не используется напрямую для оценки безопасности траектории, а лишь оценивает текущее распределение вероятностей положения ТС. Важно отметить, что алгоритм локализации Монте-Карло позволяет учитывать произвольное распределение вероятности собственного положения, что отличает предложенный подход от методов, описывающих неопределенность собственного положения нормальным распределением. Для оценки безопасности используется небольшой участок траектории, просчитанный наперед во времени при помощи математической модели и системы управления ТС. Это позволяет использовать предложенный подход в системах реального времени, а также исключает необходимость в явном виде учитывать предыдущие состояния системы.
На основе предложенного метода оценки безопасности траектории разработана система управления скоростью ТС. Предложенная система позволяет снижать скорость движения для достижения допустимого значения вероятности столкновения. Важным свойством предложенной системы, отличающей ее от ранее существующих (Schmerling, Pavone, 2016, Liu, Ang, 2014; Schreier et al., 2016; Mehta et al., 2018; Annel et al., 2016), является устойчивость к отключению сенсорных систем, использующихся для навигации. Разброс гипотез системы локализации при отключении одного или нескольких сенсорных каналов данных стремительно увеличивается, что приводит к увеличению вероятности столкновения, в свою очередь влекущей замедление и полную остановку ТС. В работе рассматривается система, учитывающая статические препятствия, однако она легко может быть расширена для учета динамических объектов.
СИСТЕМА БЕЗОПАСНОГО УПРАВЛЕНИЯ СКОРОСТЬЮ
В данной работе рассматривается задача поиска максимальной безопасной скорости ТС.
Входными данными для системы безопасного управления скоростью являются:
• оценка позы (положение + ориентация) ТС в системе координат карты ${{{\mathbf{X}}}_{t}} = \left( {{{x}_{t}},{{y}_{t}},{{\theta }_{t}}} \right)$;
• мгновенная скорость ТС ${{V}_{t}}$;
• множество частиц – гипотез о позе ТС с весами, характеризующими вероятность нахождения ТС в позе частицы ${\mathbf{X}}_{t}^{i}$: ${\mathbf{M}} = \left\{ {\left\langle {{\mathbf{X}}_{t}^{i},w_{t}^{i}} \right\rangle } \right\}$, где $w_{t}^{i}$ – вес i-й частицы, $\sum\nolimits_{i = 1}^n {{{w}_{i}} = 1} $, $i \in \left[ {1;n} \right]$, n – количество частиц;
• задание глобальной траектории ${\mathbf{T}} = \left\{ {\left\langle {{{x}_{k}},{{y}_{k}}} \right\rangle } \right\}$, $k \in \left[ {1;m} \right]$, m – количество точек траектории;
• карта проходимости ${{M}_{o}}_{c}$ – бинарное изображение, где пиксели со значением 1 принадлежат статическим препятствиям, со значением 0 – проходимым областям.
Выходом является максимальная безопасная скорость ${{V}_{s}}$ такая, что:
(1)
${{V}_{s}} = max\left\{ {{{V}_{{lim}}} \in [0;{{V}_{{max}}}]{\text{|}}P(C{\text{|}}{{{\mathbf{X}}}_{t}},{{V}_{t}},{\mathbf{M}},{\mathbf{T}},{{M}_{o}}_{c},\tau ,{{V}_{{lim}}}) < {{P}_{s}}({{V}_{{lim}}});0} \right\},$Другими словами, в формуле (1) ставится задача поиска ${{V}_{s}}$ – максимального ограничения скорости ${{V}_{{lim}}}$, которое бы удовлетворяло условию безопасности, т.е. условная вероятность столкновения БПНТС ${{P}_{C}}$ в период прогнозирования с таким ${{V}_{{lim}}}$ не превышала бы порогового значения, задаваемого функцией ${{P}_{s}}\left( {{{V}_{{lim}}}} \right)$.
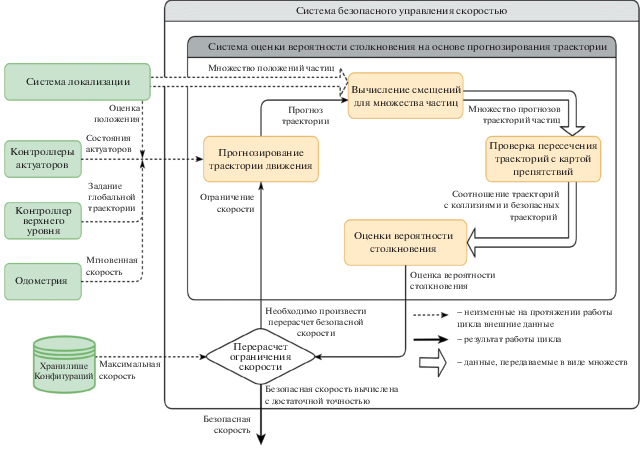
На рис. 1 изображена структура системы безопасного управления скоростью ТС. Цикл расчета безопасной скорости запускается с заданной периодичностью на всем протяжении движения ТС.
Оценка вероятности столкновения на траектории производится следующим образом: модуль прогнозирования траектории движения рассчитывает опережающую траекторию движения. Опережающая траектория затем применяется к каждой частице, с учетом их текущего положения. Другими словами, профиль траектории подвергается параллельному переносу так, чтобы его начало совпадало с текущим положением каждой частицы, и поворачивается на соответствующий угол рысканья. Таким образом, получается множество прогнозов траекторий для каждой гипотезы о положении ТС.
Затем каждая траектория ${{{\mathbf{T}}}_{i}}$ из множества прогнозов траекторий проверяется на наличие коллизий при помощи карты проходимости ${{M}_{o}}_{c}$. Траектория считается безопасной, если ни одна поза на траектории не принадлежит статическому препятствию. Чтобы проверить принадлежность позы траектории запрещенной зоне, на карте вычисляются координаты точек, задающих периметр БПТС с данной позой. Такое множество координат точек обозначим как ${\mathbf{R}}\left( {{\mathbf{X}}{\text{'}}} \right) = \left\{ {\left\langle {x,y} \right\rangle } \right\}$, где ${\mathbf{X}}{\text{'}}$ – поза на траектории. Если на ${{M}_{o}}_{c}$ координаты ни одной из этих точек не принадлежат препятствию, то точка траектории считается безопасной.
На основе имеющегося соотношения безопасных траекторий и траекторий с коллизиями вычисляется вероятность столкновения ${{P}_{C}}$:
где $\int_{\mathbf{M}} {d{{{\mathbf{X}}}_{i}}} $ – интеграл по пространству возможных поз ТС. Метод Монте-Карло аппроксимирует это пространство дискретным множеством частиц. Тогда интеграл заменяется суммой по множеству частиц; n – количество траекторий, каждая из которых относится к i-й частице, $P\left( {{{{\mathbf{X}}}_{i}}} \right) = {{w}_{i}}$ – вероятность того, что поза БПТС в настоящий момент является позой i-й частицы, иначе говоря вес i-й частицы; $P(C{\text{|}}{\mathbf{X}} = {{{\mathbf{X}}}^{i}})$ $ \in $ $\left\{ {0,1} \right\}$ – вероятность наличия коллизии на траектории при условии того, что поза БПТС в настоящий момент является позой i-й частицы:(3)
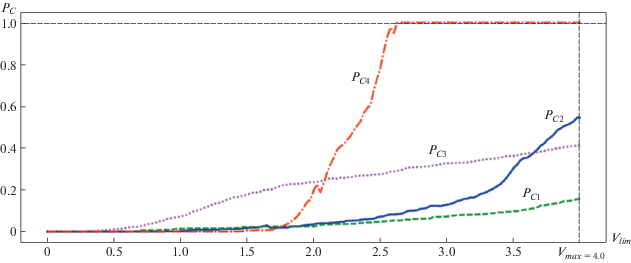
$\begin{gathered} P(C{\text{|}}{\mathbf{X}} = {{{\mathbf{X}}}_{i}}) = \\ \; = \left\{ {\begin{array}{*{20}{l}} {0,}&{{\text{е с л и }}\quad \quad\forall {\mathbf{X}}' \in {{{\mathbf{T}}}_{i}}:{\mathbf{R}}\left( {\mathbf{X}} \right) \cap {{M}_{o}}_{c} = \emptyset ,} \\ {1,}&{{\text{в }}\;\;{\text{п р о т и в н о м }}\;\;{\text{с л у ч а е }}.} \end{array}} \right. \\ \end{gathered} $Полученная вероятность используется для расчета максимальной безопасной скорости ${{V}_{s}}$. Зависимость ${{P}_{C}}$ от ограничения скорости ${{V}_{{lim}}}$ для нескольких произвольных моментов времени показана на рис. 2. Интуитивно понятно, что данная функция возрастает с увеличением ${{V}_{{lim}}}$. Эксперименты показывают, что это действительно так, но возможны незначительные отклонения. Если этими отклонениями пренебречь, то вместо полного перебора ${{V}_{{lim}}}$ расчет безопасной скорости ${{V}_{s}}$ можно производить алгоритмами быстрого поиска, например двоичным (бинарным) поиском, т.е. на каждой итерации алгоритма производится сравнение полученной вероятности столкновения ${{P}_{C}}$ для текущего ограничения скорости ${{V}_{{lim}}}$ со значением функции порогового значения вероятности ${{P}_{s}}$ для этого же ограничения скорости. После этого производится перерасчет вероятности столкновения для нового значения скорости, установленного согласно алгоритму двоичного поиска.
ПРОГНОЗИРОВАНИЕ ОПЕРЕЖАЮЩЕЙ ТРАЕКТОРИИ ДВИЖЕНИЯ
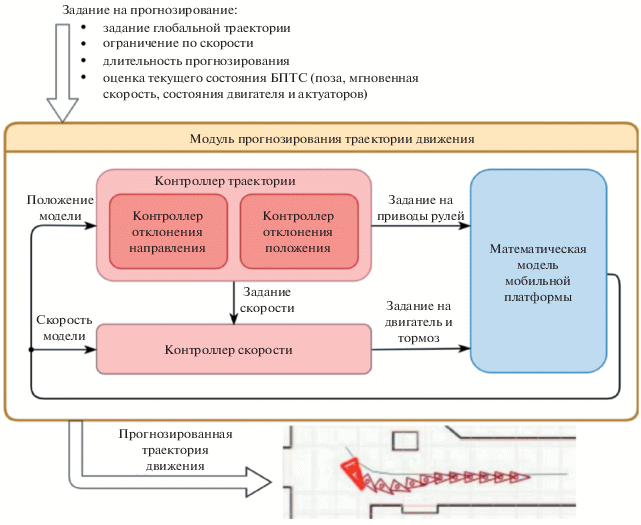
Модуль прогнозирования траектории движения (МПТД) предназначен для расчета опережающего участка траектории ТС в режиме реального времени на основе математической модели. На вход МПТД подается текущее состояние мобильной платформы (координаты и направление мобильной платформы, ее скорость, положения рулевых приводов, мгновенный момент двигателя и состояние тормоза), глобальная траектория движения ТС, ограничение по скорости, длительность прогнозирования. Выходом МПТД является прогноз траектории движения. Схема МПТД приведена на рис. 3.
МПТД объединяет в себе систему управления (СУ) движением ТС, состоящую из контроллеров траектории и скорости, и математическую модель мобильной платформы (МММП) ТС. В качестве СУ в данной работе применяется система управления, аналогичная разработанной для беспилотного автомобиля Стэндфордского университета Stanley, выигравшего в 2005 г. соревнования автономных автомобилей DARPA Grand Challenge (Hoffmann et al., 2007; Thrun et al., 2006). СУ, используемая в МПТД, идентична СУ, управляющей ТС, что гарантирует полную идентичность генерируемых СУ заданий при одинаковых значениях обратной связи от системы позиционирования ТС и математической модели.
Контроллер траектории, сравнивая желаемые значения положения и направления движения с текущими значениями, получаемыми от МММП, рассчитывает задание для рулевых приводов, а также задание текущей скорости, передаваемое контроллеру скорости. Новые задания передаются модели, и цикл замыкается. Новое состояние МММП сохраняется в виде точки траектории с привязкой к текущему симулированному времени и используется в качестве обратной связи для СУ на следующем шаге цикла. Данный цикл продолжается с заданным шагом дискретизации по времени, пока траектория не достигнет требуемой длительности прогнозирования.
Математическая модель мобильной платформы
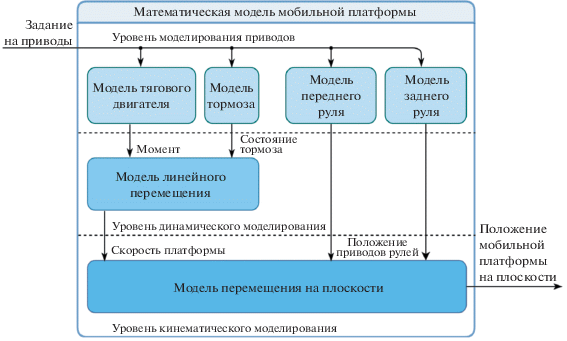
Математическая модель мобильной платформы транспортного средства описывает ее движение при подаче на входы сигналов управления, эквивалентных тем, которые подаются на настоящую платформу. Выходом МММП являются поза и мгновенная скорость движения ТС (рис. 4). МММП разработана таким образом, что для ее настройки достаточно иметь записанные управляющие сигналы и соответствующие им сигналы обратной связи исполняющих устройств. Разработанная модель не стремится описать природу и внутреннее устройство исполняемых устройств, а рассматривает их как черный ящик, минимизируя ошибку между реальными выходными сигналами и выходом модели. К преимуществам такого подхода можно отнести отсутствие необходимости знать физические особенности и характеристики тягового двигателя и рулевых приводов, что значительно упрощает процесс построения модели. Помимо этого, характеристики составляющих платформу элементов зачастую могут быть неизвестны либо отличаться от заявленных производителем. МММП является трехуровневой и состоит из шести отдельных моделей, но не все модели могут быть задействованы при моделировании платформ различной конфигурации, например, для моделирования необязательно наличие тормоза или заднего руля. Блок-схема МММП приведена на рис. 4. Подробное описание МММП приведено в Приложении 1.
Рис. 4.
Блок-схема математической модели мобильной платформы. Устройство каждого модуля приведено в Приложении 1.
АЛГОРИТМ ЛОКАЛИЗАЦИИ МОНТЕ-КАРЛО
Для оценки положения ТС в представленной системе используется алгоритм локализации Монте-Карло. Он позволяет оценить вектор состояния системы ${{{\mathbf{X}}}_{{\mathbf{t}}}}$ в момент времени t при помощи множества гипотез (так называемых частиц) и ассоциированных с ними весов (численных оценок вероятности гипотез) – $\left\{ {\langle {\mathbf{X}}_{{\mathbf{t}}}^{{\mathbf{i}}},w_{t}^{i}\rangle } \right\}$, где $i = 1,...,n$ – порядковый индекс частицы, n – количество частиц. Алгоритм локализации, примененный в данной работе, аналогичен алгоритму, описанному в работе (Абрамов и др., 2019). Каждая частица представляет собой гипотезу о положении транспортного средства в пространстве ${{{\mathbf{X}}}_{{\mathbf{t}}}} = {{({{x}_{t}},{{y}_{t}},{{\theta }_{t}})}^{T}}$, где ${{x}_{t}}$ и ${{y}_{t}}$ – двумерные координаты ТС относительно системы координат, связанной с картой в момент времени t, и ${{\theta }_{t}}$ – соответствующий угол рысканья. Вектор состояния ${{{\mathbf{X}}}_{{\mathbf{t}}}}$ зависит от предыдущего состояния системы ${{{\mathbf{X}}}_{{{\mathbf{t}} - 1}}}$ в соответствии с вероятностным законом движения $p({{{\mathbf{X}}}_{{\mathbf{t}}}}{\text{|}}{{{\mathbf{U}}}_{{\mathbf{t}}}},{{{\mathbf{X}}}_{{{\mathbf{t}} - 1}}})$, где ${{{\mathbf{U}}}_{{\mathbf{t}}}}$ – вектор управляющих сигналов, примененных к системе в момент времени $t - 1$. Вероятностный закон $p({{{\mathbf{Z}}}_{{\mathbf{t}}}}{\text{|}}{{{\mathbf{X}}}_{{\mathbf{t}}}},m)$, называемый моделью измерений, позволяет оценить вероятность измерения ${{{\mathbf{Z}}}_{{\mathbf{t}}}}$ при условии заданного положения ТС ${{{\mathbf{X}}}_{{\mathbf{t}}}}$ и известной карты m. Проблема, решаемая при помощи фильтра частиц, может быть сформулирована следующим образом: имея все последовательные измерения сенсоров ${{{\mathbf{Z}}}^{{\mathbf{t}}}} = {{{\mathbf{z}}}_{0}},...,{{{\mathbf{z}}}_{{\mathbf{t}}}}$, и управляющие сигналы ${{{\mathbf{U}}}^{{\mathbf{t}}}} = {{{\mathbf{u}}}_{0}},...,{{{\mathbf{u}}}_{{\mathbf{t}}}}$ необходимо восстановить апостериорное состояние системы ${{{\mathbf{X}}}_{{\mathbf{t}}}}$ в любой заданный момент времени t (Thrun, 2002).
Отметим, что множество частиц с соответствующими весам ${\mathbf{M}} = \left\{ {\langle {\mathbf{X}}_{{\mathbf{t}}}^{{\mathbf{i}}},w_{t}^{i}\rangle } \right\}$ является дискретной аппроксимацией плотности распределения вероятностей положения ТС. Соответственно указанное множество может быть использовано для оценки неопределенности собственного положения ТС.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Система безопасного управления скоростью была реализована в качестве подсистемы управления роботом-макетом автомобиля. Тестирование робота проводилось на полигоне, имитирующем городскую среду.
На рис. 5, слева, поэтапно отображена работа системы. Здесь синим обозначены оценка положения и опережающая траектория, темно-зеленым обозначены частицы – гипотезы о положении, светло-зеленые линии – опережающие траекторий для каждой частицы. Траектории, заканчивающиеся красным треугольником, имеют коллизии.
Рис. 5.
Слева – поэтапная визуализация работы системы безопасного управления скоростью. Справа – траектория беспилотного транспортного средства с отображением скорости.
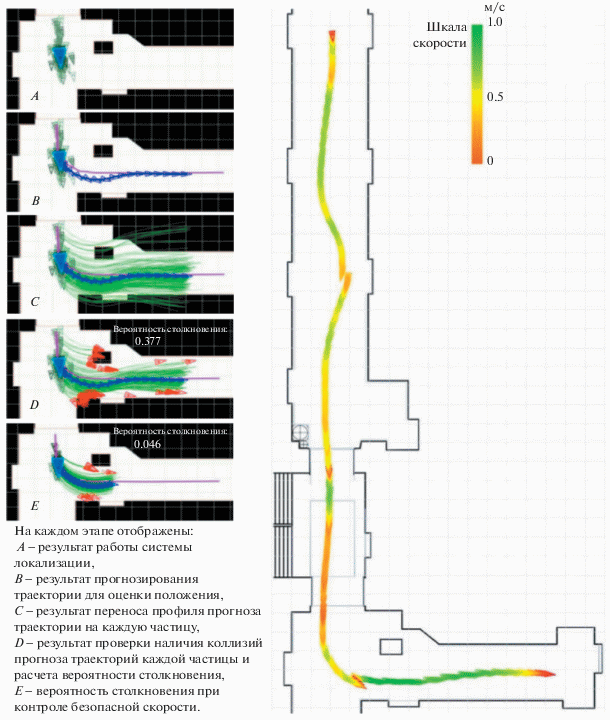
На рис. 5, справа, продемонстрирована траектория ТС, полученная в результате реального проезда. Цвет траектории в каждой ее точке соответствует мгновенной скорости движения ТС. Красный цвет соответствует нулевой скорости движения, зеленый – максимальной допустимой скорости. Наблюдаемые в траектории разрывы возникают вследствие коррекции оценки положения системой локализации. Из рисунка видно, что скорость сильно ограничивалась в местах, где движение происходило близко к стенам либо перед сложными участками траектории (повороты или въезд в узкий проход). После уточнения оценки положения либо после проезда сложных участков траектории скорость восстанавливалась.
На рис. 6 в центре изображен график изменения зависимости вероятности столкновения ${{P}_{C}}$ от ограничений скорости ${{V}_{{lim}}}$ с течением времени. По оси абсцисс отложено время от момента начала движения по маршруту. По оси ординат отложена последовательность задаваемых значений ограничений скорости от 0 до максимально возможной на данном маршруте – 4 м/с. Цветом (согласно шкале слева) отображена вероятность столкновения в течение периода прогнозирования τ для всего возможного диапазона ограничений скорости. Видно, что за некоторыми исключениями вероятность столкновения растет с увеличением скорости. Так как отклонения от монотонности возрастания функции ${{P}_{C}}$ от ограничения скорости незначительны, то при использовании монотонно убывающей или константной функции порогового значения вероятности ${{P}_{s}}$ допустимо использование алгоритмов быстрого поиска на упорядоченных данных для определения максимального допустимого ограничения скорости. Также видно, что зависимость ${{P}_{C}}$ от ограничения скорости ${{V}_{{lim}}}\quad$ сильно варьируется с течением времени. Данные скачки возникают по большей части в моменты перераспределения частиц. Для избежания нежелательных рывков (чередующихся высоких ускорений и торможений) ТС был проведен анализ функций пороговых значений вероятности ${{P}_{s}}$. На рис. 6 снизу приведены три графика изменения зависимости вероятности столкновения ${{P}_{C}}$ от ограничения скорости с течением времени с того же проезда, где черным обозначены недопустимые значения ограничения скорости, вероятность столкновения при которых превышает пороговую согласно соответствующим функциям ${{P}_{s}}$. Для наглядности аналогичные функции ${{P}_{s}}$, а также соответствующие им максимальные безопасные скорости ${{V}_{s}}_{i}$ для типовых зависимостей вероятности столкновения ${{P}_{C}}$ от ограничения скорости ${{V}_{{lim}}}$ отображены на рис. 7. Видно, что при применении убывающих функций ${{P}_{s}}_{2}$ или ${{P}_{s}}_{3}$ максимально допустимое ограничение скорости меняется значительно плавнее, чем при применении константной пороговой функции ${{P}_{s}}_{1}$, а при высоких скоростях движение становится аккуратней, тогда как на низких скоростях ТС движется более уверенно.
Рис. 6.
График изменения зависимости вероятности столкновения от ограничения скорости с течением времени.
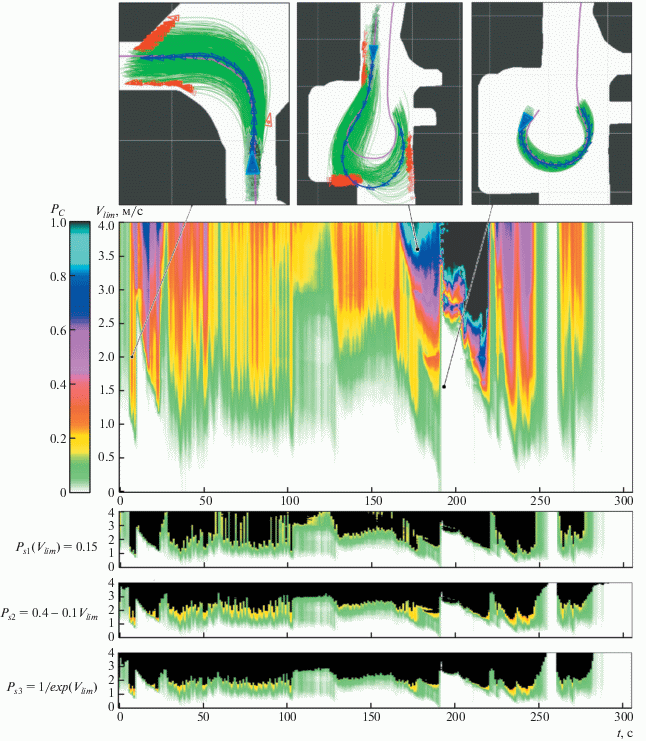
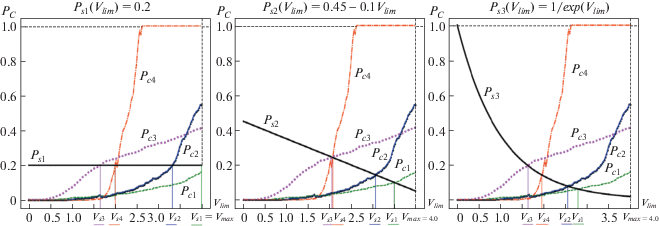
Рис. 7.
Вариации функций порогового значения вероятности столкновения и соответствующие им максимальные безопасные скорости для различных зависимостей вероятности столкновения от ограничения скорости.
На центральном графике рис. 6 после 200-й секунды заметна область, где на невысоких скоростях вероятность столкновения близка к нулевой, однако при повышении скорости она резко становится близкой к единице. Ситуации, описывающие эти случаи, отображены на рис. 6 на верхнем правом и верхнем центральном изображениях соответственно. По ним видно, что низкая вероятность при невысоких скоростях объясняется высокой точностью локализации на данном участке кругового движения. Высокая вероятность вызвана тем, что система траекторного управления не способна совершить маневр разворота при таких скоростях. В остальных областях повышенная вероятность столкновения обусловлена по большей части высокой неопределенностью собственного положения, как на верхнем левом изображении.
ЗАКЛЮЧЕНИЕ
В работе предложена система безопасного управления скоростью движения наземного беспилотного транспортного средства, основанная на математической модели ТС, системе траекторного управления движением и алгоритме локализации Монте-Карло. Центральной частью разработанной системы является оценка вероятности столкновения при движении по траектории в условиях неопределенности собственного положения. Оценка получается путем расчета опережающей траектории и анализа ее пересечения с картой проходимости для каждой гипотезы о текущем положении ТС. Полученное значение вероятности используется для расчета безопасной скорости движения.
Предложенный метод позволяет не только предотвращать столкновение с конкретным препятствием, но и может быть также использован для контроля качества работы системы локализации: при большом разбросе гипотез о положении возрастает количество коллизий с произвольными препятствиями, вследствие чего движение будет замедленно или остановлено до тех пор, пока оценка положения не станет более точной. В то время как в данной работе локальная траектория, получаемая на основе модели и системы управления ТС, считается фиксированной, предложенный метод оценки вероятности столкновения может быть использован для планирования локальной траектории движения, т.е. для выбора оптимальной траектории из нескольких доступных вариантов.
В дальнейшем предложенный метод оценки вероятности столкновения может быть расширен таким образом, чтобы учитывать динамические препятствия. Для этого препятствия, детектируемые тем или иным методом, могут наноситься на карту проходимости, что позволит учитывать их автоматически при расчете вероятности столкновения.
Список литературы
Абрамов М.П., Шипитько О.С., Лукоянов А.С., Панфилова Е.И., Кунина И.А., Григорьев А.С. Система позиционирования внутри зданий мобильной робототехнической платформы на основе детекции краев. Сенсорные системы. 2019. Т. 33. № 1. С. 30–43. https://doi.org/10.1134/S0235009219010025
Annell S., Gratner A., Svensson L. Probabilistic collision estimation system for autonomous vehicles. IEEE 19th International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2016. P. 473–478.
Bopardikar S.D., Englot B., Speranzon A. Multiobjective path planning: Localization constraints and collision probability. IEEE Transactions on Robotics. 2015. V. 31 (3). P. 562–577.
Broadhurst A., Baker S., Kanade T. Monte Carlo road safety reasoning. IEEE Proceedings. Intelligent Vehicles Symposium. IEEE, 2005. P. 319–324.
Du Toit N.E., Burdick J.W. Probabilistic collision checking with chance constraints. IEEE Transactions on Robotics. 2011. V. 27 (4). P. 809–815.
Harper C.D., Hendrickson C.T., Samaras C. Cost and benefit estimates of partially-automated vehicle collision avoidance technologies. Accident Analysis & Prevention. 2016. V. 95. P. 104–115.
Hoffmann G.M., Tomlin C.J., Montemerlo M., Thrun S. Autonomous automobile trajectory tracking for off-road driving: Controller design, experimental validation and racing. American Control Conference. IEEE, 2007. P. 2296–2301.
Houénou A., Bonnifait P., Cherfaoui V. Risk assessment for collision avoidance systems. 17th International IEEE Conference on Intelligent Transportation Systems (ITSC). IEEE, 2014. P. 386–391.
Hu X.,Chen L., Tang B., Cao D., He H. Dynamic path planning for autonomous driving on various roads with avoidance of static and moving obstacles. Mechanical Systems and Signal Processing. 2018. V. 100. P. 482–500.
Janson L., Schmerling E., Pavone M. Monte Carlo motion planning for robot trajectory optimization under uncertainty. Robotics Research. Springer, Cham, 2018. P. 343–361.
Kuffner Jr J.J., LaValle S.M. RRT-connect: An efficient approach to single-query path planning. ICRA. 2000. V. 2.
Lambert A., Gruyer D., Saint Pierre G. A fast Monte Carlo algorithm for collision probability estimation. 10th International Conference on Control, Automation, Robotics and Vision. IEEE, 2008a. P. 406–411.
Lambert A., Gruyer D., Pierre G.S., Ndjeng A.N. Collision probability assessment for speed control. 11th International IEEE Conference on Intelligent Transportation Systems. IEEE, 2008b. P. 1043–1048.
Liu P., Yang R., Xu Z. How Safe Is Safe Enough for Self-Driving Vehicles? Risk analysis. 2018. V. 39 (2). P. 315–325.
Liu W., Ang M.H. Incremental sampling-based algorithm for risk-aware planning under motion uncertainty. IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2014. P. 2051–2058.
Mehta D., Ferrer G., Olson E. C-MPDM: Continuously-parameterized risk-aware MPDM by quickly discovering contextual policies. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018. P. 7547–7554.
Patil S., Van Den Berg J., Alterovitz R. Estimating probability of collision for safe motion planning under Gaussian motion and sensing uncertainty. IEEE International Conference on Robotics and Automation. IEEE, 2012. P. 3238–3244.
Schmerling E., Pavone M. Evaluating trajectory collision probability through adaptive importance sampling for safe motion planning. arXiv preprint arXiv:1609.05399. 2016.
Schreier M., Willert V., Adamy J. An integrated approach to maneuver-based trajectory prediction and criticality assessment in arbitrary road environments. IEEE Transactions on Intelligent Transportation Systems. 2016. V. 17 (10). P. 2751–2766.
Thrun S. Particle filters in robotics. Proceedings of the Eighteenth conference on Uncertainty in artificial intelligence. Morgan Kaufmann Publishers Inc., 2002. P. 511–518.
Thrun S., Montemerlo M., Dahlkamp H., et al. Stanley: The robot that won the DARPA Grand Challenge. Journal of field Robotics. 2006. V. 23 (9). P. 661–692.
Van Den Berg J., Abbeel P., Goldberg K. LQG-MP: Optimized path planning for robots with motion uncertainty and imperfect state information. The International Journal of Robotics Research. 2011. V. 30 (7). P. 895–913.
Vitus M.P., Tomlin C.J. Closed-loop belief space planning for linear, Gaussian systems. IEEE International Conference on Robotics and Automation. IEEE, 2011. P. 2152–2159.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы