Сенсорные системы, 2020, T. 34, № 1, стр. 64-71
Ускорение свертки и обратного проецирования при реконструкции томографических изображений
А. В. Долматова 1, 2, *, Д. П. Николаев 1
1 Институт проблем передачи информации РАН
127051 Москва, Большой Каретный переулок 19, Россия
2 ООО “Смарт Энджинс Сервис”
117312 Москва, проспект 60-летия Октября 9, Россия
* E-mail: anastasiya.v.dolmatova@gmail.com
Поступила в редакцию 13.09.2019
После доработки 11.10.2019
Принята к публикации 30.10.2019
Аннотация
Метод свертки и обратной проекции (также известный как метод фильтрованных обратных проекций, FBP) широко используется для восстановления томографических изображений. Классическая реализация данного алгоритма требует выполнения $O({{N}^{3}})$ операций, где N – характерный линейный размер изображения. В данной работе предлагаются методы, позволяющие снизить вычислительную сложность алгоритма до $O({{N}^{2}}\log N)$ операций сложения и $O({{N}^{2}})$ операций умножения; тогда как ранее предложенные методы требуют $O({{N}^{2}}\log N)$ операций умножения. Показано, что операция свертки с рамп-фильтром может быть аппроксимирована последовательным применением двух рекурсивных фильтров. Также описан метод быстрого вычисления обратного дискретного преобразования Радона, позволяющий ускорить обратное проецирование.
ВВЕДЕНИЕ
Вычислительная компьютерная томография, широко используемая в медицине и промышленности, позволяет исследовать внутреннюю структуру объекта без нарушения его целостности. В основе этого метода лежит численное решение обратной задачи поглощения по набору измеренных рентгеновских проекций. Одним из распространенных способов реконструкции томографических изображений является метод свертки и обратной проекции (Filtered back projection, FBP) (Kak, Slaney, 1988). Несмотря на то что этот метод менее устойчив к шумам, чем алгебраические итерационные методы, он позволяет восстановить изображение за существенно меньшее время ($O({{N}^{3}})$, где N – линейный размер изображения). Тем не менее актуальной задачей компьютерной томографии является проведение диагностики в режиме реального времени, в этом случае скорости работы FBP оказывается недостаточно.
Существует несколько подходов, позволяющих увеличить скорость реконструкции методом свертки и обратной проекции. Один из таких подходов основан на применении теоремы о центральном сечении (Fourmont, 2003; Potts, Steidl, 2000; O’Connor, Fessler, 2006). Большинство алгоритмов данной группы использует быстрое преобразование Фурье на неоднородной сетке с последующим переходом от полярных координат к декартовым в фурье-пространстве при помощи интерполяции. При этом качество реконструкции существенно зависит от выбора метода интерполяции. Подробный анализ возникающих артефактов, искажающих восстановленное изображение, приведен в работе (Potts, Steidl, 2002).
В работе (Andersson, 2005) описан метод ускорения операции обратного проецирования с использованием перехода к логполярным координатам. Показано, что в этом случае обратное проецирование может быть представлено в виде свертки с конечным ядром и выполнено при помощи быстрого преобразования Фурье.
Еще один подход к ускорению метода FBP предложен в работах (Basu, Bresler, 2000; Xiao et al., 2002). Авторы предлагают восстанавливать не все изображение целиком, а используя свойства преобразования Радона, вычислять синограммы, соответствующие четырем квадрантам изображения, и восстанавливать их по отдельности. В этом случае, согласно теореме Найквиста-Шеннона-Котельникова, для восстановления квадранта с линейным размером в 2 раза меньше исходного изображения, можно использовать в 2 раза меньше проекций без потери качества реконструкции. Разбиение изображения на квадранты можно продолжать последовательно до тех пор, пока размер независимо восстанавливаемых участков не достигнет величины в 1 пиксел. В этом случае вычислительная сложность данного алгоритма составляет $O({{N}^{2}}\log N)$. Недостаток этого метода состоит в большом количестве промежуточных интерполяций, что может приводить к накоплению ошибки (Basu, Bresler, 2001).
Все описанные методы требуют $O({{N}^{2}}\log N)$ операций умножения. В данной работе предлагается модификация алгоритма свертки и обратной проекции, позволяющая восстановить изображение за $O({{N}^{2}}\log N)$ операций сложения и $O({{N}^{2}})$ операций умножения.
МЕТОД СВЕРТКИ И ОБРАТНОЙ ПРОЕКЦИИ
В основе математического аппарата компьютерной томографии лежит интегральное преобразование Радона, которое ставит в соответствие некоторой непрерывной финитной функции $f(x,y)$, определенной на ${{\mathbb{R}}^{2}}$, множество ее линейных интегралов вдоль всех возможных прямых $L$:
В пространстве ${{\mathbb{R}}^{2}}$ любая прямая линия L может быть однозначно задана двумя параметрами. В компьютерной томографии наиболее распространено определение прямой L углом θ наклона нормали $\vec {n} = (\cos \theta ,\sin \theta )$ к этой прямой и расстоянием от начала координат r (рис. 1, а). Такая параметризация соответствует параллельной схеме томографических измерений: объект вращается вокруг своей оси в центре системы координат, а линейный детектор зафиксирован напротив источника излучения, или, что эквивалентно, объект неподвижно зафиксирован, а линейный детектор вращается одновременно с источником. Также данная система координат актуальна для среднего слоя в конусной схеме измерений, когда объект просвечивается не параллельным, а конусным пучком рентгеновского излучения.
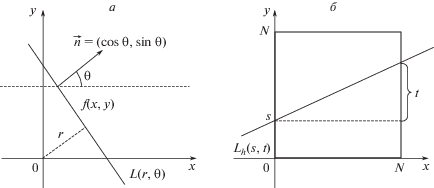
Рис. 1.
Разные виды параметризации прямых, используемые при вычислении преобразования Радона.
а – прямая L задана углом θ отклонения нормали от оси x и расстоянием до центра координат r; б – преимущественно горизонтальная прямая ${{L}_{h}}$ задана параметрами s и t, задающими координату y пересечения прямой левой границы изображения и изменение этой координаты от левой до правой границы соответственно.
Проекцией функции $f(x,y)$ называется множество всех точек в ее радон-образе, соответствующее определенному углу θ: ${{p}_{\theta }}(r) \equiv {{\left. {R[f](\alpha ,r)} \right|}_{{\alpha = \theta }}}.$ Важным свойством преобразования Радона является его обратимость. Это свойство позволяет восстановить исходную функцию $f(x,y)$ по набору измеренных проекций. Рассмотрим метод свертки и обратной проекции, широко применяемый для восстановления томографических изображений. Суть метода состоит в последовательном применении двух операций. На первом шаге выполняется свертка проекций с некоторой фильтрующей функцией $h(r)$:
Затем выполняется операция обратного проецирования:
(3)
$\tilde {f}(x,y) = \frac{1}{{2{{\pi }^{2}}}}B[\tilde {p}](x,y) = \frac{1}{{2{{\pi }^{2}}}}\int\limits_0^{2\pi } {{{{\tilde {p}}}_{\theta }}} (r)d\theta ,$(4)
$h(r) = \int\limits_{ - \infty }^\infty {\left| \omega \right|{{e}^{{2\pi i\omega r}}}d\omega } $В реальных измерительных системах получить непрерывный набор проекций не представляется возможным, поэтому все интегральные операторы заменяются соответствующим суммированием, а непрерывная свертка преобразуется в одномерный линейный фильтр. В компьютерной томографии число проекционных углов P выбирается таким образом, чтобы оно было соизмеримо с размером изображения N. В этом случае операция свертки может быть выполнена за $O({{N}^{3}})$ операций в пространстве изображения или за $O({{N}^{2}}\log N)$ операций в фурье-пространстве с использованием алгоритма быстрого преобразования Фурье (БПФ). Операция обратного проецирования требует $O({{N}^{3}})$ операций. В следующих разделах будут описаны методы, позволяющие ускорить дискретные операции свертки и обратного проецирования.
УСКОРЕНИЕ СВЕРТКИ ПРИ ПОМОЩИ РЕКУРСИВНОГО ФИЛЬТРА
При разработке быстрых алгоритмов, выполнимых за $O({{N}^{2}}\log N)$ операций, время, требуемое для вычисления свертки, становится соизмеримым со временем, требуемым для обратного проецирования. В связи с этим становится актуальным вопрос о возможности ускорения операции свертки.
Рассмотрим идеальный рамп-фильтр, импульсный отклик которого задается выражением (4). В общем случае, он имеет сингулярность в точке $r = 0$ (Wei et al., 2005). Однако на практике спектр измеренных проекций не является бесконечным ($\left| \omega \right| < W$, где W – максимальная частота, присутствующая в спектре), что позволяет избежать сингулярности. Для дискретного сигнала $W = 1{\text{/}}2\Delta $, где Δ – шаг дискретизации. Без потери общности при выборе соответствующих координат можно полагать, что $\Delta = 1$, тогда импульсный дискретный отклик фильтра (4) приобретает вид
(5)
$\begin{gathered} h(n) = 2\int\limits_0^{1/2} {\left| \omega \right|{{e}^{{2\pi i\omega n}}}d\omega } = \\ \, = \frac{1}{2}sinc(\pi n) - \frac{1}{4}{{\left( {sinc(\pi n{\text{/}}2)} \right)}^{2}}, \\ \end{gathered} $(6)
$h(n) = \left\{ \begin{gathered} {\text{1/4,}}\quad n = 0, \hfill \\ 0,\quad {\text{для нечетных }}n, \hfill \\ - 1{\text{/}}{{(n\pi )}^{2}},\quad {\text{для четных }}n. \hfill \\ \end{gathered} \right.$Дискретная свертка проекции ${{p}_{\theta }}$ с ядром (6) может быть записана в виде операции фильтрации с конечной импульсной характеристикой (КИХ-фильтр):
(7)
${{\tilde {p}}_{\theta }}(n) = {{p}_{\theta }} * h = \sum\limits_{k = n - {{L}_{0}}}^{k = n + {{L}_{0}}} {{{p}_{\theta }}} (n - k)h(k),$Рис. 2.
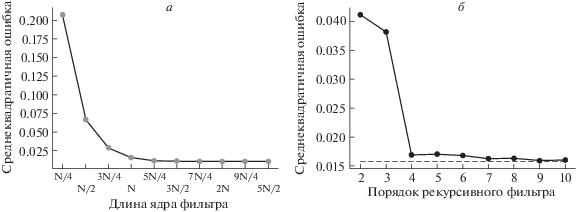
Аппроксимация рамп-фильтра двумя рекурсивными фильтрами.
а – среднеквадратичная ошибка восстановленного методом FBP изображения фантома Шеппа-Логана в зависимости от длины ядра рамп-фильтра; б – среднеквадратичная ошибка восстановленного методом FBP изображения фантома Шеппа-Логана в зависимости от порядка рекурсивного фильтра. Пунктирной линией показана ошибка, возникающая при использовании КИХ-фильтра с длиной ядра L = 256. Размер изображения N = 256, число проекций P = 256, максимальная яркость 1.0.
Вопрос снижения вычислительной сложности операции свертки является актуальным во многих задачах обработки сигналов. Так, в работах (Deriche, 1987; Young, van Vliet, 1995) приведены вычислительно эффективные способы аппроксимации фильтра Гаусса, применяемого для размытия изображений, его первой и второй производных при помощи фильтров с бесконечной импульсной характеристикой (также называемых рекурсивными или БИХ-фильтрами).
Разностное уравнение, описывающее дискретный БИХ-фильтр, имеет вид
(8)
${{\tilde {p}}_{\theta }}(n) = \sum\limits_{k = 0}^{M - 1} {{{b}_{k}}} {{p}_{\theta }}(n - k) - \sum\limits_{k = 1}^M {{{a}_{k}}} {{\tilde {p}}_{\theta }}(n - k),$Важно заметить, что импульсный отклик фильтра (8) является однонаправленным, тогда как импульсный отклик рамп-фильтра является симметричным ($r(n) = r( - n)$). Симметричный рекурсивный фильтр может быть представлен в виде суммы (Deriche, 1993) или произведения (Young, van Vilet, 1995) казуальной и антиказуальной составляющей. Оба подхода широко применяются для аппроксимации гауссового фильтра в задачах обработки изображений. В рамках данной работы мы ограничимся применением подхода Дерише.
Представим импульсную переходную функцию фильтра (6) в виде суммы казуальной и антиказульных составляющих:
(9)
$\begin{gathered} {{h}^{ + }}(n) = \left\{ \begin{gathered} h(0){\text{/}}2,\quad n = 0, \hfill \\ h(n),\quad n > 0 \hfill \\ 0,\quad n < 0. \hfill \\ \end{gathered} \right. \\ {{h}^{ - }}(n) = \left\{ \begin{gathered} h(0){\text{/}}2,\quad n = 0, \hfill \\ h(n),\quad n < 0 \hfill \\ 0,\quad n > 0. \hfill \\ \end{gathered} \right. \\ \end{gathered} $Тогда
Представим результирующий функцию ${{\tilde {p}}_{\theta }}$ в виде суммы выходов двух рекурсивных фильтров, аппроксимирующих ${{h}^{ + }}$ и ${{h}^{ - }}$:
(10)
$\begin{gathered} \tilde {p}_{\theta }^{ + }(n) = \sum\limits_{k = 0}^{M - 1} {b_{k}^{ + }} {{p}_{\theta }}(n - k) - \sum\limits_{k = 1}^M {a_{k}^{ + }} {{p}_{\theta }}(i - k), \\ \tilde {p}_{\theta }^{ - }(n) = \sum\limits_{k = 0}^{M - 1} {b_{k}^{ - }} {{p}_{\theta }}(n + k) - \sum\limits_{k = 1}^M {a_{k}^{ - }} {{p}_{\theta }}(n + k), \\ {{{\tilde {p}}}_{\theta }}(n) = \tilde {p}_{\theta }^{ + }(n) + \tilde {p}_{\theta }^{ - }(n). \\ \end{gathered} $В силу симметрии $a_{k}^{ + } = a_{k}^{ - }$ и $b_{k}^{ + } = b_{k}^{ - }$, поэтому достаточно найти коэффициенты только для казуального фильтра. Для нахождения коэффициентов будем минимизировать среднеквадратичную ошибку между откликом КИХ-фильтра (7) и БИХ-фильтра (10) на смещенную импульсную функцию вида
Эта задача может быть решена любым оптимизационным алгоритмом, например, методом сопряженных градиентов Пауэлла (Powell, 1964) или симплекс-методом (Gao, Han, 2012). Найденные коэффициенты для фильтров разного порядка приведены в табл. 1. Рисунок 2, б показывает зависимость ошибки восстановления изображения от порядка фильтра. Можно заметить, что уже при использовании рекурсивных фильтров четвертого порядка ошибка становится сопоставима с ошибкой, полученной при восстановлении изображения при помощи свертки с КИХ-фильтром.
Таблица 1.
Коэффициенты БИХ-фильтров, аппроксимирующих дискретный рамп-фильтр с длиной ядра L = 256
| k | Порядок фильтра | |||||||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 8 | 10 | |||||
| ${{b}_{{k - 1}}}$ | ${{a}_{k}}$ | ${{b}_{{k - 1}}}$ | ${{a}_{k}}$ | ${{b}_{{k - 1}}}$ | ${{a}_{k}}$ | ${{b}_{{k - 1}}}$ | ${{a}_{k}}$ | |
| 1 | 0.12499 | –0.02965 | 0.12519 | 0.01277 | 0.12488 | 0.01823 | 0.12500 | 0.00984 |
| 2 | –0.21767 | 0.93070 | –0.21002 | 0.86454 | –0.16179 | 0.48415 | –0.13253 | 0.24973 |
| 3 | 0.04041 | 0.43157 | –0.05607 | 1.15327 | –0.05081 | 0.80082 | –0.03192 | 0.45774 |
| 4 | 0.08193 | –0.39336 | 0.22527 | –0.95734 | 0.04371 | 0.21033 | –0.00396 | 0.31263 |
| 5 | –0.05358 | –0.26880 | –0.00318 | 0.23764 | –0.01208 | 0.37264 | ||
| 6 | –0.04356 | 0.20285 | 0.13462 | –0.84732 | 0.04022 | –0.01137 | ||
| 7 | –0.06360 | –0.14389 | 0.00106 | 0.01857 | ||||
| 8 | –0.04206 | 0.25214 | 0.07027 | –0.51484 | ||||
| 9 | –0.04352 | –0.05579 | ||||||
| 10 | –0.02236 | 0.14547 | ||||||
В отличие от фильтра Гаусса, рамп-фильтр не имеет шкалируемых параметров. Для обработки изображений известного размера достаточно найти коэффициенты 1 раз и не пересчитывать их для каждого изображения. На практике зачастую используют другие типы фильтров, менее чувствительные к высокочастотным шумам. Тем не менее все применяемые фильтры являются симметричными, для их представления в виде БИХ-фильтра можно использовать процедуру, аналогичную описанной выше.
УСКОРЕНИЕ ОБРАТНОГО ПРОЕЦИРОВАНИЯ ПО СХЕМЕ БРЕЙДИ $(s,t)$-ПАРАМЕТРИЗАЦИЯ
В классической реализации алгоритма FBP, операция обратного проецирования является самой затратной с вычислительной точки зрения и определяет общую асимптотическую сложность метода $O({{N}^{3}})$. В данном разделе предлагается быстрый способ вычисления дискретного обратного проецирования при помощи перехода к другой системе координат.
Введем $(s,t)$-параметризацию прямой таким образом, чтобы некоторая точка $({{x}_{0}},{{y}_{0}})$ на плоскости изображения $(x,y)$ определяла прямую на плоскости $(s,t)$. Набор проекций в пространстве параметров $(s,t)$ иногда называют линограммой (Edholm, Herman, 1987). Такая параметризация является естественной, например, для позитронной эмиссионной томографии (Hamill et al., 2003).
Пусть функция $f(x,y)$ задана в области $0 \leqslant x \leqslant N,$ $0 \leqslant y \leqslant N$. Разобьем множество всех прямых на четыре класса:
преимущественно-вертикальные прямые с уклоном вправо $L_{v}^{ + }$ $(3\pi {\text{/}}4 \leqslant \theta < \pi )$,
преимущественно-вертикальные прямые с уклоном влево $L_{v}^{ - }$ $(0 \leqslant \theta < \pi {\text{/}}4)$,
преимущественно-горизонтальные прямые с уклоном вверх $L_{h}^{ + }$ $(\pi {\text{/}}2 \leqslant \theta < 3\pi {\text{/}}4)$
и преимущественно-горизонтальные прямые с уклоном вниз $L_{h}^{ - }$ $(\pi {\text{/}}4 \leqslant \theta < \pi {\text{/}}2)$.
Тогда параметры s и t для $L_{h}^{ \pm }$ задают координаты двух точек прямой, лежащих на вертикальных границах области определения функции: $(0,s)$ и $(N,s + t)$; а для $L_{v}^{ \pm }$ – координаты двух точек, лежащих на горизонтальных границах изображения: $(s,0)$ и $(s + t,N)$ ( рис. 1, б). Параметр $t$ может принимать значения от –N до 0 для $L_{h}^{ - }$ и $L_{v}^{ - }$ и от 0 до N для $L_{h}^{ + }$ и $L_{v}^{ + }$. Между пространствами параметров $(s,t)$ и $(r,\theta )$ существует взаимно однозначная связь:
(11)
$\tan \theta = - {{\left( {\frac{N}{t}} \right)}^{p}},\quad r = \frac{{sN}}{{\sqrt {{{t}^{2}} + {{N}^{2}}} }},$Можно заметить, что $(s,t)$-параметризация обладает морфологической симметрией: для каждой из областей определения этой параметризации точка в пространстве изображения соответствует прямой в $(s,t)$-пространстве, а точка в $(s,t)$-пространстве соответствует прямой в пространстве изображений. Такая симметрия позволяет установить связь между оператором прямого проецирования (преобразования Радона) $R[f](s,t)$ и соответствующим ему оператором обратного проецирования $B[p](x,y)$. Обозначим $P_{h}^{ + }(s,t)$, $P_{h}^{ - }(s,t)$, $P_{v}^{ + }(s,t)$ и $P_{v}^{ - }(s,t)$ линограммы, соответствующие введенным семействам прямых. Заметим, что операторы прямого проецирования для преимущественно-горизонтальных прямых ${\text{R}}_{h}^{ \pm }[f]$ могут быть получены из соответствующих операторов для преимущественно-вертикальных прямых ${\text{R}}_{v}^{ \pm }[f]$ путем предварительного транспонирования изображения (поворота против часовой стрелки и отражения относительно оси x):
Перепишем выражения для операторов прямого (1) и обратного (3) проецирования в соответствии с введенной $(s,t)$-параметризацией:
(13)
$\begin{gathered} P_{v}^{ \pm }(s,t) = {\text{R}}_{v}^{ \pm }[\tilde {f}](s,t) = \int\limits_0^N {\tilde {f}} \left( {s + \frac{t}{N}y,y} \right)dx, \\ \tilde {f}_{v}^{ \pm }(x,y) = {\text{B}}_{v}^{ \pm }[P_{v}^{ \pm }](x,y) = \pm \int\limits_0^N {P_{v}^{ \pm }} \left( {x - \frac{y}{N}t,t} \right)dt. \\ \end{gathered} $Сравнивая полученные выражения, заметим, что оператор ${\text{B}}_{v}^{ \pm }$, задающий отображение из пространства $(s,t)$ в пространство $(x,y)$, может быть выражен через оператор прямого проецирования следующим образом:
(14)
${\text{B}}_{v}^{ \pm }[P_{v}^{ \pm }](x,y) = \pm {\text{R}}_{v}^{ \pm }[P_{v}^{ \pm }](x, - y).$Таким образом, при использовании $(s,t)$-параметризации операция обратного проецирования эквивалентна операции прямого проецирования со сменой знака одного из параметров. Аналогичным образом, с учетом (12),оператор ${\text{B}}_{h}^{ \pm }$ записывается в виде
ОБРАТНОЕ ПРОЕЦИРОВАНИЕ ПО СХЕМЕ БРЕЙДИ
В дискретном пространстве преобразование Радона от функции вдоль заданной прямой может быть аппроксимировано суммированием значений функции в точках, принадлежащих дискретному представлению этой прямой. Такое приближение позволяет использовать ускоренные методы вычисления оператора прямого проецирования. М. Брейди заметил, что дискретные представления прямых с близкими углами наклона обладают большим количеством общих точек (Brady, 1998). В этом случае для нахождения суммы вдоль каждой из этих прямых нет необходимости считать повторяющийся участок дважды. Брейди предложил последовательно находить частичные суммы для сегментов длины ${{2}^{i}}$, $i = 1...{{\log }_{2}}(N + 1)$. Рекурсивная реализация описанного алгоритма для двумерного и трехмерного случаев приведена в работе (Ершов и др., 2017). Важной особенностью описанного алгоритма является то, что он требует $O({{N}^{2}}\log N)$ операций, причем все эти операции являются сложением, а не умножением. В работе (Прун и др., 2013) было предложено использовать схему Брейди для ускорения вычислений обратных проекций для алгебраического метода восстановления томографических изображений.
Согласно выражению (14), операция обратного проецирования может быть представлена в виде операции прямого проецирования со сменой знака одного из параметров. Это позволяет использовать схему Брейди для ускорения алгоритма свертки и обратной проекции, позволяющего восстановления исходного изображения по набору проекций, заданных в пространстве $(s,t)$. На первом этапе выполняется сверка исходных проекций $P_{h}^{ \pm }$ и $P_{v}^{ \pm }$ с заданным фильтром. Если проекции заданы в $(r,\theta )$-пространстве, выполняется переход к $(s,t)$-координатам (11). Затем для каждого набора проекций выполняется дискретное обратное проецирование по схеме Брейди в соответствии с выражениями (14) и (15):
(16)
$\begin{gathered} \tilde {f}_{v}^{ \pm }(x,y) = \pm {\text{R}}_{v}^{ \pm }[P_{v}^{ \pm }(s,t)](x, - y), \\ \tilde {f}_{h}^{ \pm }(x,y) = \pm {{\left\{ {{\text{R}}_{v}^{ \pm }[P_{h}^{ \pm }(s,t)](x, - y)} \right\}}^{T}}. \\ \end{gathered} $Исходное изображение представляет собой сумму найденных изображений:
(17)
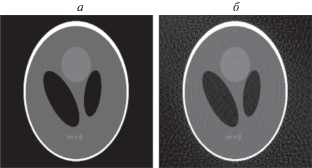
$\begin{gathered} \tilde {f}(x,y) = \tilde {f}_{h}^{ + }(x,y) + \\ + \;\tilde {f}_{h}^{ - }(x,y) + \tilde {f}_{v}^{ + }(x,y) + \tilde {f}_{v}^{ - }(x,y). \\ \end{gathered} $На рис. 3 представлен результат работы описанного алгоритма на модельном фантоме Шеппа-Логана размером 256 × 256 пикселов. Для смоделированного изображения при помощи алгоритма Брейди была найдена полная дискретная линограмма. Изображение восстанавливалось описанным методом из набора проекций в $(s,t)$-координатах.
ЗАКЛЮЧЕНИЕ
В данной работе предложена модификация алгоритма свертки и обратной проекции, позволяющая ускорить обработку изображений. Предложена аппроксимация рамп-фильтра парой рекурсивных фильтров. Показано, что для восстановления изображения в хорошем качестве достаточно фильтров четвертого порядка. Показано, что при определенном выборе параметров, задающих прямые, оператор обратного проецирования может быть выражен через оператор прямого проецирования (преобразования Радона). Это позволяет использовать схему Брейди для быстрого выполнения операции дискретного обратного проецирования. Вычислительная сложность предложенного алгоритма составляет $O({{N}^{2}})$ операций умножения, требуемых для свертки, и $O({{N}^{2}}\log N)$ операций сложения, требуемых для обратного проецирования.
Работа выполнена при частичной финансовой поддержке РФФИ (проекты 18-29-26020, 18-29-26033).
Список литературы
Ершов Е.И., Терехин А.П., Николаев Д.П. Обобщение быстрого преобразования Хафа для трехмерных изображений. Информационные процессы. 2017. Т. 17. № 4. С. 294–308.
Прун В.Е., Бузмаков А.В., Николаев Д.П., Чукалина М.В., Асадчиков В.Е. Вычислительно эффективный вариант алгебраического метода компьютерной томографии. Автоматика и телемеханика. 2013. Т. 10. С. 86–97. https://doi.org/10.1134/S000511791310007X
Andersson F. Fast inversion of the Radon transform using log-polar coordinates and partial back-projections. SIAM Journal on Applied Mathematics. 2005. V. 65. № 3. P. 818–837.
Basu S., Bresler Y. $O({{N}^{2}}\log N)$ filtered backprojection reconstruction algorithm for tomography. IEEE Transactions on Image Processing. 2000. V. 9. № 10. P. 1760–1773. https://doi.org/10.1109/83.869187
Basu S., Bresler Y. Error analysis and performance optimization of fast hierarchical backprojection algorithms. IEEE Transactions on Image Processing. 2001. V. 10. № 7. P. 1103–1117. https://doi.org/10.1109/83.931104
Brady M.L. A fast discrete approximation algorithm for the Radon transform. SIAM Journal on Computing. 1998. V. 27. № 1. P. 107–119. https://doi.org/10.1137/S0097539793256673
Deriche R. Using Canny’s criteria to derive a recursively implemented optimal edge detector. International journal of computer vision. 1987. V. 1. № 2. P. 167–187. https://doi.org/10.1007/BF00123164
Deriche R. Recursively implementating the Gaussian and its derivatives. [Research Report] RR-1893. INRIA. 1993.
Edholm P.R., Herman G.T. Linograms in image reconstruction from projections. IEEE transactions on medical imaging. 1987. V. 6. № 4. P. 301–307. https://doi.org/10.1109/TMI.1987.4307847
Fourmont K. Non-equispaced fast Fourier transforms with applications to tomography. Journal of Fourier Analysis and Applications. 2003. V. 9. № 5. P. 431–450. https://doi.org/10.1007/s00041-003-0021-1
Gao F., Han L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Computational Optimization and Applications. 2012. V. 51. № 1. P. 259–277. https://doi.org/10.1007/s10589-010-9329-3
Hamill J., Michel C., Kinahan P. Fast PET EM reconstruction from linograms. IEEE Transactions on Nuclear Science.2003. V. 50. № 5. P. 1630–2635. https://doi.org/10.1109/NSSMIC.2002.1239647
Kak A.C., Slaney M. Principles of computerized tomographic imaging. 1988 New York . IEEE press, 1988.
O’Connor Y.Z., Fessler J.A. Fourier-based forward and back-projectors in iterative fan-beam tomographic image reconstruction. IEEE transactions on medical imaging. 2006. V. 25. № 5. P. 582–589. https://doi.org/10.1109/TMI.2006.872139
Potts D., Steidl G. Fourier reconstruction of functions from their nonstandard sampled Radon transform. Journal of Fourier Analysis and Applications. 2002. V. 8. № 6. P. 513–534. https://doi.org/10.1007/s00041-002-0025-2
Potts D., Steidl G. New Fourier reconstruction algorithms for computerized tomography. Wavelet Applications in Signal and Image Processing VIII. 2000. V. 4119. P. 13–23.
Powell M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. The Computer Journal. 1964. V. 7. № 2. P. 155–162. https://doi.org/10.1093/comjnl/7.2.155
Ramachandran G.N., Lakshminarayanan A.V. Three-dimensional reconstruction from radiographs and electron micrographs: application of convolutions instead of Fourier transforms. Proceedings of the National Academy of Sciences. 1971. V. 68. № 9. P. 2236–2240. https://doi.org/10.1073/pnas.68.9.2236
Wei Y., Wang G., Hsieh J. An intuitive discussion on the ideal ramp filter in computed tomography (I). Computers and Mathematics with Applications. 2005. V. 49. № 5–6. P. 731–740. https://doi.org/10.1016/j.camwa.2004.10.034
Xiao S., Bresler Y., Munson D.C. $O({{N}^{2}}\log N)$ native fan-beam tomographic reconstruction. Proceedings IEEE International Symposium on Biomedical Imaging. IEEE press, 2002. P. 824–827.
Young I.T., Van Vliet L.J. Recursive implementation of the Gaussian filter. Signal processing. 1995. V. 44. № 2. P. 139–151. DOI: 0165-1684(95)00020-E
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы