Сенсорные системы, 2020, T. 34, № 1, стр. 72-86
Одноточечный RANSAC для оценки величины осевого вращения объекта по томографическим проекциям
М. О. Чеканов 1, 2, О. С. Шипитько 1, *, Е. И. Ершов 1
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д. 19, Россия
2 Московский физико-технический институт (национальный исследовательский университет)
141701 Московская обл., г. Долгопрудный, Институтский пер., д. 9, Россия
* E-mail: shipitko@visillect.com
Поступила в редакцию 25.09.2019
После доработки 14.10.2019
Принята к публикации 29.10.2019
Аннотация
В работе предложен алгоритм определения угла осевого вращения объекта по паре его томографических проекций, основанный на методе RANSAC. Получено аналитическое выражение для вычисления угла поворота по одному корректному сопоставлению особых точек. Алгоритм состоит из следующей последовательности этапов: выделение и сопоставление особых точек, вычисление угла поворота для каждого сопоставления, фильтрация ложных сопоставлений алгоритмом RANSAC, наконец, вычисление искомого угла методом минимизации невязки Сэмпсона по оставшимся сопоставлениям. Приведены экспериментальные результаты сравнения с методами, основанными на анализе распределения ответов. Было показано, что предложенный алгоритм обладает большей точностью. Дополнительные эксперименты продемонстрировали, что задача определения угла осевого вращения плохо обусловлена для точек объекта, лежащих вблизи оси вращения и оптического центра камеры.
ВВЕДЕНИЕ
Компьютерная томография – метод послойного представления внутренней структуры объекта, основанный на анализе ослабления рентгеновского излучения при прохождении через вещество. Данная технология применяется в различных областях: медицине (Kesminiene, Cardis, 2018), при неразрушающем контроле на производстве, для прецизионного измерения размеров объектов (Buratti et al., 2018), сельском хозяйстве (Mairhofer et al., 2017). При томографии взаимные траектории образца, детектора и источника зондирующего излучения обычно считаются известными, поскольку задаются целенаправленным перемещением компонентов прибора. Многие наиболее вычислительно эффективные алгоритмы томографической реконструкции, такие как алгоритм FDK (Feldkamp et al., 1984) и алгоритм, предложенный А. Катсевич (Katsevich, 2004), полагаются на геометрическую точность прибора и достоверно известную траекторию движения всех его составных частей. Однако по различным причинам (механические люфты, неточность датчиков угла поворота, термические деформации) реализованная траектория отличается от заданной, что негативно влияет на качество восстановленного томографического изображения. Таким образом, геометрические неточности, такие как ошибка измерения угла вращения объекта, детектора или источника, наклон образца относительно оси вращения, движение образца во время сканирования являются источником ошибок реконструкции (Ferrucci et al., 2015). В связи с этим существенное количество усилий регулярно затрачивается на калибровку систем компьютерной томографии. Геометрическая калибровка, как правило, является трудозатратным и дорогим процессом, требующим вовлечения специалистов, имеющих соответствующую квалификацию. Более того, юстировка прибора не позволяет полностью устранить влияние ошибок на результат реконструкции, а качество калибровки падает со временем. В то же время геометрические ошибки, присущие даже откалиброванной системе, все еще могут оказывать негативное влияние на качество реконструкции. Таким образом, разработка методов коррекции возникающих ошибок имеет высокую практическую значимость для повышения точности томографических измерений.
Задача определения параметров относительного перемещения подвижной камеры является актуальной и хорошо проработанной в робототехнике и компьютерном зрении. Данная работа – попытка применить существующие методы визуальной одометрии для уточнения параметров томографирования объекта с более сложной моделью формирования изображения. В работе предложен метод оценки величины осевого вращения объекта при условии неподвижности камеры (здесь и далее под терминами камера и детектор подразумевается цифровая рентгеновская камера). Оптическая ось камеры при этом перпендикулярна оси вращения объекта. Такое вращение объекта эквивалентно случаю движения камеры вокруг неподвижного объекта и хорошо описывается аппаратом эпиполярной геометрии. Далее для простоты будем рассматривать именно этот случай. Предположение, выдвигаемое в данной работе, заключается в том, что определение величины осевого вращения позволит скорректировать геометрические ошибки, обусловленные неточностью датчиков угла поворота детектора или объекта. Для определения относительного перемещения камеры осуществляется детектирование и сопоставление особых точек на паре томографических проекций (рентгенографических изображений). Далее на основе каждого сопоставления производится оценка угла поворота, путем вычисления параметров эпиполярного соответствия. Для фильтрации ложных сопоставлений применяется реализация метода Random Sample Consensus (RANSAC). Итоговая оценка угла вычисляется методом минимизации ошибки перепроекции по оставшимся после фильтрации сопоставлениям.
В целом задача геометрической коррекции в томографии широко исследована. В литературе предложено множество моделей влияния геометрических ошибок различного рода на качество реконструкции (Ferrucci et al., 2016; Kumar et al., 2011; Wenig, Kasperl, 2006). Существуют два основных способа устранения влияния этих ошибок (геометрической калибровки): калибровка, основанная на референсном объекте – объекте с известной геометрией, позволяющем оценить и скорректировать влияние геометрических ошибок методами проективной геометрии (Dewulf et al., 2013; Hermanek et al., 2017; Weiß et al., 2012); калибровка, основанная на референсных измерительных приборах, позволяющих напрямую измерить координатные неточности в томографической схеме (Welkenhuyzen et al., 2014; Bircher et al., 2018). Предложенные методы геометрической калибровки позволяют частично нивелировать координатные ошибки. Методы геометрической калибровки, как правило, разрабатываются для устранения определенного вида ошибок – ошибки масштабирования (Weiß et al., 2012) и ошибки измерения вращательного движения (Defrise et al., 2008). Процедуры калибровки, использующие данные методы, не позволяют учесть факторы, возникающие из-за отличия условий калибровочных экспериментов от экспериментов с реальными объектами. К таким факторам относятся термические деформации, возникающие вследствие значительно большей длительности реального томографического эксперимента по сравнению с калибровочным, а также ошибки, вызванные изменением геометрии исследуемого образца или его перемещением под собственным весом во время измерений.
Альтернативным подходом к уточнению результата томографической реконструкции является так называемая онлайн-калибровка. В литературе предложены методы такой калибровки, позволяющие оценить и скорректировать геометрические ошибки после или непосредственно в процессе томографического эксперимента (Xu et al., 2017; Zhang et al., 2014; Muders, Hesser, 2014; Chung et al., 2018). По опубликованным работам можно видеть, что постепенно идет переход от методов с априорно известным положением и формой калибровочного объекта (Zhang et al., 2014) к методам с одновременной реконструкцией и оценкой параметров движения (Yang et al., 2017).
Важным этапом методов томографической реконструкции с одновременным уточнением параметров движения является оценка относительного движения камеры по томографическим проекциям. В общем случае движение камеры в пространстве описывается шестью параметрами (три параметра – координаты и три – углы поворота). Однако движение детектора в томографической установке может быть приближено движением по окружности. Такое приближение при условии фиксированного радиуса сокращает количество параметров до единственного – угла поворота. Движение по окружности – широко освещенный в литературе частный случай движения камеры. Его особенности находят применение в таких областях, как калибровка параметров камеры (Hernández et al., 2007), а также восстановление 3D структуры объектов по набору их изображений (structure from motion) ( Mendonça et al., 2000; Wong, Cipolla, 2001; Vianello et al., 2018).
Для поиска соответствий между парами изображений будем применять аппарат особых точек – вычислительные алгоритмы, позволяющие детектировать, описывать и сопоставлять области изображений, инвариантные к различным преобразованиям. При поиске соответствий между особыми точками двух изображений неизбежно возникают ложные сопоставления. В контексте рассматриваемой задачи это приводит к неверной оценке угла поворота объекта. Дополнительным осложнением в контексте рентгенографических изображений является прозрачность объекта: по одному изображению трудно определить, где именно локализована точка объекта (на передней стороне, на задней или внутри), а при анализе изображений, полученных с нескольких ракурсов, диаметрально противоположные относительно оси вращения точки движутся в противоположные стороны. Таким образом, для стабильной оценки угла осевого вращения объекта необходимы методы фильтрации ложных сопоставлений.
Метод консенсус случайных выборок (Random Sample Consensus, RANSAC) является распространенным подходом к робастной оценке параметров модели по данным, содержащим выбросы (Овчинкин, Ершов, 2018; Kunina et al., 2019; Tropin et al., 2019). Известен ряд работ, в которых для оценки перемещения камеры применяется алгоритм RANSAC, строящий гипотезу по единичному сопоставлению точек пары изображений. В серии работ (Scaramuzza, 2009; 2011a; 2011b), Д. Скарамуцца и соавторы решают задачу визуальной одометрии на последовательности изображений, сделанных камерой, установленной на автомобиле. Авторами было показано, что одноточечная параметризация ведет к наибыстрейшему RANSAC-алгоритму, а также продемонстрировано, что в задаче оценки относительного перемещения автомобиля одноточечная реализация способна обеспечить точность, сопоставимую, а иногда и превосходящую стандартный пятиточечный алгоритм (Nistér, 2004). Схожая задача об оценке относительного перемещения автомобиля решалась и другим коллективом авторов. В работе (Van Cuong et al., 2013) Н.В. Куонг и соавторы подтвердили выводы Д. Скарамуццы, а также представили систему, использующую алгоритм минимизации ошибки перепроекции (bundle adjustment) для уточнения оценки относительного перемещения. В работах (Civera et al., 2009; 2010) авторами предложен алгоритм, комбинирующий RANSAC с расширенным фильтром Калмана (Grewal, 2011). Применение фильтра Калмана позволяет сократить параметризацию алгоритма RANSAC до одного сопоставления за счет использования априорной вероятностной информации о направлении движения камеры.
МОДЕЛЬ ДВИЖЕНИЯ КАМЕРЫ
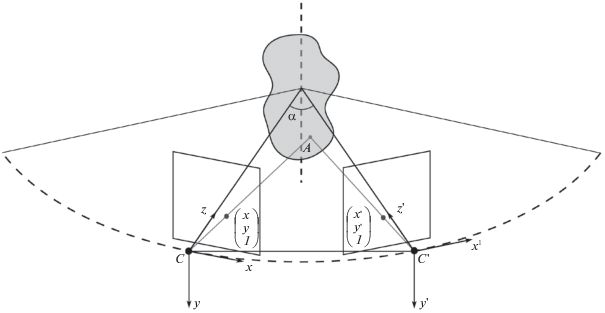
Рассмотрим камеру, движущуюся по окружности. При этом оптическая ось камеры лежит в горизонтальной плоскости, а сам объект неподвижен (рис. 1). Ставится задача оценки угла поворота камеры между двумя положениями по изображениям, полученным в них. Утверждается, что для решения данной задачи достаточно знать координаты проекции на плоскость каждого изображения одной точки пространства. Пусть $q = {{(x,y,1)}^{T}}$, $q{\text{'}}\; = {{(x{\text{'}},y{\text{'}},1)}^{T}}$ – однородные координаты некоторой точки для первого и второго положения камеры соответственно. Эти координаты связывает так называемая существенная матрица:
где R – матрица поворота вокруг оси y, ${{[t]}_{ \times }} = r\left( {\begin{array}{*{20}{c}} 0&{ - 2{\text{si}}{{{\text{n}}}^{2}}\frac{\alpha }{2}}&0 \\ {2{\text{si}}{{{\text{n}}}^{2}}\frac{\alpha }{2}}&0&{ - {\text{sin}}\alpha } \\ 0&{{\text{\;\;sin}}\alpha }&0 \end{array}} \right)$ – матричное представление векторного произведения с вектором переноса t, r – радиус окружности, по которой перемещается камера. Рассматриваемая система имеет одну степень свободы. Следовательно, можно параметризовать существенную матрицу единственным параметром, в нашем случае – углом поворота камеры:(2)
$E = r\left( {\begin{array}{*{20}{c}} 0&{ - 2{\text{si}}{{{\text{n}}}^{2}}\frac{\alpha }{2}}&0 \\ {2{\text{si}}{{{\text{n}}}^{2}}\frac{\alpha }{2}{\text{cos}}\alpha - {\text{si}}{{{\text{n}}}^{2}}\alpha }&0&{ - 2{\text{si}}{{{\text{n}}}^{2}}\frac{\alpha }{2}{\text{sin}}\alpha - {\text{sin}}\alpha {\text{cos}}\alpha } \\ 0&{{\text{\;\;sin}}\alpha }&0 \end{array}} \right).$Согласно работе (Hu et al., 2008) точки q, $q{\text{'}}$ связаны соотношением $q{{{\text{'}}}^{T}}Eq = 0$. Раскрыв это выражение, получаем выражение для угла поворота камеры:
(3)
$\alpha = 2{{\tan }^{{ - 1}}}\left( {\frac{{y - y{\text{'}}}}{{x{\text{'}}y + xy{\text{'}}}}} \right).$По этому углу однозначно восстанавливается матрица поворота и, если задан радиус окружности, вектор перемещения камеры.
ФИЛЬТРАЦИЯ ВЫБРОСОВ
Для поиска сопоставлений на паре изображений применяется алгоритм детекции и сопоставления особых точек. При работе этого алгоритма неизбежно возникают ложные сопоставления – выбросы. В данной работе в качестве алгоритма оценки угла осевого вращения, устойчивого к наличию в имеющихся данных выбросов, предлагается использовать алгоритм RANSAC. Рассмотрим его подробнее.
На каждой итерации алгоритма выбирается произвольная пара сопоставленных точек. По ней вычисляется параметр модели – угол поворота по формуле (3). Далее для оставшихся пар точек рассчитывается величина невязки Сэмпсона (Sampson distance) (Hu et al., 2008):
(4)
$d\left( {q,q{\text{'}}} \right) = \sqrt {\frac{{{{{\left( {q{{{\text{'}}}^{T}}Eq} \right)}}^{2}}}}{{\left( {Eq} \right)_{x}^{2} + \left( {Eq} \right)_{y}^{2} + \left( {{{E}^{T}}q{\text{'}}} \right)_{x}^{2} + \left( {{{E}^{T}}q{\text{'}}} \right)_{y}^{2}}}} ,$Необходимое число итераций алгоритма RANSAC может быть рассчитано как
(5)
$N \geqslant \frac{{{\text{log}}\left( {1 - p} \right)}}{{{\text{log}}(1 - \left( {1 - \epsilon {{)}^{n}}} \right)}},$ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Для тестирования предложенного алгоритма был проведен ряд экспериментов. В первую очередь алгоритм оценки угла поворота тестировали на синтетических данных. Такой эксперимент позволил изучить влияние доли ложных сопоставлений и пространственной точности детектора особых точек на качество оценки угла поворота. При помощи экспериментов на реальной последовательности томографических проекций удалось дополнительно оценить влияние свойств рентгеновских изображений на точность получаемых оценок. Последующие разделы подробно описывают методологию проводимых экспериментов и полученные результаты.
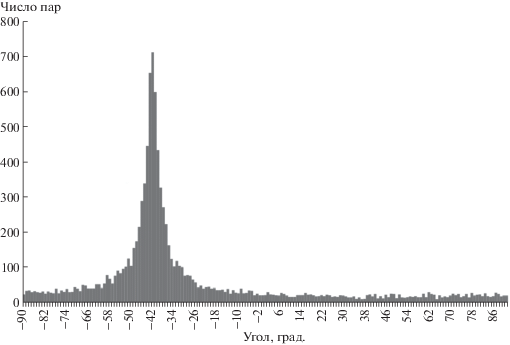
Для относительной оценки качества получаемых оценок угла осевого вращения предложенный алгоритм сравнивали с двумя альтернативными. Первый алгоритм в качестве оценки рассчитывал медиану вычисленных значений углов на всех полученных парах точек. Второй алгоритм основан на анализе гистограммы углов, вычисленных для всех сопоставлений (далее будем называть данный алгоритм гистограммным). В этом алгоритме диапазон допустимых углов разбивали на заданное число интервалов. Для каждой пары сопоставлений рассчитывали угол осевого вращения по формуле (3). Для каждого интервала гистограммы сохраняли число пар точек, задающих угол из соответствующего интервала (рис. 2). Далее выбирали интервал, в который попало наибольшее число оценок угла осевого вращения. На основе сопоставлений, попавших в этот интервал, рассчитывали угол, минимизирующий сумму квадратов отклонений оценок углов, который и принимали в качестве ответа.
ЭКСПЕРИМЕНТЫ НА СИНТЕТИЧЕСКИХ ДАННЫХ
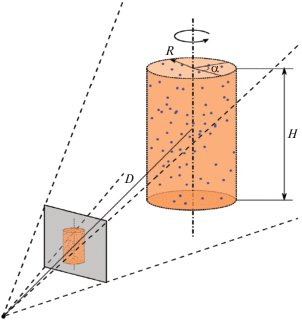
В эксперименте применяли следующую процедуру генерации данных. Точки генерировали случайным образом с равномерной плотностью распределения в объеме цилиндра, размеры и расстояние до которого задавали параметрически (рис. 3). Полученное облако точек поворачивали на заданный угол. Для обоих наборов точек (исходного и повернутого) производили переход от трехмерных координат точек к однородным координатам. К полученным однородным координатам, как исходных, так и повернутых точек, добавляли нормальный шум с нулевым средним. Таким образом, генерировался набор пар точек в однородных координатах. К полученному набору пар добавляли множество смоделированных ложных сопоставлений, получаемое сопоставлением случайно выбранных точек до и после поворота облака точек.
Для углов поворота в диапазоне (–90°, 90°) генерировали пары сопоставленных точек, на которых затем тестировали алгоритмы оценки угла поворота. Данный эксперимент был повторен $300$ раз для каждого значения угла поворота. После чего для каждого алгоритма усредняли модули отклонения оценки от истинного угла поворота. Параметры генерации точек и алгоритма RANSAC приведены в табл. 1. Результаты эксперимента представлены на рис. 4, а.
Таблица 1.
Параметры генерации данных и RANSAC в эксперименте с синтетическими данными
| Параметры | Значение |
|---|---|
| Расстояние до оси цилиндра, D | 200 |
| Высота цилиндра, H | 230 |
| Радиус цилиндра, R | 115 |
| Координатный шум детекции особых точек | нормальный |
| σ распределения | 0.0001 |
| Число выбросов | 70 |
| Число корректных сопоставлений | 30 |
| Вероятность выбрать модель без выбросов за N итераций | 0.999 |
| Необходимая доля сопоставлений, определенных алгоритмом как корректные, для конститсентной гипотезы | 0.25 |
| Порог невязки Сэмпсона | 0.01 |
Рис. 4.
a − Зависимость средней ошибки от угла поворота; б – Зависимость средней ошибки от величины шума.
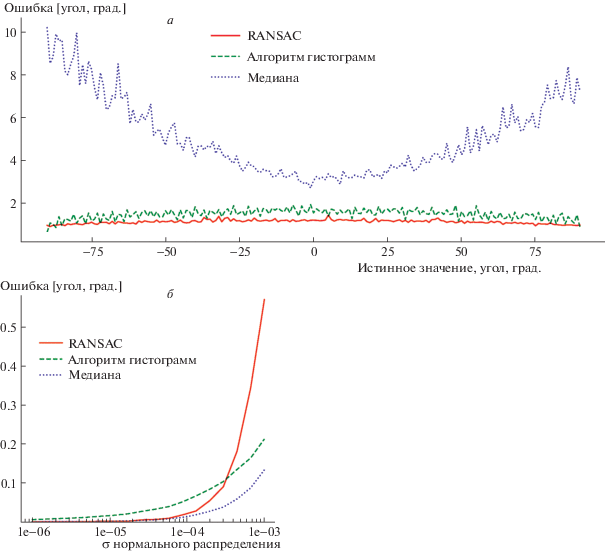
Полученные результаты демонстрируют, что предложенный алгоритм превосходит по качеству гистограммный и медианный алгоритмы на всем диапозоне исследуемых углов. Это обусловлено устойчивостью RANSAC к ложным сопоставлениям, неизбежно возникающим при поиске соответствий особых точек.
Дополнительно было оценено влияние геометрического шума детекции особых точек на ошибку оценки угла вращения. В данном эксперименте использовали те же параметры генерации точек, что и указанные в табл. 1, за исключением числа корректных сопоставлений и выбросов, которые были изменены на 100 и 0 соответственно. Шум детекции особых точек моделировали нормальным распределением с нулевым средним. Среднеквадратическое отклонение изменялось в диапазоне (10–6; 10–3). Для каждой модели шума измерение проводили 1000 раз и затем полученные значения отклонений усредняли. Зависимость ошибки от среднеквадратического отклонения изображена на рис. 4, б.
Из полученной зависимости видно, что при достаточно большом шуме ошибка оценок RANSAC начинает превышать ошибки других алгоритмов. В первую очередь это связано с тем, что во время проведения эксперимента величина порога невязки Сэмпсона не изменялась, вследствие чего корректно сопоставленные точки воспринимались алгоритмом как выбросы.
ЭКСПЕРИМЕНТЫ НА ТОМОГРАФИЧЕСКИХ ПРОЕКЦИЯХ
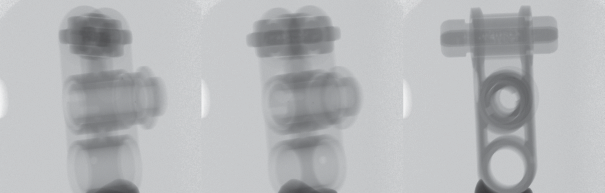
Для тестирования алгоритмов оценки угла поворота был также собран набор томографических проекций, полученных на лабораторном рентгеновском микротомографе, разработанном и функционирующем во ФНИЦ “Кристаллография и фотоника” РАН (Бузмаков, 2018; 2019). Проекции вращающегося объекта формировались с шагом 0.5° в диапазоне 0–200° (рис. 5). Все изображения получены при одинаковых условиях:
• Экспозиция 5 с;
• Энергия излучения 17 кэВ, монохроматор – пирографит, линия MoKa;
• Детектор Ximea xiRay11.
Для получения точечных сопоставлений на паре изображений применяли алгоритм детекции и дескрипции особых точек SURF (speeded up robust features) с заданным порогом гессиана – 100. Для детального описания алгоритма и его параметров можно обратиться к работе (Bay et al., 2006).
Наибольшая точность была достигнута при следующих параметрах алгоритма RANSAC: желаемая вероятность за N итераций из всех имеющихся пар точек выбрать пару, не являющуюся выбросом – 0.999; доля корректных сопоставлений – 0.05 (доля была искусственно занижена для увеличения числа итераций алгоритма); порог невзяки Сэмпсона, при которой сопоставленные точки еще считаются корректной парой – 1.73 × 10–4; минимальная доля пар, удовлетворяющих построенной модели, при которой построенная модель считается правдоподобной – 0.1. Всего было протестировано 398 пар томографических проекций. Истинное значение осевого вращения для каждой пары составляло 1°. В табл. 2 представлены результаты эксперимента, статистика считалась только по парам томографических проекций, для которых все три алгоритма смогли оценить угол вращения.
Таблица 2.
Статистика отклонения оцененного угла от истинного значения. Истинный угол вращения составлял 1° для каждой пары изображений
| Измеряемая характеристика, град. | RANSAC | Алгоритм гистограмм | Медиана |
|---|---|---|---|
| Число пар изображений, для которых был определен угол поворота объекта | 371 | 371 | 371 |
| Средний модуль ошибки | 1.02 | 1.35 | 2.77 |
| Среднеквадратическое отклонение | 0.99 | 4.85 | 9.76 |
| Минимальная величина ошибки | 0.0020 | 0.0021 | 0.0082 |
| Q1 (25%) | 0.38 | 0.19 | 0.46 |
| Q2 (50%) | 0.74 | 0.52 | 0.88 |
| Q3 (75%) | 1.25 | 2.03 | 2.09 |
| Максимальная величина ошибки | 5.66 | 91.31 | 106.87 |
На 27 изображениях RANSAC не смог определить угол. В четырех случаях гистограмма углов не имела пика выше одной пары в интервале и алгоритм гистограмм не смог вычислить угол. Средняя ошибка предложенного алгоритма меньше, чем у двух других. Максимальная величина ошибки гистограммного алгоритма составляет 91°, у RANSAC эта величина меньше 6°. Медианный алгоритм показывает худшие значения по всем характеристикам. Все три алгоритма показали среднюю величину ошибки, сравнимую с истинным углом поворота. Такая большая ошибка объясняется малым изменением координат точек объекта при повороте в 1°. При повороте на такой угол изменение координаты y (формула 3) соответствующих точек составляет приблизительно 1–3 пикселя, что сопоставимо с шумом детектора. Увеличение угла между сопоставляемыми проекциями невозможно ввиду неспособности алгоритма SURF сопоставить точки томографических проекций на углах, превышающих 3°, для исследуемого набора данных. Таким образом, надежное сопоставление томографических проекций при больших значениях угла поворота представляется дальнейшим направлением работ. Кроме того, на величину изменения координат точки влияет ее удаленность от оптической оси и оси вращения объекта. Для исследования обусловленности задачи был проведен ряд дополнительных экспериментов.
АНАЛИЗ ГРАНИЦЫ ПРИМЕНИМОСТИ ОДНОТОЧЕЧНОГО АЛГОРИТМА RANSAC
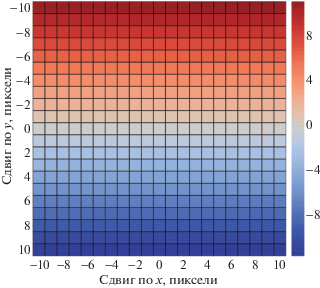
Для проверки устойчивости предложенного алгоритма к координатным ошибкам детекции особых точек был проведен следующий эксперимент: на паре томографических проекций находили сопоставления особых точек; cреди всех пар, выбранных в качестве гипотезы в процессе работы алгоритма RANSAC, выбирали наилучшую пару, т.е. ту, на которой была получена модель с наименьшим значением суммы квадратов ошибок; далее в наилучшей паре фиксировали положение первой точки и меняли положение второй; при этом заново вычисляли оценку угла поворота. Истинное значение угла осевого вращения составляло 1°. Отклонения вычисленных значений углов поворота от истинного представлены на рис. 6. Из результатов эксперимента следует, что ошибки определения положения точки вдоль оси x слабо влияют на результат работы алгоритма, в то время, как ошибка в 1 пиксель по y приводит к изменению результата более чем на градус. При этом среднее смещение точки по оси y на рассматриваемом наборе томографических проекций составило 1.75 пикселя при повороте объекта на 1°.
Рис. 6.
Вычисленное значение отклонения вычисленного угла поворота от истинного при смещении одной точки сопоставленной пары. По осям диаграммы отложены смещения вдоль координатных осей положения особой точки в пикселях.
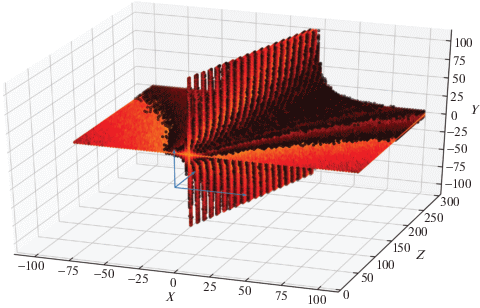
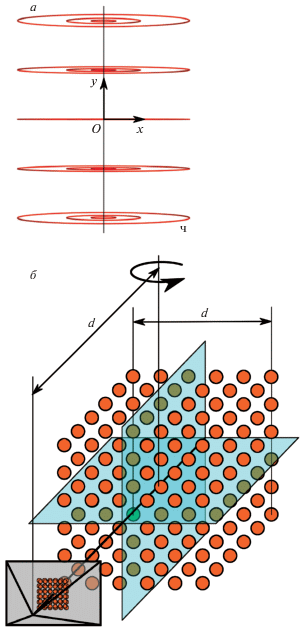
Как уже упоминалось, существуют области, в которых формула вычисления угла поворота плохо обусловлена. Так, на рис. 7, а проиллюстрированы траектории некоторых точек объекта – эллипсы. На плоскостях, близких к горизонтальной плоскости, проходящей через центр камеры, эллипсы имеют меньшую малую ось, чем на отдаленных плоскостях. Это приводит к большей ошибке вычисления угла из-за погрешности определения вертикальной составляющей перемещения точки. Чтобы изучить обусловленность формулы от положения точки объекта в пространстве, был проведен следующий эксперимент. Сгенерированную кубическую решетку размером $200$ усл.ед., центр которой располагался на расстоянии 200 усл.ед. от центра камеры, вращали на произвольный фиксированный угол 21° (рис. 7, б). Затем, как и в эксперименте на синтетических данных, координаты точек приводились к однородным с добавлением нормального шума ($\sigma = 0.004$). Для каждого сопоставления вычисляли угол поворота и его отклонение от истинного значения. Результат усредняли по 100 измерениям. Для визуализации результатов отбрасывались точки, среднее отклонение которых было меньше 60°. Отбрасывание точек было необходимо для более наглядной визуализации областей с наибольшим значением ошибки. Результат эксперимента продемонстрирован на рис. 8. Структура оставшихся точек представляет собой две плоскости. Одна из них горизонтальная, которая при проецировании на плоскость изображения переходит в горизонтальную линию, проходящую через принципиальную точку. Другая плоскость – плоскость, проходящая через ось вращения под углом, равным половине угла вращения (10.5° в нашем случае). Если подставить точки этих плоскостей в формулу вычисления угла, в ней появится неопределенность вида $\frac{0}{0}$. Таким образом, для точек вблизи этих плоскостей формула имеет плохую обусловленность.
Рис. 7.
а – Примеры траекторий точек объекта на изображении при осевом вращении. O – принципиальная точка. б – Схема эксперимента по проверке обусловленности формулы угла поворота.
Чтобы объяснить большую величину ошибки в эксперименте с томографическими снимками, последний эксперимент был повторен. На этот раз угол поворота был равен углу в эксперименте с реальными данными – 1°. Среди всех узлов решетки выбирали тот, который находился ближе всего к центру траектории детектора и при этом средний модуль отклонения которого составлял меньше 0.5°. В результате было установленно, что искомый узел находится на расстоянии 0.9 (в однородной системе координат) от центра. В имеющихся же данных размер детали составлял 0.3. Следовательно, детекция точки, для которой формула была бы хорошо обусловлена, не представляется возможной. Для решения проблемы можно предложить два пути: либо увеличить размер детали на снимках, что требует изменения геометрических параметров томографа; либо сопоставлять точки на снимках с большим углом поворота между положениями съемки, что увеличит перемещение точек объекта. Проблема последнего подхода, а именно невозможность сопоставить точки при слишком больших углах поворота, была описана в предыдущем разделе.
АНАЛИЗ СКОРОСТИ РАБОТЫ АЛГОРИТМА RANSAC
Для демонстрации эффективности одноточечного RANSAC на рис. 9, а показаны зависимости числа итераций методов RANSAC от доли выбросов. Рассматриваются методы, в которых модель строится по 1, 2 и 5 точкам. Как видно из графика, уже при количестве выбросов, равном 30% от числа корректно сопоставленных точек, число итераций одноточечного RANSAC в разы меньше 5-точечного алгоритма, который используется для восстановления движения камеры в общем случае (Nistér, 2004).
Рис. 9.
а – Число итераций RANSAC в зависимости от доли выбросов; б – Время работы алгоритма на различных этапах обработки изображений.
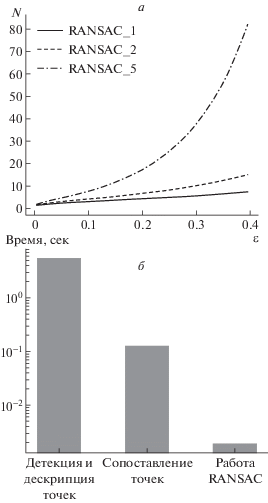
Чтобы показать, что время работы RANSAC пренебрежимо мало при вычислении угла поворота в сравнении с другими этапами обработки изображений, при проведении эксперимента на томографических данных сохранялось время, затраченное на детекцию и дескрипцию особых точек, их сопоставление и вычисление угла поворота методом RANSAC (рис. 9,б).
ЗАКЛЮЧЕНИЕ
В работе предложен алгоритм для оценки величины осевого вращения объекта по его томографическим проекциям на основе RANSAC, требующий лишь одного корректного сопоставления точек двух изображений. Проведено экспериментальное сравнение предложенного алгоритма с аналогами на синтетических и реальных данных. Показано, что предложенный алгоритм превосходит аналоги. Дополнительно проведен ряд экспериментов, направленных на изучение обусловленности задачи оценки угла вращения по паре точек изображений. Так, с одной стороны, показано, что при малых углах вращения координатный шум детекции особых точек может быть сравним с изменением координат точки, вызванным вращением, а значит, необходимы алгоритмы детекции и дескрипции особых точек, позволяющие надежно сопоставлять точки томографических проекций при больших углах поворота объекта. С другой стороны, полученные результаты демонстрируют, что близость точки объекта к оси вращения и горизонтальной плоскости, проходящей через оптическую ось камеры, делает задачу менее обусловленной и в предельном случае приводит к неопределенности оценки угла вращения. Таким образом, при выборе пар точек необходимо фильтровать точки, лежащие в описанных областях. Важно отметить, что в томографии периферийные области объекта содержат меньше наложенных сигналов, приходящих с разной глубины объекта. В связи с этим потенциально такие области лучше описываются алгоритмами особых точек, разработанными для изображений формирующихся в непрозрачной модели мира. Таким образом, области объекта, далекие от оптической оси камеры и оси вращения самого объекта, представляют наибольший интерес для оценки величины осевого вращения.
Было показано, что для применения предложенного алгоритма в решении практических задач необходимо проводить предварительный анализ обусловленности задачи для исследуемого объекта и детектируемых на нем особых точек. Предложенный алгоритм может быть в дальнейшем улучшен путем разработки механизмов детекции и дескрипции особых точек, показывающих лучшее качество на цифровых рентгенографических изображениях. Другое направление развития – минимизация ошибки опеределения угла осевого вращения при сопоставлении различных пар последовательности изображений, а не только соседних.
Список литературы
Бузмаков А.В., Асадчиков В.Е., Золотов Д.А., Рощин Б.С., Дымшиц Ю.М., Шишков В.А., Чукалина М.В., Ингачева А.С., Ичалова Д.Е., Кривоносов Ю.С., Дьячкова И.Г., Балцер М., Касселе М., Чилингарян С., Копманн А. Лабораторные микротомографы: конструкция и алгоритмы обработки данных. Кристаллография. 2018. Т. 63. № 6. С. 1007–1011.
Бузмаков А.В., Асадчиков В.Е., Золотов Д.А., Чукалина М.В., Ингачева А.С., Кривоносов Ю.С. Лабораторные рентгеновские микротомографы: методы предобработки экспериментальных данных. Известия РАН. Серия Физическая. 2019. Т. 83. № 2. С. 194–197.
Овчинкин А.А., Ершов Е.И. Алгоритм определения положения пучка эпиполярных линий для случая прямолинейного движения камеры. Сенсорные системы. 2018. Т. 32. № 1. С. 42–49.
Bay H., Tuytelaars T., Van Gool L. Surf: Speeded up robust features. European conference on computer vision. Springer. 2006. P. 404–417. https://doi.org/10.1007/11744023_32
Bircher B.A., Meli F., Küng A., Thalmann R. A geometry measurement system for a dimensional cone-beam CT. 8th Conference on Industrial Computed Tomography, Wels, Austria. 2018.
Buratti A., Bredemann J., Pavan M., Schmitt R., Carmignato S. Industrial X-Ray Computed Tomography. Springer. 2018. P. 333–369. https://doi.org/10.1007/978-3-319-59573-3_9
Chung K., Schad L.R., Zöllner F.G. Tomosynthesis implementation with adaptive online calibration on clinical c-arm systems. International journal of computer assisted radiology and surgery. 2018. V. 13 (10). P.1481–1495. https://doi.org/10.1007/s11548-018-1810-y
Civera J., Grasa O.G., Davison A.J., Montiel J. 1-point ransac for ekf-based structure from motion. 2009 IEEE/RSJ International Conferenceon Intelligent Robots and Systems. IEEE. 2009. P. 3498–3504. https://doi.org/10.1109/iros.2009.5354410
Civera J., Grasa O.G., Davison A.J., Montiel J. 1-point ransacfor extended kalman filtering: Application to real-time structure from motionand visual odometry. Journal of Field Robotics. 2010. V. 27 (5). P. 609–631. https://doi.org/10.1002/rob.20345
Defrise M., Vanhove C., Nuyts J. Perturbative refinement of thegeometric calibration in pinhole spect. IEEE transactions on medical imaging. 2008. V. 27 (2). P. 204–214. https://doi.org/10.1109/tmi.2007.904687
Dewulf W., Kiekens K., Tan Y., Welkenhuyzen F., Kruth J.-P. Uncertainty determination and quantification for dimensional measurementswith industrial computed tomography. CIRP Annals. 2013. V. 62 (1). P. 535–538. https://doi.org/10.1016/j.cirp.2013.03.017
Feldkamp L.A., Davis L., Kress J.W. Practical cone-beam algorithm. Josa a1. 1984. V. 1 (6). P. 612–619. https://doi.org/10.1016/j.cirp.2013.03.017
Ferrucci M., Ametova E., Carmignato, S., Dewulf W. Evaluating theeffects of detector angular misalignments on simulated computed tomographydata. Precision Engineering. 2016. V. 45. P. 230–241. https://doi.org/10.1016/j.precisioneng.2016.03.001
Ferrucci M., Leach R.K., Giusca C., Carmignato S., Dewulf W. Towards geometrical calibration of x-ray computed tomography systems – a review. Measurement Science and Technology. 2015. V. 26 (9). P. 092003. https://doi.org/10.1088/0957-0233/26/9/092003
Golub G.H. Least squares, singular values and matrix approximations. Aplikace matematiky. 1968. V. 13 (1). P. 44–51. https://doi.org/10.1007/978-3-662-39778-7_10
Grewal M.S. Kalman filtering. Springer. 2011 https://doi.org/10.1007/978-3-642-04898-2_321
Hermanek P., Ferrucci M., Dewulf W., Carmignato S. Optimized reference object for assessment of computed tomography instrument geometry. 7th Conference on Industrial Computed Tomography. 2017. P. 7–8.
Hernández C., Schmitt F., Cipolla R. Silhouette coherence forcamera calibration under circular motion. IEEE transactions on patternanalysis and machine intelligence. 2007. V. 29 (2). P. 343–349. https://doi.org/10.1109/tpami.2007.42
Hu M., McMenemy K., Ferguson S., Dodds G., Yuan B. Epipolar geometry estimation based on evolutionary agents. Pattern Recognition. 2008. V. 41 (2). P. 575–591. https://doi.org/10.1016/j.patcog.2007.06.016
Katsevich A. An improved exact filtered backprojection algorithm forspiral computed tomography. Advances in Applied Mathematics. 2004. V. 32 (4). P. 681–697. https://doi.org/10.1016/s0196-8858(03)00099-x
Kesminiene A., Cardis E. Cancer risk from paediatric computedtomography scanning: Implications for radiation protection in medicine. Annals of the ICRP. 2018. V. 47 (3–4). P. 113–114. https://doi.org/10.1177/0146645318756236
Kumar J., Attridge A., Wood P., Williams M. A. Analysis of the effect of cone-beam geometry and test object configuration on the measurement accuracy of a computed tomography scanner used for dimensional measurement. Measurement Science and Technology. 2011. V. 22 (3). P. 035105. https://doi.org/10.1088/0957-0233/22/3/035105
Kunina I., Panfilova E., Gladkov A. Matching of sar and optical images by independent referencing to vector map. J. Zhou. 2019. V. 11041. https://doi.org/10.1117/12.2523132
Mairhofer S., Pridmore T., Johnson J., Wells D.M., Bennett M.J., Mooney S.J., Sturrock C.J. X-ray computed tomography of crop plantroot systems grown in soil. Current Protocols in Plant Biology. 2017. V. 2 (4). P. 270–286. https://doi.org/10.1002/cppb.20049
Mendonça P.R., Wong K.-Y.K., Cipolla R. Camera pose estimationand reconstruction from image profiles under circular motion. European Conference on Computer Vision. Springer. 2000. P. 864–877. https://doi.org/10.1007/3-540-45053-x_55
Muders J., Hesser J. Stable and robust geometric self-calibrationfor cone-beam ct using mutual information. IEEE Transactions on NuclearScience. 2014. V. 61 (1). P. 202–217. https://doi.org/10.1109/tns.2013.2293969
Nistér D. An efficient solution to the five-point relative pose problem. IEEE transactions on pattern analysis and machine intelligence. 2004. V. 26 (6). P. 0756–777. https://doi.org/10.1109/tpami.2004.17
Scaramuzza D. 1-point-ransac structure from motion for vehicle-mounted cameras by exploiting non-holonomic constraints. International journal of computer vision. 2011a. V. 95 (1). P. 74–85. https://doi.org/10.1007/s11263-011-0441-3
Scaramuzza D. Performance evaluation of 1-point-ransac visualodometry. Journal of Field Robotics. 2011b. V. 28 (5). P. 792–811. https://doi.org/10.1002/rob.20411
Scaramuzza D., Fraundorfer F., Siegwart R. Real-time monocularvisual odometry for on-road vehicles with 1-point ransac. 2009 IEEEInternational Conference on Robotics and Automation. IEEE. 2009. P. 4293–4299. https://doi.org/10.1109/robot.2009.5152255
Tropin D.V., Nikolaev D.P., Slugin D.G. The method of image alignment based on sharpness maximization. J. Zhou. 2019. V. 11041. https://doi.org/10.1117/12.2522903
Van Cuong N., Heo M.B., Jee G.-I. 1-point ransac based robustvisual odometry. J. Korean GNSS Society. 2013. V. 2 (1). P. 81–89. https://doi.org/10.11003/jkgs.2013.2.1.081
Vianello A., Ackermann J., Diebold M., Jähne B. Robust houghtransform based 3d reconstruction from circular light fields. Proceedings ofthe IEEE Conference on Computer Vision and Pattern Recognition. 2018. P. 7327–7335.19 https://doi.org/10.1109/cvpr.2018.00765
Weiß D., Lonardoni R., Deffner A., Kuhn C. Geometric imagedistortion in flat-panel x-ray detectors and its influence on the accuracy ofct-based dimensional measurements. iCT conference. 2012. https://doi.org/10.1016/b978-0-12-388429-9.00008-x
Welkenhuyzen F., Boeckmans B., Tan Y., Kiekens K., Dewulf W., Kruth J.-P. Investigation of the kinematic system of a 450 kv ct scanner andits influence on dimensional ct metrology applications. Proceedings of the 5th International Conference on Industrial Computed Tomography. 2014. P. 217–225.
Wenig P., Kasperl S. Examination of the measurement uncertainty ondimensional measurements by x-ray computed tomography. Proceedingsof 9th European Conference on Non-Destructive Testing (ECNDT), Berlin,Germany. 2006.
Wong K.-Y., Cipolla R. Structure and motion from silhouettes. Proceedings Eighth IEEE International Conference on Computer Vision. 2001. V. 2. P. 217–222. https://doi.org/10.1109/iccv.2001.937627
Xu Y., Yang S., Ma J., Li B., Wu S., Qi H., Zhou L. Simultaneous calibration phantom commission and geometry calibration in cone beam ct. Physics in Medicine, Biology. 2017. V. 62 (17). № 375. https://doi.org/10.1088/1361-6560/aa77e5
Yang K., Li X., George Xu X., Liu B. Direct and fast measurementof ct beam filter profiles with simultaneous geometrical calibration. Medical physics. 2017. V. 44 (1). P. 57–70. https://doi.org/10.1002/mp.12024
Zhang F., Du J., Jiang H., Li L., Guan M., Yan B. Iterative geometric calibration in circular cone-beam computed tomography. Optik-International Journal for Light and Electron Optics. 2014. V. 125 (11). P. 2509–2514. https://doi.org/10.1016/j.ijleo.2013.10.090
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы