Сенсорные системы, 2021, T. 35, № 1, стр. 43-49
Метод ансамблирования алгоритмов кластеризации для решения задачи совместной кластеризации
И. И. Байков 1, Е. А. Семерова 1, А. И. Курмуков 1, 2, *
1 Национальный исследовательский университет, Высшая школа экономики”
101000 Москва, Мясницкая ул., 20, Россия
2 Институт проблем передачи информации им. А.А. Харкевича РАН
127994 Москва, Большой Каретный пер., д. 19, Россия
* E-mail: kurmukovai@gmail.com
Поступила в редакцию 01.09.2020
После доработки 28.09.2020
Принята к публикации 02.11.2020
Аннотация
Мы предлагаем решение задачи совместной кластеризации (multi-view clustering), в которой каждый объект описывается не одним, а несколькими независимыми наборами признаков. В настоящей работе нашими объектами являются вершины графов, которые определены на общем множестве вершин, но обладают различными множествами ребер. Задача кластеризации вершин графа заключается в разбиении множества вершин на группы таким образом, чтобы количество ребер внутри одной группы было велико, а количество ребер между вершинами из разных групп было мало. Наш подход к ансамблированию позволяет адаптировать целый класс жадных алгоритмов кластеризации вершин графа для задачи совместной кластеризации. Обход вершин каждого графа производится независимо, а присвоение меток кластеров происходит на основе усредненной метрики качества. Мы демонстрируем результаты экспериментов на реальных и синтетических данных (с известной кластерной структурой). Результаты работы нашего алгоритма на реальных данных не уступают существующим методам, а на синтетических данных с большим количеством кластеров превосходят их.
ВВЕДЕНИЕ
Поиск сообществ (кластеризация объектов) является одной из фундаментальных задач машинного обучения. Тогда как методы снижения размерности позволяют снизить признаковое представление объектов, задача кластеризации позволяет уменьшить количество рассматриваемых объектов, объединяя их в группы (кластеры) на основе схожести, подходящие для интерпретации. Традиционно задача кластеризации формулируется для объектно-признаковой матрицы ${{X}_{{n~ \times ~m}}}$, в которой каждый из n объектов описывается набором из m признаков. Однако в реальных приложениях объекты могут быть описаны наборами признаков различной природы, т.е. вместо одной объектно-признаковой матрицы мы имеем дело с несколькими. В таком случае задача кластеризации превращается в задачу совместной кластеризации (“multi-view clustering”) (Bickel, Scheffer, 2004).
В реальных приложениях часто встречаются данные, характеризующиеся наборами признаков различной природы:
● веб-страницы, описываемые, с одной стороны, своим содержанием, а с другой – активностью пользователей (Chao et al., 2017);
● медицинские МРТ снимки, характеризующиеся набором параметров пациента (пол, возраст, диагноз), параметрами съемки (сила магнитного поля, задержка и продолжительность воздействия), массивом пикселей, задающий изображение;
● видеозаписи, состоящие как из последовательности кадров, так и соответствующей им аудиодорожки, и другие.
На первый взгляд задача совместной кластеризации может быть сведена к задаче обычной кластеризации. Например, можно использовать только одну группу признаков или объединять (конкатенировать) все наборы признаков в один. Однако такие подходы могут давать не лучшие результаты: группы признаков могут быть комплементарны, и в таком случае хочется использовать всю имеющуюся информацию о структуре данных; простое объединение может приводить к тому, что признаки одной природы будут преобладать над остальными (например, из-за эффектов масштаба), вследствие чего нивелировать их влияние на структуру кластеров (Yang, Wang, 2018). Существующие методы для решения задачи совместной кластеризации можно условно разделить на три категории.
Первым широко используемым методом является подход, основанный на построении мета-графа (Strehl, Ghosh, 2002). Объекты независимо кластеризуются в каждом признаковом представлении любым выбранным алгоритмом (например, методом k-средних), после чего строится граф, в котором вершины соответствуют объектам, а вес ребра между двумя вершинами равен доле кластеризаций, в которых два соответствующих объекта попали в один и тот же кластер. Затем вершины полученного графа кластеризуются с использованием любого алгоритма кластеризации вершин графа. Результирующую раскраску можно считать решением задачи совместной кластеризации первоначальных объектов. Такой подход оказывается очень чувствителен к выбору алгоритма кластеризации на первом шаге и алгоритма поиска сообществ вершин на втором. Кроме того, структура построенного метаграфа учитывает только информацию об индивидуальных раскрасках и никак не учитывает признаковые представления, поэтому в реальных приложениях алгоритм может показывать невысокие результаты (Lancichinetti, Fortunato, 2012, Kurmukov et al., 2020).
Вторая группа методов также использует индивидуальные кластеризации, которые затем агрегируются жадным образом (Strehl, Ghosh, 2002). Сложность таких подходов может расти быстрее чем (m!)k, где m – число кластеров, а k – число индивидуальных представлений объектов (число индивидуальных кластеризаций). Такая сложность возникает из-за того, что прежде всего необходимо установить соответствие между метками кластеров во всех имеющихся кластеризациях. Для этого используется матричное представление для меток кластеров: бинарная матрица размера – число объектов на число кластеров, в которой элемент с индексами $i,~j~$ равен единице, если i-е наблюдение принадлежит j-му кластеру (и нулю в противном случае). Для установления соответствия между двумя кластеризациями необходимо перебрать расстояния (например, ${{l}_{2}}$ норму) между матрицами, с учетом всех возможных перестановок столбцов этих матриц, т.е. m!m!11, и выбрать минимальное. Во многих реальных задачах количество кластеров и количество индивидуальных представлений мало, и такое решение может быть использовано.
Вышеперечисленные подходы очень удобны, потому что позволяют использовать существующие алгоритмы кластеризации без каких-либо модификаций. Их главный недостаток заключается в том, что для получения результирующей кластеризации используется только информация об индивидуальных раскрасках (индивидуальные кластеризации на основе разных групп признаков) и не используется признаковое представление. Последняя группа методов заключается в модификации существующих алгоритмов кластеризации. Так, например, большое количество подходов модифицируют алгоритмы спектральной кластеризации, определенным образом регуляризуя Лапласианы индивидуальных представлений (Yang, Wang, 2018). Несмотря на большое количество разработанных методов совместной кластеризации для табличных данных (т.е. данных, в которых объекты описываются набором признаков), в литературе практически отсутствуют методы совместной кластеризации, специфичные для кластеризации вершин графов.
В настоящей работе мы рассматриваем задачу поиска сообществ вершин графов (совместная кластеризация вершин графов) для графов, определенных на одном множестве вершин, но обладающих разными наборами ребер. Будем называть такие графы – графами индивидуального представления. Например, это могут быть транспортные сети, в которых вершинами служат транспортные развязки, а ребрами – дороги между ними для автомобилей и пешеходов или транспортная загруженность в разное время суток. В качестве другого примера могут служить коннектомы – графы головного мозга, восстановленные по МРТ снимкам (Kurmukov et al., 2016). Вершинами в коннектомах выступают регионы головного мозга, а ребрами – связи между ними (например, пучки нейронов, тянущиеся из одного региона в другой, или функциональная коактивация этих регионов). У разных пациентов вершины их коннектомов будут относиться к одним и тем же анатомическим зонам (таким образом, разные пациенты разделяют один и тот же набор вершин), но ребра будут отличаться.
Предлагаемый нами алгоритм заключается в одновременной кластеризации вершин всех имеющихся графов. Он применим для целого класса жадных алгоритмов, в которых решение о перемещении данной вершины из одного сообщества в другое принимается на основе эвристической метрики, например, модулярности (modularity). Алгоритм сводится к одновременному обходу (в одинаковом порядке) вершин графов, принятие решения о перемещении текущей вершины в новый кластер происходит на основе взвешенного голосования большинства. В качестве примера мы демонстрируем результаты модификации алгоритма Louvain modularity (Blondel et al., 2008) для задачи совместной кластеризации, однако наш метод также может быть применен и для других алгоритмов, например, Label propagation (Raghavan et al., 2007) или Leiden (Traag et al., 2019). Мы приводим результаты экспериментов как на реальных данных (с неизвестной кластерной структурой), так и на синтетическом наборе данных.
МЕТОДЫ
Введем необходимые обозначения. Обозначим за $G\left( {V,~E} \right)$ граф (сеть) на множестве вершин V, с множеством ребер $E:V \times V$, такой граф может быть задан матрицей смежности A размера $n \times n$, где $n = \left| V \right|$, элемент матрицы ${{A}_{{ij}}}$ содержит вес ребра между вершинами i и j. Раскраской или кластеризацией графа будем называть вектор l длины n такой, что если две вершины i и j лежат в одном кластере, компоненты вектора ${{c}_{i}}$ и ${{c}_{j}}$ принимают одно значение, а если две вершины лежат в разных кластерах, то соответствующие компоненты вектора c принимают разные значения. Количество уникальных значений вектора c совпадает с количеством кластеров и обозначается буквой m. Модулярностью (Newman, 2006) называется характеристика графа и его раскраски, задаваемая формулой
(1)
$Q\left( {A,~с} \right) = ~\frac{1}{{2b}}\sum\limits_{i,~j} {\left[ {{{A}_{{ij}}} - \frac{{{{k}_{i}}{{k}_{j}}}}{{2b}}} \right]} \delta \left( {{{c}_{i}},{{c}_{j}}} \right),$Алгоритм Louvain modularity
Перед тем как описать предложенный алгоритм совместной кластеризации, опишем работу метода, который мы будем модифицировать. Алгоритм поиска сообществ Louvain modularity – это иерархический, жадный алгоритм, оптимизирующий модулярность. Алгоритм стартует с кластеризации, в которой каждая вершина принадлежит своему кластеру и состоит из двух шагов.
На первом шаге все вершины обходятся в случайном порядке, для текущей вершины i рассчитывается возможный прирост модулярности при переносе этой вершины из текущего кластера в кластер C одного из ее соседей:
На втором шаге алгоритма строится мета граф, вершины которого – это сообщества, полученные на предыдущем шаге, а веса ребер между двумя вершинами равны сумме всех ребер между вершинами соответствующих сообществ. На результирующем графе запускается первый шаг.
Алгоритм работает до тех пор, пока объединение сообществ в вершины приводит к приросту значения модулярности.
Предложенный метод ансамблирования22
Теперь дадим описание предлагаемому методу ансамблирования. Пусть дан набор графов ${{G}_{1}}\left( {V,~{{E}_{1}}} \right),~ \ldots ~,~{{G}_{k}}\left( {V,~{{E}_{k}}} \right)$, задаваемых своими матрицами смежности ${{A}^{1}},~ \ldots ~,~{{A}^{k}}$. Задача совместной кластеризации вершин заключается в поиске такой раскраски c*, которая является общей для всех графов ${{G}_{1}}\left( {V,~{{E}_{1}}} \right),~ \ldots ~,~{{G}_{k}}\left( {V,~{{E}_{k}}} \right)$, т.е. максимизирует среднюю модулярность:
(2)
$с* = ~argma{{x}_{c}}~\mathop \sum \limits_i^k Q\left( {{{{\text{A}}}^{{\text{i}}}},{\text{\;}}с} \right)~.$Пусть даны некоторый порядок обхода вершин T и числовая метрика $q\left( {i,~c} \right),$ на основе которой вершина i помещается в кластер c (в случае Louvain modularity в качестве такой числовой метрики выступает ΔQ). Вершина i помещается в кластер c* такой, что:
где $negh\left( i \right)$ – это множество уникальных кластеров соседей вершины i. Предложенная модификация алгоритма заключается в изменении этого правила: вершине i присваивается метка того кластера, для которого достигается максимальное значение метрики $q\left( {{{i}^{k}},~c} \right)$ среди всех графов ${{G}_{1}}\left( {V,~{{E}_{1}}} \right),~ \ldots ~,~{{G}_{k}}\left( {V,~{{E}_{k}}} \right)$, среди всех возможных соседей вершины i.Приведем пример модификации алгоритма Louvain modularity для решения задачи совместной кластеризации.
На первом шаге фиксируем порядок обхода вершин для всех графов. Для текущей вершины i рассчитываем прирост модулярности для каждого графа индивидуального представления: $\Delta {{Q}_{1}},...,~\Delta {{Q}_{k}}$, вершина i помещается в кластер той вершины своего соседа, в котором достигается наибольший суммарный прирост модулярности (для каждой вершины соседа мы складываем соответствующие ΔQ во всех индивидуальных представлениях). Обход вершин производится до тех пор, пока перемещение вершин позволяет увеличить модулярность.
Второй шаг аналогичен шагу в Louvain modularity с той разницей, что мы строим k метаграфов (их вершины совпадают, а ребра будут отличаться, поскольку они построены по разным графам индивидуальных представлений).
Далее будем называть предложенный алгоритм методом ансамбля.
Кластеризация на основе метаграфа
Результаты работы предложенного метаалгоритма мы сравниваем с двумя методами консенсус-кластеризации сетей:
● кластеризация графа, заданного средней матрицей смежности (далее Средний граф).
● кластеризация графа на основе метаграфа (Strehl, Ghosh, 2002) (далее Консенсус метаграф).
Первый способ заключается в том, чтобы вместо отдельных графов ${{G}_{1}},~ \ldots ~,~{{G}_{k}}$ рассматривать граф $\hat {G}$, заданный усредненной матрицей смежности: $\hat {A} = \frac{1}{k}~\sum\nolimits_i^k {{{A}^{i}}} $. Вершины такого графа можно кластеризовать с использованием любого алгоритма (мы использовали Louvain modularity).
Второй способ основан на идее построения метаграфа. Графы ${{G}_{1}},~ \ldots ~,~{{G}_{k}}$ кластеризуются индивидуально с использованием выбранного алгоритма кластеризации (мы брали традиционный Louvain modularity). На основе полученных кластеризаций33 ${{с}_{1}},...{{с}_{k}}$ строится плотный мета-граф M, в котором вершины соответствуют вершинам исходных графов, а вес ребра между двумя вершинами i и j равен доле раскрасок, в которых вершины i и j оказались в одном кластере. Полученный метаграф кластеризуется алгоритмом Louvain modularity.
Метрика качества
Для сравнения полученных средних кластеризаций мы использовали меру похожести Rand Index. Метрика Rand Index учитывает возможность переобозначения меток кластеров и рассчитывается как доля пар вершин с согласованной разметкой по отношению к общему количеству пар вершин:
где a – количество пар вершин в раскрасках ${{S}_{1}},{{S}_{2}},$ таких, что они имеют один цвет и в раскраске ${{S}_{1}}$, и в раскраске ${{S}_{2}}$; b – количество пар вершин таких, что они имеют разный цвет и в раскраске ${{S}_{1}}$, и в раскраске ${{S}_{2}}$; n – количество вершин в графе.В экспериментах мы используем Adjusted Rand Index (Hubert, Arabie, 1985) – это скорректированная на случайность версия индекса Рэнда, которая принимает значение, близкое к нулю (может быть отрицательным) в случае, если совпадения двух кластеризаций на уровне случайности, и единица для идентичных кластеров (с точностью до переобозначения меток кластеров).
Для определения качества совместной кластеризации на реальных данных использовалось значение средней модулярности (формула 2).
Синтетические данные
Задача оценки качества работы методов кластеризации осложняется тем, что их сравнение с использованием размеченной выборки не всегда может быть корректно. Сообщества вершин, выделяемые разными алгоритмами, могут быть осмысленными и оправданными с точки зрения структуры связей, но при этом не совпадать с разметкой. Например, рассмотрим граф социальной сети, в котором вершины соответствуют людям, а ребра возникают между двумя людьми, состоящими друг у друга в друзьях. В таком графе естественным образом возникают сообщества (или кластеры, т.е. группы вершин с большим количеством связей внутри сообщества и малым числом связей с вершинами из другого сообщества) людей, объединенных, например, местом учебы или проживания. Предположим, что ручная разметка этих вершин соответствует их политическим предпочтениям, это свойство может найти отражение в структуре связей (эффект, известный как ассортативность, “assortativity mixing” (Newman, 2003)), но совершенно не обязательно будет преобладать. Таким образом, для оценки качества работы алгоритмов кластеризации можно использовать следующие подходы:
● замена задачи поиска сообществ на вспомогательную, как, например, в методе k-средних, в котором минимизируется суммарное квадратичное отклонение точек кластеров от центров этих кластеров;
● использование данных малого размера с известной кластерной структурой или синтетических данных (также с известной кластерной структурой);
● экспертная интерпретация полученных кластеров.
В случае задачи совместной кластеризации для существующих реальных данных неизвестна “истинная” кластерная структура, кроме того, синтетический набор данных позволяет протестировать работу предложенного алгоритма в различных условиях: при различном числе вершин, ребер и кластеров.
Для генерации взвешенных графов с известной кластерной структурой мы использовали геометрическую модель:
1. Фиксируем количество вершин n, количество кластеров m, количество графов индивидуальных представлений k.
2. Генерируем смесь из m гауссовских распределений со средними ${{\mu }_{1}},~ \ldots ,~{{\mu }_{m}}$ и матрицами ковариации ${{\sigma }_{1}},~ \ldots ,~{{\sigma }_{m}}$ в ${{R}^{3}}$. Размеры кластеров брали одинаковыми.
3. Генерируем полный граф $G\left( {V,~E} \right)$ ,в котором вершинами служат точки из п. 2 (их принадлежность к кластеру определяется принадлежностью к компоненте гауссовской смеси), а вес ребра между двумя вершинами обратно пропорционален расстоянию между ними (чем больше расстояние, тем меньше вес).
4. Генерируем графы индивидуальных представлений ${{G}_{1}}\left( {V,~{{E}_{1}}} \right),~ \ldots ~,~{{G}_{k}}\left( {V,~{{E}_{k}}} \right)$ спарсификацией случайных ребер графа G. Таким образом, ${\text{|}}{{E}_{1}}{\text{|}} = {\text{|}}{{E}_{2}}{\text{|}}$ = … = ${\text{|}}{{E}_{k}}{\text{|}} = \left( {1 - p} \right)*\left| E \right|$.
В ходе экспериментов мы варьировали параметры m и p.
Данные ADNI
Для экспериментов на реальных данных мы использовали набор данных, подготовленный в рамках Alzheimer‘s Disease Neuroimaging Initiative (Mueller et al., 2005). Обработанные данные представляют из себя взвешенные неориентированные графы на 68 вершинах, восстановленные по снимкам магнитно-резонансной томографии (МРТ). Данные собраны по 228 участникам (807 снимков). Средний возраст пациентов на первичном осмотре 72.9 ± 7.4 года (96 женщин и 132 мужчины). Для каждого человека имеется не менее одного и не более шести снимков МРТ головного мозга. Данные включают 47 пациентов с диагностированной врачами болезнью Альцгеймера, 40 пациентов с ранними нарушениями когнитивных функций, 80 пациентов с поздней стадией умеренного нарушения когнитивных функций и 61 пациент без патологии. Для разметки вершин графа был использован атлас Десикана–Киллиани (DK) (Desikan et al., 2006), который включает 68 областей головного мозга. Веса ребер в исходной матрице кортикальных связей пропорциональны количеству трактов, обнаруженных алгоритмом трактографии.
РЕЗУЛЬТАТЫ
Описание экспериментов
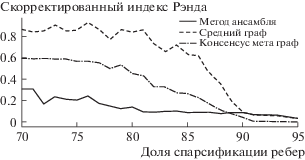
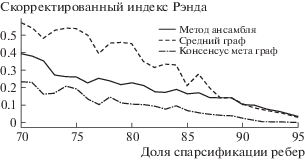
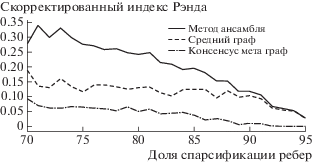
Для оценки качества работы алгоритмов граф G спарсифицировался на заданном уровне p. Мы генерировали k графов индивидуальных представлений, вершины которых кластеризовались с использованием трех различных методов: предложенный метод ансамблирования; при помощи метаграфа; при помощи графа, заданного средней матрицей смежности. Полученная кластерная структура сравнивалась с истинной (принадлежность к компонентам гауссовской смеси) с использованием меры похожести ARI (adjusted rand index). Затем уровень спарсификации p увеличивался, и вся процедура повторялась. Значение уровня спарсификации изменялось в пределах [0.8, 0.975] с шагом 0. Полученные значения ARI приведены на рис. 1, 2 и 3, качество совместной кластеризации при разных уровнях спарсификации в терминах ARI (больше – лучше). Для оценки влияния количества кластеров на качество работы алгоритма процедура, описанная выше, была проведена для графов с 10, 25 и 50 кластерами. Полученные результаты, усредненные для различных уровней спарсификции, приведены в табл. 1.
Таблица 1.
Средние значения ARI (больше – лучше). Усреднение происходило для различных уровней спарсификации, для 10 графов
| Алгоритм | 10 кластеров | 25 кластеров | 50 кластеров |
|---|---|---|---|
| (предложенный) Метод ансамбля | 0.14 | 0.19 | 0.20 |
| Средний граф | 0.57 | 0.30 | 0.12 |
| Консенсус метаграф | 0.31 | 0.09 | 0.04 |
Эксперименты с реальными данными были устроены следующим образом. Мы получили совместные кластеризации с использованием трех методов: предложенный метод ансамблирования; при помощи метаграфа; при помощи графа, заданного средней матрицей смежности. Затем полученные раскраски были использованы для расчета модулярности на всех графах из набора данных ADNI. Были получены следующие значения модулярности (среднее ± стандартное отклонение): 0.368 ± 0.028 (средняя матрица смежности), 0.356 ± 0.027 (предложенный метод ансамбля), 0.364 ± 0.029 (мета граф), 0.424 ± 0.029 (средняя модулярность для индивидуальных, близких к оптимальным, разбиений).
Анализ результатов
Результаты на синтетических данных показывают состоятельность предложенного метода в конфигурациях с большим числом сообществ (кластеров), рис. 2, 3. Для используемой схемы генерации синтетических данных можно было ожидать, что метод, использующий среднюю матрицу смежности, будет выходить победителем во всех экспериментах. Поскольку спарсификация графов происходит независимо из одного и того же графа, поэтому после усреднения ожидается значительное восстановление исходной структуры. По результатам экспериментов оказалось, что это происходит только для графов с относительно небольшим числом сообществ, а при увеличении числа кластеров предложенный алгоритм ансамблирования оказывается лучше.
Результаты на реальных данных показывают, что все подходы к получению средней кластеризации демонстрируют одинаковые результаты с точки зрения модулярности (в рамках одного стандартного отклонения). Отметим, что кластеризация, полученная предложенным алгоритмом ансамблирования, оказалась практически идентичной кластеризации, полученной на основе средней матрицы смежности (похожесть 0.84 ARI). После того как метки кластеров двух раскрасок были приведены в соответствие, только пять вершин (из 68) в двух раскрасках оказались в разных кластерах.
Исследование выполнено при поддержке РФФИ в рамках научного проекта № 19-37-90157.
Список литературы отсутствует.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы