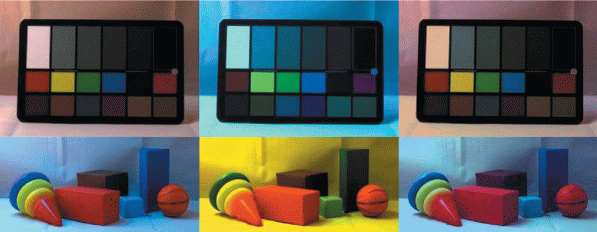Сенсорные системы, 2021, T. 35, № 3, стр. 236-259
The role of projective transformations in image normalization
I. A. Konovalenko 1, *, P. P. Nikolaev 1, 2
1 Institute for Information Transmission Problems of RAS (Kharkevich Institute)
127051 Moscow, Bolshoy Karetny pereulok, 19, Russia
2 Moscow Institute of Physics and Technology (National Research University)
141701 Moscow Region, Dolgoprudny, Institutsky pereulok 9, Russia
* E-mail: konovalenko@iitp.ru
Поступила в редакцию 25.03.2021
После доработки 12.04.2021
Принята к публикации 25.04.2021
Аннотация
The analysis of an image captured under arbitrary conditions requires preliminary normalization: a conversion to such a form as if the image was captured under normal, i.e. convenient for the further analysis, conditions. This paper presents a review of modern methods, accuracy criteria, and applications of various normalization approaches. The main stages of the problem development are described. For the first time, the two most important special cases of normalization, conventionally considered independently in the literature, are examined in a unified way. The first special case covers only geometric issues, and the second one is concerned with color aspects exclusively. We demonstrate that the normalization procedure fundamentally involves two- and three-dimensional projective transformations within a general analytical framework, without regard to its color and geometric interpretation for practical problems. This implies the advantage of the suggested unified approach.
IMAGE NORMALIZATION
Images of the same object of some visual scene differ significantly under different capturing conditions. It is obvious, for example, that images can differ radically when using image-forming optical systems (hereinafter referred to as cameras) of different spectral ranges (see Fig. 1).
Fig. 1.
Images of the same area of the Earth surface taken in the radio (left) and optical (right) spectral bands. The images are reproduced from (Abulkhanov et al., 2018).

Note that even if the spectral ranges of cameras are perfectly matching, the captured images can differ due to the divergence in their sensitivity spectra (see Fig. 2).
Images can also vary greatly when using the same camera with different camera settings (focus, aperture, color-correction). When using the same camera with fixed settings, the lighting of the scene (see Fig. 3 and 4), the angle of shooting the object (see Fig. 5) and the optical properties of the environment (see Fig. 6) have a fundamental influence on the resulting image.
Fig. 3.
Images of the same color table taken with the Canon 5D Mark III camera with fixed settings, but under different illumination conditions. This visually demonstrates the color metameric phenomenon: the colors in different areas of the color table match or differ depending on the lighting. The images are reproduced from the MLSDCR (Multiple Light Source Dataset for Colour Research) (Smagina et al., 2020).

Fig. 4.
Images of the same banknote under visible (left) and ultraviolet (right) illumination, where a bright fluorescent area stands out.

Fig. 5.
Images of the same document. Images (a), (b), and (c) are captured from different angles. Image (d) is the result of geometric normalization of image (b) assuming that the capturing angle of image (c) is chosen as the normal imaging condition.

Fig. 6.
Images of the same object. Image (a) was obtained in the air environment, (b) – in the water environment, (c) – the result of color normalization of image (b) assuming that the air environment is chosen as the normal imaging condition. Reproduced from (Shepelev et al., 2020).

The dependence of images on the capturing conditions significantly complicates the analysis of the former. Therefore, when capturing conditions can be controlled, they, as a rule, are chosen to be convenient for the subsequent analysis of the resulting images (for example, a scanner is usually used for documents image-forming) - such conditions are usually called normal. For a flat object, an important aspect of normal imaging conditions is usually the orthogonality of the camera optical axis to the plane of the object (Rodríguez-Piñeiro et al., 2011; Kholopov, 2017). However, the imaging conditions control may be technically difficult (see examples in (Nikolaev et al., 2016; Gladkov et al., 2017)), or impossible. In such cases, it is necessary to solve the normalization problem, i.e., to transform the image in such a way as if it was obtained under normal imaging conditions (see examples in Fig. 5 and 6). The initial (input) image transformed in this way is called a normalized image (see formulas (2) and (3)) (Murygin, 2010), and the imaginary camera which could have captured this normalized image is called a virtual camera (Kholopov, 2017).
In the literature, usually one of two special cases of image normalization is considered. In order to describe them, we will consider the image I, as a function:
where $\mathbb{D} \subset {{\mathbb{R}}^{2}}$ is the domain of image, $\mathbb{V}$ is codomain of image. Then, in the first case, the normalization is performed by transformation in the independent variables domain of images (see Fig. 5):(2)
${{I}_{{{\text{norm}}}}}({{{\text{H}}}_{{\text{g}}}}({\mathbf{r}})) = {{I}_{{{\text{input}}}}}({\mathbf{r}}),\quad {\mathbf{r}} \in {{\mathbb{D}}_{{{\text{input}}}}},$(3)
${{I}_{{{\text{norm}}}}}({\mathbf{r}}) = {{{\text{H}}}_{{\text{c}}}}({{I}_{{{\text{input}}}}}({\mathbf{r}})),\quad {\mathbf{r}} \in {{\mathbb{D}}_{{{\text{norm}}}}}.$We will call these types of normalizations geometric (Chen et al., 2002; Chekhlov and Ablameiko, 2004; Singh et al., 2008; Zeynalov et al., 2009), and color normalizations (Finlayson et al., 1995; Iyatomi et al., 2010; Gong et al., 2019; Kordecki, 2019) respectively. Note that formulas (2) and (3), in general, may not be sufficient to specify ${{I}_{{{\text{norm}}}}}$ at each point ${{\mathbb{D}}_{{{\text{norm}}}}}$. For example, in Fig. 5(d), the undefined region of the image ${{I}_{{{\text{norm}}}}}$ by formula (2) is shown by squares.
Active research on the topic of geometric normalization of images began with the work (Huttenlocher et al., 1993) by D. Huttenlocher published in 1993. The term normalization in the described sense was used by E. Blake for the first time in 1994 (Sinclair and Blake, 1994), but it is not widely used in English-language literature. In Russian works on image analysis, the term normalization was introduced by V.A. Gorokhovatsky in 1997 (Triputen’ and Gorokhovatskii, 1997) and it is now generally accepted (Putyatin et al., 1998; Lyubchenko and Putyatin, 2002; Chekhlov and Ablameiko, 2004; Vanichev, 2007; Kozlov et al., 2009; Bolotova et al., 2017). The term color image normalization was introduced by G. Finlayson (Finlayson et al., 1998). However, research on this topic began much earlier, for example, in the fundamental work of G. Healey (Healey, 1989) published in 1989.
If the normal imaging conditions are exclusive, then normalization is an idempotent operation: applying normalization twice to an image has the same result as applying it once (Finlayson et al., 1998; Nikolaidis, 2011). If, however, there are multiple sets of imaging conditions that can be considered normal (Murygin, 2010; Nikolayev, 2016), it is reasonable to require idempotence additionally. Then normalization will not change the image originally captured under normal conditions. The idempotence combines the operation of normalization of images with the operation of normalization of vectors (reducing them to a single unit length).
Images obtained under arbitrary imaging conditions are often considered as a result of the distortion of “imaginary” (hypothetical) images obtained under normal imaging conditions. Normalization in such a case is understood as removal (correction, compensation) of these distortions (Kholopov, 2017; Baltzopoulos, 1995; Calore et al., 2012; Tsviatkou, 2014).
Normalization of images is usually based on some model of the target object of the scene. For example, such a model can be a so-called reference image (Murygin, 2010; Nikolaev, 2010; Vanichev, 2007) – an image of a similar object obtained under normal conditions. In the described case, the geometric normalization of the image can be considered as an operation of its alignment (image registration (Goshtasby, 2005)) with the reference image.
Algorithms for the geometric normalization of images are usually based on the assumption that the target object of the scene is sufficiently rich in detail, well known a priori, and depicted informatively. Otherwise, most approaches do not yield satisfactory results. To eliminate this problem, a theory has been proposed. This theory provides methods for projective geometric normalization for the extremely complex cases where the information characterizing the object is minimal in the number of its normalizing (projectively invariant) features. An example of such an approach to geometrical normalization is known for flat smooth shapes given by the family of ovals (o). Normalization is carried out by the procedure of its redescription, invariant with respect to the 2D homography transformation, i.e. the projective transformation of the plane o in Cartesian 3D space. The algorithms of such processing are particularly simple in the case of symmetry of three kinds (radial, axial or rotational), while the detection of symmetry elements (axes and/or centers) performed via fast universal procedures (Nikolaev, 2016). It is sufficient enough to obtain an invariant description of o as a projection onto a “reference” 4-vertex shape or by calculating a closed curve of 2D wurf-mapping (Nikolaev, 2010). Let us add that the family o (their subfamily are the Lamé curves, also called “superellipses” having at least two axes plus the center of symmetry) rightfully belongs to the objects which do not include the “standard” varieties of projectively invariant points: inflection, fracture, second-order contact and etc. In the model, when the optical registration of o is adequately described by a flat central projection given by a notional pinhole camera, such an invariant representation of o (if technically necessary, for some problem of o recognition) can be transformed (up to a scale accuracy) to a normalized version of representation as if the camera was capturing o orthogonally. In the context of this approach, the cases when the target object is modeled, for example, by the composition of two ovals (Nikolaev et al, 2018), a composite oval (Nikolaev, 2010), an oval with hidden symmetries (Nikolaev, 2014; Nikolaev, 2017), an oval with an inner point (Savchik and Nikolaev, 2016), an outer straight line (Balitskiy et al., 2017), with two marked points (Savchik and Nikolaev, 2018) were studied.
THE NORMALIZATION PROBLEM AND ITS PRACTICAL APPLICATIONS
The optical systems of practical interest have geometric aberrations – deviations from the pinhole camera model. One of such aberrations is radial distortion, which disturbs the collinear correspondence between the image and the subject and is typical in inexpensive optical systems equipped with wide-angle lenses and designed for wide-scale use. Geometric aberrations are related to imaging conditions, so their elimination is a special case of normalization. In (Kunina et al., 2016), a single-image blind radial distortion compensation algorithm was proposed.
The same cameras have different radial distortions when capturing images in air and underwater conditions. The paper (Sheshkus et al., 2020) provides an analytical description of visual geometric distortions occurring when capturing underwater objects. A normalization transformation was introduced to compensate for underwater distortion without an underwater calibration procedure. In (Titov et al., 2019), a method for the normalization of underwater color images is proposed.
It is reasonable to consider the algorithms of “automatic white balance” as the color normalization of images. Conventionally, white balance is performed before converting the color coordinates of the camera to the coordinate system of a standard observer for subsequent image finalization and rendering (Karaimer, Brown, 2016), which allows for significantly improved picture quality using simple linear models (Karaimer, Brown, 2018). At the moment, there are many different white balance algorithms. There are two reviews on the subject (Gijsenij et al., 2011; Das et al., 2018), new datasets are being created (Ershov et al., 2020), and the original, more complex formulations were proposed (Savchik et al., 2019).
Another example of color normalization is the reconstruction of multispectral images. The visual non-optimality of the latter is due to various deviations of imaging conditions from normal (Kober, Karnaukhov, 2016a; Kober, Karnaukhov, 2016b; Kober, Karnaukhov, 2015; Chochia, 2016).
Normalization is used for preprocessing of images in many image analysis tasks, some examples of both types of normalization will be discussed further.
Document Image Analysis
It is common to apply geometric (Rodríguez-Piñeiro et al., 2011), (Skoryukina et al., 2020), and color (Polevoy et al., 2021) normalization to images of documents for the subsequent optical recognition of the latter. At the same time, inaccuracies in the normalization can lead to recognition errors. In (Bulatov et al., 2020), a dataset of video recordings of documents obtained from a variety of camera angles, and in (Smagina et al., 2020), a dataset of images obtained under different light conditions are presented.
In the field of automatic document analysis, the standard task is to remove the slope of letters and significant characters to be recognized, i.e. to perform geometric normalization of the image. There are many papers demonstrating the influence of tilt compensation on all subsequent stages of document processing. The main problem, in this case, is to determine this tilt angle. One of the standard approaches is the Hough image analysis of the document image. The paper (Bezmaternykh, Nikolaev, 2020) investigates the quality of tilt angle detection using the Hough image obtained using the fast Hough transform algorithm.
As part of the task of understanding a document, often the intermediate step is the recognition of certain attributes of the document. For this purpose, the localized attributes are sent as the input of the OCR module in the form of images of text fragments. Most of these modules are designed for the task of recognition of the standard font fragments, but italic and handwritten texts are quite common and also should be recognized. Often, this leads to complications of the standard fragment processing scheme, in particular, algorithms for segmentation of the string image into rasters of individual characters (Chernov et al., 2016). Correction of slanted text fragmentation is one of the classical stages of image normalization in OCR modules. Nowadays, there are many methods for determining the angle of slope of text fragments. Many of them are based on the application of fast Hough transform (Limonova et al., 2017; Bezmaternykh et al., 2018). However, the slant of the characters can occur not only because of the slanted font but also because of the inaccurate normalization of the imaging angle. In (Konovalenko et al., 2020b), an analytical expression for the maximum target direction normalization error for the document was proposed.
A classic step in automatic document processing is image segmentation. Its special case is the binarization task: all pixels of the source image are divided into two classes, which are usually referred to as object and background. Application of such segmentation is widely used in systems of document recognition, archival storage. This technique is also employed to improve the visual quality of document images, which is a special case of the problem of image normalization. The task of document binarization attracts the close attention of developers of automatic recognition procedures. There is even a special DIBCO competition to monitor the situation in this area, which is regularly held within ICDAR. Recently, the highest accuracy of binarization is demonstrated by the solutions which employ artificial neural networks. The most popular architecture is U-Net, based on of which new solutions are constantly being proposed. One such solution, for example, won a competition in 2017 (Bezmaternykh et al., 2019). The U-Net architecture has been the subject of in-depth research by scientists, both in finding optimal neuronal activation functions for training (Gayer et al., 2021) and in reducing the number of trainable coefficients in the model (Limonova et al., 2021). However, in some cases, the use of neural network solutions is not feasible, for example, due to limited resources on the device. One of the standard tools in such a case may be the Otsu method or its various generalization (Ershov et al., 2021).
Another relevant task is the recognition of matrix barcodes scanned or captured under conditions unknown a priori. Usually, the process of code recognition is divided into several stages. First, the code is localized in the image, then its corners are precisely determined and the normalization of the image is carried out. Then the code is divided into separate modules (matrix code cells), and the original message is extracted. However, sometimes it is possible to apply a generative approach to recognition, instead of individual modules extraction (Bezmaternykh et al., 2010).
In (Kunina et al., 2020), a method for color normalization of document illumination in a full-page scanner without moving parts was proposed, and in (Karnaukhov and Kober, 2017), an adaptive method for eliminating shadows in the document image was proposed.
Normalization is also used for the automatic classification of document types (Awal et al., 2017).
Algorithms for geometric normalization of document images are often based on vanishing points (Shemiakina et al., 2020; Abramov et al., 2020). In (Konovalenko et al., 2020c), a method of vanishing point detection based on the principle of maximum likelihood was introduced, and in (Sheshkus et al., 2020), a method based on neural network involvement was demonstrated.
Traffic situation recognition
In the recognition of the traffic situation by automated devices, the features that are localized in the plane of the road are of greatest interest: the markings of the roadway, its boundaries. Recognition of such features is greatly simplified if the image is received from above the plane of the roadway (the so-called birds-eye view) since in this case the parallel lines on the road are projected as the parallel lines on the image. In practice, cameras are mounted behind the windshield of cars. In order to switch from the camera images to the “birds-eye view on the road” view, a projective transformation can be applied that performs a virtual rotation of the camera. Such normalization is the first step of many well-known algorithms for the recognition of road boundaries and road markings (Panfilova et al., 2021; Shipitko et al., 2019; Shipitko et al., 2021; Prun et al., 2017), which is also used for navigation of unmanned vehicles (Abramov et al., 2019; Shipitko, Grigoryev, 2018). Image normalization is also applied to license plate recognition (Murygin, 2010; Povolotskiy et al., 2019; Povolotskiy et al., 2018).
Computed tomography scan
In classical computed tomography, the probing radiation is considered to be monochromatic and the tomographic reconstruction is reduced to the problem of reversal of the Radon transform. However, modern tomographs use X-ray tube with polychromatic radiation as a radiation source. Applying this technique to the projections registered in the polychromatic model obtained by classical reconstruction algorithms leads to distortions in the reconstructed image. To obtain a correct reconstructed image, it is necessary to bring the registered projections to monochromatic, i.e. to solve the normalization problem. It is impossible to solve the normalization problem exactly by any known mathematical transformation. There are many approaches to find an approximate solution. The works (Chukalina et al., 2017; Ingacheva, Chukalina, 2019) suggest numerically simulating monochromatic projections – by applying a one-parameter correction function with automatically found correction parameter-based on the measured in polychromatic mode.
Other image normalization applications
In addition to the above, normalization is used to search for similar images in databases (Orrite and Herrero, 2004), to identify television broadcasts from a TV screen image (Skoryukina et al., 2017), to compare space images of Earth with electronic maps (Kozlov et al., 2009), and to analyze medical images (Baltzopoulos, 1995). Brightness normalization is used to improve the accuracy of neural network methods for face verification (Ilyuhin et al., 2019a; Ilyukhin et al., 2019b). In (Nikolaev et al., 2015), normalization was applied to the detection of diamonds in the ore stream. In addition, G. Legge showed that normalization of images can be applied to facilitate the visual perception by humans (Legge et al., 1985).
IMAGE NORMALIZATION ACCURACY CRITERIA
Let us consider formally described in the literature interfaces of geometric image normalization algorithms. The image to be normalized is input ${{I}_{{{\text{input}}}}}$. In addition to it, some form of a priori information about the target object and information about what imaging conditions are considered normal may be fed to the input. Some normalization algorithms use independent data about the imaging conditions, such as illumination and perspective (Kholopov, 2017; Calore et al., 2012; Arvind et al., 2018; Karpenko et al., 2015). The normalization algorithm returns an algorithmically normalizing transformation ${{\hat {H}}}$ (or its parameters), a transformation of pixel coordinates, application of which to the input image ${{I}_{{{\text{input}}}}}$ yields an algorithmically normalized image ${{I}_{{{\text{alg}}}}}$. In this case, the image transformation itself is either not performed at all (when it is enough to know the transformation parameters) or, due to its non-triviality, is given for implementation to algorithms specially designed for this purpose. In addition, the estimation of certain imaging conditions can be returned.
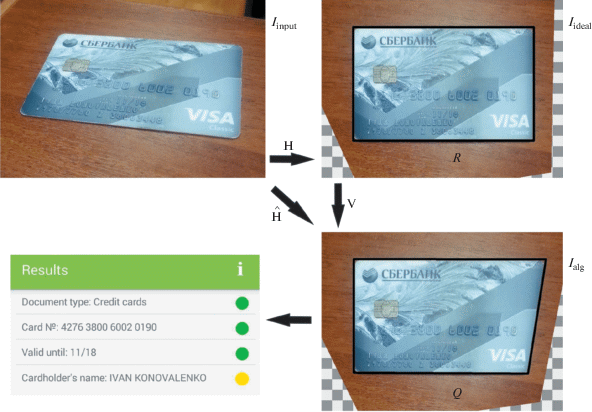
Normalization algorithms are usually not required to perform precisely. In order to formalize an estimate of the accuracy of an algorithmically normalizing transformation ${{\hat {H}}}$, an ideal normalizing transformation ${\text{H}}$ (ground truth) is usually expertly specified. The transform ${{\hat {H}}}$ may then be regarded as an estimate of the ideal transform ${\text{H}}$. Let us call the image obtained by applying ${\text{H}}$ to the input image ${{I}_{{{\text{input}}}}}$, an ideally normalized image ${{I}_{{{\text{ideal}}}}}$ (see example in Fig. 7). Naturally, the more accurate the normalization is, the closer the transformation ${{\hat {H}}}$ is to the transformation ${\text{H}}$ or the closer the image ${{I}_{{{\text{alg}}}}}$ is to the image ${{I}_{{{\text{ideal}}}}}$. However, there are many reasonable non-equivalent ways to formalize this closeness – the accuracy of geometric normalization inherently has many criteria. A large number of normalization accuracy criteria have been proposed in the literature. Before considering them, let us introduce the necessary notations.
Fig. 7.
Example of image normalization and its subsequent analysis. H – ideal normalization transformation, ${{\hat {H}}}$ – algorithmic normalization transformation, V – residual distortion, ${{I}_{{{\text{input}}}}}$ – image to be normalized, ${{I}_{{{\text{ideal}}}}}$ – algorithmically normalized image, ${{I}_{{{\text{alg}}}}}$ – algorithmically normalized image, bottom left – result (protocol) of image ${{I}_{{{\text{alg}}}}}$ analysis, R – region of interest, Q – image of the region of interest R in the image ${{I}_{{{\text{alg}}}}}$ plane.
Let us denote by ${\mathbf{r}}\;\mathop = \limits^{{\text{def}}} \;{{\left[ {\begin{array}{*{20}{c}} x&y \end{array}} \right]}^{T}}$ the Cartesian coordinates of pixels on the image plane ${{I}_{{{\text{ideal}}}}}$, and by q the Cartesian coordinates of pixels in the image plane ${{I}_{{{\text{alg}}}}}$ and let us determine the residual distortion as
for each visible point of the target object, the coordinates ${\mathbf{r}}$ which translate its image in the image ${{I}_{{{\text{ideal}}}}}$ into the coordinates q of its image in the image ${{I}_{{{\text{alg}}}}}$:If the normalization algorithm works accurately, the residual distortion ${\text{V}}$ is an identity transformation. Let us also introduce the residual distortion coordinate discrepancy (Kunina et al., 2016) (see example in Fig. 8)
(6)
${\text{d}}({\mathbf{r}})\;\mathop = \limits^{{\text{def}}} \;{\text{||}}{\mathbf{r}} - {\text{V}}({\mathbf{r}}){\text{|}}{{{\text{|}}}_{2}},$Fig. 8.
Example of coordinate discrepancy d. Left: algorithmically normalized image ${{I}_{{{\text{alg}}}}}$, the area of interest R is marked by a black frame. Right: vector field of residual distortion displacements ${\text{V}}({\mathbf{r}}) - {\mathbf{r}}$, color shows coordinate discrepancy values ${\text{d}}({\mathbf{r}}) = \;\parallel {\kern 1pt} {\text{V}}({\mathbf{r}}) - {\mathbf{r}}{\kern 1pt} {{\parallel }_{2}}$.

In some cases, the normal imaging conditions themselves determine which area of the image ${{I}_{{{\text{ideal}}}}}$ is of interest (for example, contains an image of the target object). Then we call it the region of interest and denote by
where ${{\mathbb{D}}_{{{\text{ideal}}}}}$ is the domain of the image ${{I}_{{{\text{ideal}}}}}$ (see (1)). Otherwise, we take $R = {{\mathbb{D}}_{{{\text{ideal}}}}}$. The region of interest $R$ shows exactly where in the image ${{I}_{{{\text{ideal}}}}}$ plane the normalization ${{\hat {H}}}$ is required to be accurate. We will not consider the case of an empty region of interest. Since the image domain ${{\mathbb{D}}_{{{\text{ideal}}}}}$ is always bounded, the region of interest R is also bounded. The sets R and ${{\mathbb{D}}_{{{\text{ideal}}}}}$ will be considered closed, since in this case there is no practical reason not to, and it is mathematically convenient. We will not require the convexity and connectivity of the region of interest R, since these restrictions are insufficient for practical needs. The image Q of the region of interest R in the image ${{I}_{{{\text{alg}}}}}$ plane is set by $Q\;\mathop = \limits^{{\text{def}}} \;{\text{V}}[R]\;\mathop = \limits^{{\text{def}}} \;\{ {\text{V}}({\mathbf{r}}){\kern 1pt} :\;{\mathbf{r}} \in R\} $. Ideally, $Q = R$.Hereafter, for brevity, we will use the notation as follows:
(8)
$\begin{gathered} \mathop {\max }\limits_X \;{\text{f}}\;\mathop = \limits^{{\text{def}}} \;\mathop {\max }\limits_{{\mathbf{x}} \in X} \;{\text{f}}({\mathbf{x}}), \\ \mathop {\sup }\limits_X \;{\text{f}}\;\mathop = \limits^{{\text{def}}} \;\mathop {\sup }\limits_{{\mathbf{x}} \in X} \;{\text{f}}({\mathbf{x}})\;\mathop = \limits^{{\text{def}}} \;\sup \;\{ {\text{f}}({\mathbf{x}}){\kern 1pt} :\;{\mathbf{x}} \in X\} , \\ \end{gathered} $Now let us proceed to the review of the criteria proposed in the literature for the accuracy of the geometric normalization. The works (Clark et al., 2008; Singh et al., 2008; Zeynalov et al., 2009) suggest evaluating the accuracy of normalization visually. Formal criteria can be divided into three groups: intrasystem, color, and geometric. Further, we will consider these three groups separately.
Intrasystem criteria
We have already shown that the normalization is applied as a stage of preprocessing of images for various image analysis problems Thus, there is an approach where the accuracy of the normalization is defined as the quality of the solution of the problem in which it is applied. For example, in (Merino-Gracia et al., 2013; Lu et al., 2005; Zhang et al., 2008; Tong, Zhang, 2010; Takezawa et al., 2016) the criterion for the accuracy of document image normalization is chosen as the quality of text recognition on an algorithmically normalized image ${{I}_{{{\text{alg}}}}}$; in (Awal et al, 2017; Finlayson et al., 1998) – the quality of scene object recognition; and in (Skoryukina et al., 2017) – the proportion of correctly identified TV broadcasts. Since such accuracy criteria are defined exclusively within the framework of some image analysis system and its testing system, we will call them intrasystem criteria. They depend only on a single image or a set of images ${{I}_{{{\text{alg}}}}}$.
Intrasystem criteria of accuracy are undoubtedly useful, as improvement of normalization algorithm in the sense of intrasystem criterion by its definition means the improvement of quality of solution of the final image analysis problem, and exactly in the sense in which this quality is specified. However, the criteria proposed in the literature are not limited to intrasystem criteria. The reason for this lies in the violation of the principle of software modularity, which requires that the development (and hence testing) of modules should be carried out independently. This violation results in the following problems. The system of image analysis and/or system of its testing by the time of the introduction of the normalization algorithm may not be fully developed. If both of these systems already exist, they are usually in the process of constant change, so the intrasystem criteria for normalization accuracy are also changing. In addition, they are not mathematically formalized, difficult to analyze, make the software debugging process difficult, and do not imply the universality of normalization algorithms. Zeynalov et al. (2009) describe intrasystem criteria as incorrect for these reasons. There is an opposite approach, in which it is believed that the image analysis system must be such that the quality of its performance on normalized images correlated well with some simple fixed criterion for the accuracy of normalization of these images.
Color criteria
By color criteria for the accuracy of geometric normalization, we will denote the criteria that necessarily depend on both images ${{I}_{{{\text{alg}}}}}$ and ${{I}_{{{\text{ideal}}}}}$, and may depend on the region of interest R and its image Q. For example, the articles ( Szeliski, 1996; Sawhney and Kumar, 1999; Calderon and Romero, 2007; Goshin et al., 2014) use the root mean square pointwise difference of these images throughout the region of interest as the normalization accuracy of single-channel images (see Fig. 9):
(9)
${{I}_{2}}({{I}_{{{\text{alg}}}}},{{I}_{{{\text{ideal}}}}};R)\;\mathop = \limits^{{\text{def}}} \;\sqrt {\frac{1}{{S(R)}}\int\limits_R ({{I}_{{{\text{alg}}}}}{{{\left( {{\mathbf{r}}) - {{I}_{{{\text{ideal}}}}}({\mathbf{r}})} \right)}}^{2}}d{\mathbf{r}}} ,$(10)
$\begin{gathered} PSNR({{I}_{{{\text{alg}}}}},{{I}_{{{\text{ideal}}}}};R)\mathop = \limits^{{\text{def}}} \; \\ \mathop = \limits^{{\text{def}}} \;20{{\log }_{{10}}}\left[ {{{I}_{{\max }}}{\text{/}}{{I}_{2}}({{I}_{{{\text{alg}}}}},{{I}_{{{\text{ideal}}}}};R)} \right], \\ \end{gathered} $(11)
$\begin{gathered} SSIM({{I}_{{{\text{alg}}}}},{{I}_{{{\text{ideal}}}}};R)\;\mathop = \limits^{{\text{def}}} \\ \, = \frac{{(2{{\mu }_{a}}{{\mu }_{i}} + {{c}_{1}})(2{{\sigma }_{{ai}}} + {{c}_{2}})}}{{(\mu _{a}^{2} + \mu _{i}^{2} + {{c}_{1}})(\sigma _{a}^{2} + \sigma _{i}^{2} + {{c}_{2}})}}, \\ \end{gathered} $(12)
$\begin{gathered} \sigma _{a}^{2}\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{S(R)}}\int\limits_R {{\left( {{{I}_{{{\text{alg}}}}}({\mathbf{r}}) - {{\mu }_{a}}} \right)}^{2}}d{\mathbf{r}}, \\ {{\mu }_{i}}\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{S(R)}}\int\limits_R {{I}_{{{\text{ideal}}}}}({\mathbf{r}})d{\mathbf{r}}, \\ \end{gathered} $(13)
${{\sigma }_{{ai}}}\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{S(R)}}\int\limits_R \left( {{{I}_{{{\text{alg}}}}}({\mathbf{r}}) - {{\mu }_{a}}} \right)\left( {{{I}_{{{\text{ideal}}}}}({\mathbf{r}}) - {{\mu }_{i}}} \right)d{\mathbf{r}},$(14)
$\begin{gathered} {{c}_{1}} = ({{k}_{1}}{{I}_{{\max }}}{{)}^{2}},\quad {{c}_{2}} = ({{k}_{2}}{{I}_{{\max }}}{{)}^{2}}, \\ {{k}_{1}} = 0.01,\quad {{k}_{2}} = 0.03. \\ \end{gathered} $Fig. 9.
Single-channel images ${{I}_{{{\text{ideal}}}}}$, ${{I}_{{{\text{alg}}}}}$ and their difference module $|{\kern 1pt} {{I}_{{{\text{alg}}}}} - {{I}_{{{\text{ideal}}}}}{\kern 1pt} |$. The images are reproduced from (Goshin et al., 2014).

The Wasserstein metric (Haker et al., 2004; Schmitzer and Schnörr, 2015; Su et al., 2015), informally called the “earth mover’s distance”, is also used for single-channel images:
(15)
$\begin{gathered} {{W}_{p}}({{I}_{{{\text{alg}}}}},{{I}_{{{\text{ideal}}}}};Q,R)\;\mathop = \limits^{{\text{def}}} \\ \, = \mathop {\inf }\limits_{\gamma \in \Gamma (\mu ,\nu )} {{\left[ {\int\limits_{Q \times R} {{\text{||}}{\mathbf{q}} - {\mathbf{r}}{\text{||}}_{2}^{p}} \,d\gamma ({\mathbf{q}},{\mathbf{r}})} \right]}^{{1/p}}}, \\ \end{gathered} $(16)
$\begin{gathered} \mu (X) = \frac{{\int_X {{I}_{{{\text{alg}}}}}({\mathbf{q}})d{\mathbf{q}}}}{{\int_Q {{I}_{{{\text{alg}}}}}({\mathbf{q}})d{\mathbf{q}}}},\quad X \subseteq Q, \\ \nu (X) = \frac{{\int_X {{I}_{{{\text{ideal}}}}}({\mathbf{r}})d{\mathbf{r}}}}{{\int_R {{I}_{{{\text{ideal}}}}}({\mathbf{r}})d{\mathbf{r}}}},\quad X \subseteq R \\ \end{gathered} $Radial distortion compensation is an important special case of geometric normalization. To describe its accuracy, criteria detecting the presence of straight lines in the image ${{I}_{{{\text{alg}}}}}$ are used (Kunina et al., 2016).
The main property of color criteria for geometric normalization accuracy is as follows: even for fixed transformations ${{\hat {H}}}$, H and the region of interest R, i.e. when in the geometric sense normalization is made equally accurately, the value of any color criterion changes depending on images ${{I}_{{{\text{alg}}}}}$ and ${{I}_{{{\text{ideal}}}}}$.
Geometric criteria
By geometric criteria of the normalization accuracy, we mean the criteria that depend only on transformations ${\text{H}}$ and ${{\hat {H}}}$, or on their parameters, and on the region of interest R, and on the derived objects: Q, V, d. They do not depend on the images (${{I}_{{{\text{input}}}}}$, ${{I}_{{{\text{alg}}}}}$ and ${{I}_{{{\text{ideal}}}}}$). Geometric accuracy criteria are natural for geometric normalization and are more frequently met in the literature. Let us list them below.
1. The closeness of the parameters specifying the transformations ${{\hat {H}}}$ and ${\text{H}}$. For example, in (Triputen’ and Gorokhovatskii, 1997), the accuracy of normalization by an affine transformation given by the matrix $\hat {A} = ({{\hat {a}}_{{ij}}}) \in {{\mathbb{R}}^{{2 \times 3}}}$, was calculated as follows:
(17)
${{E}_{{{\text{affin}}}}}(\hat {A},A) = \sum\limits_{i = 1}^2 \sum\limits_{j = 1}^3 \frac{{{\text{|}}{{{\hat {a}}}_{{ij}}} - {{a}_{{ij}}}{\text{|}}}}{{{\text{|}}{{a}_{{ij}}}{\text{|}}}},$2. Jaccard’s coefficient (Jaccard, 1901), equal to the area of intersection of sets $Q$ and $R$, divided by the area of their union (see Fig. 10):
(19)
${{K}_{{{\text{Jaccard}}}}}(Q,R)\;\mathop = \limits^{{\text{def}}} \;\frac{{S(Q \cap R)}}{{S(Q \cup R)}}.$It was used, for example, at the “Smartphone document capture competition” of the ICDAR conference (Zhukovskiy et al., 2018). The paper (Rezatofighi et al., 2019) suggests its more suitable modification for optimization.
3. Hausdorff metric, the greatest distance from the points of one set to their corresponding nearest points of the second set (see Fig. 11):
(20)
$\begin{gathered} {{d}_{H}}(Q,R)\;\mathop = \limits^{{\text{def}}} \; \\ \mathop = \limits^{{\text{def}}} \max \left\{ {\mathop {\sup }\limits_{{\mathbf{q}} \in Q} \mathop {\inf }\limits_{{\mathbf{r}} \in R} {\text{||}}{\mathbf{q}} - {\mathbf{r}}{\text{|}}{{{\text{|}}}_{2}},\;\mathop {\sup }\limits_{{\mathbf{r}} \in R} \mathop {\inf }\limits_{{\mathbf{q}} \in Q} {\text{||}}{\mathbf{r}} - {\mathbf{q}}{\text{|}}{{{\text{|}}}_{2}}} \right\}. \\ \end{gathered} $The Hausdorff metric has been used for arbitrary object detection (Sim et al., 1999), for alignment of partially occluded contours (Orrite and Herrero, 2004), for robust face detection (Jesorsky et al., 2001), and for calculation of closeness between two images (Huttenlocher et al., 1993). In the works (Dubuisson and Jain, 1994; Efimov and Novikov, 2016), its modifications were proposed.
4. In the case when instead of sets Q and R, two continuous curves are considered: $Q,R{\kern 1pt} :\;[0,1] \to {{\mathbb{R}}^{2}}$, the Frechette distance, related to the Hausdorff metric, is used:
(21)
$F(Q,R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\inf }\limits_{a,b} \;\mathop {\max }\limits_{t \in [0,1]} \;{\text{||}}Q(a(t)),R(b(t)){\text{|}}{{{\text{|}}}_{2}},$5. Mean square coordinate discrepancy d:
(22)
${{L}_{2}}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\left\{ \begin{gathered} \sqrt {\frac{1}{{S(R)}}\int\limits_R {{{\text{d}}}^{2}}({\mathbf{r}})d{\mathbf{r}}\quad {\text{for}}\;0 < S(R) < \infty } \hfill \\ \sqrt {\frac{1}{{{\text{|}}R{\text{|}}}}\sum\limits_{{\mathbf{r}} \in R} {{{\text{d}}}^{2}}({\mathbf{r}})} \quad {\text{for}}\;0 < {\text{|}}R{\text{|}} < \infty \hfill \\ \end{gathered} \right.,$6. The mean coordinate discrepancy d was also employed (Kunina et al., 2016; Shemiakina et al., 2017):
(23)
${{L}_{1}}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\left\{ \begin{gathered} \frac{1}{{S(R)}}\int\limits_R {\text{d}}({\mathbf{r}})d{\mathbf{r}}\quad {\text{for}}\;0 < S(R) < \infty , \hfill \\ \frac{1}{{{\text{|}}R{\text{|}}}}\sum\limits_{{\mathbf{r}} \in R} {\text{d}}({\mathbf{r}})\quad {\text{for}}\;0 < {\text{|}}R{\text{|}} < \infty . \hfill \\ \end{gathered} \right.$7. Finally, the maximum coordinate discrepancy d (minimax criterion) was also proposed as an accuracy criterion. In the general case, it is defined as the following supremum:
(24)
${{L}_{\infty }}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\sup }\limits_{{\mathbf{r}} \in R} \,{\text{d}}({\mathbf{r}}).$The maximum coordinate discrepancy was used as a criterion for the normalization accuracy in the tasks of space image georeferencing (Katamanov, 2007), face detection (Jesorsky et al., 2001), and text recognition (Shemiakina et al., 2017; Skoryukina et al., 2018). In the case of projective normalization, some works (Shemiakina et al., 2017; Skoryukina et al., 2018) applied this criterion in a non-standard way. Instead of the entire region of interest R, it used only the extreme points of the region’s convex hull ${\text{E}}({\text{Conv}}(R))$:
(25)
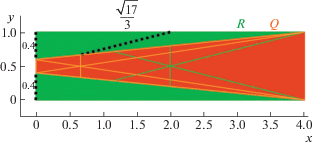
${{\hat {L}}_{\infty }}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\sup }\limits_{{\text{E}}({\text{Conv}}(R))} {\text{d}}.$The authors assumed that equality ${{\hat {L}}_{\infty }}({\text{V}};R) = {{L}_{\infty }}({\text{V}};R)$ is true. However, this assumption is not always correct. Let us consider a counterexample to the declared equality (see Fig. 12). Let
(26)
$\begin{gathered} {\text{V}}({\mathbf{r}}) = \frac{1}{{ - 2x + 10}}\left[ {\begin{array}{*{20}{c}} {2x} \\ { - x + 2y + 4} \end{array}} \right], \\ {\text{d}}({\mathbf{r}}) = \;\parallel {\kern 1pt} {\mathbf{r}} - {\text{V}}({\mathbf{r}}){\kern 1pt} {{\parallel }_{2}}, \\ \end{gathered} $(27)
$\begin{gathered} {{{\hat {L}}}_{\infty }}({\text{V}};R) = \mathop {\sup }\limits_{{\text{E}}({\text{Conv}}(R))} {\text{d}} = 0.4 < \frac{{\sqrt {17} }}{3} = {\text{d}}\left( {\left[ {\begin{array}{*{20}{c}} 2 \\ 1 \end{array}} \right] \in R} \right) \leqslant \\ \, \leqslant \mathop {\sup }\limits_R {\text{ d}} = {{L}_{\infty }}({\text{V}};R)\; \Rightarrow \;{{{\hat {L}}}_{\infty }}({\text{V}};R) < {{L}_{\infty }}({\text{V}};R). \\ \end{gathered} $Fig. 12.
A counterexample to the statement that the supremum of coordinate discrepancy of the projective transformation on a rectangle is achieved on its vertices. The projective transformation of a rectangle into a trapezoid is shown. The lengths of the dashed lines correspond to the coordinate discrepancies. The property is visually demonstrated: the coordinate discrepancy at vertices of the rectangle is smaller than at the point on its edge.
It is interesting to note that all of the listed geometric accuracy criteria depend on ${{\hat {H}}}$ and H only through the residual distortion ${\text{V}} = {{\hat {H}}}{{{\text{H}}}^{{ - 1}}}$ (4) and the coordinate discrepancy d derived from it (6). Therefore, the accuracy of the transformation H estimate ${{\hat {H}}}$ can be understood as the closeness of the residual distortion V to the identity transformation.
Let us nowexamine the listed geometric criteria. The criteria based on proximity of parameters that define transformations ${{\hat {H}}}$ and ${\text{H}}$are not suitable to describe the normalization accuracy, since they do not depend on the region of interest R, which shows where exactly in the image ${{I}_{{{\text{ideal}}}}}$ plane the normalization should be accurate. The Jaccard coefficient, the Hausdorff metric, and the Frechet distance do not have this drawback, but, being utilized as criteria for normalization accuracy, they have another general drawback. They specify only the similarity of sets Q and R, while arbitrary distortions within a set are not accounted for. For example, in Fig. 13 we can see two examples of document image normalization, correct and incorrect, which have an ideal accuracy in terms of each of the three above-mentioned criteria.
Fig. 13.
Two examples of document image normalization (left – correct, right – incorrect), which are perfectly accurate in terms of Jaccard coefficient, Hausdorff metric, and Frechette distance.

Mean, root mean square and maximum coordinate discrepancies have no obvious disadvantages compared to the previous criteria.
PROJECTIVE IMAGE NORMALIZATION AND ACCURACY CRITERIA
Theoretical justification of projective image normalization
The following classes of transformations are used to implement geometric normalization of images: isometric (Murygin, 2010; Huttenlocher et al., 1993; Bolotova et al., 2017), affine (Triputen’ and Gorokhovatskii, 1997; Putyatin et al., 1998; Nikolaidis, 2011), polynomial (Kozlov et al., 2009), fractional-polynomial (Singh et al, 2008), radial-polynomial (to compensate for radial distortion) (Kunina et al., 2016), central-projective (Rodríguez-Piñeiro et al, 2011; Zhang and He, 2007; Kholopov, 2017), projective (Safari et al., 1997; Iwamura et al., 2007; Merino-Gracia et al., 2013; Shemiakina et al., 2017; Xie et al., 2018), and arbitrary (Jesorsky et al., 2001; Zeynalov et al., 2009).
The shape of scene objects is very often modeled by a polyhedron (approximation of their 3D shape is called polyhedral), formally approximating the optical system of its registration by a pinhole camera (the laws of geometric optics are approximated in this case by the flat central projection) (Forsyth, Ponce, 2002). Under such assumptions, the images of the same object face captured from arbitrary angles are connected by a two-dimensional projective transformation (Shemiakina, 2017; Hartley, Zisserman, 2003) (see Fig. 14 and 15). Thus, the ideal normalizing transformation ${\text{H}}$ of this face image is projective, and the algorithmically normalizing transformation ${{\hat {H}}}$ is chosen to be projective. Since the transformations ${\text{H}}$ and ${{\hat {H}}}$ are projective, the residual distortion ${\text{V}} = {{\hat {H}}}{{{\text{H}}}^{{ - 1}}}$ is also projective. Such geometric normalization will be referred to as projective normalization. The projective transformation preserves straight lines. In Fig. 14 and 15, this fundamental property is expressed by the fact that the images of straight lines of the scene also remain straight.
Fig. 14.
Formation of images ${{I}_{1}}$ and ${{I}_{2}}$ of a flat rectangular object in a pinhole camera with optical centers ${{O}_{1}}$ and ${{O}_{2}}$. The object and its images are pairwise connected by projective transformations.

Fig. 15.
The real image obtained by the camera, which can be accurately simulated by a pinhole camera model. The flat faces of the scene are related to their images by projective transformations.

The projective transformation is used not only for geometric normalization of images, but also for color normalization. In 1931, the International Commission on Illumination (CIE) introduced the standard CIE XYZ color space and formalized the concept of chromaticity (color without luminance) as an ordered pair of chromatic coordinates ($x$, $y$) of the CIE xy color space (Smith et al., 1931), with the relationship between color and chromaticity specified as a projective mapping. Projective CIE xy chromaticity transformations have been considered since MacAdam’s work (1937) published in 1937. However, due to their projective definition, we can assume that the projective chromaticity transformations have been considered since their introguction in 1931. Nevertheless, a formal theoretical justification for projective color normalization was published only in 2016 by G. Finlayson (Finlayson et al., 2016). It is worth noting several works where all three color coordinates are projectively transformed. The first appears to be a paper (Wallace et al., 2003) by a Princeton University Computer Science Department team, published in 2003. A three-dimensional projective transformation was used to compare the color bodies of different projection frameworks. Later, the same approach was applied to photorealistic color palette transfer between images (Gong et al., 2019) (see Fig. 16 for examples). In both cases, it is a mutual calibration of the two images, rather than a transition to a color space with the required properties. In the article (Smagina et al., 2019), the projective transformation was suggested to be used precisely for the transition to space with a simple, but meaningful, metric. In this work, it was shown that a fixed three-dimensional projective transformation of color coordinates can improve the results of color segmentation algorithms. In 2020, another paper (Kim et al., 2020) demonstrated the use of a three-dimensional projective transformation for color normalization (calibration) of micro-LED displays.
Accuracy criteria for projective image normalization
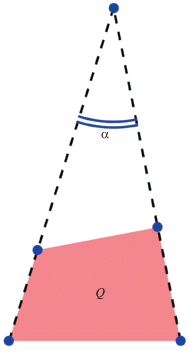
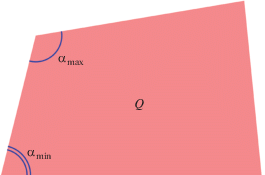
All the criteria described above are universal, and therefore applicable to the description of the projective normalization accuracy. However, for the case of projective normalization, special criteria have been proposed in the literature. They all assume that the region of interest R is a rectangle. Then its image Q is a quadrilateral. For example, in (Calore et al., 2012), the angle between the left and right sides of the quadrilateral $Q$ was proposed as an accuracy criterion: $\alpha (Q)$ (see Fig. 17), and in (Kholopov, 2017), the ratio between the minimum and maximum angles of the quadrilateral Q (see Fig. 18):
in (Takezawa et al., 2016), the total relative proximity of the lengths of the opposite sides of Q was chosen:(29)
$D(Q) = \frac{{{\text{|}}a - c{\text{|}}}}{{a + c}} + \frac{{{\text{|}}b - d{\text{|}}}}{{b + d}}.$The articles (Rodríguez-Piñeiro et al., 2011; Zhang and He, 2007) define normalization accuracy as the accuracy of the normalization algorithm’s estimate of the aspect ratio of a rectangle R. All the criteria listed here are invariant to the similarity transformation.
THEORETICAL JUSTIFICATION OF THE NORMALIZATION ACCURACY CRITERIA
It was shown above that a large number of normalization accuracy criteria have been already proposed, including those introduced specifically for projective normalization. Thus, the question of the proposed criteria applicability to various image analysis problems is relevant. The introduction of problem-oriented criteria allows for a theoretically justified approach to the choice of optimal algorithm among existing algorithms of geometric normalization, and to the development of new algorithms.
In (Konovalenko et al., 2020d), for the case of a document with a fixed structure (Povolotskiy and Tropin, 2019), a normal probabilistic recognition model was introduced, according to which the probability of correct recognition of a symbol jumps to zero as the coordinate discrepancy of this symbol increases. For this model, it was proved that the accuracy criterion of image normalization, expressed as the maximum (by text fields of the document) coordinate discrepancy, is monotonically related to the probability of correct recognition of the entire document.
In (Konovalenko et al., 2020a), another model of recognition was introduced, according to which the probability of correct recognition of a symbol decays according to Gaussian with the growth of the coordinate discrepancy of this symbol. For this model, it was proved that the accuracy criterion of image normalization, equal to the mean square of the coordinate misalignment in the text fields of the document, is monotonically related to the probability of true recognition of the entire document.
In (Konovalenko and Shemiakina, 2018; Konovalenko et al., 2020a), the maximum and root mean square coordinate discrepancies were expressed analytically for the case of projective normalization.
LIMITS OF APPLICABILITY OF NORMALIZATION ACCURACY CRITERIA
The case of arbitrary normalization
All the above mentioned criteria of images normalization accuracy, except intrasystem, are not intended for the case when some part of the region of interest image is not mapped on the image ${{I}_{{{\text{alg}}}}}$. In this regard, it is necessary that the algorithmically normalized image completely contains the image of the region of interest:
and that the input image completely contains the preimage of the region of interest:In addition, a residual distortion that is too “bad” at the region of interest also makes all of the above non-intrasystem accuracy criteria meaningless. Therefore, let us require that at each point the transformation has a Jacobian matrix and a positive Jacobian
because a zero Jacobian usually leads to loss of information, and a negative one means “reflection” of the image and corresponds to imitation of the view of the object surface “from the back” (see Fig. 19).Fig. 19.
An example of projective normalization in which the Jacobian of residual distortion V equals to either positive or negative values in the region of interest R. Above – ideally normalized image ${{I}_{{{\text{ideal}}}}}$. Bottom – algorithmically normalized image ${{I}_{{{\text{alg}}}}}$, obtained as a result of splitting the image ${{I}_{{{\text{ideal}}}}}$ by residual projective distortion into two parts: for the right side the Jacobian of residual distortion is positive, and for the left side it is negative, which corresponds to “reflecting” the image.

The case of projective normalization
Let us consider in detail what these constraints mean for the case of projective normalization, when the camera is modeled by a pinhole camera and the object surfaces are modeled by planes. Let us introduce the projective transformation P, the inverse of H:
– it translates the points of the image ${{I}_{{{\text{ideal}}}}}$ into the points of the image ${{I}_{{{\text{input}}}}}$. The projective transformation V is parameterized by a homogeneous matrix (homography matrix) $V\;\mathop = \limits^{{\text{def}}} \;({{v}_{{ij}}}) \in {{\mathbb{R}}^{{3 \times 3}}}$ in the following standard way:
(34)
${\text{V}}({\mathbf{r}})\;\mathop = \limits^{{\text{def}}} \;\frac{{\left[ {\begin{array}{*{20}{c}} {{{v}_{{11}}}x + {{v}_{{12}}}y + {{v}_{{13}}}} \\ {{{v}_{{21}}}x + {{v}_{{22}}}y + {{v}_{{23}}}} \end{array}} \right]}}{{{{v}_{{31}}}x + {{v}_{{32}}}y + {{v}_{{33}}}}}.$Similarly, the projective transformations ${{\hat {H}}}$, H and P are parameterized by the matrices $\hat {H}$, H and p respectively. Let
Let us introduce the function
(36)
$Z({\mathbf{r}})\;\mathop = \limits^{{\text{def}}} \;{{v}_{{31}}}x + {{v}_{{32}}}y + {{v}_{{33}}}.$From the constraints (30), (31), and (32) it follows that the function Z has a constant sign on the set R:
(37)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{r}} \in R\quad \Rightarrow \quad Z({\mathbf{r}}) < 0,} \\ {{\mathbf{r}} \in R\quad \Rightarrow \quad Z({\mathbf{r}}) > 0.} \end{array}} \right.$Let us prove this for the general case when the set R is not necessarily connected. Indeed, if for a point ${\mathbf{r}} \in R$ is satisfied $Z({\mathbf{r}}) = 0$, then the corresponding point ${\text{V}}({\mathbf{r}})$ in the image ${{I}_{{{\text{alg}}}}}$ plane is infinitely distant (see (34)) and therefore cannot belong to this image, which violates the condition (30). Moreover, it follows from (34) and (36) that:
(38)
$\det (J({\mathbf{r}})) = \frac{{{{v}_{{11}}}{{v}_{{22}}}{{v}_{{33}}} - {{v}_{{11}}}{{v}_{{23}}}{{v}_{{32}}} - {{v}_{{12}}}{{v}_{{21}}}{{v}_{{33}}} + {{v}_{{12}}}{{v}_{{23}}}{{v}_{{31}}} + {{v}_{{13}}}{{v}_{{21}}}{{v}_{{32}}} - {{v}_{{13}}}{{v}_{{22}}}{{v}_{{31}}}}}{{{{Z}^{3}}({\mathbf{r}})}}.$I.e. the sign $Z({\mathbf{r}})$ either everywhere coincides with the sign of the Jacobian of the projective transformation V, or differs from it everywhere, which means that to satisfy condition (32) it has to be either uniformly on R negative or positive, what was required to prove. If condition (37) is ignored, the coordinate discrepancy (6) is predetermined naturally:
(39)
${\text{d}}({\mathbf{r}})\;\mathop = \limits^{{\text{def}}} \;\left\{ \begin{gathered} {\text{||}}{\mathbf{r}} - {\text{V}}({\mathbf{r}}){\text{|}}{{{\text{|}}}_{2}}\quad {\text{for}}\;Z({\mathbf{r}}) \ne 0, \hfill \\ + \infty \quad \,\,\,\,\,\,\,\,\,\,\,\,{\kern 1pt} \,\,{\text{for}}\;Z({\mathbf{r}}) = 0. \hfill \\ \end{gathered} \right.$AFFINE APPROXIMATION OF PROJECTIVE IMAGE NORMALIZATION
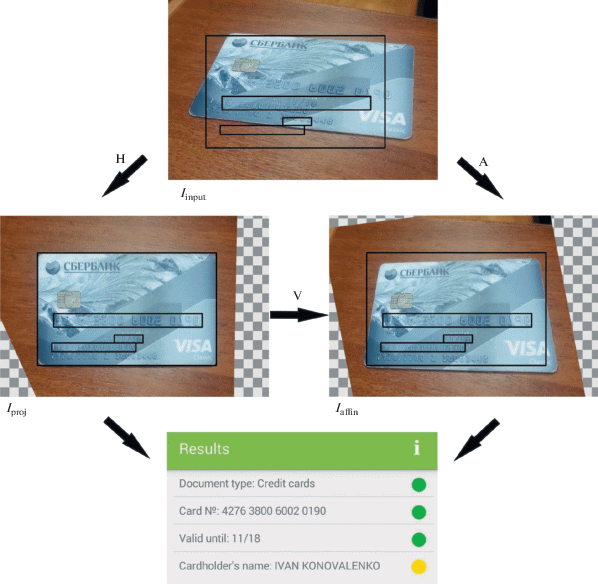
Due to the growing technical capabilities of mobile devices in recent years, autonomous image analysis on mobile devices without the involvement of the server has become relevant. A significant contribution to the development of this approach was made by V.V. Arlazarov. The computational power of modern mobile devices is such that the time required for projective image transformation turns out to be a critical factor (Trusov, Limonova, 2020). A competitive approach that increases the speed of image processing could be the affine transformation (Putyatin et al., 1998; Wolberg, 1990). Note that a typical variant of the orientation of the camera optical axis with respect to the plane of the target object can be represented by an orthogonal view model. In this approximation, the camera-object system is naturally described by an affine projection model (Forsyth and Ponce, 2002), and the generally required projective normalization is replaced by frequently used affine normalization without significant loss of accuracy Triputen’ and Gorokhovatskii, 1997; Putyatin et al., 1998; Nikolaidis, 2011) (see Fig. 20). Such a transition to a less computationally expensive model can provide the required acceleration of the normalization step.
Рис. 20.
Projective (left) and affine (right) geometric normalizations of the document image ${{I}_{{{\text{input}}}}}$ (top) and the result of its recognition (bottom). H – projective transformation, A – affine transformation, ${\text{V}} = {\text{A}}{{{\text{H}}}^{{ - 1}}}$ – residual projective distortion. The black boxes show the ideal localization of a document and its text fields. Even though the camera’s optical from normal, the text fields of the document were accurately normalized via affine normalization.
The notion that in practice the projective transformation can be replaced by the affine transformation was suggested earlier in (Gruen, 1985). This property was used in (Ohta et al., 1981) to simplify further mathematical constructions. The affine approximation is widely used in image augmentation (Pavić et al., 2006) and in rendering (Wolberg, 1990; Heckbert, 1989; Lorenz and Döllner, 2009). In (Huang et al., 2015), the projective transformation is replaced by a simpler affine transformation in order to eliminate overtraining. A similar idea is used in the weak perspective camera model (Alter, 1992; Kutulakos and Vallino, 1996; Aradhye and Myers, 2010), where within each scene object the equidistance of its parts from the camera is assumed. Developing affine invariant methods instead of the much more complex projective invariant ones is common in the popular technology of special points (Mikolajczyk and Schmid, 2002; Mikolajczyk and Schmid, 2004; Morel and Yu, 2009), and in the related problem of significant regions detection (Kadir et al., 2004), although both approaches are practically invariant to the capturing perspective. The division into affine and projective methods also exists in the field of stereoreconstruction (Faugeras, 1995). Replacing a projective transformation with an affine one for rendering and image normalization purposes leads to the loss of accuracy (Putyatin et al., 1998; Zwicker et al., 2004).
In (Konovalenko et al., 2019), the maximum and root mean square coordinate discrepancies were proposed as accuracy criteria for affine approximation of projective normalization. Based on these criteria, the problems of the search for optimal affine approximations are formulated. The convexity of the obtained optimization problems is proved. A method for the employment of optimal affine approximations to save computational resources during image transformation is proposed. In (Konovalenko et al., 2021), the problem of finding an affine approximation optimal according to the criterion of coordinate mean square discrepancy was solved analytically.
CONCLUSION
In the analytical part of this review paper, the authors demonstrated the following original results:
1. Among the known criteria for the accuracy of image normalization, several were chosen based on the following attributes. Ones that do not violate the software modularity principle, do not depend on the values of images, do take into account the area of interest, and do not require an ideal accuracy in the case of loose normalization. Such criteria include mean, root mean square, and maximum coordinate discrepancies (see section Theoretical justification of the normalization accuracy criteria).
2. For the case of projective normalization, an analytical expression for the maximum coordinate discrepancy was previously described in the literature. This expression, however, was refuted by the authors: it is shown that the supremum of the coordinate discrepancy of 2D projective transformation on a closed bounded set is not necessarily reached at the extreme points of its convex hull (see item 7 in Geometrical Criteria section).
3. Limits of applicability of normalization accuracy criteria were introduced.
4. We proposed mean square and maximum coordinate discrepancies as accuracy criteria of affine approximation of projective normalization. It significantly reduces computational complexity when choosing optimal affine approximations, and the problem of affine approximation search has been studied analytically (Konovalenko et al., 2021).
Список литературы
Abramov M.P., Shipitko O.C., Grigoryev A.S., Ershov E.I. Poisk tochki skhoda dlya dinamicheskoi kalibrovki vneshnikh parametrov monokulyarnoi kamery pri uslovii pryamolineinogo dvizheniya [Vanishing point detection for monocular camera extrinsic calibration under translation movement] Sensornye sistemy [Sensory systems]. 2020. V. 34 (1). P. 32–43 (in Russian). https://doi.org/10.31857/S0235009220010023
Abramov M.P., Shipitko O.S., Lukoyanov A.S., Panfilova E.I., Kunina I.A., Grigoryev A.S. Sistema pozitsionirovaniya vnutri zdanii mobil’noi robototekhnicheskoi platformy na osnove detektsii kraev [Edge detection based mobile robot indoor localization] Sensornye sistemy [Sensory systems]. 2019. V. 33 (1). P. 30–43 (in Russian). https://doi.org/10.1134/S0235009219010025
Abulkhanov D.A., Sidorchuk D.S., Konovalenko I.A. Obuchenie neirosetevykh deskriptorov osobykh tochek dlya sopostavleniya radiolokatsionnykh i opticheskikh izobrazhenii [Neural network-based feature point descriptors for registration of optical and SAR images] Sensornye sistemy [Sensory Systems]. 2018. V. 32 (3). P. 222–229 (in Russian). https://doi.org/10.1134/S0235009218030034
Alter T.D. 3d pose from 3 corresponding points under weak-perspective projection. Technical report. Massachusetts Inst Of Technology Artificial Intelligence Lab. 1992.
Aradhye H., Myers G.K. Method and apparatus for recognition of symbols in images of three-dimensional scenes. US Patent. No. 7.738.706. 2010.
Arvind C.S., Mishra R., Vishal K., Gundimeda V. Vision based speed breaker detection for autonomous vehicle. Tenth International Conference on Machine Vision (ICMV 2017). International Society for Optics and Photonics. 2018. V. 106960E. P. 1–9.
Awal A.M., Ghanmi N., Sicre R., Furon T. Complex document classification and localization application on identity document images. IAPR 2017-International Conference on Document Analysis and Recognition. 2017. P. 427–431. https://doi.org/10.1109/ICDAR.2017.77
Balitskiy A.M., Savchik A.V., Gafarov R.F., Konovalenko I.A. O proektivno invariantnykh tochkakh ovala s vydelennoy vneshney pryamoy [On projectively invariant points of an oval with a distinguished exterior line] Problemy peredachi informatsii [Problems of Information Transmission]. 2017. V. 53 (3). P. 84–89 (in Russian).
Baltzopoulos V. A video fluoroscopy method for optical distortion correction and measurement of knee-joint kinematics. Clinical Biomechanics. 1995. V. 10 (2). P. 85–92.
Bezmaternykh P.V., Ilin D.A., Nikolaev D.P. U-Net-bin: hacking the document image binarization contest. Computer Optics. 2019. V. 43 (5). P. 825–832. https://doi.org/10.18287/2412-6179-2019-43-5-825-832
Bezmaternykh P.V., Nikolaev D.P. A document skew detection method using fast Hough transform. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 114330J. https://doi.org/10.1117/12.2559069
Bezmaternykh P.V., Nikolaev D.P., Arlazarov V.L. Textual Blocks Rectification Method Based on Fast Hough Transform Analysis in Identity Documents Recognition. Tenth International Conference on Machine Vision (ICMV 2017). International Society for Optics and Photonics. 2018. V. 10696. P. 1069606. https://doi.org/10.1117/12.2310162
Bezmaternykh P.V., Vylegzhanin D.V., Gladilin S.A., Nikolaev D.P. Generativnoe raspoznavanie dvumernykh shtrikhkodov. Iskusstvennyi intellekt i prinyatie reshenii [Scientific and Technical Information Processing]. 2010. V. 2010 (4). P. 63–69 (in Russian).
Bolotova Yu.A., Spitsyn V.G., Osina P.M. Obzor algoritmov detektirovaniya tekstovykh oblastei na izobrazheniyakh i videozapisyakh [Review Of Algorithms For Text Detection In Images And Videos] Komp’yuternaya optika [Computer Optics]. 2017. V. 41 (3). P. 441–452 (in Russian).
Bulatov K., Matalov D., Arlazarov V.V. MIDV-2019: Challenges of the Modern Mobile-Based Document OCR. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 114332N. https://doi.org/10.1117/12.2558438
Calderon F., Romero L. An accurate image registration method using a projective transformation model. Eighth Mexican International Conference on Current Trends in Computer Science (ENC2007). IEEE. 2007 P. 58–64.
Calore E., Pedersini F., Frosio I. Accelerometer based horizon and keystone perspective correction. Instrumentation and Measurement Technology Conference (I2MTC). 2012 IEEE International. IEEE. 2012. P. 205–209.
Chekhlov D.O., Ablameiko S.V. Normalizatsiya izobrazhenii otnositel’no perspektivnogo preobrazovaniya na osnove geometricheskikh parametrov [Normalization of images relating to perspective transformation based on geometric options] Informatika [Informatics]. 2004. V. (3). P. 67–76 (in Russian).
Chen H., Sukthankar R., Wallace G., Li K. Scalablealignment of large-format multi-projector displays using camera homography trees. Proc. Conf. Visualization’02. IEEE Computer Society. 2002. P. 339–346.
Chernov T.S., Ilin D.A., Bezmaternykh P.V., Faradzhev I.A., Karpenko S.M. Research of Segmentation Methods for Images of Document Textual Blocks Based on the Structural Analysis and Machine Learning. Vestnik RFFI. 2016. I. 4. P. 55–71. (in Russian).https://doi.org/10.22204/2410-4639-2016-092-04-55-71
Chochia P.A. Vosstanovlenie amplitudnykh kharakteristik monokhromnykh i mul’tispektral’nykh izobrazhenii, ispol’zuya funktsiyu gradientov [Recovering of the Amplitude Characteristics of Monochrome and Multispectral Images Using the Function of Gradients] Informatsionnye protsessy. 2016. V. 16 (2). P. 112–120. (in Russian).
Chukalina M., Ingacheva A., Buzmakov A., Polyakov I., Gladkov A., Yakimchuk I., Nikolaev D. Automatic beam hardening correction for CT reconstruction. Proc. ECMS 2017, European Council for Modeling and Simulation 2017. 2017. P. 270–275. https://doi.org/10.7148/2017-0270
Clark A.J., Green R.D., Grant R.N. Perspective correction for improved visual registration using natural features. Image and Vision Computing New Zealand. 2008. IVCNZ 2008. 23rd International Conference. 2008. P. 1–6.
Dance C.R. Perspective estimation for document images. Document Recognition and Retrieval IX. International Society for Optics and Photonics. 2001. V. 4670. P. 244–255.
Das P., Baslamisli A.S., Liu Y., Karaoglu S., Gevers T. Color constancy by GANs: an experimental survey. 2018. arXiv preprint arXiv:1812.03085.
Dubuisson M.P., Jain A.K. A modified hausdorff distance for object matching. Proc. of 12th international conference on patternrecognition. IEEE. 1994. V. 1. P. 566–568.
Efimov A.I., Novikov A.I. Algoritm poetapnogo utochneniya proektivnogo preobrazovaniya dlya sovmeshcheniya izobrazhenii [An algorithm for multistage projective transformation adjustment for image superimposition] Komp’yuternaya Optika [Computer Optics]. 2016. V. 40 (2). P. 258–265 (in Russian). https://doi.org/10.18287/2412-6179-2016-40-2-258-265
Ershov E., Savchik A., Semenkov I., Banic N., Belokopytov A., Senshina D., Koscevic K., Subasi M., Loncaric S. The Cube++ Illumination Estimation Dataset. IEEE Access. 2020. V. 8. P. 227511–227527. https://doi.org/10.1109/ACCESS.2020.3045066
Ershov E.I., Korchagin S.A., Kokhan V.V., Bezmaternykh P.V. A generalization of Otsu method for linear separation of two unbalanced classes in document image binarization. Computer Optics. 2021. V. 45 (1). P. 66–76. https://doi.org/10.18287/2412-6179-CO-752
Faugeras O.D. What can be seen in three dimensions with anuncalibrated stereo rig? European conference on computer vision. Springer. 1992. P. 563–578.
Finlayson G.D., Funt B.V., Barnard K. Color constancy under varying illumination. Proc. of IEEE International Conference on Computer Vision. 1995. P. 720–725.
Finlayson G.D., Gong H., Fisher R.B. Color homography color correction. Color and Imaging Conference. 2016. V. 2016 (1). P. 310–314.
Finlayson G.D., Schiele B., Crowley J.L. Comprehensive colour image normalization. European conference on computer vision. 1998. P. 475–490.
Forsyth D.A., Ponce J. Computer vision: a modern approach. Prentice Hall Professional Technical Reference, 2002. 720 p.
Gayer A.V., Sheshkus A.V., Nikolaev D.P., Arlazarov V.V. Improvement of U-Net Architecture for Image Binarization with Activation Functions Replacement. Thirteenth International Conference on Machine Vision (ICMV 2020). 2021. V. 11605. P. 116050Y. https://doi.org/10.1117/12.2587027
Gijsenij A., Gevers T., Van De Weijer J. Computational color constancy: Survey and experiments. IEEE Transactions on Image Processing. 2011. V. 20 (9). P. 2475–2489.
Gladkov A.P., Kuznetsova E.G., Gladilin S.A., Gracheva M.A. Adaptivnaya stabilizatsiya yarkosti izobrazheniya v tekhnicheskoi sisteme raspoznavaniya krupnykh dvizhushchikhsya ob"ektov [Adaptive image brightness stabilization for the industrial system of large moving object recognition] Sensornye sistemy [Sensory systems]. 2017. V. 31 (3). P. 247–260 (in Russian). https://doi.org/10.31857/S0235009220010047
Gong H., Finlayson G.D., Fisher R.B., Fang F. 3D color homography model for photo-realistic color transfer re-coding. The Visual Computer. 2019. V. 35 (3). P. 323–333.
Goshin Y.V., Kotov A.P., Fursov V.A. Dvukhetapnoe formirovanie prostranstvennogo preobrazovaniya dlya sovmeshcheniya izobrazhenii [Two-stage formation of a spatial transformation for image matching] Komp’yuternaya optika [Computer Optics]. 2014. V. 38 (4). P. 886–891 (in Russian).
Goshtasby A.A. 2-D and 3-D Image Registration: for Medical, Remote Sensing, and Industrial Applications. John Wiley & Sons, 2005. 280 p.
Gruen A. Adaptive least squares correlation: a powerful image matching technique. South African Journal of Photogrammetry. RemoteSensing and Cartography. 1985. V. 14 (3). P. 175–187.
Haker S., Zhu L., Tannenbaum A., Angenent S. Optimal mass transport for registration and warping. International Journal of computer vision. 2004. V. 60 (3). P. 225–240.
Har-Peled S. New similarity measures between polylines with applications to morphing and polygon sweeping. Discrete & Computational Geometry. 2002. V. 28 (4). P. 535–569.
Hartley R., Zisserman A. Multiple view geometry in computer vision. Cambridge, England, Cambridge university press. 2003. 655 p.
Healey G. Using color for geometry-insensitive segmentation. JOSAA. 1989. V. 6 (6). P. 920–937.
Heckbert P.S. Fundamentals of texture mapping and image warping. University of California. Berkeley. 1989. V. 2 (3). P. 1–86.
Hsu S.C., Sawhney H.S. Influence of global constraints and lens distortion on pose and appearance recovery from a purely rotating camera. Applications of Computer Vision. 1998. WACV’98. Proc. of the Fourth IEEE Workshop on. IEEE. 1998. P. 154–159.
Huang J.B., Singh A., Ahuja N. Single image super-resolution from transformed self-exemplars. Proc. of the IEEE Conference on Computer Vision and Pattern Recognition. 2015. P. 5197–5206.
Huttenlocher D.P., Klanderman G.A., Rucklidge W.J. Comparing images using the hausdorff distance. IEEE Transactions on pattern analysis and machine intelligence. 1993. V. 15 (9). P. 850–863.
Ilyuhin S.A., Chernov T.S., Polevoy D.V., Fedorenko F.A. A method for spatially weighted image brightness normalization for face verification. Proc. SPIE 11041. Eleventh International Conference on Machine Vision (ICMV 2018). 2019a. V. 11041. P. 1104118. https://doi.org/10.1117/12.2522922
Ilyukhin S.A., Chernov T.S., Polevoy D.V. Povyshenie tochnosti neirosetevykh metodov verifikatsii lits za schet prostranstvenno-vzveshennoi normalizatsii yarkosti izobrazheniya [Improving the Accuracy of Neural Network Methods of Verification of Persons by Spatial-Weighted Normalization of Brightness Image] Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2019b. V. 2019 (4). P. 12–20 (in Russian). https://doi.org/10.14357/20718632190402
Ingacheva A.S., Chukalina M.V. Polychromatic CT Data Improvement with One-Parameter Power Correction. Mathematical Problems in Engineering. 2019. V. 2019. P. 1405365. https://doi.org/10.1155/2019/1405365
Iwamura M., Niwa R., Kise K., Uchida S., Omachi S. Rectifying perspective distortion into affine distortion using variants and invariants. Proc. of the Second International Workshop on Camera-Based Document Analysis and Recognition. 2007. P. 138–145.
Iyatomi H., Celebi M.E., Schaefer G., Tanaka M. Automated color normalization for dermoscopy images. 2010 IEEE International Conference on Image Processing. IEEE. 2010. P. 4357–4360.
Jaccard P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull Soc Vaudoise Sci Nat. 1901. V. 37. P. 241–272.
Jesorsky O., Kirchberg K.J., Frischholz R.W. Robust face detection using the hausdorff distance. International Conference on Audio-and Video-Based Biometric Person Authentication. Springer. 2001. P. 90–95.
Kadir T., Zisserman A., Brady M. An affine invariantsalient region detector. European conference on computer vision. Springer. 2004. P. 228–241.
Karaimer H.C., Brown M.S. A software platform for manipulating the camera imaging pipeline. European Conference on Computer Vision. 2016. P. 429–444. https://doi.org/10.1007/978-3-319-46448-0_26
Karaimer H.C., Brown M.S. Improving color reproduction accuracy on cameras. Proc. of the IEEE Conference on Computer Vision and Pattern Recognition. 2018. P. 6440–6449.
Karnaukhov V.N., Kober V.I. A locally adaptive algorithm for shadow correction in color images. Applications of Digital Image Processing XL, International Society for Optics and Photonics, Nov. 2017. 2017. V. 10396. P. 10396–23. https://doi.org/10.1117/12.2272692
Karpenko S., Konovalenko I., Miller A., Miller B., Nikolaev D. Uav control on the basis of 3d landmark bearing-only observations. Sensors. 2015. V. 15 (12). P. 29802–29820. https://doi.org/10.3390/s151229768
Katamanov S.N. Avtomaticheskaya privyazka izobrazhenii geostatsionarnogo sputnika mtsat-1r. Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa [Current Problems In Remote Sensing Of The Earth From Space]. 2007. V. 1 (4). P. 63–68 (in Russian).
Kholopov I.S. Algoritm korrektsii proektivnykh iskazhenii pri malovysotnoi s"emke [Projective distortion correction algorithm at low altitude photographing] Komp’yuternaya optika [Computer Optics]. 2017. V. 41 (2). P. 284–290 (in Russian).
Kim K., Lim T., Kim C., Park S., Park C., Keum C. High-precision color uniformity based on 4D transformation for micro-LED. Proc. SPIE 11302, Light-Emitting Devices, Materials, and Applications XXIV. 2020. V. 11302. P. 113021U. https://doi.org/10.1117/12.2542728
Kober V.I., Karnaukhov V.N. Adaptivnaya korrektsiya neravnomernogo osveshcheniya na tsifrovykh mul’tispektral’nykh izobrazheniyakh [Adaptive correction of nonuniform illumination of multispectral digital images] Informatsionnye protsessy. 2016a. V. 19 (2). P. 152–161 (in Russian).
Kober V.I., Karnaukhov V.N. Vosstanovlenie mul’tispektral’nykh izobrazhenii, iskazhennykh prostranstvenno-neodnorodnym dvizheniem kamery [Restoration of multispectral images degraded by non-uniform camera motion] Informatsionnye protsessy. 2015. V. 15 (2). P. 269–277 (in Russian).
Kober V.I., Karnaukhov V.N. Adaptive correction of nonuniform illumination of multispectral digital images. JCTE. 2016b. V. 61 (12). P. 1419–1425. https://doi.org/10.1134/S1064226916120123
Konovalenko I.A. Srednekvadratichnaya nevyazka koordinat kak kriterii tochnosti normalizatsii izobrazhenii pri opticheskom raspoznavanii dokumentov [RMS coordinate discrepancy as accuracy criterion of images normalization at optical document recognition] Informatsionnye protsessy. 2020a. V. 20 (3). P. 215–230 (in Russian).
Konovalenko I.A., Shemiakina J.A. Error values analysis for inaccurate projective transformation of a quadrangle. Journal of Physics: Conference Series. 2018. V. 1096 (1). P. 012038. https://doi.org/10.1088/1742-6596/1096/1/012038
Konovalenko I.A., Kokhan V.V., Nikolaev D.P. Optimal’naya affinnaya approksimatsiya proektivnogo preobrazovaniya izobrazhenii [Optimal affine approximation of image projective transformation] Sensornye sistemy [Sensory systems]. 2019. V. 33 (1). P. 7–14 (in Russian). https://doi.org/10.1134/S0235009219010062
Konovalenko I.A., Kokhan V.V., Nikolaev D.P. Optimal affine image normalization approach for optical character recognition. Computer Optics. 2021. V. 45 (1). P. 90–100. https://doi.org/10.18287/2412-6179-CO-759
Konovalenko I.A., Polevoy D.V., Nikolaev D.P. Maksimal’naya nevyazka napravlenii kak kriterii tochnosti proektivnoi normalizatsii izobrazheniya pri opticheskom raspoznavanii teksta [Maximal directions discrepancy as accuracy criterion of images projective normalization for optical text recognition] Sensornye sistemy [Sensory systems]. 2020b. V. 34 (2). P. 131–146 (in Russian). https://doi.org/10.31857/S0235009220020079
Konovalenko I.A., Shemyakina Y.A., Faradzhev I.A. Otsenka tochki skhoda otrezkov metodom maksimal’nogo pravdopodobiya [Calculation of a vanishing point by the Maximum likelihood estimation method] Vestnik YuUrGU MMP [Bulletin of the South Ural State University, Series: Mathematical Modelling, Programming and Computer Software]. 2020c. V. 13 (1). P. 107–117 (in Russian). https://doi.org/10.14529/mmp200108
Konovalenko I.A., Kokhan V.V., Nikolaev D.P. Maximal coordinate discrepancy as accuracy criterion of image projective normalization for optical recognition of documents. Bulletin of the South Ural State University, Series: Mathematical Modelling, Programming and Computer Software. 2020d. V. 13 (3). P. 43–58. https://doi.org/10.14529/mmp200304
Kordecki A. Practical testing of irradiance-independent camera color calibration. Proc. SPIE 11041. Eleventh International Conference on Machine Vision (ICMV 2018). 2019. V. 11041. P. 340–345.
Kozlov E.P., Egoshkin N.A., Eremeev V.V. Normalizatsiya kosmicheskikh izobrazhenii Zemli na osnove ikh sopostavleniya s elektronnymi kartami. Tsifrovaya obrabotka signalov. [Digital Signal Processing]. 2009. V. (3). P. 21–26 (in Russian).
Kunina I.A., Aliev M.A., Arlazarov N.V., Polevoy D.V. A method of fluorescent fibers detection on identity documents under ultraviolet light. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 1–8. https://doi.org/10.1117/12.2558080
Kunina I.A., Gladilin S.A., Nikolaev D.P. Blind radial distortion compensation in a single image using fast Hough transform. Computer Optics. 2016. V. 40 (3). P. 395–403. https://doi.org/10.18287/2412-6179-2016-40-3-395-403
Kutulakos K.N., Vallino J. Affine object representations for calibration-free augmented reality. Virtual Reality Annual International Symposium. Proc. of the IEEE 1996. IEEE. 1996. P. 25–36.
Legge G.E., Pelli D.G., Rubin G.S., Schleske M.M. Psychophysics of reading–I. Normal vision. Vision research. 1985. V. 25 (2). P. 239–252.
Limonova E., Bezmaternykh P.V., Nikolaev D., Arlazarov V. Slant Rectification in Russian Passport OCR System Using Fast Hough Transform. Ninth International Conference on Machine Vision (ICMV 2016). 2017. V. 10341. P. 103410P. https://doi.org/10.1117/12.2268725
Limonova E., Nikolaev D., Arlazarov V.V. Bipolar Morphological U-Net for Document Binarization. Thirteenth International Conference on Machine Vision (ICMV 2020). 2021. V. 11605. P. 116050P. https://doi.org/10.1117/12.2587174
Lorenz H., Döllner J. Real-time piecewise perspective projections. GRAPP. 2009. P. 147–155.
Lu S., Chen B.M., Ko C.C. Perspective rectification of document images using fuzzy set and morphological operations. Image and Vision Computing. 2005. V. 23 (5). P. 541–553.
Lyubchenko V.A., Putyatin E.P. Matematicheskie modeli razlozheniya proektivnykh preobrazovanii v zadachakh normalizatsii. Radioelektronika i informatika. 2002. V. 2 (19). P. 57–59 (in Russian).
MacAdam D.L. Projective Transformations of I. C. I. Color Specification. J. Opt. Soc. Am. 1937. V. 27 (8). P. 294–299. https://doi.org/10.1364/JOSA.27.000294
Merino-Gracia C., Mirmehdi M., Sigut J., González-Mora J.L. Fast perspective recovery of text in natural scenes. Image and Vision Computing. 2013. V. 31 (10). P. 714–724.
Mikolajczyk K., Schmid C. An affine invariant interest point detector. European conference on computer vision. Springer. 2002. P. 128–142.
Mikolajczyk K., Schmid C. Scale & affine invariant interest point detectors. International journal of computer vision. 2004. V. 60 (1). P. 63–86.
Morel J.M., Yu G. ASIFT: A new framework for fully affine invariant image comparison. SIAM journal on imaging sciences. 2009. V. 2 (2). P. 438–469.
Murygin K.V. Normalizatsiya izobrazheniya avtomobil’nogo nomera i segmentatsiya simvolov dlya posleduyushchego raspoznavaniya [Normalization of the Image of a Car Plate and Segmentation of Symbols for the Subsequent Recognition] Shtuchny jintelekt [Artificial Intelligence]. 2010. V. (3). P. 364–369 (in Russian).
Nikolaev D.P., Gladkov A., Chernov T., Bulatov K. Diamond Recognition Algorithm using Two-Channel X-ray Radiographic Separator. Seventh International Conference on Machine Vision (ICMV 2014). International Society for Optics and Photonics. 2015. V. 9445. P. 944507. https://doi.org/10.1117/12.2181204
Nikolaev D.P., Grigoryev A.S., Gladkov A.P. Programma avtomaticheskogo soglasovaniya chuvstvitel’nostei kamer stereopary. Patent RF. No. RU 2016617966. 2016.
Nikolaev P.P. Metod proektivno invariantnogo opisaniya ovalov s osevoi libo tsentral’noi simmetriei. Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2014. V. (2). P. 46–59 (in Russian).
Nikolaev P.P. Proektivno invariantnoe raspoznavanie sostavnykh ovalov. Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2010. V. (4). P. 3–15 (in Russian).
Nikolaev P.P. Raspoznavanie proektivno preobrazovannykh ploskikh figur. X. Metody poiska okteta invariantnykh tochek kontura ovala - itog vklyucheniya razvitoy teorii v skhemy ego opisaniya [Recognition of projectively transformed planar figures. X. Methods for finding an octet of invariant points of an oval contour – the result of introducing a developed theory into the schemes of oval description] Sensornye sistemy [Sensory systems]. 2017. V. 31 (3). P. 202–226 (in Russian).
Nikolaev P.P., Savchik A.V., Konovalenko I.A. Proektivno invariantnoe predstavlenie kompozitsii dvukh ovalov [A Projectively Invariant Representation of a Composition of Two Ovals] Informatsionnye protsessy. 2018. V. 18 (4). P. 304–321 (in Russian).
Nikolayev P.P. Proektivno invariantnoe opisanie ovalov s simmetriyami trekh rodov [A Projective Invariant Description of Ovals with Three Possible Symmetry Genera] Vestnik RFFI [Vestnik RFFI]. 2016. V. (4). P. 38–54 (in Russian). https://doi.org/10.22204/2410-4639-2016-092-04-38-54
Nikolaidis A. Affine transformation invariant image watermarking using moment normalization and radial symmetry transform. 18th IEEE International Conference on Image Processing. IEEE. 2011. P. 2729–2732.
Ohta T.I., Maenobu K., Sakai T. Obtaining surface orientation from texels under perspective projection. IJCAI. 1981. P. 746–751.
Orrite C., Herrero J.E. Shape matching of partially occluded curves invariant under projective transformation. Computer Vision and Image Understanding. 2004. V. 93 (1). P. 34–64.
Panfilova E.I., Shipitko O.S., Kunina I.A. Fast Hough Transform-Based Road Markings Detection For Autonomous Vehicle. Thirteenth International Conference on Machine Vision (ICMV 2020). 2021 V. 11605. P. 116052B. https://doi.org/10.1117/12.2587615
Pavić D., Schönefeld V., Kobbelt L. Interactive image completion with perspective correction. The Visual Computer. 2006. V. 22 (9–11). P. 671–681.
Polevoy D.V., Panfilova E.I., Ershov E.I., Nikolaev D.P. Color correction of the document owner’s photograph image during recognition on mobile device. Thirteenth International Conference on Machine Vision (ICMV 2020). 2021. V. 11605. P. 1160510. https://doi.org/10.1117/12.2587627
Povolotskiy M.A., Kuznetsova E.G., Utkin N.V., Nikolaev D.P. Segmentatsiya registratsionnykh nomerov avtomobilei s primeneniem algoritma dinamicheskoi transformatsii vremennoi osi [Segmentation of vehicle registration plates based on dynamic time warping] Sensornye sistemy [Sensory systems]. 2018. V. 32 (1). P. 50–59 (in Russian). https://doi.org/10.7868/S0235009218010080
Povolotskiy M.A., Tropin D.V. Dynamic Programming Approach to Template-based OCR. Proc. SPIE 11041. Eleventh International Conference on Machine Vision (ICMV 2018). 2019. V. 11041. P. 110411T. https://doi.org/10.1117/12.2522974
Povolotskiy M.A., Tropin D.V., Chernov T.S., Savel’ev B.I. Metod segmentatsii strukturirovannykh tekstovykh ob"ektov na izobrazhenii s pomoshch’yu dinamicheskogo programmirovaniya [Dynamic programming approach to textual structured objects segmentation in images] Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2019. V. 69 (3). P. 66–78 (in Russian). https://doi.org/10.14357/20718632190306
Pritula N., Nikolaev D.P., Sheshkus A., Pritula M., Nikolaev P.P. Comparison of two algorithms modifications of projective-invariant recognition of the plane boundaries with the one concavity. Seventh International Conference on Machine Vision (ICMV 2014). International Society for Optics and Photonics. ICMV 2014. 2015. V. 944508. P. 1–5. https://doi.org/10.1117/12.2181215
Prun V.E., Polevoy D.V., Postnikov V.V. Forward Rectification – Spatial Image Normalization for a Video from a Forward Facing Vehicle Camera. Ninth International Conference on Machine Vision (ICMV 2016). 2017. V. 10341. P. 103410W. https://doi.org/10.1117/12.2268605
Putyatin E.P., Prokopenko D.O., Pechenaya E.M. Voprosy normalizatsii izobrazhenii pri proektivnykh preobrazovaniyakh. Radioelektronika i informatika [Radioelectronics & Informatics]. 1998. V. 2 (3). P. 82–86 (in Russian).
Rezatofighi H., Tsoi N., Gwak J., Sadeghian A., Reid I., Savarese S. Generalized intersection over union: A metric and a loss for bounding box regression. Proc. of the IEEE Conference on Computer Vision and Pattern Recognition. 2019. P. 658–666.
Rodríguez-Piñeiro J., Comesaña-Alfaro P., Pérez-González F., Malvido-García A. A new method for perspective correction of document images. Document Recognition and Retrieval XVIII. International Society for Optics and Photonics. 2011. V. 787410. P. 1–12.
Safari R., Narasimhamurthi N., Shridhar M., Ahmadi M. Document registration using projective geometry. IEEE transactions on image processing. 1997. V. 6 (9). P. 1337–1341.
Savchik A., Ershov E., Karpenko S. Color Cerberus. ISPA 2019. 2019. P. 355–359. https://doi.org/10.1109/ISPA.2019.8868425
Savchik A.V., Nikolaev P.P. Metod proektivnogo sopostavleniya dlya ovalov s dvumya otmechennymi tochkami. Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2018. V. (1). P. 60–67 (in Russian).
Savchik A.V., Nikolaev P.P. Teorema o peresechenii T-i H-polyar [The Theorem of T- and H- Polars Intersections Count]. Informatsionnye protsessy. 2016. V. 16 (4). P. 430–443 (in Russian).
Sawhney H.S., Kumar R. True multi-image align mentand its application to mosaicing and lens distortion correction. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1999. V. 21 (3). P. 235–243.
Schmitzer B., Schnörr C. Globally optimal joint image segmentation and shape matching based on Wasserstein modes. Journal of Mathematical Imaging and Vision. 2015. V. 52 (3). P. 436–458.
Shemiakina J., Konovalenko I., Tropin D., Faradjev I. Fast projective image rectification for planar objects with Manhattan structure. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 114331N. https://doi.org/10.1117/12.2559630
Shemiakina J.A., Zhukovsky A.E., Faradjev I.A. Issledovanie algoritmov vychisleniya proektivnogo preobrazovaniya v zadache navedeniya na planarnyi ob"ekt po osobym tochkam [The research of the algorithms of a projective transformation calculation in the problem of planar object targeting by feature points] Iskusstvennyi intellekt i prinyatie reshenii [Artificial Intelligence And Decision Making]. 2017. V. 2017 (1). P. 43–49 (in Russian).
Shemiakina Yu.A. Ispol’zovanie tochek i pryamykh dlya vychisleniya proektivnogo preobrazovaniya po dvum izobrazheniyam ploskogo ob"ekta [The usage of points and lines for the calculation of projective transformation by two images of one plane object] Informatsionnye tekhnologii i vychislitel’nye sistemy [Journal Of Information Technologies And Computing Systems]. 2017. V. 2017 (3). P. 79–91 (in Russian).
Shepelev D.A., Bozhkova V.P., Ershov E.I., Nikolaev D.P. Modelirovanie drobovogo shuma tsvetnykh podvodnykh izobrazhenii [Simulating shot noise of color underwater images] Komp’yuternaya optika [Computer Optics]. 2020. V. 44 (4). P. 671–679 (in Russian). https://doi.org/10.18287/2412-6179-CO-754
Sheshkus A., Ingacheva A., Arlazarov V., Nikolaev D. HoughNet: neural network architecture for vanishing points detection. ICDAR 2019, IEEE. 2020. V. 8978201. P. 844–849. https://doi.org/10.1109/ICDAR.2019.00140
Shipitko O., Grigoryev A. Ground Vehicle Localization With Particle Filter Based On Simulated Road Marking Image. ECMS 2018. 2018. P. 341–347. https://doi.org/10.7148/2018-0341
Shipitko O., Kibalov V., Abramov M. Linear Features Observation Model for Autonomous Vehicle Localization. ICARCV 2020, Institute of Electrical and Electronics Engineers Inc. 2021. V. 9305434. P. 1360–1365. https://doi.org/10.1109/ICARCV50220.2020.9305434
Shipitko O.S., Abramov M.P., Lukoyanov A.S., Panfilova E.I., Kunina I.A., Grigoryev A.S. Edge detection based mobile robot indoor localization system. Proc. SPIE 11041. Eleventh International Conference on Machine Vision (ICMV 2018). 2019. V. 11041. P. 110412V. https://doi.org/10.1117/12.2522788
Sim D.G., Kwon O.K., Park R.H. Object matching algorithms using robust hausdorff distance measures. IEEE Transactions on image processing. 1999. V. 8 (3). P. 425–429.
Sinclair D., Blake A. Isoperimetric normalization of planar curves. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1994. V. 16 (8). P. 769–777.
Singh S.K., Naidu S.D, Srinivasan T.P., Krishnaa B.G, Srivastava P.K. Rational polynomial modelling for cartosat-1 data. The International Archives of the Photogrammetry. Remote Sensing and Spatial Information Sciences. 2008. V. 37. P. 885–888.
Skoryukina N., Arlazarov V.V., Nikolaev D.P. Fast method of ID documents location and type identification for mobile and server application. ICDAR 2019. 2020. P. 850–857. https://doi.org/10.1109/ICDAR.2019.00141
Skoryukina N., Chernov T., Bulatov K., Nikolaev D.P., Arlazarov V. Snapscreen: Tv-stream frame search with projectively distorted and noisy query. Ninth International Conference on Machine Vision (ICMV 2016). 2017. V. 103410Y. P. 1–5. Bellingham. https://doi.org/10.1117/12.2268735
Skoryukina N., Shemiakina J., Arlazarov V. L., Faradjev I. Document localization algorithms based on feature points and straight lines. Tenth International Conference on Machine Vision (ICMV 2017). International Society for Optics and Photonics. 2018. V. 106961H. P. 1–8. https://doi.org/10.1117/12.2311478
Smagina A., Bozhkova V.P., Gladilin S., Nikolaev D. Linear colour segmentation revisited. Proc. SPIE 11041. Eleventh International Conference on Machine Vision (ICMV 2018). 2019. V. 11041. P. 110410F. https://doi.org/10.1117/12.2523007
Smagina A., Ershov E., Grigoryev A. Multiple Light Source Dataset for Colour Research. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 114332C. https://doi.org/10.1117/12.2559491
Smith T., Guild J. The C.I.E. colorimetric standards and their use. Transactions of the Optical Society. 1931. V. 33 (3). P. 73–134. https://doi.org/10.1088/1475-4878/33/3/301
Stein G.P. Lens distortion calibration using point correspondences. Computer Vision and Pattern Recognition, 1997. Proc. of the IEEE Computer Society Conference. 1997. P. 602–608.
Su Z., Zeng W., Wang Y., Lu Z.L., Gu X. Shape classification using Wasserstein distance for brain morphometry analysis. International Conference on Information Processing in Medical Imaging. Springer. 2015. P. 411–423.
Szeliski R. Video mosaics for virtual environments. IEEE computer Graphics and Applications. 1996. P. 16 (2). P. 22–30.
Takezawa Y., Hasegawa M., Tabbone S. Camera-captured document image perspective distortion correction using vanishing point detection based on Radon transform. Pattern Recognition (ICPR). 2016 23rd International Conference on. IEEE. 2016. P. 3968–3974.
Titov V., Shepelev D., Nikolaev D. Opredelenie parametrov pogloscheniya i rasseyaniya na osnove bystrogo preobrazovaniya Khafa. Sbornik trudov 43-i mezhdistsiplinarnoi shkoly-konferentsii IPPI RAN “Informatsionnye tekhnologii i sistemy 2019" (ITiS 2019). [Proc. of the ITaS 2019]. 2020. P. 495–500 (in Russian).
Tong L., Zhang Y. Correction of perspective text image based on gradient method. Information Networking and Automation (ICINA). International Conference on. IEEE. 2010. V. 2. P. 312–316.
Triputen’ V.V., Gorokhovatskii V.A. Algoritm parallel’noi normalizatsii affinnykh preobrazovanii dlya tsvetnykh izobrazhenii. Radioelektronika i informatika [Radioelectronics & Informatics]. 1997. V. (1). P. 97–98. (in Russian).
Trusov A., Limonova E. The analysis of projective transformation algorithms for image recognition on mobile devices. Proc. SPIE 11433. Twelfth International Conference on Machine Vision (ICMV 2019). Wolfgang Osten and Dmitry P. Nikolaev editors. 2020. V. 11433. P. 250–257.
Tsviatkou V.Yu. Geometricheskie modeli mnogorakursnykh izobrazhenii i proektivnaya kompensatsiya dvizheniya kamery [Geometric models of multi-angle images and projective compensation of camera motion] Doklady Belorusskogo gosudarstvennogo universiteta informatiki i radioelektroniki [Doklady BGUIR]. 2014. V. 86 (8). P. 41–47 (in Russian).
Vanichev A.Yu. Normalizatsiya siluetov ob"ektov v sistemakh tekhnicheskogo zreniya. Programmnye produkty i sistemy. [Software & Systems]. 2007. V. (3). P. 86–88 (in Russian).
Wallace G., Chen H., Li K. Color gamut matching for tiled display walls. EGVE '03: Proc. of the workshop on Virtual environments 2003. 2003. P. 293–302. https://doi.org/10.1145/769953.769988
Wolberg G. Digital Image Warping. IEEE Computer Society Press, LosAlamitos, CA, 1990. 318 p.
Xie Y., Tang G., Hoff W. Geometry-based populated chessboard recognition. Tenth International Conference on Machine Vision (ICMV 2017). International Society for Optics and Photonics. 2018. V. 1069603. P. 1–5.
Zeynalov R., Velizhev A., Konushin A. Vosstanovlenie formy stranitsy teksta dlya korrektsii geometricheskikh iskazhenii [Document images geometrical distortions correction using text lines shape extraction]. Proc. of the 19 International Conference GraphiCon-2009. 2009. P. 125–128 (in Russian).
Zhang W., Li X., Ma X. Perspective correction method for Chinese document images. Intelligent Information Technology Application Workshops. 2008. IITAW’08. International Symposium on. IEEE. 2008. P. 467–470.
Zhang Z., He L.W. Whiteboard scanning and image enhancement. Digital signal processing. 2007. V. 17 (2). P. 414–432.
Zhukovskiy A.E., Nikolaev D.P., Arlazarov V.V., Postnikov V.V., Polevoy D.V., Skoryukina N.S., Chernov T.S., Shemyakina Yu.A., Mukovozov A.A., Konovalenko I.A., Povolotskiy M.A. Segments graph-based approach for document capture in a smartphone video stream. ICDAR2017. IEEE Computer Society. 2018. V. 1. P. 337–342. https://doi.org/10.1109/ICDAR.2017.63
Zwicker M., Rasanen J., Botsch M., Dachsbacher C., Pauly M. Perspective accurate splatting. Proc. of the Graphics interface 2004. Canadian Human-Computer Communications Society. 2004. P. 247–254.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы