Сенсорные системы, 2023, T. 37, № 1, стр. 78-88

ВВЕДЕНИЕ

Одной из актуальных задач в сфере космических технологий является задача сближения и стыковки космических аппаратов (КА).

Первая автоматическая стыковка была проведена 30 октября 1967 г. Тогда на орбите состыковались при помощи системы “Игла”, разработанной в Советском Союзе, две испытательные машины: “Космос – 186” и “Космос – 188”. В настоящее время стыковка с Международной космической станцией (МКС) является регулярной и проводится уже несколько десятков лет.

В космической отрасли отечественного производства активно используется радиотехническая система “Курс” – это система взаимных измерений параметров движения для поиска сближения и стыковки КА с МКС. Система “Курс” позволяет обеспечить стыковку в полностью автоматическом режиме без встречной ориентации орбитальной станции. Надежность комплекса повышается за счет современных датчиков измерения скорости и дальности, а также автоматического контроля критичных параметров. Однако характеристики радиотехнических систем стыковки являются не вполне удовлетворительными.

Одной из проблем является сложная конфигурация объектов, с которыми осуществляется стыковка. Радиочастотный сигнал испытывает множественные переотражения от элементов конструкции, которые вносят заметные ошибки в результаты измерений и вызывают сбои слежения за измеряемыми параметрами движения (Медведев, 2012). Также данные системы требуют размещения сложной и громоздкой аппаратуры на обоих сближающихся бортах и большого энергопотребления.

В крупные частные американские космические компании процесс автоматической стыковки пришел совсем недавно. Впервые капсула Crew Dragon от SpaceX состыковалась полностью автоматически в 2019 г. До этого момента стыковку осуществлял член экипажа, который находился на борту МКС. Такая стыковка производилась при помощи роботизированной руки, которая перемещала капсулу в доступный порт. Первая автоматическая стыковка являлась демонстрацией безопасной доставки грузов, но не людей, хотя наиболее значимым событием является именно автоматическая стыковка аппаратов с людьми на борту (Grush, 2019). Уже на следующий год компания SpaceX произвела автоматическую стыковку капсулы с МКС, в которой находились двое астронавтов (Grush, 2020). Эти стыковки были организованы с использованием лазеров, датчиков и программного обеспечения для автоматической стыковки оборудования с доступным портом за пределами МКС.

Российский транспортный пилотируемый космический корабль “Союз МС-21 С.П. Королев” был запущен к МКС с космодрома Байконур 18 марта 2022 г. На данный момент это один из последних запусков космического корабля. Процесс стыковки КА с модулем “Причал” сначала проходил штатно в автоматическом режиме с использованием вышеописанной системы “Курс”, но примерно на дальности 180 м пришлось перейти в ручной режим. На данный момент точные причины отказа системы не установлены, но факт отказа подтверждает актуальность задачи повышения надежности автоматической стыковки.

Еще одним из последних примеров отказа “Курса” служит стыковка, выполненная 5 октября 2021 г. Начало запуска ракеты, выход на орбиту, подход к МКС прошли штатно, но, когда до МКС оставалось около 29 м, корабль “Союз МС-19” вдруг отошел обратно, после он начал еще одну попытку стыковки, которая снова закончилась неудачно. После стало ясно, что отказала система автоматического сближения, и командиру экипажа пришлось провести стыковку в ручном режиме. Отметим, что этот выход в космос был произведен для съемок первого в мире фильма в космосе, таким образом, большинство состава экипажа были российские актеры, а не профессиональные космонавты, одному из которых пришлось выполнять функции бортинженера.

Все стыкующиеся КА в течение последних 45 лет оснащаются специальным набором камер и средств передачи данных, при помощи которых осуществляется визуальный контроль процесса сближения и стыковки (Мюллер и др., 2019). Видеоизображение, полученное с этих камер, может использоваться для решения навигационных задач в процессе сближения и стыковки. Продолжительное время это видеоизображение использовалось в так называемом “ручном” режиме: космонавт на станции управляет стыкующимся с ней КА, руководствуясь телевизионным изображением, получаемым с телекамеры, находящейся на корабле. Такой режим использовался при стыковке беспилотного корабля “Прогресс” с орбитальной станцией “Мир” в мае 2010 г. Ручной режим стыковки накладывает дополнительную ответственность на космонавта, а также увеличивает его психическую нагрузку. Современная аппаратура и вычислительная техника позволяют строить системы компьютерного зрения, которые дают возможность автоматизировать многие процессы сбора и обработки зрительных данных и включить зрительную обратную связь в систему управления КА без участия человека (Сайгираев и др., 2004). Рассмотрим некоторые подходы и существующие системы, основанные на этом.

Б.М. Миллер и соавторы в своей работе (Миллер и др., 2017) предлагают подход к навигации беспилотного летательного аппарата (БПЛА) при помощи оптического потока. Изображение фиксируется с использованием камеры, расположенной на борту. Автор указывает, что применение оптического потока для определения элементов движения дает дополнительное средство навигации, которое можно достаточно эффективно использовать для некоторых специфических задач, решаемых на БПЛА в автономном режиме.

В работе (Попов и др., 2018) исследуется задача визуальной навигации для автоматической посадки БПЛА. Авторами было показано, что использование последовательности изображений с двух камер, установленных на разных высотах на борту БПЛА, позволяет существенно повысить точность оценки высоты в сравнении с применением имеющихся бортовых средств.

В статье (Богуславский, Соколов, 2011) представлена система автоматического мониторинга процесса сближения и стыковки космических аппаратов. Система основана на обработке видеосигнала, идущего с камер, расположенных на КА. В каждом кадре выделяются детали стыковочных узлов, размеры и геометрические параметры взаимного расположения которых используются как первичные измерения. Обработка кадров происходит в реальном времени. Исследования, представленные в работе С.М. Соколова, показывают возможность успешного использования системы технического зрения для информационного обеспечения процессов сближения, стыковки и посадки космических аппаратов.

В статье (Бахшиев и др., 2013) представлена система контроля положения КА относительно МКС. Так, для решения этой задачи, как и в предыдущих примерах, воспользовались телевизионным изображением, формируемым существующими камерами, установленными на КА и МКС. Благодаря проведенным экспериментам был сделан вывод, что ошибка определения экранных координат ключевых точек конструкции наблюдаемого объекта наиболее существенно влияет на определение углов отклонения объекта от линии визирования и угла взаимного крена.

Проведя анализ множества статей, можно сказать, что существуют системы, решающие задачу стыковки КА с МКС различными методами и алгоритмами. Современная техника способна решать задачи определения взаимного местоположения и параметров движения космического аппарата, используя информацию с камеры, установленной на нем. Использование камеры требует решения задачи калибровки, которую необходимо проводить периодически в условиях космической съемки.

Для решения задачи калибровки на данный момент применяются различные методы и алгоритмы. Наиболее распространенной является калибровка с использованием некоторого шаблона, например шахматной доски. Применение таких методов в космических условиях не является преимущественным.

Существуют и другие методы калибровки. В работах (Hartley, 1997; Stein, 1995) представлены методы, использующие разные изображения одной сцены. Основой для анализа в таких методах служат априорные знания о геометрии сцены или траектории движения камеры. В нашем случае такие методы тоже являются неприменимыми, так как отсутствует возможность получения нужного изображения с бортовой камеры КА, а в доступе находятся некоторые кадры процесса стыковки. При этом информация о камере, формировавшей снимки, и ее внутренних параметрах отсутствует. Экспертного истинного значения фокусного расстояния камеры тоже нет. В нашем случае необходимо оценить фокусное расстояние на основе анализа кадров. Такой способ носит название автоматической калибровки. К таким способам относят: анализ изображения в частотной области, исследование структуры изображения и другие.

В работе (Кунина и др., 2016) описан метод калибровки, основанный на предположении, что классическая сцена имеет прямые линии. При центрально-проективном преобразовании прямые линии должны отобразиться в прямые, но на изображении они могут быть искривлены вследствие радиальной дисторсии. Знание этого факта может помочь разрешить задачу калибровки. Преимуществом алгоритма, предложенного в работе, является использование единственного изображения сцены без знания априорной информации о внутренних параметрах камеры. Алгоритм продемонстрировал практическую применимость и высокую точность исправления радиальной дисторсии. Недостатком же является факт должного существования прямых линий на сцене, изображенной на кадре. Этот недостаток говорит о невозможности применения данного метода для решения задачи автокалибровки в космосе.

Резюмируя все вышесказанное, можно утверждать, что существует множество методов калибровки камеры, но применение большинства из них невозможно в условиях космического пространства.

ПОСТАНОВКА ЗАДАЧИ

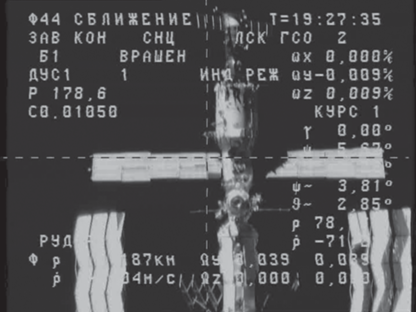
Имеются кадры процесса сближения КА с МКС. Полагаем, что съемка процесса осуществлялась камерой-обскурой. Один из кадров представлен на рис. 1.

Известно, что кадры получены в момент вращения камеры относительно МКС, т.е. положение камеры не менялось, но при этом изменились углы Эйлера (крен, тангаж, рысканье). Как утверждалось выше, МКС имеет сложную конфигурацию, но независимо от того, объемная она или нет, ее изображение на кадре не будет меняться, так как кадры получены в момент, когда камера только вращалась. Исходя из этого, можно считать, что облако особых точек на поверхности МКС лежит в одной плоскости (сцена плоская). Координаты точки на сцене обозначим за x₁, x₂. Известно, что плоская сцена связана с ее изображением центрально-проективным преобразованием (Karpenko et al., 2015)

в котором матрица преобразования H_c = [h_ij] имеет следующий вид:

Как видно, такое преобразование задается матрицей камеры C, произвольным не нулевым числом γ, вектором сдвига t и матрицей поворота R. Будем предполагать, что фокусные расстояния по ширине и высоте пикселя равны, и пиксели не скошены. Тогда матрица камеры имеет следующий вид:

где c = [c₁c₂]^T – принципиальная точка камеры (в пикселях), f – фокусное расстояние камеры.

Ортонормированная матрица поворота $R \in {{\mathbb{R}}^{{3 \times 3}}}$ имеет следующий вид:

где [y p r]^T – углы Эйлера (y – рысканье, p – тангаж, r – крен). Обозначим вектор углов Эйлера за $\vec {\alpha }$.

Матрица камеры содержит внутренние параметры камеры, процесс их определения по отснятым ею фотографиям называется внутренней калибровкой. Процесс определения матрицы поворота и вектора смещения по имеющимся кадрам носит название внешней калибровки (Бохоева, Курохтин, 2016). Существует ряд методов калибровки камеры (Гошин, Фурсов, 2012; Medioni, Kang, 2004; Hartley, 1995; Heikkila, Silver, 1997), каждый из которых имеет определенные преимущества и недостатки.

Внутренние параметры описывают устройство камеры. Обычно внутренняя калибровка производится 1 раз. Это связано с тем, что внутренние геометрические параметры, оптические характеристики линз и параметры устройства отображения, как правило, не меняются во время съемки. В нормальных условиях калибровка камеры осуществляется в лаборатории. В нашем случае параметры камеры, используемой в процессе съемки стыковки КА с МКС, неизвестны, а калибровка камеры в космическом пространстве с использованием шаблона (метод гибкой калибровки Чжана (Zhang, 2000)) является затратной. Регулярный процесс калибровки камеры тоже является необходимым, так как сбитая калибровка может сказаться на точности системы автоматической стыковки, использующей получаемую визуальную информацию.

Будем считать принципиальную точку камеры известной (поделенные пополам размеры кадра). Тогда неизвестными в центрально-проективном преобразовании параметрами останутся углы Эйлера, вектор сдвига и фокусное расстояние (Konovalenko et al., 2015). При этом в нашем распоряжении имеются кадры процесса стыковки. Таким образом, возникает задача определения фокусного расстояния бортовой камеры КА по данным стыковки с МКС. Дальнейшее использование полученного фокусного расстояния необходимо для решения более глобальной задачи – разработка системы автоматической стыковки.

СВЯЗЬ ИЗОБРАЖЕНИЙ ПЛОСКОЙ СЦЕНЫ

Выведем связь двух изображений одной плоской сцены. Трехмерные координаты сцены обозначим как [x₀, y₀, z₀]. В соответствии с постановкой задачи МКС считаем плоской, так как камера только вращается. В связи с этим введем координату z₀ равной 1. Тогда преобразование координат точек сцены [x₀, y₀] в координаты на первом кадре выглядит следующим образом:

Преобразуем выражение (8) к выражению (9):

Аналогично выражению (8) в выражении (10) представлено преобразование координат точек сцены в координаты на втором кадре:

Подставляя выражение (9) в (10), получим формулу, соответствующую преобразованию координат между двумя кадрами одной сцены. Откуда следует, что матрица преобразования может быть записана как произведение центрально-проективных матриц преобразований

Распишем каждую матрицу преобразования:

Так как для исследования выбраны кадры последовательности с наблюдаемым процессом вращения камеры, следовательно t₁ = t₂ = t. Собирая все в одну формулу, получим:

Заметим, что матрица поворота является ортогональной и, следовательно, обратная ей матрица есть транспонированная матрица. Произведение ${{R}_{1}} \cdot R_{2}^{{ - 1}}$ обозначим за R и в дальнейшим будем искать углы, определяющие эту матрицу поворота. Из всего вышесказанного имеем

МИНИМИЗАЦИЯ КВАДРАТИЧНОГО ФУНКЦИОНАЛА

Обозначим двухмерные точки на первом кадре за x₁, x₂, …, x_n. Соответствующие им точки на втором обозначим за y₁, y₂, …, y_n. Вектор всех неизвестных параметров матрицы проективного преобразования обозначим за θ.

Тогда квадратичный функционал ошибки запишется следующим образом:

Минимизация функционала (16) по содержащимся в преобразовании H параметрам приведет к решению поставленной задачи:

МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Для построения функционала максимального правдоподобия необходимо определить вероятностную модель перехода ключевых точек первого кадра в соответствующие точки второго кадра. Будем считать, что выбранные точки на первом кадре не шумят, а ключевые точки второго кадра шумят. Такое модельное предположение позволит построить более простой функционал оптимизации и упростить решение. Шум координат этих точек опишем с использованием вектора независимых нормально распределенных случайных величин:

Распишем формулу полученных при помощи проективного преобразования координат точек второго кадра с учетом шума:

где f – фокусное расстояние (в пикселях), $\vec {\alpha }$ – вектор углов Эйлера. Вектор параметров получившейся вероятностной модели обозначим

Обозначим матрицу наблюдений

Далее запишем функцию правдоподобия с учетом независимости y_i:

В дальнейшем будем использовать логарифмическую функцию правдоподобия l(θ) = lnL(θ). Так как она строго монотонно возрастает на всей области определения, максимум любой функции L(θ) является максимумом функции lnL(θ), и наоборот (Коноваленко, 2020):

Распишем функцию правдоподобия (22) как логарифмическую

Заметим, что первое слагаемое каждой суммы не зависит от f и 0.5σ^–2 константа по f, поэтому оптимизация по σ для поиска оценки фокусного расстояния может быть опущена. Откуда следует, что метод максимального правдоподобия сводится к инженерному подходу к решению (17) и служит его вероятностным обоснованием.

ОЦЕНКА АПОСТЕРИОРНОГО МАКСИМУМА

Предположим, что априорное распределение g(f) известно. Это позволяет рассматривать f как случайную величину байесовской статистики. Тогда апостериорная плотность вероятности фокусного расстояния при условии полученных данных Y:

Метод оценки априорного максимума затем оценивает  f  как моду апостериорного распределения этой случайной величины:

Заметим, что в формуле (27) знаменатель выражения не зависит от f и никак не влияет на значения максимума аргумента, откуда следует, что при максимизации этой функции по f его можно приравнять к 1. Также отметим факт того, что при равновероятностном распределении функция g( f ) принимает какое-либо постоянное значение, тогда при оптимизации ее тоже можно не учитывать. Таким образом, если считать все параметры равновероятными, придем к методу максимального правдоподобия (частный случай метода апостериорного максимума), который описан в предыдущей части.

Аналогично методу максимального правдоподобия, для решения оптимизационной задачи будем использовать логарифмирование. Исходя из этого, получим:

Для поиска оптимальной $\vec {\sigma }$ приравняем к нулю частную производную функцию правдоподобия l(θ) = g(Y | f) по σ:

Умножим обе части выражения на ${{\sigma }^{3}}$:

Выразим ${{\sigma }^{2}}$ из выражения (30):

Используя факт того, что $g\left( f \right)$ не зависит от σ, получим

РЕАЛИЗАЦИЯ ПРЕДЛОЖЕННЫХ МЕТОДОВ

Определение фокусного расстояния камеры производилось с использованием имеющихся кадров, полученных во время вращения камеры. Расстояние между положениями МКС на двух имеющихся кадрах велико. Так как экспертное значение фокусного расстояния неизвестно, оценку достаточно провести для одной пары кадров. Предлагаемый метод выбран из модельных предположений и не является эвристикой, поэтому оценка носит лишь демонстративный характер.

С использованием алгоритма поиска особых точек (SIFT (Lowe, 1999)), были найдены все особые точки на имеющихся изображениях, вычислены их дескрипторы. Далее дескрипторы ключевых точек были сопоставлены и с применением алгоритма RANSAC (Fischer et al., 1981) отброшены все пары точек, которые не удовлетворяют модели.

В процессе визуального осмотра было выяснено, что среди всех сопоставленных точек почти не было точек, соответствующих расположению солнечных батарей МКС. Поэтому решено вручную выбрать особые точки на кадрах и добавить их к множеству всех точек, найденных алгоритмом SIFT. В конечном итоге получены два множества особых точек (для каждого выбранного кадра свое), имеющие мощность 132. На рис. 2 представлены выбранные для решения задачи кадры с обозначенными на них особыми точками.

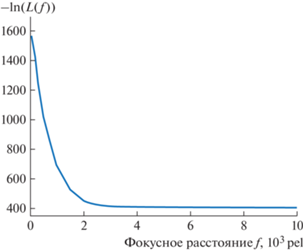
Метод максимального правдоподобия был реализован с использованием библиотеки с открытым исходным кодом Scipy. Для решения задачи оптимизации использовался метод Нелдера–Мида (Nealder, Mead, 1965). Оптимизация функции правдоподобия (22) проводилась по трем параметрам (углы Эйлера) с фиксированным значением фокусного расстояния. Для наглядного представления и упрощения процесса расчетов было решено не максимизировать значения функции правдоподобия, а минимизировать негативную ей функцию. В процессе минимизации негативной функции правдоподобия были получены оптимальные значения для каждого фиксированного значения фокусного расстояния. Зависимость минимального значения функции от фокусного расстояния представлена на рис. 3.

Минимизация же функции правдоподобия по всем четырем параметрам (фокусное расстояние и три угла Эйлера) приводит к следующим оптимальным значениям: $f = 5502~$ pel, $y = - 0.00228~$ rad, $p = 0.0035~$ rad, $r = 0.03469~$ rad.

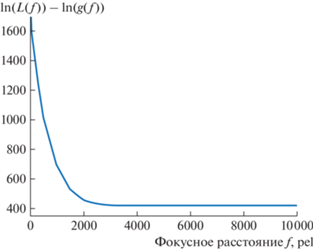
Изучив полученную зависимость, приходим к выводу о том, что функция выходит на плато и, начиная с некоторого момента, значения фокусного расстояния одинаково правдоподобны. Для подтверждения выхода функции на плато был построен график, представленный на рис. 4, который будет более полезен для сравнения метода максимального правдоподобия с методом апостериорного максимума.

Оценка метода апостериорного максимума была проведена с использованием аналогичного методу максимального правдоподобия инструмента. Для метода апостериорного максимума, в соответствии в формулой (32), необходимо задать случайное распределение фокусного расстояния. В качестве распределения можно выбрать любое непрерывное распределение. В текущей реализации было выбрано логнормальное распределение – двупараметрическое абсолютно непрерывное распределение с плотностью вероятности:

Значения параметров логнормального распределения были выбраны в соответствии с модой распределения равной диагонали выбранного для исследования кадра, как наиболее часто встречаемого значения, равного 900 пикселов. Математические расчеты привели к следующим значениям распределения: μ = 7.05, σ = 0.5. Плотность вероятности выбранного распределения с подобранными параметрами представлена на рис. 5.

Оптимизация функционала (32) проводилась по трем параметрам (углы Эйлера) с фиксированным значением фокусного расстояния, аналогично процессу исследования метода максимального правдоподобия. Зависимость оптимального значения функции от фокусного расстояния представлена на рис. 6.

Минимизация функционала по четырем параметрам приводит к следующим оптимальным значениям: $f = 4780~$ pel, $y = - 0.00227~$ rad, $p = 0.0036~$ rad, $r = 0.03548$ rad .

Изучив полученную зависимость, приходим к выводу о том, что функция имеет минимум в точке с фокусным расстоянием 4780, которое и является результатом работы метода.

На рис. 7 представлен тот же график, но в меньшем масштабе для более детального рассмотрения.

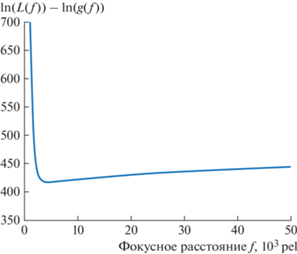
Сравнивая график рис. 7 с графиком рис. 4, видим, что метод апостериорного максимума на плато не выходит. Применения априорных знаний демонстрирует большую устойчивость MAP и сходимость к одному значению оценки фокусного расстояния.

ЗАКЛЮЧЕНИЕ

В данной работе представлены методы оценки фокусного расстояния камеры, расположенной на КА. Метод максимального правдоподобия (MLE) и метод апостериорного максимума (MAP) представляют два функционала, оптимизация которых приводит к решению задачи нахождения фокусного расстояния камеры, расположенной на КА. В ходе вычислительных экспериментов было выяснено, что значение фокусного расстояния камеры, снимающей процесс сближения и стыковки, примерно равно 4780 пикселям. Такая оценка была произведена впервые. Вычисленное значение внутреннего параметра камеры и предложенные методы могут быть использованы для решения более глобальной задачи – разработки системы автоматической стыковки, основанной на использовании визуального канала.