Известия РАН. Теория и системы управления, 2019, № 1, стр. 52-77

Введение. Переключаемые системы (ПС) служат математическими моделями многорежимных систем автоматического управления технологическими процессами и движущимися объектами [1, 2]. Функционирование таких систем представляется непрерывно-дискретными процессами, которые имеют разнородное представление. В рассматриваемых в статье системах непрерывное изменение, задающее движение объекта управления, описывается дифференциальными уравнениями, а дискретное изменение, моделирующее работу устройства управления, – рекуррентными уравнениями. ПС являются частным случаем гибридных систем [1], в которых непрерывный процесс, как правило, отражает физические законы, технологические или технические принципы, а дискретный процесс показывает работу устройства управления, например цифровых автоматов с памятью. Обе составляющих процесса управления взаимосвязаны и влияют друг на друга. Обычно дискретная составляющая характеризует операционную ситуацию, в которой происходит функционирование, определяя режим непрерывного движения объекта управления. Переключение соответствует изменению операционной ситуации и смене режима работы системы. Качество управления оценивается функционалом, в котором учитываются затраты на непрерывное управление и на каждое переключение. Выбор количества переключений, самих моментов переключений, а также собственно переключений – скачков состояния, вместе с выбором управления непрерывной частью определяют траекторию ПС и подлежат оптимизации. При этом не исключаются многократные переключения в фиксированный момент времени [2]. Исследуемая модель ПС обобщает дискретные системы автоматного типа, непрерывно-дискретные, логико-динамические и переключающие системы [3]. В свою очередь ПС являются частным случаем систем со сменой моделей движения [4].

Достаточные условия оптимальности управления динамическими системами, как правило, связаны с определением функции цены (функции Гамильтона–Якоби–Беллмана (ГЯБ)). Для синтеза оптимальных ПС предлагается, как и в [4], искать вспомогательные функции – так называемые образующие функции цены, из которых потом можно построить “настоящую” функцию цены. Дифференциальные и рекуррентные уравнения для этих вспомогательных функций выводятся на основе метода динамического программирования [5], при этом “настоящая” функция цены оказывается, вообще говоря, не нужна.

Вместе с задачей оптимального управления при полной информации рассматривается задача управления в условиях параметрической неопределенности. Предполагается, что в начальный момент времени состояние ПС точно не известно, а известно множество возможных начальных состояний. Поэтому ставится задача оптимального в среднем [6, 7] управления пучком траекторий. Для ее решения предлагается применить принцип разделения, который заключается в том, что оптимальное управление пучком траекторий совпадает с оптимальным управлением одной траекторией. Если принцип разделения выполняется, то для пучка траекторий можно использовать управление, оптимальное для одной специальным образом выбранной траектории пучка. Например, это может быть траектория, исходящая из геометрического центра тяжести множества возможных состояний. Если принцип разделения не выполняется, то получаемое таким способом управление пучком будет субоптимальным. Однако оно может оказаться удовлетворительным для практики. Такой подход к синтезу управления аналогичен применяемому в стохастических системах, когда для управления пучком траекторий используют оптимальное замкнутое управление для математического ожидания состояния системы. Обоснование этого метода опирается на теорему разделения [8], которая справедлива не для всех стохастических систем. На практике такой подход часто применяется даже без обоснования.

Управление пучком траекторий ПС осуществляется при наличии дискретных неточных измерений. Предполагается, что в результате каждого измерения определяется множество возможных в этот момент состояний системы. Моменты измерений задаются заранее. Накопление поступающей информации происходит естественным образом [9] – путем пересечения всех известных (“измеренных”) к настоящему времени множеств. Такой метод позволяет без потерь учитывать всю поступающую информацию. Однако его реализация затруднительна. Действительно, для этого нужно иметь полное и точное описание получаемых в процессе управления множеств возможных состояний. Для линейных систем можно использовать эллипсоиды [10] или линейные неравенства. Для нелинейных систем приходится применять приближенные аппроксимации этих множеств. Наиболее простой способ состоит в выборе достаточно большого количества точек в заданном множестве возможных начальных состояний, например подходящих узлов некоторой сетки в пространстве состояний, а затем моделировать траектории движения, исходящие из этих точек, удаляя при каждом измерении недопустимые состояния. Конечно, такой способ дает только приближенное описание множества, но его точность может оказаться достаточной для практики.

Применение двух подходов – принципа разделения и учета дискретных измерений – сочетается следующим образом. Множество возможных состояний системы корректируется при каждом измерении путем его пересечения с “измеренным” в этот момент времени множеством. Для пучка траекторий, исходящих из этого пересечения, применяется программное управление, оптимальное для некоторой траектории этого пучка, например для траектории, исходящей из геометрического центра тяжести этого пересечения. Такой способ позволяет синтезировать субоптимальное позиционное управление, т.е. управление с обратной связью по множеству возможных состояний системы.

Представляют интерес задачи, в которых принцип разделения выполняется. В этом случае субоптимальное управление пучком оказывается оптимальным. Известно, что в линейно-квадратичных задачах управления непрерывными [6], дискретными, непрерывно-дискретными системами [11] управления принцип разделения выполняется. Однако для линейных систем автоматного типа принцип разделения выполняется только в стационарном случае [12]. Поэтому для линейно-квадратичных задач управления ПС принцип разделения заведомо не выполняется, так как они являются обобщением систем автоматного типа. Однако принцип разделения в системах с переключениями можно модифицировать [13]: “оптимальное управление пучком траекторий совпадает с условным оптимальным управлением одной траекторией”, т.е. с управлением, оптимальным при фиксированном наборе моментов переключений. Такой условный принцип разделения для линейно-квадратичных задач оказывается справедливым.

В работе доказаны достаточные условия оптимальности управления ПС и условия субоптимальности управления пучком траекторий. Получены уравнения для нахождения оптимального управления с обратной связью, а также уравнения для синтеза субоптимального в среднем и субоптимального гарантирующего управлений при наличии дискретных неточных измерений. Рассмотрены академические примеры, демонстрирующие применение принципа разделения и достаточных условий оптимальности и субоптимальности ПС. В частности, приведен контрпример линейно-квадратичной задачи управления ПС, в которой принцип разделения не выполняется.

1. Постановки задач. Пусть на заданном промежутке времени $T = [{{t}_{0}},{{t}_{F}}]$ динамическая система совершает N переключений (скачков) в моменты времени t_i, $i = 1,\; \ldots ,\;N$, образующие неубывающую последовательность $\mathcal{T} = \{ {{t}_{1}},\; \ldots ,\;{{t}_{N}}\} $:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальному уравнению

а в моменты переключений – дискретно в соответствии с рекуррентным уравнением

В соотношениях (1.2) обозначены: $\mathcal{N}\dot { = }\{ i = 0,\;1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}}\dot { = }[{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in {{T}_{i}}$, $i \in \mathcal{N}$, $x(t) \in X\dot { = }{{\mathbb{R}}^{n}}$; $u(t)$ – управление непрерывным движением системы в момент времени $t \in T$, $u(t) \in U \subset {{\mathbb{R}}^{p}}$, U – заданное множество допустимых значений управления. При ${{t}_{i}} = {{t}_{{i + 1}}}$ дифференциальное уравнение (1.2) опускается ($i \notin \mathcal{N}$), а значение $u({{t}_{i}})$ управления в этой точке ${{T}_{i}}\, = \,\,\{ {{t}_{i}}\} $ несущественно. В уравнении (1.3) ${{x}_{i}}\dot { = }x({{t}_{i}})$ – состояние системы сразу после i-го переключения, ${{x}_{{i - }}}$ – состояние системы непосредственно перед i-м переключением:

${{v}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, ${{v}_{i}} \in V \subset {{\mathbb{R}}^{q}}$, V – заданное множество допустимых управлений переключениями. Функция $f{\text{:}}\;T \times X \times U \to {{\mathbb{R}}^{n}}$ непрерывна на всей области определения вместе с производной $\partial f{\text{/}}\partial x$; функция $g{\text{:}}\;T \times X \times V \to {{\mathbb{R}}^{n}}$, $i = 1,\; \ldots ,\;N$, ограничена. Предполагаем, что в уравнении (1.3) исключаются так называемые фиктивные переключения, при которых состояние системы не изменяется (${{x}_{i}} = {{x}_{{i - }}}$) и фактического переключения нет.

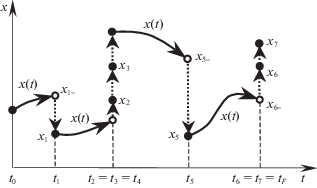
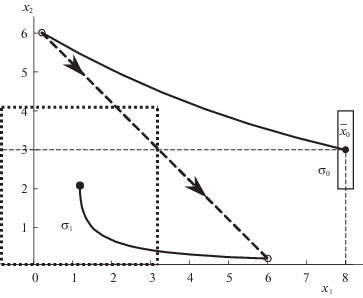
Возможное равенство последовательных моментов в (1.1) означает, что система совершает мгновенные многократные переключения [2, 3]. Например, на рис. 1 изображена кусочно-гладкая траектория с семью моментами переключений ${{t}_{1}},\; \ldots ,\;{{t}_{7}}$, которые образуют неубывающую последовательность ${{t}_{0}} < {{t}_{1}} < {{t}_{2}} = {{t}_{3}} = {{t}_{4}} < {{t}_{5}} < {{t}_{6}} = {{t}_{7}}$. В точках t₁ и t₅ траектория имеет обычные (однократные) переключения, например скачок ${{x}_{{1 - }}} \to {{x}_{1}}$ из состояния ${{x}_{{1 - }}} = x({{t}_{1}} - 0)$ в состояние x₁ в момент t₁. В точках t₄ и t₇ траектория имеет многозначные разрывы, а система совершает мгновенные многократные переключения: тройное переключение ${{x}_{{2 - }}} \to {{x}_{2}} \to {{x}_{3}} \to {{x}_{4}}$ в момент t₄ и двойное ${{x}_{{5 - }}} \to {{x}_{6}} \to {{x}_{7}}$ в момент t₇. Между неравными моментами переключений – на четырех промежутках ${{T}_{0}} = [{{t}_{0}},{{t}_{1}})$, ${{T}_{1}} = [{{t}_{1}},{{t}_{2}})$, ${{T}_{4}} = [{{t}_{4}},{{t}_{5}})$, ${{T}_{5}} = [{{t}_{5}},{{t}_{6}})$ – изменение состояния системы является непрерывным, а траектории x(t) – гладкими кривыми. Множество номеров ненулевых промежутков $\mathcal{N} = \{ 0,\;1,\;4,\;5\} $. Точки ${{T}_{2}} = \{ {{t}_{2}}\} $, ${{T}_{3}} = \{ {{t}_{3}}\} $, ${{T}_{6}} = \{ {{t}_{6}}\} $ – “промежуточные” для мгновенных многократных переключений. Заметим, что характер разрыва (многозначный или обычный – однозначный) траектории не влияет на ее непрерывное изменение между моментами переключений.

Начальное состояние системы задано

Условие (1.5) не исключает одного или нескольких переключений в начальный момент времени ${{t}_{0}}$, поскольку первые несколько моментов переключений (1.1) могут совпадать. Момент t_F окончания процесса управления задан, а конечное состояние свободно – терминальных ограничений нет.

Множество допустимых процессов $\mathcal{D}({{t}_{0}},{{x}_{0}})$ составляют тройки $d = (x( \cdot ),u( \cdot ),\{ v\} )$, включающие последовательность $x( \cdot ) = {{\{ {{x}_{i}}( \cdot )\} }_{{i \in \mathcal{N}}}}$ абсолютно непрерывных на T_i функций ${{x}_{i}}( \cdot )$; ограниченную измеримую на T функцию $u{\text{:}}\;T \to U$; последовательность $\{ v\} \dot { = }\{ {{v}_{i}}\} _{{i = 1}}^{N}$ векторов ${{v}_{i}} \in V$; причем пары $({{x}_{i}}( \cdot ),u( \cdot ))$, $i \in \mathcal{N}$, удовлетворяют уравнению (1.2) почти всюду на промежутке T_i, тройки $({{x}_{{i - }}},{{x}_{i}},{{v}_{i}})$, $i = 1,\; \ldots ,\;N$, на $\mathcal{T}$ – рекуррентному уравнению (1.3); в начальный момент времени выполняется условие (1.5). Подчеркнем, что количество $N = \left| {\mathcal{T}(x( \cdot ))} \right|$ переключений и моменты $\mathcal{T}(x( \cdot )) = \{ {{t}_{1}},\; \ldots ,\;{{t}_{N}}\} $ переключений не фиксированы и у разных допустимых процессов могут не совпадать.

На множестве $\mathcal{D}({{t}_{0}},{{x}_{0}})$ допустимых процессов задан функционал качества

где функции ${{f}^{0}}{\text{:}}\;T \times X \times U \to \mathbb{R}$ и $F{\text{:}}\;X \to \mathbb{R}$ непрерывны и ограничены снизу, а функция g⁺ : $T \times X \times V \to {{\mathbb{R}}_{ + }}$ неотрицательная, ${{g}^{ + }}( \cdot ) \geqslant 0$. Последнее условие позволяет рассматривать каждое слагаемое ${{g}^{ + }}({{t}_{i}},{{x}_{{i - }}},{{v}_{i}})$ в (1.6) как затраты (или “штраф”) при переключении ${{x}_{{i - }}} \to {{x}_{i}}$. В силу непрерывности функции ${{f}^{0}}(t,x,u)$ по всем аргументам функция ${{f}^{0}}[t] = {{f}^{0}}(t,x(t),u(t))$ будет измеримой и ограниченной, т.е. суммируемой, для любого допустимого процесса $d = (x( \cdot ),u( \cdot ),\{ v\} )$. Поэтому функционал (1.6) определен на $\mathcal{D}({{t}_{0}},{{x}_{0}})$. Отметим, что в функционале (1.6) количество переключений N и моменты переключений не заданы, а находятся в результате оптимизации.

1.1. Задача оптимального управления одной траекторией. Требуется найти минимальное значение функционала (1.6) и оптимальный процесс d* = $d* = (x{\text{*}}( \cdot ),u{\text{*}}( \cdot ),\{ v*\} ) \in \mathcal{D}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:

Если наименьшее значение (1.7) не существует, то может быть поставлена задача нахождения минимизирующей последовательности допустимых процессов [14]. Количество переключений у процессов минимизирующей последовательности может оставаться конечным или неограниченно возрастать. Бесконечное количество переключений у оптимального процесса становится невозможным, если усилить условие неотрицательности функции g⁺ в (1.6):

Применение таких “штрафов” в функционале качества исключает последовательности процессов с неограниченным ростом числа переключений как неминимизирующие.

Условие ${{g}^{ + }}( \cdot ) \geqslant 0$ неотрицательности затрат на переключение позволяет при решении задачи (1.7) не рассматривать процессы с фиктивными переключениями. Действительно, исключая фиктивное переключение ${{x}_{i}} = {{x}_{{i - }}}$, в функционале (1.6) удаляется неотрицательное слагаемое ${{g}^{ + }}({{t}_{i}},{{x}_{{i - }}},{{v}_{i}}) \geqslant 0$. Поэтому значение функционала не увеличивается. Значит, если у процесса есть фиктивные переключения, то эти переключения можно исключить, при этом получим допустимый процесс без фиктивных переключений, на котором значение функционала будет не больше. Если же выполняется условие (1.8) положительности затрат, то фиктивных переключений у оптимальных процессов не может быть.

1.2. Задача управления с фиксированным числом переключений. В прикладных задачах нередко возникают ограничения на количество переключений. Задача минимизации функционала (1.6) на множестве допустимых траекторий с заданным числом переключений формулируется следующим образом. Пусть ${{\mathcal{D}}^{N}}({{t}_{0}},{{x}_{0}})$ – множество допустимых процессов из $\mathcal{D}({{t}_{0}},{{x}_{0}})$ с N переключениями, быть может фиктивными. Подчеркнем, что количество переключений N у всех процессов из ${{\mathcal{D}}^{N}}({{t}_{0}},{{x}_{0}})$ одинаковое (равное N), но моменты переключений (1.1) у разных процессов могут не совпадать. Обозначим через ${{I}^{N}}({{t}_{0}},{{x}_{0}},d)$ функционал (1.6) при фиксированном количестве переключений N. Он определен на подмножестве ${{\mathcal{D}}^{N}}({{t}_{0}},{{x}_{0}})$ множества ${{\mathcal{D}}_{0}}({{t}_{0}},{{x}_{0}})$. Требуется найти минимальное значение функционала (1.6) на множестве ${{\mathcal{D}}^{N}}({{t}_{0}},{{x}_{0}})$ и процесс ${{d}^{N}} \in {{\mathcal{D}}^{N}}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:

Такой процесс d^N будем называть условно оптимальным, имея в виду его оптимальность при дополнительном условии – заданном количестве переключений N.

Поставленные задачи (1.7), (1.9) представляют собой так называемые задачи со свободным конечным состоянием и фиксированным временем. В более общей постановке [14] на правый конец траектории могут быть наложены терминальные ограничения. Отметим, что поставленные задачи являются частным случаем задачи оптимального управления со сменой модели движения [4].

1.3. Задача оптимального в среднем управления пучком траекторий. Обозначим через $\mathcal{W}({{t}_{0}},{{x}_{0}})$ множество допустимых программных управлений $w = (u( \cdot ),\{ v\} )$. Программное управление u(⋅) непрерывным движением – это, как и ранее, ограниченная измеримая функция $u{\text{:}}\;T \to U$. Программное управление $\{ \text{v}\} $ переключениями – это последовательность $v( \cdot ) = \{ {{v}_{i}}\} _{{i = 1}}^{N}$ дискретных управлений ${{v}_{i}} \in V$, соответствующая последовательности моментов переключений (1.1). Предполагаем, что каждое допустимое программное управление $w = (u( \cdot ),\{ v\} ) \in \mathcal{W}({{t}_{0}},{{x}_{0}})$ порождает в силу уравнений движения (1.2), (1.3) такую единственную траекторию x(⋅), исходящую из начального состояния (1.5), что процесс $d = (x( \cdot ),u( \cdot ),\{ v\} )$ оказывается допустимым $d \in \mathcal{D}({{t}_{0}},{{x}_{0}})$. Функционал (1.6) при этом можно считать зависящим от программного управления I(t₀, x₀, $w)\dot { = }I({{t}_{0}},{{x}_{0}},d)$.

Пусть в отличие от задачи (1.7) начальное состояние ${{x}_{0}} \in X$ точно не известно, а известно множество ${{\sigma }_{0}}$ возможных начальных состояний (${{\sigma }_{0}} \subset X$). Обозначим через $\mathcal{W}({{t}_{0}},{{\sigma }_{0}})$ множество допустимых программных управлений $w = (u( \cdot ),\{ v\} )$, каждое из которых порождает допустимую траекторию $x( \cdot )$ для любого начального состояния $x({{t}_{0}}) \in {{\sigma }_{0}}$. Объединение этих траекторий образует пучок $t \to \sigma (t)$, исходящий из множества возможных начальных состояний $\sigma ({{\tau }_{0}}) = {{\sigma }_{0}}$.

Пусть, по-прежнему, качество управления одной траекторией характеризуется функционалом (1.6), который можно считать зависящим от программного управления $I = I({{t}_{0}},{{x}_{0}},w)$. Качество программного управления пучком траекторий, исходящих из множества σ₀, оценивается средним значением функционала (1.6):

при этом считаем, что множество σ₀ имеет положительную меру $mes{{\sigma }_{0}} > 0$. В (1.10) измеримую неотрицательную весовую функцию $\rho {\text{:}}\;X \to {{\mathbb{R}}_{ + }}$, в частности, можно считать плотностью вероятности начального состояния системы, предполагая при этом, что

Требуется найти оптимальное в среднем управление ${{w}^{{\text{с }}}}$, минимизирующее функционал (1.10):

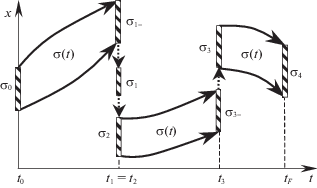
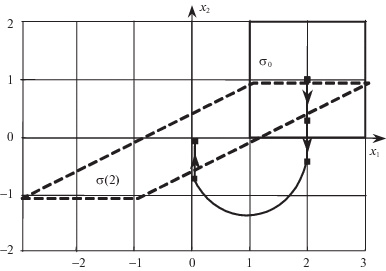
Как и в случае управления одной траекторией (см. разд. 1.2), минимизация в (1.11) может проводиться при дополнительном условии – заданном количестве N переключений. На рис. 2 представлен типовой пучок траекторий σ(t), исходящий из множества начальных состояний σ₀. Моменты переключений t₁, t₂, t₃ образуют неубывающую последовательность ${{t}_{0}} < {{t}_{1}} = {{t}_{2}} < {{t}_{3}} < {{t}_{F}}$.

1.4. Задача субоптимального управления пучком траекторий. Для управления пучком траекторий предлагается применять управление, оптимальное для одной траектории, возможно, не принадлежащей этому пучку. Такое управление для пучка траекторий не обязательно будет оптимальным. Наилучшее для пучка траекторий управление, оптимальное хотя бы для одной траектории системы, будем называть субоптимальным управлением пучком траекторий. Субоптимальное управление, вообще говоря, не является оптимальным для пучка траекторий, но оно может оказаться вполне приемлемым для практики. Сформулируем задачу поиска такого управления.

Пусть $\hat {\mathcal{W}}({{t}_{0}})$ – множество оптимальных программных управлений $\hat {w} = (\hat {u}( \cdot ),\{ \hat {v}\} )$ отдельными траекториями, т.е. каждое программное управление $\hat {w} \in \hat {\mathcal{W}}$ хотя бы для одного начального состояния ${{\hat {x}}_{0}} \in X$ порождает в силу уравнений движения (1.2), (1.3) оптимальный процесс, минимизирующий функционал (1.6). Начальное состояние ${{\hat {x}}_{0}}$ может не принадлежать множеству σ₀. В рассматриваемой задаче любое управление, оптимальное для одной траектории, считаем допустимым для всех траекторий пучка, т.е. $\hat {\mathcal{W}}({{t}_{0}}) \subset \mathcal{W}({{t}_{0}},{{\sigma }_{0}})$.

Требуется найти субоптимальное в среднем управление ${{\hat {w}}^{{\text{c}}}}$, минимизирующее функционал (1.10) на множестве $\hat {\mathcal{W}}({{t}_{0}})$:

Наименьшее значение (1.12) не меньше минимального значения (1.11), так как $\hat {\mathcal{W}}({{t}_{0}}) \subset \mathcal{W}({{t}_{0}},{{\sigma }_{0}})$.

Если для каждого начального состояния ${{\hat {x}}_{0}}$ известно оптимальное программное управление $\hat {w}({{t}_{0}},{{\hat {x}}_{0}}) \in \hat {\mathcal{W}}({{t}_{0}})$, то минимизацию по управлению в (1.12) можно заменить минимизацией по состоянию ${{\hat {x}}_{0}}$:

Наилучшее состояние $\hat {x}_{0}^{{\text{c}}}$, для которого достигается минимум в (1.13), известно для некоторых типов задач. Такое состояние будем называть субоптимальным в среднем состоянием системы. Например, как показано в [6], для задач управления линейными непрерывными системами с квадратичным функционалом качества наилучшим (субоптимальным в среднем) состоянием $\hat {x}_{0}^{{\text{c}}}$ будет геометрический центр тяжести множества σ₀. Для других линейно-квадратичных задач имеются аналогичные результаты [11–13].

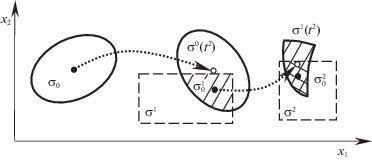
1.5. Задача субоптимального управления пучком траекторий с дискретными неточными измерениями. Пусть в некоторые моменты времени ${{t}^{1}},\; \ldots ,\;{{t}^{m}}$, образующие возрастающую последовательность ${{t}_{0}} < {{t}^{1}} < \; \ldots \; < {{t}^{m}} < {{t}_{F}}$ на промежутке $[{{t}_{0}},{{t}_{F}}]$, производятся неточные измерения, в результате которых соответственно определяются “измеренные” множества ${{\sigma }^{1}},\; \ldots ,\;{{\sigma }^{m}}$ возможных состояний системы. Предполагаем, что моменты измерений не совпадают с моментами мгновенных многократных переключений из последовательности (1.1). Измерения позволяют “сузить” пучок траекторий [9]. В самом деле, пусть ${{\sigma }^{i}}(t)$ – пучок траекторий после i-го измерения, ${{t}^{i}} < t < {{t}^{{i + 1}}}$, $i = 1,\; \ldots ,\;m - 1$, а $\sigma _{0}^{m}$ – множество всех возможных состояний системы в момент времени t^m с учетом начального множества σ₀ и всех m измерений, проведенных до этого момента включительно. Это множество получается путем последовательного пересечения множества возможных состояний системы с “измеренными” множествами

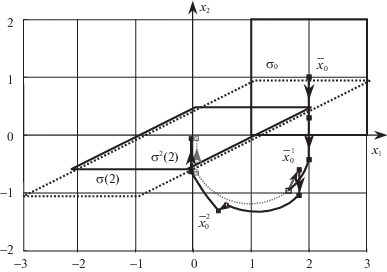
На рис. 3 изображены состояния пучка траекторий с учетом двух измерений в моменты t ¹ и t ². “Измеренные” множества представлены прямоугольниками σ¹ и σ², множество σ₀ начальных состояний – эллипсом, пересечение $\sigma _{0}^{1} = {{\sigma }^{0}}({{t}^{1}}) \cap {{\sigma }^{1}}$ отмечено штриховкой, а $\sigma _{0}^{2} = {{\sigma }^{1}}({{t}^{2}}) \cap {{\sigma }^{2}}$ – двойной штриховкой. Полужирными точками отмечены геометрические центры тяжести множеств ${{\sigma }_{0}}$, $\sigma _{0}^{1}$, $\sigma _{0}^{2}$, маленькими окружностями – центры тяжести множеств ${{\sigma }^{0}}({{t}^{1}})$, ${{\sigma }^{1}}({{t}^{2}})$.

Задача субоптимального управления пучком траекторий с учетом измерений формулируется так же, как в разд. 1.4, только процесс управления пучком происходит на промежутке времени $[{{t}^{m}},{{t}_{F}}]$ и начинается из множества в $\sigma _{0}^{m}$. Требуется найти субоптимальное в среднем управление w^c, минимизирующее функционал ${{I}^{{\text{c}}}}({{t}^{m}},\sigma _{0}^{m},w)$ на множестве $\hat {\mathcal{W}}({{t}^{m}})$:

Заметим, что задача управления фактически отделена от задачи наблюдения, т.е. определения множества возможных состояний. Каждое измерение позволяет уточнить это множество, при этом субоптимальное управление заново формируется с учетом полученной информации. Например, если в качестве субоптимального в среднем состояния пучка выбирается геометрический центр тяжести, то при каждом измерении этот центр изменяется, возможно, скачком, при этом виртуальная траектория, проходящая через центры тяжести (пунктирные стрелки на рис. 3), может иметь разрывы в моменты измерений.

2. Достаточные условия оптимальности управления. Решения поставленных задач (1.7), (1.9) управления одной траекторией будем искать на основе достаточных условий оптимальности управления с обратной связью. Так как задачи (1.7), (1.9) являются частным случаем задач оптимального управления со сменой моделей движения [4], то для них можно применить разработанный в [4] метод синтеза позиционного управления. Отличие системы (1.2), (1.3) от системы со сменой моделей движения [4] заключается в том, что пространство функционирования рассматриваемой системы, т.е. пространства состояний и управлений, при переключениях (1.3) не меняются. Поэтому рекуррентная процедура нахождения функции цены, а также достаточные условия оптимальности упрощаются по сравнению с [4].

2.1. Функция цены и ее образующие. Процедура построения функции цены (функции ГЯБ), разработанная в [4], заключается в использовании для этой цели вспомогательных функций, так называемых образующих функции цены. Приведем определения этих функций для задач (1.7), (1.9).

Обозначим через $\mathcal{D}(t,x)$ множество допустимых процессов, удовлетворяющих начальному условию $x(t) = x$, каждый из которых имеет конечное число переключений на $[t,{{t}_{F}}]$. Оставшиеся переключения происходят в моменты ${{t}_{1}},\; \ldots ,\;{{t}_{k}}$, образующие неубывающую последовательность на промежутке $[t,{{t}_{F}}]$:

Заметим, что количество k оставшихся переключений и сами моменты ${{t}_{1}},\; \ldots ,\;{{t}_{k}}$ переключений не фиксированы и у разных допустимых процессов могут не совпадать.

На множестве $\mathcal{D}(t,x)$ допустимых процессов определим функционал оставшихся потерь, аналогичный (1.6):

Функция цены $\varphi (t,x)$, по определению, равна значению функционала оставшихся потерь (2.2), вычисленному на оптимальном процессе с начальным условием $x(t) = x$. Иначе говоря, функция цены равна минимальному значению функционала оставшихся потерь (2.2) на множестве допустимых процессов $\mathcal{D}(t,x)$:

Для задачи (1.7) определим образующую функции цены с $k$ переключениями, значение ${{\varphi }^{k}}(t,x)$ которой равно значению функционала оставшихся потерь (2.2), вычисленному на процессе, который оптимален среди всех допустимых процессов, исходящих из начальной позиции (t, x) и имеющих ровно k переключений, быть может фиктивных. Если обозначить через ${{\mathcal{D}}^{k}}(t,x)$ множество допустимых управлений из $\mathcal{D}(t,x)$, имеющих ровно k переключений, быть может фиктивных, а через ${{I}^{k}}(t,x,d)$ – функционал (2.2) при фиксированном количестве k оставшихся переключений, то

Согласно определению, функция цены (2.3) является нижней огибающей своих образующих

а наименьшее значение функционала (1.6) вычисляется по функции цены

Вспомогательные функции (2.4) аналогичны функциям, введенным в [4]. Отличие заключается в том, что у образующих отсутствует нумерация моделей движения, так как при переключениях (1.3) модель движения не меняется. Это приводит к упрощению процедуры нахождения функции цены и достаточных условий оптимальности по сравнению с [4].

2.2. Уравнения для образующих функции цены. Вывод уравнений, которым удовлетворяют образующие функции цены, опирается на принцип оптимальности Беллмана, модифицированный для задач с переключениями. Согласно этому принципу, часть оптимального процесса с k оставшимися переключениями, следующая после первого переключения, является оптимальным процессом с k – 1 переключениями.

Нулевая образующая ${{\varphi }^{0}}(t,x)$ соответствует оптимальному процессу без переключений. Поэтому она удовлетворяет уравнению ГЯБ

с терминальным условием

Существование решения уравнения (2.6) предполагается. Заметим, что нулевая образующая совпадает с обычной функцией цены в задаче оптимального управления без переключений с функционалом Больца.

Остальные образующие находятся в результате рекуррентной процедуры, в которой ключевую роль играет так называемая [15] двухпозиционная функция цены $\phi (\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }})$. Она определяется как решение задачи Лагранжа для системы (1.2) с фиксированными концами траектории:

Эта функция, как функция начальной позиции $(t,x) \to \phi (t,x{\mathbf{|}}\tau ,{{x}_{\tau }})$, удовлетворяет уравнению ГЯБ с нулевыми терминальными условиями

Двухпозиционная функция $\phi (\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }})$ определяется для всех пар позиций $(\theta ,{{x}_{\theta }}) \in T \times X$, $(\tau ,{{x}_{\tau }}) \in T \times X$, $\theta < \tau $. Если для некоторых позиций решение задачи (2.8) не существует, то можно доопределить функцию, полагая $\varphi (\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }}) = + \infty $, чтобы исключить недопустимые процессы.

Пусть известна образующая ${{\varphi }^{{k - 1}}}$, $k \in \mathbb{N}$. Тогда, согласно принципу оптимальности, следующая образующая φ^k удовлетворяет уравнению

Действительно, непрерывное движение на промежутке $[t,\tau ]$ до первого переключения происходит, учитывая (2.6), при оптимальном управлении, переводящим систему из позиции (t, x) в позицию $(\tau ,{{x}_{\tau }})$, в которой совершается скачок. Оптимальность первого переключения обеспечивает операция минимизации по управлению $v$ в (2.10). Поэтому выражение в фигурных скобках равно минимальному значению функционала оставшихся потерь при заданной позиции $(\tau ,{{x}_{\tau }})$ переключения. Первые две операции минимизации в (2.10) устанавливают лучшую позицию для переключения. Таким образом, правая часть (2.10) дает минимальное значение функционала (2.2) с k оставшимися переключениями, которое определяет образующую (2.4).

Выведенное уравнение (2.10) представляет собой рекуррентное уравнение для последовательности функций ${{\varphi }^{k}}(t,x)$, зависящих от позиции системы. Уравнение осложняется тремя операциями конечномерной минимизации. Однако наибольшую сложность для решения представляет двухпозиционная функция цены $\phi \left( {\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }}} \right)$, входящая в это уравнение. Она удовлетворяет уравнению ГЯБ (2.9), так же как функция цены ${{\varphi }^{0}}(t,x)$. Однако зависимость функции $\phi \left( {\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }}} \right)$ от двух позиций фактически “удваивает” область ее определения по сравнению с функцией цены ${{\varphi }^{0}}(t,x)$. Это существенно повышает требования к вычислительным ресурсам, необходимым для численного решения. Можно сказать, что “проклятие размерности” [5], характерное для задачи синтеза оптимального позиционного управления, удваивается в случае двухпозиционной функции цены. Отметим, что в силу симметрии

объем требуемой для численного решения компьютерной памяти можно уменьшить. Отметим еще, что исследованию решений уравнения ГЯБ посвящены многочисленные работы, так как это связано с обоснованием метода динамического программирования [16, 17].

Начальным условием для уравнения (2.10) служит нулевая образующая ${{\varphi }^{0}}(t,x)$, т.е. функция цены для процессов без переключений. Она находится как решение уравнения ГЯБ (2.6) с ненулевым терминальным условием (2.7). Однако если известна двухпозиционная функция цены $\phi (\theta ,{{x}_{\theta }}|\tau ,{{x}_{\tau }})$, то образующую ${{\varphi }^{0}}(t,x)$ можно получить, решая задачу конечномерной минимизации:

Равенство (2.11) выражает связь между решениями задач с функционалами Лагранжа и Больца.

2.3. Оптимальное позиционное управление. При решении уравнений (2.6)–(2.10) выполняются пять операций минимизации. В результате минимизации левой части (2.6) определяется оптимальное позиционное управление

непрерывным движением при отсутствии переключений. Минимизируя левую часть (2.9), получаем позиционное управление

При минимизации правой части (2.10) определяются оптимальное позиционное управление переключением системы

и оптимальная позиция $({{\tau }^{k}},{{{\mathbf{x}}}^{k}})$ первого из оставшихся k переключений, т.е. оптимальный момент переключения: и оптимальное состояние перед переключением:

Точки минимума (2.13)–(2.16) находятся при дополнительном условии – заданном количестве k оставшихся переключений, а оптимальное количество переключений определяется в результате минимизации (2.5):

Позиционные конструкции (2.12)–(2.17) позволяют найти оптимальный процесс. Действительно, пусть система находится в позиции $({{t}_{0}},{{x}_{0}})$, т.е. удовлетворяет начальным условиям (1.5). Для этой позиции определяем оптимальное количество оставшихся переключений $N = {\mathbf{k}}({{t}_{0}},{{x}_{0}})$, а также позицию $({{t}_{1}},{{x}_{{1 - }}})$ первого переключения: ${{t}_{1}} = {{\tau }^{N}}({{t}_{0}},{{x}_{0}})$, ${{x}_{{1 - }}} = {{{\mathbf{x}}}^{N}}({{t}_{0}},{{x}_{0}})$. Если t₁ = t₀, то ${{{\mathbf{x}}}^{N}}({{t}_{0}},{{x}_{0}}) = {{x}_{0}}$, т.е. позиция перед первым переключением совпадает с начальной ${{x}_{{1 - }}} = {{x}_{0}}$. Система сразу совершает скачок ${{x}_{0}} \to {{x}_{1}} = g({{t}_{1}},{{x}_{0}},{{v}_{1}})$ под действием управления ${{v}_{1}} = {{{\mathbf{v}}}^{N}}({{t}_{1}},{{x}_{0}})$. Если ${{t}_{1}} > {{t}_{0}}$, то сначала на промежутке $[{{t}_{0}},{{t}_{1}}]$ происходит непрерывное движение, согласно уравнению (1.2), с программным управлением ${{u}_{0}}(t) = {{{\mathbf{u}}}^{N}}\left( {t,x(t)|{{t}_{1}},{{x}_{{1 - }}}} \right)$, а в конце этого промежутка из состояния ${{x}_{{1 - }}} = x({{t}_{1}} - 0)$ происходит скачок ${{x}_{{1 - }}} \to {{x}_{1}} = g({{t}_{1}},{{x}_{{1 - }}},{{v}_{1}})$ под действием управления ${{v}_{1}} = {{{\mathbf{v}}}^{N}}({{t}_{1}},{{x}_{{1 - }}})$. И в том и в другом случае система приходит в позицию $({{t}_{1}},{{x}_{1}})$, в которой выполняются те же действия, за исключением поиска оптимального количества переключений, так как оно равно N – 1. Если в начальной позиции $({{t}_{0}},{{x}_{0}})$ оптимальное количество переключений равно нулю: ${{{\mathbf{k}}}_{0}}({{t}_{0}},{{x}_{0}}) = 0$, то переключений нет и непрерывное движение системы совершается, согласно уравнению (1.2), под действием программного управления $u(t) = {{{\mathbf{u}}}^{0}}(t,{{x}_{0}}(t))$.

Таким образом, оптимальное позиционное управление для рассматриваемых систем представляет собой целый “управляющий комплекс”, состоящий из шести функций: ${{{\mathbf{u}}}^{0}}(t,x)$ и ${{{\mathbf{u}}}^{k}}(t,x|\tau ,\xi )$ – условные оптимальные управления (2.12), (2.13) непрерывным движением системы, ${{{\mathbf{v}}}^{k}}(t,x)$ – условное оптимальное управление (2.14) переключениями, ${{\tau }^{k}}(t,x)$ – оптимальный момент (2.15) первого из k оставшихся переключений, ${{{\mathbf{x}}}^{k}}(t,x)$ – оптимальное состояние (2.16) для этого переключения, ${\mathbf{k}}(t,x)$ – оптимальное количество (2.17) переключений процесса, исходящего из позиции $(t,x)$.

2.4. Достаточные условия оптимальности. В формулировке достаточных условий предполагается, что описанная выше рекуррентная процедура нахождения образующих функций цены реализуема. При этом, разумеется, будет существовать и “настоящая” функция цены (функция ГЯБ).

Теорема 1. Если для задачи (1.1)–(1.7) существуют последовательности функций φ^k, $k \in {{\mathbb{Z}}_{ + }}$, удовлетворяющих на области определения уравнениям (2.6)–(2.10), то для оптимальности допустимого процесса $d = (x( \cdot ),u( \cdot ),\{ v\} ) \in \mathcal{D}({{t}_{0}},{{x}_{0}})$ с моментами переключений ${{t}_{1}},\; \ldots ,\;{{t}_{N}}$, образующими неубывающую последовательность (1.1), достаточно, чтобы выполнялись следующие условия:

где ${{T}_{i}} = \left[ {{{t}_{i}},{{t}_{{i + 1}}}} \right]$, $\mathcal{N} = \left\{ {i = 0,\;1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}} \right\}$. При N = 0 равенства (2.18)–(2.20) опускаются.

Доказательство теоремы аналогично доказательству теоремы 1 в [4]. Решаемая задача (1.7) является частным случаем задачи, исследуемой в [4], поскольку модель непрерывного движения (1.2) не меняется. Учитывая это, опускаем нумерацию моделей движения, принятую в [4]. Рассмотрим так называемую в [4] условную функцию цены с k оставшимися переключениями, значение которой ${{\phi }^{k}}(t,x|\tau ,\xi )$ по определению равно значению функционала оставшихся потерь (2.2), вычисленному на процессе, который оптимален среди всех допустимых процессов, исходящих из начальной позиции (t, x) и имеющих ровно k переключений, быть может фиктивных, первое из которых происходит в позиции $(\tau ,\xi ) \in [t,{{t}_{F}}] \times X$. При k = 0 полагаем по определению ${{\phi }^{0}}(t,x|\tau ,\xi ) = {{\varphi }^{0}}(t,x)$ для всех $(\tau ,\xi ) \in [t,{{t}_{F}}] \times X$. Если обозначить через ${{\mathcal{D}}^{k}}(t,x|\tau ,\xi )$ множество допустимых управлений из ${{\mathcal{D}}^{k}}(t,x)$ с первым из оставшихся k переключением в позиции $(\tau ,\xi ) \in [t,{{t}_{F}}] \times X$, то

Эту функцию, учитывая модифицированный принцип оптимальности, можно выразить через двухпозиционную функцию цены:

Действительно, производная функции $(t,x) \to {{\varphi }^{k}}(t,x|\tau ,\xi )$ в силу уравнения движения (1.2) имеет вид

Следовательно, учитывая (2.9), эта функция удовлетворяет уравнению ГЯБ:

с терминальным условием

Уравнения (2.22), (2.23) совпадают с уравнениями (3.3), (3.4) в [4]. Значит, из существования двухпозиционной функции цены следует существование последовательности условных функций цены. В свою очередь, образующая функции цены связана с условной функцией цены равенством

Подставляя в правую часть выражение (2.21), получаем уравнение (2.10). Следовательно, соотношения (2.21)–(2.23) определяют ту же самую образующую, что и уравнение (2.10). При этом условия теоремы 1 в [4] будут совпадать с условиями доказываемой теоремы, учитывая обозначения (1.4). Теорема доказана.

3. Субоптимальное управление пучком траекторий. Управление пучком траекторий ПС будем искать на основе принципа разделения: “оптимальное управление пучком траекторий совпадает с оптимальным управлением одной траекторией”. Эта траектория, будем ее называть опорной, может принадлежать пучку или не принадлежать ему. Оптимальное программное управление для опорной траектории можно получить, используя оптимальное управление с полной обратной связью (см. разд. 2). Поэтому остается только выбрать наилучшую опорную траекторию. Для этого достаточно указать начальное состояние опорной траектории. Таким образом, если принцип разделения справедлив, то решение задачи оптимального управления пучком можно разбить (разделить) на два этапа: синтез оптимального управления с обратной связью и нахождение начального состояния для опорной траектории. На втором этапе фактически строится оценка начального состояния, которая затем используется в оптимальном управлении с обратной связью.

Получим достаточные условия субоптимальности управления пучком траекторий. Обозначим через $\mathcal{W}(t,x)$ множество допустимых программных управлений $w = (u( \cdot ),\{ v\} )$, каждое из которых порождает в силу уравнений движения (1.2), (1.3) такую единственную траекторию x(⋅), исходящую из начального состояния $x(t) = x$, что процесс $d = (x( \cdot ),u( \cdot ),\{ v\} )$ оказывается допустимым $d \in \mathcal{D}(t,x)$. Качество программного управления $w \in \mathcal{W}(t,x)$ одной траекторией оценивается функционалом оставшихся потерь (2.2), который обозначим $I(t,x,w) = I(t,x,d)$, подчеркивая зависимость от управления.

3.1. Функция стоимости полуоптимального процесса. Рассмотрим функцию, значение которой $\beta (t,x,\hat {x})$ по определению равно значению функционала оставшихся потерь (2.2):

вычисленному на траектории, исходящей из позиции (t, x), при управлении $\hat {w}$, оптимальном для траектории $\hat {x}( \cdot )$, исходящей из позиции $(t,\hat {x})$. Иначе говоря, функция $\beta (t,x,\hat {x})$ равна значению функционала оставшихся потерь (2.2) на полуоптимальном процессе $d = (x( \cdot ),\hat {w})$, в котором управление $\hat {w}$ оптимальное (правда, для траектории $\hat {x}( \cdot )$), а траектория $x( \cdot )$ неоптимальная, хотя получается при управлении $\hat {w}$. Будем называть функцию $\beta (t,x,\hat {x})$ стоимостью полуоптимального процесса. Заметим, что функция цены $\varphi (t,\hat {x})$ показывает стоимость оптимального процесса $\hat {d} = (\hat {x}( \cdot ),\hat {w})$, так как по определению $\varphi (t,\hat {x}) = I(t,\hat {x},\hat {d})$. При совпадении аргументов $x = \hat {x}$ функция стоимости полуоптимального процесса совпадает с функцией цены

3.2. Субоптимальная оценка состояния. Используя функцию стоимости (3.1), можно определить субоптимальное управление пучком траекторий. Действительно, для программного управления $\hat {w}$, оптимального для траектории, удовлетворяющей начальному условию $x({{t}_{0}}) = \hat {x}$, имеем равенство

Качество управления $\hat {w}$ пучком траекторий, исходящих из множества ${{\sigma }_{0}}$, оценивается средним значением функционала (1.10):

Выбор наилучшего управления $\hat {w}$ можно заменить, согласно (3.2), выбором наилучшего начального состояния $\hat {x}$ опорной траектории:

Если выполняется принцип разделения, то управление ${{\hat {w}}^{{\text{с }}}}$, оптимальное для траектории, исходящей из позиции $({{t}_{0}},{{\hat {x}}^{{\text{с }}}})$, будет оптимальным в среднем управлением пучком траекторий.

3.3. Образующие функции стоимости. Для нахождения функции стоимости $\beta (t,x,\hat {x})$ будем использовать, как и для функции цены, вспомогательные функции – образующие ${{\beta }^{k}}(t,x,\hat {x})$, $k \in {{\mathbb{Z}}_{ + }}$, которые определим следующим образом. Обозначим, как и ранее, через ${{I}^{k}}(t,x,w)$ функционал (2.2) при фиксированном количестве k оставшихся переключений, быть может фиктивных. Значение образующей ${{\beta }^{k}}(t,x,\hat {x})$ функции стоимости полагаем равным значению ${{I}^{k}}(t,x,\hat {w})$ функционала оставшихся потерь (2.2), вычисленному на траектории с k переключениями, исходящей из позиции (t, x), при управлении $\hat {w}$, оптимальном для траектории, исходящей из позиции $(t,\hat {x})$. Таким образом, образующая ${{\beta }^{k}}(t,x,\hat {x})$ отличается от функции $\beta (t,x,\hat {x})$ дополнительным ограничением на количество переключений.

Функция стоимости находится по своим образующим

где $\hat {k} = {\mathbf{k}}(t,\hat {x})$ – оптимальное количество переключений (2.17). Образующие функции цены и стоимости связаны между собой, согласно (2.4), равенством

3.4. Уравнения для образующих функций стоимости. Получим по определению уравнения, которым удовлетворяют образующие функции стоимости. При непрерывном движении изменение функции ${{\beta }^{k}}$ происходит при управлении

Это оптимальное позиционное управление переводит систему (1.2) из позиции $(t,\hat {x})$ в оптимальную позицию $({{\tau }^{k}}(t,\hat {x}),\;{{{\mathbf{x}}}^{k}}(t,\hat {x}))$ первого из оставшихся k переключений. При этом управлении функция ${{\beta }^{k}}$ удовлетворяет уравнению

с терминальным условием

Дискретное изменение функции стоимости происходит под действием управления ${{{\mathbf{v}}}^{k}}(\tau ,\hat {x})$:

В процедуре нахождения образующих функции стоимости используется оптимальное позиционное управление, получение которого описано в разд. 2. Поэтому в уравнениях (3.5), (3.7) нет дополнительных операций минимизации, как в уравнениях для образующих функции цены.

3.5. Достаточные условия субоптимальности управления пучком траекторий. В формулировке достаточных условий предполагается, что описанная выше рекуррентная процедура нахождения образующих функций стоимости реализуема. При этом будет существовать и сама функция стоимости полуоптимальных процессов.

Теорема 2 (достаточные условия субоптимальности управления пучком траекторий). Если существует последовательность функций ${{\beta }^{k}}(t,x,\hat {x})$, $k \in {{\mathbb{Z}}_{ + }}$, удовлетворяющая на всей области определения уравнениям (3.5)–(3.7), то программное управление ${{\hat {w}}^{{\text{с }}}}$, оптимальное для траектории, исходящей из начального состояния (3.3), будет субоптимальным в среднем управлением пучком траекторий.

Действительно, из уравнений (3.5)–(3.7) следует, что указанные в формулировке функции ${{\beta }^{k}}(t,x,\hat {x})$ представляют собой образующие функции стоимости, по которым строится функция $\beta $, согласно (3.4). Оценка (3.3) начального состояния обеспечивает субоптимальность управления пучком траекторий. Теорема доказана.

3.6. Условное субоптимальное управление пучком траекторий. Оценку (3.3) можно улучшить, если использовать не оптимальное управление опорной траекторией, а условное оптимальное (см. разд. 1.2), т.е. оптимальное управление с фиксированным числом переключений. Действительно, учитывая связь (3.4), для начальной позиции $({{t}_{0}},{{x}_{0}})$ имеем равенство

где $\hat {k} = {\mathbf{k}}({{t}_{0}},\hat {x})$. Подставляя функцию стоимости в (3.2), получаем неравенство

Каждое из этих неравенств выполняется как равенство, если минимум по $k \in {{\mathbb{Z}}_{ + }}$ в правой части достигается при $k = \hat {k}$. Значит, вместо формулы (3.3) выбор наилучшего начального состояния $\hat {x}$ опорной траектории лучше делать так:

В самом деле, оптимальное значение k, получаемое при минимизации правой части неравенства (3.8), может отличаться от оптимального количества переключений $\hat {k} = {\mathbf{k}}({{t}_{0}},\hat {x})$. Поэтому опорная траектория $\hat {x}( \cdot )$ с начальным состоянием (3.9) не будет оптимальной, а будет условно оптимальной с k переключениями.

В задаче субоптимального управления функционал (1.12) минимизируется на множестве $\hat {\mathcal{W}}$ оптимальных программных управлений, каждое из которых оптимально хотя бы для одной траектории. Обозначим через ${{\hat {\mathcal{W}}}^{k}}$ множество условно оптимальных управлений, имеющих ровно k переключений, быть может фиктивных. Каждое управление ${{\hat {w}}^{k}} \in {{\hat {\mathcal{W}}}^{k}}$ является оптимальным для некоторой траектории с k переключениями. Объединение этих управлений

будет включать множество оптимальных управлений, т.е. $\hat {\mathcal{W}} \subset {{\hat {\mathcal{W}}}_{{{{\mathbb{Z}}_{ + }}}}}$. Поэтому минимизация функционала (1.12) по условным оптимальным управлениям из ${{\hat {\mathcal{W}}}_{{{{\mathbb{Z}}_{ + }}}}}$, которой соответствуют состояния (3.9), оказывается не хуже, чем минимизация по оптимальным управлениям $\hat {\mathcal{W}}$, которой соответствуют состояния (3.3). Наилучшее для пучка траекторий управление, условно оптимальное хотя бы для одной траектории системы, будем называть условным субоптимальным управлением пучком траекторий.

Теорема 3 (достаточные условия условной субоптимальности управления пучком траекторий). Если существует последовательность функций ${{\beta }^{k}}(t,x,\hat {x})$, $k \in {{\mathbb{Z}}_{ + }}$, удовлетворяющая на всей области определения уравнениям (3.5)–(3.7), то программное управление ${{\hat {w}}^{{\text{с }}}}$, оптимальное для траектории, исходящей из начального состояния (3.9), будет условным субоптимальным в среднем управлением пучком траекторий.

Действительно, из уравнений (3.5)–(3.7) следует, что указанные в формулировке функции ${{\beta }^{k}}(t,x,\hat {x})$ представляют собой образующие функции стоимости, по которым строится функция $\beta $, согласно (3.4). Оценка (3.9) начальных состояний обеспечивает условную субоптимальность управления пучком траекторий. Теорема доказана.

Если выполняется модифицированный (условный) принцип разделения: “оптимальное управление пучком траекторий совпадает с условным оптимальным управлением одной траекторией”, то управления, удовлетворяющие условиям теоремы 3, будут оптимальным гарантирующим и оптимальным в среднем управлениями пучками траекторий соответственно. Для дискретных и непрерывно-дискретных систем эта модификация принципа расширения не имеет смысла, так как количество переключений в этих системах фиксировано.

3.7. Условное субоптимальное управление пучком траекторий с дискретными неточными измерениями. Для пучка траекторий с измерениями предлагается использовать субоптимальное управление, которое совпадает с условным оптимальным управлением для опорной траектории, исходящей из некоторого состояния системы, выбираемого оптимальным образом. Начальное состояние опорной траектории после $m$ измерений находится по формуле, аналогичной (3.9):

Процедура управления при этом следующая. В начальный момент времени известна позиция $({{t}_{0}},{{\sigma }_{0}})$ пучка траекторий. По множеству ${{\sigma }_{0}}$ возможных начальных состояний находим оценку $\hat {x}_{0}^{{\text{c}}} = {{\hat {x}}^{{\text{c}}}}({{t}_{0}})$, согласно (3.9). При этом также определяется оптимальное количество переключений $N = {\mathbf{k}}({{t}_{0}},{{x}_{0}})$. Под действием программного управления, условно-оптимального для опорной траектории, исходящей из начального состояния $\hat {x}_{0}^{{\text{c}}}$ и имеющей ровно N переключений, выполняем моделирование движения пучка. Движение пучка начинается в момент t₀ из начального множества ${{\sigma }^{0}}({{t}_{0}}) = {{\sigma }_{0}}$ и заканчивается в момент t¹ первого измерения. В этот момент находим пересечение $\sigma _{0}^{1} = {{\sigma }^{0}}({{t}^{1}}) \cap {{\sigma }^{1}}$ множества возможных состояний ${{\sigma }^{0}}({{t}^{1}})$ и “измеренного” множества σ¹. В результате получаем позицию $({{t}^{1}},\sigma _{0}^{1})$ пучка траекторий с учетом первого измерения. В этой позиции выполняем те же действия, начиная с выбора оценки ${{\hat {x}}^{{\text{с }}}}({{t}^{1}})$ на множестве $\sigma _{0}^{1}$.

Как указано во Введении, в статье не рассматриваются методы моделирования пучков траекторий, связанные с проблемами адекватного описания множеств возможных состояний системы и множеств, полученных при неточных измерениях, а также их пересечения. Приемлемое решение этих проблем в общем случае вряд ли возможно. Для “экономичного” описания множеств состояний нужно использовать практические соображения, учитывающие прикладную область исследования, динамические свойства системы, характер оптимального движения и т.п. Общие рекомендации тоже возможны. Например, для линейных систем можно использовать линейные неравенства или эллипсоиды [10].

4. Примеры. Рассмотрим два академических примера оптимального управления пучками траекторий линейных ПС с квадратичным критерием качества. Первая линейно-квадратичная задача служит контрпримером, в котором принцип разделения не выполняется. Оптимальное в среднем управление не совпадает с субоптимальным, и оба этих управления отличаются от оптимального управления для геометрического центра тяжести пучка траекторий. Во второй задаче принцип разделения выполняется и применяется для получения оптимального в среднем управления при наличии дискретных неточных измерений.

Пример 1. Пусть на заданном промежутке времени $T = [0,\;3]$ динамическая система совершает N переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,\; \ldots ,\;N$, которые образуют неубывающую последовательность:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальным уравнениям:

а в моменты переключений – дискретно в соответствии с рекуррентными уравнениями

Здесь $\mathcal{N} = \left\{ {i = 0,\;1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}} \right\}$ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}} = [{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in T$, $x = {{({{x}_{1}},{{x}_{2}})}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}$; $u(t)$ – значение управления непрерывным движением системы в момент времени $t \in T$, $u \in \mathbb{R}$. Дискретное управление (переключениями) отсутствует.

Качество процесса управления оценивается квадратичным функционалом

где x₀ – начальное состояние системы, $w = (u( \cdot ),\mathcal{T})$ – “управляющий комплекс”, включающий управление $u( \cdot )$ непрерывным движением и моменты переключений $\mathcal{T} = \{ {{t}_{1}},\; \ldots ,\;{{t}_{N}}\} $. Коэффициент λ = 100 определяет затраты на каждое переключение. Количество N и моменты переключений ${{t}_{1}},\; \ldots ,\;{{t}_{N}}$ заранее не заданы и подлежат оптимизации.

Начальное состояние точно не известно, а известно множество (прямоугольник) σ₀ = $[7.8,8.2] \times [2,4]$ возможных начальных состояний. Качество управления пучком траекторий, исходящих из множества σ₀, оценивается средним значением функционала (4.3):

Требуется найти:

1) оптимальное программное управление $\bar {w} = (\bar {u}( \cdot ),\bar {\mathcal{T}})$ для начального состояния ${{\bar {x}}_{0}} = {{(8,3)}^{{\text{T}}}}$ – центра прямоугольника σ₀;

2) среднее значение ${{\bar {I}}^{{\text{c}}}}$ при управлении $\bar {w} = (\bar {u}( \cdot ),\bar {\mathcal{T}})$, оптимальном для траектории, исходящей из центра ${{\bar {x}}_{0}}$;

3) субоптимальное в среднем состояние $\hat {x}_{0}^{{\text{c}}}$ системы и среднее значение ${{\hat {I}}^{{\text{c}}}}$ при управлении $\hat {w} = (\hat {u}( \cdot ),\bar {\mathcal{T}})$, оптимальном для траектории, исходящей из $\hat {x}_{0}^{{\text{c}}}$;

4) наименьшее среднее значение I  ^c и оптимальное в среднем управление ${{w}^{{\text{c}}}} = ({{u}^{{\text{c}}}}( \cdot ),{{\mathcal{T}}^{{\text{c}}}})$.

Рассматривается линейно-квадратичная задача. По сравнению с общей постановкой (1.1)–(1.3), (1.6), (1.10) имеем: t₀ = 0, t_F = 3, $X = {{\mathbb{R}}^{2}}$, $U = \mathbb{R}$, $f(t,x,u) = {{(u\,{{x}_{2}})}^{{\text{T}}}}$, $g(t,x,v) = {{({{x}_{2}}\;{{x}_{1}})}^{{\text{T}}}}$, ${{f}^{0}}(t,x,u) = ({{u}^{2}} + x_{1}^{2} + x_{2}^{2}){\text{/}}2$, ${{g}^{ + }}(t,x,v) = \lambda $, F(x) = 0. Дискретное управление отсутствует.

В системе (4.1), (4.2) один канал управления: первая координата управляема, а вторая – нет (она экспоненциально отклоняется от нуля). В момент переключения фактически происходит взаимная замена координат состояния – неуправляемая координата становится управляемой и наоборот. Таким образом, совершая переключения (т.е. меняя канал управления), можно попеременно управлять координатами системы. Ненулевые затраты $\lambda $ на каждое переключение исключают из числа оптимальных процессов режимы с мгновенными многократными переключениями.

Найдем образующие функции цены. Сначала рассмотрим процессы без переключений (при N = 0). Составляем уравнение (2.6) для нулевой образующей функции цены:

Решая его с нулевым терминальным условием ${{\varphi }^{0}}(3,x) = 0$, получаем образующую

и нулевое оптимальное позиционное управление ${{{\mathbf{u}}}^{0}}(t,x) = - {{x}_{1}}th(3 - t)$.

Для получения остальных образующих рассмотрим вспомогательную задачу Лагранжа с фиксированными краевыми условиями:

Решением этой задачи служит двухпозиционная функция цены:

Она как функция первых двух аргументов $(t,x) \to \phi (t,x|\tau ,{{x}_{\tau }})$ удовлетворяет уравнению ГЯБ:

с нулевым терминальным условием $\phi (\tau ,{{x}_{\tau }}|\tau ,{{x}_{\tau }}) = 0$. При решении уравнения (4.5) находим позиционное оптимальное управление

При помощи двухпозиционной функции цены составляем рекуррентное уравнение для образующих

где $y{\text{'}} = ({{y}_{2}},{{y}_{1}})$ – точка фазовой плоскости, симметричная точке y относительно прямой y₁ = y₂.

1. Находим оптимальное управление $\bar {w} = (\bar {u}( \cdot ),\bar {\mathcal{T}})$ для траектории, исходящей из центра тяжести ${{\bar {x}}_{0}} = {{(8,3)}^{{\text{T}}}}$ прямоугольника σ₀. Вычисляем значения образующих в этой точке (все значения приближенные):

Как видим, при большом штрафе $\lambda = 100$ лучшим оказывается оптимальный процесс с одним переключением ${{\bar {x}}_{{1 - }}} = {\text{(1}}{\text{.2065,}}\;{\text{2}}{\text{.0585)}} \to {{\bar {x}}_{1}} = {\text{(2}}{\text{.0585,}}\;{\text{1}}{\text{.2065)}}$ в момент ${{\bar {t}}_{1}} = 0.703$. Оптимальное программное управление находится по позиционному управлению (4.6):

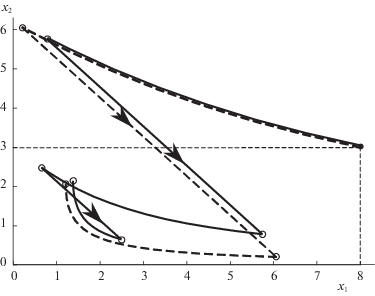
Без учета затрат на переключение (т.е. при $\lambda = 0$) оптимальный процесс с двумя переключениями ${\text{(0}}{\text{.785,}}\;{\text{5}}{\text{.7409)}} \to {\text{(5}}{\text{.7409,}}\;{\text{0}}{\text{.785)}}$ в момент ${{t}_{1}} = 0.649$ и (0.649, 18.2035) → (18.2035, 0.649) в момент ${{t}_{2}} = 1.803$ был бы немного лучше ${{I}^{2}} = 76.33175 < 76.61338 = {{I}^{1}}$. Но при большом штрафе ($\lambda $ = 100) одно переключение выгоднее. Таким образом, оптимальный “управляющий комплекс” $\bar {w} = (\bar {u}( \cdot ),\bar {\mathcal{T}})$ для начального состояния ${{\bar {x}}_{0}}$ включает оптимальное управление (4.7) непрерывным движением и один момент переключения $\bar {\mathcal{T}} = \{ {{\bar {t}}_{1}}\} $. На рис. 4 показаны фазовые траектории, оптимальные при одном переключении (штриховая линия) и при двух (сплошная линия). Скачки траекторий обозначены стрелками.

2. Вычисляем среднее значение (4.4) при управлении $\bar {w} = (\bar {u}( \cdot ),\bar {\mathcal{T}})$, оптимальном для траектории, исходящей из центра тяжести ${{\bar {x}}_{0}}$. Для этого записываем условную функцию стоимости полуоптимальных процессов для управления с одним переключением в позиции $({{t}_{1}},{{\hat {x}}_{1}})$:

где $\tau = {{t}_{1}} - {{t}_{0}}$, ${{x}_{0}} = {{({{x}_{{10}}},{{x}_{{20}}})}^{{\text{T}}}}$, ${{\hat {x}}_{0}} = {{({{\hat {x}}_{{10}}},{{\hat {x}}_{{20}}})}^{{\text{T}}}}$, ${{\hat {x}}_{1}} = {{({{\hat {x}}_{{11}}},{{\hat {x}}_{{21}}})}^{{\text{T}}}}$. Подставляем ${{t}_{0}} = 0$, $\hat {x} = {{\bar {x}}_{0}} = {{(8,3)}^{{\text{T}}}}$, ${{t}_{1}} = {{\bar {t}}_{1}}$ = 0.703, ${{\hat {x}}_{1}} = {{{\text{(0}}{\text{.207,}}\;{\text{6}}{\text{.0594)}}}^{{\text{T}}}}$ и вычисляем среднее значение ${{\bar {I}}^{{\text{c}}}} = {{I}^{{\text{c}}}}({{\sigma }_{0}},\bar {u}( \cdot ))$ = 178.762803.

3. Найдем теперь субоптимальное управление. Для этого записываем среднее значение функции (4.8):

для управления $\hat {w} = (\hat {u}( \cdot ),{{\hat {t}}_{1}})$, оптимального для траектории, исходящей из некоторого состояния ${{\hat {x}}_{0}}$. Позиция после переключения $({{\hat {t}}_{1}},{{\hat {x}}_{1}})$ и управление $\hat {u}( \cdot )$ непрерывным движением полностью определяются состоянием ${{\hat {x}}_{0}}$ (см. п. 1)). Поэтому среднее значение (4.9) также определяется только этим состоянием, т.е. ${{I}^{{\text{c}}}}({{\sigma }_{0}},\hat {u}( \cdot )) = {{I}^{{\text{c}}}}({{\hat {x}}_{0}})$. Минимизируя ${{I}^{{\text{c}}}}({{\hat {x}}_{0}})$ по ${{\hat {x}}_{0}}$, находим субоптимальное в среднем состояние $\hat {x}_{0}^{{\text{c}}} = {{{\text{(8,}}3.03{\text{)}}}^{{\text{T}}}}$ и наименьшее среднее значение ${{\hat {I}}^{{\text{с }}}} = 178.75771$. Субоптимальное управление имеет переключение в момент ${{\hat {t}}_{1}} = 0.699$ из состояния ${{\hat {x}}_{{1 - }}}$ = ${{{\text{(0}}{\text{.207,6}}{\text{.0956)}}}^{{\text{T}}}}$ в состояние ${{\hat {x}}_{1}} = {{{\text{(6}}{\text{.0956,0}}{\text{.207)}}}^{{\text{T}}}}$. Как видим, субоптимальное управление лучше, чем управление центром тяжести множества возможных состояний системы. Это важная особенность рассматриваемого примера. Для широкого круга линейно-квадратичных задач оптимального в среднем управления пучками траекторий детерминированных (да и стохастических) систем наилучшей оценкой начального состояния служит его среднее значение (соответственно математическое ожидание). Другими словами, субоптимальное управление пучком совпадает с оптимальным управлением для центра тяжести пучка. Это выполняется для непрерывных, дискретных, непрерывно-дискретных систем, в которых моменты переключений дискретной части фиксированы. В рассматриваемом примере это правило нарушается.

4. Найдем теперь оптимальное в среднем управление ${{w}^{{\text{с }}}} = ({{u}^{{\text{с }}}}( \cdot ),{{\mathcal{T}}^{{\text{с }}}})$. Для этого будем минимизировать среднее значение (4.9) по управлению ${{u}^{{\text{с }}}}( \cdot )$ с одним переключением. При фиксированной позиции $({{t}_{1}},{{x}_{1}})$ переключения наилучшей оценкой начального состояния служит центр тяжести, поэтому $x_{0}^{{\text{c}}} = {{\bar {x}}_{0}}$. Оптимальное программное управление вида (4.7) определяется заданной начальной позицией $({{t}_{0}},{{\bar {x}}_{0}})$ и некоторой позицией $(t_{1}^{{\text{c}}},x_{1}^{{\text{c}}})$ переключения. Поэтому функционал (4.9) оказывается функцией, зависящей только от позиции переключения, т.е. ${{I}^{{\text{c}}}}({{\sigma }_{0}},{{w}^{{\text{c}}}})$ = ${{I}^{{\text{c}}}}(t_{1}^{{\text{c}}},x_{1}^{{\text{c}}})$. Минимизируя по этим аргументам, получаем наименьшее среднее значение ${{I}^{{\text{с }}}}$ = 178.752432. Оптимальное в среднем управление имеет переключение в момент $t_{1}^{{\text{c}}}$ = 0.695 в позиции $\hat {x}_{1}^{{\text{c}}} = {{{\text{(0}}{\text{.207,6}}{\text{.0111)}}}^{{\text{T}}}}$. Как видим, оптимальное в среднем управление не является субоптимальным. Значит, принцип разделения в этом примере не выполняется. На рис. 5 изображены начальное σ₀ и конечное σ₁ множества возможных состояний системы сплошной и пунктирными линиями соответственно, а также траектория, исходящая из центра ${{\bar {x}}_{0}}$ при оптимальном в среднем управлении (непрерывные участки представлены сплошными линиями, а скачок – штриховой).

Пример 2. Пусть на заданном промежутке времени $T = [0,2]$ динамическая система совершает N переключений (скачков) в моменты времени ${{t}_{i}}$, $i = 1,\; \ldots ,\;N$, которые образуют неубывающую последовательность:

Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальным уравнениям:

а в моменты переключений – дискретно в соответствии с рекуррентными уравнениями:

Здесь $\mathcal{N} = \left\{ {i = 0,\;1,\; \ldots ,\;N|{{t}_{i}} < {{t}_{{i + 1}}}} \right\}$ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}}\, = \,\,[{{t}_{i}},{{t}_{{i + 1}}})$ непрерывного движения системы; x(t) – состояние системы в момент времени $t \in T$, $x = {{({{x}_{1}},{{x}_{2}})}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}$; $u(t)$ – значение управления непрерывным движением системы в момент времени $t \in T$, $u(t) \in \mathbb{R}$; ${{x}_{{i - }}}$ – состояние системы перед переключением в момент t_i (см. (1.4)), ${{x}_{i}}\dot { = }x({{t}_{i}})$ – состояние после i-го переключения, ${{v}_{i}}$ – дискретное управление в момент переключения ${{t}_{i}}$, ${{v}_{i}} \in \mathbb{R}$, $i = 1,\; \ldots ,\;N$.

Качество процесса управления оценивается квадратичным функционалом

где x₀ – начальное состояние системы, $w = (u( \cdot ),\{ v\} )$ – программное управление u(⋅) непрерывным движением и последовательность $\{ v\} = \{ {{v}_{1}},\; \ldots ,\;{{v}_{N}}\} $ – дискретных управлений переключениями, а $\mu = 0.05$, $\eta = 0.1$, $\lambda = 0.02$ – коэффициенты, определяющие затраты на непрерывное управление и переключения. Количество переключений N и моменты переключений ${{t}_{1}},\; \ldots ,\;{{t}_{N}}$ заранее не заданы и подлежат оптимизации.

Начальное состояние точно не известно, а известно множество (квадрат) ${{\sigma }_{0}} = [1,\;3] \times [0,\;2]$ возможных начальных состояний. Качество управления пучком траекторий, исходящих из множества σ₀ оценивается средним значением функционала (4.10):

В заданные моменты ${{t}^{1}},\; \ldots ,\;{{t}^{m}}$ производятся неточные измерения скорости движения x₂, при этом координата x₁ (расстояние) не измеряется. В каждый момент t ^j, $j = 1, \ldots ,\;m$, измеренное значение скорости $\bar {x}_{2}^{j}$ является случайной величиной с равномерным распределением на промежутке $[{{x}_{{2\min }}}({{t}^{j}}),\;{{x}_{{2\max }}}({{t}^{j}})]$ возможных значений ${{x}_{2}}({{t}^{j}})$, а погрешность измерений $2{{\Delta }^{j}}$ равна длине этого промежутка. Иначе говоря, в момент t ^j становится известной полоса σ ^j = $\{ x \in {{\mathbb{R}}^{2}}|\bar {x}_{2}^{j} - {{\Delta }^{j}} \leqslant {{x}_{2}} \leqslant \bar {x}_{2}^{j}$ + Δ^j} возможных (“измеренных”) состояний. Множество $\sigma _{0}^{j}\dot { = }{{\sigma }^{j}}({{t}^{j}})$ возможных состояний системы в момент времени t ^j с учетом всех предыдущих измерений определяется пересечениями (1.14).

Предполагаем, что измерения скорости происходят в моменты времени ${{t}^{1}} = 0.5$, ${{t}^{2}} = 1.5$. В каждый момент t ^j, $j = 1,\;2$, измеренное значение скорости $\bar {x}_{2}^{j}$ является случайной величиной с равномерным распределением на промежутке $[{{x}_{{2\min }}}({{t}^{j}}),\;{{x}_{{2\max }}}({{t}^{j}})]$ возможных значений ${{x}_{2}}({{t}^{j}})$, а погрешность измерений $2{{\Delta }^{j}}$ равна длине этого промежутка. Иначе говоря, в момент t ^j определяется полоса ${{\sigma }^{j}} = \{ x \in {{\mathbb{R}}^{2}}|\bar {x}_{2}^{j} - {{\Delta }^{j}} \leqslant {{x}_{2}} \leqslant \bar {x}_{2}^{j} + {{\Delta }^{j}}\} $ возможных (“измеренных”) состояний. Множество $\sigma _{0}^{j}\dot { = }{{\sigma }^{j}}({{t}^{j}})$ возможных состояний системы в момент времени t ^j с учетом всех предыдущих измерений определяется пересечениями (1.14).

Требуется найти:

1) оптимальное программное управление $\bar {w} = (\bar {u}( \cdot ),\{ \bar {v}\} )$ для траектории, исходящей из центра ${{\bar {x}}_{0}} = {{(2,1)}^{{\text{T}}}}$ квадрата σ₀;

2) наименьшее среднее значение ${{\bar {I}}^{{\text{c}}}}$ при управлении $\bar {w}$, оптимальном для траектории, исходящей из центра ${{\bar {x}}_{0}}$;

3) наименьшее среднее значение $\bar {I}_{2}^{{\text{c}}}$ функционала

после двух неточных измерений скорости движения x₂ в моменты времени ${{t}^{1}} = 0.5$, ${{t}^{2}} = 1.5$.

Рассматривается линейно-квадратичная задача. По сравнению с общей постановкой (1.1)–(1.3), (1.6), (1.11) имеем: ${{t}_{0}} = 0$, ${{t}_{F}} = 2$, $X = {{\mathbb{R}}^{2}}$, $U = \mathbb{R}$, $V = \mathbb{R}$, $f(t,x,u) = {{({{x}_{2}}\;u)}^{{\text{T}}}}$, g(t, x, $\text{v}) = {{({{x}_{1}},{{x}_{2}} + v)}^{{\text{T}}}}$, ${{f}^{0}}(t,x,u) = {{u}^{2}}{\text{/}}2$, ${{g}^{ + }}(t,x,v) = \lambda + {{v}^{2}}{\text{/}}2$, $F(x) = x_{1}^{2}{\text{/}}2 + x_{2}^{2}{\text{/}}2$. Требуется привести систему в окрестность начала координат, чтобы уменьшить терминальные слагаемые функционала (4.10) с минимальными затратами на управление. При помощи переключения можно скачком улучшить состояние системы, после чего затраты на непрерывное управление, определяемые интегральным членом функционала, уменьшатся. Поэтому переключение нужно делать как можно раньше, а именно в начальный момент времени. В конечный момент времени скачки траектории могут привести к уменьшению терминальных членов функционала. Таким образом, у оптимального процесса переключения происходят только в начальный и/или конечный моменты времени. Этот вывод подтверждается расчетами.

1. Пусть процесс имеет  j переключений в начальный момент времени и k – в конечный. Тогда моменты переключений образуют неубывающую последовательность:

Обозначим через ${{\varphi }_{{jk}}}(t,x)$ образующие функции цены, $j,k \in {{\mathbb{Z}}_{ + }}$, полагая для уменьшения количества индексов ${{\varphi }_{k}}(t,x)\dot { = }{{\varphi }_{{0k}}}(t,x)$. Уравнения для образующих получаем из достаточных условий оптимальности. В конечный момент времени t = 2:

на промежутке $t \in [0,\;2]$: в начальный момент времени t = 0:

Будем искать образующие в виде квадратичных функций:

Подставляя функции (4.15), (4.16) в уравнения (4.12)–(4.14), получаем соотношения для нахождения коэффициентов квадратичных функций. В конечный момент времени t = 2:

на промежутке $t \in [0,\;2]$: в начальный момент времени t = 0:

Решая уравнения (4.17)–(4.19), получаем

где $\tau = 2 - t$, $\Delta = {{\mu }^{2}} + \mu (F_{{11}}^{k}{{\tau }^{3}}{\text{/}}3 + F_{{12}}^{k}{{\tau }^{2}} + F_{{22}}^{k}) + \,{\text{|}}{{F}^{k}}{\text{|}}{{\tau }^{4}}{\text{/}}12$, $F_{{11}}^{k} = {{\Phi }_{k}}(2)$, $F_{{12}}^{k} = {{\Psi }_{k}}(2)$, $F_{{22}}^{k} = {{\Gamma }_{k}}(2)$, |F  ^k| = $F_{{11}}^{k}F_{{22}}^{k} - {{(F_{{12}}^{k})}^{2}}$. В правых частях уравнений (4.21), (4.22) у всех функций не указаны значения аргумента t = 2 и t = 0 соответственно.

Позиционные условные оптимальные управления определяем, выполняя операции минимизации в (4.12)–(4.14):

Оптимальное количество переключений ${{{\mathbf{k}}}_{0}}(0,x)$, ${{{\mathbf{k}}}_{F}}(0,x)$ находим по образующим (4.15), решая задачу дискретной оптимизации

Для начального состояния ${{\bar {x}}_{0}} = {{(2,\;1)}^{{\text{T}}}}$ получаем: ${{k}_{0}} = 2$, ${{k}_{1}} = 1$, ${{\bar {v}}_{1}} = {{\bar {v}}_{2}} = - 0.70859$, ${{\bar {v}}_{3}} = 0.59173$, $\bar {u}(t) = 1.3003\,t - 1.4172$, $\bar {I} = 0.16045$ (вычисления приближенные). На рис. 6 изображена оптимальная траектория, характерные состояния представлены полужирными квадратиками, скачки траектории – стрелками.

2. Обозначим через ${{\beta }_{{j\,k}}}(t,x,\hat {x})$ образующие функции стоимости полуоптимального процесса, $j,k \in {{\mathbb{Z}}_{ + }}$, полагая, как и ранее, для уменьшения количества индексов ${{\beta }_{k}}(t,x,\hat {x})\dot { = }{{\beta }_{{0k}}}(t,x,\hat {x})$. Уравнения для этих образующих получаем из достаточных условий оптимальности. В конечный момент времени t = 2:

где ${{{\mathbf{\hat {v}}}}_{k}} = {{{\mathbf{v}}}_{k}}(2,\hat {x})$ – позиционное управление переключениями (4.24);

на промежутке $t \in [0,\;2]$:

где ${{{\mathbf{\hat {u}}}}_{k}} = {{{\mathbf{u}}}_{k}}(t,\hat {x})$ – позиционное управление непрерывным движением (4.23);

в начальный момент времени t = 0:

где ${{{\mathbf{\hat {v}}}}_{{jk}}} = {{{\mathbf{v}}}_{{jk}}}(2,\hat {x})$ – позиционное управление переключениями (4.24).

Будем искать образующие в виде квадратичных функций:

где ${{\varphi }_{{jk}}}(t,x)$ и ${{\varphi }_{k}}(t,x)$ – образующие функции цены (4.15), (4.16), $\Delta x = x - \hat {x}$ – отклонение от состояния $\hat {x}$ оптимальной траектории. Подставляя функции (4.28), (4.29) в уравнения (4.26), (4.27), получаем соотношения для нахождения коэффициентов квадратичных функций. В конечный момент времени t = 2: на промежутке $t \in [0,\;2]$: в начальный момент времени t = 0:

В правых частях уравнений (4.30), (4.32) у всех функций не указаны значения аргумента t = 2 и t = 0 соответственно. Решения уравнений (4.30)–(4.32) выражаются через коэффициенты $\Phi $, $\Psi $, $\Gamma $ образующих функции цены (4.20)–(4.22):

Здесь, как и ранее, $\tau = 2 - t$, $j \in {{\mathbb{Z}}_{ + }}$, $k \in {{\mathbb{Z}}_{ + }}$, $0 \leqslant t \leqslant 2$.

Среднее значение (4.11) функционала (4.10) на программном управлении $\hat {w}$, оптимальном для траектории $\hat {x}( \cdot )$, исходящей из позиции $({{t}_{0}},{{\hat {x}}_{0}})$, вычисляем по функции стоимости полуоптимального процесса:

где ${{{\mathbf{\hat {k}}}}_{0}} = {{{\mathbf{k}}}_{0}}(0,{{\hat {x}}_{0}})$, ${{{\mathbf{\hat {k}}}}_{F}} = {{{\mathbf{k}}}_{F}}(0,{{\hat {x}}_{0}})$ – количество переключений (4.25) у оптимальной траектории $\hat {x}( \cdot )$ в начальный и конечный моменты времени соответственно. Подставляя ${{\hat {x}}_{0}} = {{\bar {x}}_{0}}$ в формулу (4.33), получаем среднее значение ${{\bar {I}}^{{\text{c}}}} = {{I}^{{\text{c}}}}({{t}_{0}},{{\sigma }_{0}},\bar {w}) = {\text{1}}{\text{.160446}}$ при управлении $\bar {w}$, оптимальном для траектории, исходящей из центра ${{\bar {x}}_{0}}$. На рис. 6 изображены множества возможных начальных и конечных состояний – квадрат σ₀ и параллелограмм $\sigma (2)$ соответственно, а также оптимальная траектория, исходящая из центра ${{\bar {x}}_{0}} = {{(2,1)}^{{\text{T}}}}$ квадрата σ₀.

3. Множество σ₀ возможных начальных состояний представляет собой квадрат со сторонами, параллельными координатным осям. В процессе непрерывного движения квадрат преобразуется в параллелограмм $\sigma (t)$ с основаниями, параллельными оси абсцисс (x₁). При переключениях меняется только скорость движения x₂, поэтому параллелограмм смещается вдоль оси ординат (x₂). При каждом неточном измерении скорости множество “измеренных состояний” представляет собой полосу, например, ${{\sigma }^{m}} = \{ x \in {{\mathbb{R}}^{2}}|\bar {x}_{2}^{m} - {{\Delta }^{m}} \leqslant {{x}_{2}} \leqslant \bar {x}_{2}^{m} + {{\Delta }^{m}}\} $ в момент $t = {{t}^{m}}$. Пересечение этой полосы с параллелограммом ${{\sigma }^{{m - 1}}}({{t}^{m}})$ дает новый параллелограмм $\sigma _{0}^{m}$, основания которого параллельны оси абсцисс. Таким образом, в процессе движения с учетом неточных измерений множество возможных состояний системы является параллелограммом. Для описания такого множества достаточно использовать три его вершины. Моделируя движения вершин параллелограмма от начального момента времени t₀ = 0 до момента t¹ первого измерения, получаем параллелограмм ${{\sigma }^{0}}({{t}^{1}})$. По измеренному значению скорости $\bar {x}_{2}^{1}$ и погрешности измерения Δ¹ определяем полосу ${{\sigma }^{1}} = \{ x \in {{\mathbb{R}}^{2}}|\bar {x}_{2}^{1} - {{\Delta }^{1}} \leqslant {{x}_{2}} \leqslant \bar {x}_{2}^{1} + {{\Delta }^{1}}\} $, которую пересекаем с ${{\sigma }^{0}}({{t}^{1}})$. В результате получаем параллелограмм $\sigma _{0}^{1}$. Находим его центр $\bar {x}_{0}^{1}$ и вычисляем среднее значение $\bar {I}_{1}^{{\text{c}}}$ = ${{I}^{{\text{c}}}}({{t}^{1}},\sigma _{0}^{1},\bar {x}_{0}^{1})$. Затем моделируем движение вершин параллелограмма от момента t ¹ до момента t² второго измерения и вычисляем $\bar {I}_{2}^{{\text{c}}} = {{I}^{{\text{c}}}}({{t}^{2}},\sigma _{0}^{2},\bar {x}_{0}^{2})$. Далее процедура повторяется до последнего измерения. При моделировании используется оптимальное в среднем управление, которое совпадает с оптимальным управлением для центра параллелограмма. При каждом измерении j = $1, \ldots ,m$ положение центра $\bar {x}_{0}^{j}$ возможных состояний системы меняется и оптимальное управление синтезируется заново.

Для пучка с двумя измерениями получаем:

– до первого измерения управление совпадает с найденным в п. 1;

– после первого измерения в момент ${{t}^{1}} = 0.5$ определяем центр $\bar {x}_{0}^{1} = {{(1.8263, - 0.59324)}^{{\text{T}}}}$ множества $\sigma _{0}^{1}$, синтезируем для него оптимальное управление: k₀ = 1, ${{k}_{1}} = 0$, ${{\bar {v}}_{1}} = - {\text{0}}{\text{.45335}}$, $\bar {u}(t) = 1.4899t$ – 1.65171, вычисляем наименьшее среднее значение функционала $\bar {I}_{1}^{{\text{c}}} = 0.64735$ с учетом затрат на промежутке $[0,\;0.5]$;

– после второго измерения в момент ${{t}^{2}} = 1.5$ имеем $\bar {x}_{0}^{2} = {{(0.43318,\; - 1.30027)}^{{\text{T}}}}$, k₀ = 0, k₁ = 0, $\bar {u}(t) = - 0.82161t + 2.7861$, $\bar {I}_{2}^{{\text{c}}} = 0.54809$ с учетом затрат на промежутке $[0,\;1.5]$.

На рис. 7 изображены множество начальных состояний (квадрат σ₀), виртуальное (без учета измерений) множество конечных состояний – параллелограмм $\sigma (2)$ (представленный пунктирными линиями), фактическое (с учетом двух измерений) множество конечных состояний – параллелограмм ${{\sigma }^{2}}(2)$. Траектория центра множества состояний показана полужирными линиями, характерные состояния представлены квадратами, скачки траектории обозначены стрелками. Двойными стрелками отмечены изменения центра в результате измерений.

Эффективность измерений можно оценить, сравнивая средние значения функционала без измерений и с измерениями: ${{\bar {I}}^{{\text{c}}}} = {\text{1}}{\text{.160446}} > \bar {I}_{1}^{{\text{c}}} = {\text{0}}{\text{.64735}} > \bar {I}_{2}^{{\text{c}}} = {\text{0}}{\text{.54809}}$. Заметим, что величины $\bar {I}_{1}^{{\text{c}}}$, $\bar {I}_{2}^{{\text{c}}}$ случайные. Поэтому для объективной оценки нужно использовать статистические методы.

Заключение. Достаточные условия оптимальности управления ПС позволяют синтезировать субоптимальное в среднем управление в условиях параметрической неопределенности. При этом получается позиционное управление с обратной связью по множеству возможных состояний детерминированной системы. Разработанный метод синтеза распространяется на задачи с неточными дискретными измерениями. Трудности применения этого подхода заключаются в первую очередь в необходимости решать вспомогательную задачу Лагранжа с фиксированными, но произвольными терминальными состояниями. Эта трудность, кажется преодолимой, учитывая разработанные численные методы [18]. Остальные операции, выполняемые при синтезе управления, сводятся к задачам конечномерной оптимизации. Их решение, как правило, не вызывает особых затруднений. В целом, трудоемкость и алгоритмическая сложность предлагаемого метода гораздо выше, чем при синтезе оптимальных процессов без переключений. “Проклятие размерности” усугубляется тем, что кроме текущей позиции системы в алгоритмах используются также и все последующие позиции переключений. Поэтому выбор комбинаций численных методов, решающих задачу Лагранжа с последующей конечномерной минимизацией, кажется актуальным.

Применяя субоптимальное управление, нужно считаться с тем, что принцип разделения в ПС, вообще говоря, не выполняется. Даже в линейно-квадратичной задаче, как показано в примере 1, оптимальное в среднем управление пучком не только не совпадает с оптимальным управлением его центром тяжести, но даже отличается от субоптимального. Это обстоятельство необходимо учитывать при решении прикладных задач, в которых принцип разделения, как правило, применяется без обоснования. Целесообразно уточнить класс линейно-квадратичных задач синтеза ПС, в которых выполняется принцип разделения, а также установить те задачи, в которых оптимальные процессы имеют переключения только в начальный и/или конечный моменты времени (см. пример 2).

Дальнейшие исследования могут быть связаны также с распространением предлагаемого подхода на задачи гарантирующего управления. Синтез субоптимального гарантирующего управления, как правило, оказывается несколько сложнее, чем синтез управления, оптимального в среднем. Это связано с недифференцируемостью функции максимума. При этом алгоритмы синтеза становятся более громоздкими [11].