Известия РАН. Теория и системы управления, 2019, № 1, стр. 42-51

УПРАВЛЕНИЕ ТВЕРДЫМ ТЕЛОМ, НЕСУЩИМ ДИССИПАТИВНЫЕ ОСЦИЛЛЯТОРЫ, В ПРИСУТСТВИИ ВОЗМУЩЕНИЙ

И. М. Ананьевский^a, b, *, Т. А. Ишханян^a, b, **

^a ИПМех РАН
Москва, Россия

^b ИФИ НАН РА
Аштарак, Армения

^* E-mail: anan@ipmnet.ru
^** E-mail: tishkhanyan@gmail.com

Поступила в редакцию 31.07.2018
После доработки 31.08.2018

DOI: 10.1134/S0002338819010025

Полный текст (PDF)

Аннотация

Рассматривается система, состоящая из несущего тела и присоединенных к ней двух линейных диссипативных осцилляторов. Тело движется по горизонтальной прямой под действием ограниченной управляющей силы и малого неизвестного возмущения. Предполагается, что координата и скорость тела в каждый момент времени известны, а фазовые состояния осцилляторов не доступны измерениям. Предложен закон управления, который останавливает несущее тело в начале координат за конечное время. Эффективность предложенного закона управления проиллюстрирована с помощью численного моделирования.

Введение. Исследуется задача об управляемом перемещении тела, содержащего упругие элементы или полость с жидкостью. Предполагается, что тело испытывает неконтролируемое и непостоянное воздействие внешней среды, а переменные, описывающие динамику упругих элементов или жидкости, не доступны измерениям. В качестве упрощенной модели такой механической системы рассматривается твердое тело с присоединенными к нему двумя линейными диссипативными осцилляторами. Тело движется по горизонтальной прямой под действием ограниченной управляющей силы и малого неизвестного возмущения. Требуется построить ограниченное по модулю управление в форме обратной связи, т.е. как функция фазовых переменных несущего тела, которое приводит тело в наперед заданное терминальное положение за конечное (нефиксированное) время, при этом полное успокоение колебаний осцилляторов не требуется.

Одним из технических объектов, который описывает данная модель, является прецизионная поворотная платформа, устанавливаемая на орбитальном космическом аппарате. С помощью платформы можно изменять ориентацию закрепленного на ней контейнера с полезной нагрузкой, что повышает эффективность проводимых на орбите технологических процессов [1, 2]. Ранее [3, 4] задача управления платформой была исследована для случая, когда контейнер моделировался твердым телом, а платформа представляла собой одно- или двустепенной карданов подвес. Предполагалось, что в подшипниках осей вращения рамок подвеса присутствует сухое трение, которое существенно влияет на управление и точность ориентации. Был предложен алгоритм построения гладкого ограниченного управления, приводящего платформу в заданное состояние за конечное время в предположении, что параметры трения неизвестны и могут изменяться в процессе движения.

Поскольку среда, используемая в контейнере, при проведении некоторых технологических процессов может рассматриваться как вязкая жидкость, то в качестве упрощенной модели такой системы контейнер можно считать твердым телом, несущим несколько прикрепленных к нему гармонических диссипативных осцилляторов. Состояние среды в контейнере в каждый момент времени неизвестно, поэтому фазовые состояния осцилляторов также считаются неизвестными. Таким образом, несущее тело испытывает не только неконтролируемое воздействие внешней среды, но и действие упругих сил со стороны осцилляторов, что существенно затрудняет управление.

Задача локального управления такой системой решена в [5]. Построено управление, приводящее несущее тело за конечное время в заданное состояние покоя и удерживающее его там (на поведение осцилляторов после остановки несущего тела условий не накладывалось). При этом предполагалось, что начальное состояние всей системы находится вблизи терминального положения, что влекло за собой малость возмущений, действующих на несущее тело со стороны осцилляторов. В изучаемой ниже постановке задачи предположение о близости начального и терминального состояний отсутствует, т.е. влияние осцилляторов на несущее тело может быть сколь угодно велико.

Задача управления твердым телом, несущим один диссипативный осциллятор, решена в [6].

Исследуемая ниже система представляет собой систему с дефицитом управлений, так как число ее степеней свободы превосходит размерность вектора управляющих сил. Используемый в данной работе для управления такой системой подход основан на методике, развитой в [7, 8].

1. Постановка задачи и уравнения движения. Рассмотрим движущееся по горизонтальной прямой под действием ограниченной управляющей силы и малого неконтролируемого возмущения твердое тело с присоединенными к нему двумя линейными диссипативными осцилляторами. Динамика такой системы подчиняется уравнениям

(1.1)

$\begin{gathered} {{m}_{0}}\ddot {\xi } = {{\kappa }_{1}}{{\varphi }_{1}} + {{\kappa }_{2}}{{\varphi }_{2}} + {{\gamma }_{1}}{{{\dot {\varphi }}}_{1}} + {{\gamma }_{2}}{{{\dot {\varphi }}}_{2}} + {{u}_{0}} + {{v}_{0}}, \\ {{m}_{1}}(\ddot {\xi } + {{{\ddot {\varphi }}}_{1}}) = - {{\kappa }_{1}}{{\varphi }_{1}} - {{\gamma }_{1}}{{{\dot {\varphi }}}_{1}}, \\ {{m}_{2}}(\ddot {\xi } + {{{\ddot {\varphi }}}_{2}}) = - {{\kappa }_{2}}{{\varphi }_{2}} - {{\gamma }_{2}}{{{\dot {\varphi }}}_{2}}. \\ \end{gathered} $

Здесь ξ – координата несущего тела на прямой, ${{m}_{0}}$ – масса тела, ${{m}_{i}}$ – массы осцилляторов, ${{\varphi }_{i}}$ – удлинение пружины i-го осциллятора, ${{\kappa }_{i}} > 0$ – жесткости пружин, ${{\gamma }_{i}} > 0$ – коэффициенты вязкого трения осцилляторов, $i = 1,2$.

Предполагается, что управляющая сила ${{u}_{0}}$ и возмущение ${{v}_{0}}$ удовлетворяют условию

(1.2)

$\left| {{{u}_{0}}} \right| \leqslant {{U}_{0}},\quad \left| {{{v}_{0}}} \right| \leqslant \rho {{U}_{0}},\quad 0 < \rho < 1.$

Перейдем к безразмерным переменным. С этой целью введем новое время

$\begin{gathered} \tau = \frac{{{{\kappa }_{1}}t}}{{{{\gamma }_{1}}}} \\ \end{gathered} $

и следующие обозначения:

$\begin{gathered} {{\mu }_{1}} = \frac{{{{m}_{0}} + {{m}_{1}}}}{{{{m}_{1}}}},\quad {{\mu }_{2}} = \frac{{{{m}_{0}} + {{m}_{2}}}}{{{{m}_{2}}}},\quad a = \frac{{\gamma _{1}^{2}}}{{{{m}_{0}}{{\kappa }_{1}}}},\quad \kappa = \frac{{{{\kappa }_{2}}}}{{{{\kappa }_{1}}}},\quad \gamma = \frac{{{{\gamma }_{2}}}}{{{{\gamma }_{1}}}} \\ \end{gathered} .$

Зададим вектор $x \in {{\mathbb{R}}^{6}}$ новых переменных:

$\begin{gathered} {{x}_{1}} = \frac{{\kappa _{1}^{2}{{m}_{0}}}}{{\gamma _{1}^{2}}}\xi ,\quad {{x}_{2}} = x_{1}^{'} = \frac{{{{\kappa }_{1}}{{m}_{0}}}}{{{{\gamma }_{1}}}}\dot {\xi }, \\ {{x}_{3}} = {{\kappa }_{1}}{{\varphi }_{1}},\quad {{x}_{4}} = x_{3}^{'} = {{\gamma }_{1}}{{{\dot {\varphi }}}_{1}}, \\ {{x}_{5}} = {{\kappa }_{1}}{{\varphi }_{2}},\quad {{x}_{6}} = x_{5}^{'} = {{\gamma }_{1}}{{{\dot {\varphi }}}_{2}}. \\ \end{gathered} $

Уравнения движения (1.1) примут вид

(1.3)

$\begin{gathered} x_{1}^{'} = {{x}_{2}},\quad x_{2}^{'} = {{x}_{3}} + {{x}_{4}} + \kappa {{x}_{5}} + \gamma {{x}_{6}} + {{u}_{0}} + {{v}_{0}}, \\ x_{3}^{'} = {{x}_{4}},\quad x_{4}^{'} = - a({{\mu }_{1}}({{x}_{3}} + {{x}_{4}}) + \kappa {{x}_{5}} + \gamma {{x}_{6}}) - a({{u}_{0}} + {{v}_{0}}), \\ x_{5}^{'} = {{x}_{6}},\quad x_{6}^{'} = - a(({{x}_{3}} + {{x}_{4}}) + {{\mu }_{2}}(\kappa {{x}_{5}} + \gamma {{x}_{6}})) - a({{u}_{0}} + {{v}_{0}}). \\ \end{gathered} $

Обозначая теперь производную по новому времени τ точкой, перепишем систему (1.3) в векторной форме

(1.4)

$\dot {x} = {{A}_{0}}x + {{B}_{0}}({{u}_{0}} + {{v}_{0}}).$

Здесь

$\begin{gathered} {{A}_{0}} = \left( {\begin{array}{*{20}{c}} 0&1&0&0&0&0 \\ 0&0&1&1&\kappa &\gamma \\ 0&0&0&1&0&0 \\ 0&0&{ - a{{\mu }_{1}}}&{ - a{{\mu }_{1}}}&{ - a\kappa }&{ - a\gamma } \\ 0&0&0&0&0&1 \\ 0&0&{ - a}&{ - a}&{ - a{{\mu }_{2}}\kappa }&{ - a{{\mu }_{2}}\gamma } \end{array}} \right),\quad {\text{ }}{{B}_{0}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \\ { - a} \\ 0 \\ { - a} \end{array}} \right) \\ \end{gathered} {\kern 1pt} {\kern 1pt} .$

Считается, что координата и скорость тележки в каждый момент времени известны, поэтому в системе (1.4) наблюдаемыми переменными являются компоненты x₁ и x₂, а уравнение для вектора выходных переменных $p \in {{\mathbb{R}}^{2}}$ имеет вид

$\begin{gathered} p = {{C}_{0}}x,\quad {{C}_{0}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&0&0&0 \end{array}} \right) \\ \end{gathered} .$

Будем предполагать, что параметры системы таковы, что пара $({{A}_{0}},{{B}_{0}})$ управляема, а пара $({{A}_{0}},{{C}_{0}})$ наблюдаема [9–11].

Задача. Построить ограниченное управление в форме обратной связи, т.е. как функцию наблюдаемых переменных x₁, x₂, которое остановит несущее тело в заданной точке прямой (не нарушая общности – в точке x₁ = 0) за конечное время для любых начальных состояний из некоторой ограниченной области фазового пространства $x \in {{\mathbb{R}}^{6}}$.

Процесс управления состоит из двух этапов. На первом этапе система приводится в малую окрестность начала координат фазового пространства $x \in {{\mathbb{R}}^{6}}$ с помощью управления, зависящего от всего фазового вектора x. Поскольку по условию задачи этот вектор неизвестен, то используется его приближенное значение, получаемое стандартными методами теории наблюдений линейных систем. Оказывается, что вдали от начала координат подстановка в управляющую функцию приближенных значений фазовых переменных вместо точных не оказывает существенного влияния на эффективность управления. В результате к концу первого этапа несущее тело приводится в окрестность терминального положения, а энергия колебаний осцилляторов становится достаточно малой.

На втором этапе рассматривается только первое уравнение системы (1.1), описывающее динамику несущего тела. Силы, действующие на несущее тело со стороны осцилляторов, становятся малыми по сравнению с управляющей силой, что позволяет остановить несущее тело в заданном положении.

2. Первый этап управления. Приведем систему (1.4) к более удобному для построения управления виду [12]. Поскольку пара $({{A}_{0}},{{B}_{0}})$ управляема, то, согласно критерию Калмана, матрица

${{F}_{0}} = ({{B}_{0}}\,\,{{A}_{0}}{{B}_{0}}\,\,\, \ldots \,\,A_{0}^{5}{{B}_{0}})$

обратима. Обозначим через f₀ последнюю строку матрицы $F_{0}^{{ - 1}}$ и составим построчно матрицу

$S = \left( {\begin{array}{*{20}{c}} {{{f}_{0}}} \\ {{{f}_{0}}{{A}_{0}}} \\ {{{f}_{0}}A_{0}^{2}} \\ \ldots \\ {{{f}_{0}}A_{0}^{5}} \end{array}} \right).$

Невырожденное линейное преобразование координат

$\begin{gathered} z = {{S}_{1}}Sx \\ \end{gathered} $

с диагональной матрицей ${{S}_{1}} = {\text{diag}}\{ {{( - 1)}^{i}}i!,\;i = 0,\; \ldots ,\;5\} $ приводит систему (1.4) к виду

(2.1)

$z = {{A}_{1}}z + B({{u}_{0}} + {{v}_{0}}),\quad {{A}_{1}} = \left( {\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}&{{{a}_{3}}}&{{{a}_{4}}}&0&0 \\ { - 1}&0&0&0&0&0 \\ 0&{ - 2}&0&0&0&0 \\ 0&0&{ - 3}&0&0&0 \\ 0&0&0&{ - 4}&0&0 \\ 0&0&0&0&{ - 5}&0 \end{array}} \right),\quad B = \left( \begin{gathered} 1 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right).$

Здесь

$\begin{gathered} {{a}_{1}} = - a\left( {{{\mu }_{1}} + \gamma {{\mu }_{2}}} \right),\quad {{a}_{2}} = a\left( {a\gamma \left( {{{\mu }_{1}}{{\mu }_{2}} - 1} \right) + {{\mu }_{1}} + \kappa {{\mu }_{2}}} \right), \\ {{a}_{3}} = - \frac{1}{2}{{a}^{2}}\left( {{{\mu }_{1}}{{\mu }_{2}} - 1} \right)(\gamma + \kappa ),\quad {{a}_{4}} = \frac{1}{6}{{a}^{2}}\kappa \left( {{{\mu }_{1}}{{\mu }_{2}} - 1} \right). \\ \end{gathered} $

Вектор наблюдаемых переменных теперь задается соотношением

$\begin{gathered} p = Cz,\quad C = {{C}_{0}}{{S}^{{ - 1}}}S_{1}^{{ - 1}} \\ \end{gathered} .$

Обозначим через a¹ верхнюю строку матрицы A₁ и введем новое управление

(2.2)

$\begin{gathered} u = {{u}_{0}} - ({{a}^{1}},z) \\ \end{gathered} $

(здесь и далее (⋅, ⋅) означает скалярное произведение). Тогда система (2.1) примет форму

(2.3)

$\dot {z} = Az + B(u + {{v}_{0}})$

где

$\begin{gathered} A = \left( {\begin{array}{*{20}{c}} 0&0&0& \ldots &0 \\ { - 1}&0&0& \ldots &0 \\ 0&{ - 2}&0& \ldots &0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0& \ldots &0&{ - 5}&0 \end{array}} \right) \\ \end{gathered} {\kern 1pt} {\kern 1pt} .$

Сформулируем вспомогательную задачу. Построить управление в форме обратной связи, т.е. как функцию u(z) всего фазового вектора z, которое удовлетворяет условию

(2.4)

${\text{|}}u(z){\text{|}} \leqslant {{U}_{1}},\quad {{U}_{1}} > 0$

и приводит систему (2.3) в окрестность начала координат фазового пространства $z \in {{\mathbb{R}}^{6}}$.

Заметим, что если ${{U}_{1}} < {{U}_{0}}$ и выполнено (2.4), то управление u₀ будет удовлетворять неравенству (1.2) в некоторой ограниченной области, содержащей начало координат.

Сформулируем закон управления, предложенный в [7, 8], который применяется на первом этапе и позволяет приводить всю систему, т.е. несущее тело и осцилляторы, в окрестность начала координат за конечное время, если фазовый вектор системы точно известен.

Введем в рассмотрение скалярную функцию $T(z)$, диагональные матрицы

$\delta (T) = {\text{diag}}\{ {{T}^{{ - 1}}},{{T}^{{ - 2}}}, \ldots ,{{T}^{{ - 6}}}\} ,\quad M = {\text{diag}}\{ - 1, - 2, \ldots , - 6\} ,$

положительно определенные матрицы R, Q и вектор $f \in {{\mathbb{R}}^{6}}$:

$\begin{gathered} {{R}_{{ij}}} = \frac{1}{{(i + j)(i + j - 1)}},\quad i,j = 1, \ldots ,6,\quad Q = {{R}^{{ - 1}}},\quad f = - \frac{1}{2}QB \\ \end{gathered} .$

Зададим функцию T(z) неявно уравнением

(2.5)

$\left( {Q\delta (T)z,\delta (T)z} \right) = d,\quad d > 0,\quad z \ne 0.$

Установлено [8], что уравнение (2.5) относительно T имеет единственное положительное решение для любого $z \in {{\mathbb{R}}^{6}}$, $z \ne 0$. Функция $T(z) > 0$ является аналитической, обладает свойствами

(2.6)

$\begin{gathered} \mathop {\lim }\limits_{\zeta \to 0} \,\mathop {\max }\limits_{|z| = \zeta } T(z) = 0, \\ \end{gathered} \quad \mathop {\lim }\limits_{\zeta \to \infty } \,\mathop {\min }\limits_{|z| = \zeta } T(z) = \infty ,$

может быть доопределена в нуле $T(0) = 0$ с сохранением непрерывности и служит функцией Ляпунова для системы (2.3).

Определим управляющую функцию формулой

(2.7)

$u(z) = (f,\delta (T)z).$

В [8] показано, что функция u(z) во всем фазовом пространстве подчиняется ограничению

${\text{|}}u(z){\text{|}} \leqslant \frac{1}{2}\sqrt {d{{Q}_{{11}}}} ,$

где Q₁₁ – левый верхний элемент матрицы Q. В частности, выбором постоянной d в уравнении (2.5) можно обеспечить выполнение условия (2.4).

В [8] доказано, что при ${{v}_{0}} \equiv 0$ для производной функции T в силу системы (2.3) справедливо равенство

$\dot {T} = - 1,$

из которого следует, что в отсутствие возмущений функция T(z) обращается в нуль через конечный промежуток времени, т.е. все траектории системы (2.3) приходят в начало координат за конечное время, причем время движения из точки z равно T(z).

Обозначим через q(t) приближенное значение фазового вектора z(t), способ вычисления которого описан ниже, и пусть

(2.8)

$r(t) = z(t) - q(t).$

Подставим в управление (2.7) вместо вектора z его оценку q. С учетом соотношения (2.2) получим

${{u}_{0}}(q) = {{u}_{0}}(z) + u(q) - u(z) + ({{a}^{1}},r).$

Положим

(2.9)

$v = {{v}_{0}} + {{v}_{1}} + {{v}_{2}},\quad {{v}_{1}} = u(q) - u(z),\quad ({{a}^{1}},z - q).$

Система (2.3) примет вид

(2.10)

$\dot {z} = Az + B(u(z) + v).$

Пусть

(2.11)

$y = \delta (T)z,\quad z \ne 0.$

Производная функции T в силу системы (2.10) удовлетворяет равенству

(2.12)

$\dot {T} = - \frac{{(Py,y) + 2v(QB,y)}}{{(Py,y)}},$

где отрицательно определенная матрица P задана выражением

$\begin{gathered} P = QM + MQ,\quad M = {\text{diag}}\{ - 1, - 2, \ldots , - 6\} \\ \end{gathered} .$

Из соотношения (2.12) вытекает следующее достаточное условие убывания функции T вдоль траекторий системы (2.10), управляемой с помощью (2.7):

(2.13)

$\sup {\text{|}}v{\text{|}} < \frac{1}{{2D}},\quad D = \mathop {\max }\limits_{(Qy,y) = d} \frac{{(QB,y)}}{{(Py,y)}}.$

Действительно, при выполнении данного условия имеет место неравенство

$\dot {T} \leqslant - \sigma ,\quad \sigma > 0,$

которое гарантирует убывание функции T до нуля за конечное время.

Оценим теперь $v$. Первое слагаемое ${{v}_{0}}$ в (2.9) ограничено в силу условия (1.2). Для оценки величины ${{v}_{1}}$ воспользуемся линейным приближением приращения управляющей функции u(z):

$\begin{gathered} {{v}_{1}}(z) = \left( {f,\delta (T(z - r))(z - r) - \delta (T(z)z} \right) \approx \left( {f,\;\frac{{2(Qy,\delta (T)r)}}{{(Py,y)}}My - \delta (T)r} \right) \\ \end{gathered} .$

Уравнение (2.5) с учетом соотношения (2.11) принимает вид

$(Qy,y) = d,$

откуда вытекают неравенства

$\frac{d}{{{{Q}_{ + }}}} \leqslant {{\left| y \right|}^{2}} \leqslant \frac{d}{{{{Q}_{ - }}}},$

где ${{Q}_{ + }},{{Q}_{ - }} > 0$ – максимальное и минимальное собственные числа положительно определенной матрицы Q. Принимая во внимание вид матрицы $\delta (T)$ и свойство (2.6) функции T(z), получаем, что при больших по модулю z величина ${{v}_{1}}(z)$ мала и стремится к нулю при $\left| z \right| \to \infty $, т.е. $\left| {{{v}_{1}}(z)} \right|$ тем меньше, чем дальше от начала координат находится фазовое состояние системы.

Из приведенного ниже соотношения (3.6) видно, что ошибка в определении текущего фазового состояния системы r(t) пропорциональна постоянной ρ, ограничивающей возмущения ${{v}_{0}}$ в условии (1.2). Следовательно, при малых значениях $\rho $ величина ${{v}_{2}}$ также мала.

Таким образом, условие (2.13), которое гарантирует убывание функции T(z) вдоль траектории системы (2.10), выполнено при достаточно больших z и малых $\rho $.

3. Оценка вектора фазового состояния. Изложенный выше закон управления требует знания текущего фазового состояния системы. Однако по условию задачи вектор фазовых переменных z(t) неизвестен, измерениям доступны лишь компоненты выходного вектора p(t). Вычислим приближенное значение q(t) вектора z(t) для фиксированного момента времени t.

Пусть [s, t] – интервал времени, на котором наблюдается вектор выходного сигнала $p(\theta )$, $\theta \in [s,t]$, системы (2.1), и $Z(\theta )$ – фундаментальная матрица решений однородной системы

$\begin{gathered} \dot {z} = {{A}_{1}}z \\ \end{gathered} ,$

нормированная в точке s, т.е. $Z(s) = I$, где I – единичная матрица. Тогда

(3.1)

$p(\theta ) = Cz(\theta ) = CZ(\theta )\left( {z(s) + \int\limits_s^\theta {{Z}^{{ - 1}}}(\tau )B({{u}_{0}}(\tau ) + {{v}_{0}}(\tau ))d\tau } \right).$

Положим

$H(\theta ) = CZ(\theta )$

и перепишем соотношение (3.1) в виде

$H(\theta )z(s) = p(\theta ) - H(\theta )\int\limits_s^\theta {{Z}^{{ - 1}}}(\tau )B({{u}_{0}}(\tau ) + {{v}_{0}}(\tau ))d\tau .$

Домножим обе части данного равенства на ${{H}^{{\rm T}}}(\theta )$ и проинтегрируем их на отрезке [s, t]. Получим

(3.2)

$\hat {H}(s)z(s) = \hat {p}(s) - \int\limits_s^t {{H}^{{\rm T}}}(\theta )H(\theta )\int\limits_s^\theta {{Z}^{{ - 1}}}(\tau )B({{u}_{0}}(\tau ) + {{v}_{0}}(\tau ))d\tau d\theta .$

Здесь использованы обозначения

$\begin{gathered} \hat {H}(s) = \int\limits_s^t {{H}^{{\rm T}}}(\theta )H(\theta )d\theta ,\quad \hat {p}(s) = \int\limits_s^t {{H}^{{\rm T}}}(\theta )p(\theta )d\theta \\ \end{gathered} .$

Соотношение (3.2) представляет собой уравнение для определения начальной точки z(s) наблюдаемого отрезка траектории. В силу наблюдаемости системы матрица $\hat {H}(s)$ обратима [10, 11], а уравнение (3.2) однозначно разрешимо относительно z(s).

В правой части уравнения (3.2) управляющая функция ${{u}_{0}}(t)$ считается заданной, поэтому в отсутствие возмущений вектор z(s) находится однозначно. Затем с помощью интегрирования системы (2.1) может быть восстановлена вся траектория, в том числе вычислено точное значение вектора z(t). Поскольку возмущение ${{v}_{0}}$ присутствует, то для определения приближенных значений фазовых координат будем использовать систему

(3.3)

$\dot {q} = {{A}_{1}}q + B{{u}_{0}},$

которая совпадает с системой (2.2) при ${{v}_{0}} \equiv 0$. Рассмотрим отрезок траектории системы (3.3), для которого интеграл от выходного вектора $p(\theta )$ на интервале наблюдения [s, t] принимает то же значение $\hat {p}(s)$. Начальная точка q(s) этого отрезка удовлетворяет уравнению

$\hat {H}(s){{q}_{t}}(s) = \hat {p}(s) - \int\limits_s^t {{H}^{{\rm T}}}(\theta )H(\theta )\int\limits_s^\theta {{Z}^{{ - 1}}}(\tau )B{{u}_{0}}(\tau )d\tau d\theta $

(индекс t в обозначениях ${{q}_{t}}(s)$ указывает, что начальная точка рассматриваемого участка траектории зависит от правого конца интервала наблюдения). Таким образом, если для определения начальной точки участка траектории вместо системы (2.1) использовать систему (3.3), игнорируя наличие возмущений, то погрешность окажется равной вектору

(3.4)

$z(s) - {{q}_{t}}(s) = - {{\hat {H}}^{{ - 1}}}(s)\int\limits_s^t {{H}^{{\rm T}}}(\theta )H(\theta )\int\limits_s^\theta {{Z}^{{ - 1}}}(\tau )B{{v}_{0}}(\tau )d\tau d\theta .$

Оценим теперь ошибку в определении вектора фазового состояния в момент времени t, если вместо системы (2.1) использовать систему (3.3). С учетом (2.8) получим соотношение

(3.5)

$r(t) = Z(t)\left( {z(s) - {{q}_{t}}(s) + \int\limits_s^t {{Z}^{{ - 1}}}(\tau )B{{v}_{0}}(\tau )d\tau } \right),$

в которое нужно подставить выражение (3.4) для $z(s) - {{q}_{t}}(s)$.

Будем считать, что интервал времени [s, t], по наблюдениям на котором определяется текущее состояние системы z(t), может быть сколь угодно мал без потери точности вычислений. Используя соотношение (3.5), можно найти асимптотическое поведение при $s \to t$ вектора $r(t)$, максимального по модулю для всех возмущений ${{v}_{0}}$, удовлетворяющих ограничению (1.2). Тем самым в любой момент времени t может быть найдено приближенное выражение для максимальной по модулю погрешности определения вектора $z(t)$.

Пример. Пусть рассматриваемая система обладает следующим набором значений физических параметров:

(3.6)

${{m}_{0}} = 5,\quad {{m}_{1}} = 1,\quad {{m}_{2}} = 2,\quad {{\kappa }_{1}} = {{\kappa }_{2}} = 1,\quad {{\gamma }_{1}} = {{\gamma }_{2}} = 1.$

Нетрудно проверить, что в этом случае пара $({{A}_{0}},{{B}_{0}})$ управляема, а пара $({{A}_{0}},{{C}_{0}})$ наблюдаема.

С помощью изложенного выше метода оценки текущего фазового состояния системы можно показать, что при данных значениях параметров максимальный по модулю для всех допустимых возмущений вектор ошибки определения фазового состояния в каждый момент времени приблизительно равен

$r \approx \left( {\begin{array}{*{20}{c}} {17.5} \\ {12.5} \\ { - 25} \\ { - 165} \\ { - 60} \\ {5100} \\ {} \end{array}} \right)\rho .$

4. Второй этап движения. Положим

$\begin{gathered} g(t,{{\varphi }_{1}},{{\varphi }_{2}},{{{\dot {\varphi }}}_{1}},{{{\dot {\varphi }}}_{2}}) = {{v}_{0}} + {{\kappa }_{1}}{{\varphi }_{1}} + {{\kappa }_{2}}{{\varphi }_{2}} + {{\gamma }_{1}}{{{\dot {\varphi }}}_{1}} + {{\gamma }_{2}}{{{\dot {\varphi }}}_{2}} \\ \end{gathered} $

и рассмотрим первое уравнение системы (1.1), описывающее динамику несущего тела:

(4.1)

$\begin{gathered} {{m}_{0}}\ddot {\xi } = {{u}_{0}} + g \\ \end{gathered} .$

Применим управление вида

(4.2)

$\begin{gathered} {{u}_{0}}(\xi ,\dot {\xi }) = - \frac{{6{{m}_{0}}\xi }}{{T_{1}^{2}(\xi ,\dot {\xi })}} - \frac{{3{{m}_{0}}\dot {\xi }}}{{{{T}_{1}}(\xi ,\dot {\xi })}} \\ \end{gathered} ,$

где функция ${{T}_{1}}(\xi ,\dot {\xi })$ задается неявно уравнением

$\begin{gathered} dT_{1}^{4} - 6{{{\dot {\xi }}}^{2}}T_{1}^{2} - 24\xi \dot {\xi }{{T}_{1}} - 36{{\xi }^{2}} = 0,\quad d > 0 \\ \end{gathered} .$

Как и выше, это уравнение относительно ${{T}_{1}}$ имеет единственное положительное решение во всем фазовом пространстве $(\xi ,\dot {\xi }) \in {{\mathbb{R}}^{2}}$, кроме нуля, причем функция ${{T}_{1}}$ может быть доопределена в нуле ${{T}_{1}}(0,0) = 0$ с сохранением непрерывности. Выбор параметра d в виде

$\begin{gathered} d = \frac{{2U_{0}^{2}}}{{3m_{0}^{2}}} \\ \end{gathered} $

обеспечивает выполнение условия (1.2). В [3] показано, что если выполнено соотношение

(4.3)

${\text{|}}g(t,{{\varphi }_{1}},{{\varphi }_{2}},{{\dot {\varphi }}_{1}},{{\dot {\varphi }}_{2}}){\text{|}} < \frac{{(3 - \sqrt 3 ){{U}_{0}}}}{{6{{m}_{0}}}},$

то существует такое $\sigma > 0$, что производная функции T₁ в силу уравнений (4.1), (4.2) удовлетворяет неравенству

(4.4)

$\begin{gathered} {{{\dot {T}}}_{1}} < - \sigma \\ \end{gathered} .$

Следовательно, при выполнении условия (4.3) через конечный промежуток времени функция ${{T}_{1}}$ обратится в нуль, а несущее тело остановится в заданном положении.

Покажем, что неравенство (4.3) выполнено вдоль траекторий системы (1.1), начинающихся в некоторой окрестности нуля фазового пространства $\xi ,\dot {\xi },{{\varphi }_{1}},{{\dot {\varphi }}_{1}},{{\varphi }_{2}},{{\dot {\varphi }}_{2}}$.

Для системы (1.1) введем в рассмотрение функцию Ляпунова

$\begin{gathered} V(\xi ,\dot {\xi },{{\varphi }_{1}},{{{\dot {\varphi }}}_{1}},{{\varphi }_{2}},{{{\dot {\varphi }}}_{2}}) = {{T}_{1}}(\xi ,\dot {\xi }) + \frac{1}{2}\sum\limits_{i = 1,2} ({{\kappa }_{i}}\varphi _{i}^{2} + {{m}_{i}}{{(\dot {\xi } + {{{\dot {\varphi }}}_{i}})}^{2}}) \\ \end{gathered} .$

Эта функция положительно определена, а ее производная в силу системы (1.1) при использовании управления (4.2) равна

$\begin{gathered} \dot {V} = {{{\dot {T}}}_{1}} - \sum\limits_{i = 1,2} ({{\gamma }_{i}}\dot {\varphi }_{i}^{2} + ({{\kappa }_{i}}{{\varphi }_{i}} + {{\gamma }_{i}}{{{\dot {\varphi }}}_{i}})\dot {\xi }) \\ \end{gathered} .$

При достаточно малых $\rho $ существует такое ${{V}_{0}} > 0$, что в окрестности

$W = \{ (\xi ,\dot {\xi },{{\varphi }_{1}},{{\dot {\varphi }}_{1}},{{\varphi }_{2}},{{\dot {\varphi }}_{2}}) \in {{\mathbb{R}}^{6}}{\text{:}}\;V(\xi ,\dot {\xi },{{\varphi }_{1}},{{\dot {\varphi }}_{1}},{{\varphi }_{2}},{{\dot {\varphi }}_{2}}) < {{V}_{0}}\} $

имеют место неравенства (4.3) и

$\left| {\sum\limits_{i = 1,2} ({{\kappa }_{i}}{{\varphi }_{i}} + {{\gamma }_{i}}{{{\dot {\varphi }}}_{i}})\dot {\xi }} \right| < \sigma .$

Следовательно, в этой окрестности $\dot {V} < 0$ и траектории ее не покидают. Тогда в соответствии с (4.4) функция T₁ вдоль траекторий через конечный промежуток времени обратится в нуль.

Из проведенных рассуждений можно заключить, что если параметр $\rho $ таков, что вне области W выполнено неравенство (2.13), то управление (2.7), применяемое вне W, и управление (4.2), применяемое внутри W, остановят несущее тело в начале координат за конечное время.

5. Результаты численного моделирования. Для иллюстрации работы предложенного алгоритма управления было проведено компьютерное моделирование динамики системы с набором физических параметров (3.6) и постоянной $\rho = 0.1$ в ограничении (1.2). Начальные состояния несущего тела и осцилляторов выбраны следующими:

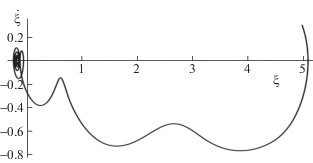
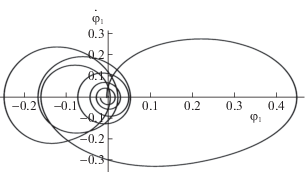
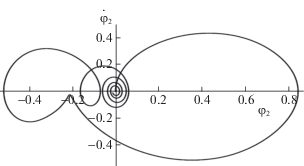
${{\xi }^{0}} = 5,\quad {{\dot {\xi }}^{0}} = 0.3,\quad \varphi _{1}^{0} = \dot {\varphi }_{1}^{0} = \varphi _{2}^{0} = \dot {\varphi }_{2}^{0} = 0.$

На рис. 1–3 изображены фазовые траектории несущего тела и осцилляторов на первом этапе движения. Продолжительность этапа оказалась равной ${{t}_{1}} = 25.7$. В момент окончания первого этапа и начала второго фазовые состояния несущего тела и осцилляторов принимали значения

$\xi = - 0.168,\quad \dot {\xi } = 0.018,\quad {{\varphi }_{1}} = - 0.015,\quad {{\dot {\varphi }}_{1}} = - 0.005,\quad {{\varphi }_{2}} = - 0.012,\quad {{\dot {\varphi }}_{2}} = - 0.013.$

Рис. 1.

Первый этап. Несущее тело

Рис. 2.

Первый этап. Первый осциллятор

Рис. 3.

Первый этап. Второй осциллятор

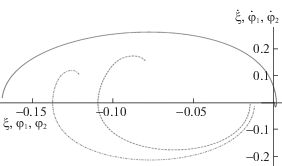
На рис. 4 представлены фазовые траектории несущего тела (сплошная линия) и осцилляторов на втором этапе движения. Продолжительность второго этапа оказалась равной ${{t}_{2}} = 1.1$.

Рис. 4.

Второй этап. Несущее тело и осцилляторы

Заключение. Проведенный анализ и численное моделирование показывают, что используемый на первом этапе закон управления в форме обратной связи оказывается нечувствительным по отношению к неточности определения текущего фазового состояния системы, если это состояние находится далеко от начала координат. При достаточно малом уровне возмущений это позволяет к окончанию первого этапа привести несущее тело в окрестность терминального положения, а энергию колебаний осцилляторов сделать малой. На втором этапе, когда возмущения, действующие со стороны осцилляторов, малы, управление, зависящее только от координаты и скорости несущего тела, останавливает тело в заданном положении за конечное время.

Список литературы

Акуленко Л.Д., Болотник Н.Н., Борисов А.E., Гавриков А.А., Емельянов Г.А. Управление кажущимся ускорением твердого тела, закрепленного в двухстепенном подвесе на подвижном основании // Изв. РАН. ТиСУ. 2012. № 3. С. 3–12.
Акуленко Л.Д., Болотник Н.Н., Борисов А.E., Гавриков А.А., Емельянов Г.А. Квазиоптимальное управление поворотом твердого тела вокруг неподвижной оси с учетом трения // Изв. РАН. ТиСУ. 2015. № 3. С. 3–21.
Ананьевский И.М., Ишханян Т.А. Управление поворотной платформой на подвижном основании в присутствии возмущений // Изв. РАН. ТиСУ. 2016. № 3. С. 154–162.
Ананьевский И.М., Ишханян Т.А. Управление двухкаскадной электромеханической системой, подверженной возмущениям // ПММ. 2016. Т. 80. Вып. 5. С. 515–524.
Ананьевский И.М., Ишханян Т.А. Управление платформой с осцилляторами в присутствии сухого трения // Тр. ИММ УрО РАН. 2017. Т. 23. № 1. С. 20–26.
Ananievski I. Control of a Cart with Viscoelastic Links Under Uncertainty // Cybernetics and Physics. 2017. V. 6. № 4. P. 160–165.
Ананьевский И.М., Анохин Н.В., Овсеевич А.И. Синтез ограниченного управления линейными динамическими системами с помощью общей функции Ляпунова // ДАН. 2010. Т. 434. № 3. С. 319–323.
Ovseevich A. A Local Feedback Control Bringing a Linear System to Equilibrium // JOTA. 2015. V. 165. № 2. P. 532–544.
Kalman R.E., Falb P.L., Arbib M.A. Topics in Mathematical System Theory. N.Y.: McGraw-Hill, 1969. 358 p.
Красовский Н.Н. Теория управления движением. М.: Наука, 1968. 476 с.
Sontag E.D. Mathematical Control Theory: Deterministic Finite-dimensional Systems. N.Y.: Springer, 1998. 544 p.
Brunovsky P.A. A Classification of Linear Controllable Systems // Kybernetika. 1970. V. 6. № 3. P. 173–188.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал