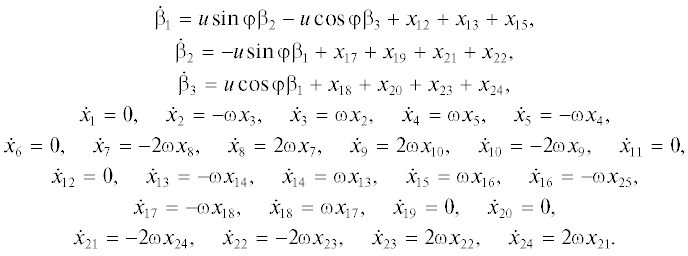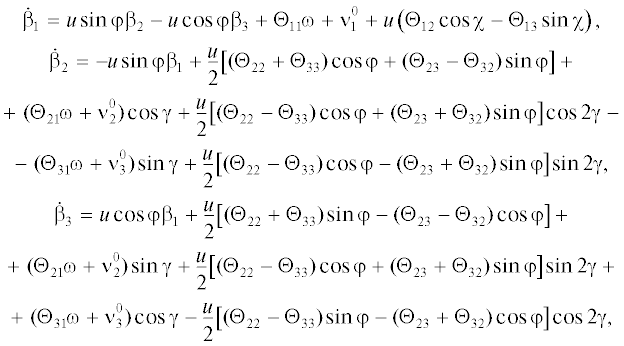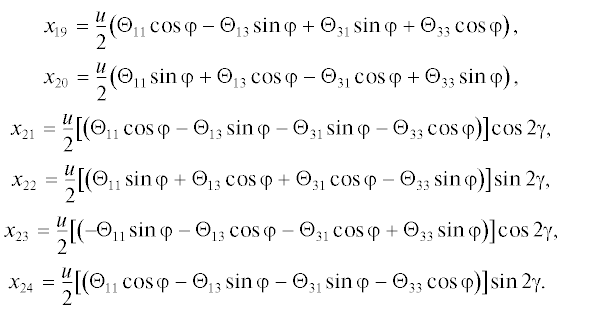Известия РАН. Теория и системы управления, 2019, № 1, стр. 3-12

Введение. Многие задачи механики и техники, в частности задачи динамики и управления движущимися объектами, приводят к необходимости исследования нестационарных нелинейных систем и их линеаризованных моделей. Одним из основных методов изучения линейных нестационарных систем (ЛНС), как однородных, так и содержащих управления и наблюдения, является метод их преобразования к стационарным системам. ЛНС, допускающие такое преобразование, называют приводимыми. Понятие приводимой системы, впервые введенное А.М. Ляпуновым для линейных однородных нестационарных систем [1], было распространено на линейные нестационарные системы, содержащие управления и наблюдения в [2, 3]. Там же были изложены основы теории приводимости ЛНС с управлением и наблюдением, сформулированы условия приводимости таких систем.

В данной работе описываются некоторые новые классы ЛНС с управлением и наблюдением, которые допускают приведение путем конструктивного преобразования к стационарным системам большего порядка, чем исходная система. Рассматривается задача калибровки бескарданной инерциальной навигационной системы (БИНС), иллюстрирующая эффективность предложенного подхода к анализу наблюдаемости ЛНС указанного класса.

1. Приводимые линейные нестационарные системы с управлением и наблюдением. Напомним сначала некоторые результаты по приводимости ЛНС. Рассмотрим ЛНС

где x – n-мерный вектор состояния системы, $u$ – k-мерный вектор управляющих воздействий, $\sigma $ – l-мерный вектор измерений; $A$ – постоянная (n × n)-матрица, B(t) и C(t) – матрицы (n × k) и (l × n) соответственно, зависящие от времени.

Условия приводимости ЛНC (1.1) к стационарной системе того же порядка представлены в [2, 3]. Если условия приводимости к системе того же порядка не выполняются, то при определенных условиях ЛНC (1.1) может быть преобразована в стационарную систему большего порядка [2, 3].

Рассмотрим систему с наблюдением, но без управления:

Пусть матрица C(t) представляется в виде линейной комбинации постоянных (l × n)-матриц $\quad{{C}_{1}},{{C}_{2}},...,{{C}_{r}}$:

Будем полагать, что скалярные функции ${{\alpha }_{i}}(t),i = 1,2,\;...\;r$, таковы, что можно ввести m-мерный вектор f(t), r компонент которого – функции ${{\alpha }_{i}}(t)$, а остальные $(m - r)$ компонент выбраны так, чтобы поведение вектора f(t) описывалось некоторой линейной системой дифференциальных уравнений с постоянными коэффициентами:

Это означает, что к выделенному таким образом классу функций ${{\alpha }_{i}}(t)$, входящих в матрицу C(t), относятся такие функции, как полиномы, экспоненты, синусы и косинусы различных частот, а также всевозможные линейные комбинации этих функций.

Если представление (1.3), (1.4) имеет место, то система (1.2) при помощи преобразования

E_n – единичная (n × n)-матрица, приводится к полностью стационарной системе [2, 3]

Здесь $ \otimes $ означает кронекеровское произведение матриц [4], O – нулевые матрицы соответствующих размеров.

Для систем, нестационарных по управлению,

где матрица B(t) представима в виде, аналогичном (1.3), (1.4):

Преобразование

приводит систему (1.7) к стационарной системе размерности $mn$:

Возможность приведения к стационарным системам ЛНС второго порядка, нестационарных по наблюдению и управлению, рассмотрена в [5, 6].

2. Системы специального вида с наблюдением. Рассмотрим нестационарную систему более общего, чем (1.2), вида

Здесь ${{x}^{{(j)}}}$ – ${{n}_{j}}$-мерные векторы состояния системы ($j = 1,2$), ${{A}_{{jj}}}$ – постоянные $({{n}_{j}} \times {{n}_{j}})$-матрицы, $(l \times {{n}_{2}})$- матрица ${{C}_{1}}(t)$ может быть записана в виде (1.3), (1.4), ${{C}_{0}}$ – постоянная $(l \times {{n}_{1}})$-матрица, а $({{n}_{1}} \times {{n}_{2}})$-матрица ${{A}_{{12}}}(t)$ представляется аналогично матрице ${{C}_{1}}(t)$:

Функции ${{\gamma }_{j}}(t),i = 1,2,\;...,\;q,$ являются функциями, принадлежащими совокупности функций ${{f}_{1}}(t),\;...,\;{{f}_{m}}(t)$. Введем новые переменные аналогично формулам (1.5):

Дифференцируя выражение (2.3), получим

По свойствам кронекеровского произведения $F(t){{A}_{{22}}} = ({{E}_{m}} \otimes {{A}_{{22}}})F(t)$. Тогда

Выражение ${{A}_{{12}}}(t){{x}^{{(2)}}}$ при помощи соотношений (2.2) и (2.3) приводится к виду

где $\mathop {{{G}_{{12}}}}\limits_{({{n}_{1}} \times m{{n}_{2}})} = [\begin{array}{*{20}{c}} {\mathop {{{D}_{1}}}\limits_{({{n}_{1}} \times {{n}_{2}})} }&{...}&{{{D}_{r}}}&O&{...}&O \end{array}]$.

Измерение записывается следующим образом:

где $\mathop {{{\Gamma }_{1}}}\limits_{(l \times m{{n}_{2}})} = [\begin{array}{*{20}{c}} {\mathop {{{C}_{1}}}\limits_{(l \times {{n}_{2}})} }&{...}&{{{C}_{r}}}&O&{...}&O \end{array}]$.

Таким образом, система (2.1) преобразуется в стационарную систему

В частном случае, если A₂₂ = 0, система (2.1) принимает вид

Пример 1.

Здесь функции ${{f}_{i}}(t)$ имеют вид ${{f}_{1}}(t) = \alpha (t) = \cos \omega t,\;{\kern 1pt} {{f}_{2}}(t) = \gamma (t) = \sin \omega t$ и подчиняются уравнению

Преобразование ${{y}_{1}} = {{x}_{2}}\sin \omega t,{{y}_{2}} = {{x}_{2}}\cos \omega t$ приводит систему (2.6) к стационарной системе (2.4):

Матрица наблюдаемости стационарной системы (2.7) имеет вид

Определитель этой матрицы $\det N = \omega {{C}_{0}}(C_{1}^{2}{{({{a}_{{22}}} - {{a}_{{11}}})}^{2}} + {{\left( {{{C}_{0}}{{a}_{{12}}} - {{C}_{1}}\omega } \right)}^{2}})$. Система (2.7) ненаблюдаема, если

Отметим, что этот же результат получается при применении критерия Hautus [7] или критерия наблюдаемости для нестационарных систем [8, 9].

Для стационарной системы (2.7) можно аналитически построить алгоритм оценивания с постоянными коэффициентами, в то время как для исходной системы (2.1) это сделать не удастся.

3. Системы специального вида с управлением. Рассмотрим нестационарную систему вида

Здесь ${{x}^{{(j)}}}$ – ${{n}_{j}}$-мерные векторы состояния системы ($j = 1,2$), ${{A}_{{jj}}}$ – постоянные $({{n}_{j}} \times {{n}_{j}})$-матрицы, представляется в виде (1.3), (1.4), B₀ – постоянные $({{n}_{1}} \times k)$-матрицы, а $({{n}_{2}} \times k)$-матрица $\quad\quad{{B}_{1}}(t)$ и $({{n}_{2}} \times {{n}_{1}})$-матрица A₂₁(t) записываются в виде, аналогичном (1.3) и (2.2):

Скалярные функции ${{\beta }_{i}}(t)$ и ${{\delta }_{i}}(t)$ являются функциями, принадлежащими совокупности функций ${{f}_{1}}(t),\;...,\;{{f}_{m}}(t)$, удовлетворяющих системе (1.4).

Введем замену переменных

Тогда

В новых переменных система (3.1) становится стационарной и имеет вид

Здесь ${{R}_{{22}}} = ({{E}_{m}} \otimes {{A}_{{22}}}) - ({{S}^{T}} \otimes {{E}_{{{{n}_{2}}}}})$.

Пример 2.

Преобразование ${{x}_{2}} = {{y}_{1}}\cos \omega t + {{y}_{2}}\sin \omega t$ приводит систему (3.4) к стационарной системе вида (3.3):

Замечание 1. Следует иметь в виду, что начальные условия для исходной системы (3.4) заданы, но определение начальных условий для расширенной системы (3.5) имеет некоторый произвол – в данном случае ${{y}_{1}}(0) = {{x}_{2}}(0)$, ${{y}_{2}}(0)$ – свободно. Значением ${{y}_{2}}(0)$ можно распоряжаться в зависимости от конкретной задачи управления. Подобная ситуация имеет место во всех задачах синтеза управления, решаемых путем приведения к стационарным системам большей размерности, например для систем вида (3.3).

Условие управляемости системы (3.5) имеет вид

Для стационарной системы (3.5) при наличии свойства управляемости закон управления можно построить в виде

выбирая коэффициенты ${{k}_{j}}$ так, чтобы замкнутая этим управлением система (3.5) была асимптотически устойчивой.

Для того, чтобы управление u можно было вводить непосредственно в нестационарную систему (3.4), следует перейти от переменных ${{x}_{1}},{{y}_{1}},{{y}_{2}}$ к переменным ${{x}_{1}},{{x}_{2}},x_{2}^{'}$, введя [2, 3] дополнительную переменную $x_{2}^{'}$ по формуле

Тогда ${{y}_{1}} = {{x}_{2}}\cos \omega t - x_{2}^{'}\sin \omega t,\quad {{y}_{2}} = {{x}_{2}}\sin \omega t + x_{2}^{'}\cos \omega t$. Переменная $x_{2}^{'}$ удовлетворяет уравнению

Переменные $x = {{({{x}_{1}},{{x}_{2}},x_{2}^{'})}^{{\text{T}}}}$ подчиняются системе уравнений

Интересно отметить, что матрица A(t) удовлетворяет матричному дифференциальному уравнению

и однородная система, соответствующая системе (3.8), приводима путем преобразования x = $[\exp (Dt)]y$ к стационарной системе [3, 10]. При этом неоднородная нестационарная система (3.8) становится полностью стационарной системе (3.5).

Управление, вводимое в систему (3.4), (3.7) в соответствии с выражением (3.6), имеет вид

Замечание 2. Для систем (2.4) и (3.3) удобно применять критерии наблюдаемости и управляемости Хаутуса [7], имеющие здесь вид

Матрицы ${{G}_{{22}}},{{R}_{{22}}}$ запишем как

Критерий (3.9) следует проверять только для значений $\lambda $, являющихся корнями характеристического уравнения $\det \left( {({{A}_{{11}}} - \lambda {{E}_{{{{n}_{1}}}}})({{G}_{{22}}} - \lambda {{E}_{{m{{n}_{2}}}}})} \right) = 0$, а критерий (3.10) – для корней уравнения $\det \,({{R}_{{22}}} - \lambda {{E}_{{m{{n}_{2}}}}}) = 0$.

Собственные значения матриц ${{G}_{{22}}},{{R}_{{22}}}$ равны соответственно ${{\nu }_{{ij}}} = {{\lambda }_{i}} + {{\mu }_{j}}$ и ${{\nu }_{{ij}}} = {{\lambda }_{i}} - {{\mu }_{j}}$, где ${{\lambda }_{i}}$ – собственные значения матрицы ${{A}_{{22}}}$, а ${{\mu }_{j}}$ – собственные значения матрицы S. Матрицы ${{A}_{{11}}},{{A}_{{22}}},S$ имеют порядок меньший, чем ${{n}_{1}} + m{{n}_{2}}$, и их собственные значения легче определить. Поэтому в данном случае критерий Хаутуса предпочтительнее известного критерия Калмана [11].

В частности, если A₂₂ = 0, собственные значения матриц G₂₂ и R₂₂ будут ${{\mu }_{j}}$ и $ - {{\mu }_{j}}$, $j = 1,2,\;...,\;m$.

4. Калибровка бескарданной инерциальной навигационной системы. Рассмотрим задачу калибровки БИНС при помощи одностепенного стенда с горизонтальной осью вращения [12–14]. В [12] была предложена процедура калибровки, состоящая из трех этапов. На каждом этапе осуществляется вращение БИНС на поворотном стенде вокруг одной из фиксированных осей. Поэтому в модели системы явным образом возникает нестационарность, вызванная изменением ориентации.

4.1. Уравнения ошибок измерений. Согласно [12–14], уравнение, описывающее динамику ошибок ориентации, имеет вид

Здесь $\beta = {{\left[ {\begin{array}{*{20}{c}} {{{\beta }_{1}}}&{{{\beta }_{2}}}&{{{\beta }_{3}}} \end{array}} \right]}^{{\text{T}}}}$ – вектор малого поворота приборного трехгранника $Oz$ относительно географического Ox; L – матрица, задающая поворот стенда; $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$ – компоненты вектора погрешностей нулей, $\Theta = \left[ {{{\Theta }_{{ij}}}} \right]$, ${{\Theta }_{{ij}}}$ – погрешности неортогональности осей чувствительности датчиков угловых скоростей, ${{\Theta }_{{ii}}}$ – погрешности масштабных коэффициентов;

${{u}_{1}},{{u}_{2}},{{u}_{3}}$ – компоненты вектора угловой скорости вращения Земли в проекциях на оси географического трехгранника Ox; вектор угловой скорости стенда ${{\Omega }_{z}} = {{\left[ {\begin{array}{*{20}{c}} {{{\Omega }_{1}}}&{{{\Omega }_{2}}}&{{{\Omega }_{3}}} \end{array}} \right]}^{{\text{T}}}}$ в проекциях на оси приборного трехгранника: ${{\Omega }_{1}} = \omega $ – величина угловой скорости вращения стенда, Ω₂ = $ = u{\text{cos}}\varphi ,{{\Omega }_{3}} = u{\text{sin}}\varphi $, $u$ – величина угловой скорости вращения Земли, $\varphi $ – географическая широта нахождения стенда.

В качестве измерений используется информация о векторе удельной силы ${{f}_{z}}{\text{/}}g$, доставляемая ньютонометрами. Соответствующее уравнение измерений в проекциях на оси географического трехгранника имеет вид [12]

Здесь $\varepsilon _{1}^{0},\varepsilon _{2}^{0},\varepsilon _{3}^{0}$ – погрешности нулей, матрица $\Gamma $ погрешностей масштабов и неортогональности осей чувствительности ньютонометров имеет вид [12]

4.2. Первый этап калибровки. На первом этапе матрица $L$ имеет вид

В скалярной форме уравнение (4.1) и измерение (4.2) имеют вид ($\chi = \gamma - \varphi $)

Согласно методике, изложенной выше, введем новые переменные:

В переменных (4.5) уравнения (4.3) и измерения (4.4) имеют вид:

Для анализа наблюдаемости системы (4.6), (4.7) рассмотрим сначала измерение σ₃. Введем наблюдаемые комбинации z_i путем последовательного дифференцирования σ₃:

Учитывая формулы (4.5), имеем следующие наблюдаемые переменные:

Далее, аналогично рассматривая измерения σ₁ и σ₂, получим наблюдаемые комбинации:

Учитывая формулы (4.5), из (4.8) и (4.9), получим 16 следующих наблюдаемых комбинаций исходных переменных:

4.3. Второй этап калибровки. На втором этапе матрица $L$ имеет вид

В этом случае уравнение (4.1) и измерение (4.2) представляются следующим образом:

Для системы (4.11), (4.12) можно провести ту же процедуру перехода к стационарной системе и выделения наблюдаемых комбинаций, при этом получатся 16 других наблюдаемых комбинаций исходных переменных. Однако, учитывая результаты первого этапа, можно далее рассматривать следующие модифицированные измерения:

Введем новые переменные:

Анализ полученной стационарной системы позволяет получить следующие наблюдаемые комбинации исходных приборных погрешностей:

В результате проведенных двух этапов калибровки при объединении наблюдаемых комбинаций приборных погрешностей в совокупностях (4.10) и (4.14) остаются неизвестными ${{\Gamma }_{{21}}},{{\Theta }_{{21}}},\nu _{1}^{0}$.

4.4. Третий этап калибровки. На третьем этапе матрица L имеет вид

В этом случае уравнения измерений запишем как

С учетом выражений (4.10), (4.14) можно ввести модифицированные измерения

Это означает, что из выражения для ${{\bar {\sigma }}_{3}}$ можно получить ${{\Gamma }_{{21}}}$, затем из (4.10) и (4.14) – величины ${{\Theta }_{{21}}}$ и $\nu _{1}^{0}$. Таким образом определяются все приборные погрешности.

Заключение. Предложена методика исследования наблюдаемости и управляемости для нестационарных линейных многомерных систем определенного класса, основанная на конструктивном приведении их к стационарным системам большего порядка, чем исходные. Анализ наблюдаемости и управляемости для стационарных систем существенно проще. В качестве приложения рассмотрена задача калибровки бескарданной инерциальной системы, где проведено исчерпывающее аналитическое исследование наблюдаемости.