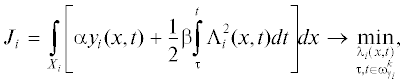Известия РАН. Теория и системы управления, 2019, № 1, стр. 31-41
ОПТИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОГО ПОИСКА ОБЪЕКТОВ ДЛЯ МОДЕЛИ РАСПРЕДЕЛЕННОГО ПУАССОНОВСКОГО ПОТОКА ИХ ПОЯВЛЕНИЯ
В. В. Хуторцев *
* E-mail: hvv.56@mail.ru
Поступила в редакцию 21.03.2017
После доработки 21.08.2018
Аннотация
Сформированы математические модели оптимизируемых фиктивных динамических систем для вероятностей нахождения необнаруженных объектов наблюдения в различных секторах зоны поиска. Сформулировано условие инвариантности управления поиском, позволяющее объединять текущий и терминальный критерии качества. Определена процедура синтеза закона оптимального управления последовательно-параллельным поиском, проведен анализ ее свойств. Приведен пример.
Введение. Поиск объектов наблюдения (ОН) является одной из важных задач, стоящих перед системами, которые осуществляют контроль космического или воздушного пространства, локацию земной поверхности, поверхности океана и т.д. [1–4]. От качества ее решения во многом зависит эффективность работы информационно-измерительных систем (ИИС), связанная со своевременным и достоверным обнаружением ОН, которые появляются в зоне их обзора.
Управление наблюдениями при поиске объектов составляет одну из разновидностей общего класса задач планирования наблюдений [5–8].
Существующие методы управления поиском могут быть условно разделены на две группы. Методы первой группы основаны на предположении о том, что ОН, количество которых известно заранее и в отношении которых осуществляется поиск, уже находятся в зоне поиска, однако еще не найдены [1–4]. Такой подход является достаточно ограниченным. Он не может использоваться для решения задач, характеризуемых высокой степенью априорной неопределенности относительно как количества находящихся в зоне поиска объектов наблюдения, так и динамики их появления, например, задач контроля воздушного движения или космического пространства.
Вторая группа методов [9–11] свободна от указанных ограничений, поскольку базируется на использовании закономерностей случайных потоков, положенных в основу модели появления ОН в зоне поиска.
Для второй группы методов предложены две процедуры решения задачи поиска.
Первая разработана для ИИС, у которых размеры области обзора не меньше размеров зоны поиска. Для закона управления поиском осуществлена оптимизация в текущем времени или текущая оптимизация [9], приводящая, например, к закону перераспределения во времени излучаемой мощности между диаграммами направленности многолучевых антенных систем для активных ИИС или закону изменения во времени параметров, регулирующих ширину диаграмм направленности различных лучей для пассивных ИИС [12]. Такое управление может быть интерпретировано как управление параллельным поиском, поскольку управляющая функция или интенсивность поиска зависит как от времени, так и от пространственных координат, и может быть реализовано параллельно во всей области обзора.
Вторая процедура ориентирована на наиболее часто встречающиеся на практике поисковые системы, у которых размеры области обзора меньше, чем размеры зоны поиска. Она предполагает секторизацию [13] зоны поиска или разбиение зоны поиска на несколько секторов, размеры которых определяются размерами области обзора ИИС, и последовательный их опрос [11]. Порядок такого опроса оптимизируется по терминальному критерию качества. При этом закон управления поиском внутри каждого сектора полагается равномерным. Повысить качество второй процедуры возможно за счет рационального перераспределения энергетического потенциала ИИС внутри каждого из секторов зоны поиска за счет применения принципов текущей оптимизации, использованной при реализации процедуры первого типа.
В связи с этим представляется актуальным объединение подходов, предложенных в [9, 11], и рассмотрение вопроса определения последовательно-параллельных поисковых стратегий, которые были бы, с одной стороны, ориентированы на возможность последовательного просмотра нескольких секторов зоны поиска [11], а с другой – обеспечивали бы при каждом обращении к соответствующему сектору оптимальное решение задачи по критерию качества текущей оптимизации управления параллельным поиском [9].
1. Анализ потоковых закономерностей появления объектов наблюдения. Определим зону поиска $\overline X \in {{R}^{n}}$, в которой ОН появляются в соответствии с закономерностями распределенного случайного потока $\varphi (x,t)$ с плотностью интенсивности $\nu (x,t)$. Интенсивность интегрального потока
в $\overline X $ в целом составляетВероятность появления в $\overline X $ очередного ОН за интервал времени Δt (Δt – малая величина) определяется соотношением $\nu (t)\Delta t + O(\Delta t)$, где $O(\Delta t)$ – имеет порядок малости ${{(\Delta t)}^{2}}$ и выше.
Предположим, что технические характеристики ИИС таковы, что область обзора X, внутри которой ИИС способна обеспечить поиск, меньше, чем зона поиска $\overline X $, т.е. $X \in \overline X $.
Разобьем зону поиска $\overline X $ на $G$ секторов контроля Xi, соизмеримых с областью обзора ИИС X, таких, что
(1.1)
${{X}_{i}} \in \overline X ,\quad i = \overline {1,G} ,\quad {{X}_{i}} \cap {{X}_{j}} = 0;\quad i,j = \overline {1,G} ,\quad i \ne j,\quad \bigcup\limits_{i = 1}^G {{{X}_{i}} = } \overline X .$Для каждой из них определим соответствующий индикатор:
(1.2)
${{\delta }_{i}}(x) = \left\{ {\begin{array}{*{20}{c}} {1,\quad x \in {{X}_{i}},} \\ {0,\quad x \notin {{X}_{i}}.} \end{array}} \right.$Пусть ИИС осуществляет последовательный контроль секторов ${{X}_{i}},i = \overline {1,G} $, на интервале времени $\omega \in \left[ {0,T} \right]$. Определим для каждой из секторов контроля закон управления поиском
где(1.4)
${{\lambda }_{i}}(x,t)\left\{ {\begin{array}{*{20}{c}} { \geqslant 0,\quad x \in {{X}_{i}},} \\ { = 0,\quad x \notin {{X}_{i}},} \end{array}} \right.$– непрерывные на $\omega \times {{X}_{i}}$ функции, задающие интенсивность поиска или структуру закона управления поиском внутри соответствующих секторов;
(1.5)
${{\gamma }_{i}}(t) \in \Gamma = \left[ {0,1} \right]\;\;\forall t,\;t \in \omega ,\quad i = \overline {1,G} $– управления, характеризующие временную программу обращение ИИС к секторам контроля.
Для ${{\gamma }_{i}}(t),i = \overline {1,G} $, выполняется ограничение
Соотношение (1.6) определяет невозможность одновременного контроля ИИС более чем в одном секторе.
Предположим, что для $\overline X $ справедливым является условие [9], отражающее закономерности функционирования большинства существующих ИИС и связанные с существенным превышением интенсивности поисковых усилий таких систем над интенсивностью потока ОН. С учетом структуры (1.3) указанное условие может быть интерпретировано следующим образом:
(1.7)
$\frac{{\bar {\nu }}}{{\overline \lambda }} \ll 1,\quad \bar {\nu } = \mathop {\max }\limits_{t \in \omega } \nu (t),\quad \overline \lambda = \mathop {\max }\limits_{x \in X,\,t \in \omega } \left\{ {\sum\limits_{i = 1}^G {{{\gamma }_{i}}(t){{\lambda }_{i}}(x,t)} } \right\}.$С учетом ограничения (1.7) приближенно можно полагать [9], что вероятность обнаружения информационной системой объекта в $\overline X $ за интервал времени Δt (Δt – малая величина) при условии, что ОН находится в точке $x \in {{X}_{i}}$ и ${{\gamma }_{i}}(t) = 1$, определяется соотношением ${{\lambda }_{i}}(x,t)\Delta t + O(\Delta t).$
Выполнение условия (1.7) предоставляет возможность приближенного описания процессов появления и обнаружения ОН в области поиска с помощью модели дискретного случайного процесса с двумя состояниями [9, 14, 15].
2. Постановка задачи. Введем для зоны поиска $\overline X $ ненормированную вероятностную меру $y(x,t)$, определяющую вероятность наличия в ней необнаруженного ОН:
и разобьем интервал $\left[ {0,T} \right]$ на локальные подынтервалы оптимизации поиска:(2.2)
${{\omega }_{k}} = \left[ {{{t}_{k}},{{t}_{{k + 1}}}} \right],\quad k = \overline {0,(K - 1)} ,$Будем полагать $y(x,t)$ функцией, непрерывно дифференцируемой по $t$ на ${{\omega }_{k}}$ и кусочно-непрерывной по $x$ на $\overline X $.
В соответствии с (1.7) эволюция во времени ненормированной меры $y(x,t)$ при $t \in {{\omega }_{k}}$ для зоны поиска $\overline X $ определяется соотношением [9]
(2.3)
$\begin{gathered} \frac{{\partial y(x,t)}}{{\partial t}} = - y(x,t)\left( {\sum\limits_{i = 1}^G {{{\Lambda }_{i}}(x,t)} + \nu (t)} \right) + \nu (x,t), \\ y(x,{{t}_{k}}) = {{y}_{k}}(x),\quad {{\left. {{{y}_{k}}(x)} \right|}_{{x \notin \overline X }}} = 0, \\ {{y}_{k}}(x) = \left\{ \begin{gathered} 0,{\text{ е с л и }}{\kern 1pt} {\text{о ч е р е д н о й О Н н а }}{{\omega }_{{k - 1}}}\;{\text{в }}\overline X \;{\text{о б н а р у ж е н ; }} \hfill \\ {{y}^{{k - 1}}}(x,{{t}_{k}}),{\text{е с л и }}{\kern 1pt} {\text{о ч е р е д н о й О Н н а }}{{\omega }_{{k - 1}}}\;{\text{в }}\overline X \;{\text{н е о б н а р у ж е н ;}} \hfill \\ \end{gathered} \right. \\ \end{gathered} $Представим (2.3) для каждой из подобластей поиска с учетом (1.2). В результате получим
(2.4)
$\frac{{\partial {{y}_{i}}(x,t)}}{{\partial t}} = - {{y}_{i}}(x,t)({{\Lambda }_{i}}(x,t) + \nu (t)) + {{\nu }_{i}}(x,t),\quad {{y}_{i}}(x,{{t}_{k}}) = {{y}_{{ik}}}(x),$(2.5)
${{y}_{i}}(x,t) = y(x,t){{\delta }_{i}}(x),\quad {{\nu }_{i}}(x,t) = \nu (x,t){{\delta }_{i}}(x)$;Нетрудно показать, что с учетом (1.4), (2.5)
Предположим, что внутри ${{\omega }_{k}}$ в случае обращения ИИС к какому-либо из секторов Xi, $i = \overline {1,G} $, поиск в нем осуществляется в соответствии с критерием качества текущей оптимизации управления параллельным поиском [9]:
где $\alpha ,\;\beta $ – весовые коэффициенты; $t - \tau \ll 1$; $\omega _{{{{\gamma }_{i}}}}^{k}:\{ t = \arg [{{\gamma }_{i}}(t) = 1]\} ,\omega _{{{{\gamma }_{i}}}}^{k} \in {{\omega }_{k}}$.Критерий (2.7) включает две составляющие. Первая определяет вероятность нахождения в Xi необнаруженного ОН, вторая характеризует аналог элементарной энергии закона управления поиском.
Определение. Условно-оптимальным управлением параллельным поиском в Xi будем называть управление $\lambda _{i}^{{{\text{о п т }}}}(x,t)$, оптимальное по критерию (2.7) при условии, что ${{\gamma }_{i}}(t) = 1.$
Утверждение 1. Условно-оптимальное управление параллельным поиском инвариантно к временной программе обращения ИИС к сектору Xi и определяется соотношением
Доказательство утверждения 1 приведено в Приложении.
Проведем математическую постановку задачи.
Закон управления поиском (2.8) (закон изменения интенсивности поисковых усилий ИИС) для одного из секторов Xi, выбранного в соответствии с планом поиска
из зоны обзора поисковой системы, может определять закон перераспределения излучаемой мощности между диаграммами направленности многолучевых антенных систем для активных ИИС или закон изменения параметров, регулирующих ширину диаграмм направленности различных лучей для пассивных ИИС.С учетом (2.8) математическая модель эволюции во времени ненормированной меры $y_{i}^{{{\text{о п т }}}}(x,t)$ в подобласти контроля Xi приобретает вид
(2.10)
$\begin{gathered} \frac{{\partial y_{i}^{{{\text{о п т }}}}(x,t)}}{{\partial t}} = - \frac{\alpha }{\beta }{{\gamma }_{i}}(t){{(y_{i}^{{{\text{о п т }}}}(x,t))}^{2}} - y_{i}^{{{\text{о п т }}}}(x,t)\nu (t) + {{\nu }_{i}}(x,t), \\ {\text{ }}y_{i}^{{{\text{о п т }}}}(x,{{t}_{k}}) = y_{{ik}}^{{{\text{о п т }}}}(x),\quad x \in {{X}_{i}},\quad i = \overline {1,G} . \\ \end{gathered} $Отметим, что результат решения системы дифференциальных уравнений в частных производных (2.10) зависит от управлений ${{\gamma }_{i}}(t),\;i = \overline {1,G} .$ В свою очередь указанный результат в соответствии с (2.1), (2.6) однозначно определяет вероятность $p({{t}_{{k + 1}}})$ наличия в $\overline X $ необнаруженного ОН в конце интервала поиска ${{\omega }_{k}}$.
Таким образом, необходимо найти такую систему функций ${{\gamma }_{i}}(t),\;i = \overline {1,G} ,$ удовлетворяющих ограничениям (1.5), (1.6) и образующих план поиска (2.9), которая бы обеспечивала минимум функционала качества:
Иными словами, план поиска (2.9) должен удовлетворять терминальному критерию качества
(2.11)
${{J}_{{\text{т }}}} = p({{t}_{{k + 1}}}) = \sum\limits_{i = 1}^G {\int\limits_{{{X}_{i}}} {y_{i}^{{{\text{о п т }}}}(x,{{t}_{{k + 1}}})dx} \to \mathop {\min }\limits_\Pi } .$Поставим задачу для математических моделей фиктивных динамических систем (2.9), описываемых дифференциальными уравнениями в частных производных относительно ненормированных вероятностных мер $y_{i}^{{{\text{о п т }}}}(x,t)$, в условиях ограничения (1.6) определить на интервале ωk план поиска (2.9), оптимальный в смысле критерия (2.11).
Приведенная математическая формулировка задачи соответствует объединению подходов, рассмотренных в [9, 11], и определению поисковых стратегий последовательно-параллельного типа, которые, с одной стороны, ориентированы на возможность последовательного оптимального в смысле критерия (2.11) просмотра нескольких секторов контроля зоны поиска, а с другой – обеспечивают при каждом обращении к соответствующему сектору оптимальное решение задачи по критерию качества (2.7) текущей оптимизации управления параллельным поиском.
3. Синтез оптимального плана поиска. Дифференциальные уравнения в частных производных (2.10) могут быть интерпретированы как распределенные по x дифференциальные уравнения Риккати. Воспользуемся их аналитическими свойствами. Применительно к (2.10) справедливо следующее утверждение.
Утверждение 2. Для непрерывных по x на Xi и непрерывно дифференцируемых по t на ωk функций ${{s}_{i}}(x,t),\;{\kern 1pt} {{q}_{i}}(x,t)$, таких, что
(3.1)
${{\left. {{{s}_{i}}(x,t)} \right|}_{{x \notin {{X}_{i}}}}} = 0,\quad {{\left. {{{q}_{i}}(x,t)} \right|}_{{x \notin {{X}_{i}}}}} = 0,$(3.2)
$\begin{gathered} \frac{{\partial {{s}_{i}}(x,t)}}{{\partial t}} = a(t){{s}_{i}}(x,t) + {{\gamma }_{i}}(t)b{{q}_{i}}(x,t), \\ \frac{{\partial {{q}_{i}}(x,t)}}{{\partial t}} = {{c}_{i}}(x,t){{s}_{i}}(x,t) - a(t){{q}_{i}}(x,t),\quad t \in {{\omega }_{k}},\quad x \in {{X}_{i}}, \\ \end{gathered} $(3.3)
$y_{i}^{{{\text{о п т }}}}(x,{{t}_{k}}){{s}_{i}}(x,{{t}_{k}}) - {{q}_{i}}(x,{{t}_{k}}) = 0,\quad x \in {{X}_{i}},$(3.4)
$y_{i}^{{{\text{о п т }}}}(x,t){{s}_{i}}(x,t) = {{q}_{i}}(x,t),\quad \forall x,x \in {{X}_{i}},\quad \forall t,t \in {{\omega }_{k}}.$Доказательство утверждения приведено в Приложении.
Определим критерий качества (2.11) в терминах (3.2). Для этого в тождествах $y_{i}^{{{\text{о п т }}}}(x,{{t}_{{k + 1}}}){{s}_{i}}(x,{{t}_{{k + 1}}})$ = ${{q}_{i}}(x,{{t}_{{k + 1}}})$, $\forall x,x \in {{X}_{i}}$, $i = \overline {1,G} ,$ зададим значение произвольных функций
Тогда критерий (2.11) приобретает вид
(3.6)
${{J}_{{\text{т }}}} = \sum\limits_{i = 1}^G {{{p}_{i}}} ({{t}_{{k + 1}}}) = \sum\limits_{i = 1}^G {\int\limits_{{{X}_{i}}} {{{q}_{i}}(x,{{t}_{{k + 1}}})dx} \to \mathop {\min }\limits_\Pi } .$Совокупность фиктивных динамических систем, описываемых двухточечными краевыми задачами (ДТКЗ) (3.2), (3.3), (3.5) для $i = \overline {1,G} $, ограничения (1.6) и критерия качества (3.6) составляют эквивалентную оптимизационную задачу для определения плана поиска для ИИС.
В соответствии с принципом максимума запишем гамильтониан
(3.7)
$\begin{gathered} {\rm H} = \sum\limits_{i = 1}^G {\int\limits_{{{X}_{i}}} {\{ {{\psi }_{{si}}}(x,t)[a(t){{s}_{i}}(x,t) + {{\gamma }_{i}}(t)b{{q}_{i}}(x,t)]} } + \\ + \;{{\psi }_{{qi}}}(x,t)[{{c}_{i}}(x,t){{s}_{i}}(x,t) - a(t){{q}_{i}}(x,t)]\} dx, \\ \end{gathered} $Найдем из (3.7) программные функции, задающие последовательность обращения ИИС к секторам:
(3.8)
$\frac{{\partial {\rm H}}}{{\partial {{\gamma }_{i}}}} = {{M}_{i}}(t) = b\int\limits_{{{X}_{i}}} {{{\psi }_{{si}}}(x,t){{q}_{i}}(x,t)} dx,\quad i = \overline {1,G} .$Таким образом, решающее правило, отвечающее условию максимума гамильтониана, приобретает вид
(3.9)
$\begin{gathered} {{\gamma }_{i}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad {\text{е с л и }}\quad {{M}_{i}}(t) \geqslant \overline M (t),} \\ {0,\quad {\text{е с л и }}\quad {{M}_{i}}(t) < \overline M (t),} \end{array}} \right. \\ t \in {{\omega }_{k}},\quad i = \overline {1,G} , \\ \end{gathered} $Уравнения для сопряженных переменных определяются соотношениями [5, 16]
(3.10)
$\begin{gathered} \frac{{\partial {{\psi }_{{si}}}(x,t)}}{{\partial t}} = - \frac{{\partial {\rm H}}}{{\partial {{s}_{i}}}} = - a(t){{\psi }_{{si}}}(x,t) - {{c}_{i}}(x,t){{\psi }_{{qi}}}(x,t), \\ \frac{{\partial {{\psi }_{{qi}}}(x,t)}}{{\partial t}} = - \frac{{\partial {\rm H}}}{{\partial {{q}_{i}}}} = - {{\gamma }_{i}}(t)b{{\psi }_{{si}}}(x,t) + a(t){{\psi }_{{qi}}}(x,t), \\ t \in {{\omega }_{k}},\quad x \in {{X}_{i}},\quad i = \overline {1,G} . \\ \end{gathered} $По аналогии с [5] можно показать, что ${{\psi }_{{qi}}}(x,t) = - {{s}_{i}}(x,t),{{\psi }_{{si}}}(x,t) = {{q}_{i}}(x,t)$. Тогда, пренебрегая константой b в (3.8), для программных функций получим
В соответствии с [5] определение оптимального закона поиска может быть проведено на основе принципа частичного обновления плана [17] с учетом распределенного по x характера полученных исходных моделей. Соответствующая процедура является итерационной и включает следующие этапы.
Этап 1. Задание начального плана поиска ${{\Pi }^{0}}{\text{:}}\,\{ \gamma _{i}^{0}(t) \in \Gamma ,i = \overline {1,G} \} $.
Этап 2. Решение ДТКЗ (3.2), (3.3), (3.5) для каждого из секторов ${{X}_{i}},i = \overline {1,G} $, и определение зависимостей $q_{i}^{0}(x,t),t \in {{\omega }_{k}}$.
Этап 3. Расчет по ним в соответствии с (3.11) программных функций
Этап 4. Определение из (3.9) переходного плана поиска Π01 : $\{ \gamma _{i}^{{01}}(t) \in \Gamma ,i = \overline {1,G} ,t \in {{\omega }_{k}}\} $.
Этап 5. Формирование закона поиска на основе принципа частичного обновления плана ${{\Pi }^{1}} = \Pi _{{{{\varepsilon }_{0}}}}^{{01}} \cup \Pi _{{1 - {{\varepsilon }_{0}}}}^{0}$, где $0 < {{\varepsilon }_{0}} < 1$ – параметр, характеризующий степень обновления плана на первом шаге итерационной процедуры. Требования к значениям ${{\varepsilon }_{0}}$ определены в [5].
Далее процедура повторяется с соответствующей заменой индексов.
Практическая реализация рассмотренной процедуры возможна на основе перехода в секторах ${{X}_{i}},i = \overline {1,G} $, к дискретному базису. Пусть для секторов поиска определим сетки равноотстоящих узлов ${{x}_{{iu}}} \in {{X}_{i}},u = \overline {1,U} $, где $U$ полагается одинаковым для всех подобластей поиска с шагом, обеспечивающим требуемую точность приближенного представления интегральных соотношений в (3.6), (3.11). Тогда уравнение (2.10) для каждого сектора ${{X}_{i}},i = \overline {1,G} $, может быть приближенно представлено с помощью системы обыкновенных дифференциальных уравнений Риккати:
(3.12)
$\begin{gathered} \frac{{dy_{{iu}}^{{{\text{о п т }}}}(t)}}{{dt}} = - \frac{\alpha }{\beta }{{\gamma }_{i}}(t){{(y_{{iu}}^{{{\text{о п т }}}}(t))}^{2}} - y_{{iu}}^{{{\text{о п т }}}}(t)\nu (t) + {{\nu }_{{iu}}}(t), \\ y_{{iu}}^{{{\text{о п т }}}}({{t}_{k}}) = y_{{iuk}}^{{{\text{о п т }}}},\quad t \in {{\omega }_{k}},\quad u = \overline {1,U} , \\ \end{gathered} $Уравнениям (3.12) могут быть поставлены в соответствие двухточечные краевые задачи, аналогичные (3.2), (3.3), (3.5):
(3.13)
$\begin{gathered} \frac{{d{{s}_{{iu}}}(t)}}{{dt}} = a(t){{s}_{{iu}}}(t) + {{\gamma }_{i}}(t)b{{q}_{{iu}}}(t), \\ \frac{{d{{q}_{{iu}}}(t)}}{{dt}} = {{c}_{{iu}}}(t){{s}_{{iu}}}(t) - a(t){{q}_{{iu}}}(t),\quad t \in {{\omega }_{k}},\quad u = \overline {1,U} , \\ \end{gathered} $(3.14)
$\begin{gathered} y_{i}^{{{\text{о п т }}}}({{x}_{u}},{{t}_{k}}){{s}_{{iu}}}({{t}_{k}}) - {{q}_{{iu}}}({{t}_{k}}) = 0, \\ {{s}_{{iu}}}({{t}_{{k + 1}}}) = 1,\quad u = \overline {1,U} . \\ \end{gathered} $Критерий качества (2.11) в дискретном базисе определяется соотношением
(3.15)
${{J}_{{\text{т }}}} = \sum\limits_{i = 1}^G {\sum\limits_{u = 1}^U {{{q}_{{iu}}}({{t}_{{k + 1}}})} \to \mathop {\min }\limits_\Pi } .$Для программных функций (3.11) получим
Формирование субоптимального (с учетом введенного дискретного базиса) закона поиска может быть проведено в соответствии с ранее рассмотренной итерационной процедурой, примененной к моделям (3.13), (3.14). Указанные модели могут иметь высокую размерность, вместе с тем их структура аналогична структуре моделей, использовавшихся при оптимизации наблюдений, например в [5–7]. Таким образом, для базирующейся на них процедуры поиска законов управления наблюдениями справедливы приведенные в [5] условия сходимости, в том числе релаксационной, а необходимые условия оптимальности, определяемые из принципа максимума, являются в том числе и достаточными [5, 18].
Необходимо отметить, что структура математической модели (3.12) эволюции во времени ненормированной вероятностной меры в приведенной задаче не может быть сведена к уравнению Бернулли ни при каких условиях, что влечет за собой необходимость интегрировании (3.13) на основе фундаментальных матриц.
Рассмотрим достаточно часто встречающийся случай, когда ИИС может обращаться на ${{\omega }_{k}}$ только к одной из подобластей контроля ${{X}_{i}},i = \overline {1,G} $. Указанное условие порождает дополнительные к (1.6) ограничения на управляющие функции:
(3.17)
$\int\limits_{{{\omega }_{k}}} {{{\gamma }_{i}}(t)dt \in {{\Gamma }_{h}} = \{ 0,h\} } ,\quad i = \overline {1,G} ,\quad k = \overline {0,(K - 1)} .$Решение оптимизационной задачи в этом случае осуществляется путем последовательного обращения к подобластям ${{X}_{i}},i = \overline {1,G} $, при $k = 0,1,\;...$ и не требует реализации итерационной процедуры определения закона управления поиском. Покажем это.
Рассмотрим системы уравнений (3.13) для $i = \overline {1,G} $. Каждой из них могут быть поставлены в соответствие две фундаментальные матрицы для ${{\gamma }_{i}}(t) = 0$ и для ${{\gamma }_{i}}(t) = 1$, описываемые уравнениями
(3.18)
$\begin{gathered} \frac{d}{{dt}}{{\Lambda }_{{iu}}} = {{A}_{{iu}}}{{\Lambda }_{{iu}}},\quad \frac{d}{{dt}}{{\Lambda }_{{iu\gamma }}} = {{A}_{{iu\gamma }}}{{\Lambda }_{{iu\gamma }}},\quad t \in {{\omega }_{k}}, \\ {{\Lambda }_{{iu}}}({{t}_{k}}) = {{\Lambda }_{{iu\gamma }}}({{t}_{k}}) = E,\quad u = \overline {1,U} , \\ \end{gathered} $(3.19)
${{\Lambda }_{{iu}}} = \left[ {\begin{array}{*{20}{c}} {\lambda _{{iu}}^{{ss}}}&{\lambda _{{iu}}^{{sq}}} \\ {\lambda _{{iu}}^{{qs}}}&{\lambda _{{iu}}^{{qq}}} \end{array}} \right];\quad {{\Lambda }_{{iu\gamma }}} = \left[ {\begin{array}{*{20}{c}} {\lambda _{{iu\gamma }}^{{ss}}}&{\lambda _{{iu\gamma }}^{{sq}}} \\ {\lambda _{{iu\gamma }}^{{qs}}}&{\lambda _{{iu\gamma }}^{{qq}}} \end{array}} \right];$По результатам решения (3.18) с учетом (3.14) могут быть сформированы значения ${{q}_{{iu}}}({{t}_{{k + 1}}})$, $q_{{iu}}^{\gamma }({{t}_{{k + 1}}})$, определяемые соотношениями соответственно
(3.20)
$\begin{gathered} {{q}_{{iu}}}({{t}_{{k + 1}}}) = \frac{{\lambda _{{iu}}^{{qs}}({{t}_{{k + 1}}}) + \lambda _{{iu}}^{{qq}}({{t}_{{k + 1}}}){{y}_{{i{\text{у }}u}}}({{t}_{k}})}}{{\lambda _{{iu}}^{{ss}}({{t}_{{k + 1}}}) + \lambda _{{iu}}^{{sq}}({{t}_{{k + 1}}}){{y}_{{i{\text{у }}u}}}({{t}_{k}})}}, \\ q_{{iu}}^{\gamma }({{t}_{{k + 1}}}) = \frac{{\lambda _{{iu\gamma }}^{{qs}}({{t}_{{k + 1}}}) + \lambda _{{iu\gamma }}^{{qq}}({{t}_{{k + 1}}}){{y}_{{i{\text{у }}u}}}({{t}_{k}})}}{{\lambda _{{iu\gamma }}^{{ss}}({{t}_{{k + 1}}}) + \lambda _{{iu\gamma }}^{{sq}}({{t}_{{k + 1}}}){{y}_{{i{\text{у }}u}}}({{t}_{k}})}}, \\ \end{gathered} $Таких решений будет $2UG$. Тогда для значений целевой функции критерия (3.15) получим
(3.21)
${{J}_{{{\text{т }}i}}} = \sum\limits_{u = 1}^U {q_{{iu}}^{\gamma }({{t}_{{k + 1}}})} \sum\limits_{j = 1j \ne i}^G {\sum\limits_{u = 1}^U {{{q}_{{iu}}}({{t}_{{k + 1}}})} } .$Значение номера сектора, к которому необходимо обращаться ИИС на ${{\omega }_{k}}$, определяется из соотношения
Если на ${{\omega }_{k}}$ ИИС обнаружила ОН, то ${{y}_{{i{\text{у }}u}}}({{t}_{{k + 1}}}) = 0$, если же нет, то
(3.23)
$\begin{gathered} y_{{i*u}}^{{{\text{о п т }}}}({{t}_{{k + 1}}}) = q_{{i*u}}^{\gamma }({{t}_{{k + 1}}}),\quad y_{{ju}}^{{{\text{о п т }}}}({{t}_{{k + 1}}}) = {{q}_{{ju}}}({{t}_{{k + 1}}}), \\ u = \overline {1,U} ,\quad j = \overline {1,G} ,\quad j \ne i{\text{*}}. \\ \end{gathered} $Условия (3.23) являются исходными для решения задачи на ${{\omega }_{{k + 1}}}$.
4. Пример. Пример опишем в условиях ограничений (3.17) для ωρ, $\rho = k,\;...,\;k + 8$. Рассмотрим вначале ${{\omega }_{k}}$. Пусть заданы два сектора поиска ${{X}_{1}},{{X}_{2}}$, для которых
(4.1)
${{\nu }_{i}}(x,t) = {{\nu }_{i}} = {\text{const}};\quad \nu (t) = \nu = У ;\quad \mu ({{X}_{i}}) = 2,\quad i = 1,2,$(4.2)
$\begin{gathered} \frac{{d{{s}_{i}}(t)}}{{dt}} = a{{s}_{i}}(t) + {{\gamma }_{i}}(t)b{{q}_{i}}(t), \\ \frac{{d{{q}_{i}}(t)}}{{dt}} = {{c}_{i}}{{s}_{i}}(t) - a{{q}_{i}}(t),\quad t \in {{\omega }_{k}}. \\ \end{gathered} $Будем полагать, что очередной ОН обнаружен на ${{\omega }_{{k - 1}}}$, следовательно
(4.3)
$y_{i}^{{{\text{о п т }}}}(x,{{t}_{k}}) = 0,\quad {{q}_{i}}({{t}_{k}}) = 0,\quad {{s}_{i}}({{t}_{{k + 1}}}) = 1.$Целевая функция критерия качества (3.15) может быть представлена в виде
или в терминах (3.21):(4.5)
${{J}_{{{\text{т 1}}}}} = q_{1}^{\gamma }({{t}_{{k + 1}}}) + {{q}_{2}}({{t}_{{k + 1}}}),\quad {{J}_{{{\text{т 2}}}}} = {{q}_{1}}({{t}_{{k + 1}}}) + q_{2}^{\gamma }({{t}_{{k + 1}}}).$Для (3.19) из (4.2) получим
(4.6)
${{\Lambda }_{{i\gamma }}} = \left[ {\begin{array}{*{20}{c}} {\frac{{a + {{w}_{i}}}}{{{{c}_{i}}}}{{e}^{{2(t - {{t}_{k}}){{w}_{i}}}}} - \frac{{a - {{w}_{i}}}}{{{{c}_{i}}}}}&{\frac{b}{{{{c}_{i}}}}({{e}^{{2(t - {{t}_{k}}){{w}_{i}}}}} - 1)} \\ {{{e}^{{2(t - {{t}_{k}}){{w}_{i}}}}} - 1}&{ - \frac{{a - {{w}_{i}}}}{{{{c}_{i}}}}{{e}^{{2(t - {{t}_{k}}){{w}_{i}}}}} + \frac{{a + {{w}_{i}}}}{{{{c}_{i}}}}} \end{array}} \right]\frac{{{{c}_{i}}}}{{2{{w}_{i}}}}{{e}^{{ - (t - {{t}_{k}}){{w}_{i}}}}},$(4.7)
${{\Lambda }_{i}} = \left[ {\begin{array}{*{20}{c}} {{{e}^{{a(t - {{t}_{k}})}}}}&0 \\ {\frac{{{{c}_{i}}}}{{2a}}({{e}^{{a(t - {{t}_{k}})}}} - {{e}^{{ - a(t - {{t}_{k}})}}})}&{{{e}^{{ - a(t - {{t}_{k}})}}}} \end{array}} \right],$(4.8)
$i_{{k + 1}}^{*} = 1,\quad i_{{k + 2}}^{*} = 1,\quad i_{{k + 3}}^{*} = 2,\quad i_{{k + 4}}^{*} = 1,\quad i_{{k + 5}}^{*} = 1,\quad i_{{k + 6}}^{*} = 1,\quad i_{{k + 7}}^{*} = 2,\quad i_{{k + 8}}^{*} = 1.$Более частое обращение к первому сектору поиска связано с тем, что плотность интенсивности появления ОН в ней превышает аналогичный показатель для X2 (${{c}_{1}} > {{c}_{2}}$) более чем в 2 раза.
На рисунке 1 приведен график зависимости целевой функции $J{\text{*}}$ критерия (3.21) от номера $\rho $ локального интервала оптимизации (кривая 1) при оптимальной стратегии поиска (4.8).
Рис. 1.
Графики зависимостей целевой функции от номера локального интервала оптимизации при оптимальной (кривая 1) и неоптимальной (кривая 2) стратегиях поиска
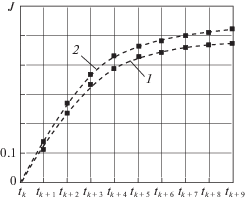
Первоначальный рост представленной зависимости обусловлен ростом вероятности появления в ${{X}_{1}},\;{{X}_{2}}$ очередного объекта наблюдения. Ее установившееся значение связано с взаимной компенсацией факторов, определяемых, с одной стороны, интенсивностью потока ОН, а с другой – поисковыми усилиями ИИС. Кривая 2 характеризует значения целевой функции $\overline J $ в случае выбора на каждом интервале оптимизации неоптимального решения. Средний относительный выигрыш
Необходимо отметить, что если в процессе реализации стратегии поиска (4.8) на каком-либо локальном интервале оптимизации $k + \varsigma ,\varsigma = \overline {0,8} ,$ очередной ОН будет обнаружен, то формирование последующего плана наблюдений осуществляется, исходя из начальных условий $y_{i}^{{{\text{о п т }}}}(x,{{t}_{{k + \varsigma + 1}}}) = 0;{{q}_{i}}({{t}_{{k + \varsigma + 1}}})$ = 0, ${{s}_{i}}({{t}_{{k + \varsigma + 2}}})$ = 1.
Заключение. Рассмотренный подход ориентирован на ИИС, размер области обзора у которых меньше, чем размер зоны поиска. Связанная с указанным обстоятельством необходимость секторизации зоны поиска привела к последовательно-параллельной структуре поисковых стратегий.
Использование предложенного подхода дает возможность осуществлять рациональное перераспределение поисковых усилий как внутри каждого выделенного сектора, например, за счет наилучшего перераспределения излучаемой мощности между диаграммами направленности многолучевой антенной решетки, так и между секторами за счет оптимизации последовательности их опроса.
Рассмотренная процедура основана на стохастической потоковой модели появления ОН. С учетом использования при ее реализации принципов локальной оптимизации [19, 20] она предоставляет возможность расширить класс решаемых задач поиска и включить в него задачи, характеризуемые интенсивно изменяющейся обстановкой и ее априорной неопределенностью. Указанные черты, в частности, характерны для задач контроля воздушного движения и космического пространства.
Полученный результат является обобщением подходов к оптимальному поиску ОН, представленных в [9, 11].
ПРИЛОЖЕНИЕ
Доказательство утверждения 1. Представим (2.4) в интегральной форме
(П.1)
${{y}_{i}}(x,t) = {{y}_{i}}(x,\tau ) + \int\limits_\tau ^t {[ - {{y}_{i}}(x,t)({{\gamma }_{i}}(t){{\lambda }_{i}}(x,t) + {{\nu }_{i}}(t)) + {{\nu }_{i}}(x,t)} ]dt$(П.2)
${{J}_{i}} = \int\limits_{{{X}_{i}}} \{ \alpha {{y}_{i}}(x,\tau ) + \int\limits_\tau ^t {\{ \alpha [ - {{y}_{i}}(x,t)({{\lambda }_{i}}(x,t) + \nu (t)) + {{\nu }_{i}}(x,t)] + \frac{1}{2}\beta \lambda _{i}^{2}(x,t)\} dt} \} dx.$Положим
где $\lambda _{i}^{{{\text{о п т }}}}(x,t)$ – условно-оптимальное управление параллельным поиском; $\eta (x,t)$ – некоторая произвольная вариация управления; $\theta $ – малое положительное число.Запишем с учетом (П.3) необходимое условие минимума для (П.2):
(П.4)
${{\left. {\frac{{\partial {{J}_{i}}(\theta )}}{{\partial \theta }}} \right|}_{{\theta = 0}}} = 0,$(П.5)
$\begin{gathered} {{J}_{i}}(\theta ) = \int\limits_{{{X}_{i}}} {\left\{ {\alpha {{y}_{i}}(x,\tau ) + \int\limits_\tau ^t {\{ \alpha [ - {{y}_{i}}(x,t)[(\lambda _{i}^{{{\text{о п т }}}}(x,t) + \theta \eta (x,t)) + \nu (t)]} } \right.} + \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} + \,{{\nu }_{i}}(x,t)] + \frac{1}{2}\beta {{{(\lambda _{i}^{{{\text{о п т }}}}(x,t) + \theta \eta (x,t))}}^{2}}\} dt} \right\}dx. \\ \end{gathered} $Из (П.4), (П.5) следует, что
(П.6)
$\int\limits_{{{X}_{i}}} {\int\limits_\tau ^t {[ - \alpha {{y}_{i}}(x,t) + \beta \lambda _{i}^{{{\text{о п т }}}}(x,t)]\eta (x,t)dt} dx = 0.} $В силу произвольного характера вариации $\eta (x,t)$ вне зависимости от структуры $\omega _{{{{\gamma }_{i}}}}^{k} \in {{\omega }_{k}}$, т.е. для любых управлений ${{\gamma }_{i}}(t) = 1,$ задающих временную программу обращение ИИС к i-му сектору контроля на интервале ${{\omega }_{k}}$, структура закона непрерывного условно-оптимального по критерию (2.7) поиска определяется соотношением (2.8). Утверждение доказано.
Доказательство утверждения 2. Доказательство проведем по аналогии с [5].
Представим (2.10) в виде
(П.7)
$\begin{gathered} \frac{{\partial y_{i}^{{{\text{о п т }}}}(x,t)}}{{\partial t}} = - \frac{\alpha }{\beta }{{\gamma }_{i}}(t){{(y_{i}^{{{\text{о п т }}}}(x,t))}^{2}} - \frac{1}{2}y_{i}^{{{\text{о п т }}}}(x,t)\nu (t) - \frac{1}{2}y_{i}^{{{\text{о п т }}}}(x,t)\nu (t) + {{\nu }_{i}}(x,t), \\ t \in {{\omega }_{k}},\quad x \in {{X}_{i}},\quad i = \overline {1,G} . \\ \end{gathered} $С учетом (П.7) продифференцируем по времени (3.4). В результате получим
(П.8)
$\begin{gathered} \left[ { - \frac{\alpha }{\beta }{{\gamma }_{i}}(t){{{(y_{i}^{{{\text{о п т }}}}(x,t))}}^{2}} - \frac{1}{2}y_{i}^{{{\text{о п т }}}}(x,t)\nu (t) - \frac{1}{2}y_{i}^{{{\text{о п т }}}}(x,t)\nu (t) + {{\nu }_{i}}(x,t)} \right] \times \\ \times \;{{s}_{i}}(x,t) + y_{i}^{{{\text{о п т }}}}(x,t)\frac{{\partial {{s}_{i}}(x,t)}}{{\partial t}} = \frac{{\partial {{q}_{i}}(x,t)}}{{\partial t}}, \\ t \in {{\omega }_{k}},\quad x \in {{X}_{i}},\quad i = \overline {1,G} . \\ \end{gathered} $Перегруппировка слагаемых в (П.8) с учетом (3.4) приводит к следующему соотношению:
(П.9)
$\begin{gathered} y_{i}^{{{\text{о п т }}}}(x,t)\left[ {\left. { - \frac{\alpha }{\beta }{{\gamma }_{i}}(t){{q}_{i}}(x,t) - \frac{1}{2}\nu (t){{s}_{i}}(x,t) + \frac{{\partial {{s}_{i}}(x,t)}}{{\partial t}}} \right]} \right. + \\ + \;\left[ { - \frac{1}{2}\nu (t){{q}_{i}}(x,t) + {{\nu }_{i}}(x,t){{s}_{i}}(x,t) - \frac{{\partial {{q}_{i}}(x,t)}}{{\partial t}}} \right] = 0, \\ t \in {{\omega }_{k}},\quad x \in {{X}_{i}},\quad i = \overline {1,G} . \\ \end{gathered} $Равенство (П.9) выполняется, если функции ${{s}_{i}}(x,t),{{q}_{i}}(x,t)$ удовлетворяют системе уравнений (3.2) с начальными условиями (3.3). Утверждение доказано.
Список литературы
Хеллман О. Введение в теорию оптимального поиска. М.: Наука, 1985.
Альведе Р., Вегснер И. Задачи поиска. М.: Мир, 1985.
Абчук В.А., Суздаль В.Г. Поиск объектов. М.: Сов. радио, 1977.
Аркин В.И. Задача оптимального распределения поисковых усилий // Теория вероятностей и ее применения. 1964. Т. 9. № 1. С. 179–180.
Малышев В.В., Красильщиков М.М., Карлов В.И. Оптимизация наблюдения и управления летательных аппаратов. М.: Машиностроение, 1989.
Карлов В.И., Красильщиков М.Н. Оптимизация процесса измерений в динамических системах при различных критериях оптимальности // Изв. АН СССР. Техн. кибернетика. 1987. № 3. С. 191–197.
Хуторцев В.В., Карга А.В. Метод прогнозирующей модели в теории управления наблюдениями. М.: Радио и связь, 2004.
Карга А.В., Хуторцев В.В. Оптимизация наблюдений в комплексной измерительной системе // Изв. РАН. ТиСУ. 2002. № 1. С. 14–19.
Баранов И.В., Хуторцев В.В. Текущая оптимизация поиска объектов для модели распределенного пуассоновского потока их появления // Изв. РАН. ТиСУ. 2011. № 6. С. 24–34.
Болдырихин Н.В., Хуторцев В.В. Управление наблюдениями за потоками случайных процессов // АиТ. 2006. № 12. С. 43–55.
Хуторцев В.В., Баранов И.В. Оптимальное управление наблюдениями в задаче дискретного поиска для пуассоновской модели потока объектов наблюдения // Радиотехника. 2010. № 3. С. 20–24.
Проблемы антенной техники / Под. ред. Л.Д. Бахраха, Д.И. Воскресенского. М.: Радио и связь, 1989.
Дегтярев О.В., Минаенко А.Н., Орехов М.О. Решение задачи секторизации района управления воздушным движением. 1. Основные принципы и проблемы секторизации воздушного пространства и ее формализация для оптимизационной задачи // Изв. РАН. ТиСУ. 2009. № 3. С. 56–72.
Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, 1964.
Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов. радио, 1977.
Сейдж Э.П., Уайт Ч.С., III. Оптимальное управление системами. М.: Радио и связь, 1982.
Черноусько Ф.Л., Колмановский В.Б. Оптимальное управление при случайных возмущениях. М.: Наука, 1978.
Миллер Б.М. Оптимальное управление наблюдениями при фильтрации процессов диффузионного типа // АиТ. 1985. № 2. С. 79–86.
Хуторцев В.В., Свиженко А.В. Локальная оптимизация наблюдений за случайными потоками объектов в многоканальных измерительных системах // Информационно-измерительные и управляющие системы. 2008. № 12. С. 61–64.
Свиженко А.В., Хуторцев В.В. Локально-оптимальное управление наблюдениями за пуассоновскими потоками фильтруемых процессов // Изв. РАН. ТиСУ. 2010. № 3. С. 33–39.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления