Известия РАН. Теория и системы управления, 2019, № 2, стр. 75-89
ПРЯМОЙ МЕТОД ФОРМИРОВАНИЯ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМ АППАРАТОМ
О. Н. Корсун 1, 2, *, А. В. Стуловский 1, 3
1 ФГУП ГосНИИАС
Москва, Россия
2 МАИ (национальный исследовательский ун-т)
Москва, Россия
3 МФТИ
г. Долгопрудный, Россия
* E-mail: marmotto@rambler.ru
Поступила в редакцию 12.11.2018
После доработки 23.11.2018
Принята к публикации 26.11.2018
Аннотация
Рассмотрен прямой метод формирования оптимального программного управления летательным аппаратом самолетного типа, заключающийся в предварительной параметризации управляющих сигналов с последующим определением значений входящих в них коэффициентов посредством многопараметрической минимизации заданного функционала. Обсуждаются условия применимости и возможные ограничения. Работоспособность метода подтверждается примерами, использующими данные математического моделирования и натурного эксперимента. Проводится сравнение результатов с решениями, полученными в рамках классического подхода к формированию оптимального управления, предусматривающего решение двухточечной краевой задачи.
Введение. В настоящее время разработан широкий спектр различных подходов к решению задачи оптимального управления динамическими системами [1–3]: классическая теория, основанная на вариационном исчислении и принципе максимума Понтрягина, динамическое программирование, метод обратных задач динамики [4], алгебраическая теория вложения систем и т.д. Общепризнанной основой при формировании оптимального программного управления являются вариационные методы и принцип максимума [5]. Однако в случае многомерных нелинейных динамических систем нередко возникают трудности, связанные с решением двухточечной краевой задачи. В этой связи в последнее время усилился интерес к прямым методам нахождения программного управления [6–9].
Прямой метод основывается на предположении, что в рассматриваемой задаче множество управлений может быть представлено в виде конечномерного пространства, каждая точка которого взаимно однозначно соответствует возможному управляющему сигналу [10, 11]. Координаты точки являются, например, коэффициентами разложения управления по какому-либо базису линейно независимых функций. В результате задача сводится к поиску экстремума рассматриваемого функционала в этом пространстве, т.е. к задаче многомерной параметрической оптимизации. Традиционно для решения используют градиентные методы оптимизации, а в последние годы [12] – генетические и популяционные алгоритмы [13–17]. Теоретической основой такого подхода является известная теорема о единственности решения конечномерной системы нелинейных дифференциальных уравнений [18]. Такой прямой подход существенно проще, чем классические методы, требующие решения двухточечной краевой задачи [19–21]. Однако актуален вопрос об условиях его применимости и о соотношении полученных результатов с классическими решениями [22]. Эта проблема рассмотрена в данной работе применительно к управлению летательным аппаратом (ЛА) самолетного типа.
1. Постановка задачи. Начнем с краткого описания предлагаемого метода. Общая постановка задачи достаточно традиционна [19]. Пусть нелинейная нестационарная модель объекта управления задана в виде
где ${\mathbf{x}}$ и ${\mathbf{\dot {x}}}$ – векторы фазовых координат (выходных сигналов) и их производных по времени; ${\mathbf{u}}$ – искомый вектор управления (входной сигнал); $f(\, \cdot \,)$ – известная векторозначная функция векторных аргументов. Начальные условия ${\mathbf{x}}({{t}_{0}}) = {{{\mathbf{x}}}_{{\mathbf{0}}}}$ принимаются заданными.Минимизируемый скалярный функционал имеет вид
(1.2)
$J({\mathbf{x}},{\mathbf{u}}) = \int\limits_{{{t}_{0}}}^T {F({\mathbf{x}},{\mathbf{u}},t)dt,} $Пусть требуется найти управление, обеспечивающее на рассматриваемом интервале времени минимальные отклонения выходных сигналов от желаемых. Тогда функционал можно конкретизировать следующим образом:
(1.3)
$J({\mathbf{x}},{\mathbf{\tilde {x}}},{\mathbf{u}}) = \int\limits_{{{t}_{0}}}^T {{{{({\mathbf{x}}(t) - {\mathbf{\tilde {x}}}(t))}}^{T}}{\mathbf{K}}(} {\mathbf{x}}(t) - {\mathbf{\tilde {x}}}(t))dt,$Несложно заметить, что постановка (1.1)–(1.3) соответствует известной задаче Лагранжа со свободным концом, поскольку границы ${{t}_{0}}$, $T$ рассматриваемого участка фиксированы, а начальные условия заданы. Для нахождения оптимального управления ${\mathbf{\tilde {u}}}$, доставляющего минимум функционалу (1.3), традиционно рекомендуется переход к двухточечной краевой задаче. При этом формируется функция Гамильтона
где $(\lambda ,{\mathbf{f}})$ – скалярное произведение векторов $\lambda $ и ${\mathbf{f}}$, а сама сопряженная вектор-функция $\lambda $ удовлетворяет уравнению(1.5)
$\dot {\lambda } = - {\mathbf{f}}_{x}^{T}\lambda + {{F}_{x}} = - \frac{{\partial G}}{{\partial x}}$Оптимальное управление ${\mathbf{\tilde {u}}}$ предлагается искать из необходимого условия минимума функции Гамильтона
(1.6)
$\frac{{\partial G}}{{\partial {\mathbf{\tilde {u}}}}} = \lambda {{{\mathbf{f}}}_{u}} - {{F}_{u}} = 0.$Рассмотренный вариант соответствует случаю, когда на управление не наложены ограничения. При наличии ограничений вместо уравнений (1.4)–(1.6) рассматриваются их модификации, полученные на основе принципа максимума. В обоих вариантах возникает двухточечная краевая задача, поскольку начальные условия для модели объекта (1.1) заданы в начале интервала, а для сопряженной функции (1.3) – в конце. В общем случае при решении задачи могут возникать значительные трудности, например высокая вычислительная сложность. Дополнительным осложняющим фактором является отсутствие очевидной физической интерпретации для сопряженной вектор-функции [19, 23].
В предлагаемом прямом методе нахождение оптимального управления ${\mathbf{\tilde {u}}}$ осуществляется только на основе уравнений (1.1) и (1.3), уравнения (1.4)–(1.6) не используются. Каждый из скалярных управляющих сигналов, входящих в вектор ${\mathbf{\tilde {u}}}$, предлагается искать в виде разложения по базису линейно независимых функций. В данной работе используются Эрмитовы сплайны третьего порядка [24]. Приведем их краткое описание. Пусть на некотором интервале времени $t \in [{{t}_{1}},{{t}_{M}}]$ заданы М значений ${{t}_{j}}$, $j = 1,2 \ldots M$, которые называются узлами сплайна. Тогда для точки $t$ из отрезка $[{{t}_{i}},{{t}_{{i + 1}}}]$ значение сплайна рассчитывается по формуле
Они являются непрерывными скалярными функциями, имеют непрерывные первые производные [24]. Этим выбором определяются свойства гладкости формируемых управлений. Значения аппроксимируемой функции и ее производной в узлах сплайна формируют вектор априорно неизвестных параметров, однозначно описывающих сплайн. Для учета интенсивного изменения управляющих сигналов или большой длительности участка необходимо увеличивать число узлов, т.е. число параметров.
Таким образом, управляющие сигналы оказываются представлены набором коэффициентов, и задача представляет собой поиск минимума функционала в пространстве коэффициентов
(1.7)
$J({\mathbf{x}},{\mathbf{\tilde {x}}},{\mathbf{u}}({\mathbf{a}})) \to \mathop {min}\limits_{a \in A} ,$Для численного решения оптимизационной задачи целесообразно применять генетические или популяционные алгоритмы, особенно если размерность полученного пространства превышает 20–30. В данной работе выбран метод роя частиц. Описание этого класса алгоритмов приведено в [25, 26], применение конкретных вариантов демонстрируется в [27, 28].
Итак, предлагаемый метод заключается в прямой минимизации функционала (1.3) с учетом модели объекта (1.1), для чего выполняется параметризация управлений в виде Эрмитова сплайна 3-го порядка. Полученная в результате многомерной параметрической оптимизации задача решается одним из популяционных алгоритмов оптимизации – методом роя частиц.
Подтверждение работоспособности предложенного алгоритма, а также сравнение его с традиционной задачей Лагранжа выполняется далее на примере ЛА самолетного типа.
2. Формирование модели объекта управления. Прежде чем перейти к решению конкретной задачи, необходимо сформулировать модель объекта управления. В качестве основы рассмотрим достаточно полную нелинейную модель пространственного движения самолета, выведенную при условии, что оси связанной системы координат совпадают с главными осями инерции [29]:
(2.1)
$\frac{{d{{\omega }_{z}}}}{{dt}} = \frac{{{{J}_{x}} - {{J}_{y}}}}{{{{J}_{z}}}}{{\omega }_{x}}{{\omega }_{y}} + q\frac{{S{{b}_{A}}}}{{{{J}_{z}}}}{{m}_{z}} - \frac{{{{k}_{{{\text{д в }}}}}{{\omega }_{y}}}}{{{{J}_{z}}}} - \frac{{({{P}_{{{\text{п р }}}}} + {{P}_{{{\text{л е в }}}}}){{y}_{{{\text{д в }}}}}}}{{{{J}_{z}}}},$Очевидно, что универсальная система уравнений (2.1) является достаточно громоздкой. В частности, она предполагает использование полного банка аэродинамических коэффициентов исследуемого самолета. Поэтому для дальнейшей работы систему (2.1) предлагается упростить.
Конкретизируем решаемую задачу. Пусть требуется оптимизировать процесс разворота маневренного самолета по курсу, не допуская при этом значительной потери высоты и скорости. Предположим, что маневр осуществляется за счет изменения угла атаки, т.е. создания дополнительной подъемной силы, а собственно разворот происходит за счет изменения угла крена. Тогда угол скольжения можно положить равным нулю.
Получим следующую систему уравнений:
(2.2)
$\dot {V} = - \frac{{qS}}{m}{{c}_{{xe}}}(\alpha ) + \frac{{{{P}_{x}}}}{m}\cos \alpha (t) + g( - \cos \alpha (t)\sin \nu (t) + \sin \alpha (t)\cos \nu (t)\cos \gamma (t)),$Система дифференциальных уравнений (2.2) дополняется алгебраическим уравнением для угловой скорости тангажа ${{\omega }_{z}}$:
(2.3)
${{\omega }_{z}} = \dot {\nu }(t)\cos \gamma (t) - \dot {\tilde {\psi }}\cos \nu (t)\sin \gamma (t),$Система (2.2) также описывает пространственное движение, но включает всего четыре дифференциальных уравнения и требует только значения тяги двигателей ${{P}_{x}}$, аэродинамических коэффициентов подъемной силы ${{c}_{{ye}}}(\alpha )$ и силы сопротивления ${{c}_{{xe}}}(\alpha )$ в полусвязанной системе координат [30]. В системе (2.2) в качестве управляющих сигналов выбраны углы тангажа и крена, чем исключается необходимость использования специальных уравнений для их расчета. Кроме того, эти углы являются относительно медленно изменяющимися функциями, что уменьшает размерность пространства параметров при решении задачи оптимизации.
Для системы (2.2) функционал включает желаемые значения угла атаки, скорости, высоты и угла рыскания. Поскольку вычисления выполняются в дискретном времени, интеграл (1.3) следует заменить суммой:
(2.4)
$F({\mathbf{x}},{\mathbf{u}},t) = \sum\limits_{i = 0}^N {({{k}_{1}}{{{(\alpha ({{t}_{i}}) - \tilde {\alpha }({{t}_{i}}))}}^{2}} + {{k}_{2}}{{{(V({{t}_{i}}) - \tilde {V}({{t}_{i}}))}}^{2}} + {{k}_{3}}{{{(H({{t}_{i}}) - \tilde {H}({{t}_{i}}))}}^{2}} + {{k}_{4}}{{{(\psi ({{t}_{i}}) - \tilde {\psi }({{t}_{i}}))}}^{2}}} ),$Полученная система уравнений является удобной в силу своей простоты, однако остается возможность, что система (2.2) окажется чрезмерно упрощенной. Поэтому сформируем более сложную модель, в которой учтено изменение угла скольжения, а в качестве управлений выбраны угловые скорости ${{\omega }_{x}}(t)$, ${{\omega }_{y}}(t)$, ${{\omega }_{z}}(t)$.
Такая система имеет вид
(2.5)
$\dot {\psi }(t) = \frac{1}{{\cos \nu (t)}}({{\omega }_{y}}(t)\cos \gamma (t) - {{\omega }_{z}}(t)\sin \gamma (t));$Для системы (2.5) в функционал дополнительно вводится желаемые значения угла скольжения $\tilde {\beta }$ с коэффициентом усиления ${{k}_{5}}$:
(2.6)
$\begin{gathered} F({\mathbf{x}},{\mathbf{u}},t) = \sum\limits_{i = 0}^N {({{k}_{1}}{{{(\alpha ({{t}_{i}}) - \tilde {\alpha }({{t}_{i}}))}}^{2}} + {{k}_{2}}{{{(V({{t}_{i}}) - \tilde {V}({{t}_{i}}))}}^{2}} + {{k}_{3}}{{{(H({{t}_{i}}) - \tilde {H}({{t}_{i}}))}}^{2}} + } \\ + \;{{k}_{4}}{{(\psi ({{t}_{i}}) - \tilde {\psi }({{t}_{i}}))}^{2}} + {{k}_{5}}{{(\beta ({{t}_{i}}) - \tilde {\beta }({{t}_{i}}))}^{2}}). \\ \end{gathered} $3. Формулировка задачи Лагранжа для выбранных объектов управления. После определения модели объекта управления и сигналов управления можно сформулировать необходимые условия оптимальности (1.4)–(1.6) в явном виде. Вначале рассмотрим модель (2.2)–(2.3) с функционалом (2.4).
Напомним, что необходимое условие (1.6) в общем случае имеет вид
где ${{f}_{u}}$ и ${{F}_{u}}$ – частные производные по управлению.Это уравнение можно упростить, учитывая, что функционал (2.4) не зависит явно от управления. Тогда
Подставляя модель (2.2)–(2.3), в которой вектор фазовых переменных имеет размерность 4, а размерность вектора управления равна 2, и определяя аналитически частные производные по углам тангажа и крена, т.е. по вектору управляющих сигналов, получим следующие два уравнения, в каждое из которых входят по четыре частных производных:
(2.8)
$\begin{gathered} {{\lambda }_{1}}f_{\nu }^{1} + {{\lambda }_{2}}f_{\nu }^{2} + {{\lambda }_{3}}f_{\nu }^{3} + {{\lambda }_{4}}f_{\nu }^{4} = 0; \hfill \\ {{\lambda }_{1}}f_{\gamma }^{1} + {{\lambda }_{2}}f_{\gamma }^{2} + {{\lambda }_{3}}f_{\gamma }^{3} + {{\lambda }_{4}}f_{\gamma }^{4} = 0, \hfill \\ \end{gathered} $Сопряженная вектор-функция в общем случае находится из уравнения (1.5):
Применительно к модели (2.2)–(2.3) с функционалом (2.4) это уравнение можно представить следующим образом:
(2.9)
$\begin{gathered} {{{\dot {\lambda }}}_{1}} = 2{{k}_{1}}(\alpha (t) - \tilde {\alpha }(t)) - {{\lambda }_{1}}f_{\alpha }^{1} - {{\lambda }_{2}}f_{\alpha }^{2} - {{\lambda }_{3}}f_{\alpha }^{3}, \\ {{{\dot {\lambda }}}_{2}} = 2{{k}_{2}}(V(t) - \tilde {V}(t)) - {{\lambda }_{1}}f_{V}^{1} - {{\lambda }_{2}}f_{V}^{2} - {{\lambda }_{3}}f_{V}^{3}, \\ {{{\dot {\lambda }}}_{3}} = 2{{k}_{3}}(H(t) - \tilde {H}(t)) - {{\lambda }_{1}}f_{H}^{1} - {{\lambda }_{2}}f_{H}^{2}, \\ {{{\dot {\lambda }}}_{4}} = 2{{k}_{4}}(\psi (t) - \tilde {\psi }(t)),{\text{ }} \\ \end{gathered} $Если же выбрать в качестве модели объекта управления систему (2.5) размерности 7, функционал (2.6), а в качестве управляющих сигналов – вектор угловых скоростей размерности 3, то уравнение (2.7) является системой размерности 3:
Общее дифференциальное уравнение (1.5) для сопряженной вектор-функции $\lambda $ принимает форму системы из семи уравнений:
4. Проверка работоспособности метода. Проверка работоспособности предлагаемого метода выполнялась путем решения специально сформированной тестовой задачи. Для генерации данных выполнялось моделирование движения объекта согласно уравнениям (2.2)–(2.3), при этом в качестве входных сигналов задавались известные функции времени. Моделировалось движение маневренного самолета, выполняющего быстрый разворот по углу рыскания на 180° с выходом на закритические углы атаки. Параметры модели объекта принимались согласно работе [31], где представлена методика их идентификации по полетным данным. Таким образом, тестирование проводилось на примере сложного существенно нелинейного динамического объекта. С другой стороны, сгенерированные выходные сигналы являлись весьма точным решением известных уравнений (2.2)–(2.3) при заданных входных сигналах, т.е. в тестовой задаче все компоненты известны с высокой точностью. Для проверки работоспособности алгоритма ставилась задача по известной модели и выходным сигналам восстановить входные сигналы. Эти оценки алгоритм находит, минимизируя функционал (2.4), в который сгенерированные на модели выходные сигналы входят как желаемые. Можно ожидать, что при такой постановке точность оценок входных сигналов должна быть очень высокой, поскольку погрешности минимальны, а однозначность обеспечивается теоремой о единственности решения системы нелинейных дифференциальных уравнений [18]. Область поиска в методе роя частиц задавалась ±90° для угла тангажа, ±180° для угла крена, в качестве начального приближения выбирались нулевые значения. На временном интервале задавалась равномерная сетка с шестью узлами. Таким образом, для нахождения двух управляющих сигналов требовалось найти 24 параметра (значения управлений и их производных в узлах сплайнов). С этой целью брался выходной сигнал, сгенерированный моделью, и для него подбиралось управление, которое затем сравнивалось с исходным. При такой постановке задачи обеспечивалось полное соответствие модели объекту управления, а кроме того искомые входные сигналы заведомо находились в пределах области поиска. Как можно видеть на рис. 1, степень совпадения по выходным сигналам оказалась очень высокой, вплоть до визуальной неразличимости. Точность соответствия оценок входных сигналов значениям, заданным при моделировании, также весьма высокая (рис. 2), хотя заметны небольшие отличия. Этот результат соответствует ожидаемому и подтверждает способность алгоритма находить единственную оценку входных сигналов при произвольном начальном приближении.
Рис. 1.
Сравнение исходных выходных сигналов (сплошная линия) и выходных сигналов, полученных с помощью оптимизационного алгоритма (штрихованная линия)
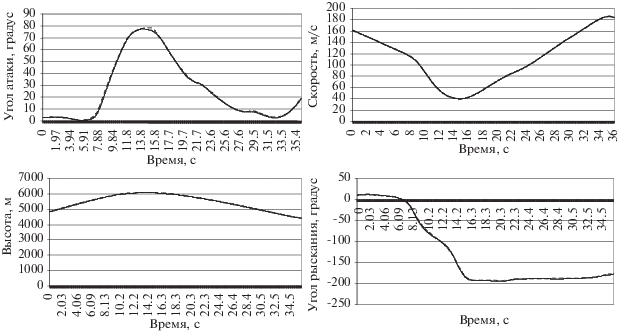
Рис. 2.
Сравнение заданных входных сигналов (сплошная линия) с сигналами, полученными с помощью оптимизационного алгоритма (штрихованная линия)
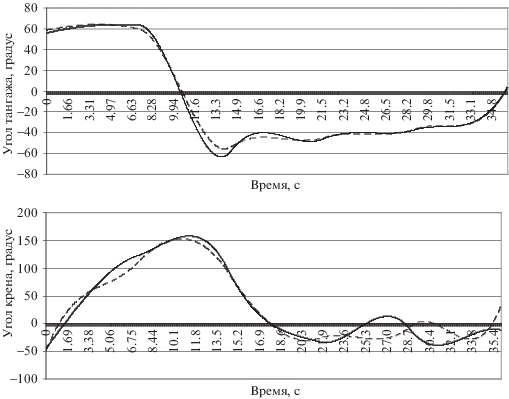
Как можно видеть на рис. 2, входные сигналы тоже с высокой точностью воспроизводят свои заданные значения.
На следующем этапе ставилась задача убедиться в том, что модель может верно описывать движение реального объекта. Для этого было решено обработать с помощью описанного алгоритма данные, полученные в результате летных испытаний.
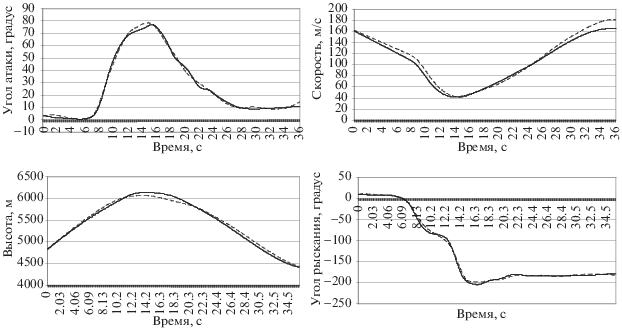
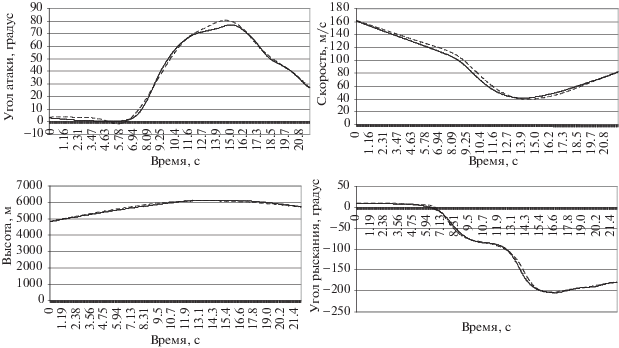
Как можно видеть на рис. 3 даже при использовании достаточно простой модели (2.2)–(2.3) выходные сигналы с высокой точностью соответствуют экспериментальным данным.
Рис. 3.
Сравнение выходных сигналов в натурном эксперименте (сплошная линия) и выходных сигналов, полученных с помощью оптимизационного алгоритма с использованием системы (2.2)–(2.3) (штрихованная линия)
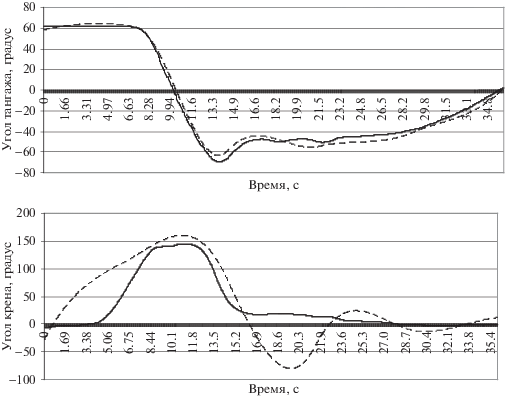
Остается проверить сходство наблюдаемых в натурном эксперименте управляющих сигналов и сигналов, полученных в результате работы оптимизационного алгоритма. Как видно на рис. 4, для угла тангажа наблюдается достаточно высокая степень совпадения. Расхождения для угла крена оказываются существенно больше, но, как было замечено выше, это не сказывается на выходных сигналах и может быть объяснено существующими расхождениями между реальным объектом и описывающей его идеализированной моделью.
Рис. 4.
Сравнение входных сигналов в натурном эксперименте (сплошная линия) с сигналами, полученными с помощью оптимизационного алгоритма (штрихованная линия)
Применение более подробной модели (2.5) позволяет добиться столь же хорошего соответствия выходных сигналов (рис. 5).
Рис. 5.
Сравнение выходных сигналов в натурном эксперименте (сплошная линия) и выходных сигналов, полученных с помощью оптимизационного алгоритма с использованием системы (2.5) (штрихованная линия)
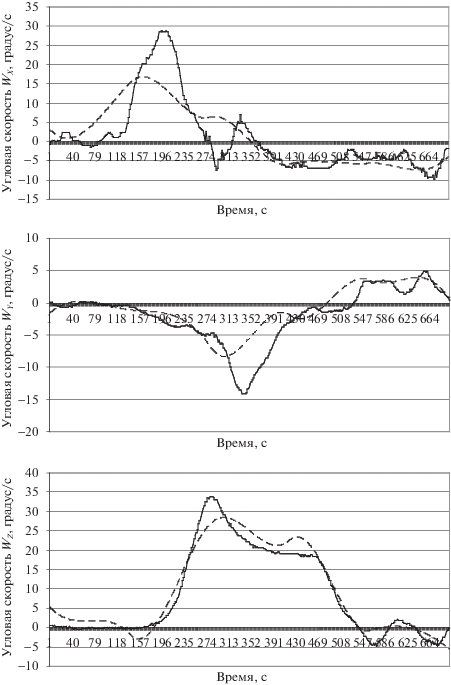
Сравнение полученных при помощи алгоритма входных сигналов (угловых скоростей) с соответствующими сигналами, измеренными в эксперименте, показано на рис. 6. Здесь степень рассогласования выше, чем в предыдущем случае, когда в качестве управлений рассматривались углы крена и тангажа. Очевидно, это вызвано тем, что в сигналах угловых скоростей доля высокочастотных составляющих выше и принятый сплайн с шестью узлами не воспроизводит точно все изменения. Отметим однако, что соответствие по выходным сигналам и в этом случае весьма высокое.
Рис. 6.
Сравнение входных сигналов в натурном эксперименте (сплошная линия) с сигналами, полученными с помощью оптимизационного алгоритма (штрихованная линия)
5. Сравнение решения задачи с решением, основанным на решении двухточечной задачи. На следующем этапе работы ставился вопрос о сравнении полученных результатов с классическими методами оптимального управления, в частности, с рассмотренной выше задачей Лагранжа. Как известно, оптимальное управление должно удовлетворять необходимому условию (1.6). Поэтому было выполнено сравнение предложенного прямого метода с решением на основе условия (1.6), т.е. равенства нулю производных функции Гамильтона по управлению.
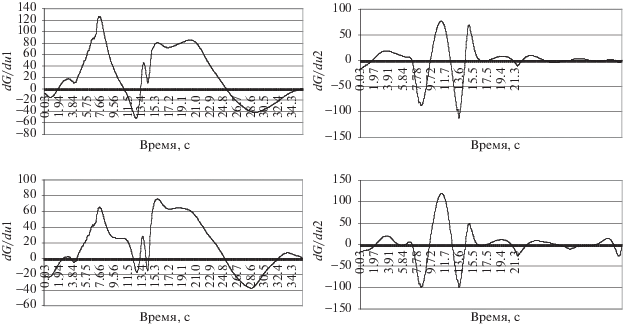
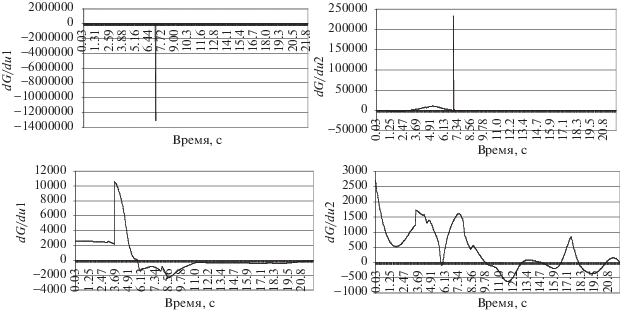
Проверка выполнялась для описанного выше примера нахождения управления по модельным данным с моделью объекта вида (2.2)–(2.3). Сравнивались два варианта. В первом применялся прямой метод с функционалом (2.4), а производные функции Гамильтона вычислялись, но для формирования управления не использовались. Во втором варианте квадраты производных функции Гамильтона включались в минимизируемый функционал. В обоих вариантах достигалась высокая степень соответствия как между выходными, так и между входными сигналами, идентичная наблюдаемой на рис. 1 и 2. Полученные значения производных функции Гамильтона для обоих вариантов приведены на рис. 7. Как видим, значения производных в обоих случаях сопоставимы.
Рис. 7.
Значения производных функции Гамильтона для случая, когда производные не включены в состав функционала (верхний ряд) и когда они включены (нижний ряд)
Таким образом, проведенное сравнение показало, что предложенный прямой метод, не использующий функцию Гамильтона, позволяет получить решение, практически совпадающее с решением, полученным с использованием классического необходимого условия (1.6).
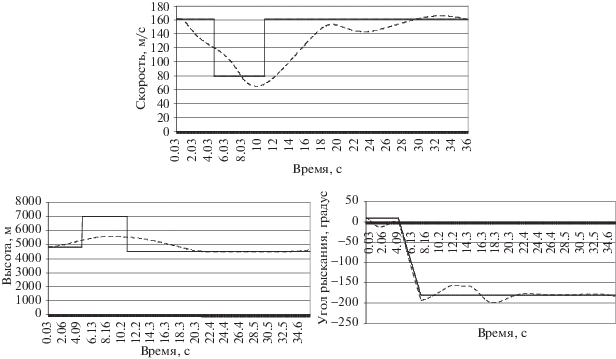
6. Формирование оптимального управления. Применим представленные выше методы для формирования управления. Рассмотрим задачу быстрого разворота по углу рыскания без потери высоты и скорости. Желаемые выходные сигналы показаны на рис. 8 сплошными линиями. Выходные сигналы, полученные прямым методом, представлены на том же рисунке пунктиром. Можно видеть, что угол рысканья объекта с высокой точностью соответствует заданному, а скорость и высота после выполнения маневра восстанавливают исходные значения. Для метода с использованием функции Гамильтона выходные сигналы аналогичны.
Рис. 8.
Значения выходных сигналов, полученные при решении задачи формирования управления (штрихованная линия) и заданные значения выходных сигналов (сплошная линия)
Различия наблюдаются только для значений самих производных функции Гамильтона (рис. 9). В прямом методе они существенно больше, но это не влияет на конечный результат.
Рис. 9.
Значения производных функции Гамильтона для случая, когда производные не включены в состав функционала (верхний ряд) и когда они включены (нижний ряд)
Заключение. В работе предложен прямой метод нахождения оптимального программного управления, использующий параметризацию управляющих сигналов в форме сплайнов и нахождение оценок параметров при помощи популяционного алгоритма. Сформировано несколько вариантов модели движения летательного аппарата, различающихся по степени сложности. Работоспособность метода подтверждена по данным математического моделирования и натурного эксперимента.
Кроме того, в работе на примере математического моделирования выполнено сравнение предложенного метода с решением, полученным в рамках классической задачи Лагранжа. Показано, что при этом обеспечивается высокая степень соответствия.
Особенностью представленных выше задач является допущение о том, что используемые сплайны аппроксимируют управления с высокой точностью. Другими словами, предполагается достаточная степень гладкости управляющих сигналов.
Таким образом, предложенный прямой метод в рамках рассмотренного класса задач нахождения оптимального программного управления летательным аппаратом обеспечивает получение решений, практически совпадающих с классическими методами. В то же время реализация предложенного метода существенно проще.
Список литературы
Методы классической и современной теории автоматического управления / Под ред. К.А. Пупкова, Н.Д. Егупова. М.: Изд-во МГТУ им. Баумана, 2004. 656 с.
Rao A.V. Survey of Numerical Methods for Optimal Control // Advances Astronautical Sciences. 2010. V. 135. P. 497–528.
Conway B.A. A Survey of Methods Available for Numerical Optimization of Continuous Dynamic Systems // J. Optimization Theory Appl. 2012. V. 152. № 2. P. 271–306.
Крутько П.Д. Обратные задачи динамики управляющих систем. Нелинейные модели. М.: Наука, 1988. 237 с.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. Изд. 4-е. М: Наука, 1983. 392 с.
Лапин М.С., Мельц И.О. Применение прямого метода для оптимизации управляющих функций динамической системы и их ограничений // Тр. ЦАГИ. 1970. Вып. 1190. С. 20–39.
Hargraves C.R., Paris S.W. Direct Trajectory Optimization Using Nonlinear Programming Techniques // J. Guidance, Control, Dynamics. 1987. V. 10. P. 338–342.
Von Stryk O., Bulirsch R. Direct and Indirect Methods for Trajectory Optimization // Annals of Operation Research. 1992. № 37. P. 357–373.
Bulirsh R., Nerz E., Pesh H.J., Von Stryk O. Combining Direct and Indirect Methods in Optimal Control: Range Maximization of a Hang Glider // Intern. Series of Numerical Mathematics. 1993. V. 111. P. 273–286.
Goh C.J., Teo K.L. Control Parametrization: A Unified Approach to Optimal Control Problems with General Constraints // Automatica. 1988. V. 24. P. 3–18.
Hull D.G. Conversion of Optimal Control Problems into Parameter Optimization Problems // J. Guidance, Control, Dynamics. 1997. V. 20. № 1. P. 57–60.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. 447 с.
Davis L. Handbook of Genetic Algorithms. N. Y., USA: Van Nostrand Reinhold, 1991. 385 p.
Wuerl A., Crain T., Braden E. Genetic Algorithm and Calculus of Variation-Based Trajectory Optimization Technique // J. Spacecraft Rockets. 2003. V. 40. P. 882–888.
Won T.-H., Hwang G.-H., Park J.H., Lee M.H. Design of FLC for High-angle-of-attack Using Adaptive Evolutionary Algorithm // KSME Intern. J. 2003. V. 12. № 2. P. 187–196.
Дивеев А.И., Шмалько Е.Ю. Методы генетического программирования для решения задачи синтеза оптимального управления // Вопросы теории безопасности и устойчивости систем. 2015. № 17. С. 38–63.
Дивеев А.И., Софронова Е.А., Шмалько Е.Ю. Эволюционные численные методы решения задачи синтеза управления группой роботов // Информационные и математические технологии в науке и управлении. 2016. № 3. С. 11–23.
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. Изд. 4-е. М.: Наука, 1974. 331 с.
Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 328 с.
Roberts S.M., Shipman J.S. Multipoint Solution of Two-point Boundary Value Problems // J. Optimization Theory Appl. 1971. V. 7. № 4. P. 301–318.
Miele A., Well K.P., Tietze J.L. Multipoint Approach to the Two-point Boundary Value Problem // J. Mathematical Analysis Appl. 1973. V. 44. P. 625–642.
Лёвин С.А. Сравнение решений задачи оптимизации траектории полета управляемой ракеты с РДТТ прямым и непрямым методом // Уч. зап. ЦАГИ. 2017. Т. XLVIII. № 6. С. 53–63.
Моисеев Н.Н. Численные методы в теории оптимальных систем. М.: Наука, 1971. 424 с.
Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. М.: Наука, 1980. 352 с.
Eberhardt R.C., Kennedy J.A. Particle Swarm Optimization // Proc. IEEE Intern. Conf. on Neural Networks. Piscataway, N.J., 1995. P. 1942–1948.
Olsson A.E. Particle Swarm Optimization: Theory, Techniques and Applications. Hauppage, USA: Nova Science Publishers, 2011. 305 p.
Lu Y., Yan D., Levy D. Parameter Estimation of Vertical Takeoff and Landing Aircrafts by Using a PID Controlling Particle Swarm Optimization Algorithm // Applied Intelligence. 2016. V. 44. № 4. P. 793–815.
Буковский Г.А., Корсун О.Н., Стуловский А.В. Формирование оптимального управления самолетом на закритических углах атаки на основе популяционного алгоритма оптимизации // Вестник компьютерных и информационных технологий. 2018. № 6. С. 27–37.
Аэродинамика, устойчивость и управляемость сверхзвуковых самолетов / Под ред. Г.С. Бюшгенса. М.: Наука. Физмалит, 1998. 816 с.
ГОСТ 20058-80. Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. М.: Изд-во стандартов, 1981. 54 с.
Канышев А.В., Корсун О.Н., Овчаренко В.Н., Стуловский А.В. Идентификация аэродинамических коэффициентов продольного движения и оценка погрешностей бортовых измерений на закритических углах атаки // Изв. РАН. ТиСУ. 2018. № 3. С. 33–47.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


