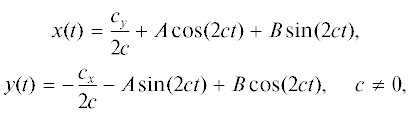Известия РАН. Теория и системы управления, 2019, № 2, стр. 98-105
ПЕРЕОРИЕНТАЦИЯ ТВЕРДОГО ТЕЛА, УПРАВЛЯЕМОГО ПОСРЕДСТВОМ ПОДВИЖНОЙ ВНУТРЕННЕЙ МАССЫ
Н. Ю. Наумов 1, *, Ф. Л. Черноусько 1, **
1 ИПМех им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: nikita.naumov@phystech.edu
** E-mail: chern@ipmnet.ru
Поступила в редакцию 14.11.2018
После доработки 22.11.2018
Принята к публикации 26.11.2018
Аннотация
Рассматривается задача об управлении ориентацией твердого тела при помощи внутренней подвижной массы. Предложен метод расчета движения материальной точки относительно твердого тела, при котором тело совершает заданное изменение ориентации в пространстве. Построенный способ переориентации состоит из трех плоских поворотов вокруг главных центральных осей инерции твердого тела. Плоские повороты основаны на решении соответствующих задач оптимального управления.
Введение. Одним из способов управления движением робототехнических систем является управление посредством внутренних подвижных масс, совершающих заданные движения относительно корпуса робота. Мобильные роботы, движение которых основано на этом принципе, называют капсульными роботами или вибророботами. Поступательное движение таких роботов возможно при наличии сил сопротивления внешней среды, например сил сухого трения или вязкого сопротивления. Особенностью капсульных роботов является отсутствие внешних движителей, таких, как колеса, ноги, гусеницы, пропеллеры, что позволяет делать эти роботы герметичными и использовать их для движения в опасных или ранимых средах. Описанный принцип перемещения применяется в микророботах [1, 2] и в роботах, движущихся внутри труб [3].
Управление при помощи подвижных внутренних масс возможно использовать также и при отсутствии внешних сил для изменения ориентации тела в пространстве. Соответствующая задача о плоском повороте рассмотрена в [4], где дано решение, оптимальное по быстродействию, в случае, когда вспомогательная подвижная масса мала по сравнению с массой основного тела, и в [5], где исследован общий случай. Ниже рассмотрена трехмерная задача о пространственном развороте при помощи подвижной массы.
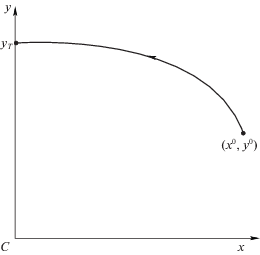
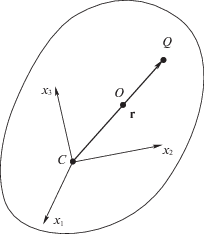
1. Механическая система. Предположим, что твердое тело P массы M содержит вспомогательную подвижную материальную точку Q массы m, которая управляется посредством актюатора и может перемещаться относительно тела P. Силы взаимодействия между телами P и Q являются единственными силами, действующими на систему P + Q. Примем, что в начальный момент t = 0 система покоится, и обозначим через O центра масс системы P + Q, через C – центр масс тела P, а через RQ, RC и r – векторы RQ = $\overline {OQ} $, RC = $\overline {OC} $, r = $\overline {CQ} $ (см. рис. 1).
Так как центр масс O системы сохраняет свое положение, имеем
откуда следует Ввиду отсутствия внешних сил, импульс системы P + Q и ее кинетический момент сохраняются и равны своим начальным нулевым значениям. Обозначая через ${{v}_{c}}$ скорость точки C, условие сохранения импульса можно записать в виде(1.3)
$M{{v}_{C}} + m({{v}_{C}} + \omega \times r + \dot {r}) = 0,\quad {{v}_{C}} = {{\dot {R}}_{C}},$(1.5)
$M{{R}_{C}} \times {{v}_{C}} + J \cdot \omega + m({{R}_{C}} + r) \times ({{v}_{C}} + \omega \times r + \dot {r}) = 0,$2. Постановка задачи. Введем декартову систему координат Cx1x2x3, связанную с твердым телом P (рис. 1), оси которой Cxi совпадают с главными центральными осями инерции тела, i = 1, 2, 3. Поставим задачу о переводе тела P из заданного начального состояния в заданное конечное состояние. Как в начальном, так и в конечном состоянии определяется ориентация тела P в пространстве, т.е. направления осей Cxi, i = 1, 2, 3. Этот перевод можно осуществить посредством трех плоских поворотов, кинематика которых описывается при помощи углов Эйлера–Крылова [6].
Пусть заданная конечная ориентация тела P может быть реализована в результате последовательных поворотов тела на углы αi вокруг осей Cxi, i = 1, 2, 3. Эти плоские повороты можно осуществить при помощи плоских движений точки Q.
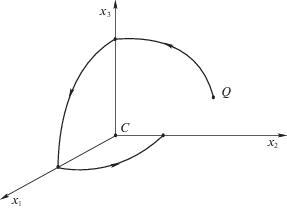
Предположим для определенности, что в начальный момент точка Q находится в плоскости Cx2x3 и имеет координаты (0, $x_{2}^{0}$, $x_{3}^{0}$) в системе координат Cx1x2x3 (рис. 2). Осуществим такое плоское движение точки Q в плоскости Cx2x3, при котором тело P повернется вокруг оси Cx1 на заданный угол α1, а точка Q перейдет в точку на оси Cx3 с координатами (0, 0, $x_{3}^{'}$), где $x_{3}^{'}$ произвольно. Затем осуществим плоское движение точки Q в плоскости Cx1x3, при котором тело P повернется на заданный угол α2 вокруг оси Cx2, а точка Q перейдет в точку на оси Cx1 с координатами ($x_{1}^{'}$, 0, 0), где $x_{1}^{'}$ произвольно. Наконец, осуществим плоское движение точки Q в плоскости Cx1x2, при котором тело P повернется на заданный угол α3 вокруг оси Cx3, а точка Q перейдет в точку (0, $x_{2}^{'}$, 0) на оси Cx2 при произвольном $x_{2}^{'}$.
Для реализации описанной переориентации тела P необходимо и достаточно решить плоскую задачу о повороте тела P на заданный угол посредством такого движения точки Q в плоскости поворота, при котором она переходит в точку на одной из осей координат.
3. Плоский поворот. Перейдем к рассмотрению задачи о плоском повороте тела P на заданный угол α вокруг одной из его главных центральных осей инерции посредством плоского движения точки Q. Введем декартову систему координат Cxy в плоскости поворота и запишем векторное уравнение (1.6) в проекции на ось, перпендикулярную плоскости Cxy. Обозначая через x, y и u, $v$ проекции на оси Cx и Cy векторов r и $\dot {r}$ соответственно, получим из (1.6) уравнение [4]
Здесь I – главный центральный момент инерции тела P вокруг оси, перпендикулярной плоскости Cxy, φ – угол поворота тела вокруг этой оси. Обозначим через a радиус инерции тела вокруг указанной оси, определяемый соотношениемПредположим, что величина скорости точки Q относительно тела P ограничена величиной V. Имеем
Введем безразмерные переменные
перепишем уравнение (3.1) в виде системы, опуская штрихи у безразмерных переменных:(3.5)
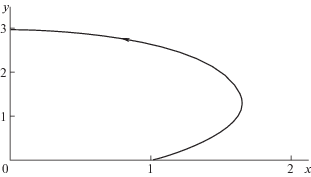
$\dot {x} = u{\text{,}}\quad \dot {y} = v{\text{,}}\quad\quad \dot {\varphi } = \frac{{\mu (yu - xv)}}{{1 + \mu ({{x}^{2}} + {{y}^{2}})}}{\text{.}}\quad$Задача о плоском повороте, которую следует решить для реализации пространственной переориентации тела P, можно сформулировать следующим образом (см. рис. 3).
Задача 1. Найти управления u(t) и $v(t)$, удовлетворяющие ограничению (3.6) на интервале t ∈ [0, T] и такие, чтобы для решения системы уравнений (3.5) выполнялись краевые условия:
(3.7)
$x(0) = {{x}^{0}}{\text{,}}\quad\quad y(0) = \quad{{y}^{0}}{\text{,}}\quad \varphi (0) = 0{\text{,}}\quad x(T) = 0{\text{,}}\quad\quad \varphi (T) = \alpha $Поскольку желательно выполнить маневр переориентации как можно быстрее, целесообразно сделать время T ориентации как можно меньше. Не решая точно задачу оптимального управления, поступим следующим образом. Сначала, следуя подходу [4], найдем оптимальное по быстродействию управление для упрощенной задачи в случае μ ≪ 1, а затем на его основе построим точное, но не оптимальное решение исходной задачи 1.
4. Оптимальное управление. В случае μ ≪ 1 система (3.5) упрощается и принимает вид
(4.1)
$\dot {x} = u{\text{,}}\quad \dot {y} = v{\text{,}}\quad \dot {z} = yu - xv,\quad z = \varphi {\text{/}}\mu .$Задача 2. Найти управления u(t) и $v(t)$, удовлетворяющие ограничению (3.6) на интервале t ∈ [0, T] и такие, что для системы (4.1) выполняются краевые условия (3.7) при наименьшем T.
Следуя принципу максимума [7], составим функцию Гамильтона для системы (4.1):
Здесь px, py, pz – сопряженные переменные, удовлетворяющие уравнениям(4.3)
${{\dot {p}}_{x}} = {{p}_{z}}v{\text{,}}\quad {{\dot {p}}_{y}} = - {{p}_{z}}u{\text{,}}\quad\quad {{\dot {p}}_{z}} = 0.$(4.4)
${{p}_{x}} = cy + {{c}_{x}}{\text{,}}\quad {{p}_{y}} = - cx + {{c}_{y}}{\text{,}}\quad {{p}_{z}} = c,$Определяя максимум гамильтониана (4.2) по u, $v$ при ограничении (3.6), найдем
где введено обозначение Заметим, что максимум достигается при выполнении равенства в (3.6), так что имеем Вставляя формулы (4.5) в гамильтониан (4.2), получим H = D. Так как в автономной системе гамильтониан постоянен, то за счет нормализации сопряженных переменных можно без ограничения общности положить Подставляя соотношения (4.4) и (4.8) в формулы (4.5), а затем вставляя полученные выражения для u и $v$ в первые два уравнения (4.1), получим уравнения Интегрируя уравнения (4.9), имеем где A и B – произвольные постоянные. Из начальных условий (3.7) находим Так как значение y(T) свободно, то имеем условие трансверсальности py(T) = 0. Принимая во внимание также краевое условие x(T) = 0 из (3.7), из второго соотношения (4.4) при t = T получим cy = 0. Следовательно, согласно (4.11), имеем A = x0. Подставляя найденное значение $A$ соотношения (4.11) в равенства (4.10), получим Подставляя первое равенство (4.12) в краевое условие x(T) = 0 из (3.7), найдем Вставляя соотношения (4.12) в первые два уравнения (4.1), получим выражения для управлений: где B определено равенством (4.13). Управления (4.14) должны удовлетворять равенству (4.7). Подставив соотношения (4.13) и (4.14) в (4.7), получим после упрощений Подставим теперь соотношения (4.12) и (4.14) в правую часть третьего уравнения (4.1). После преобразований имеемПроинтегрируем полученное уравнение от 0 до T и воспользуемся краевыми условиями (3.7) для φ и соотношением (4.13). В результате получим
(4.16)
${{\mu }^{{ - 1}}}\alpha = - {{x}^{0}}{{y}^{0}} + \frac{{{{{({{x}^{0}})}}^{2}}}}{{{\text{si}}{{{\text{n}}}^{2}}(2cT)}}{\text{[}}2cT - \sin (2cT)\cos (2cT){\text{]}}{\text{.}}$Соотношения (4.15) и (4.16) представляют собой два трансцендентных уравнения для определения двух неизвестных параметров c и T. Обозначим
и введем в рассмотрение функцию Тогда равенство (4.16) представляется как(4.19)
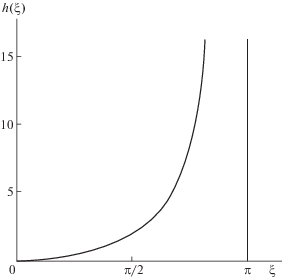
$h(\xi ) = \frac{{{{\mu }^{{ - 1}}}\alpha + {{x}^{0}}{{y}^{0}}}}{{{{{({{x}^{0}})}}^{2}}}}\quad$Функция h(ξ), определяемая равенством (4.19), является нечетной функцией ξ. Она монотонно возрастает от 0 до ∞ на интервале изменения ξ от 0 до π; ее график представлен на рис. 4.
Таким образом, процедура решения задачи 2 состоит в следующем. Сначала по заданным параметрам x0, y0, α, μ из уравнения (4.19) определяем параметр ξ. Это уравнение, в силу свойств функции h(ξ), имеет единственное решение ξ ∈ (–π, π). Затем определяем время быстродействия T по формуле (4.20). Параметр c находится из равенства (4.17). Оптимальное управление и оптимальная траектория определены соотношениями (4.14) и (4.12) соответственно, причем константа B в этих равенствах задана, согласно (4.13), соотношением B = –x0ctgξ. Отметим, что при ξ = c = 0 имеем вырожденный случай: оптимальная траектория состоит из одной начальной точки x = y = 0. Из равенств (4.12) вытекает соотношение
Следовательно, оптимальная траектория представляет собой дугу окружности с центром в точке K с координатами xK = 0, yK = y0 – B. Используя соотношения (4.13) и (4.17), получим Радиус окружности (4.21), согласно формулам (4.13) и (4.17), определяется равенством(4.23)
$R = {{[{{({{x}^{0}})}^{2}} + {{B}^{2}}]}^{{1/2}}} = {\text{|}}{{x}^{0}}{\text{/}}\sin \xi {\text{|}}{\text{.}}$В конечной точке оптимальной траектории имеем, согласно равенствам (4.12), (4.13) и (4.17):
Так как построенное решение основано на упрощающем предположении μ ≪ 1, оно является приближенным. В работе [5] получено точное решение системы уравнений для оптимального управления в квадратурах, однако удовлетворение краевых условий для этого решения представляет определенные трудности.
Поэтому предлагается, следуя [4], использовать найденные выше сравнительно простые соотношения для построения допустимого решения поставленной задачи 1.
5. Решение задачи 1. Рассмотрим невырожденный случай ξ ≠ 0. Для построения решения используем полученные выше соотношения (4.12) и (4.14) для траекторий и управлений соответственно. В этих равенствах константа A = x0, а константа B задана соотношением (4.13). При этом имеется три неизвестных параметра ξ, T, c, связанных равенством (4.17). Для их нахождения проинтегрируем третье уравнение из системы (3.5), а также воспользуемся краевыми условиями (3.7). Тогда
(5.1)
$\alpha = \mathop \smallint \limits_0^T \frac{{\mu (yu - xv)}}{{1 + \mu ({{x}^{2}} + {{y}^{2}})}}dt{\text{.}}$Сведем уравнение (5.1) к одному неизвестному параметру ξ. Для этого воспользуемся соотношениями (4.15) и (4.17), из которых выразим T и c через ξ. Так как подынтегральная функция из уравнения (5.1) непрерывна, и, кроме того, как и функция h(ξ), монотонна на отрезке от 0 до π, применим метод Ньютона решения нелинейных уравнений для нахождения параметра ξ.
Таким образом, найдя все неизвестные параметры ξ, T, c, мы полностью определим решение задачи 1.
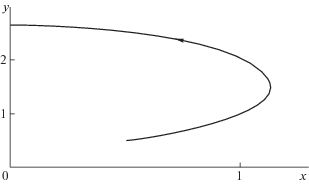
Примеры. Рассмотрим некоторые примеры решения задачи 1 для различных значений параметров μ, α и при различных начальных условиях. Будут найдены параметры ξ, T, а также построены траектории точки Q.
1. Общие параметры и начальные условия:
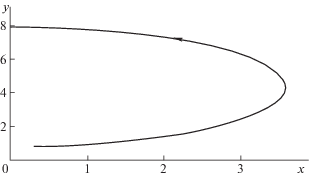
2. Общие параметры и начальные условия:
3. Общие параметры и начальные условия:
Заключение. Рассмотрена задача об изменении ориентации твердого тела при помощи внутренней подвижной массы. Предложен метод расчета движения материальной точки относительно твердого тела, при котором тело совершает заданное изменение ориентации в пространстве. Приведено несколько примеров.
Список литературы
Schmoeckel F., Worn H. Remotely Controllable Mobile Microrobots Acting as Nano Positioners and Intelligent Tweezers in Scanning Electron Microscopes (SEMs) // Proc. Intern. Conf. Robotics and Automation, IEEE. N.Y., 2001. P. 3903–3913.
Vartholomeos P., Papadopoulos E. Dynamics, Design and Simulation of a Novel Microrobotic Platform Employing Vibration Microactuators // J. Dynamical Systems, Measurement and Control. 2006. V. 128. № 1. P. 122–133.
Gradetsky V., Solovtsov V., Kniazkov M., Rizzoto G.G., Amato P. Modular Design of Electro-magnetic Mechatronics Microrobots // Proc. 6th Intern. Conf. Climbing and Walking Robots CLAWAR. 2003. P. 651–658.
Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы // ДАН. 2018. Т. 480. № 5. С. 528–532.
Шматков А.М. Поворот тела за кратчайшее время перемещением точечной массы // ДАН. 2018. Т. 481. № 5.
Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 672 с.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983. 392 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


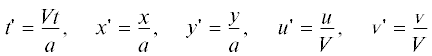 .
.