Известия РАН. Теория и системы управления, 2019, № 2, стр. 106-116

Введение. В недавно опубликованной статье [1] кратко представлен новый подход к решению проблемы обеспечения эффективности использования однокарданных безупорных силовых гироскопов – гиродинов (в англоязычной технической терминологии – single-gimbal control moment gyros (SGCMG’s)). Эта проблема изучается со времени начала эксплуатации гиродинов в системах управления (СУ) ориентацией космических аппаратов (КА) – с 60-х годов прошлого века [2–4]. В поисках ее решения рассматриваются вопросы оптимизации конфигурирования гиросистемы и создания технологии расчета законов управления КА, надежно реализуемых гиродинами.

Уже в первых публикациях по этому вопросу предлагались решения в виде использования механически спаренных гироскопов. К ним можно отнести гиросистемы “Twin-Gyro” [2, 3], “стригущие пары” (Scissored-Pair) [4], гирорамы [5] и другие конструкции, в частности 4FACS (4 gyro Fine Attitude Control System) [6]. Целью этих поисков было ослабление чувствительности законов управления, исполняемых гиродинами, к так называемой “проблеме сингулярности”.

В терминах законов управления, вычисляемых предлагаемым новым методом, эти законы представлены изменением во времени виртуальных углов прецессии $\alpha (t)$ и $\beta (t)$ [7], по которым вычисляются прецессии реальных гироузлов ${{\delta }_{{ij}}}(t)$ [7]. “Проблема сингулярности” таких управлений заключается в наличии особых положений гироузлов гиродинов на осях прецессий, в которых вычисленные законы перестают исполняться, КА теряет управляемость, и рабочий процесс прерывается.

Широко распространенный на сегодняшний день способ расчета законов программного управления ориентацией КА, исполняемых инерционными органами (ИО), основан на решении так называемой в классической терминологии “прямой задачи динамики” [8, с. 139], в современных терминах – “первой задачи динамики” [9, с. 24]. Эта задача заключается в вычислении сил по априори заданному закону движения. На этом пути расчета законов управления возникает необходимость обращения якобиана, порожденного дифференцированием кинетического момента гиросистемы – суммарного момента количеств движения роторов всех ее гироскопов относительно несущего корпуса КА [10] (краткое название гиростатический момент). Элементы этого якобиана зависят от углов прецессии гироузлов (кардановых колец с несомыми роторами), изменение которых во времени предопределено априори заданным движением КА. Это обстоятельство является причиной вырождения ранга якобиана в рабочем процессе на множестве совместных нулей системы его миноров одного порядка – на так называемом множестве “сингулярных состояний гиросистемы”.

При попадании гироузлов в эти особые положения при исполнении вычисленных управлений КА теряет управляемость. Вывод гироузлов из сингулярных состояний (или обеспечение обхода этих состояний) требует использования дополнительных управлений, так называемых управлений настройки гиросистемы [10]. Эти управления обеспечивают восстановление управляемости аппарата при сохранении в процессе этой настройки его состояния, достигнутого в момент потери управляемости. Отметим, что восстановление управляемости при наличии сингулярных состояний гиросистемы связано с обеспечением ее избыточности [10]. С другой стороны, процесс настройки гиросистемы происходит за счет времени рабочего процесса.

Несмотря на приведенные обстоятельства, сопровождающие исполнение законов управления, вычисленных как решение прямой задачи динамики, эта технология расчета используется вот уже более полувека. Проблеме сингулярности и сегодня посвящен бурный поток работ [11], однако для этой, по образному выражению Crenshaw J.W. “чумы однокарданных управляющих гироскопов” (“…the singularity problems which have plagued other SGCMG concepts” [4]), эффективного средства расчета управлений, обеспечивающего их беспроблемное исполнение, пока найдено не было.

Исходным “рабочим инструментом” гироскопов является гироузел, несущий ротор с собственным кинетическим моментом. Направление кинетического момента ротора изменяется посредством изменения угла прецессии гироузла. Это позволяет создавать нужной величины и направления гиростатический момент. Этот гиростатический момент и определяет управляющую способность гиросистемы. В настоящей статье предлагается обеспечивать решение задачи управляемости КА последовательным использованием непосредственно гиростатического момента, а не его относительной (локальной) производной, применяемой сегодня повсеместно. (Заметим, что относительная производная с точностью до переносного члена в выражении абсолютной производной гиростатического момента определяет управляющий момент, создаваемый гиросистемой. При малых угловых скоростях вращения КА этим переносным членом обосновано пренебрегают [10].)

Предлагаемый здесь новый метод вычисляет закон управления ориентацией аппарата из условия выполнения заданных краевых условий и априори заданной структуры траектории движения, а не закона движения. Закон же движения по заданной траектории в новом методе вычисляется через управление в процессе решения задачи. Рассматривая закон изменения гиростатического момента в качестве непосредственного инструмента управления КА, примем вместо традиционно используемых в качестве законов управления скоростей прецессий гироузлов сами их прецессии – изменение углов прецессий гироузлов в функции времени. В такой постановке задачи расчета законов управления переориентацией КА новый метод, не связанный с дифференцированием, не порождает при расчете управления особых (сингулярных) положений гироузлов. Это гарантирует непрерывное изменение во времени углов прецессии гироузлов, которые определяют закон изменения гиростатического момента и, таким образом, гарантируют безостановочное исполнение гиродинами вычисленных управлений. Отметим, что для осуществления расчета и реализации законов управления новым методом – методом перманентных поворотов – исполнительная гиросистема в процессе ее настройки на выполнение очередного рабочего этапа переориентации не возмущает состояния КА и потому не нуждается в дополнительных исполнительных гироскопах для компенсации таких возмущений.

Обоснование данного утверждения будет приведено во второй части этой статьи. Таким образом, гиросистема, исполняющая новые законы ориентации, не нуждается в избыточности состава гироскопов. В этом ее важное отличие от гиросистем, исполняющих традиционные управления переориентацией. Дополнительный двухкарданный (трехстепенной) гироскоп обеспечивает реализацию новой идеологии расчета законов управления, а не исполнение вычисленных законов.

Важный шаг в создании нового метода расчета управлений, исполняемых гиродинами, заключается и в использовании кинетического момента всего КА в качестве переменной состояния динамической модели. Эта модель наглядно демонстрирует исключительную роль обмена гиростатического момента гиросистемы с кинетическим моментом всего КА в природе эффекта его управляемости. В этом обмене проявляется и важная роль закона сохранения кинетического момента КА.

Дифференцирование гиростатического момента КА открывает “окно”, через которое в процесс расчета управления проникает вирус “проблемы сингулярности”. Использование кинетического момента КА в качестве переменной состояния явилось решающим дополнением к введенной J.W. Crenshaw комбинации кинематических переменных (углов прецессии гироузлов) в создании “противочумной прививки” от “заболевания” проблемой сингулярности.

1. О кинематическом конфигурировании силовых гиросистем. Распространенное на сегодня конфигурирование системы однокарданных силовых безупорных гироскопов (гиродинов), заключающееся в жестком закреплении осей прецессии гироузлов в корпусе аппарата, можно называть геометрическим конфигурированием. Предлагаемое в статье конфигурирование заключается в дополнении традиционного размещения осей прецессии гироузлов в корпусе аппарата не механическим, а кинематическим, программно реализуемым связыванием углов прецессии пар гироузлов с коллинеарными осями прецессии.

Характер этих кинематических связей определился при анализе результатов итерационных расчетов программных управлений с позиции обеспечения управляемости краевых условий в задаче ориентации для достаточно широкого класса динамических моделей КА [12, 13] – КА с инерционными исполнительными органами СУ. Реализуется дополнительное конфигурирование виртуально: вычисленные программные связи скоростей прецессии коллинеарных пар гироузлов численно “прошиваются” в законах вращения гироузлов предварительно и независимо от рабочих программных законов управления гироузлами [7], получаемых в результате расчетов. При пересчете рабочих законов для измененных постановок задач параметры кинематических связей могут настраиваться. Такой подход к конфигурированию исполнительных гиросистем обеспечивает возможность конечношагового расчета в реальном времени таких законов программного управления рабочими режимами КА, которые безостановочно исполняются гиродинами. Результативность предложенного пути решения “проблемы сингулярности” силовых гиросистем будет продемонстрирована во второй части настоящей статьи, посвященной численной реализации нового метода на примере расчета программного управления переориентацией жесткого космического телескопа в общей постановке задачи – для произвольно заданных значений переменных состояния (угловых скоростей и положений) КА в начальный и конечный моменты времени.

К вопросу решения задачи ориентации КА в классе программных управлений логично подойти как к конструктивному решению задачи управляемости в двухточечной нелинейной краевой задаче. Строгому аналитическому обоснованию разработанного на этом пути итерационного метода последовательной линеаризации для расчета управления и численной реализации этого решения посвящены публикации [12, 13], а для расчетов программных управлений и их обоснования в задаче сканирования заданной траектории на подстилающей поверхности планеты – публикации [14–18].

Результаты этих исследований и тестирующих их расчетов, часть которых представлена в названных сейчас работах, оправдали выбор нового пути: ни в одном из моделируемых процессов исполнения гиродинами вычисленных законов для динамических моделей с реальными значениями параметров не было остановок в работе гиросистемы при управлении и жестким, и нежестким аппаратами, а такие остановки возникают при традиционном расчете управлений по априори заданному закону движения в процессе ориентации.

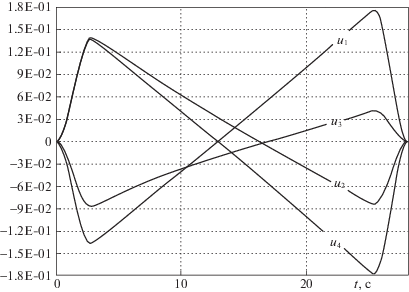
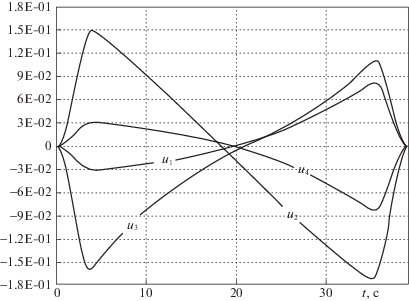
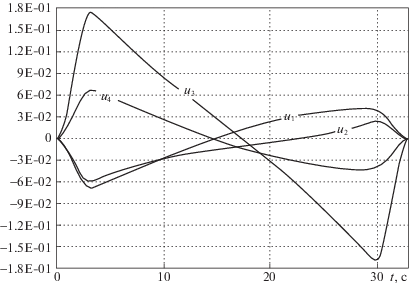
Все законы управления по итерационному алгоритму вычислялись посредством обеспечения свойства вполне управляемости для каждого члена сходящейся последовательности линеаризованных динамических моделей к исходной нелинейной модели системы, состоящей из несущего корпуса КА, несомой полезной нагрузки и СУ с гироскопическими ИО. При анализе результатов расчетов для примеров с системами гиродинов, включающими коллинеарные пары, было замечено, что вычисленные программные законы для отдельных коллинеарных пар были виртуально (программно) синхронизированы следующим простым образом: алгебраическая сумма графиков законов управления (в итерационном методе расчета это – скорости прецессии гироузлов) для отдельных коллинеарных пар тождественно равнялась нулю. Ниже приведены графики программных управлений, вычисленных итерационным методом для отдельных тестовых задач.

Подчеркнем важное обстоятельство: итерационный расчет искомого управления основан на обеспечении управляемости линеаризованной модели объекта. Сходимость последовательности управляемых линейных моделей [13] гарантирует существование решения исходной нелинейной краевой задачи. Таким образом, обнаруженная синхронизация вычисленных законов управления (скоростей вращения гироузлов гиродинов с коллинеарными осями прецессии) при обеспечении управляемости свидетельствует о связи кинематической синхронизации со свойством управляемости – существованием искомого управления.

Однако, как показал анализ вычисленных итерационным путем программных управлений, существуют задачи, для которых полученные безостановочно реализуемые исполнительными гиродинами законы управления могут не обладать свойством описанной выше простейшей синхронизации, а сопровождаются синхронизацией более сложного типа, когда ось виртуального маховика, определяемая алгебраической полусуммой скоростей прецессий гироузлов, для отдельных коллинеарных пар гиросистемы не остается неподвижной, а вращается по особому программному закону. На каждом графике законов управления, полученных из условия управляемости краевых условий для трех задач ориентации, синхронизация простейшего типа имеет место только для одной пары скоростей гироузлов. Таким образом, демонстрируемая на графиках (рис. 1–3) синхронизация простейшего типа, сопровождающая эти решения, не является необходимым условием управляемости в общей ситуации.

Важный для приложений вопрос заключается в определении типа синхронизации, обеспечивающей управляемость для достаточно широкого класса двухточечных нелинейных краевых задач. Обнаруженная связь управляемости краевых условий в нелинейной двухточечной задаче с синхронизацией скоростей вращения гироузлов (производных углов прецессий) коллинеарных пар указывает на целесообразность дополнительно к геометрическому конфигурированию осей прецессии гироузлов связывать углы прецессий коллинеарных пар. Такое расширенное конфигурирование обеспечит управляемость краевых условий в задаче переориентации и, как следствие, – осуществление конечношагового расчета законов управления, нечувствительных к наличию сингулярных положений гироузлов.

Отметим здесь, что в рамках итерационного расчета безостановочно реализуемых управлений гироузлами гиродинов не обеспечивалось отсутствие сингулярных состояний гироузлов. Присутствующие в законах управления сингулярные состояния не прерывали процесса исполнения таких управлений, оказываясь так называемыми “проходимыми состояниями” [10], что обеспечивалось выполнением условий управляемости, лежащих в основе расчета законов управления [11, 12].

В дополнение к конечным геометрическим связям на размещение коллинеарных осей прецессии гироузлов для обеспечения управляемости объекта наложим связи на углы прецессий гироузлов. Поскольку кинематика представляет собой геометрию движения, то для определения расширенного конфигурирования приемлем термин “кинематическое конфигурирование” [18].

Как уже указывалось, механически реализованные кинематические связи использовались и ранее. В работах [2–5] они вводились для механической синхронизации двухстепенных гироскопов. Применялись механические связи и для синхронизации вращения однотипных кардановых колец, спариваемых трех степенных гироскопов (см., например, [19], а также указанные в ней другие работы). В трех степенных гироскопах синхронизация использовалась для компенсации влияния нелинейностей и перекрестных связей за счет измерения моментов на выходных синхронизированных осях гироблоков и введения на основе этих измерений компенсирующих обратных связей.

Приведенные выше графики результатов расчетов управлений итерационным методом посредством обеспечения на каждом линейном шаге свойства управляемости показывают возможность осуществить кинематическую связь программно. Механическая реализация простейшей кинематической синхронизации осей прецессии коллинеарных гироузлов возможна с помощью простейшего редуктора. Однако такая синхронизация повышает сухое трение.

2. Кинематическое конфигурирование гиросистемы заданной структуры. Связанную с КА правую систему координат (ССК) Оxyz выберем по главным центральным осям тензора инерции КА. Чтобы не заслонять основную цель статьи – новую идеологию расчета закона управления, рассмотрим структуру гиросистемы, состоящей из шести гиродинов с тремя коллинеарными парами осей прецессии гироузлов. Применение такой гиросистемы для расчета законов перманентного гашения произвольных значений угловой скорости КА существенно проще решения этой задачи при использовании исполнительной гиросистемы из двух коллинеарных пар четырех гиродинов.

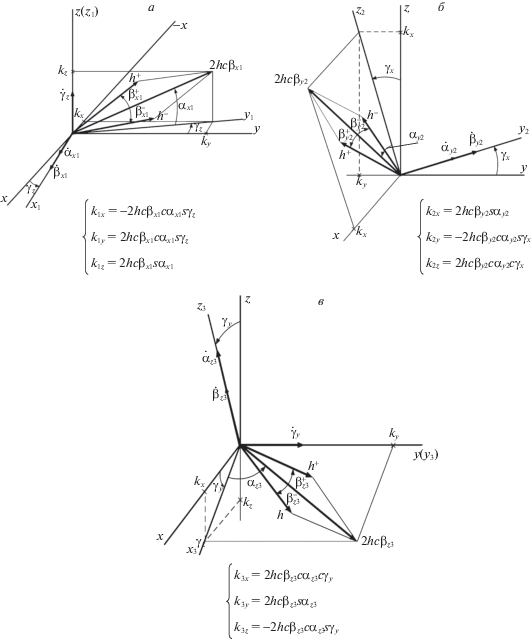
Для синхронизации прецессий гироузлов коллинеарных пар введем параметры J.W. Crenshaw [4]: ${{\alpha }_{i}}(t) = ({{\delta }_{{i1}}}(t) + {{\delta }_{{i2}}}(t)){\text{/}}2$,${{\beta }_{i}}(t) = ({{\delta }_{{i1}}}(t) - {{\delta }_{{i2}}}(t)){\text{/}}2$, где ${{\delta }_{{ij}}}(t)$ – углы реальных прецессий гироузлов, $i = x{\text{'}},y{\text{'}},z{\text{'}}$ – оси прецессий, и $j$ – номер пары коллинеарных гироузлов. Синхронизацию их скоростей прецессий осуществим наложением простейших кинематических связей для каждой из трех коллинеарных пар осей прецессий гироузлов: ${{\alpha }_{i}} = const$, $\beta _{i}^{{}}$ – величина симметризованных углов виртуальной прецессии i-й пары гироузлов: $\beta _{i}^{ + } = ({{\delta }_{{i2}}} - {{\delta }_{{i1}}}){\text{/}}2$ и $\beta _{i}^{ - } = - ({{\delta }_{{i2}}} - {{\delta }_{{i1}}}){\text{/}}2$, одинаковых по величине, но отсчитываемых в противоположные стороны от диагоналей параллелограммов ${{k}_{i}} = h_{{i1}}^{ + } + h_{{i2}}^{ - }$, построенных на собственных кинетических моментах каждой коллинеарной пары гиродинов. Условимся для краткости синхронизированную пару гиродинов с коллинеарными осями прецессии называть “спаркой”. Определим положение осей виртуальной прецессии каждой из трех спарок в связанной с КА системе координат $Oxyz$ – в главных центральных осях тензора инерции. Поскольку кинетические моменты – свободные векторы (таковы, в частности, собственные кинетические моменты гироскопов), то при реальном размещении гироскопов в корпусе КА эти оси могут быть разнесены параллельно их формальным положениям. Промежуточные шаги процедуры кинематического конфигурирования гиросистемы, состоящей из трех коллинеарных пар гиродинов, проиллюстрируем рис. 4а–в.

Положение оси виртуальной прецессии гироузлов первой спарки − линии действия вектора ее суммарного кинетического момента первой спарки (${{k}_{1}} = h_{1}^{ + } + h_{1}^{ - }$ или ${{\alpha }_{1}}(t) = ({{\delta }_{{11}}}(t) + {{\delta }_{{12}}}(t)){\text{/}}2$) определим следующим образом. Повернем систему Oxyz вокруг оси Oz на угол γ_z. Систему координат обозначим Ox₁y₁z. Ось виртуального маховика получим, повернув ось $O{{y}_{1}}$ вокруг оси виртуальной прецессии $O{{x}_{1}}$ на угол ${{\alpha }_{{{{x}_{1}}}}}$.

Здесь использованы обозначения: $c{{\beta }_{{{{x}_{1}}}}} \triangleq cos{{\beta }_{{{{x}_{1}}}}}$, $s{{\alpha }_{{{{x}_{1}}}}} \triangleq sin{{\alpha }_{{{{x}_{1}}}}}$, и аналоги; ${{\beta }_{{{{x}_{1}}}}} \triangleq {\text{|}}\beta _{{{{x}_{1}}}}^{ + }{\text{|}} \equiv {\text{|}}\beta _{{{{x}_{1}}}}^{ - }{\text{|}}$, где $\beta _{{{{x}_{1}}}}^{ + }$, $\beta _{{{{x}_{1}}}}^{ - }$ – углы прецессии гироузлов первой спарки, отсчитываемые в противоположных направлениях от диагонали.

Построим положение осей прецессии гироузлов второй спарки. Систему осей $O{{x}_{2}}{{y}_{2}}{{z}_{2}}$ получим поворотом ССК $Oxyz$ вокруг оси $Ox$ на угол ${{\gamma }_{x}}$. Затем поворотом вокруг оси $O{{y}_{2}}$ на угол ${{\alpha }_{{{{y}_{2}}}}}(t)$ ось $O{{z}_{2}}$ переведем в диагональ ромба ${{k}_{2}} = h_{2}^{ + } + h_{2}^{ + }$ – ось виртуального маховика.

Определим положение оси виртуального маховика третьей спарки. Систему координат Oxyz повернем вокруг оси Oy на угол γ_y против часовой стрелки. Новую систему назовем Ox₃yz₃. Ось прецессии третьей спарки получим, повернув ось Ox₃ вокруг оси Oz₃ на угол ${{\alpha }_{{{{z}_{3}}}}}(t)$.

Положим значения величин ${\text{|}}{{h}_{i}}{\text{|}}$ (здесь i – “имя” спарки) собственных кинетических моментов $h_{i}^{ + }$, $h_{i}^{ - }$ одинаковыми для всех гиродинов – $h$. Общий гиростатический момент ${{k}_{\Sigma }}$ трех спарок представлен его проекциями:

Рассмотрим конфигурацию для случая ${{\gamma }_{i}} = \pi {\text{/}}2$:

3. Расчет гиростатического момента при управлении ориентацией не полностью разгруженного аппарата. Рассмотрим аппарат, состоящий из жесткого корпуса, несущего оборудование, включая систему гиродинов, которая представляет инерциальные исполнительные органы СУ. Считаем, что после расстыковки аппарата с разгонным блоком его кинетический момент полностью не разгружен, а внешний момент не действует. В этих условиях суммарный кинетический момент несущего корпуса аппарата с несомым оборудованием и гиросистемой в инерциальной системе отсчета (ИСО) будет постоянен и не равен нулю: $K_{p}^{{И С О }} = const \ne 0$. В связанной с аппаратом системе отсчета (ССО) кинетический момент системы будем обозначать $K_{р }^{{{\text{С С О }}}}(t)$. Вектор $K_{р }^{{С С О }}(t)$ это – тот же вектор $K_{p}^{{И С О }}$, только наблюдаемый из “окна” CCO. В случае $\omega (t) \ne 0$ ССО вращается, и суммарный кинетический момент аппарата представляется наблюдателю, находящемуся в ССО, переменным во времени вектором $K_{р }^{{{\text{С С О }}}}(t)$. Таким образом, кинетический момент $K_{р }^{{{\text{С С О }}}}(t)$ в связанной с аппаратом системе отсчета определяется как моментом $K_{р }^{{{\text{С С О }}}}(t)$, оставшимся после разгрузки аппарата, так и угловой скоростью вращения аппарата $\omega (t)$. При этом если вращением аппарата вокруг центра масс управляют с помощью инерциальных исполнительных элементов, то его угловая скорость $\omega (t)$ является параметром кинетического момента $K_{р }^{{{\text{С С О }}}}(t)$, независимым от него, и определяется только гиростатическим моментом гиросистемы.

В связанной с КА ССО суммарный кинетический момент аппарата, несущего гиросистему, определяется равенством:

где $I$ – тензор инерции в ССО, включающий инертную массу всех несомых аппаратом элементов; $\omega (t)$ – его угловая скорость КА в ССО, вектор $I\omega (t)$ – кинетический момент несущего корпуса КА; $k(t)$ – кинетический момент гиросистемы в ее движении относительно корпуса (в дальнейшем – гиростатический момент), вычисленный в ССО и играющий роль независимого параметра кинетического момента $K_{р }^{{{\text{С С О }}}}(t).$

Поскольку после разгрузки КА его кинетический момент в ИСО сохраняет постоянное значение $K_{р }^{{И С О }} = const$, его производная в инерциальной системе – абсолютная производная – тождественно равна нулю: $(K_{р }^{{И С О }}){\text{'}} \equiv 0.$ Выразим эту абсолютную производную через локальную производную $\dot {K}_{р }^{{С С О }}$ – производную в осях, связанных с аппаратом:

Отметим, что в осях ССО величинат.е. сохраняет свое значение во все время движения аппарата (для проверки этого утверждения достаточно правую часть равенства (3.2) умножить скалярно на $K_{р }^{{С С О }}$ и проинтегрировать результат). В силу (3.3) угловая скорость аппарата $\omega \left( t \right)$ определяется только гиростатическим моментом $k(t)$.

Из определения (3.1) и установленного свойства угловой скорости ясно, что управлять вращением КА вокруг центра масс, полностью описываемым вектором угловой скорости $\omega \left( t \right)$, возможно только за счет изменения гиростатического момента $k(t)$.

Рассмотрим перманентное вращении КА вокруг оси, определяемой постоянным ортом ${{n}_{0}}$: $\omega (t) = \omega (t){{n}_{0}}$. Перепишем уравнение (3.2):

Примем вектор $K_{р }^{{{\text{С С О }}}}(t)$ за переменную состояния КА и будем рассматривать $\omega (t)$ в (3.3) в качестве независимого от $K_{р }^{{{\text{С С О }}}}(t)$ параметра, определяемого только гиростатическим моментом $k(t)$. Поскольку скалярно зависящая от времени матрица коэффициентов $ - \omega (t)\langle {{n}_{0}}\rangle $ уравнения (3.4) коммутирует со своим интегралом, проинтегрируем это уравнение. В результате интегрирования получим

где принято ${{t}_{0}} = 0$; $\varphi (t)$ – угол поворота КА вокруг перманентной оси, $K_{{р 0}}^{{С С О }} \triangleq K_{р }^{{С С О }}(0)$. Вычислив экспоненту, уравнение перманентного вращения аппарата (3.5) приведем к виду

Заменив, следуя определению (3.1), кинетический момент $K_{р }^{{С С О }}(t)$ его составляющими $I\omega (t)$ и $k(t)$ и учитывая, что (3.6) – описывает перманентное вращение аппарата, перепишем его как

где $L(\varphi (t))$ – ортогональная матрица, представляющая выражение в квадратных скобках в (3.6); (свойство ортогональности матрицы $L(\varphi (t))$ – очевидно из (3.5) в силу кососимметричности $\langle {{n}_{0}}\rangle $). Разложим вектор $k(t)$ на аддитивные составляющие, соответствующие векторам $\omega (t)$ и $K_{р }^{{С С О }}(t)$:

При этом разделении величину ${\text{|}}{{k}_{K}}(t){\text{|}}$ вектора ${{k}_{K}}(t)$ выберем равной постоянному в ССО значению ${\text{|}}K_{р }^{{С С О }}(t){\text{|}} \equiv {\text{|}}K_{p}^{{{\text{И С О }}}}{\text{|}} \equiv {\text{|}}\omega (t)I{{n}_{0}} + k(t){\text{|}} = const$ – первому интегралу уравнений (3.2) в общем случае движения аппарата.

Уравнение перманентного вращения (3.7) при этом примет вид:

При указанном выборе вектора ${{k}_{K}}(t)$ величина вектора $\omega (t)I{{n}_{0}} + {{k}_{\omega }}(t)$ будет тождественно равна нулю: ${\text{|}}\omega (t)I{{n}_{0}} + {{k}_{\omega }}(t){\text{|}} \equiv 0$, следовательно, вовсе время перманентного вращения аппарата будет иметь место векторное равенство:

Таким образом, по построению вектора ${{k}_{K}}(t)$ уравнение перманентного вращения (3.7) распалось на два уравнения: (3.10) и (3.11)

Реализация кинетического момента ${{k}_{K}}(t)$, обеспечивающего выполнение равенства (3.11), осуществляется установкой в КА трехстепенного гироскопа с собственным кинетическим моментом ротора, равным величине ${\text{|}}K_{p}^{{И С О }}{\text{|}}$ неразгруженного кинетического момента $K_{p}^{{И С О }}$. Векторное равенство (3.11) обеспечивается безопорными кардановыми кольцами, несущими ротор, и управляемые электроприводами. Необходимый закон изменения перманентной угловой скорости $\omega (t) = \omega (t){{n}_{0}}$ исполняется вектором ${{k}_{\omega }}(t)$ в силу уравнения (3.10). При известном законе вращения ССО $\omega (t)$ будет известен закон вращения неразгруженного кинетического момента аппарата $L(\varphi (t))K_{{р 0}}^{{С С О }}$. Из (3.11) вычисляются компоненты момента ${{k}_{K}}(t)$, которые реализуются электроприводами кардановых колец. Осуществление всех перечисленных операций представляет чисто техническую проблему.

Активно управляемый вектор гиростатического момента ${{k}_{\omega }}(t)$, определяющий в силу (3.10) в связанной с аппаратом системе отсчета закон перманентного гашения $\omega (t)$, формируется законами прецессий гироузлов, вращаемых электроприводами. Направление же гиростатического момента ${{k}_{K}}(t)$ величиной, равной ${\text{|}}K_{р }^{{И С О }}{\text{|}} = {\text{|}}I\omega (t) + k(t){\text{|}}$, в связанной с аппаратом системе отсчета ССО в процессе гашения скорости $\omega {\text{*}}(t) \to 0$ определяется в синхронном вращении векторов ${{k}_{K}}(t)$ и $K_{{}}^{{С С О }}(t)$: ${{k}_{K}}(t) \equiv L(\varphi {\text{*}}(t))K_{{р 0}}^{{С С О }} \equiv K_{р }^{{С С О }}(t)$. Таким образом, в процессе гашения скорости вектор гиростатического момента ${{k}_{K}}(t)$ индуцирован неразгруженным кинетическим моментом аппарата $K_{p}^{{И С О }}.$ В момент остановки вращения КА связанная система отсчета ССО останавливается и выполняется равенство ${{k}_{K}}({{T}_{0}}) = K_{р }^{{{\text{С С О }}}}({{T}_{0}}) = K_{р }^{{{\text{И С О }}}}$.

Таким образом, при неразгруженном кинетическом моменте аппарата-гиростата по природе его динамики (в отличие от динамики твердого тела) для расчета закона управления, гасящего вращение аппарата, можно воспользоваться уравнением $\omega (t)I{{n}_{0}} + {{k}_{\omega }}(t) = 0$, подобным уравнению, используемому в расчетах управления, для полностью разгруженного аппарата [18]. Формально уравнение (3.10) совпадает с интегралом кинетического момента КА разгруженного аппарата, однако в рассматриваемом случае таковым не является. Обеспечить такой расчет можно за счет разделения гиростатического момента на две части: активную часть ${{k}_{\omega }}(t)$, управляемую гиросистемой и обеспечивающую гашение скорости аппарата, и пассивную часть ${{k}_{K}}(t)$, индуцированную неразгруженным постоянным кинетическим моментом $K_{p}^{{И С О }}$.

Заключение. В работе достаточно подробно изложена новая технология расчета программных управлений ориентацией КА. Прикладному аспекту этой технологии посвящена вторая часть статьи. Результаты численной реализации подтверждают отсутствие в законах управления, вычисленных новым методом, особых положений гироузлов, в которых теряется способность гиросистемы, состоящей из гиродинов, продолжать исполнение вычисленного закона управления. Таким образом, новая технология расчета законов управления не порождает в этих законах сингулярных значений углов прецессии и тем самым решает известную “проблему сингулярности”.