Известия РАН. Теория и системы управления, 2019, № 3, стр. 87-96
Построение математической модели функционирования пенсионных фондов в рамках задачи оценки их устойчивости
А. А. Белолипецкий a, М. А. Лепская b, *
a ВЦ ФИЦ ИУ РАН
Москва, Россия
b МФТИ (ГУ)
Москва, Россия
* E-mail: maria.lepskaya@gmail.com
Поступила в редакцию 22.11.2018
После доработки 25.12.2018
Принята к публикации 28.01.2019
Аннотация
Рассматривается задача моделирования деятельности пенсионных фондов и оценки их финансовой устойчивости. Взяв за базовую стандартную модель Крамера–Лундберга, авторы работы модифицируют ее в результате задания параметров поступления и выплат в фонд в виде случайных величин. При этом имитационное решение задачи функционирования пенсионной схемы и оценки ее устойчивости рассматривается на данных российских реалий, где начальные демографические значения полагаются равными соответствующим значениям на 2018 г., а прогнозные данные и результаты функционирования пенсионной схемы, в том числе исследование ее на устойчивость, – с 2018 по 2036 г. Имитационное моделирование проводится с учетом прогнозируемой динамики ожидаемых показателей смертностей с учетом половозрастной структуры населения.
Введение. В основе проблематики находится поиск вероятности разорения пенсионной схемы на конечном временном интервале и оценка эффективности набора экономических стратегий повышения устойчивости пенсионных схем с учетом возможных сценариев развития демографической обстановки в долгосрочном периоде.
Математическая модель функционирования пенсионных фондов, положенная в основу этой статьи, была детально изложена в предыдущей работе данных авторов [1]. Исследования устойчивости пенсионных схем, нашедшие отражение в настоящей публикации, также базируются на модифицированной модели Камера–Лундберга с учетом задания параметров поступлений и выплат в фонд в виде случайных величин. В качестве случайных величин в модели могут быть рассмотрены время смерти участников пенсионной схемы, количество участников схемы, индексация пенсий, доходность резервов, заработная плата участников пенсионной схемы и прочие экономические параметры. В качестве случайных факторов в постановке задачи приводятся количество человек, вступающих в пенсионную схему в год рассмотрения, и случайная смертность.
В виду долгосрочного характера функционирования пенсионной схемы при описании финансовых потоков пенсионного фонда необходимо учитывать изменения основных демографических параметров общества: уровней рождаемости и ожидаемой продолжительности жизни.
Для рассмотрения долгосрочной динамики этих показателей на российских реалиях предлагается использовать прогноз Росстата [2], представленный в трех сценариях: пессимистичном, среднем и оптимистичном. Половозрастная структура населения Российской Федерации (в расчете на 1 млн. чел.) по состоянию на 2018 г. представлена в левой части рис. 1, в правой части рис. 1 – три сценария прогноза Росстата на 2036 г.
Рис. 1.
Текущий и прогнозный половозрастной состав населения Российской Федерации (в расчете на 1 млн. чел.)
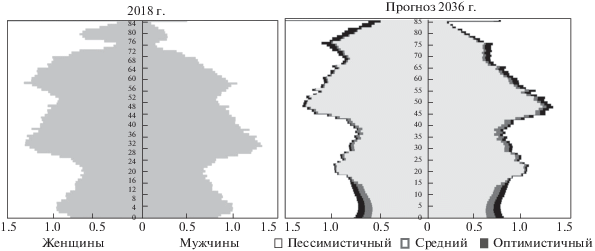
Текущие значения состояния общества показывают, что в ближайшие 20 лет будет наблюдаться сильное увеличение доли пенсионеров в виду неравномерного распределения по возрастным группам населения страны (левая часть рис. 1). Правая же часть рис. 1 говорит о прогнозном увеличении средней продолжительности жизни. Из этого можно сделать предположение, что в течение последующих 20 лет возможны несколько экономических сценариев и/или их комбинаций для обеспечения потенциальной устойчивости пенсионной схемы: повышение нагрузки выплат на рабочее население, недоиндексация пенсий и отставание роста доходов пенсионеров, повышение пенсионного возраста.
Особенно чувствительными к колебаниям демографического состава участников оказываются негосударственные пенсионные фонды, обладающие большей дисперсией финансовых результатов.
В настоящей работе ставится задача оценки эффективности вышеописанных стратегий повышения устойчивости пенсионных схем с учетом возможных сценариев развития демографической обстановки в долгосрочном периоде.
1. Постановка задачи и математические модели. 1.1. Моделирование демографического состава участников пенсионной схемы. В произвольный момент времени $t$ возрастной состав общества может быть представлен в виде вектора
Первый элемент этого вектора соответствует числу новорожденных, которое в каждый год t мы будем считать случайной величиной с некоторым известным распределением
Рассмотрим группу $N(t,x)$ людей, которые в год $t$ находятся в возрасте $x$ лет. В год t + 1 их возраст составит соответственно x + 1 лет, а их число может быть представлено следующим образом:
где сумма берется по всей рассматриваемой группе, а величины ${{\xi }_{i}}(t,x)$ являются индикаторами события, состоящего в том, что $i$-й член рассматриваемой группы пережил прошедший годЗдесь сделано предположение об однородности членов заданной возрастной группы, выражающейся в фиксированный год t в равенстве вероятностей $p(t,x)$ пережить x + 1 год жизни для всех членов группы. С учетом такого определения величин ${{\xi }_{i}}(t,x)$ выражение (1.1) представляет из себя сумму числа успехов в $N(t,x)$ одинаковых испытаниях Бернулли, а величина $N(t + 1,x + 1)$ имеет биномиальное распределение
Зависимость вероятности пережить $x + 1$ год жизни $p(t,x)$ от времени отражает в себе изменение ожидаемой продолжительности жизни в долгосрочном периоде.
В результате обобщения вышесказанного для всех возрастных групп возрастной состав общества в $t + 1$ год может быть представлен как
(1.2)
${{{\mathbf{N}}}_{{t + 1}}} = \left[ \begin{gathered} N(t + 1,0) \\ N(t + 1,1) \\ ... \\ N(t + 1,x) \\ ... \\ N(t + 1,R) \\ \end{gathered} \right] \sim \left[ \begin{gathered} n(t) \\ Bin(N(t,a),p(t,1)) \\ ... \\ Bin(N(t,х - 1),p(t,x - 1)) \\ ... \\ Bin(N(t,R - 1),p(t,R - 1)) + Bin(N(t,R),p(t,R)) \\ \end{gathered} \right].$Таким образом, зная возрастной состав общества в произвольный год $t$, можно спрогнозировать его динамику в течение любого временного промежутка.
1.2. Математическая модель пенсионной схемы. Введем следующие предположения относительно рассматриваемой пенсионной схемы:
1) участники вступают в пенсионную схему и начинают платить взносы в возрасте $a$ лет;
2) достигнув возраста $r$ лет, участник выходит на пенсию и начинает получать пенсионные выплаты;
3) число людей возраста a, вступающих в пенсионную схему в $t$-й год, пропорционально совокупному числу членов общества возраста $a$ с коэффициентом пропорциональности $k$;
4) вступление и выход из пенсионный схемы в возрасте, отличном от $a$, невозможны.
Тогда возрастной состав участников пенсионной схемы в произвольном году $t + 1$ может быть представлен следующим вектором
(1.3)
${{{\mathbf{M}}}_{{t + 1}}} = \left[ \begin{gathered} M(t + 1,a) \\ ... \\ M(t + 1,x) \\ ... \\ M(t + 1,r) \\ ... \\ M(t + 1,R) \\ \end{gathered} \right] \sim \left[ \begin{gathered} kN(t + 1,a) \\ ... \\ Bin(M(t,х - 1),p(t,x - 1)) \\ ... \\ Bin(M(t,r - 1),p(t,r - 1)) \\ ... \\ Bin(M(t,R - 1),p(t,R - 1)) \\ \end{gathered} \right],$Умножая вектор ${{{\mathbf{M}}}_{t}}$ на квадратную матрицу E+ соответствующей размерности с единицами на первых $r$ диагональных элементах, получим вектор ${\mathbf{M}}_{t}^{ + }$, содержащий только работающую часть участников пенсионной схемы. Аналогично умножением ${{{\mathbf{M}}}_{t}}$ на квадратную матрицу E– соответствующей размерности с единицами на последних $R - r$ диагоналях получим вектор ${\mathbf{M}}_{t}^{ - }$, характеризующий число пенсионеров.
Введем в рассмотрение функцию $s(x)$, характеризующую средний размер заработной платы, получаемый работником возраста $x$. Будем считать, что средний уровень заработных плат ежегодно изменяется на $\Theta $ процентов.
Начальная годовая ставка пенсионных выплат является долей f от последней ставки заработной платы перед выходом на пенсию. Таким образом, для участника схемы, выходящего на пенсию (т.е. достигающего возраста $r$) в момент времени $t$, прогнозируемая годовая ставка пенсионных выплат составит $fs(r){{e}^{{\theta t}}}$, где ${{e}^{\theta }} = 1 + \Theta $.
Введем поправочный коэффициент $h(x)$, применяемый к исходной ставке пенсионных выплат размера $fs(r){{e}^{{\theta (t - (x - r))}}}$ тем лицам, которые вышли на пенсию $x - r$ лет назад. Заметим, что $h(r)$ = 1. Например, $h(x)$ может быть экспоненциальной функцией ${{e}^{{\omega (x - r)}}}$, где $\omega $ – постоянный коэффициент прироста, определяемый уровнем ежегодной индексации пенсий $\Omega = {{e}^{\omega }} - 1$.
Таким образом, для пенсионера возраста $x$ в момент времени $t$ прогнозируемая годовая ставка пенсионных выплат будет определена следующим выражением:
(1.4)
${{b}_{t}} = fs(r){{e}^{{\theta (t - (x - r))}}}{{e}^{{\omega (x - r)}}} = fs(r){{e}^{{\theta t}}}{{e}^{{(\omega - \theta )(x - r)}}} = {{e}^{{\theta t}}}F(x).$Взносы работающих участников пенсионной схемы будем считать долей $z$ от получаемой ими заработной платы, таким образом, взнос участника возраста $x$ в момент времени $t$ составит
1.3. Математическая модель процесса накопления и расходования средств пенсионного фонда. Составим вектор следующего вида:
Тогда, с учетом выражения (1.5), совокупный годовой объем взносов всех работающих в пенсионный фонд в год $t$ может быть найден как
а совокупный годовой объем всех пенсионных выплат с учетом выражения (1.4) составит где вектор Mt представляет собой вектор (1.3), характеризующий возрастной состав участников пенсионной схемы.Сумма этих двух показателей представляет собой приращение объема пенсионного фонда в t-м году и определяется как
(1.6)
$\Delta {{H}_{t}} = {{Q}_{t}} + {{B}_{t}} = {{e}^{{\theta t}}}{{{\mathbf{V}}}^{{\text{T}}}}{{{\mathbf{M}}}_{t}}.$Здесь учтен тот факт, что сумма матриц ${{E}^{ + }}$ и ${{E}^{ - }}$ дает единичную матрицу, вследствие чего произведение векторов становится скалярным.
С учетом выражения (1.6) объем средств пенсионного фонда в произвольный момент времени $t$ может быть найден следующим образом:
(1.7)
${{{\mathbf{H}}}_{t}} = {{H}_{0}} + \sum\limits_{j = 1}^t {{{e}^{{\theta j}}}{{{\mathbf{V}}}^{{\text{T}}}}{{{\mathbf{M}}}_{t}}} ,$Предположим также, что по результатам каждого финансового года средства фонда, оставшиеся после всех выплат, размещаются на финансовом рынке с фиксированной средней ставкой доходности $i$ процентов. Тогда выражение (1.6) для приращения объема фонда в t-м году должно быть переписано с учетом инвестиционного дохода от размещения средств, накопленных к концу предыдущего периода:
а выражение для процесса (1.7) может быть представлено как(1.8)
${{H}_{t}} = {{H}_{0}}{{(1 + i)}^{t}} + \sum\limits_{j = 1}^{t - 1} {{{e}^{{\theta (t - j)}}}{{{(1 + i)}}^{j}}{{{\mathbf{V}}}^{T}}{{{\mathbf{M}}}_{{t - j}}}} .$Важно отметить, что в силу линейности процесса (1.8) относительно вектора состава участников Mt рассмотрение пенсионных схем с возможностью вступления/выхода в произвольном возрасте, отличном от $a$, равно как и схем с неоднородным (например, по половому признаку) составом участников, может быть произведено через суперпозицию соответствующих процессов (1.8).
Так, процесс накопления и расходования средств пенсионного фонда с учетом различия социально-демографических характеристик по половому признаку может быть представлен в виде следующего выражения:
(1.9)
${{{\mathbf{H}}}_{t}} = {{H}_{0}}{{(1 + i)}^{t}} + \sum\limits_{j = 1}^{t - 1} {{{e}^{{\theta (t - j)}}}{{{(1 + i)}}^{j}}[{{{\mathbf{V}}}^{{\text{T}}}}({{r}_{w}}){\mathbf{M}}_{{t - j}}^{w} + {{{\mathbf{V}}}^{{\text{T}}}}({{r}_{m}}){\mathbf{M}}_{{t - j}}^{m}]} ,$В качестве меры устойчивости пенсионного фонда на конечном временном промежутке [0, T] будем использовать вероятность его разорения, определенную следующим образом:
Процесс (1.9) не является Марковским в силу того, что его значения зависят от всей предыстории развития процессов (1.3) и (1.4). Благодаря этому факту, а также общей сложности рассматриваемых взаимосвязей решение задачи нахождения вероятности (1.18) в аналитическом виде представляется затруднительным. В такой ситуации представляется целесообразным использование методов имитационного моделирования.
2. Имитационное моделирование. 2.1. Постановка эксперимента. Рассмотрим пенсионный портфель при фиксированных параметрах $a$ и $R$. Имитационный эксперимент поставим следующим образом: для $t = \overline {1,T} $ будем последовательно генерировать потоки случайных величин $n(t)$ и $\{ N(t,x)\} _{{x = 0}}^{R}$, на основании которых сформируем выборки значений процесса изменения возрастного состава участников фонда Mt.
Далее, для фиксированных значений параметров $i$, $\Theta $ и $\Omega $, а также пенсионных возрастов ${{r}_{w}}$ и ${{r}_{m}}$ с использованием полученных значений Mt рассчитаем динамику финансовых потоков пенсионного фонда и составим выборку значений процесса его накопления (1.9). На основе полученных выборок вероятность разорения фонда определяется как отношения числа реализаций соответствующего процесса, содержащих значения $H(t) < 0$, к общему числу проведенных экспериментов. Далее, повторяя описанную последовательность действий при различных значениях параметров, получим оценку влияния этих параметров на устойчивость пенсионного фонда.
В качестве распределения величины $n(t)$ – числа новорожденных в $t$-м году – используем распределение Пуассона, описывающее число независимых событий, произошедших на конечном временном интервале. Параметр распределения $\lambda (t)$ будем описывать прогнозируемой Росстатом численностью новорожденных в период 2019–2036 гг. [2].
Вероятность индивида пережить $x + 1$ год своей жизни $p(t,x)$, определяющая распределения случайных величин $\{ N(t,x)\} _{{x = 0}}^{a}$ и $\{ M(t,x)\} _{{x = a}}^{R}$, может быть оценена как отношение прогнозной численности группы населения возраста $x + 1$ в год $t + 1$ к численности группы возраста $x$ в год $t$. При моделировании динамики ожидаемых уровней рождаемости и смертности рассмотрим все три представленных в прогнозе Росстата сценария.
В качестве параметра $k$, определяющего долю населения, который участвует в пенсионном фонде, используем значение 10–3, примерно соответствующее негосударственному пенсионному фонду средних размеров [3]. Начальное распределение участников пенсионной схемы по возрастам и полу будем считать соответствующим социально-демографическому распределению населения в 2018 г.
Долю забортной платы, подлежащей отчислению в пенсионный фонд, положим равной 22%, в соответствии со значением основного тарифа страховых взносов на обязательное пенсионное страхование Пенсионного фонда Российской Федерации. Для моделирования зависимости заработной платы от возраста работника $s(x)$ воспользуемся статистикой средних уровней заработной платы по различным возрастным группам в первом квартале 2018 г., представленной в статистических сборниках Росстата [4]. На основании данных Росстата о среднем уровне назначенных пенсий за первый квартал 2018 г. [4] рассчитаем показатель f (отношение первой полученной пенсии к последней зарплате) как отношение среднего уровня назначенной пенсии к среднему уровню заработной платы в предпенсионной возрастной группе, который по указанным данным оказывается равным 40.87%. За единицу измерения денежных средств принимается пиковый уровень средней по стране годовой заработной платы, приходящийся на промежуток 30–35 лет и равный 510 тыс. руб.
В каждом проведенном эксперименте были использованы 103 реализаций модели. Возраст вступления в пенсионную схему полагается равным a = 18 лет, старшая возрастная группа соответствует возрастам $R \geqslant 85$ лет. Если не оговорено иное, темп роста заработных плат $\Theta $ соответствует уровню 2018 г. и равен 4.1%, уровень индексации пенсий $\Omega = $ 2.5%, доходность резервов определена на характерном для банковских вкладов уровне i = 8%. Пенсионный возраст, по умолчанию, полагается равным 60 и 55 лет для мужчин и женщин соответственно. Период прогнозирования $T$ определяется наличием данных и составляет 18 лет [5, 6].
2.2. Результаты экспериментов. Рассмотрим распределения конечного объема фонда к 2036 г. при нулевом начальном объеме и описанных выше экономических параметрах, представленных на рис. 2.
Рис. 2.
Эмпирические распределения объема пенсионного фонда к 2036 г. для различных демографических сценариев
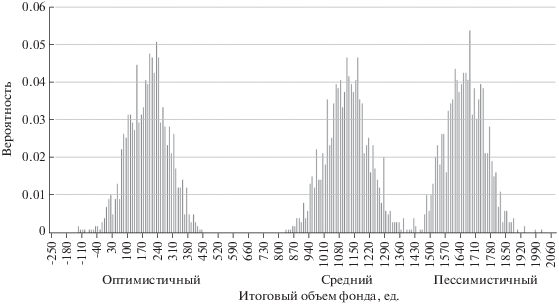
Видно, что наилучший финансовый результат пенсионного фонда достигается при реализации пессимистичного демографического сценария, а наихудший – в случае оптимистичного. Такое положение дел объясняется заметным увеличением средней продолжительности жизни в среднем сценарии по сравнению с пессимистичным при значительно меньших различиях в количестве работающего населения. Оптимистичный сценарий включает в себя также существенное увеличение старшей возрастной группы, создающей дополнительную нагрузку на пенсионный фонд.
Эмпирические распределения на рис. 2 позволяют оценить уровень неопределенности результатов фонда, который при разумных экономических параметрах оказывается сопоставим с абсолютными объемами фонда. Данный факт, иллюстрирующий существенную зависимость итогов деятельности фонда от случайных колебаний демографического состава его участников (характерную для пенсионных фондов с относительно небольшим числом участников, составляющим порядка 105–106 чел.), подтверждает обоснованность стохастического подхода к моделированию финансовой деятельности негосударственных пенсионных фондов [7].
Рассмотрим характер влияния основных параметров модели на ожидаемые результаты деятельности фонда. Минимальным требованием к успешной пенсионной схеме является неуменьшение реальных доходов пенсионеров, которое в рамках настоящей модели может быть интерпретировано как превышение темпами индексации пенсий Ω темпа роста заработных плат Θ [8].
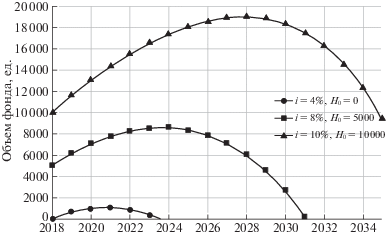
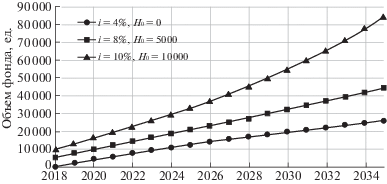
На рис. 3 показана ожидаемая динамика объема пенсионного фонда в среднем демографическом сценарии при темпе индексации пенсий Ω, равном темпу роста заработных плат Θ = 4.1% и различных параметрах доходности резервов i и начального объема фонда ${{H}_{0}}$. Видно, что выполнение требования сохранения реальных доходов пенсионеров неизбежно приводит к более раннему или позднему разорению пенсионного фонда. Увеличение параметров i и ${{H}_{0}}$ в разумных пределах может оттянуть этот срок, но не изменить характер зависимостей. Таким образом, доходность и объем резервов имеют достаточно ограниченное воздействие на устойчивость пенсионной схемы.
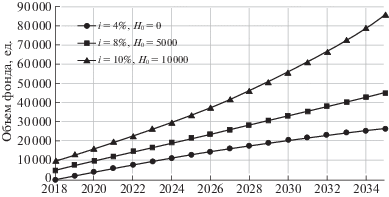
Для сравнения уменьшение уровня индексации пенсий в 2 раза, при прочих равных, приводит к принципиальному изменению картины (рис. 4). В этих условиях ожидаемый объем фонда неограниченно растет. Характер этого роста в зависимости от совокупности параметров i и ${{H}_{0}}$ может варьироваться от логарифмического до экспоненциального [9].
Схожего результата можно добиться за счет увеличения порога пенсионного возраста. Так, при используемых значениях параметров увеличение пенсионного возраста для мужчин и женщин на один год позволяет обеспечить уровень индексации пенсий равный темпам роста заработной платы (рис. 5).
Рис. 5.
Ожидаемая динамика объема пенсионного фонда при Ω = Θ = 4.1%, ${{r}_{m}} = $ 61, ${{r}_{w}} = $ 56
Описанная картина наблюдается в независимости от абсолютных значений параметров Ω и Θ. Таким образом, при фиксированном пороге пенсионного возраста и уровне нагрузки на работающее население соотношение темпа индексации пенсий и темпа роста заработных плат является основным параметром, определяющим устойчивость пенсионной схемы. На рис. 6 представлены значения максимального уровня темпа индексации пенсий, обеспечивающего 95% уверенность в неразорении пенсионного фонда на рассматриваемом временном промежутке, в зависимости от наблюдаемого уровня темпов роста заработной платы (используется средний демографический сценарий).
Рис. 6.
Зависимость максимального темпа индексации пенсий, обеспечивающего 95%-ную вероятность неразорения фонда, от темпа роста заработной платы при различных уровнях пенсионного возраста
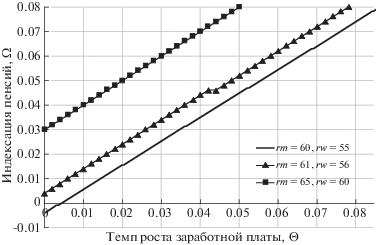
Видно, что максимальный достижимый уровень индексации пенсий прямо пропорционален темпу роста заработной платы. Расстояние от прямой до начала координат при этом определяется в первую очередь порогом пенсионного возраста. Таким образом, в рамках рассматриваемой модели для заданного порога пенсионного возраста существует максимально достижимое соотношение уровня индексации пенсий и темпа роста заработной платы.
В частности, из рис. 6 видно, что при порогах пенсионного возраста 60 и 55 лет для мужчин и женщин соответственно при определенных ранее параметрах модели по умолчанию уровень индексации пенсий, больший или равный темпам роста заработной платы, оказывается недостижим.
При соотношениях Ω и Θ, близким к критическим, важную роль начинают играть иные параметры модели. Так, на рис. 7 показана характерная зависимость вероятности разорения пенсионного фонда от доходности резервов и реализации различных демографических сценариев при Ω = Θ и порогах пенсионного возраста 61 и 56 лет для мужчин и женщин соответственно.
Рис. 7.
Зависимость вероятности разорения пенсионного фонда от ставки доходности резервов в различных демографических сценариях
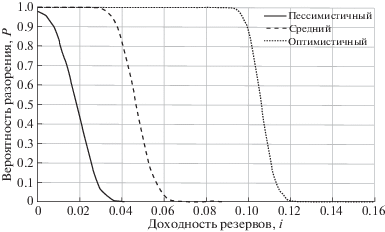
Наконец, при заданных значениях доходности резервов и ожидаемых демографических показателей может быть оценен минимальный уровень пенсионного возраста, позволяющий с достаточной уверенностью обеспечить требуемый уровень роста благосостояния пенсионеров.
Так, на рис. 8 показаны минимальные уровни пар порогов пенсионного возраста $({{r}_{m}},{{r}_{w}})$, позволяющие обеспечить тот или иной уровень индексации пенсий с 95%-ной вероятностью неразорения фонда при прочих параметрах, взятых по умолчанию (средний демографический сценарий).
Рис. 8.
Минимальные уровни пенсионного возраста, обеспечивающие 95%-ную вероятность неразорения фонда
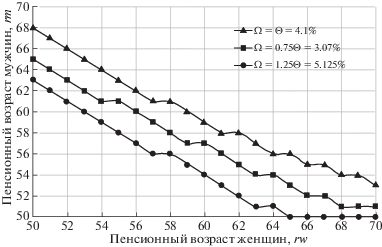
В частности, из графиков на рис. 6 и рис. 8 следует, что повышение порогов пенсионного возраста до уровня 65 и 55 лет для мужчин и женщин соответственно должно обеспечить возможность индексации пенсий на уровне, в 1.73 раза превышающем темп роста заработных плат.
Заключение. Стохастический характер финансовых потоков пенсионных фондов требует применения при их рассмотрении теоретико-вероятностного подхода. В рамках такого подхода факторами неопределенности должны выступать как параметры страхового портфеля фонда, так и колебания макроэкономических параметров. В виду сложности рассматриваемых закономерностей для оценки устойчивости пенсионного фонда эффективным оказывается применение методов имитационного моделирования.
Подобный подход к моделированию деятельности негосударственных пенсионных фондов на реальных демографических и экономических данных Российской Федерации при минимальном количестве исходных предположений позволил получить достаточно обоснованные результаты, хорошо соотносящиеся с действительным положением дел.
В частности, анализ финансовых потоков пенсионного фонда, основанный на текущих демографических прогнозах при разумных значениях актуальных экономических параметров (уровень инфляции, индексации заработной платы и пр.) подтвердил невозможность обеспечения роста реальных доходов пенсионеров в долгосрочном периоде при сохранении порогов пенсионного возраста на уровне 60/55 лет. В то же время реализуемое в рамках пенсионной реформы повышение пенсионного возраста при сохранении значений прочих параметров должно обеспечить возможность индексации пенсий на уровне, более чем в 1.5 раза превышающем темпы роста заработной платы.
Предложенные имитационные алгоритмы могут быть использованы для оценки влияния на устойчивость пенсионных фондов параметров формирования пенсионных взносов и выплат, а также стратегий управления резервами, исследования чувствительности результатов деятельности фонда к изменениям внешних факторов и макроэкономических показателей.
Список литературы
Belolipetskii A.A., Lepskaya M.A. A Mathematical Model of Pension Fund Operation and Methods of Fund Stability Analysis // Computational Mathematics and Modeling. 2018. V. 29. Iss. 2. P. 233–243.
Предположительная численность населения Российской Федерации до 2035 года: Статистический бюллетень. М.: Росстат, 2018. 331 с.
Обзор ключевых показателей негосударственных пенсионных фондов: информационно аналитическое издание // Центральный банк Российской Федерации. 2-й квартал, 2017. М.: Центральный банк РФ, 2017. 19 с.
Социально-экономическое положение России. № 9. Январь–сентябрь 2018 года: Статистический сборник. М.: Росстат, 2018. 366 с.
Демографический ежегодник России. 2017: Статистический сборник / Под ред. Г.К. Оксенойта, С.Ю. Никитана, Е.М. Андреева и др. М.: Росстат, 2017. 265 с.
Королев В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска. М.: Физматлит, 2007. 542 с.
Виноградов О.П. Об одном элементарном методе получения оценок вероятности разорения // Обозрение прикладной и промышленной математики. 1998. Т. 5. Вып. 1. С. 134–149.
Бойков А.В. Модель Крамера-Лундберга со стохастическими премиями // Теория вероятностей и ее применение. 2002. Т. 47. Вып. 3. С. 549–553.
Глухова Е.В., Змеев О.А., Ливщиц К.И. Математические модели страхования. Томск: Изд-во Томск. ун-та, 2004. 180 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления