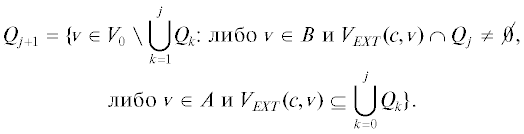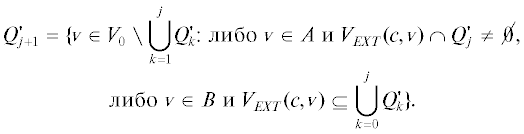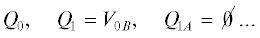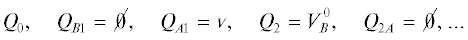Известия РАН. Теория и системы управления, 2019, № 3, стр. 97-105
ОЦЕНКА СЛОЖНОСТИ АЛГОРИТМА ПОТЕНЦИАЛЬНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЦИКЛИЧЕСКИХ ИГР НА ГРАФАХ
И. А. Башлаева a, *, Д. В. Ковков b
a Волгоградский государственный ун-т
Волгоград, Россия
b Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
* E-mail: bashlaeva_ia@volsu.ru
Поступила в редакцию 01.10.2018
После доработки 27.12.2018
Принята к публикации 28.01.2019
Аннотация
Дано уточнение верхней оценки сложности алгоритма потенциальных преобразований для решения циклических игр на графах. Оценка близка к нижней оценке сложности алгоритма потенциальных преобразований. Получено сведение задачи об оптимальном уклонении к решению циклических игр на ориентированных графах.
Введение. В работе рассматриваются циклические игры с полной информацией на графах и проводится анализ сложности алгоритма потенциальных преобразований данного алгоритма решения таких игр. Циклические игры анализировались в [1], близкие постановки и результаты представлены в [2, 3].
В [4] изучается сложность нахождения цены и оптимальных стратегий со средними платами на графах, семейства игр с полной информацией, введенных Эренфехтом и Мичельским и рассмотренных в [1]. Описывается алгоритм псевдополиномиального времени для решения таких игр. Представлено их полиномиальное сведение к простым стохастическим играм, изученным Кондоном.
В [5] рассматриваются некоторые хорошо известные семейства стохастических игр двух лиц с нулевой суммой на конечных ориентированных графах. Сюда включают стохастические паритетные игры, стохастические средние игры с выигрышем и простые стохастические игры. Установлено, что решения игр в каждом из этих классов (количественно или стратегически) являются все полиномиальными по времени. Кроме того, строится линейный по времени алгоритм, который для заданной простой стохастической игры и значений всех положений этой игры вычисляет пару оптимальных стратегий.
В [6] представлены алгоритмы и их сложность для задачи нахождения равновесий (смешанные равновесия Нэша, чистые равновесия Нэша и коррелированные равновесия) в играх, которые определены на высокорегулярных графах, таких, как $d$-мерная решетка; утверждается, что такие игры представляют интерес для моделирования больших систем взаимодействующих агентов. Показано, что смешанные равновесия Нэша могут быть найдены за экспоненциальное время, в то время как коррелированные равновесия могут быть найдены за полиномиальное время.
В [7] доказывается NP-полнота двух задач на орграфах, связанных с игровыми стратегиями. Изучается сложность классических задач абстрактной алгебры относительно существования решений алгебраических уравнений.
В [8] предлагается новый параметр для сложности конечных ориентированных графов, который измеряет, в какой степени циклы графов переплетаются. Эта мера, называемая запутанностью, определяется посредством игры, которая несколько похожа по духу на игры полицейских и разбойников, используемых для описания ширины дерева. На многих классах графов существуют значительные различия между запутанностью и различными воплощениями ширины дерева. Запутанность тесно связана с вычислительной и описательной сложностью модального исчисления. С одной стороны, количество переменных с фиксированной точкой, необходимых для описания конечного графа до бисимуляции, фиксируется его запутанностью. Это играет решающую роль в доказательстве строгой иерархии исчисления. В дополнение к этому доказано, что паритетные игры, ограниченные запутанностью, могут быть решены за полиномиальное время. В частности, установлено, что сложность решения паритетной игры может быть параметризована через минимальную запутанность подыгры, вызванной выигрышной стратегией.
В [9] грабитель и k полицейских выбирают стартовые вершины в графе и чередуются от вершины к вершине по дугам графа; захват происходит, если полицейский когда-либо разделяет вершину с грабителем. Если $k$ не фиксировано и если граф является ориентированным или указаны начальные положения, то показано, что данная задача является EXPTIME-полной. Подобные методы приводят к PSPACE- и EXPTIME-полноте некоторых других комбинаторных игр, которые ранее были известны только как NP- и PSPACE-трудные.
В [10] представлены несколько игр двух лиц, основанных на простых комбинаторных идеях, для которых проблема решения, выиграл ли первый игрок, является полной в полиномиальном пространстве. Это дает убедительное подтверждение, хотя и не абсолютное доказательство того, что эффективных общих алгоритмов для определения победителя этих игр не существует. Если бы был известен полиномиальный по времени алгоритм для решения какой-либо из этих игр, то это означало бы возможность полиномиального по времени решения для а) всех остальных таких игр, б) всех NP-полных задач и в) вообще любой задачи, разрешимой полиномиальной лентой, ограниченной машиной Тьюринга.
В [1] $I(n)$ обозначает число линейных итераций вспомогательного алгоритма. Из доказательства конечности алгоритма следует верхняя оценка его битовой сложности, которая равна $O({{n}^{2}}{\text{log}}(nM)I(n))$. Непосредственная оценка, вытекающая из конструкции алгоритма числа итераций, есть $I(n) = O({{2}^{{nlog(n)}}})$. Число применений вспомогательного алгоритма полиномиально от размера исходной задачи, а число итераций вспомогательного алгоритма экспоненциально от размера задачи. В работе проведен анализ экспоненциальной оценки $I(n)$ числа итераций вспомогательного алгоритма. Дана верхняя оценка сложности от размера исходной задачи I(n) = = $O({{2}^{n}})$. Известны примеры с достижимой экспоненциальной сложностью вспомогательного алгоритма, равной $I(n) = \Omega ({{2}^{{n/2 - 1}}})$. Таким образом, общая оценка сложности алгоритма потенциальных преобразований есть $O(mlog(nM){{2}^{n}})$. Алгоритм потенциальных преобразований из [1] превосходит в гарантированном варианте алгоритм, приведeнный в [11]. Оценка сложности алгоритма из цитируемой работы равна $O(mnlog(M){{2}^{n}})$. Известно, что алгоритм потенциальных преобразований имеет также и псевдополиномиальную оценку сложности $O({\text{poly(}}Mn))$.
Хотя теоретическая оценка сложности данного алгоритма экспоненциальна, но на практике число итераций алгоритма не превосходит более чем в несколько раз числа вершин в графе игровой сети. Во многом данный алгоритм близок к симплекс-методу решения задачи линейного программирования. Случай отсутствия конфликта существенно проще, возникает задача поиска максимального по среднему весу цикла. Эта задача полиномиально разрешима.
Представленные циклические игры имеют важные применения к вопросам корректности параллельных распределенных систем. Анализ паралельных программ, использующих общую память или анализ корректности управляющих схем на логических элементах [12], сводим к анализу соответствующей циклической игры. Практические задачи параллельных распределенных систем имеют большую размерность, поэтому эффективность алгоритмов решения важна в практике циклических игр, где M – максимальная по модулю стоимость перехода игровой сети, а $n$ – число вершин в графе переходов. В настоящей статье представлена близкая к оптимальной оценка сложности данного алгоритма и решен один из вопросов, сформулированных в [11]. В цитируемой работе вводятся в рассмотрение игры об оптимальном уклонении веса траектории от нуля и с помощью введенных игр решаются циклические игры с средним выигрышем по траектории. Другими словами, построено полиномиальное сведение циклических игр к играм на оптимальное уклонение и представлен алгоритм решения игр на уклонение. Поставлен вопрос о полиномиальной эквивалентности циклических игр и игр на оптимальное уклонение и дан положительный ответ на него. Полученный результат выделяет алгоритм потенциальных преобразований как наилучший алгоритм (в теоретическом смысле) из имеющихся алгоритмов решения циклических игр. Этот алгоритм не хуже динамического программирования – в общем случае метод потенциальных преобразований имеет такую же псевдополиномиальную оценку сложности, что и динамическое программирование и превосходит динамическое программирование уже на игровых сетях с фиксированным числом вершин.
В [1] рассматриваются минимаксные средние циклы (о теории минимакса см. также [13, 14]).
1. Постановка задачи. Пусть $G = (V;E)$ – ориентированный граф, $A$ и $B$ – выделенные подмножества вершин: 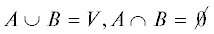 , $c:V \to Z$ – целочисленная весовая функция, определенная на ребрах графа. Ориентированное ребро
с началом в вершине $u$ и концом в вершине $v$ обозначим $(u,v)$. Далее $E({{V}_{1}},{{V}_{2}})$ – ребра с началами в вершинах ${{V}_{1}}$ и концами в вершинах ${{V}_{2}}$; $E({{V}_{1}})$ – ребра с началами в вершинах ${{V}_{1}}$; $V({{V}_{1}})$ – множество концевых вершин ребер с началами в вершинах ${{V}_{1}}$. Предполагаем беступиковость графа, т.е. множество $E(v)$ не пусто для каждой вершины $v \in V$.
, $c:V \to Z$ – целочисленная весовая функция, определенная на ребрах графа. Ориентированное ребро
с началом в вершине $u$ и концом в вершине $v$ обозначим $(u,v)$. Далее $E({{V}_{1}},{{V}_{2}})$ – ребра с началами в вершинах ${{V}_{1}}$ и концами в вершинах ${{V}_{2}}$; $E({{V}_{1}})$ – ребра с началами в вершинах ${{V}_{1}}$; $V({{V}_{1}})$ – множество концевых вершин ребер с началами в вершинах ${{V}_{1}}$. Предполагаем беступиковость графа, т.е. множество $E(v)$ не пусто для каждой вершины $v \in V$.
Вершины B $(A)$ называют вершинами первого (второго) игроков. Рассматривается следующая позиционная антагонистическая игра двух лиц. Имеется фишка, которая в начальный момент располагается в некоторой вершине ${{v}_{0}} \in V$. Игроки шаг за шагом передвигают фишку по ребрам графа по следующему правилу.
Если в текущий момент времени фишка находится в позиции $v \in B$ $(v \in A)$, тогда первый (второй) игрок выбирает некоторое ребро $(v,u) \in E(v)$ и передвигает ее в следующую вершину $u$. Игра длится до тех пор, пока не будет пройден первый цикл, и платеж первого игрока второму составит $\left( {c({{e}_{1}}) + \ldots + c({{e}_{t}})} \right){\text{/}}t$, где ${{e}_{1}},\; \ldots ,\;{{e}_{t}}$ – все ребра цикла. Первый игрок минимизирует платеж, а второй максимизирует. Оказывается, что оптимальные (равновесные по Нэшу) стратегии игроков достигаются на множестве стационарных стратегий, т.е. таких стратегий, у которых очередной переход из текущего состояния $u(t)$ не зависит ни от всей предшествующей траектории, ни от момента времени $t$. Таким образом, стационарная стратегия первого, второго игроков есть отображения вида:
В [1] доказана справедливость следующего равновесного условия: найдется пара стационарных стратегий $s_{1}^{'}$ и $s_{2}^{'}$ первого и второго игроков соответственно, что для любой вершины ${{v}_{0}}$ справедливо следующее:
В [1] дано конструктивное доказательство сформулированного равновесного условия и предложен метод потенциальных преобразований нахождения оптимальных стационарных стратегий $s_{1}^{'},s_{2}^{'}$.
Для решения данной задачи используется вспомогательный алгоритм, определяющий $\forall v \in V$ и для произвольного рационального $p$, знак цены (т.е. либо $c(v) \geqslant p$, либо $c(v) \leqslant p$). Далее, применяя дихотомию, можно найти все цены вершин с точностью $1{\text{/}}{{n}^{2}}$ (две различные величины средних циклов отличаются по крайней мере на $1{\text{/}}{{n}^{2}}$). При этом стационарные стратегии будут требуемыми. Таким образом, общее число применений вспомогательного алгоритма есть $O(nlogMn)$.
Алгоритм потенциальных преобразований Гурвича–Карзанова–Хачияна, описанный в [1], использует тот факт, что если $c'(u,v) = c(u,v) + \varepsilon (u) - \varepsilon (v)$, где $\varepsilon $ – некоторая функция, определенная на множестве вершин графа, то стоимости всех циклов в графе относительно весовых функций c и $c'$ совпадают. Коротко дадим формальное описание алгоритма и результатов его корректности из [1].
2. Метод потенциалов. Пусть
В результате работы алгоритма будет построена новая весовая функция c'(u, $v$) = = $c(u,v) + \varepsilon (u) - \varepsilon (v)$ и найдено разбиение $V$ на непересекающиеся подмножества $V'$ и $V''$ (возможно, что либо 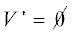 , либо
, либо 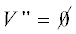 ), такие, что:
), такие, что:
(a) ${\text{extr}}{\kern 1pt} (c',v) \leqslant p,\;\forall v \in V'$ и ${\text{extr}}{\kern 1pt} (c',v) \geqslant p,\;\forall v \in V''$;
(b) 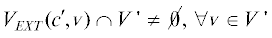 ;
; 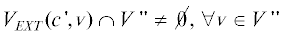 ;
;
(c) 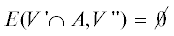 ,
,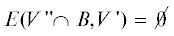 .
.
Тогда нетрудно заметить, что $\forall v \in V'c(v) \leqslant p$ и $\forall v \in V''c(v) \geqslant p$.
В дальнейшем будем предполагать целочисленность $p$, так как поиск для произвольного рационального $p = q{\text{/}}r$ легко сводится к поиску требуемого потенциального преобразования для стоимостной функции $c' = rc$ и целого числа $p' = q$.
Алгоритм состоит из итераций. Структура одной итерации такова.
Строим “помеченное множество”
Содержательно это означает следующее. Сначала помечаем множество вершин с экстремумом меньше $p$ (т.е. ${{V}^{ - }}$). Затем помечаем те вершины минимизирующего игрока с экстремумом, равным p, из которых есть переход по экстремальной дуге в уже помеченное множество, и те вершины максимизирующего игрока с экстремумом, равным p, из которых все экстремальные дуги ведут в помеченное множество. Помеченное множество $L$ удобно представлять в виде “слоев” (${{Q}_{j}}$ в описании, приведенном выше).
Отметим, что 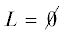 , тогда и только тогда, когда
, тогда и только тогда, когда 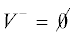 . Однако в случае
. Однако в случае 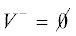 можно сразу заключить, что $\forall v \in V:c(v) \geqslant p$ (требуемое разбиение:
можно сразу заключить, что $\forall v \in V:c(v) \geqslant p$ (требуемое разбиение: 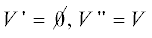 ). Аналогично можно заметить, что если
). Аналогично можно заметить, что если 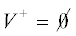 , то $\forall v \in V:c(v) \leqslant p$.
, то $\forall v \in V:c(v) \leqslant p$.
Далее производим потенциальное преобразование вида $c'(u,v) = c(u,v) + \delta \left( {\chi (u) - \chi (v)} \right)$, где $\chi $ – индикаторная функция множества $L$. Величина $\delta > 0$ выбирается максимальной, не нарушающей условие монотонности: $\forall v \in V{\text{|extr}}{\kern 1pt} (c',v) - p{\text{|}} \leqslant {\text{|extr}}{\kern 1pt} (c,v) - p{\text{|}}$, а, кроме того, сохраняются “знаки” экстремумов, т.е. если ${\text{extr}}{\kern 1pt} (c,v) \leqslant p$, то ${\text{extr}}{\kern 1pt} (c',v) \leqslant p$, а если ${\text{extr}}{\kern 1pt} (c,v) \geqslant p$, то ${\text{extr}}{\kern 1pt} (c',v) \geqslant p$. Отметим, что, в частности, это означает, что множества ${{V}^{ - }}$ и ${{V}^{ + }}$ могут только сокращаться.
Для определения $\delta $ нужно просмотреть множества: ${{E}_{1}} = E(B \cap \overline L ,L)$ (цены всех таких дуг больше p по построению $L$), ${{E}_{2}} = E(A \cap L,\overline L )$ (цены всех таких дуг меньше $p$), V1 = = $\{ v\, \in \,{{V}^{ + }}\, \cap \,AV_{{EXT}}^{'}(v)\, \subseteq \,L\} $, здесь для вершины $v \in A \cap {{V}^{ + }}$ $V_{{EXT}}^{'}(v) = \{ w \in V:c(v,w) \geqslant p$. Также V2 = = $\{ v \in {{V}^{ - }} \cap B:V_{{EXT}}^{'}(v) \subseteq \overline L \} $ для вершины $v \in B \cap {{V}^{ - }}$ $V_{{EXT}}^{'}(v) = \{ w \in V:c(v,w) \leqslant p$.
Если все эти множества пусты, то $(L,\overline L )$ – искомое разбиение. В противном случае полагаем
Приведем основные утверждения о корректности из [1].
1. Выполняется условие монотонности: $\forall v \in V{\text{|extr}}{\kern 1pt} (c',v) - p{\text{|}} \leqslant {\text{|extr}}{\kern 1pt} (c,v) - p{\text{|}}$, а, кроме того, сохраняются “знаки” экстремумов, т.е. если ${\text{extr}}{\kern 1pt} (c,v) \leqslant p$, то ${\text{extr}}{\kern 1pt} (c',v) \leqslant p$, а если ${\text{extr}}{\kern 1pt} (c,v) \geqslant p$, то ${\text{extr}}{\kern 1pt} (c',v) \geqslant p$.
2. На двух идущих подряд итерациях помеченные множества $L,L'$ различны.
3. Рассмотрим следующую последовательность множеств на двух подряд идущих итерациях:
Тогда эти последовательности различны. И первое различие в нечетном слое обусловлено сокращением соответствующего множества, первое изменение в четном слое обусловлено расширением соответствующего множества. Другими словами, числовая последовательность
Утверждение 1. Остановка вспомогательного алгоритма произойдет не более чем через ${{2}^{n}}$ итераций.
Доказательство. Не теряя общности, будем предполагать, что циклов среднего веса p в игровой сети нет. Поэтому множество ${{V}^{0}}{\text{/}}L$ разбивается аналогичным образом:
Выполнены аналогичные условия лексического уменьшения.
1. На двух идущих подряд итерациях помеченные множества $Q{\text{'}}$ различны.
2. Рассмотрим следующую последовательность множеств на двух подряд идущих итерациях:
Тогда эти последовательности различны. И первое различие в нечетном слое обусловлено сокращением соответствующего множества, первое изменение в четном слое обусловлено расширением соответствующего множества, т.е. числовая последовательность
Достаточно показать, что существует не более ${{2}^{k}}$ (где k – число остальных вершин множества ${{V}^{0}}$) идущих друг за другом итераций, на которых последовательность множеств $3$ не меняется до слоя ${{Q}_{t}} \cap A,t = 0,...$ включительно. Вершины неменяющихся слоев назовем стационарными, остальные вершины множества ${{V}^{0}}$ – динамическими; ряд таких идущих друг за другом итераций будем называть стационарной последовательностью для слоя $t$. Это доказывается индукцией по числу динамических вершин.
Достаточно показать это утверждение для стационарной последовательности нулевого слоя, т.е. что не более чем через ${{2}^{{|{{V}^{0}}|}}}$ итераций числовая последовательность $3$ достигнет своего лексикографически наименьшего варианта:
Другими словами, максимальное число итераций, при которых множества ${{V}^{ + }}$, ${{V}^{ - }}$ фиксированы, не превосходит ${{2}^{{|{{V}^{0}}|}}}$. Докажем это индукцией по числу вершин в множестве $k = {\text{|}}{{V}^{0}}{\text{|}}$.
На начальном шаге индукции k = 0, поэтому ${{V}^{0}}$ – пусто, по лексикографическому убыванию числовой последовательности на следующей итерации в множестве ${{V}^{0}}$ появится хотя бы одна вершина.
Пусть утверждение справедливо для начальной итерации с ${{V}^{0}} = k - 1,k \geqslant 1$. Тогда длина стационарной последовательности не превосходит ${{2}^{{k - 1}}}$. Рассмотрим начальную итерацию с ${{V}^{0}} = k$. Стационарную последовательность $h$ для нулевого слоя разделим на две части ${{h}_{1}},{{h}_{2}}$, первая длиной не более ${{2}^{{k - 1}}},$ и вторая – остаток.
Можно предполагать, что на первом этапе ${{h}_{1}}$ черные вершины в первом слое отсутствуют 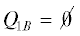 . Действительно, если на некоторой итерации первого этапа возникает вершина в множестве
${{Q}_{{1B}}}$, то это означает, что будет фиксирована еще одна вершина в множестве ${{Q}_{{1B}}}$. Множество ${{Q}_{{1B}}}$ может только расширяться, поэтому лексическое уменьшение последовательности множеств
3 может быть связано с изменениями только остальной нефиксированной части ${{Q}_{{A1}}},{{Q}_{2}},\;...$, но число вершин в этой части будет не больше $k - 1$, поэтому длина второго этапа по предположению индукции – также не более ${{2}^{{k - 1}}}$.
. Действительно, если на некоторой итерации первого этапа возникает вершина в множестве
${{Q}_{{1B}}}$, то это означает, что будет фиксирована еще одна вершина в множестве ${{Q}_{{1B}}}$. Множество ${{Q}_{{1B}}}$ может только расширяться, поэтому лексическое уменьшение последовательности множеств
3 может быть связано с изменениями только остальной нефиксированной части ${{Q}_{{A1}}},{{Q}_{2}},\;...$, но число вершин в этой части будет не больше $k - 1$, поэтому длина второго этапа по предположению индукции – также не более ${{2}^{{k - 1}}}$.
Черную вершину из множества ${{Q}_{{1B}}}$ можно перевести в множество ${{V}^{ - }}$, последовательность преобразованных весовых функций при этом не изменится. Действительно, разбиение на $L,V - L$ при этом не изменится (это можно доказать индукцией по построению слоев Qi множества L). Не изменится и выбор δ. Действительно выбор $\delta $ на такой черной вершине не произойдет. В множестве ${{Q}_{{1B}}}$ вообще нет вершин, которые могут нарушить свойство монотонности. Если мы отнесем эту вершину в класс ${{V}^{ - }}$, то $\delta $ не достигается; на такой вершине (такая вершина не попадет в множество ${{V}_{2}}$, в силу того что у такой вершины есть экстремальное ребро идущее в L).
Возможны два случая.
1. Существует белая вершина, которая на первом этапе присутствует в первом слое постоянно: ${{v}_{A}} \in {{Q}_{1}}$. Но тогда эту белую вершину можно также отнести в множество ${{V}^{ - }}$. По индукции следует, что разбиения $L,V - L$ будут одинаковыми. Выбор $\delta $ для белых вершин множества ${{V}^{ - }}$ и слоев ${{Q}_{1}},...$ происходит одинаковым образом. Поэтому последовательности преобразованных весовых функций будут аналогичными.
Последовательность множеств $3$ по предположению индукции не более чем через ${{2}^{{k - 1}}}$ итераций получит наименьший лексикографический вариант:
Поэтому на начальной итерации второго этапа будет зафиксирована вершина множества V 0 – либо белая вершина, которая получит экстремальное ребро в множество ${{V}^{ + }}$, либо появится черная вершина с экстремальным ребром в множестве ${{V}^{ - }}$. Поэтому второй этап будет проходить с дополнительной фиксированной вершиной. По предположению индукции он не может длиться более ${{2}^{{k - 1}}}$ итераций.
2. На некоторой итерации первого этапа множество Q1 становится пустым, поэтому $L = {{V}^{ - }}$. Тогда на очередной итерации появится черная вершина в множестве Q1. Следовательно эта вершина становится фиксированной на втором этапе. По предположению индукции второй этап также не может проходить более чем ${{2}^{{|{{V}_{0}}| - 1}}}$ итераций.
Известно утверждение о том, что множества L во вспомогательном алгоритме не повторяются. Поэтому общее число итераций вспомогательного алгоритма не превышает 2n. Такая оценка сложности не улучшаема. Построены достижимые примеры задач.
Так как число этапов дихотомического применения вспомогательного алгоритма составляет не более $log(c{{n}^{2}})$, а сложность итерации линейна $O({\text{|}}E{\text{|}})$, то сложность алгоритма, приведенного в [1], равна $O({\text{|}}E{\text{|}}log{\text{|}}V{\text{|}}logc)$.
3. Игры на оптимальное уклонение веса траектории. Основные определения можно найти в работе [11]. Рассмотрим следующую игру, которая определяется игровой сетью $(G:V;A,B;c:E \to Z;u \in V)$. Игра происходит по ребрам данной сети, в вершинах $A$ переход совершает игрок A, в вершинах $B$ – игрок $B$.
Рассмотрим общую стратегию максимизирующего игрока A, что для некоторого p выполнено ${{y}_{n}} + p \geqslant 0$ без разницы, какую стратегию выбрал минимизирующий игрок $B$ для всех $n$. Здесь ${{y}_{n}}$ – суммарный вес начала бесконечной траектории игры из первых $n$ первых ребер, согласно выбранным стратегиям. Инфинум таких p по всем стратегиям игрока $A$ называется потенциалом игрока $A$ и обозначается $a(u)$ (если p не существует, то $a(u) = + \infty $). Аналогично определяется потенциал $b(u)$ минимизирующего игрока $B$.
Аналогично рассмотрим общую стратегию минимизирующего игрока B, что для некоторого p выполнено $ - {{y}_{n}} + p \geqslant 0$ без разницы, какую стратегию выбрал максимизирующий игрок $A$ для всех $n$. Обозначим потенциал игрока $B$ как $b(u)$ (если $p$ не существует, то $b(u) = + \infty $).
Примечание 1. Собственно потенциал – это цена игры на бесконечности, где игрок $A$ максимизирует, а $B$ минимизирует минимальное отрицательное уклонение веса траектории от нуля. Цель игрока $A$ – минимизировать уклонение, а $B$ – максимизировать. Данную игру обозначим через $P$.
Примечание 2. Если в обычной игре $h(u) \geqslant 0$, то потенциал $a(u) \geqslant 0$, в противном случае $h(u) < 0$, тогда $a(u) = + \infty $.
Утверждение 2. Поиск потенциала $a(u)$ (аналогично $b(u)$) полиномиально сводим к решению циклической игры на средний выигрыш по циклу.
Доказательство. Не теряя общности, будем считать, что в игровой сети циклов веса ноль нет. Рассматриваем бесконечную игру из начальной вершины $u$, в которой выигрывает игрок $A$. Поэтому цена циклической игры $h(u) > 0$ и $a(u) \geqslant 0$ конечна.
Теорема 1. Следующая система равенств имеет точно одно решение. Это решение соответсвует системе потенциалов игроков $A$ и $B$ соответственно.
1) $a(u) = \mathop {min}\limits_{v \in out(v)} max\left\{ {0,a(v) - w} \right\}$, если вершина $u \in A$,
2) $a(u) = \mathop {max}\limits_{v \in out(v)} max\left\{ {0,a(v) - w} \right\}$, если вершина $u \in B$,
3) $b(u) = \mathop {min}\limits_{v \in out(v)} max\left\{ {0,b(v) + w} \right\}$, если вершина $u \in B$,
4) $b(u) = \mathop {max}\limits_{v \in out(v)} max\left\{ {0,b(v) + w} \right\}$, если вершина $u \in A$.
Точно одно из чисел $a(u),b(u)$ конечно.
Из доказательства основной теоремы [11] следует, что решение игры достигается на стационарных стратегиях.
Более точно достижимые стационарные стратегии ${{s}_{A}},{{S}_{B}}$ для экстремальных равенств в 1), 2) дают следующее. Пусть $f$ – вес текущей траектории. Если игрок $A$ придерживается стационарной стратегии ${{s}_{A}}$, то величина $f - a(v)$ не уменьшается на протежении всей игры, независимо от стратегии $B$.
Если игрок $B$ придерживается стационарной стратегии ${{s}_{B}}$, то величина $f - a(v)$ не увеличивается до тех пор, пока не встретится вершина $a(u) = 0$, независимо от стратегии игрока A. Поэтому при стационарной стратегии ${{s}_{B}}$ положительный цикл до момента, когда встретится вершина $a(u) = 0$, невозможен. (Конечная игра до первого цикла по отклонению от нуля не эквивалентна бесконечной игре.)
Вначале сведем игру $P$ к циклической игре с заданной временной функцией на вершинах.
Вершины $A$ растягиваем в ребра с нулевым весом и единичным временем. Другими словами, вершину $v \in A$ заменяем ребром $ww':w \in B,w' \in A$ с нулевым весом и единичным временем. Ребра, входившие в вершину $v$, теперь направляем в вершину $w$, а выходившие из вершины $v$ теперь направляем из вершины $w'$, вес не меняем, время остается тоже единичное. Из вершины $w$ добавляем ребро в начальную вершину $u$ с нулевым весом и временем $t = {\text{const}}$ (большое положительное число). Для вершин $v \in B$ также добавляем ребро в начальную вершину $u$ с нулевым весом и временем $t = {\text{const}}$ (большое положительное число).
Рассмотрим оптимальные стационарные стратегии в игре на уклонение ${{s}_{A}},{{s}_{B}}$ и построим следующие стационарные стратегии $s_{A}^{'},s_{B}^{'}$ в циклической игре для преобразованной игровой сети. Если $a(v) > 0$, $v \in B$, то стационарное ребро не меняем, если $a(v) = 0$, $v \in B$, то переход в начальную вершину $u$ по добавленному ребру. Если $a(v) > 0$, $v \in A$, то в вершине добавленной $w \in B$ переходим в добавленную вершину $w'$, а в вершине $w' \in A$ стационарный переход не меняем. Если $a(v) = 0,v \in A,$ то в вершине добавленной $w \in B$ переходим в начальную вершину $u$, а в вершине $w' \in A$ стационарный переход не меняем.
Стратегия ${{s}_{A}}$ гарантирует коридор $[ - a(u), + \infty ]$, который траектория никогда не покинет, стратегия ${{s}_{B}}$ гарантирует, что траектория когда-то получит вес $ - a(u)$ или меньший. Рассмотрим стратегию $s_{A}^{'}$ против любой стратегии игрока $B$ в игре $P'$. Стратегия ${{s}_{A}}$ гарантирует цикл не хуже $ - a(u){\text{/}}(t + r)$, где $a(u)$ – потенциал вершины $u$, $r$ – число ребер в оптимальной по отклонению траектории (при большом $t$ имеем $ - a(u){\text{/}}(t + r) \approx - a(u){\text{/}}t$). Действительно, начальные отрицательные циклы не допускаются при оптимальной стационарной стратегии игрока $A$, а из новых циклов минимален будет следующий: от начальной вершины рассматриваем путь с весом $ - a(u)$ и из конечной вершины этого пути переходим в начальную вершину $u$ с нулевым весом и временем движения $t = {\text{const}}$.
Наоборот рассмотрим стационарную стратегию $s_{B}^{'}$ против любой стратегии первого игрока в $P'$ (стратегия ${{s}_{B}}$ позволяет достичь отклонения $ - a(u)$), и в этот момент игра игроком $B$ переводится в начальную вершину. Средний вес полученного цикла приблизительно равен $ - a(u){\text{/}}t$. Начальные циклы отрицательного веса игроку $A$ не выгодны, так как $t$ – большое, новые циклы больше старых по средней величине. Время $t$ нужно выбрать из двух условий.
1. Минимальный новый цикл должен быть больше максимального отрицательного старого цикла $ - c{\text{|}}V{\text{|/}}t > - 1/{\text{|}}V{\text{|}}$ ($c = \mathop {max}\limits_e {\text{|}}c(e){\text{|}}$).
2. Усреднение не должно менять порядка весов траекторий. Если f – вес траектории ${{T}_{n}}$, а $r$ – вес траектории ${{T}_{m}}$ и $f < r$, то $f{\text{/}}(t + 2n) < r{\text{/}}(t + 2m)$. Отсюда $(t + 2m)f < r(t + 2n)$, приведя подобные, получим $t > 2(mf - rn){\text{/}}(r - f)$. Также ${\text{|}}2mf - 2rn{\text{/}}(r - f){\text{|}} \leqslant 4{\text{|}}V{{{\text{|}}}^{2}}c$, т.е. $t = 4{\text{|}}V{{{\text{|}}}^{2}}c$. Таким образом, если цена игры $P'$ в вершине $u$ равна $c(u)$, то потенциал $a(u)$ приближенно равен $c(u)t$ (по приближению можно восстановить точное значение).
Теперь циклическая игра с временной функцией сводима к обычной циклической игре с единичной функцией на ребрах посредством стандартной дихотомической процедуры.
Пусть нам нужно определить: верно ли, что цена игры $p'$ с временной функцией в вершине $u$ удовлетворяет неравенству $p' \geqslant h$. Вычитаем из веса каждого ребра $e \in E$ величину $ht(e)$, т.е. преобразованная весовая функция удовлетворяет равенству $c'(e) = c(e) - ht(e)$ для каждого ребра $e \in E$. Цена циклической игры с единичиной временной фукцией и преобразованной весовой функцией $c'$ больше нуля в вершине $u \in V$, $c'(u) > 0$, тогда и только тогда, когда в циклической игре с временной функцией на ребрах в начальной вершине $u$ цена игры удовлетворяет неравенству $a(u) > h$.
В силу равносильных условий: $c'({{e}_{1}}) + ... + c'({{e}_{k}}) = c({{e}_{1}}) + ... + c({{e}_{k}}){{t}_{1}}{{h}_{1}} - ... - {{t}_{k}}{{h}_{k}} > 0$ тогда и только тогда, когда $(c'({{e}_{1}}) + ... + c'({{e}_{k}})){\text{/}}({{t}_{1}} + ... + {{t}_{k}}) > h$.
Сведение полиномиально $t = O(c\,{\text{poly}}{\kern 1pt} {\kern 1pt} {\text{|}}V{\text{|}}),c' = O({{c}^{2}}{\kern 1pt} {\text{poly}}{\kern 1pt} {\text{|}}V{\text{|}})$.
Заключение. В работе дано уточнение верхней оценки сложности алгоритма потенциальных преобразований для решения циклических игр на графах $I(n) = O({{2}^{n}})$. Оценка близка к нижней оценке сложности алгоритма потенциальных преобразований.
Список литературы
Гурвич В.А., Карзанов А.В., Хачиян Л.Г. Циклические игры и нахождение минимаксных средних циклов в ориентированных графах // ЖВМиМФ. 1988. Т. 28. № 9. С. 1407–1417.
Алифанов Д.В., Лебедев В.Н., Цурков В.И. Оптимизация расписаний с логическими условиями предшествования // Изв. РАН. ТиСУ. 2009. № 6. С. 88–93.
Лебедев В.Н., Цурков В.И. Степенной в среднем алгоритм решения антагонистических игр на графе // Изв. РАН. ТиСУ. 2018. № 1. С. 89–97.
Zwick U., Paterson M. The complexity of mean payoff games on graphs // Theoretical Computer Science. 1996. V. 158. P. 343–359.
Andersson D., Miltersen P.B. The Complexity of Solving Stochastic Games on Graphs // Lecture Notes in Computer Science. V. 5878 / Eds Y. Dong, D. Z. Du, O. Ibarra. Berlin, Heidelberg: Springer, 2009.
Daskalakis K., Papadimitriou C.H. The Complexity of Games on Highly Regular Graphs // Lecture Notes in Computer Science. V. 3669 / Eds. G.S. Brodal, S. Leonardi. Berlin, Heidelberg: Springer, 2005.
Fraenkel A.S., Yesha Y. Complexity of Problems in Games, Graphs and Algebraic Equations // Discrete Applied Mathematics. 1979. V. 1. № 1–2. P. 15–30.
Berwanger D., Graedel E. Entanglement – A Measure for the Complexity of Directed Graphs with Applications to Logic and Games // Lecture Notes in Computer Science. V. 3452 / Eds. F. Baader, A. Voronkov. Berlin, Heidelberg: Springer, 2005.
Goldstein A.S., Reingold E.M. The Complexity of Pursuit on a Graph // Theoretical Computer Science. 1995. V. 143. № 1. P. 93–112.
Schaffer T.J. On the Complexity of Some Two-Person Perfect-Information Games // J. Computer and System Sci. 1978. V. 16. P. 185–225.
Lifshits Y.M., Pavlov D.S. Potenial Theory for Mean Pay-off Games // Записки научных семинаров ЛОМИ. 2006. Т. 340. С. 61–75.
Кларк Э.М., мл. Грамберг О., Пелед Д. Верификация моделей программ. М.: Изд-во Московского центра непрерывного математического образования, 2002.
Миронов А.А., Федорчук В.В., Цурков В.И. Минимакс в моделях транспортного типа с интегральными ограничениями. I // Изв. РАН. ТиСУ. 2003. № 4. С. 69–81.
Миронов А.А., Федорчук В.В., Цурков В.И. Минимакс в моделях транспортного типа с интегральными ограничениями. II // Изв. РАН. ТиСУ. 2005. № 5. С. 66–86.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления