Известия РАН. Теория и системы управления, 2019, № 3, стр. 127-139
НЕОРТОГОНАЛЬНАЯ ДИСКРЕТИЗАЦИЯ КАК ОСНОВА СЖАТИЯ И ВОССТАНОВЛЕНИЯ ВИДЕОИНФОРМАЦИИ
В. Н. Дрынкин a, *, С. А. Набоков a, Т. И. Царева a
a ФГУП ГосНИИАС
Москва, Россия
* E-mail: drynkin-v@mail.ru
Поступила в редакцию 03.07.2018
После доработки 15.01.2019
Принята к публикации 28.01.2019
Аннотация
Предложены методы сжатия видеоинформации от 4 до 16 раз с последующим восстановлением путем интерполяции с уровнем информационных потерь ниже порога зрительного восприятия, основанные на различных неортогональных пространственно-временных структурах субнайквистовой дискретизации. Эти методы могут быть реализованы в реальном времени, что продемонстрировано в рамках исследования, и применяться как самостоятельно, так и в сочетании с другими способами видеокомпрессии и кодирования, обеспечивая дополнительное сжатие.
Введение. В качестве основы современных систем управления все чаще выступают системы технического зрения, при этом нередко возникает задача передачи информации, формируемой данными системами, на пункт управления в режиме реального времени для ее оперативной обработки и хранения. В случае использования оптико-электронных систем технического зрения, основанных на многоэлементных приемниках излучения различных спектральных диапазонов, объемы передаваемой видеоинформации оказываются весьма значительны и кратно увеличиваются с каждым новым поколением видеодатчиков. При этом пропускная способность канала передачи видеоинформации, несмотря на развитие скоростных линий связи, ограничивается нормативными, массогабаритными и стоимостными требованиями.
Проблема роста объемов данных усугубляется тем, что практически во всех современных цифровых системах обработки видеоизображений используется ортогональная структура растра дискретизации (при которой отсчеты изображения (пиксели) располагаются в узлах прямоугольной решетки), получающаяся в результате простого обобщения одномерной (1D) теоремы отсчетов Котельникова–Найквиста–Шеннона на многомерный случай [1]. Такая структура видеорастра не является оптимальной по критерию информационной плотности и приводит к слишком большому количеству избыточных данных, которые необходимо существенно сжимать перед хранением или передачей. Например, для видеопоследовательности цветных ортогонально дискретизированных кадров, являющейся типичным случаем многомерного сигнала, общая скорость передачи информации имеет порядок 1010 бит/с для современных форматов 2160p/50–60, что крайне велико.
Задача сжатия данных и, в частности, сжатия изображений предполагает преобразование информации в такую форму, в которой она занимала бы минимально возможный объем, передачу (сохранение), получение (считывание) и восстановление, по возможности, без или с минимумом искажений [2]. На сегодняшний день разработано значительное количество методов сжатия видеоинформации, основанных на разнообразных подходах. Наиболее широко распространенные стандарты сжатия, такие, как MPEG H.26x и VP8/9, а также перспективный AV1, используют так называемый гибридный подход, основанный на сочетании ряда процедур – разбиения на блоки, вычисления межкадровых разностей, внутри- и межкадрового предсказания, компенсации движения, различных вариантов трансформирующего кодирования, квантования и др. Дальнейшее повышение степени сжатия видеоизображений при сохранении высокого качества восстановления в рамках гибридного подхода весьма затруднительно, поскольку обычно сопряжено с повышением вычислительной сложности, выражающейся в серьезных временны́х затратах для эффективной аппаратной реализации. Это побуждает к поиску альтернативных подходов для достижения дополнительного сжатия видеоинформации.
Один из возможных подходов к сжатию видеоизображений основан на использовании неортогональных видов дискретизации, более оптимальных по сравнению с ортогональными, позволяющих снизить плотность отсчетов дискретизации видеосообщений и тем самым уменьшить объем цифровой памяти, необходимой для хранения и передачи видеоизображений [1].
В данной работе речь пойдет о нескольких методах сжатия с потерями и соответствующих им методах восстановления видеоизображений, имеющих сравнительно низкую вычислительную сложность и основанных на так называемой треугольной дискретизации движущихся изображений, которая приводит к шахматному расположению отсчетов цифровой видеоинформации [3].
1. Сжатие и восстановление видеоинформации в 4 раза. В [4] описаны методы сжатия и соответствующий им метод восстановления видеоизображений, основанные на частотном уплотнении спектра видеосигнала за счет его передискретизации с целью достижения более эффективной (оптимальной), по сравнению с ортогональной, дискретизации движущихся изображений.
Ортогональная структура расположения отсчетов дискретизации на прямоугольном растре, получающаяся в результате простого распространения теоремы отсчетов на многомерный случай, приводит к образованию пустот и избыточной протяженности дискретного спектра видеоизображений в области пространственно-временных частот. Это происходит вследствие того, что ортогональная структура дискретизации не согласована ни с формой спектра реальных изображений, ни со свойствами зрительной системы человека, характеристики которых имеют ярко выраженную ромбовидную анизотропию [3].
Для получения оптимальной дискретизации и сокращения полосы частот дискретного сигнала видеоизображения (т.е. его сжатия) необходимо более плотно “упаковать” основную и побочные составляющие дискретного спектра сигнала видеоизображения в частотной области {ν1, ν2, ν3}, где ν1, ν2, ν3 – соответствующие нормированные пространственные горизонтальные, вертикальные и временные частоты. С учетом ромбической анизотропии спектров реальных изображений этого можно достичь, если сместить центры побочных составляющих спектра в диагональных направлениях в области пустот с помощью передискретизации, приводящей к треугольной дискретизации, при которой отсчеты располагаются в шахматном порядке.
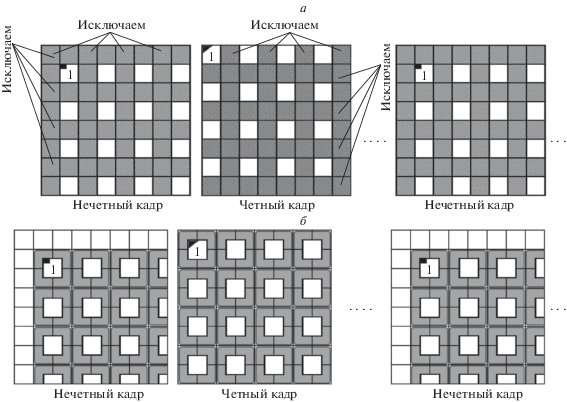
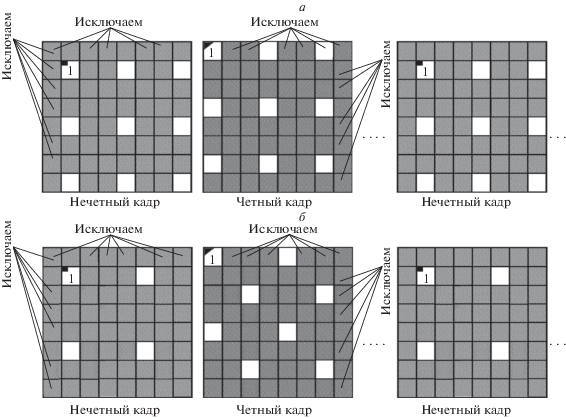
Согласно [4], передискретизацию кадров видеоизображения можно осуществить путем прореживания (децимации) исходного видеорастра с помощью исключения, например, из нечетных кадров нечетных столбцов и строк, а из четных кадров – четных столбцов и строк (рис. 1, а), или путем билинейной интерполяции (усреднения значений яркостей отсчетов видеокадров в окрестности 2 × 2) со сдвигом усредняемых областей на один отсчет по диагонали в соседних кадрах (рис. 1, б).
В обоих случаях достигается 4-кратное сжатие видеопоследовательности за счет 2-кратного уменьшения числа отсчетов и разрешающей способности по горизонтальной и вертикальной пространственным координатам. При этом остается всего 25% исходной информации.
Помимо билинейной интерполяции возможно также использование других методов взвешенного усреднения, например бикубического, а также основанных на оконных функциях высокого разрешения, например Ланцоша, Фейера (известного также как окно Бартлетта или треугольное окно), Ханна, Кайзера–Бесселя.
При ортогональной пространственно-временной дискретизации видеосигнала минимальное L1-расстояние (т.е. расстояние Минковского первого порядка) d1 ∈ $\mathbb{N}{\text{*}}$ между любыми двумя соседними отсчетами любых двух соседних кадров равно 1, при неортогональной оно равно 2. Исходя из этого, возьмем минимизацию ${{\ell }_{1}}$-нормы в качестве основы для критерия оптимальности неортогональной пространственно-временной дискретизации.
Будем называть оптимальной по критерию ${{\ell }_{1}}$ (или ${{\ell }_{1}}$-оптимальной) такую неортогональную пространственно-временную дискретизацию видеорастра, при которой d1 = 2, т.е.
(1.1)
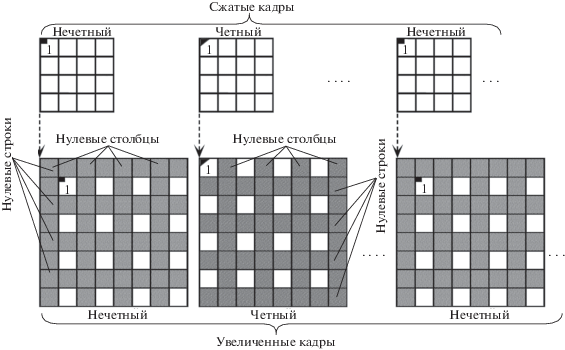
${\text{||}}{{p}_{{i,j}}} - {{q}_{{i - 1,j - 1}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i + 1,j - 1}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i - 1,j + 1}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i + 1,j + 1}}}{\text{|}}{{{\text{|}}}_{1}},$Восстановление кадров видеопоследовательности, сжатых одним из указанных выше путей, осуществляют в два этапа, включающих в себя восстановление размеров сжатых кадров до исходного и интерполяцию. На первом этапе размеры нечетных и четных кадров сжатой видеопоследовательности увеличивают, перемежая значения яркостей отсчетов восстанавливаемых сжатых кадров нулевыми столбцами и строками в соответствии с исключенными при сжатии столбцами и строками. В результате в двух соседних кадрах образуется пространственно-временная решетка с треугольной дискретизацией (рис. 2).
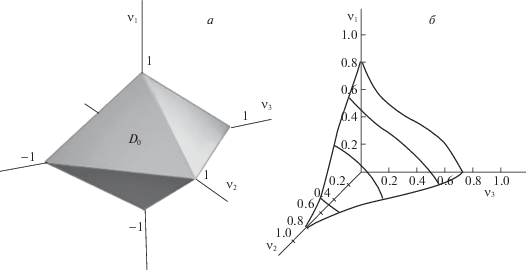
На втором этапе производят интерполяцию последовательности увеличенных видеокадров с помощью пространственно-временного восстанавливающего трехмерного (3D) интерполяционного фильтра нижних частот (ФНЧ) с областью пропускания D0 в виде октаэдра, т.е. ${{\ell }_{1}}$-шара единичного радиуса (рис. 3, а):
(1.2)
${{D}_{0}}:\left| {{{\nu }_{1}}} \right| + \left| {{{\nu }_{2}}} \right| + \left| {{{\nu }_{3}}} \right| = a,\quad 0 < a \leqslant 1,\quad a \in \mathbb{R}.$Рис. 3.
Область пропускания 3D интерполяционного ФНЧ (а) и результирующая ПЧХ 3D интерполяционного ФНЧ (б)
Необходимо отметить, что наиболее плотной упаковки спектра в частотном 3D-пространстве {ν1,ν2,ν3} можно достичь, если в качестве формы области пропускания D0 выбрать один из пяти заполняющих пространство многогранников, например ромбододекаэдр [5]. Октаэдрическая форма выбрана нами как аппроксимация, дающая достаточную точность с практической точки зрения.
Область пропускания D0 (1.2) восстанавливающего ФНЧ наиболее просто реализуется на основе метода синтеза комбинированных фильтров, приводящего к каскадному соединению 3D, двумерного (2D) и 1D рекурсивно-нерекурсивных звеньев [3]. Зададим a = 0.8 и на основе Чебышевского аналогового прототипа получим пространственно-частотную характеристику (ПЧХ) восстанавливающего 3D интерполяционного ФНЧ в следующем виде:
(1.3)
$\begin{gathered} K\left( {{{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}} \right) = \frac{{0.125\left( {1 + \exp \left( { - j\pi {{\nu }_{3}}} \right)} \right)\left[ {1 - {{\beta }_{m}}\left( {{{\nu }_{1}},{{\nu }_{2}}} \right)} \right]}}{{1 - {{\beta }_{m}}\left( {{{\nu }_{1}},{{\nu }_{2}}} \right)\exp \left( { - j\pi {{\nu }_{3}}} \right)}} \times \\ \times \;\frac{{\left( {1 + \exp \left( { - j\pi {{\nu }_{2}}} \right)} \right)\left[ {1 - \beta \left( {{{\nu }_{1}}} \right)} \right]}}{{1 - \beta \left( {{{\nu }_{1}}} \right)\exp \left( { - j\pi {{\nu }_{2}}} \right)}}\frac{{\left( {1 + \exp \left( { - j\pi {{\nu }_{1}}} \right)} \right)\left[ {1 + 0.716} \right]}}{{1 + 0.716\exp \left( { - j\pi {{\nu }_{1}}} \right)}}, \\ \end{gathered} $(1.4)
$\begin{gathered} \beta \left( {{{\nu }_{1}}} \right) = 0.534 - 0.277\cos \pi {{\nu }_{1}} - 0.266\cos 2\pi {{\nu }_{1}} + \\ + \;0.005\cos 3\pi {{\nu }_{1}} + 0.03\cos 4\pi {{\nu }_{1}}; \\ \end{gathered} $(1.5)
${{\beta }_{3}}\left( {{{\nu }_{1}},{{\nu }_{2}}} \right) = 0.657\gamma - 0.308(\cos \pi {{\nu }_{1}} + \cos \pi {{\nu }_{2}}) - 0.416\cos \pi {{\nu }_{1}}\cos \pi {{\nu }_{2}}.$Двумерная ПЧХ нерекурсивной цепи обратной связи β3(ν1, ν2) (1.5) с апертурой 3 × 3 элемента кадра полностью определяет заданную конфигурацию области пропускания D0 (1.2) 3D восстанавливающего ФНЧ (1.3) в направлении временных частот ν3. Коэффициент γ = 0.8 выбирается из соображений обеспечения устойчивости ФНЧ.
Конфигурация области пропускания D0 восстанавливающего 3D интерполяционного пространственно-временного ФНЧ (1.3) в плоскости изображения (ν1, ν2) формируется 1D нерекурсивной цепью обратной связи β(ν1) (1.4) с протяженностью апертуры в 9 элементов строки.
На рис. 3, б показана результирующая ПЧХ восстанавливающего ФНЧ в виде поверхности уровня K(ν1, ν2, ν3) = 0.8 для положительного октанта 3D-области нормированных частот {ν1, ν2, ν3}.
Таким образом, можно говорить о том, что предложенные методы четырехкратного сжатия и восстановления видеосигнала являются оптимальными как в спектральной, так и в пространственной области. Область пропускания (1.2) учитывает свойства спектров реальных изображений и зрительной системы человека, что позволяет при восстановлении видеоизображений наилучшим образом выделять из дискретного спектра основную составляющую, подавляя побочные составляющие и высокочастотные шумы. Это дает возможность практически полностью восстановить исходную видеопоследовательность за счет 2-кратного повышения числа отсчетов и практически 2-кратного повышения разрешающей способности сжатых видеокадров по горизонтальной и вертикальной пространственным координатам [6]. Как будет показано далее, уровень потерь восстановления при этом лежит ниже порога зрительного восприятия.
2. Сжатие и восстановление видеоинформации в 16 раз. На основе базовых методов сжатия и восстановления видеоизображений, рассмотренных выше, можно рассмотреть сжатие и восстановление с бо́льшими коэффициентами.
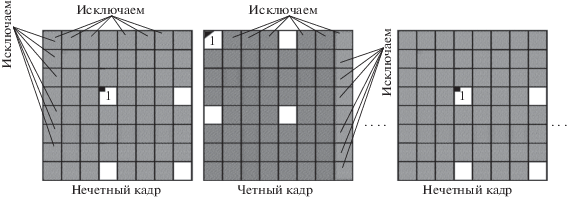
Применим дополнительную передискретизацию одним из указанных выше способов (рис. 1) к уже сжатой в 4 раза видеопоследовательности кадров, изображенной в верхней части рис. 2. Тогда получим структуру дискретизации исходных кадров, при которой остается 1/16 часть кадра (6.25%). Пример одной из возможных в данном случае структур приведен на рис. 4.
Восстановление такой видеопоследовательности после дополнения ее кадров нулевыми столбцами и строками в соответствии с рис. 4, как и в случае сжатия в 4 раза, осуществим с помощью пространственно-временного восстанавливающего 3D интерполяционного ФНЧ с областью пропускания D0 в виде ${{\ell }_{1}}$-шара (1.2). При этом восстанавливающий ФНЧ должен иметь протяженность апертуры двумерной цепи обратной связи βm(ν1, ν2) трехмерного звена, которая захватывает соседние отсчеты сжатых видеокадров, т.е. не менее 5 × 5 элементов. В этом случае m = 5 и вместо выражения (1.5) 2D ПЧХ β5(ν1, ν2) будет иметь вид
(2.1)
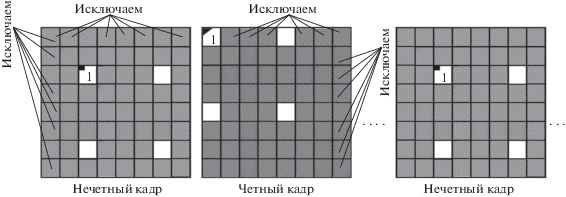
$\begin{gathered} {{\beta }_{5}}\left( {{{\nu }_{1}},{{\nu }_{2}}} \right) = 0.657\gamma + 2[ - 0.154(\cos \pi {{\nu }_{1}} + \cos \pi {{\nu }_{2}}) - \\ - \;0.06(\cos 2\pi {{\nu }_{1}} + \cos 2\pi {{\nu }_{2}})] + 4[ - 0.104\cos \pi {{\nu }_{1}}\cos \pi {{\nu }_{2}} - \\ - \;0.017(\cos 2\pi {{\nu }_{1}}\cos \pi {{\nu }_{2}} + \cos \pi {{\nu }_{1}}\cos 2\pi {{\nu }_{2}}) + 0.027\cos 2\pi {{\nu }_{1}}\cos 2\pi {{\nu }_{2}}]. \\ \end{gathered} $Анализ полученной структуры дискретизации, изображенной на рис. 4, показывает, что при достижении 16-кратного сжатия видеокадров путем 2-кратного применения базовых методов сжатия в 4 раза с диагональным сдвигом на один отсчет в соседних кадрах, как описано выше, нарушается симметрия треугольной дискретизации. Симметрируем ее, сдвинув выбор остающихся в нечетных кадрах отсчетов на один элемент по диагонали (рис. 5). Реконструкция исходной видеопоследовательности осуществляется с помощью 3D восстанавливающего ФНЧ (1.3) с учетом (2.1).
Введем обозначение полного набора L1-расстояний любой пространственно-временной решетки в виде {L1(i), L1(i+ 1), …, L1(i+n– 1)}, где n – общее число L1-расстояний в данной решетке, n ∈ $\mathbb{N}{\text{*}}$; i – порядковый номер L1-расстояния, начиная с наименьшего, $i \in \overline {0;n--1} $.
Очевидно, что обе полученные пространственно-временные решетки, изображенные на рис. 4 и 5, не являются строго ${{\ell }_{1}}$-оптимальными, поскольку не удовлетворяют условию (1.1). Можно заметить, что набор L1-расстояний равен {2, 4, 4, 6} для несимметрированной версии и {4, 4, 4, 4} для симметрированной, т.е. в обоих случаях используются расстояния, кратные двум. В этом смысле обе решетки близки к ${{\ell }_{1}}$-оптимальной дискретизации {2, 2, 2, 2}. Будем называть такие решетки ${{\ell }_{1}}$-квазиоптимальными.
Можно сравнить симметрированную и несимметрированную версии структуры дискретизации, обеспечивающей 16-кратное сжатие, по следующему критерию.
Будем называть ${{\ell }_{1}}$-равномерной (или ${{\ell }_{1}}$-симметрированной) такую неортогональную пространственно-временную дискретизацию видеорастра, при которой любые два соседние отсчета любых двух соседних кадров расположены друг относительно друга на одинаковом L1-расстоянии d1 = С + 1, где C ∈ $\mathbb{N}{\text{*}}$ – некоторая константа, т.е.
(2.2)
${\text{||}}{{p}_{{i,j}}} - {{q}_{{i - C,j - C}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i + C,j - C}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i - C,j + C}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{{p}_{{i,j}}} - {{q}_{{i + C,j + C}}}{\text{|}}{{{\text{|}}}_{1}}.$Очевидно, что при C = 1 критерий ${{\ell }_{1}}$-равномерности соответствует более строгому критерию ${{\ell }_{1}}$-оптимальности (1.1).
Таким образом, по критерию (2.2) симметрированная структура, изображенная на рис. 5, является ${{\ell }_{1}}$-равномерной, а приведенная на рис. 4 таковой не является. Но поскольку последняя использует расстояния, кратные двум, будем называть ее ${{\ell }_{1}}$-квазиравномерной (или ${{\ell }_{1}}$-квазисимметрированной).
3. Сжатие и восстановление видеоинформации в 9 и 12 раз. Полученные выше результаты позволяют сделать предположение о том, что, варьируя структуру дискретизации кадров, можно получить другие степени сжатия. В рамках данного исследования мы приведем два примера.
На рис. 6 показаны возможные структуры дискретизации, позволяющие сжимать видеопоследовательность в 9 (рис. 6, а) и 12 раз (рис. 6, б), при этом остается примерно 11 и 8% от исходного объема информации соответственно. Поясним, что сжатие в 12 раз достигается за счет сжатия одного кадра в 16 раз, а соседнего – в 8 раз, поэтому данную структуру дискретизации можно считать гибридной или составной. Для восстановления видеоинформации, сжатой в 9 и 12 раз, используются звенья β3(ν1, ν2) (1.5) и β5(ν1, ν2) (2.1) соответственно.
Наборы L1-расстояний для структур дискретизации, обеспечивающих 9- и 12-кратное сжатие, равны {2, 3, 3, 4} и {2, 2, 4, 4}. В обоих случаях пространственно-временные решетки дискретизации не являются строго ${{\ell }_{1}}$-оптимальными или ${{\ell }_{1}}$-равномерными, поскольку не удовлетворяют условиям (1.1) и (2.2). Однако при сжатии в 12 раз структура дискретизации может считаться ${{\ell }_{1}}$‑квазиоптимальной и ${{\ell }_{1}}$‑квазиравномерной, поскольку, как упоминалось ранее, использует расстояния, кратные двум.
Полученные результаты являются предварительными и требуют дальнейшего анализа. В частности, в данном исследовании мы ограничились апертурами 3 × 3 и 5 × 5 элементов импульсной характеристики первого звена восстанавливающего фильтра в качестве компромиссных вариантов между вычислительной сложностью и качеством реконструкции. Оптимальные же значения такой апертуры определяются, помимо заданного коэффициента сжатия, силой внутри- и межкадровых корреляционных связей, поэтому интерес для дальнейших исследований может представлять синтез восстанавливающего фильтра с переменной (адаптивной) апертурой.
4. Результаты экспериментов. С целью проверки возможностей разработанных методов сжатия и восстановления видеопоследовательностей было проведено имитационно-математическое моделирование с использованием разработанного программного обеспечения (ПО) и предварительно зарегистрированных реальных видеоизображений.
Рассматриваемые методы сжатия и восстановления применимы для видеоизображений любого разрешения и кадровой частоты, но в особенности актуальны для видеопотоков с высоким пространственно-временным разрешением. Поэтому для отработки предлагаемых методов были выбраны видеопоследовательности (см. табл. 1) формата 2160p, которые получают широкое распространение в службах потокового мультимедиа и становятся актуальными в системах цифрового телевизионного вещания.
Таблица 2.
Результаты объективной оценки качества восстановления
| Видеопоследовательность | Рейтинги VMAF качества восстановления после сжатия с различными коэффициентами | |||
|---|---|---|---|---|
| в 4 раза | в 9 раз | в 12 раз | в 16 раз | |
| American Football 60p | 97.72 | 92.22 | 85.07 | 77.98 |
| Animals 60p | 98.81 | 97.63 | 97.15 | 93.39 |
| FoodMarket | 99.05 | 96.41 | 96.29 | 89.95 |
| Narrator | 99.38 | 99.37 | 99.11 | 99.17 |
| PeirSeaside | 99.42 | 95.53 | 93.31 | 92.12 |
Видеопоследовательности, выбранные в качестве тестовых, характеризуются статичными и динамичными сценами, изображающими природные и искусственные объекты, которые обладают различными размерами, детализацией, скоростью и направлением движения в кадре, что позволило исследовать предлагаемые методы сжатия и восстановления на достаточно разнообразных видеосюжетах.
Моделирование осуществлялось на персональном компьютере с аппаратной поддержкой центрального и графического процессоров суммарной производительностью около 1.5 Тфлопс в режиме чисел с плавающей запятой одинарной точности. В качестве центрального процессора использовался 6-ядерный 12-поточный процессор Intel Core i7-3930K, работающий на базовой тактовой частоте 3.2 ГГц. В роли графического процессора выступал видеопроцессор AMD Radeon HD 5970. Разработанное ПО с помощью программных библиотек и инструментов FFmpeg [9] с открытым исходным кодом осуществляло декодирование исходного видеопотока с последующим сжатием и восстановлением в режиме реального времени. При использовании связки центрального и графического процессоров общая межкадровая задержка процесса декодирования, сжатия, восстановления и воспроизведения видеопотока не превышала 5.6 мс, т.е. на вышеуказанном оборудовании обработка видеопотоков, представленных в табл. 1, выполнялась со скоростью не менее 180 видеокадров в секунду. Режим использования вычислительных возможностей только центрального процессора в рамках исследования не рассматривался.
Заметим, что при моделировании сжатию и восстановлению предшествовал этап декодирования ввиду того, что исходные видеопоследовательности были изначально закодированы. Реальные же сценарии применения предложенных методов сжатия предполагают их использование в начале конвейера видеообработки, т.е. как можно “ближе” к источнику видеосигнала, после чего осуществляется его кодирование, передача, декодирование и восстановление.
На рис. 7 изображены примеры восстановления кадра сжатой путем прореживания видеопоследовательности “PierSeaside”, согласно предложенным методам. По представленным изображениям можно видеть, что артефакты восстановления почти незаметны для зрительной системы человека и закономерно проявляются главным образом на тонких структурах и малоразмерных объектах (например, в верхней части приведенных на рисунках одиночных кадров). Также можно заметить, что вертикальная синусоидальная структура в крайней левой части кадра, восстановленного после сжатия в 9 раз (рис. 7, в), имеет ошибку дискретизации, проявляющуюся на изображении в виде муарового узора, вследствие неоптимальности и неравномерности по критериям (1.1) и (2.2) структуры дискретизации, о чем упоминалось ранее. Однако же при наблюдении этих кадров в движении данные артефакты из 2D-пространства статичных изображений переходят в 3D-пространство видеоизображений, в котором дефекты малоразмерных и одновременно движущихся объектов становятся малозаметны для зрительной системы человека.
Рис. 7.
Исходный (а) и восстановленные после сжатия в 4 раза (б), 9 раз (в), 12 раз (г), 16 раз с симметрированной (д) и несимметрированной (е) структурами дискретизации кадры видеопоследовательности “PierSeaside”

5. Оценка качества восстановления сжатой видеоинформации. В настоящее время существует два подхода к оценке качества движущихся изображений: субъективная (качественная) визуальная экспертная оценка и объективная (количественная) оценка на основе математических методов.
Субъективная экспертиза, методики проведения которой описаны в рекомендации Международного союза электросвязи ITU-R BT.500 [10], считается достаточно надежным способом определения качества видеоизображений. Однако она представляет собой довольно медленный и дорогостоящий процесс, вследствие чего субъективную оценку качества видеоинформации в последнее время стараются заменить количественными оценками, позволяющими в значительной мере ускорить и автоматизировать данный процесс.
На сегодняшний день предложено множество количественных мер качества изображений, наиболее известными из которых являются пиковое отношение сигнала к шуму (ПОСШ), среднеквадратичная погрешность (СКП), показатель структурного сходства SSIM [11] и его многомасштабная, трехкомпонентная и пространственно-временная вариации, и индекс визуального качества VIF [12]. Все они в большей или меньшей степени коррелируют с визуальной оценкой качества, хотя ПОСШ и СКП в качестве метрик качества видео следует использовать с осторожностью. При количественной оценке потерь качества видеоинформации, вызванных сжатием и/или масштабированием, метрика VMAF [13] показала лучшие результаты в сравнении с другими метриками по точности корреляции с предсказанной субъективной оценкой в смысле Пирсона и Спирмена [14].
Суть метрики VMAF сводится к следующему. Данная метрика является эталонной (полнореференсной) мерой качества видео, разработанной на основе методов машинного обучения. В качестве обучающей выборки для расчетной модели использовались данные субъективной оценки набора видеопоследовательностей, выполненной в соответствии с ITU-R BT.500. Алгоритм VMAF оценивает воспринимаемое зрительной системой человека качество видео путем объединения методом опорных векторов нескольких метрик, включая “антишумовое” отношение сигнал/шум (ОСШ), меру потери детальности, индекс VIF, средний модуль разности между значениями яркостной составляющей отсчетов соседних кадров.
Рейтинговая шкала VMAF имеет диапазон от 0 до 100 баллов. Чем выше балл, тем выше качество восстановленного после сжатия видеоизображения относительно исходного, принимаемого за эталон, с точки зрения человека-наблюдателя. Максимальный рейтинг в 100 баллов говорит о полной идентичности сравниваемых видеопоследовательностей для зрительной системы человека. И наоборот, чем ниже балл, тем заметнее падает качество восстановленного видео относительно исходного.
Для оценки качества восстановления из каждой видеопоследовательности были отобраны фрагменты, содержащие не менее 300 последовательно идущих кадров в исходном разрешении и формате (см. табл. 1). В ходе эксперимента данные видеофрагменты декодировались, сжимались в 4, 9, 12 или 16 раз методом прореживания (в соответствии со схемами, представленными на рис. 1, а, 5, 6, а, б) и восстанавливались до исходного разрешения с помощью предложенных интерполяционных фильтров. Процесс декодирования, сжатия и восстановления видеопотока осуществлялся в реальном времени. Во время воспроизведения видеопоследовательностей не использовалось масштабирование для исключения влияния данного фактора на результаты эксперимента.
Субъективная оценка качества восстановления с участием 12 разновозрастных респондентов обоих полов, семь из которых не являются экспертами в области видеообработки, не показала наличия существенно заметных и/или раздражающих отличий восстановленных после сжатия видеокадров от исходных во всех случаях сжатия. Оговоримся, что условия проведения экспертной оценки не в полной мере соответствовали рекомендациям ITU-R BT.500, поэтому ее результаты следует считать предварительными.
Для получения численной оценки восстановленные после декодирования и сжатия видеофрагменты были сохранены на накопитель в формате YUV без потерь для последующего анализа с помощью ПО с открытым исходным кодом Netflix VMAF [15], реализующего автоматизированный расчет качества видео по одноименной метрике. Каждая из восстановленных видеопоследовательностей сравнивалась со своим исходным несжатым видеоэталоном, и на основании данного сравнения выставлялась оценка качества восстановления. Результаты данной оценки представлены в табл. 2 .
Перед расчетом качества восстановления каждой видеопоследовательности метрика проверялась на адекватность путем попарного сравнения одинаковых видеопоследовательностей, как восстановленных после сжатия, так и исходных. Очевидно, что идеальным результатом в данном случае будет максимальная оценка (100 баллов), т.е. полное совпадение. На практике во всех случаях оценка не опускалась ниже 99.84 балла, таким образом абсолютная и относительная погрешности измерения составили ±0.16 балла и 0.16% соответственно, что можно считать приемлемыми значениями.
Известно, что разница между исходным и восстановленным видео, равная 6 баллам VMAF, соответствует визуальному порогу различения изменения качества видеоизображения [16]. Это означает, что порог зрительного восприятия потерь видеоинформации по метрике VMAF равен 94 баллам. Исходя из этого, для каждой видеопоследовательности можно определить максимально возможный коэффициент сжатия с незаметными для зрительной системы человека потерями, для которого соответствующие значения метрики VMAF в табл. 2 выделены полужирным.
Из результатов численной оценки качества восстановления следует, что в большинстве рассмотренных случаев сжатия информационные потери после сжатия и восстановления видеоизображений находятся ниже порога зрительного восприятия (≥ 94 баллов). При увеличении коэффициента сжатия заметнее других снижается качество видеопоследовательности “American Football 60p” (несмотря на несоответствие с предварительными результатами субъективной оценки). Это объясняется наличием в ней динамичных сцен и высокодетализированных быстродвижущихся объектов, что является наименее благоприятными условиями для рассматриваемых методов видеокомпрессии и восстановления.
Полученные результаты также подтверждают актуальность дальнейших исследований в части создания адаптивного конвейера сжатия с переменным коэффициентом компрессии на основе, например детектора движения и/или межкадровой разности.
6. Сходства и различия с compressive sensing. Полученные результаты можно рассматривать с точки зрения парадигмы compressive sensing (CS) [17] – сжатые измерения, сжатые ощущения или опознание со сжатием [18], набирающей популярность и активно развивающейся в последнее время. Применительно к фото- и видеоинформации также применяют более точный термин compressive imaging [19].
Схожесть предложенного подхода с CS заключается в идее использования разреженной выборки, не удовлетворяющей главному критерию теоремы отсчетов, для реконструкции исходного сигнала (точнее, воссоздания его близкой аппроксимации или “ощущения”, отсюда и название данной парадигмы). Кроме того, основой алгоритма восстановления в парадигме CS также является ${{\ell }_{1}}$-оптимизация, позволяющая найти разреженную точку касания ${{\ell }_{1}}$-шара (с высокой вероятностью совпадающую с искомой) со случайно ориентированной гиперплоскостью, содержащей набор разреженных векторов.
Применительно к парадигме CS известен класс методов сжатия фото- и видеоизображений путем их векторизации, т.е. замены растрового описания векторным, заключающийся, в общем случае, в поиске базиса некоего интегрального преобразования с использованием базисных функций (как правило, гладких) и их дискретного представления для двумерного разложения изображения внутри ограниченного окна. К наиболее перспективным методам данного класса относится сжатие на основе преобразования Карунена–Лоэва [20], также известного как преобразование Хотеллинга или сингулярное разложение, а также метод главных компонент на основе ${{\ell }_{1}}$-нормы (например, [21]).
Как и в случае с CS, в предлагаемом подходе не используется трансформирующее кодирование, что позволяет применять предлагаемые методы как самостоятельно, так и совместно с другими методами сжатия видеоинформации [22]. Различие двух подходов состоит в том, что методы, предложенные в данном исследовании, не используют замену базиса видеоизображения, а осуществляют его частотное перестроение с учетом особенностей строения фурье-спектра дискретных изображений. К тому же CS работает, в общем случае, с рандомизированными (случайными) измерениями сигнала, в то время как предложенный подход имеет строго детерминированную структуру отсчетов, априорно заложенную в алгоритм реконструкции.
В исследовании [23] приводятся результаты восстановления статичного изображения в градациях серого, полученного с помощью односенсельной камеры, основанной на пространственных модуляторах света и разработанной в соответствии с теорией CS. Сообщается о том, что изображение формата 64 × 64 пикселя (4096 отсчетов) удалось восстановить по 1600 измерениям, что составляет около 40% от общего числа отсчетов, т.е. достигнуто 2.5-кратное сжатие информации.
Работа [24] является одной из первых, в которой приведены результаты восстановления не только изображений в градациях серого, но и цветного изображения. С помощью вариационной оптимизации, связанной с ${{\ell }_{1}}$-реконструкцией в вейвлетной области, изображение в градациях серого формата 256 × 256 элементов удалось восстановить по 2%, а цветное изображение того же размера – по 10% от общего количества отчетов исходного изображения, т.е. соответственно достигнуты 50-кратное и 10-кратное сжатие статичных монохромных и цветных полутоновых изображений. При этом в [18] справедливо отмечается, что качество изображений, восстанавливаемых по методологии CS, обычно значительно ниже по сравнению с исходными, хотя все характерные детали передаются верно.
Применительно к восстановлению видеоизображений с помощью технологии адаптивных распределенных сжатых измерений [25] исходная видеопоследовательность восстанавливается по ~13.5% отсчетов (что соответствует 7.5-кратному сжатию) при ПОСШ восстановленного изображения около 36 дБ. Однако про время, затрачиваемое на реконструкцию каждого видеокадра, в исследовании не упоминается.
Артефакты восстановления изображений, представленных в [19], находятся ниже порога зрительного восприятия, однако скорость их реконструкции все еще недостаточно высока, чтобы говорить о практической возможности восстановления видеосигналов с высоким пространственно-временным разрешением (например, таких, которые представлены в табл. 1).
Согласно более актуальным данным [26], с помощью вычислительных методов CS удается реконструировать изображения размером 512 × 512 пикселей, получаемые сенсором коротковолнового инфракрасного диапазона формата 64 × 64 сенселя, т.е. используется всего 12.5% исходного числа отсчетов (коэффициент сжатия равен 8 : 1). Уровень помех восстановления можно считать приемлемым; другим важным достижением данного исследования является сравнительно короткое (по меркам CS) время реконструкции каждого кадра, составляющее единицы секунд.
В нашем случае мы имеем дело с 6.25–25% от общего числа отсчетов исходной видеоинформации, при этом результаты субъективной и объективной оценок показывают, артефакты восстановления движущихся изображений находятся преимущественно ниже порога зрительного восприятия.
Другими преимуществами предлагаемых методов над CS с практической точки зрения являются задержка всего на один кадр, требуемая для начала процесса сжатия, а также возможность реализации методов на современных видеопроцессорах. Как было показано выше, сжатие и восстановление видеорастра больших многокадровых форматов в реальном времени возможно даже на неспециализированном оборудовании с относительно невысокой по современным меркам производительностью.
Заключение. Полученные положительные результаты восстановления сжатой в 4, 9, 12 и 16 раз видеоинформации в случае применения методов сжатия с помощью прореживания или усреднения отсчетов позволяют сделать вывод о том, что использование неортогональных структур дискретизации, приводящих к частотному уплотнению спектра видеосигнала, позволяет восстанавливать видеоизображения по числу отсчетов, существенно меньшему, чем того требует главная теорема современной теории информации. С одной стороны, это объясняется наличием сильных корреляционных связей как в кадрах, так и между кадрами видеопоследовательности. С другой стороны, это свидетельствует о том, что видеоизображения, полученные традиционными методами ортогональной дискретизации, обладают существенной информационной избыточностью.
С учетом этих фактов можно подойти к проблеме формирования видеоизображений по редким выборкам отсчетов в соответствии с предложенными структурами дискретизации, не прибегая к полному считыванию видеосигнала с фотоприемной матрицы высокого разрешения. Современные матрицы и интегрированные схемы считывания (ИСС) на основе комплементарных структур металл-оксид-полупроводник (КМОП) позволяют организовать разреженную выборку сигнала с необходимыми пространственно-временными структурами.
Это позволяет, во-первых, формировать на выходе с фотоприемного устройства уже сжатый видеосигнал для дальнейшего кодирования другими методами (например, MPEG-кодерами), обеспечивая дополнительное сжатие. После передачи видеосигнала его восстановление на приемной стороне осуществляется в обратном порядке: сначала происходит декодирование, за которым следует реконструкция с помощью предложенных интерполяционных фильтров.
Во-вторых, “разреженное” (или прореженное) считывание с матрицы дает возможность существенного (в данной работе – до 16 раз или на ~94%) сокращения числа аналогово-цифровых преобразований (АЦП) в ИСС, что положительно сказывается на сокращении энергопотребления сенсорного модуля [27]. По мере распространения видеостандартов высокого разрешения, таких как 4K и более новых, проблема сокращения энергопотребления при формировании высококачественного видеосигнала, особенно на устройствах с автономным питанием, становится только актуальнее.
В-третьих, разреженное считывание позволяет повысить скорость считывания сигнала и тем самым увеличить кадровую частоту сенсора, что повысит качество передачи движения в динамичных быстродвижущихся сценах.
Наконец, на основе разреженного считывания можно создавать матрицы с гораздо меньшим числом чувствительных элементов и/или устройств АЦП, правда в этом случае встает вопрос об изменении уже устоявшегося технологического процесса их производства. Тем не менее, подобные сенсоры со сниженной топологической плотностью фоточувствительного слоя и слоя ИСС позволят разместить в них высокоэффективные компоненты, например трансимпедансные усилители, обладающие сравнительно низкими уровнями шума темнового тока и рассеиваемой мощности.
Восстановление разреженного видеосигнала, согласно предлагаемым методам, может быть реализовано в реальном времени на современных цифровых сигнальных процессорах, созданных на основе программируемых логических интегральных схем или схем специального назначения, в том числе встраиваемых в гибридные стековые сенсорные модули или “системы на чипе”.
Список литературы
Даджион Д.Е., Мерсеро Р.М. Цифровая обработка многомерных сигналов / Пер. с англ. М.: Мир, 1988. 488 с.
Визильтер Ю.В. Конструирование операторов сегментации и сжатия данных на основе проективных морфологических разложений // Изв. РАН. ТиСУ. 2009. № 3. С. 89–104.
Дрынкин В.Н. Разработка и применение многомерных цифровых фильтров. М.: ФГУП ГосНИИАС, 2016. 180 с.
Дрынкин В.Н., Царева Т.И. Способы и устройство сжатия изображений. Способ и устройство восстановления изображений. Пат. RU 2669874 от 15.09.2017 // Бюл. изобр. 2018. № 29.
Entezari A. Towards Computing on Non-Cartesian Lattices. Technical Report. Simon Fraser University, 2006. URL. https://www.cise.ufl.edu/~entezari/research-desc/docs/tvcg.pdf (дата обращения 12.03.2018).
Дрынкин В.Н., Царева Т.И. Способ повышения разрешающей способности видеосистем. Пат. RU 2549353 от 03.02.2014 // Бюл. изобр. 2015. № 12.
Harmonic, Inc., Free 4K Demo Footage. URL. https://www.harmonicinc.com/4k-demo-footage-download (дата обращения 12.03.2018).
Xiph.org, Video test media [derf’s collection]. URL. https://media.xiph.org/video/derf (дата обращения 12.03.2018).
FFmpeg Group, FFmpeg 3.4, 2018. URL. http://ffmpeg.org (дата обращения 12.03.2018).
Methodology for the Subjective Assessment of the Quality of Television Pictures. Recommendation ITU-R BТ.500-13 // International Telecommunication Union. URL. http://www.itu.int/dms_pubrec/itu-r/rec/bt/R-REC-BТ.500-13-201201-I!!PDF-E.pdf (дата обращения 12.03.2018).
Wang Z., Bovik A.C., Sheikh H.R., Simoncelli E.P. Image Quality Assessment: From Error Visibility to Structural Similarity // IEEE Transactions on Image Processing. 2004. V. 13. № 4. P. 600–612.
Sheikh H.R., Bovik A.C. Image Information and Visual Quality // IEEE Transactions on Image Processing. 2006. V. 15. № 2. P. 430–444.
Aaron A., Li Z., Manohara M., Lin J.Y., Wu E.C.H., Kuo C.C.J. Challenges in Cloud Based Ingest and Encoding for High Quality Streaming Media // 2015 IEEE Intern. Conf. on Image Processing (ICIP). Quebec City, QC, 2015. P. 1732–1736.
Li Z., Aaron A., Katsavounidis I., Moorthy A., Manohara M. Toward a Practical Perceptual Video Quality Metriс. 2016. URL. https://medium.com/netflix-techblog/toward-a-practical-perceptual-video-quality-metric-653f208b9652 (дата обращения 12.03.2018).
Netflix, VMAF. 2018. URL. https://github.com/Netflix/vmaf (дата обращения 12.03.2018).
Ozer J. Finding the Just Noticeable Difference with Netflix VMAF. 2017. URL. https://streaminglearningcenter.com/codecs/finding-the-just-noticeable-difference-with-netflix-vmaf.html (дата обращения 12.03.2018).
Donoho D.L. Compressed Sensing // IEEE Trans. Inform. Theory. 2006. V. 52. P. 1289–1306.
Граничин О.Н., Павленко Д.В. Рандомизация получения данных и ${{\ell }_{1}}$-оптимизация (опознание со сжатием) // АиТ. 2010. № 11. С. 3–28.
Sankaranarayanan A.C., Herman M.A., Turaga P., Kelly K.F. Enhanced Compressive Imaging Using Model-based Acquisition: Smarter Sampling by Incorporating Domain Knowledge // IEEE Signal Processing Magazine. 2016. V. 33. № 5. P. 81–94.
Солодовщиков А.Ю. Исследование метода Карунена–Лоэва // Изв. РАН. ТиСУ. 2007. № 4. С. 122–128.
Liu Y., Pados D.A. Compressed-sensed-domain L1-PCA Video Surveillance // IEEE Trans. on Multimedia. 2016. V. 18. № 3. P. 351–363.
Дрынкин В.Н., Набоков С.А., Царева Т.И., Павлов Ю.В., Головнев И.Г. Сжатие и восстановление видеоинформации в авиационных системах технического зрения на основе методов неортогональной дискретизации // Сб. тез. докл. III Всероссийск. научно-технической конф. “Моделирование авиационных систем”. М.: ФГУП ГосНИИАС, 2018. С. 171–173.
Takhar D., Laska J.N., Wakin M.B., Duarte M.F., Baron D., Sarvotham S., Kelly K.F., Baraniuk R.G. A New Compressive Imaging Camera Architecture Using Optical-Domain Compression // Proc. Computational Imaging IV. 2006. V. 6065. P. 42–52.
Duarte M.F., Davenport M.A., Takhar D., Laska J.N., Sun T., Kelly K.F., Baraniuk R.G. Single-pixel Imaging via Compressive Sampling // IEEE Signal Processing Magazine. Mar. 2008. V. 25. № 2. P. 83–91.
Zhang X., Wang A., Zeng B., Liu L. Adaptive Distributed Compressed Video Sensing // Information Hiding and Multimedia Signal Processing. 2014. V. 5. № 1.
McMackin L. InView Multi-pix Camera Demonstrates 1FPS SWIR Imaging. 2017. URL. http://inviewcorp.com/news/inview-multi-pix-camera-demonstrates-1fps-swir-imaging/ (дата обращения 12.03.2018).
Schneider D. New Camera Chip Captures Only What it Needs // IEEE Spectrum. 2013. V. 50. № 3. P. 13–14.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления