Известия РАН. Теория и системы управления, 2019, № 3, стр. 140-146

Введение. Одна из главных задач, решаемая перед применением летательного аппарата (ЛА), заключается в прокладке маршрута полета. Оптимальность маршрута может оцениваться не только длиной, но и другими характеристиками, которые могут иметь достаточно сложный вид. Например, в гражданской авиации основной показатель – затраты топлива, которые зависят не только от пространственного положения ЛА, но и скоростных характеристик. Одной из распространенных задач, связанной с расходами топлива, является “задача о наборе высоты и скорости” [1] и заключается в выборе оптимального профиля набора высоты.

При полете на малых высотах, зачастую, решается не топливная задача, а задача облета различного рода препятствий, которую принято решать на цифровых картах рельефа местности. Препятствия могут быть статические (неподвижные) или динамические (подвижные), известные или обнаруживаемые в ходе полета. Построение маршрута в случае с неизвестными или движущимися препятствиями относится к теме принятия решений [2]. В данной работе основной упор делается на построение маршрута в среде с заранее известными препятствиями. Также не рассматриваются задачи большой размерности (исходные данные которых не помещаются в оперативной памяти компьютера), так как при поиске маршрута на них плохо работает традиционная оценка сложности алгоритма – общая сложность больше зависит от числа обращений к жесткому диску, нежели от числа арифметических операций. При работе с такими графами используются специфические алгоритмы с предобработкой данных, например Arc-Flags [3] и ALT [4].

Основным алгоритмом поиска оптимального пути является алгоритм Дейкстры [5] (расширение алгоритма поиска в ширину [6] на графы) и его модификации, самые распространенные из которых – $A{\text{*}}$ [7] и JPS [8]. Основное отличие алгоритмов $A{\text{*}}$ и JPS от алгоритма Дейкстры заключается в том, что в них используется эвристическая функция оценки оставшегося пути, что позволяет находить оптимальный путь, не рассматривая всех точек в графе. Это приводит к ускорению поиска маршрута до конкретной точки, но делает невозможным поиск маршрута до нескольких точек одновременно. Алгоритм JPS является улучшением алгоритма $A{\text{*}}$ и применяется при нахождении пути на сетках равномерной стоимости (все переходы имеют одинаковую стоимость). Как будет видно далее, не всегда удается свести условие задач поиска пути к нахождению пути на сетках равномерной стоимости или поиска до одной точки.

В данной статье описаны две задачи построения маршрута на цифровых картах рельефа местности:

построение скрытого маршрута через горный хребет;

построение маршрута в обход зон обнаружения радиолокационных станций.

Основная особенность данных задач состоит в сложной форме препятствий, что не позволяет применить аналитические подходы, базирующиеся на формульном задании ограничений [9]. Более того, большинство ограничений в представленных задачах носит не геометрический характер (некоторые точки и переходы запрещены), а весовой (некоторые точки и переходы более предпочтительней, чем другие), что не позволяет применить классические подходы робототехники [2, 10].

1. Задача построения скрытого маршрута через горный хребет. Данная задача заключается в построении маршрута или маршрутов перелета с одной стороны гор на другую. Полагается, что свой полет ЛА выполняет эквидистантно (высота полета неизменна относительно рельефа). Рассмотрим следующие исходные данные настоящей задачи.

Матрица высот H (матрица, в ячейках которой записана высота рельефа в данной точке). Ячейки матрицы высот являются множеством вершин $V$ графа $G$, на котором выполняется поиск маршрута. Ребрами (множество всех ребер принято обозначать $E$, а отдельные ребра – буквой $e$) соединены вершины, соответствующие соседним элементам матрицы высот.

Множество стартовых точек $S = \left\{ {{{s}_{0}},{{s}_{1}},\;...} \right\}$, например аэродромы.

Множество финальных точек $T = \left\{ {{{t}_{0}},{{t}_{1}},\;...} \right\}$. Это могут быть важные объекты инфраструктуры, такие как электростанции, железнодорожные узлы или любые другие точки интереса.

Весовая функция $f{\text{:}}\;E \to {{R}^{ + }}$, отображающая множество ребер $E = \{ {{e}_{1}},{{e}_{2}},\;...\} $ на их стоимость (рациональное положительное число).

Необходимо для каждой финальной точки ${{t}_{i}}$ найти стартовую точку ${{s}_{j}}$ и соединяющий их путь L, чтобы стоимость получившегося пути $F(L)$ была минимальной. Стоимостью пути обозначается сумма стоимостей всех ребер, входящих в него:

В формульном виде описанная задача выглядит следующим образом:

В статье будут рассмотрены разные весовые функции  f, а также результаты, получаемые при каждой из них.

Приведем конкретный пример. На рис. 1 представлена цифровая карта рельефа местности Кавказского хребта. Она задана в виде матрицы H размером $2500 \times 2500$. Шаг сетки равномерен и равен 100 м. Необходимо построить маршрут с южной стороны (точки с координатами $(0,i),i \in [0,2499]$) на северную сторону (точки с координатами $(2499,i),i \in [0,2499]$).

Так как поиск пути необходимо выполнить до множества финальных точек, хорошим выбором будет алгоритм Дейкстры. Другие алгоритмы являются алгоритмами направленного поиска и их применение целесообразно в случае одной финальной точки или небольшого количества финальных точек.

Для начала найдем оптимальный путь при функции оценки пути следующего вида: f = = $\sqrt {\partial {{x}^{2}} + \partial {{h}^{2}}} $, где $\partial x$ – шаг цифровой карты, $\partial h$ – разница по высоте между соответствующими вершинами матрицы высот. Найденный путь будет оптимальный с точки зрения длины (так как мы записали длину отрезка в качестве его оценки). Заметим, что при рассматриваемом шаге сетки (100 м) почти всегда $\partial h \ll \partial x \to f \approx \partial x = {\text{const}}$, что приводит к невыгодности обхода различных гор (маршрут через горы получается короче). Поэтому оптимальные маршруты, построенные при данной подробности карты высот, почти всегда будут совпадать с прямым отрезком, соединяющим конечную и начальную точки. Чтобы обходить вершины гор и хребты, необходимо взять карту высот более высокой подробности, которая, в силу сложности создания, является закрытой информацией.

Теперь рассмотрим задачу построения скрытого маршрута полета низколетящего ЛА, например крылатой ракеты. В данном случае необходимо минимизировать не только расстояние, но и “видимость” ЛА. Логичным решением является построение пути через ущелья без прохождения над пиками. Чтобы добиться такого маршрута, возьмем следующую функцию оценки пути: $f = 1 + {{C}_{1}} \times \partial h + {{C}_{2}} \times \partial {{h}^{2}}$, где ${{С }_{1}}$ и ${{С }_{2}}$ – параметры свертки. Опишем параметры и разъясним их смысл подробнее.

Цифра 1 – это $\partial x$, так как оно всегда постоянно, то уместно заменить его на 1.

Константа ${{С }_{1}}$ отвечает за то, насколько важно перемещение по высоте. Часто хочется уменьшить высоту полета (сделать $\partial h < 0$). Если положить ${{С }_{1}} > 0$, то при отрицательном изменении высоты стоимость ребра пути будет меньше.

Константа ${{С }_{2}}$ отвечает за штраф в изменении абсолютного значения высоты. Маневренность ЛА, таких, как крылатые ракеты, не позволяет резко изменять высоту, поэтому логично при больших абсолютных изменениях высот накладывать штраф. Значение данной константы можно посчитать из тактико-технических характеристик или же ввести другую нелинейную зависимость от изменения высоты, чтобы учесть маневренные особенности ЛА.

На рис. 2 представлен пример построения маршрутов со следующими параметрами (данные значения были подобранны эвристическим путем): ${{С }_{1}} = 0.4;{{C}_{2}} = 0.02$. Получившиеся маршруты обозначены белым цветом. Как можно заметить, маршруты проходят по ущельям и преодолевают хребты только в случае необходимости. Это является более рациональным вариантом, чем полет по прямой, если необходимо добиться скрытого преодоления горной гряды.

2. Задача построения маршрута в обход зон обнаружения радиолокационных станций. Перед постановкой задачи опишем некоторые особенности работы радиолокационных станций. Чтобы обнаружить цель, радиолокационной станции необходимо облучить ее. Для облучения цели нужно, чтобы между целью и станцией не было преград, так как радиосигнал не проходит сквозь препятствия на местности. Поэтому одним из распространенных способов “спрятаться” от радиолокационных станций является полет ЛА за естественными препятствиями, такими, как горы и холмы.

Чтобы лучше понимать, где ЛА может быть обнаружен, строятся “зоны прямой видимости”. Зона прямой видимости – это множество всех точек, для каждой из которых существует такая радиолокационная станция, что отрезок, их соединяющий, не проходит через препятствия (для расчета пересечений с препятствиями используется цифровая карта рельефа местности). В общем случае данная зона строится в 3-мерном пространстве. Из-за допущения об эквидистантном движении (на постоянной высоте над рельефом) ЛА можно сделать срез, чтобы решать задачу в 2-мерном пространстве.

Для обнаружения ЛА радиолокационной станцией, кроме существования прямой видимости, необходимо, чтобы дальность между ними была меньше определенного числа. Данное число вычисляется из тактико-технических характеристик станций и эффективной площади рассеяния (ЭПР) цели, однако на малых высотах оно зачастую больше, чем максимальная дальность прямой видимости, поэтому им можно пренебречь.

Исходными данными задачи являются:

матрица прямых видимостей H, на основе которой построен граф аналогично задаче “построения маршрута через горный хребет”;

начальная точка $s$ и конечная точка $t$;

весовая функция $f{\text{:}}\;E \to {{R}^{ + }}$, отображающая ребра на их стоимость.

Необходимо построить маршрут минимальной длины с минимальным “шансом обнаружения” (шанс быть обнаруженным хоть одним радиолокационным комплексом) из начальной точки в конечную точку. Понятие “шанс обнаружения” в зависимости от подхода к решению задачи будет трактоваться по-разному. В формульном виде описанная задача выглядит следующим образом:

Основная проблема данной задачи состоит в том, что имеется два критерия оценки маршрута (длина и шанс обнаружения), а весовая функция f является отображением ребер в одномерное пространство.

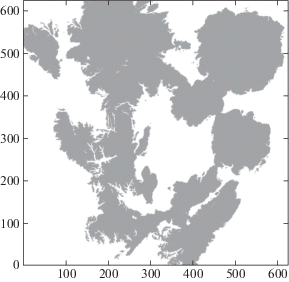
Разберем приведенную задачу и различные способы ее решения на конкретном примере. На рис. 3 представлена карта прямых видимостей радиолокационных станций, предварительно расставленных (эвристическим образом). Серым цветом отмечено пространство, на котором ЛА выходит на прямую видимость. Она задана матрицей размером 600 × 600. Шаг сетки составляет 250 м. Начальная точка имеет координаты (0, 0), а конечная – координаты (599, 599) (на рисунке соответствует левому нижнему и правому верхнему углам).

Простейший подход к построению маршрута минимальной длины с минимальным шансом обнаружения состоит в следующем: переходы в зоны прямой видимости запрещаются (выбрасываются те ребра, одна из вершин которых лежит в прямой видимости), а веса оставшихся ребер принимаются равными единице (f = 1). Данный способ обусловлен тем, что если не заходить в зоны прямой видимости, то шанс обнаружения будет равен нулю. В рассматриваемом случае находить путь можно любым из перечисленных в начале статьи способов. Основным недостатком является возможность отсутствия решения, а оно необходимо. Например, если финальная точка полностью окружена зонами прямой видимости или лежит в зоне, то маршрут до нее не будет найден.

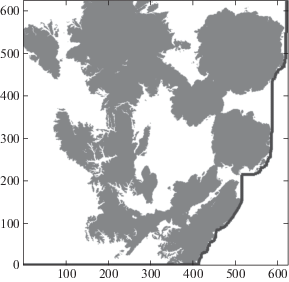
Чтобы путь существовал всегда, вместо запрета перемещения в зоны прямой видимости накладывается штраф за перемещение: если какая-либо вершина из двух попадает в прямую видимость, то весовая функция $f = 1 + С $ (размер константы $С $ обуславливает штраф за вход и нахождение в зонах прямой видимости), иначе f = 1. Данная формула фактически является сверткой двух критериев (шанс обнаружения зависит линейно от вхождений в зоны прямой видимости (что не совсем точно с математической точки зрения)). При достаточно большом размере константы алгоритм будет искать путь в обход зон обнаружения при условии существования такого пути (если такой путь не найдется, то он будет проложен через зону(ы) прямой видимости). И хотя не все веса одинаковы, использование алгоритма JPS допустимо вследствие небольшого количества вариантов этих весов. Построенный путь для значений константы $С = 100$ (данное значение было выбрано эвристическим путем) представлена на рис. 4 (черным цветом обозначен маршрут).

Получившийся результат лучше тем, что позволяет достичь финальной вершины в любом случае, однако данный способ не учитывает важную особенность работы радиолокационных станций, а именно время, затрачиваемое на завязку трассы [11]. Для завязки трассы радиолокационной станции не достаточно, чтобы цель вошла в зону прямой видимости, ей необходимо нахождение цели там некоторое время, причем чем больше время непрерывного нахождения, тем выше шанс обнаружения. Исходя из вышеописанного, есть различие между путем, в котором есть ровно два непрерывных участка прямой видимости длиной x, и путем с одним непрерывным участком длиной 2x (во втором случае шанс обнаружения существенно выше). Однако рассмотренный алгоритм (как и предыдущий) не делает разницы между этими двумя путями, если они одинаковой длины. Необходимо отметить, что настоящую особенность нельзя учесть в весах ребер изначально.

Чтобы как-то учитывать путь, приведший в данную точку, был применен подход, основанный на идее “слоеного” графа. Вместо одной вершины каждому элементу матрицы прямой видимости соответствует N вершин, по одной вершине на каждый слой. Чтобы номер слоя (нумерация слоев начинается с нуля) соответствовал времени непрерывного нахождения в зоне прямой видимости, переходы (ребра) между вершинами были сделаны ориентированными (граф становится ориентированным) и определялись следующими правилами.

Любое ребро должно соединять вершины, соответствующие соседним элементам матрицы прямой видимости.

Если конечная вершина ребра соответствует элементу матрицы с прямой видимостью, то номер слоя конечной вершины на один больше, чем номер начальной вершины, что показывает увеличение времени непрерывного нахождения в зоне прямой видимости на одну условную единицу. Если номер слоя конечной вершины больше допустимого, то номер слоя конечной совпадает с номером слоя начальной вершины ребра (данная особенность накладывает ограничение на максимальное время непрерывного нахождения в зоне прямой видимости).

Если конечная вершина ребра соответствует элементу матрицы с непрямой видимостью, то номер слоя конечной вершины равен нулю, что показывает выход из зоны прямой видимости.

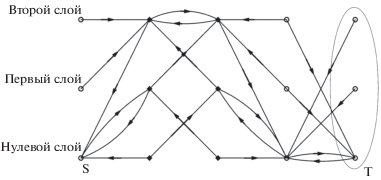
На рис. 5 представлен слоеный граф, построенный по описанному выше алгоритму, для матрицы прямой видимости размером 5 × 1 с количеством слоев, равным трем. Буквой S обозначено положение стартовой вершины (она расположена на нулевом слое, так как полагается, что прокладка маршрута начинается с нулевого времени нахождения в зоне прямой видимости). Эллипсом выделено множество финальных вершин T (множество из-за того, что финальной вершине на матрице прямой видимости соответствуют три вершины, по одному на каждом слое). Направление ребер обозначено стрелками, ромбами – вершины, соответствующие зонам прямой видимости, а кругами – все остальные вершины.

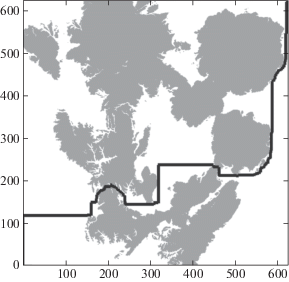
Для карты прямых видимостей, представленной на рис. 3, был построен граф с количеством слоев, равным 20, и квадратичной зависимостью весовой функции от номера слоя (непрерывного пути в зоне прямой видимости): $f = 1 + m \times m$, где $m$ – это номер слоя, на котором расположена конечная вершина данного ребра, цифра 1 – цена перемещения по первому слою. Квадратичная зависимость была выбрана с целью сильного увеличения штрафа в зависимости от времени непрерывного нахождения в зоне прямой видимости.

Пример построенного маршрута представлен на рис. 6. Можно заметить, что маршрут отличается от предыдущего. Вместо пролета по одному большому участку прямой видимости данный алгоритм предпочел полет по двум более маленьким участкам (хотя в сумме они длиннее), что является более рациональным решением с точки зрения вероятности обнаружения.

Заключение. В статье сформулирована задача скрытого пролета ЛА горного хребта на цифровых картах рельефа местности. Рассмотрен классический подход решения данной задачи, основанный на минимизации расстояния с помощью алгоритма Дейкстры, и показаны его недостатки, главным из которых является плохой учет перепада высот. Предложен метод с использованием свертки расстояния и величины изменения высоты в качестве весов ребер. Приведенный метод исправляет недостатки классического подхода.

Представлена постановка задачи обхода зон обнаружения радиолокационных станций низколетящим объектом на картах прямых видимостей, рассчитанных с помощью цифровых карт рельефа местности. Описана физика данной задачи, а также ряд решений на основе алгоритма Дейкстры. Предложена модификация графа поиска пути для учета накопительной особенности работы радиолокационных станций.

Основной особенностью вышеизложенных алгоритмов является необходимость использования всей матрицы высот или матрицы прямых видимостей, что налагает ограничения на минимальный объем памяти электронно-вычислительной машины (ЭВМ) для их хранения.